Strain Rate Effect on the Thermomechanical Behavior of NiTi Shape Memory Alloys: A Literature Review

Abstract

A review of experiments and models for the strain rate effect of NiTi Shape Memory Alloys (SMAs) is presented in this paper. Experimental observations on the rate-dependent properties, such as stress responses, temperature evolutions, and phase nucleation and propagation, under uniaxial loads are classified and summarized based on the strain rate values. The strain rates are divided into five ranges and in each range the deformation mechanism is unique. For comparison, results under other loading modes are also reviewed; however, these are shorter in length due to a limited number of experiments. A brief discussion on the influences of the microstructure on the strain-rate responses is followed. Modeling the rate-dependent behaviors of NiTi SMAs focuses on incorporating the physical origins in the constitutive relationship. Thermal source models are the key rate-dependent constitutive models under quasi-static loading to account for the self-heating mechanism. Thermal kinetic models, evolving from thermal source models, address the kinetic relationship in dynamic deformation.

1. Introduction

NiTi Shape Memory Alloys (SMAs) are the most widely used in the shape memory material family, and have important applications in electronic components, medical devices, shock absorption devices, etc., thanks to their unique thermomechanical behaviors [1,2,3,4]. Reliable and predictive simulations of NiTi SMA wires under high strain rates are always required for actuation and auxiliary control. An example of a hybrid device with SMA wires is shown in Figure 1, which is designed for anti-seismic structure to restrict the strain within 6% [5]. These growing demands push investigations on both quasi-static and dynamic responses of NiTi SMAs [6,7,8,9,10].

Researchers have conducted experiments on NiTi SMAs at a wide range of strain rates and most experiments have been under uniaxial loads [11]. While the SMA specimens could be bars, wires, or plates depending on the specific experiments, general observations and mechanisms could be extracted and summarized regardless of the shape and size of specimens. The stress responses and temperature evolutions during transformation have varied depending on the strain rate. At a very low strain rate $\dot{ϵ}<{10}^{-4}{\mathrm{s}}^{-1}$, the stress and temperature scarcely changed since the latent heat dissipated to surroundings sufficiently [11,12,13]. As the strain rate rises to ${10}^{-4}{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^{-1}{\mathrm{s}}^{-1}$, the stress and temperature increases with increasing strain rate because part of the heat by transformation is left in the material [11,14,15,16]. The heat exchange rate between the specimen and the environment is found to be greatly influenced by the temperature rise in this strain rate range, as demonstrated in a comparison test by Shaw and Kyriakides [11] between water-enclosed and air-enclosed NiTi SMA wires. In the medium range of strain rate ${10}^{-1}{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^3{\mathrm{s}}^{-1}$, the stress stopped increasing but the temperature increased quickly since an adiabatic process was reached [17,18,19,20,21]. A quickly-recovered residual strain was reported by Chen et al. [17] around 81~750 s⁻¹, which was ascribed to the significant thermal hysteresis as a result of an adiabatic process. In strain rates between ${10}^3{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^4{\mathrm{s}}^{-1}$, a sudden rise of the critical transformation stress takes place, and this can be attributed to the drag effect of dislocations surrounding the phase interface [22]. Nemat-Nasser et al. [23,24,25] observed considerably increased rate sensitivity and curved interfaces of martensite in TEM micrographs. The final strain rate range was $\dot{ϵ}>{10}^4{\mathrm{s}}^{-1}$, in which plastic deformation occurs in austenite without martensitic transformation because martensitic transformation no longer satisfies the demand of quick deformation [24,26,27,28].

Furthermore, the nucleation and propagation of phase transformation under various strain rates have also been investigated by many researchers [11,29,30]. When the strain rate is very low, the martensite nucleates at a few locations and then extends to all fields [11,29,31]. As the strain rate increases, the number of nucleation locations grows, and martensitic transformation domains propagate in a parallel mode rather than entirely [30,31].

Compared to uniaxial tests, experiments under shear and indentation have been conducted less frequently [32]. Simple shear tests on NiTi SMAs were performed early by Manach and Favier [33], while a more comprehensive study within a wider range of strain rates from 10⁻⁴ s⁻¹ to 10³ s⁻¹ was accomplished by Huang et al. [34]. As for indentation tests, Amin et al. [35] and Shahirnia et al. [36] both pointed out that the maximum indentation was influenced by the loading rate. In cases of cyclic loading, superelasticity degeneration and temperature variations have been found to be strongly dependent on the strain rate [37,38].

Besides the loading mode, microstructure also has an important impact on the rate-dependent behaviors of NiTi SMAs [25,39,40,41]. The influences of R-phase, precipitated phase, and grain size on the strain rate responses of general SMAs have been explored in many studies [39,40,42,43]. The influence of R-phase transformation on the strain effect sensitivity has been investigated by Helbert et al. [39] on NiTi SMA wires. The precipitation evolution of Ni₄Ti₃ and transformation behaviors have been studied and characterized by Fan et al. [42] in quasi-static loading and Yu et al. [43] in impact loading. The grain size influenced the amount of transformable martensite and heat generation, and therefore influenced the temperature field and transformation stress [40]. For porous and composite SMAs, higher strain rates brought in a greater transformation stress similar to general NiTi SMAs [25,41].

Modeling the strain rate effect of NiTi SMAs at low and medium strain rates is focused on characterizing and qualifying the thermal effect during transformation, where the latent heat plays an important role. Thermal source models were proposed to represent the strain rate effect as extra heat sources added to the energy equation [44,45,46,47]. The thermodynamic potential is usually adopted in thermal source models to derive the temperature evolution equation, and can be obtained either empirically or theoretically [48,49]. Many simulations have been performed at strain rates ranging from very low to medium on the basis of the thermal source models, and their predictions have matched well with experiments at corresponding strain rates [50,51,52,53,54,55]. However, the drag effect surpasses the thermal effect at high strain rates. By considering the kinetic effect and adding a resistance force into the constitutive relationship, thermal kinetic models have been extended from thermal source models to describe the thermomechanical behaviors of NiTi SMAs at high strain rates [56,57,58].

Multiple studies have conducted experiments and developed models for the deformation behaviors of NiTi SMAs under various strain rates. However, there is hardly any systematic analysis of the strain rate effect, except for some subsections touching on the strain rate effect in general reviews for NiTi SMA microstructure evolution and thermodynamic behaviors [59,60,61]. Therefore, this paper aims to present a comprehensive review and summarize the common physical mechanisms of the strain rate effects in a wide strain-rate range from quasi-static to dynamic loading. The strain rate effect under uniaxial loads will be elaborated in the first place since the number of uniaxial tests is the largest. The rate effect under other loading modes, such as shear, indentation, and cyclic loading, will be discussed later. A brief summary of the dependence of the strain rate effect on microstructure is presented at the end of Section 2. Section 3 recapitulates the main constitutive models capturing the strain rate effect. The approach is to construct the thermal source model which will first be introduced and then followed by a discussion of thermal-source components. Thermal kinetic models will be discussed next. Simulation examples will be given in both models. Final remarks with future research directions are given in Section 4.

2. Experimental Observations

Great progress has been made in uniaxial experiments to investigate the pseudo-elastic and yielding behaviors of NiTi SMAs under different strain rates. Shear and indentation tests have also been conducted, though less frequently compared to uniaxial. Experimental results under different loading rates have shown that the critical transformation stress increases as the strain rate grows. In addition to the loading mode, microstructure is another factor to influence the strain rate effect, which will be discussed at the end of this section.

2.1. Strain Rate Effect under Uniaxial Loads

The uniaxial experimental tests have been conducted by either tension or compression. Tensile test experiments are more common and frequent at low and medium loading rates, while the quantity of compression tests under shock conditions with the split Hopkinson bar are more numerous [18,26,32,62]. Compared to those in tension, stress-strain curves in compression tests have less recoverable strain, a steeper transformation slope, and higher critical stress. Tension-compression asymmetry is strongly dependent on the level of strain rate and temperature [63,64].

Under the uniaxial loading mode, the critical transformation stress is an important indicator of the strain rate effect on NiTi SMAs. To better explain the rate effects on the transformation stress over a wide range of strain rates, the transformation stress is constructed as a function of the strain rate by this review in Figure 2, based on the previous work by Nemat-Nasser et al. [23,24,25,65] and Zurbitu et al. [20,21]. On the whole, at a temperature below the maximum temperature for stress-induced martensite formation, the martensitic transformation stress (${\sigma }_t$) and the austenite yield stress (${\sigma }_y$) increase with strain rate. Specifically, at $\dot{ϵ}<{10}^4{\mathrm{s}}^{-1}$, stress-induced martensitic transformation always happens devoid of austenite yielding as ${\sigma }_y>{\sigma }_t$, where ${\sigma }_y$ can be obtained using tensile experiments under high temperature. In shock conditions where $\dot{ϵ}>{10}^4{\mathrm{s}}^{-1}$, austenite yields without any martensitic transformation as now ${\sigma }_y<{\sigma }_t$.

The features for the deformation mechanisms of NiTi SMAs at various strain rates can be classified into categories in five strain ranges separated by four critical strain rate values, which are 10⁻⁴ s⁻¹, 10¹ s⁻¹, 10³ s⁻¹, and 10⁴ s⁻¹.

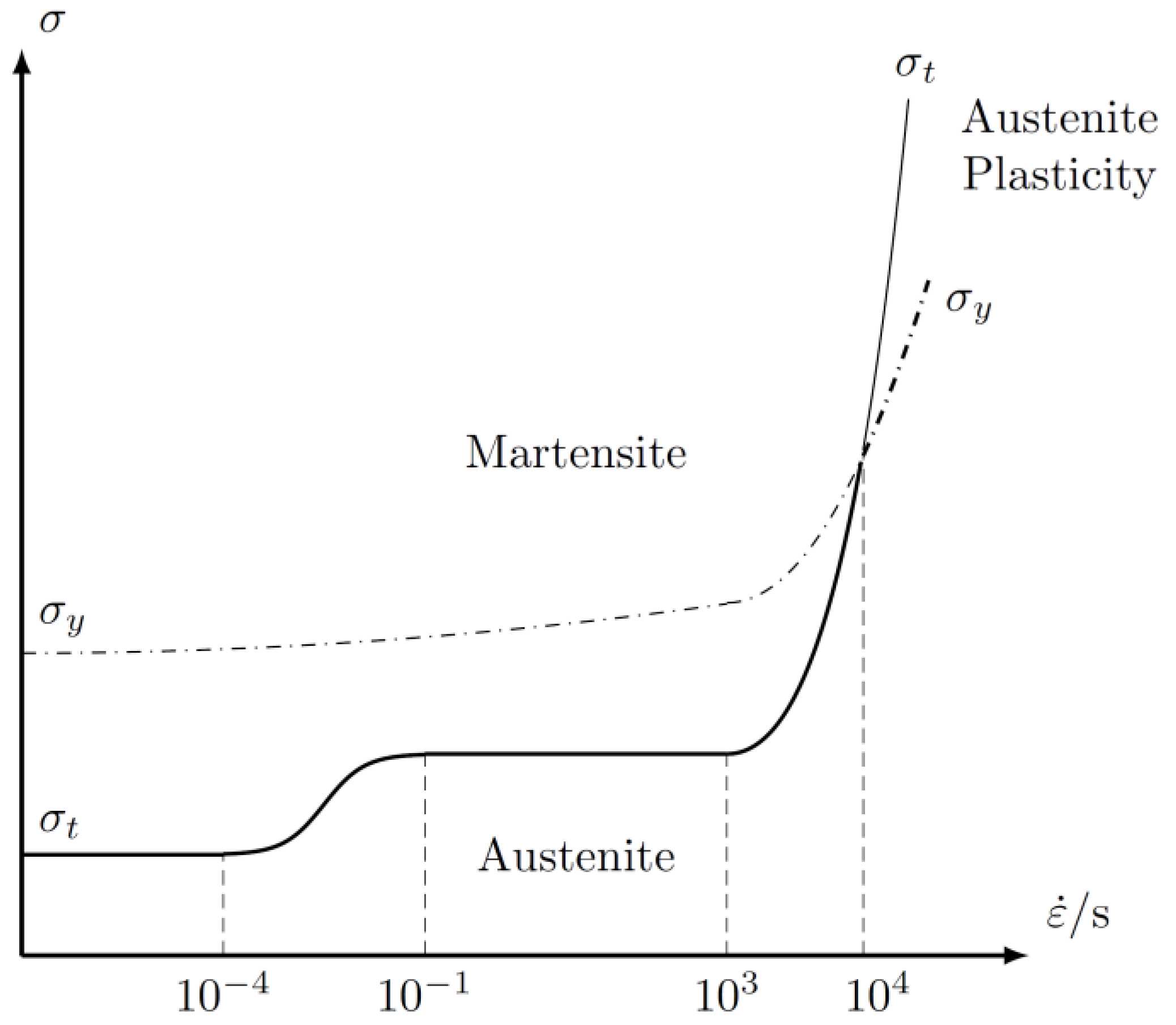
• Basically, at a very low strain rate $\dot{ϵ}<{10}^{-4}{\mathrm{s}}^{-1}$, phase transformation heat dissipates sufficiently to the environment, thus the temperature change of the material can be ignored [11,12,13]. The martensitic transformation stress is therefore not sensitive to the strain rate in this isothermal process, which is shown as a stress platform in Figure 2.
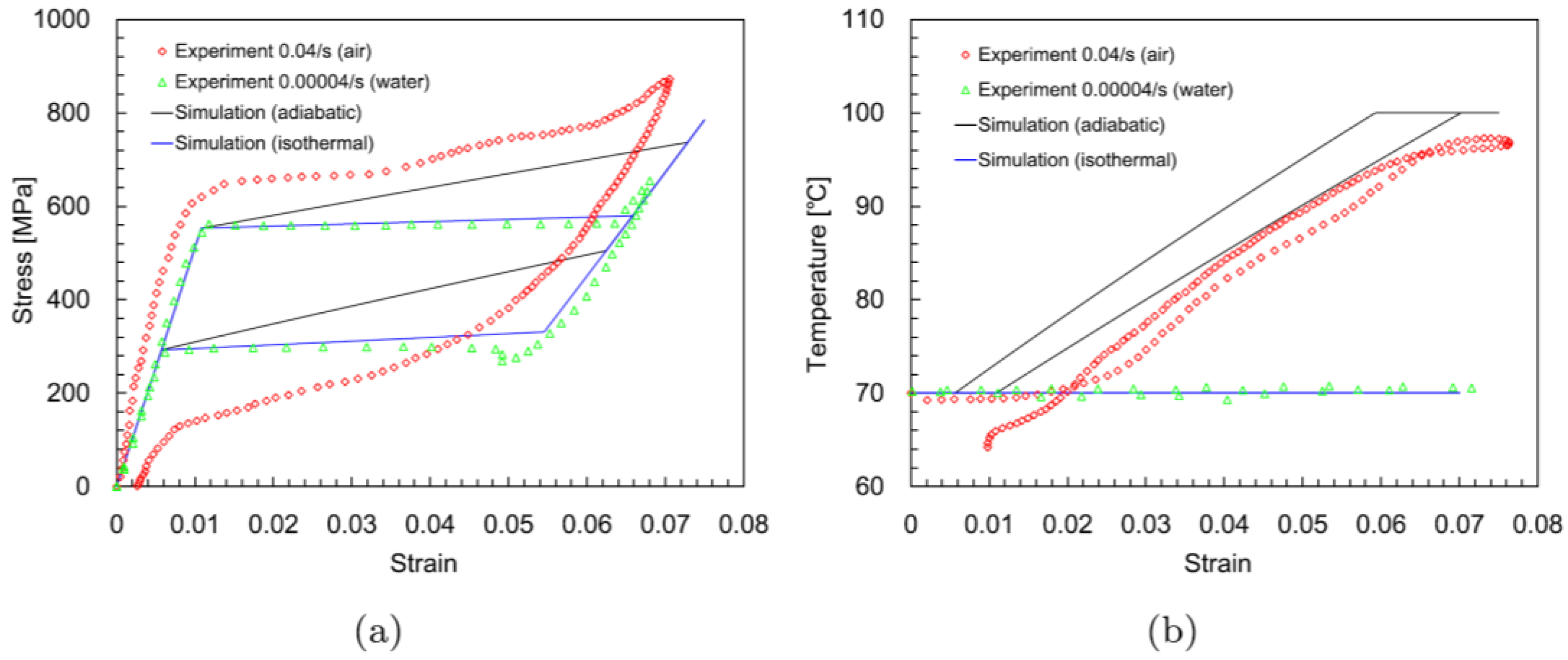
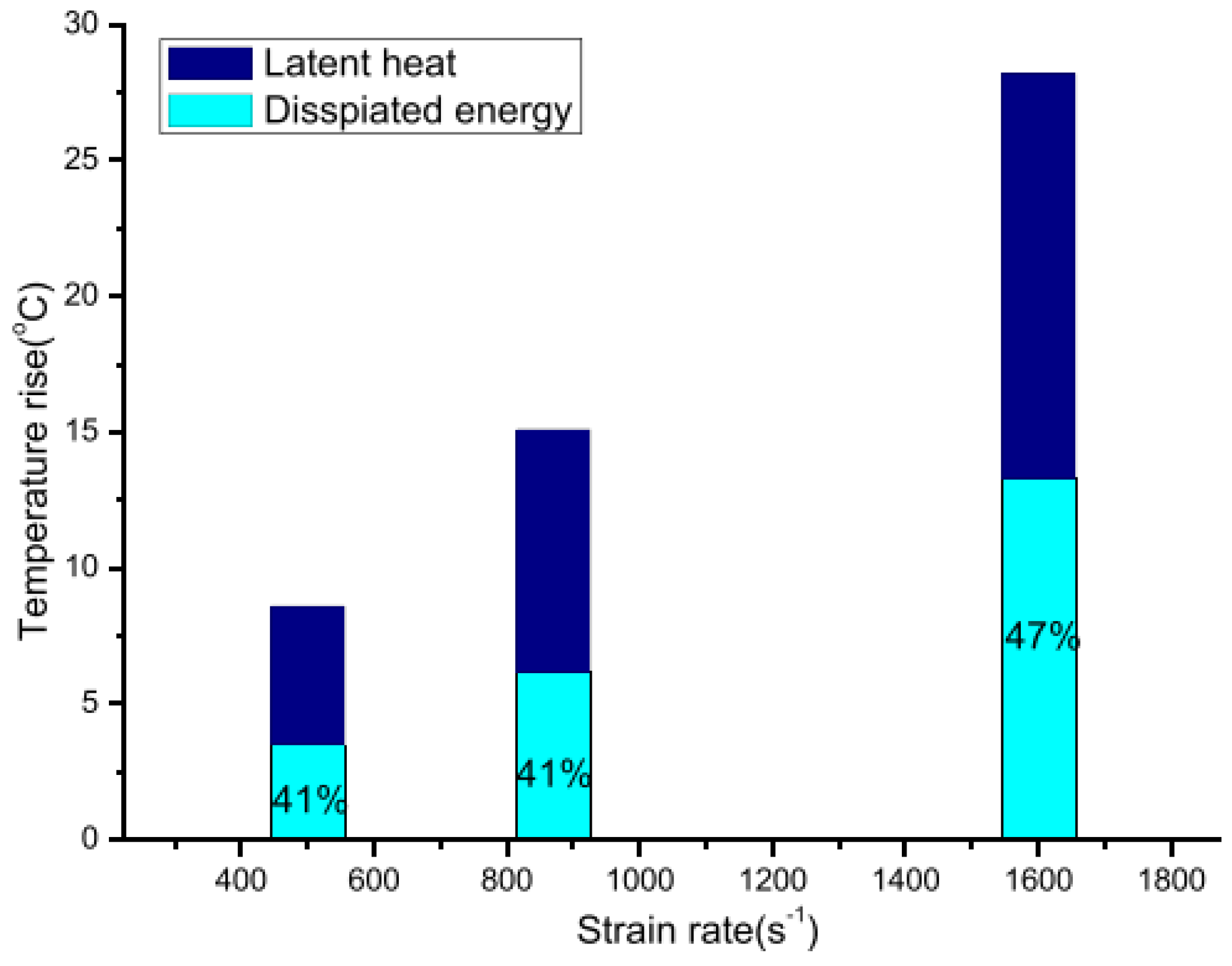
• In a relatively low strain range, ${10}^{-4}{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^{-1}{\mathrm{s}}^{-1}$, the influence of the latent heat, dissipation energy, and elastic heat gradually grows, leading to small temperature variations of the material [11,14,15,16]. The strain rate influences the temperature field and brings an increase in the martensitic transformation stress.
• As the strain rate climbs to a medium range of ${10}^{-1}{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^3{\mathrm{s}}^{-1}$, the transformation stress is nearly unchanged [17,18,19,20,21]. This is because the temperature evolution is insensitive to the strain rate as the deformation process is adiabatic. The heat produced, with amount proportional to the volume of transformed martensite, is totally used to warm up the sample, while the rate-sensitive heat produced by the transformation-induced plasticity strain is negligible.
• A sudden rise of the transformation stress appears at strain rates between ${10}^3{\mathrm{s}}^{-1}<\dot{ϵ}<{10}^4{\mathrm{s}}^{-1}$, where the dislocation drag effect becomes more significant and the flow stress is more sensitive to the strain rate [22,23,24,25,65,66,67,68,69]. The overall stress level increases remarkably as well as the transformation stress.
• The final strain rate region is $\dot{ϵ}>{10}^4{\mathrm{s}}^{-1}$, in which martensitic transformation cannot provide enough deformation, thus parent austenitic phase plastic deformation occurs due to the extremely high strain rate [24,26,27,28].

Experimental results and deformation mechanisms in all these five strain-rate ranges will be elaborated individually in the next section.

2.1.1. Less Than 10⁻⁴ s⁻¹

Isothermal processes are always observed in NiTi SMA experiments under very low loading rates. This is because the heat energy generated by transformation dissipated sufficiently into the environment [11,12,13]. In the last century, researchers measured the strain rate threshold, below which the sample temperature and transformation stress only changed in a negligible small range [11,12,13]. The threshold value is finally given around 10⁻⁴ s⁻¹.

According to the experimental results obtained by Shaw and Kyriakides [11], martensite nucleates at few locations and subsequently extends to all NiTi crystallites when the strain rate is below 10⁻⁴ s⁻¹. They installed four strain sensors on the wire to monitor the nuclear situation of the martensite during transformation in 70 ℃ water. The locations of four sensors are shown in Figure 3.

Based on the temperature, stress, and strain histories obtained with four sensors (Figure 4a), the propagation path can be captured by connecting the transformation points between austenite and martensite along the time, as shown in Figure 4b. The stress level was not sufficient to drive multiple phase fronts in this very slow loading test; therefore, only one front propagates from one side to the other during loading and unloading. The symbol A and M represent, respectively, the region of austenite and martensite. Note that small temperature jumps were recorded (depicted with T1 squares in Figure 4a) when the A/M interface crossed the thermocouple at the middle point of the wire. The two temperature jumps peak during loading and valley during unloading, indicating rapid local loss and gain of heat, respectively, which confirms the isothermal hypothesis. It can be seen from Figure 4a that the stress roughly changes with the strain in both forward and reverse transformation under this very low strain rate.

2.1.2. From 10⁻⁴ s⁻¹ to 10⁻¹ s⁻¹

As the loading rate grows, the heat energy generated during transformation, such as the latent heat, dissipation heat, and thermal expansion heat, cannot be released into the environment sufficiently. Excessive heat will lead to a temperature rise in the material, which in turn influences the transformation rate. The critical transformation stress typically increases with the strain rate; however, the environment temperature and heat exchange rate also play crucial roles in this thermal-mechanical coupling mechanism. Among the studies, Shaw and Kyriakides [11] compared the tensile properties between water-enclosed and air-enclosed NiTi SMA wires. Their experiments showed that the wire temperature varied remarkably between two surroundings and they found that the transformation stress in the water-enclosed wire was much lower than that of the air-enclosed one. The strain rate effect is weaker in the water-enclosed wire considering a higher efficiency of heat exchange. Bruhns [15] and Grabe’s group [16] spent some effort on decoupling the thermal effect from strain-rate viscous effects at high temperatures and came to the conclusion that for a specified temperature range NiTi SMA wires can be seen as deformation-rate independent materials.

The number of martensite nucleation sites increases with increasing strain rate, and these martensite domains propagate in a parallel mode. Gadaj et al. [29] applied a thermovision camera to record the infrared radiation emitted by the specimen surface. They observed the number of martensite domains became greater as the strain rate increased, and these domains propagated parallel to the austenite strip. Similar nucleation and propagation modes were observed by Zhang et al. [31].

Tobushi et al. [14] investigated the deformation behaviors of NiTi SMA under strain-controlled and stress-controlled conditions. At a low strain rate in strain-controlled situations, they pointed out a stress overshoot at the temperature Ms and a stress undershoot at the temperature As, respectively. In contrast, the overall stress-strain curves subjected to the stress control are similar to those in strain-controlled cases with high strain rate. While at a high strain rate, stress-controlled experimental results have exhibited a smooth transition in stress around the transformation temperature M_s and A_s. The difference can be explained by the excessive energy needed for nucleation when the phase interface starts moving, since greater stress is needed to transform during strain-controlled situations.

In the case of compression tests, the transformation stress also increases with increasing strain rate; however, the transformation mode does not change with the strain rate from 10⁻⁴ s⁻¹ to 10³ s⁻¹ and the strain field is generally more uniform compared with tension tests. In contrast to the localized nucleation and propagation of martensite bands under tensile loading, NiTi SMA subjected to compressive loading always exhibits a more homogeneous transformation. Elibol and Wagner [64] employed a digital image correlation in situ technique to show that the surface strain fields in compression were always uniform during transformation without any strain localization. Meanwhile, the transformation mode was barely influenced by an increase of the strain rate in both quasi-static and dynamic conditions.

The finishing point of the martensitic transformation becomes harder to distinguish when the strain rate is higher. Dayananda and Rao [70] have tested NiTi SMA wires at strain rates from 3.3 × 10⁻⁵ s⁻¹ to 3.0 × 10⁻² s⁻¹. Three “elastic” segments were identified in the stress-strain curves when the strain rate was low, which were the elastic austenite segment, superelasticity segment, and elastic Stress-Induced Martensite (SIM) segment. As the strain rate increased above 5.0 × 10⁻³ s⁻¹, a fourth segment emerged between the superelasticity and elastic stress-induced martensite segments. This intermediate segment resulted from the overlapping of the SIM formation and elastic SIM deformation, and its length increased with increasing strain rate.

2.1.3. From 10⁻¹ s⁻¹ to 10³ s⁻¹

An adiabatic process happens under this medium strain rate. The energy generated by phase transformation accumulates in the transformed region and cannot be released in such a short time. The temperature of the transformed region increases dramatically; however, the stress level remains the same. This is because the total transformed heat production is finite.

The range of strain rate from 10² s⁻¹ to 10³ s⁻¹ can be reached by the split Hopkinson bar. Experiments conducted by Chen et al. [17] showed that when the strain rate came to 81~750 s⁻¹, there would be a residual deformation in the specimen, which recovered in a few seconds to several hours. This residual deformation can be attributed to the thermal hysteresis as a result of the adiabatic process. Another paper published by Chen and Bo [62] in 2006 paid close attention to the unload progress of split Hopkinson bar systems. They reached a stable strain rate around 430 s⁻¹ under both loading and unloading conditions, which used to have difficulties in dynamic experiment design. Nemat-Nasser and Choi [18] also found that the initial temperature affected the deformation mechanism when strain rates came to 500~700 s⁻¹. The transformation stress increased with the initial temperature, and austenite plastic deformation happened eventually. Regarding to the compression test, Adharapurapu et al. [63] discovered that the asymmetry between compression and tension became weaker with higher temperature, and this phenomenon was more conspicuous under high strain rates, as shown in Figure 5. Recently, Shen et al. [19] focused on the thermal evolution in this medium strain rate range by the split Hopkinson bar system and an infrared detection system. They compared martensite NiTi SMA wires with superelastic wires between the transformation temperature A_s and A_f, and pointed out that martensite wires had higher dissipated energy than superelastic ones. This could be explained by larger plastic deformation observed in martensite wires.

At medium strain rates, nucleation sites are too numerous to distinguish but merge into large martensite zones. As observed by Saletti et al. [30] at a strain rate round 20 s⁻¹, two large martensite zones emerge on the ends of the bar specimen (one at each end) where the loading is applied, and the length of transformed martensite enlarged with two fronts move in opposite direction towards the specimen center. However, the details of the localized phase nucleation and propagation are still obscure due to the experimental difficulty [30].

However, methods are lacking to test material properties around 10⁻¹~10² s⁻¹, where car crashes and gravity-dropped bombs are the typical examples. Conventional mechanical test methods such as tension, compression, and bending test performed with screw-driven or servohydraulic load-frames are only applicable below this strain rate range. The split-Hopkinson bar technique has permitted the evaluation of mechanical properties over durations shorter than a millisecond, which is higher than this rate range. In another word, testing at intermediate rates is inherently challenging due to the possibility of elastic wave reflections and the difficulty in establishing dynamic equilibrium in the sample and the load sensors [71].

This problem can be partly solved by improving experimental devices. Xu et al. [72] used an impact testing system for the first time to show the influence of temperature and impact velocity. However, the device cannot control the strain rate precisely. Zurbitu et al. [20,21] explored NiTi SMA wire properties on the order of 1~10² s⁻¹ using an instrumented tensile-impact technique. Different from low strain rates, medium strain rates led to more stable critical transformation stresses for both austinite and martensite phases. Zurbitu’s paper compared the critical transformation stress results with those at low strain rates and demonstrated the adiabatic process during stretching in SMA wires.

2.1.4. From 10³ s⁻¹ to 10⁴ s⁻¹

The critical transformation stress increases remarkably with the strain rate in this range. The rise of transformation stress can be explained by the dislocation drag mechanism in the plastic deformation around the martensite interface [73,74]. Dislocation slips at very high strain rates need a much higher driving stress compared to those at the low strain rate due to the phono drag effect [60]. The phase interface moves with the high-speed dislocations on it and is thus subjected to the dislocation drag effect as well. Since the velocity of dislocations is a key factor in shock dynamics, the velocity of martensite interfaces should be considered in the transformation mechanism at high strain rates [23,65,74].

Split-Hopkinson bar systems are commonly used to conduct experimental tests in this strain rate range. Hudspeth et al. [75] developed a new technique to investigate the dynamic behaviors of SMA materials through simultaneous X-ray imaging and diffraction and gained a strain rate of 5000 s⁻¹. Nemat-Nasser et al. [23,24,25] improved the Split-Hopkinson bar systems at a high strain rate in 2005. They showed that strain rate sensitivity increased sharply and observed a curved interface of martensite in TEM micrographs. Therefore, the velocity of the martensite interface migration plays an important role at this stage. Yang et al. [28] used a dynamic ex-situ neutron diffraction technique to characterize the rate effect of NiTi SMAs. Based on Yang’s results, as the strain rate increases, plastic deformation replaces the martensite reorientation and the volume fraction of detwinning martensite decreases.

Recently, several Molecular-Dynamics (MD) models have been built to analyze the deformation mechanism of NiTi SMAs at a high strain rate level of around 10³ s⁻¹. For instance, Wang et al. [76] and Yazdandoost et al. [77] studied SMA crystallographic structure change in the transformation progress with MD in the shock condition. Yin et al. [78] and Ko et al. [79] simulated a NiTi nanopillar with MD under various strain rates and temperatures. They showed that the phase stress of B19 → B19′ increased at a high strain rate because there was not enough time for atoms to reach new positions. Yazdandoost et al. [80] focused on the dissipation energy in the shock condition and indicated that transformation provided the main dissipative function.

2.1.5. Greater Than 10⁴ s⁻¹

When the strain rate reaches 7000 s⁻¹, plastic deformation of austenite occurs without any martensitic transformation [27,28], which implies the yielding stress for austenite rises with the strain rate more slowly than that of the transformation stress. In the meantime, Nemat-Nasser and Choi [24] found dislocation-induced plastic slips in the austenite phase with TEM, and a similar situation was observed in NiTiCr. In other words, plastic deformation takes place before the phase interface moves, thus martensite cannot emerge at this very high strain rate. Zhang et al. [26] tested NiTi alloys in the range from 10⁴ s⁻¹ to 10⁷ s⁻¹ by the technique of magnetically driven quasi-isentropic compression and shock compression. They discovered that the elastic limit increased dramatically compared to that at the low strain rate. Some other shock tests with very high strain rates [81] are beyond the scope of this paper.

2.2. Strain Rate Effect in Different Loading Modes

Besides the uniaxial loading mode, it is common for NiTi SMAs to serve in complex mechanical loading modes including shear and indentation. The number of shear and indentation tests is much smaller than that of uniaxial ones. In general, the critical transformation stress increases with increasing strain rate for all loading types. In cases of cyclic loading, superelasticity degeneration and temperature variations become more remarkable as the strain rate grows.

2.2.1. Shear

A regular transformation hardening is observed under shear loads, and the hardening is enhanced by increasing the strain rate. Simple shear experiments on NiTi SMAs were early performed by Manach and Favier [33] in quasi-static conditions. Later, a more comprehensive study on NiTi SMA behaviors under shear stress was conducted by Huang et al. [34] over a large range of strain rates from 10⁻⁴ s⁻¹ to 10³ s⁻¹. The low and intermediate loading rates were realized on a modified MTS machine, while the impact loading rate was achieved by Split Hopkinson bars. Heterogeneous strain fields and increased transformation stress were found in all three strain-rate conditions. A shear band was observed in the 10° direction of shear loading at low and intermediate strain rates, as shown in Figure 6a, while two separated bands emerge at the impact strain rate of 290 s⁻¹, as shown in Figure 6b. Apart from the strain localization, the thermomechanical behaviors of NiTi SMA under shear loading was similar to those under tensile loading.

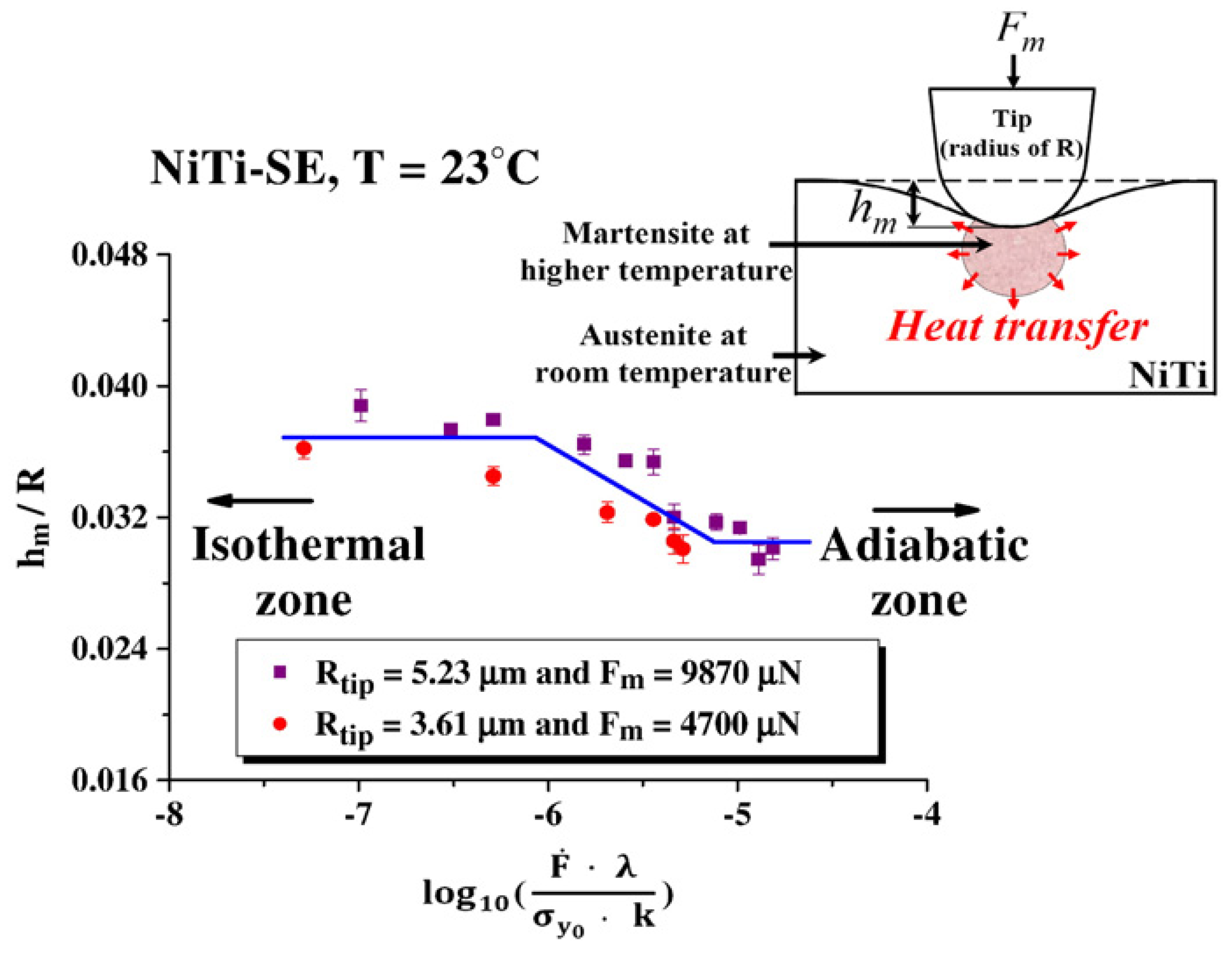
2.2.2. Indentation

Similar to the strain rate effect under uniaxial loading, an increase in loading rate in indentation tests leads to a rise of transformation stress. Moreover, a higher loading rate brings a smaller indentation depth and a drop in the recoverable deformation [36]. The interpretation in most studies [35,36,82] is that the underlying mechanism can be attributed to the increased release rate of latent heat during transformation with increasing strain rate and the strong temperature dependence of NiTi SMAs.

Considering the effect of the released latent heat conduction within the material, Amini et al. [35] adopted a normalized loading rate parameter to represent the rate effect in the experiment. The normalized loading rate was defined as a ratio of the loading rate $\dot{\mathrm{F}}$ to the transformation stress ${\sigma }_{y0}$ times the conduction coefficient $k$, and the normalized indentation depth was defined as a ratio of the indentation depth $h$ to the radius of the tip $R$, as shown in Figure 7. Based on the level of the normalized loading rate, the indentation process could be roughly classified into isothermal, adiabatic, and a transition between them, which resembles the strain-rate-dependent ranges under uniaxial loads. Amini et al. compared NiTi SMA with copper and quartz showing that the indentation depth of NiTi SMA decreased more rapidly with the loading rate. This can be explained by the enhanced transformation hardening caused by the latent heat accumulation around the indentation.

However, Farhat et al. [82] developed a simple heat model to predict the impact of temperature in indentation and suggested that the decrease of the indentation depth was not because of the temperature accumulation during transformation. Farhat et al. argued that the indentation depth decreased with the strain rate even at extremely low loading rates, where the generated heat could hardly accumulate. The loss of superelasticity might be due to the retardation of the transformation process during indentation, though more studies are needed to prove this claim.

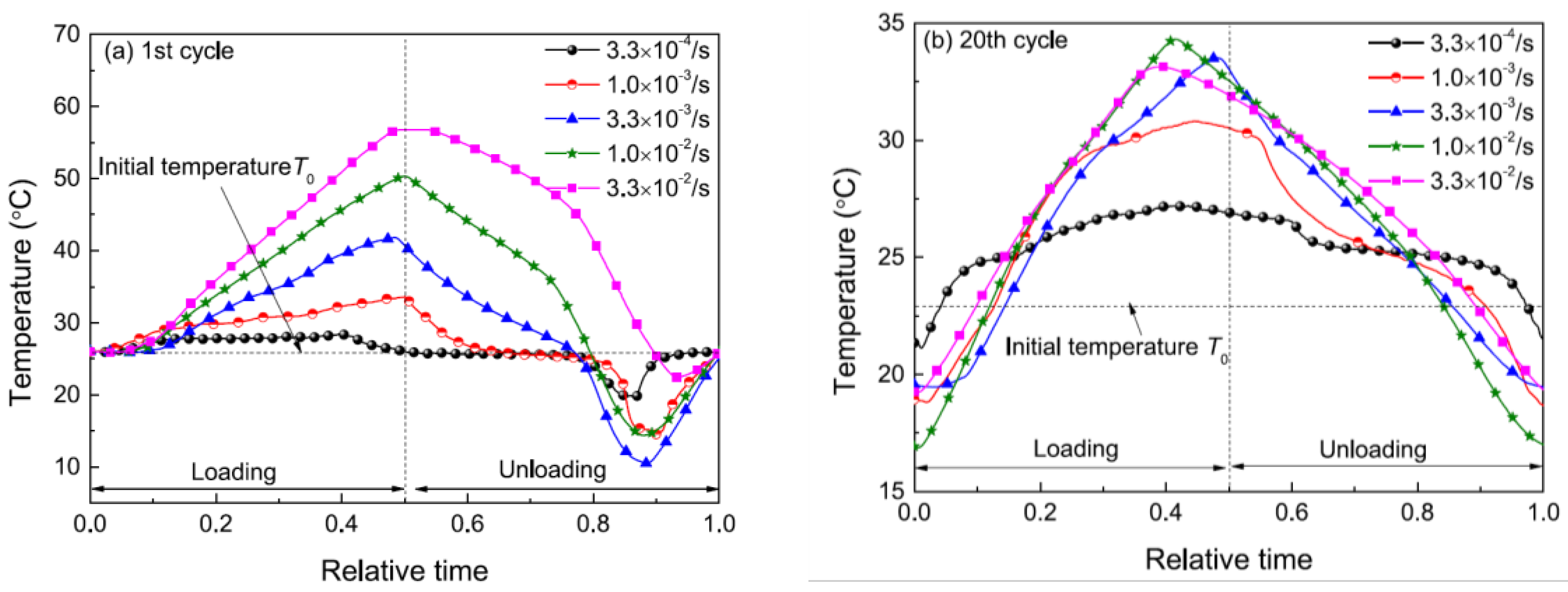
2.2.3. Cyclic Loading

The thermomechanical cyclic behaviors of NiTi SMA have been widely studied under strain- or stress-controlled uniaxial loading mode [37,38,83,84,85]. The rate-dependence under quasi-static cyclic strain-controlled loadings was systematically investigated by Kan et al. [37]. Impact fatigue tests were conducted less frequently than quasi-static ones [38]. Superelasticity degeneration and temperature variations were found strongly dependent on the strain rate, while the cyclic transformation path did not changed with strain rate.

Superelasticity degeneration indicated by transformation stress decrease, residual strain accumulation, and hysteresis loss takes place at all strain rates. Generally, the start and peak of transformation stress decrease with increasing number of cycles [37,38,83]. In Kan’s experiments, cyclic tests were performed at six strain rates ranging from 10⁻⁴ s⁻¹ to 10⁻² s⁻¹ with the maximum strain fixed at 9%. The corresponding stress-strain curves in different cycles are shown in Figure 8. The drop of transformation stress at each cycle becomes more conspicuous with increasing strain rate. Residual strain accumulation during cyclic loadings increases remarkably with increasing strain rate. The dissipation energy, i.e., the area of the stress-strain hysteresis loop, decreases with cycles, but the rate-dependence of the dissipation energy loss could be more complicated.

Superelasticity degeneration of NiTi SMA is mainly attributed to the interactions between transformation and dislocations [37,84,85]. Dislocations can be nucleated by high local stress near the phase interface and accumulate with the loading cycles. The internal stress caused by the dislocations assists stress-induced martensitic transformation, accounting for a decreasing critical transformation stress, and hindering the reverse martensitic transformation, resulting in an increasing residual strain. Therefore, superelasticity degeneration is speeded up by high strain rates.

Temperature variations during the cyclic deformation are also greatly influenced by the strain rate [37,84,85]. The evolution of temperature at five different strain rates in the 1st and 20th cycle are shown in Figure 9. In the loading part the temperature increases due to the release of transformation latent heat, while in the unloading part the temperature decreases first since the latent heat is absorbed in the reverse transformation and finally returns to the initial ambient temperature. Higher strain rates bring higher average temperatures. Generally, the amplitude of temperature oscillation decreases with increasing number of cycles; however, it increases with increasing strain rate.

Due to the temperature effect, the transformation hardening is enhanced as the strain rate grows [37]. The driving force in forward transformation progressively increases as the temperature rises. At a strain rate below 10⁻² s⁻¹, the heat generated by latent heat has to compete with heat conduction and convection in order to raise the temperature. This is similar to the mechanism under monotonic uniaxial loadings.

The number of impact fatigue tests is fewer than that of quasi-static ones. Zurbitu et al. [38] investigated the superelastic repeated-impact behaviors of NiTi SMA wires at a strain rate of 10 s⁻¹. They discovered that the critical transformation stress decreased with increasing cycles in both quasi-static and impact fatigue situations. However, the transformation stress dropped more slowly with cycles in the impact condition since rapid deformation caused a high level of dislocation density which hindered the reduction of martensitic transformation stress. Furthermore, Fitzka et al. [86] found that the intermediate R-phase still occurred in both forward and reverse martensitic transformation when the test frequency was increased to ultrasonic (10² s⁻¹). Therefore, the cyclic transformation path is independent of the strain rate.

In summary, the cyclic deformation of NiTi SMA is strongly dependent on the strain rate in the range from 10⁻⁴ s⁻¹ to 10² s⁻¹. As the strain rate increases, the superelasticity degenerates more rapidly and the sample temperature increases. The thermo-mechanical coupling effect determines the rate-dependent cyclic behaviors of NiTi SMA.

2.3. Dependence of the Strain Rate Effect on Microstructure

In addition to the loading condition, microstructure also have an important effect on the strain-rate dependent behaviors of NiTi SMAs. For general NiTi SMAs, the strain rate effect of R-phase transformation should be taken into consideration when the total strain is less than 2%. Precipitated phases, such as Ni4Ti3 precipitates, could improve the pseudoelasticity. A smaller grain size of austinite could neutralize the strain rate effect since the temperature effect decreases with a smaller latent heat. Porous SMAs are found with a similar strain rate effect, while SMA composites exhibit excellent impact-resisting performance.

2.3.1. General SMAs

• R-phase

A rhombohedral (R) phase transformation is much more sensitive to the strain rate compared to martensitic transformation. Since the elongation strain caused by R-phase is usually less than 1% (total martensitic transformation strain is 8%), the R-phase effect can be ignored in most situations. However, when the total strain is less than 2%, the influence of R-phase is worth considering carefully. Helbert et al. [39] built a three-phase pseudo-diagram and took R-phase transformation into consideration in explaining the strain effect on sensitivity of NiTi SMA wires. They found that the temperature sensitiveness of R-phase transformation stress was more than 10 MPa/K, which was approximately twice the sensitiveness of martensite phase, as shown in Figure 10. As the strain rate influences the temperature, R-phase transformation stress increases with the strain rate more rapidly than that of martensitic transformation.

b.

Precipitated phase

The influence of precipitates on the transformation behaviors of Ni-rich NiTi SMAs has been investigated by a large number of researchers [42,43,87,88,89]. The precipitated phase of Ni-rich NiTi SMAs is highly dependent on the aging temperature and time, among which the most studied are Ni₄Ti₃ precipitates. The Ni₄Ti₃ precipitates usually introduce R-phase transformation and result in a multistage transformation behavior [87]. Experimental results have shown that the precipitate influence varies with the strain rate.

The precipitation evolution and transformation behavior at quasi-static strain rates were studied and characterized by Fan et al. [42]. The critical transformation stress found was mainly determined by the magnitude of martensitic transformation temperature rather than the appearance of precipitates after aging treatment. Generally, the transformation temperature increases with decreasing aging temperature and increasing aging time.

A recent study by Yu et al. [43] showed that Ni4Ti3 precipitates could improve the pseudoelasticity of NiTi SMAs under impact loading. The critical transformation stress increases with increasing size and volume fraction of precipitates. The best performance in strength is found in the sample with the precipitates dispersed homogeneously within the grains. However, a more comprehensive study on the dependence of the strain rate effect on the precipitated phase is still needed.

c.

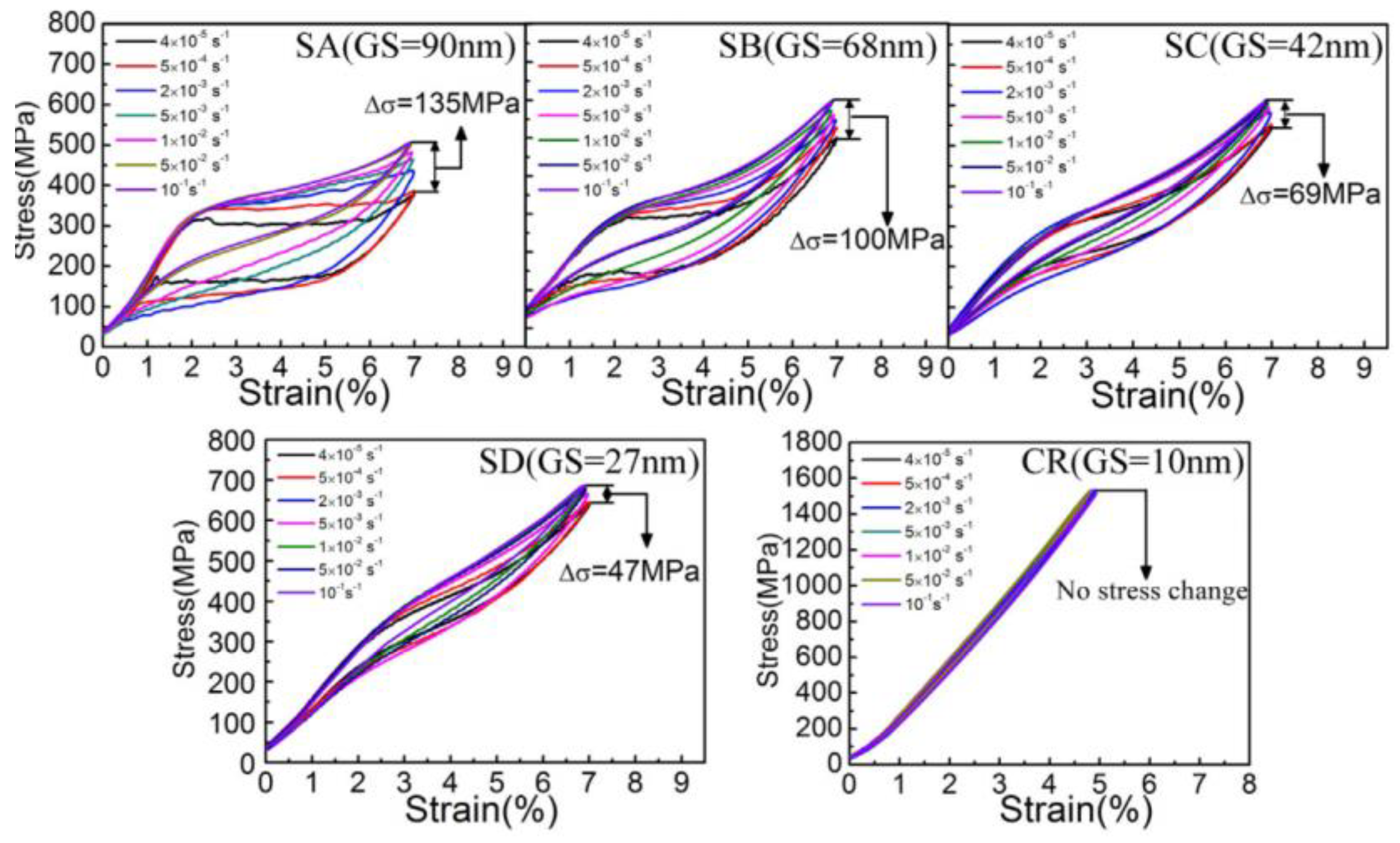
Grain size

Smaller grains typically reduce the rate-sensitivity of the transformation behavior. Ahadi and Sun [40] studied the rate-dependence of NiTi SMAs on the grain size systematically. Weaker rate dependence was found with smaller grain size, i.e., the difference between the transformation stresses at high and low strain rates diminished as the grain size became smaller. As shown in Figure 11, when the grain shrinks from 90 nm to 10 nm, $\Delta \sigma$ decreases from 135 MPa to zero. Such decreased rate dependence can be explained by smaller temperature variations due to the reduction of latent heat.

2.3.2. Porous SMAs and Composites

The rate dependence of porous SMAs is similar to general solid NiTi SMAs [25], as greater transformation stress is found at higher strain rates.

SMA composites commonly have lamellar structures with NiTi SMAs embedded and exhibit excellent impact-resisting performance [41]. For example, Pappadà et al. dropped a heavy ball on a composite plate to test the impact effect around the strain rate of 10 s⁻¹. They compared the SMA-embedded and steel-embedded plates and showed that the SMA-embedded composites had a better performance in absorbing the impact energy.

3. Models

Typically, the stress increases gradually during transformation, and this transformation hardening is enhanced by increasing the strain rate. In those models that did not directly consider the strain rate effect [90,91,92,93], the enhanced transformation hardening was modeled by a phenomenological hardening function with parameters fitted for different strain rates rather than a physical model that inherently considers the hardening mechanism. The hardening function provided extra resistance to transformation, and was generally described as a function of internal state variables with temperature-dependent parameters. These parameters were calibrated by experiments under a specific strain rate and needed to be updated when the strain rate changed. As a result, these models could only give accurate predictions in cases of limited change of the strain rate with a specific group of parameters.

To directly account for the strain rate effects discussed in Section 2, thermal source models are proposed for modeling the NiTi SMA behaviors at low and medium strain rates, and as extended versions, thermal kinetic models are proposed for high strain rates to consider the kinetic effect in shock conditions. These models that take account of the self-heating mechanism and represent the strain rate effect by means of thermal sources can be termed as thermal source models. This is because the strain rate influences the martensitic transformation rate, in turn influences the heat production rate and temperature field. In shock conditions, the velocity of dislocations and phase interfaces set in, so the thermal source model has been extended to thermal kinetic models to consider these kinetic effects.

3.1. Thermal Source Models

At low and medium strain rates, the strain rate effect of NiTi SMA is mainly attributed to temperature variations during transformation, which can be modeled by means of thermal sources in the material [44,45]. The thermal source releases heat in the forward martensitic transformation and absorbs heat in the reverse. The temperature field is hence influenced by a transformation rate that scales with the strain rate.

There are two basic ways to develop the temperature evolution equation in thermal source models. The first method is to directly add external thermal sources to the energy equation, including the latent heat, dissipation heat, and elastic heat [46,47]. The specific form of the thermal source can be constructed empirically. For instance, the released latent heat rate can be represented by a function of the rate of change in a martensitic volume fraction, while the dissipation heat is calculated by a fixed proportion (e.g., 90%) of the total mechanical dissipation energy [48,49].

The second method is to derive the energy equation from an explicit thermodynamic potential with added energy terms related to thermal sources [94,95]. The thermodynamic potential can be either Gibbs or Helmholtz free energy, which is constructed from physical or phenomenological considerations as a function of stress (or strain), temperature, and a set of internal state variables. The chosen form of the free energy should contain the thermal effect introduced by the latent heat, dissipation heat, etc. The evolution equations are then established following a standard thermodynamic procedure.

Two methods lead to similar temperature evolution equations that contain terms with the same physical origins, and both methods need extra constitutive equations for internal state variables [44,45,46,47]. The first method that directly adds thermal sources to the energy equation seems to be more simple and easier to realize; however, the second potential method is more favored among researchers in view of its thermodynamic consistency. Therefore, our review will focus on this potential method in explaining the thermal source model. Details of the potential method will be presented in the perspective of thermodynamic theory in Section 3.1.1, followed by a discussion on thermal source components in Section 3.1.2. Simulation examples based on the thermal source model will be shown in Section 3.1.3.

3.1.1. Framework of the Potential Method and the Temperature Evolution Equation

Taking the Gibbs free energy ($G$) for example, the free energy is usually expressed as a function of a stress tensor $S$, a temperature $T$, and other internal variables:

$$G=G\left(S,T,{\gamma }^i\right),$$

(1)

where ${\gamma }^i$ represents the i^th internal variable. The derivative of Gibbs free energy can then be written by:

$$\dot{G}=\frac{\partial G}{\partial S}:\dot{S}+\frac{\partial G}{\partial T}\dot{T}+\frac{\partial G}{\partial {\gamma }^i}:{\dot{\gamma }}^i,$$

(2)

where the Einstein summation convention is assumed. Three conjugate relationships from the second law of thermodynamics are applied:

$$E=-\rho \frac{\partial G}{\partial S},$$

(3)

$$s=-\frac{\partial G}{\partial T},$$

(4)

$${\pi }^i=-\rho \frac{\partial G}{\partial {\gamma }^i},$$

(5)

where $E$ is the strain tensor, $\rho$ is the density, $s$ is the entropy, and ${\pi }^i$ is the thermodynamic driving force conjugated to ${\gamma }^i$. Thus, Equation (2) can be simplified to:

$$\dot{G}=-s\dot{T}-\frac{1}{\rho }E:\dot{S}-\frac{1}{\rho }{\pi }^i:{\dot{\gamma }}^i.$$

(6)

The first law of thermodynamics can be express as

$$\rho \dot{u}=S:\dot{E}+\rho r-\nabla ·q,$$

(7)

where $u$ is the specific internal energy, $r$ is the external heat source density, and $q$ is the heat flux. Note that the mechanical dissipation is well considered in Equation (7). The expression of the internal energy rate is necessary for acquiring the progress of temperature change, which can be obtained from a Legendre transformation:

$$\dot{u}=\dot{G}+T\dot{s}+s\dot{T}+\frac{1}{\rho }\left(S:\dot{E}+E:\dot{S}\right).$$

(8)

Substitute (6) into (8), two terms can be removed:

$$\dot{u}=T\dot{s}-\frac{1}{\rho }{\pi }^i:{\dot{\gamma }}^i+\frac{1}{\rho }S:\dot{E}.$$

(9)

Equations (6), (7), and (9) suggest:

$$-\rho T\frac{\partial }{\partial t}\left(\frac{\partial G}{\partial T}\right)={\pi }^i:{\dot{\gamma }}^i+\rho r-\nabla ·q,$$

(10)

The form of the Gibbs free energy is not unique. If the internal state variables are selected to be the martensitic volume fraction $\xi$ and the transformation strain ${\epsilon }^t$, as used by Boyd and Lagoudas [94], the explicit form of the Gibbs free energy ($G_L$) can then be defined as:

$$\begin{array}{ll}{G}_L\left(S,T,\xi ,{\epsilon }^t\right)=& -\frac{1}{2\rho }S:C:S-\frac{1}{\rho }S:\left[\alpha \left(T-T_0\right)+{\epsilon }^t\right]+c\left[\left(T-T_0\right)-T\ln \left(\frac{T}{T_0}\right)\right]\\ & -s_{0}T+u_0+\frac{1}{\rho }f\left(\xi \right),\end{array}$$

(11)

where $C$ is the effective compliance tensor, $\alpha$ is the effective thermal expansion coefficient tensor, $T_0$ is a reference temperature, $c$ is the effective specific heat capacity, $s_0$ is the effective specific entropy at the reference state, $u_0$ is the effective specific internal energy at reference state, and $f\left(\xi \right)$ is a transformation hardening function.

The effective parameters in (11) are determined by terms of the properties for the pure phases. For instance, the effective thermal expansion coefficient is defined as:

$$\alpha \left(\xi \right)={\alpha }^{\mathrm{A}}+\xi \left({\alpha }^{\mathrm{M}}-{\alpha }^{\mathrm{A}}\right)={\alpha }^{\mathrm{A}}+\xi \mathsf{\Delta }\alpha ,$$

(12)

where the superscripts A and M represent pure austenite and martensite, respectively.

With the assumption that the martensitic transformation happens with no martensitic variant reorientation, the evolution of the transformation strain is then postulated as

$${\dot{\epsilon }}^t=\mathsf{\Lambda }\dot{\xi },$$

(13)

where $\mathsf{\Lambda }$ is the transformation tensor. Assume that the specific heat and the thermal expansion coefficients of the two phases are identical:

$$\frac{\partial G_L}{\partial T}=-\frac{1}{\rho }S:\alpha -c\ln \left(\frac{T}{T_0}\right)-s_0,$$

(14)

and the driving force ${\pi }^{\xi }$ can be evaluated by:

$${\pi }^{\xi }=S:\mathsf{\Lambda }+\frac{1}{2}S:\Delta C:S+\rho \Delta s_{0}T-\rho \mathsf{\Delta }{u}_0-\frac{\partial f}{\partial \xi }.$$

(15)

Substitute (14) and (15) into (10):

$$\rho c\dot{T}=-\rho \Delta s_{0}T\dot{\xi }+{\pi }^{\xi }\dot{\xi }-\alpha :\dot{S}T+\rho r-\nabla ·q,$$

(16)

which is the governing equation of temperature based on the proposed form of Gibbs free energy in (11).

3.1.2. Components Related to the Thermal Sources

Each term in the temperature evolution Equation (16) corresponds to a specific thermal source, which includes the latent heat, irreversible dissipation heat, elastic heat, heat flux, and external heat sources. These heat components will be discussed individually below.

a.

Latent heat

The temperature variations of NiTi SMAs are mainly caused by the latent heat during transformation. Previous phenomenological models assumed that the absorbed or released rate of latent heat had a linear relationship with the change rate of transformation strain [44], while recent models tended to assume a linear relationship with the change rate of martensitic volume fraction [96,97,98]. For example, the term $\rho \Delta s_{0}T\dot{\xi }$ in (16) corresponds to the latent heat, which is determined by the difference of entropy $\rho \Delta s_0$ between two phases, the temperature T, and the martensitic volume fraction change rate $\dot{\xi }$ [99,100].

b.

Irreversible dissipation heat

The influence of the dissipation heat on the temperature evolution is second only to that of the latent heat. The mechanism of dissipation of heat are complex, which usually include dissipation by martensitic transformation, martensite reorientation and detwinning, transformation-induced plasticity, and structural plasticity due to the increasing density of dislocations [60,97]. The specific dissipation process depends on the microstructure and external loading conditions.

The contribution of the dissipation heat depends on the strain rate. When the strain rate is low, the dissipation heat by the martensitic transformation in NiTi SMA is smaller than the latent heat by an order of magnitude, which only needs a simple approximation [49] and sometimes can even be ignored [99,101]. In contrast, at medium and high strain rates the dissipation heat could reach a high proportion of the total heat [102,103].

The irreversible dissipation rate can be modeled by a sum of product terms of the thermodynamic driving forces and the change rates of corresponding internal state variables. In general, the thermodynamic driving force is assumed to reach a critical value before the corresponding dissipation process initializes, and then remains a constant during the dissipation. The evolutions of internal state variables are governed by the driving forces during transformation, and they eventually determine the dissipation rate in cases of constant driving forces.

In the potential method, the free energy form is modified to take account of the corresponding dissipation heat in the temperature evolution equation. These modifications basically address the relevant dissipation mechanisms mentioned above. Examples include: (1) The dissipation heat by martensitic transformation as considered by Boyd and Lagoudas [94] in the Gibbs free energy (11) with the corresponding term ${\pi }^{\xi }\dot{\xi }$ in the temperature evolution equation (3–16). (2) The dissipation heat by the martensite reorientation was taken into account by Šittner et al. [60] in the Gibbs free energy with a function of the volume fraction of each martensite variant. (3) The dissipation heat by transformation-induced plasticity was modeled by Xu et al. [104] in the Gibbs free energy with a term depending on the plastic strain accumulated during transformation. (4) The dissipation heat by general dislocation plasticity was taken into consideration by Heller et al. [105] in the free energy with a term depending on the elevated stress subject to a yield criterion.

c.

Elastic heat

The elastic heat rate here is referred to as the power of stress owing to the thermal expansion, which is the term $\alpha :\dot{S}T$ in (16). However, the elastic heat is often neglected in most calculations for its insignificant amount compared to the latent heat [100].

d.

Heat flux and external heat source

The heat flux and external heat source, as indicated by the term $\rho r-\nabla ·q$ on the right-hand side in (16), correspond to the surface heat conduction/convection and bulk heat production. The heat release and production rates due to external factors also have important influences on the temperature evolution. For example, water-enclosed NiTi SMA wires more readily dissipate heat than air-enclosed ones, and the power of the electricity current greatly influences the temperature of current-driven NiTi SMA wires [5].

3.1.3. Simulation Results with the Thermal Source Model

Quite a few simulations of NiTi SMAs have been carried out under isothermal (quasi-static) or adiabatic conditions based on the thermal source models [50,51,54,55]. Simulation examples have been selected and arranged in the following paragraphs to show the strength of thermal source models in capturing the strain rate effect on both macro- and micro- behaviors of NiTi SMAs. The first simulation case shows the ability of thermal source models to simulate the stress-strain curves with transformation hardening when the strain rate increases. The stress response is attributed to the self-heating mechanism, so the next simulation example investigates the strain rate effect on the temperature variation. Following this, several simulations are presented in studying the contributions of thermal-source components to the temperature variation under various strain rates. The last simulation example discusses the strain rate effect on the nucleation and propagation of phase transformations.

The rate responses of the stress-strain curves are one of the major concerns in simulating the thermomechanical behaviors of NiTi SMAs. Thermal source models can catch the transformation hardening process in the stress-strain curves owing to an increase in strain rate. Simulation examples of isothermal and adiabatic deformation performed by Wang et al. [95] are shown in Figure 12. The simulated stress-strain curves were compared with experimental data in Figure 12a. In the isothermal situation ($\dot{\epsilon }=4\times {10}^{-5}{\mathrm{s}}^{-1}$), the stress stayed constant during transformation; while in the approximately-adiabatic situation ($\dot{\epsilon }=4\times {10}^{-2}{\mathrm{s}}^{-1}$), the stress increased with increasing strain exhibiting a transformation hardening process.

The increase of stress during transformation is caused by temperature change. The corresponding simulated temperature-strain curves were compared with experimental data in Figure 12b. The temperature remained constant during transformation in the isothermal situation, while the temperature increased with increasing strain in the approximately adiabatic situation. The strain rate effect on the temperature evolution compares well with experiments as the self-heating mechanism is accounted for in thermal source models.

The influences of the thermal-source components on the temperature change vary with strain rate. The contribution of the dissipation heat component to the temperature rise was investigated under various strain rates [99,101]. At low strain rates, the dissipation heat only had a small effect on the specimen temperature compared to the latent heat, so the dissipation accumulation, calculated by the mechanical dissipation in one cycle, was carefully studied. Grandi et al. [51] measured the areas of the hysteresis cycles in the simulated stress-strain curves and found that the dissipation accumulation increased with increasing strain rate first and then decreased after the peak. The non-monotone trend of the dissipated energy with the strain rate was supported by the experimental results obtained by Zhang et al. [31]. However, the contribution of the dissipation heat to the temperature rise approached that of the latent heat when the strain rate grew above 10² s⁻¹. The simulations performed by Shen and Liu [103] showed that the temperature rise increased with increasing strain rate, and the percentage of the dissipation heat ascended to 47% at a strain rate of 1600 s⁻¹, as shown in Figure 13.

In addition to the influences of the dissipation heat, the influences of the heat flux component on the temperature change were also explored at different strain rates. For instance, the trends of the maximum temperature rise with the strain rate were studied by Grandi et al. [51] under three different heat transfer coefficients, as shown in Figure 14. Either a low heat transfer coefficient or a high strain rate resulted in a rise in the specimen temperature. This demonstrated the equivalence of the thermal effects caused by decreasing the heat transfer coefficient and increasing the strain rate.

The strain rate effect on the nucleation and propagation of phase transformation was also captured by thermal source models. Ahmadian et al. [100] simulated the transformation process at strain rates ranging from 10⁻⁴ s⁻¹ to 10⁻¹ s⁻¹ showing that the number of martensite bands increased as the strain rate increased. The martensitic transformation domains in simulations propagated and widened in a parallel mode. These features are similar to those in experiments (Figure 15).

In conclusion, thermal source models are capable of describing the thermomechanical behaviors of NiTi SMAs at low and medium strain rates. However, these models do not consider the kinetic effect, which is one of the main causes for the strain rate effect in dynamic loading conditions. The thermal kinetic model has hence been developed and will be discussed in the next section.

3.2. Thermal Kinetic Models

Thermal source models are not able to capture the sudden rise of stress under dynamic loading conditions. It is observed in experiments that the overall stress level of NiTi SMA increases dramatically when the strain rate increases above 10³ s⁻¹. In contrast with the rapid growth of stress, the temperature rise reaches a saturation value as the heat by transformation is fully released in the adiabatic process. Thus, the self-heating mechanism can only partially explain the large flow stress in the high-strain-rate deformation.

The rise of overall stress, as well as transformation stress, can be ascribed to the dislocation drag mechanism in the plastic deformation around the phase interface [73,74], as discussed in Section 2. The interface between the austenite and martensite phases contains dislocations that need a much higher driving stress at high strain rates due to the phono drag effect. As a result, the resistance of the phase interface increases sharply leading to a rapid increase in transformation stress. The kinetic properties of the phase interface are therefore of fundamental importance in explaining the great increase in stress during shock conditions.

Some of the earliest phenomenological models were developed by simply introducing a strain rate term into the thermal source model. For instance, Hiroyuki et al. [106] and Auricchio et al. [107] constructed rate-dependent models with thermal sources containing strain rate terms to account for the sole strain-rate effect. Though their simulation results matched well with the experimental results at medium strain rates, their models could hardly reproduce the significant stress rise in dynamic conditions due to the neglect of the kinetic relationship at the phase interface.

Yu et al. [56,57,58] extended the thermal source model to thermal kinetic model by considering both the self-heating mechanism and kinetic relationship at high strain rates. Based on the thermal source model by Hartl et al. [108], Yu et al. added a term in the traditional transformation driving force to describe the global resistance force of the phase front on transformation. The added resistance force incorporated the velocity of the phase front, and was derived from calculating the needed energy for the kinetic energy change during transformation. The large flow stress and the strain rate effect in the dynamic loading conditions were eventually well-predicted by the thermal kinetic model.

Our review will focus on Yu’s model in explaining the thermal kinetic model in view of the limited number of rate-dependent models for dynamic deformation of NiTi SMAs. Necessary numerical verifications based on Yu’s model will be presented at the end.

On the basis of the thermal source model proposed by Hartl et al. [108], Yu’s model assumes that the dislocation drag effect on the phase interface can be modeled by adding a resistance term to the driving force of the martensitic transformation:

$${\pi }_{tr}^{\prime }={\pi }_{tr}-f_D\left(\xi \right),$$

(17)

where ${\pi }_{tr}$ is the driving force in the original quasi-static thermal source model and $f_D\left(\xi \right)$ is the added resistance force defined as a linear function of the volume fraction of martensite $\xi$:

$$f_D\left(\xi \right)=K\xi ,$$

(18)

where $K$ is a constant parameter and described the kinetics related to the strain rate. This parameter can be derived from calculating the kinetic energy change in the wave equation and its form is given as:

$$K=\frac{1}{4}{\rho }_0{\kappa }^2{g}_{tr}^2{(\dot{\epsilon })}^2,$$

(19)

where $g_{tr}$ is the complete (or maximum) transformation strain, and $\kappa$ is material parameter which describes the relationship between the strain rate $\dot{\epsilon }$ and phase boundary velocity $C_P$ as:

$$C_P=\kappa \dot{\epsilon }.$$

(20)

When the strain rate decreases to quasi-static, the resistance force decreases rapidly and finally the thermal kinetic model reduces back to the thermal source model.

Yu and Young [57] then extended the model to three dimensions and applied the thermal kinetic model to simulate the energy band evolutions under high strain rates by the finite element method [58]. The stress-strain curves from experiment data [27] and the thermal kinetic model at five different high strain rates are shown in Figure 16. The critical stress for forward phase transformation increased with increasing strain rate and the hysteresis area shrank when the strain rate was above 9000 s⁻¹. In addition to the experiment results by Guo et al., the kinetic models can match well with other austenitic SMAs.

Compared to the thermal source model, the thermal kinetic model considers both the self-heating effect and the kinetics of the phase interface in dynamic loading. However, the resistance force on the phase interface is estimated globally by a calculation of kinetic energy change, and therefore more effort is still needed to improve the thermal kinetic model in order to consider the localized microstructure of the phase front.

4. Final Remarks

This paper has reviewed experimental results and constitutive models for the strain rate effect of NiTi SMAs from quasi-static to dynamic loading conditions. An attempt has been made to summarize the physical mechanisms, experimental observations, and models relevant to different strain rates, as shown in

Table 1. A summary of mechanisms, experimental observations, and models at different strain rates.

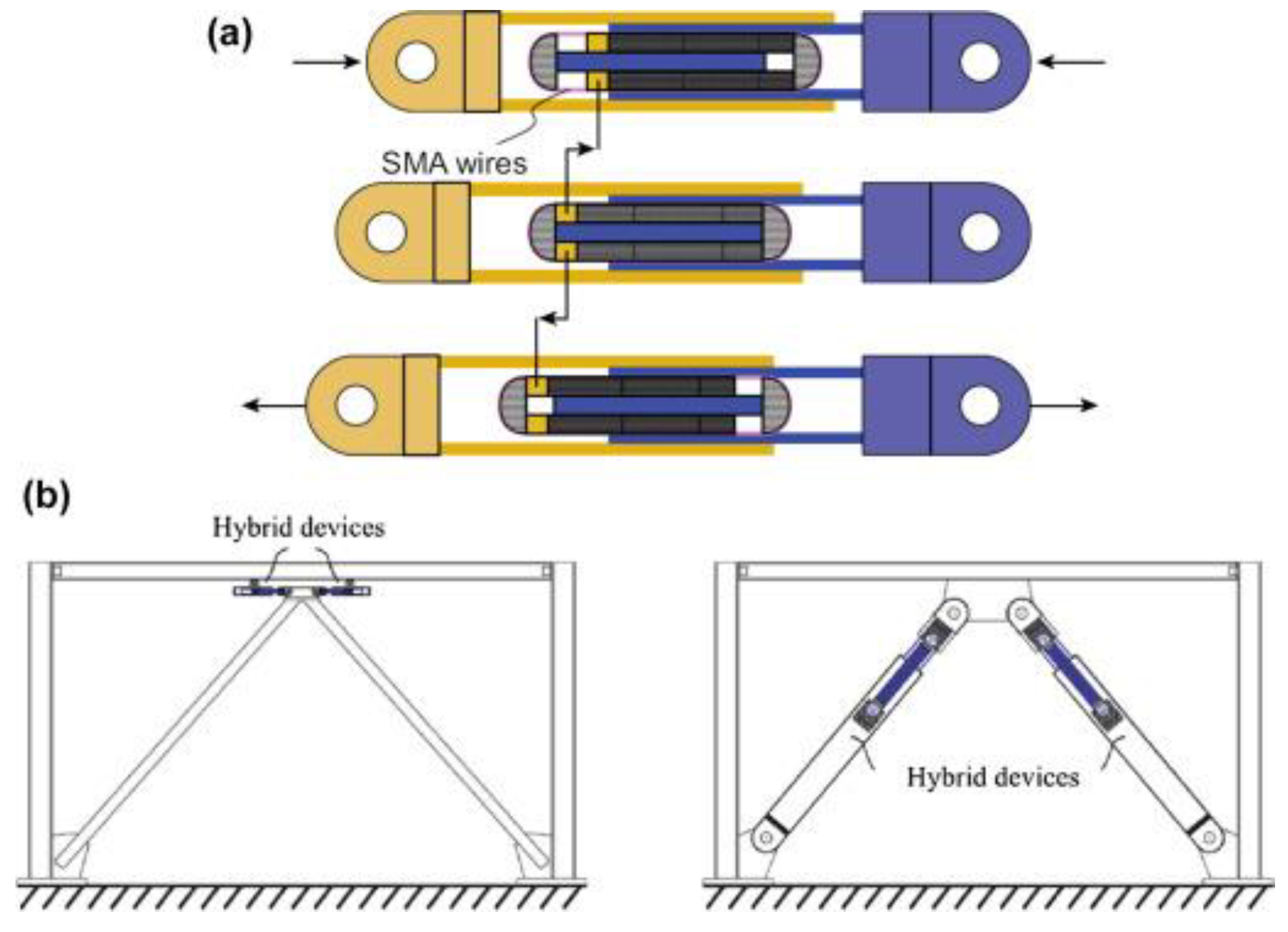
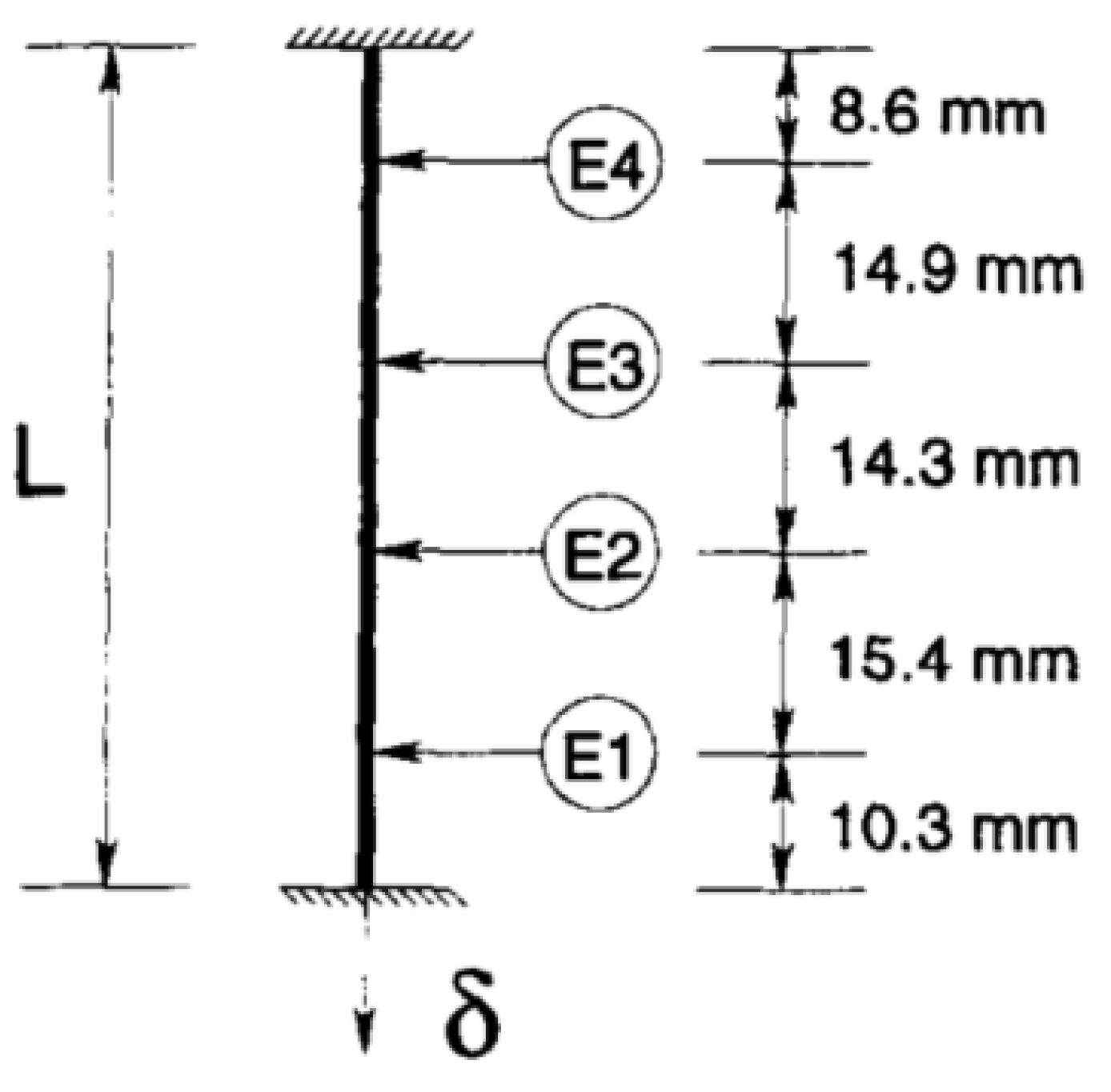
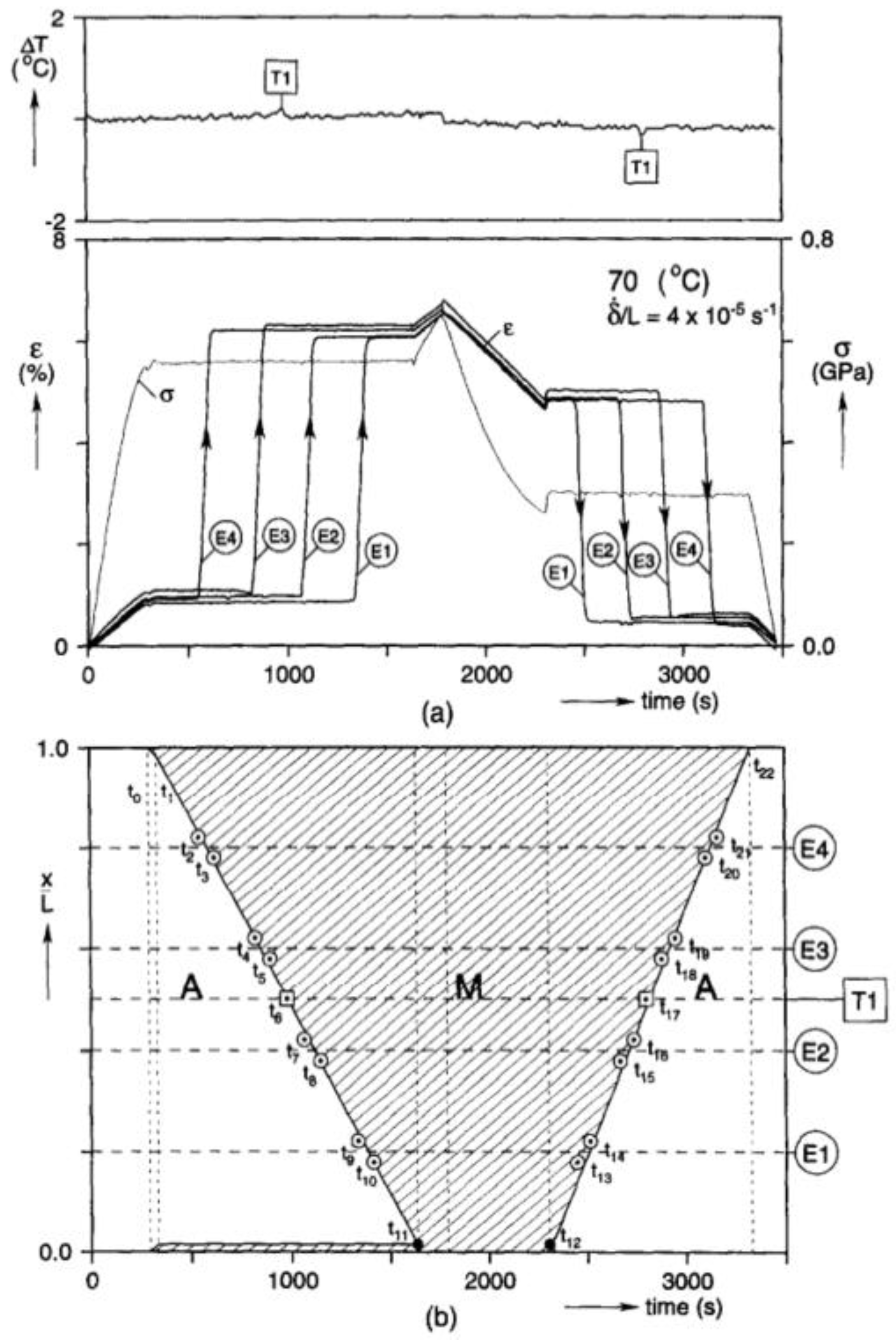
Strain Rate		Mechanisms	Experimental Observations (Uniaxial Loading, with Increasing Strain Rate)			Models
Range	Rank		Temperature Rise	Transformation Stress	Transformation Mode
$<{10}^{-4}{\mathrm{s}}^{-1}$	Very low	Isothermal process; heat by transformation dissipates to the environment sufficiently	Unnoticeable	Nearly unchanged	Martensite nucleates at few locations and then extends to all fields	Thermal source
${10}^{-4}{\mathrm{s}}^{-1}$ $~{10}^{-1}{\mathrm{s}}^{-1}$	Low	Transition from isothermal to adiabatic; part of heat by transformation is left in the specimen	Increases	Increases gradually	Number of nucleation sites increases and transformation domains propagate in a parallel mode	Thermal source
${10}^{-1}{\mathrm{s}}^{-1}$ $~{10}^3{\mathrm{s}}^{-1}$	Medium	Adiabatic process; heat by transformation is fully applied to warm up the specimen	Reaches the maximum	Nearly unchanged	Large martensite zones nucleate at loading ends and spread towards the specimen center	Thermal source
${10}^3{\mathrm{s}}^{-1}$ $~{10}^4{\mathrm{s}}^{-1}$	High	Adiabatic process; resistance of the phase interface increases dramatically due to the drag effect	Reaches the maximum	Increases dramatically	-	Thermal kinetic
$>{10}^4{\mathrm{s}}^{-1}$	Very high	Adiabatic process; austenite yields without transformation	-	-	-	Plasticity

for uniaxial loading conditions.

Most experimental results reviewed in this paper were under uniaxial loads, while those under shear, indentation, and cyclic loading have also been discussed. Experiments in shear and indentation exhibit similar behaviors to those in uniaxial; as for cyclic loading, superelasticity degeneration and temperature variations are enhanced by increasing the strain rate. The microstructure features such as appearance of the R-phase and precipitated phase, and grain size, also have influences on the strain-rate responses of general NiTi SMAs.

Rate-dependent constitutive models of NiTi SMAs have been built based on the physical mechanisms under different strain rates. Thermal source models have been developed for low and medium strain rates where the strain rate effect could be modeled as thermal sources working in the energy equation. Thermal kinetic models have been extended from thermal source models to consider the kinetic relationship at high strain rates. Both models are effective in modeling the thermodynamic behaviors of NiTi SMAs under corresponding strain rates.

In conclusion, new information provided by this analysis includes; (1) a general plot of the martensitic transformation stress and the austenite yield stress as a function of the strain rate in Figure 2, (2) categorizations of theoretical models based on the physical origins, and (3) a summary of connections between experimental observations, mechanisms, and models for NiTi SMAs at different strain rates in Table 1.

In addition to the information analyzed and summarized above, future research directions are suggested in the following three aspects: (1) new devices and experimental methods for maintaining a stable strain rate in the medium range; (2) comprehensive studies on the influences of microstructure on the strain rate effect; (3) improvements on thermal kinetic models to take account of the localized microstructure of the phase front.