Flow and Reaction Characteristic in a Stirred Reactor for Corrosion Process of Reduced Ilmenite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Method
2.2. Physical Properties
3. Results
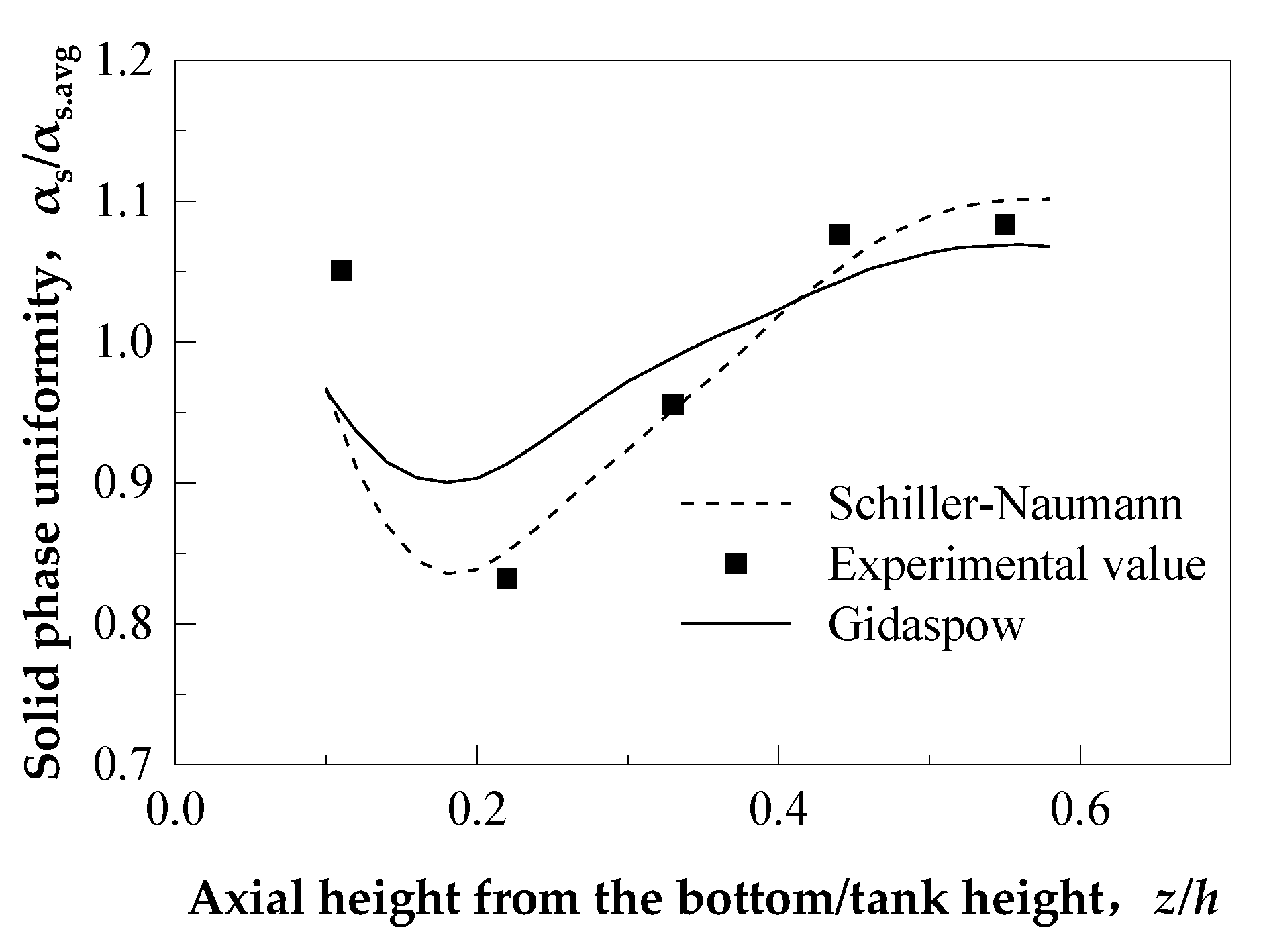
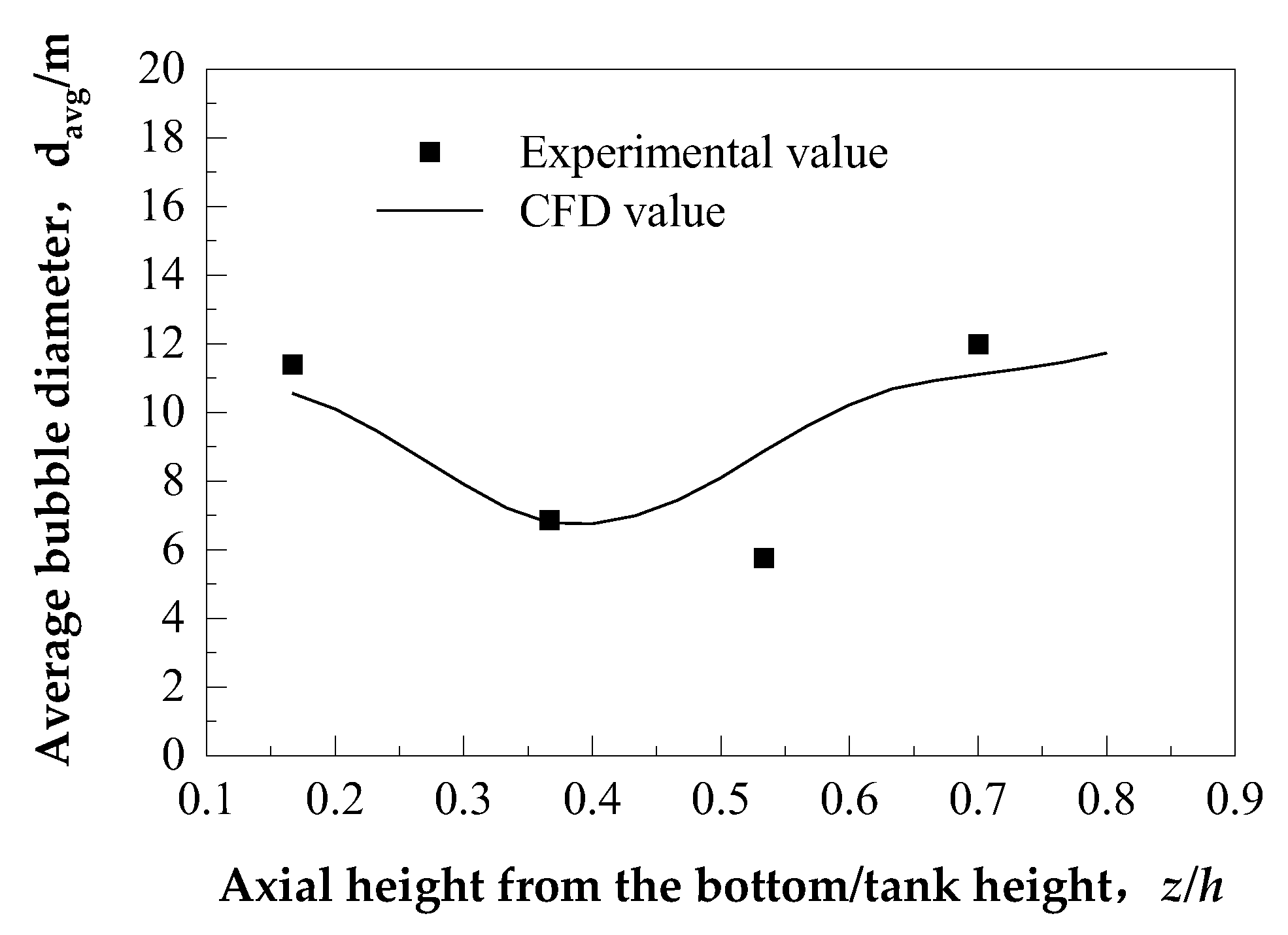
3.1. Model Validation
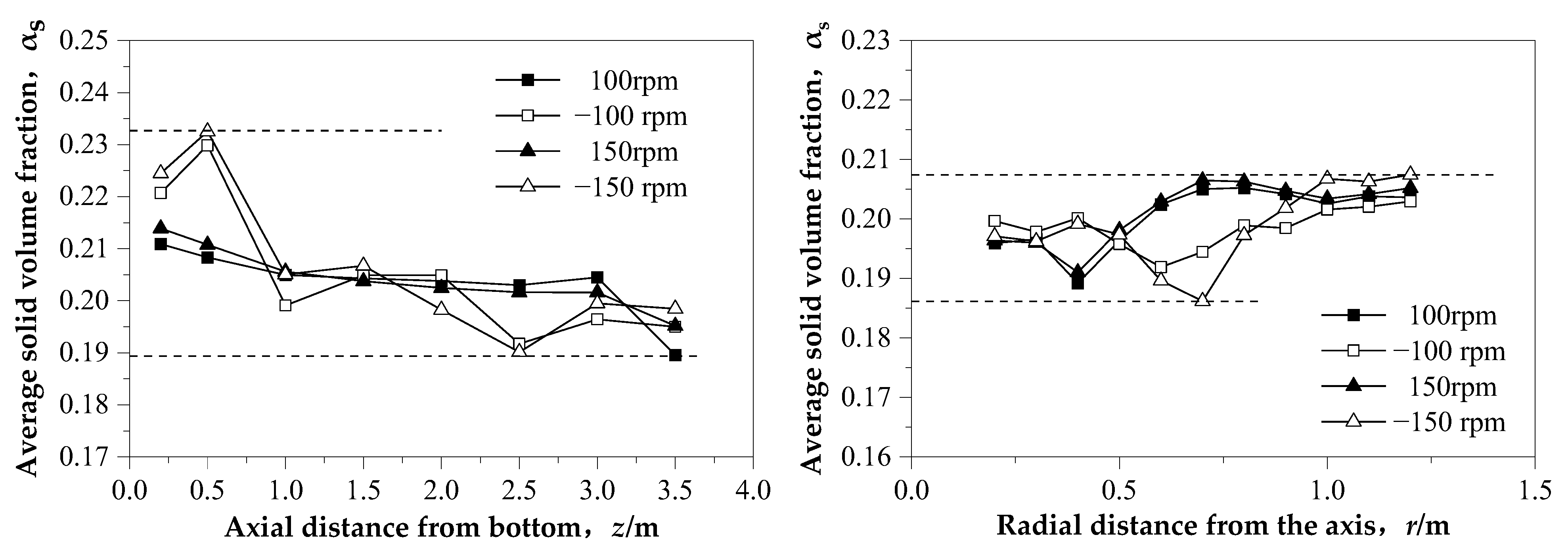
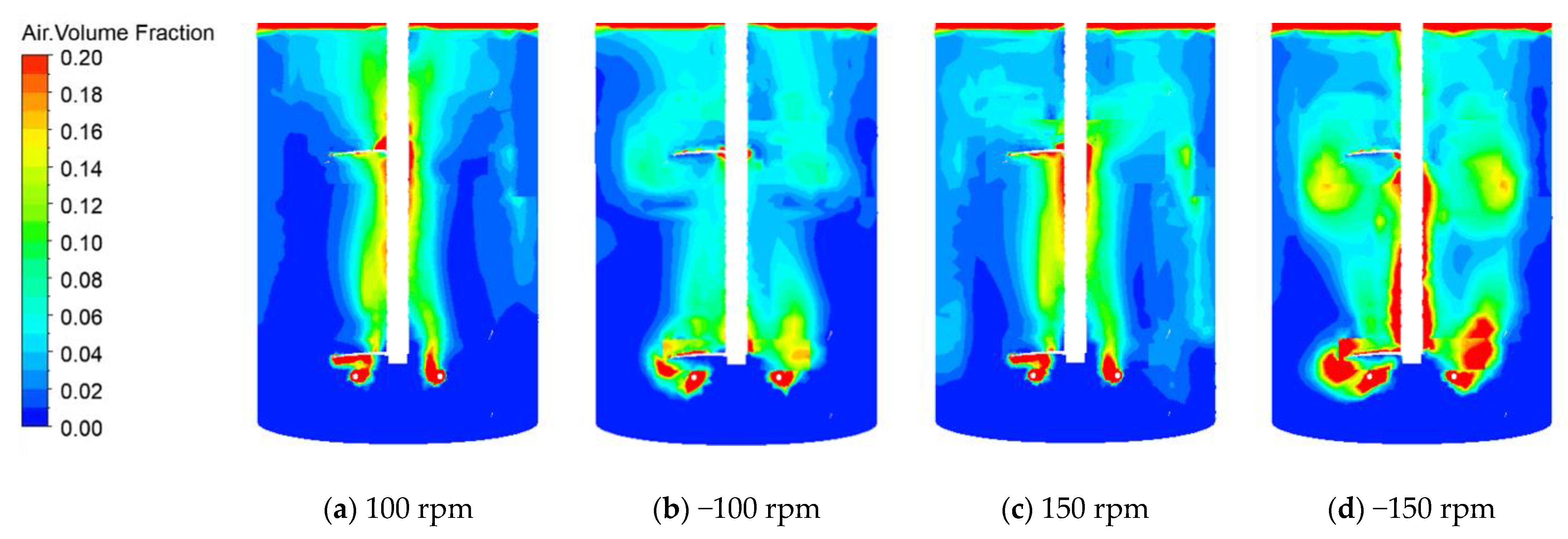
3.2. The Flow under Different Stirring Speed and Stirring Direction
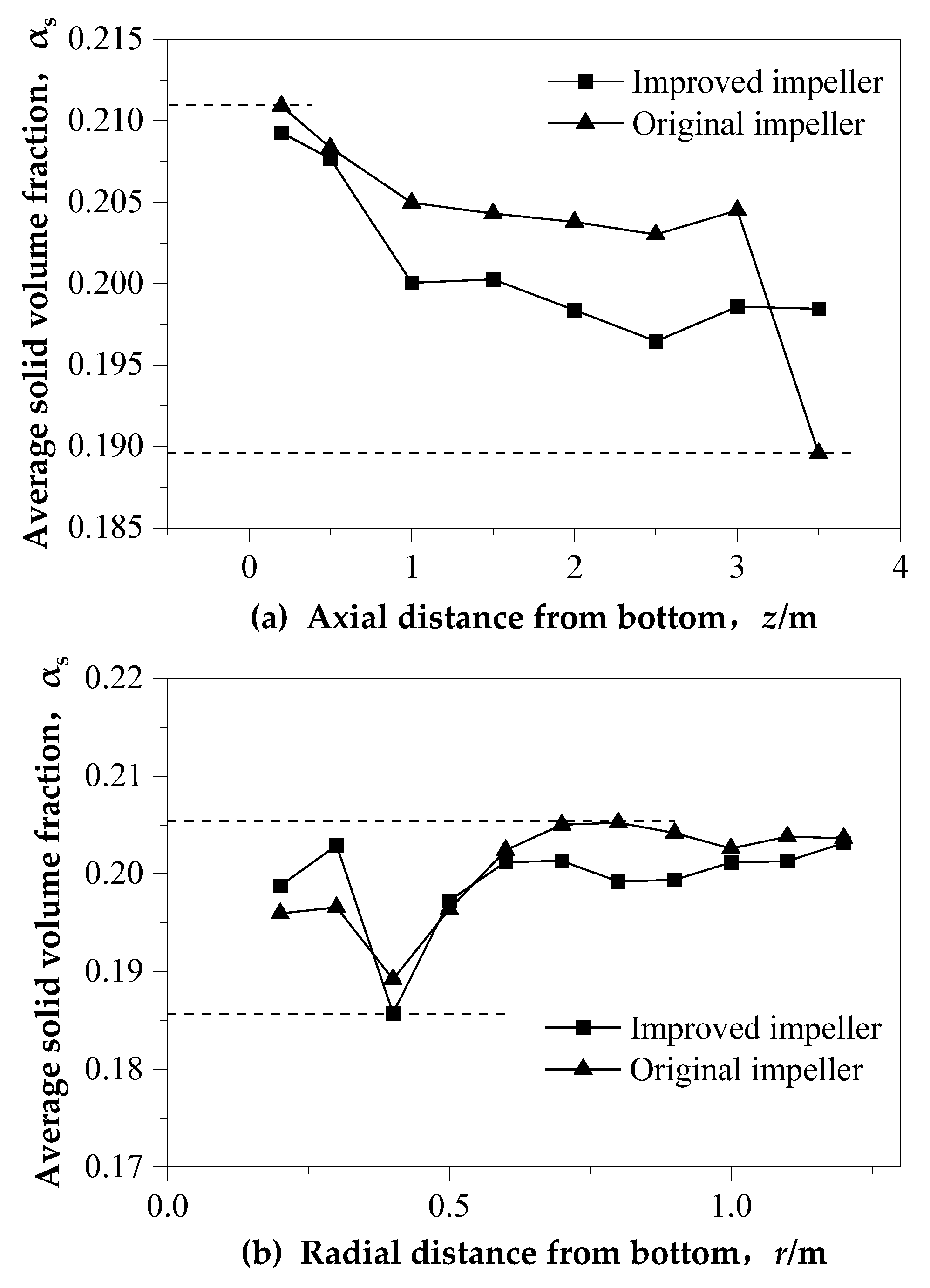
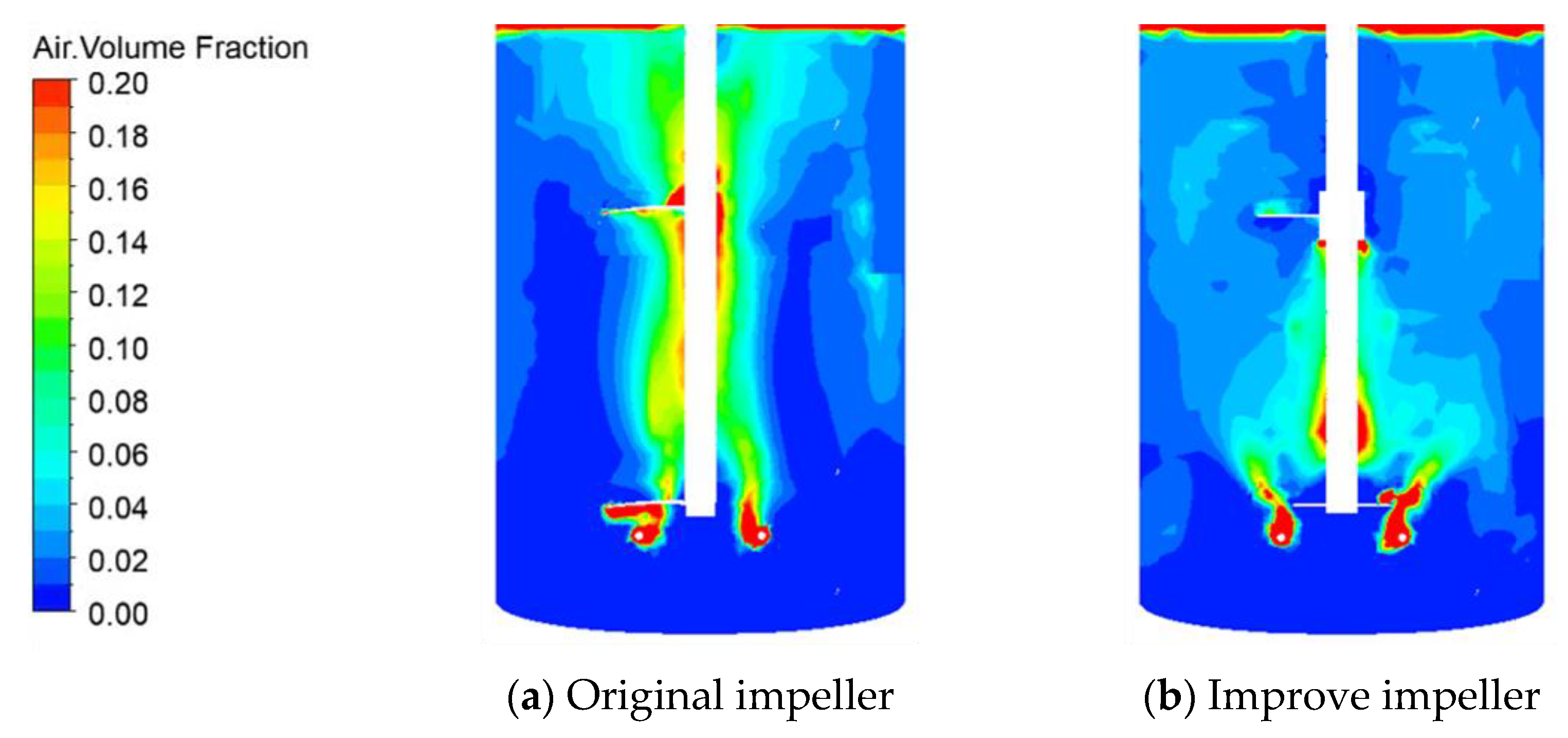
3.3. The Flow under Different Impeller Types
3.4. Corrosion Reaction Results
4. Discussion
4.1. Influence of Stirring Speed and Stirring Direction on the Flow
4.2. Influence of Different Combined Impeller Types on the Flow
4.3. Amplification Criterion for Corrosion Reactor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahmoud, M.; Afifi, A.; Ibrahim, I. Reductive leaching of ilmenite ore in hydrochloric acid for preparation of synthetic rutile. Hydrometallurgy 2004, 73, 99–109. [Google Scholar] [CrossRef]
- Chen, Y.C. Chemical Equipment Design Book-Mixing Equipment Design; Shanghai Science and Technology Press: Shanghai, China, 1985; pp. 1–3. [Google Scholar]
- Gu, D.Y.; Liu, Z.H.; Zhang, J.Y.Z.; Qiu, F.C.; Li, J.; Tao, C.Y.; Wang, Y.D. Chaotic mixing and dispersion characteristics of gas-liquid two-phase in a stirred tank. J. Chem. Ind. 2018, 69, 625–632. [Google Scholar]
- Bao, Y.; Wang, B.; Lin, M.; Gao, Z.; Yang, J. Influence of impeller diameter on overall gas dispersion properties in a sparged multi-impeller stirred tank. Chin. J. Chem. Eng. 2015, 23, 890–896. [Google Scholar] [CrossRef]
- Buffo, A.; Vanni, M.; Marchisio, D.L. Multidimensional population balance model for the simulation of turbulent gas–liquid systems in stirred tank reactors. Chem. Eng. Sci. 2012, 70, 31–44. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, H.W.; Zheng, J.K. Numerical simulation of the influence of baffle structure on mixing energy consumption in vertical mixing tank. Water Resour. Power 2013, 31, 162–197. [Google Scholar]
- Cappello, V.; Plais, C.; Vial, C.; Augier, F. Bubble size and liquid-side mass transfer coefficient measurements in aerated stirred tank reactors with non-Newtonian liquids. Chem. Eng. Sci. 2020, 211, 115280. [Google Scholar] [CrossRef]
- Mesa, D.; Brito-Parada, P.R. Bubble size distribution in aerated stirred tanks: Quantifying the effect of impeller-stator design. Chem. Eng. Res. Des. 2020, 160, 84–93. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Two-fluids RANS predictions of gas cavities, power consumption, mixing time and oxygen transfer rate in an aerated fermenter scale-down stirred with multiple impellers. Biochem. Eng. J. 2021, 166, 107867. [Google Scholar] [CrossRef]
- Kalaga, D.V.; Ansari, M.; Turney, D.E.; Hernandez-Alvarado, F.; Kleinbart, S.; ArunKumar, K.E.; Joshi, J.B.; Banerjee, S.; Kawaji, M. Scale-up of a down flow bubble column: Experimental investigations. Chem. Eng. J. 2019, 386, 121447. [Google Scholar] [CrossRef]
- Panneerselvam, R.; Savithri, S.; Surender, G.D. CFD modeling of gas-liquid-solid mechanically agitated contactor. Chem. Eng. Res Des. 2008, 86, 1331–1344. [Google Scholar] [CrossRef]
- Lapin, A.; Schmid, J.; Reuss, M. Modeling the dynamics of E. coli populations in the three-dimensional turbulent field of a stirred-tank bioreactor-a structured–segregated approach. Chem. Eng. Sci. 2006, 61, 4783–4797. [Google Scholar] [CrossRef]
- Delvigne, F.; Takors, R.; Mudde, R.; van Gulik, W.; Noorman, H. bioprocess scale-up/down as integrative enabling technology: From fluid mechanics to systems biology and beyond. Microb. Biotechnol. 2017, 10, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Haringa, C.; Deshmukh, A.T.; Mudde, R.F.; Noorman, H.J. Euler-lagrange analysis towards representative down-scaling of a 22 m3 aerobic S. cerevisiae fermentation. Chem. Eng. Sci. 2017, 170, 653–669. [Google Scholar] [CrossRef]
- Zheng, M.Z. Simulation Research on Multiphase Stirred Reactor Based on Corrosion Reaction; Northeastern University: Shenyang, China, 2021; pp. 74–75. [Google Scholar]
- Zhang, C.Y. Study on Gas-Liquid-Solid Three-Phase Stirring Performance in Corrosion Reactor; Northeastern University: Shenyang, China, 2019; pp. 29–50. [Google Scholar]
- Qiao, S.C. Numerical Simulation of Fluid Flow and Suspension of Floating Solids in Stirred Tanks Using CFD Method; Tianjin University: Tianjin, China, 2014; pp. 67–81. [Google Scholar]
- Xu, B.; Yu, J.; Shu, D.H.; Yin, D.C. Numerical Simulation of Gas Liquid Solid Three-phase Flow in Airlift Loop Reactor. Chin. J. Process Eng. 2017, 17, 944951. (In Chinese) [Google Scholar]
- Xiao, W.Z.; Wang, J.J.; Gu, X.P.; Feng, L.F. Study on cold simulation experiment of p-xylene oxidation reactor. Petrochem. Technol. 2004, 33, 632–635. [Google Scholar]
- Story, A.; Jaworski, Z.; Major-Godlewska, M.; Story, G. Influence of rheological properties of stirred liquids on the axial and tangential forces in a vessel with a PMT impeller. Chem. Eng. Res Des. 2018, 138, 398–404. [Google Scholar] [CrossRef]
- Shamlow, A.P. Mechanism of suspension of coarse particles in liquids in stirred vessels. Inst. Chem. Eng. Symp. Ser. 1992, 121, 397–412. [Google Scholar]
- Srilatha, C.; Mundada, T.P.; Patwrdhan, A.W. Scale-up of pump-mix mixers using CFD. Chem. Eng. Res. Des. 2010, 88, 10–22. [Google Scholar] [CrossRef]
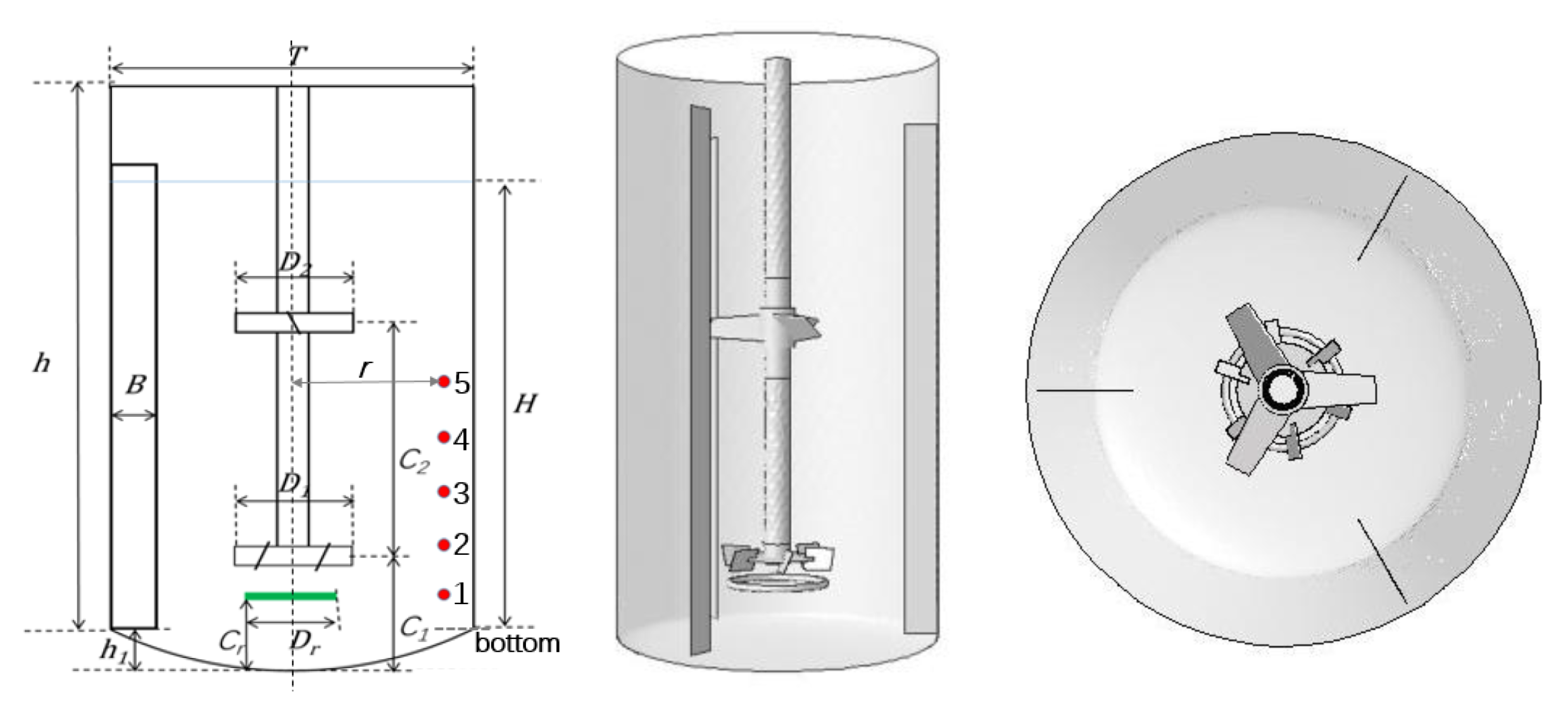
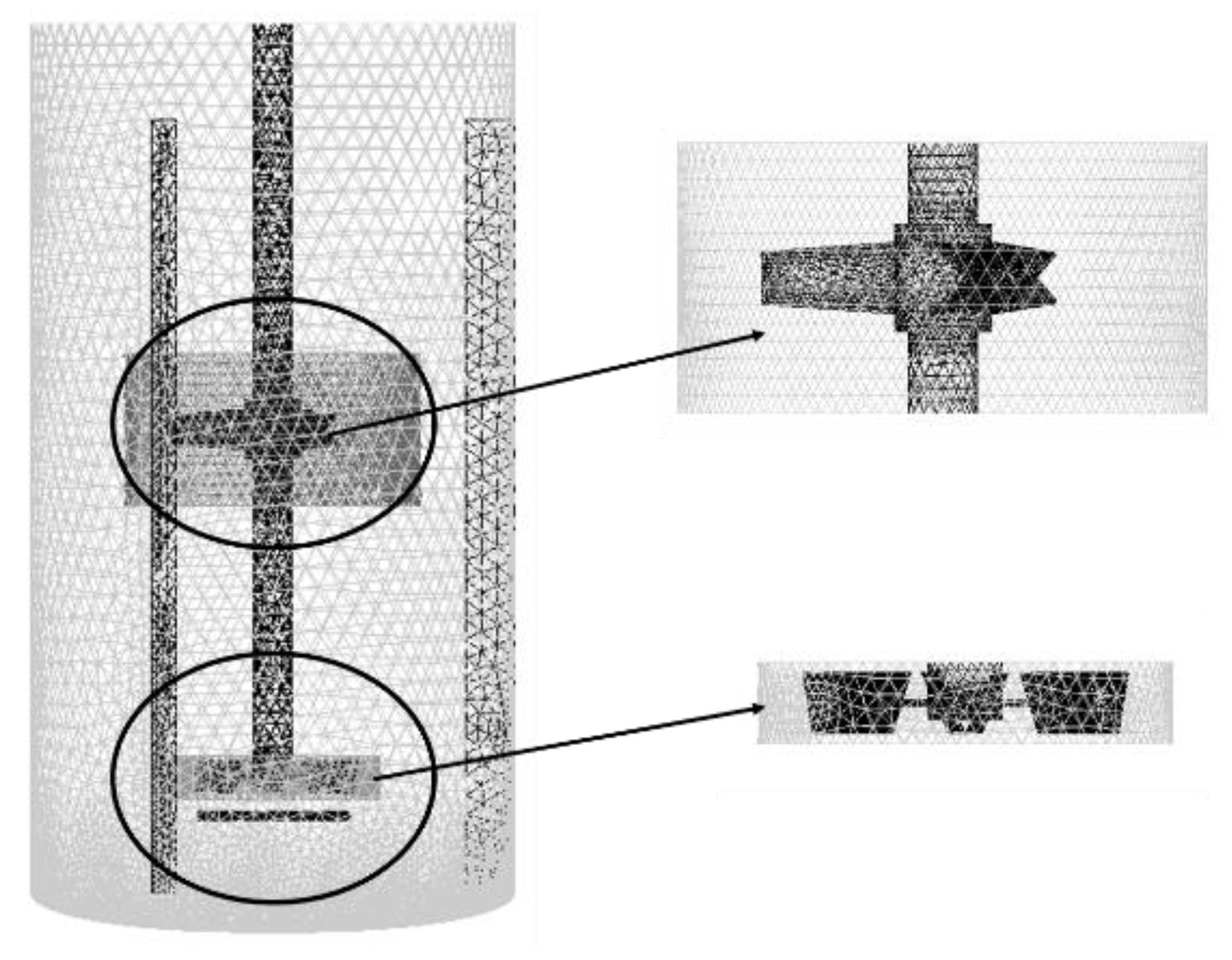

| Parameter | Value/mm |
|---|---|
| Reactor diameter, T | 2500 |
| Reactor body height, h | 4500 |
| Height of reactor bottom, h1 | 200 |
| Baffle width, B. | 250 |
| Three-blade propeller diameter, D2 | 900 |
| Disc oblique blade impeller, D1 | 1050 |
| Distance from bottom, C1 | 800 |
| Distance between impellers, C2 | 1600 |
| Distance from the bottom to the air inlet, Cr | 600 |
| Annular distributor diameter, Dr | 750 |
| Liquid level, H | 3800 |
| 1, 2, 3, 4, 5 | detection positions of solid phase volume fraction |
| Item | Upper Impeller | Lower Impeller |
|---|---|---|
| original | Three-blade propeller diameter (45°) | Three-blade propeller diameter (45°) |
| After improvement | Three-blade propeller diameter (45°) | Disc oblique blade impeller (135°) |
| Parameter | Value |
|---|---|
| Solid particle density/(kg/m3) | 4000 |
| Average diameter of solid articles/µm | 106 |
| Liquid density/(kg/m3) | 998.2 |
| Liquid Viscosity/Pa · s | 1.003 × 10−3 |
| Gas density/(kg/m3) | 1.225 |
| Gas Viscosity/Pa · s | 1.7894× 10−5 |
| Initial solid phase volume fraction/% | 20 |
| Ventilatory capacity/(m3/h) | 1479 |
| Parameter | Value, m | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Axial distance from bottom | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |||
| Radial off-axis distance | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 |
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| component | TiO2% | P% | FeO% | C% | S% | MFe% | TFe% |
| content | 64.38 | 0.067 | 6.15 | 0.069 | 0.014 | 24.41 | 29.24 |
| component | CaO % | MgO % | Al2O3 % | SiO2 % | Mn % | ||
| content | 0.15 | 0.23 | 1.55 | 1.84 | 1.89 | ||
| Parameter | Value | |||
|---|---|---|---|---|
| Corrosion system | TiO2 % | MFe % | TFe % | FeO % |
| 2%NH4Cl + 3%HCl | 74.47 | 1.67 | 16.03 | 14.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Li, Y.; Zheng, M.; Gang, S.; Zhang, T.-A. Flow and Reaction Characteristic in a Stirred Reactor for Corrosion Process of Reduced Ilmenite. Metals 2023, 13, 119. https://doi.org/10.3390/met13010119
Zhao Q, Li Y, Zheng M, Gang S, Zhang T-A. Flow and Reaction Characteristic in a Stirred Reactor for Corrosion Process of Reduced Ilmenite. Metals. 2023; 13(1):119. https://doi.org/10.3390/met13010119
Chicago/Turabian StyleZhao, Qiuyue, Yang Li, Mingzhao Zheng, Shuangfu Gang, and Ting-An Zhang. 2023. "Flow and Reaction Characteristic in a Stirred Reactor for Corrosion Process of Reduced Ilmenite" Metals 13, no. 1: 119. https://doi.org/10.3390/met13010119
APA StyleZhao, Q., Li, Y., Zheng, M., Gang, S., & Zhang, T.-A. (2023). Flow and Reaction Characteristic in a Stirred Reactor for Corrosion Process of Reduced Ilmenite. Metals, 13(1), 119. https://doi.org/10.3390/met13010119





