Evolution of Symmetrical Grain Boundaries under External Strain in Iron Investigated by Molecular Dynamics Method
Abstract
:1. Introduction
2. Method
3. Results and Discussion
3.1. Grain Boundary Energy and Structure after Different Relaxation Processes
3.2. Evolution and Related Failure Mechanisms of GBs under the External Strain Effect
3.2.1. Phase Transformation Induced Grain Boundary Failure
3.2.2. Mechanical Failure Induced by Activation of Slip System from GB Plane
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bonny, G.; Terentyev, D.; Elena, J.; Zinovev, A.; Minov, B.; Zhurkin, E.E. Assessment of Hardening Due to Dislocation Loops in Bcc Iron: Overview and Analysis of Atomistic Simulations for Edge Dislocations. J. Nucl. Mater. 2016, 473, 283–289. [Google Scholar] [CrossRef]
- Messina, L.; Nastar, M.; Sandberg, N.; Olsson, P. Systematic Electronic-Structure Investigation of Substitutional Impurity Diffusion and Flux Coupling in Bcc Iron. Phys. Rev. B 2016, 93, 184302. [Google Scholar] [CrossRef]
- Bauer, K.D.; Todorova, M.; Hingerl, K.; Neugebauer, J. A First Principles Investigation of Zinc Induced Embrittlement at Grain Boundaries in Bcc Iron. Acta Mater. 2015, 90, 69–76. [Google Scholar] [CrossRef]
- Terentyev, D.; He, X.; Serra, A.; Kuriplach, J. Structure and Strength of <1 1 0> Tilt Grain Boundaries in Bcc Fe: An Atomistic Study. Comput. Mater. Sci. 2010, 49, 419–429. [Google Scholar] [CrossRef]
- Ratanaphan, S.; Olmsted, D.L.; Bulatov, V.V.; Holm, E.A.; Rollett, A.D.; Rohrer, G.S. Grain Boundary Energies in Body-Centered Cubic Metals. Acta Mater. 2015, 88, 346–354. [Google Scholar] [CrossRef]
- Singh, D.; Parashar, A. Effect of Symmetric and Asymmetric Tilt Grain Boundaries on the Tensile Behaviour of Bcc-Niobium. Comput. Mater. Sci. 2018, 143, 126–132. [Google Scholar] [CrossRef]
- Samaras, M.; Derlet, P.M.; Van Swygenhoven, H.; Victoria, M. Radiation Damage near Grain Boundaries. Philos. Mag. 2003, 83, 3599–3607. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.M. Grain-Boundary Sliding in Nanocrystalline Fcc Metals. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 64, 224105. [Google Scholar] [CrossRef]
- Hasnaoui, A.; Van Swygenhoven, H.; Derlet, P.M. Cooperative Processes during Plastic Deformation in Nanocrystalline Fcc Metals: A Molecular Dynamics Simulation. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 66, 184112. [Google Scholar] [CrossRef]
- Chen, J.; Hahn, E.N.; Dongare, A.M.; Fensin, S.J. Understanding and Predicting Damage and Failure at Grain Boundaries in BCC Ta. J. Appl. Phys. 2019, 126, 165902. [Google Scholar] [CrossRef]
- Gui-Jin, W.; Vitek, V. Relationships between Grain Boundary Structure and Energy. Acta Metall. 1986, 34, 951–960. [Google Scholar] [CrossRef]
- Van Beers, P.R.M.; Kouznetsova, V.G.; Geers, M.G.D.; Tschopp, M.A.; McDowell, D.L. A Multiscale Model of Grain Boundary Structure and Energy: From Atomistics to a Continuum Description. Acta Mater. 2015, 82, 513–529. [Google Scholar] [CrossRef]
- Gao, N.; Fu, C.C.; Samaras, M.; Schäublin, R.; Victoria, M.; Hoffelner, W. Multiscale Modelling of Bi-Crystal Grain Boundaries in Bcc Iron. J. Nucl. Mater. 2009, 385, 262–267. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-Principles Study on the Interaction of H Interstitials with Grain Boundaries in α- and γ-Fe. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 144121. [Google Scholar] [CrossRef]
- Spearot, D.E.; Jacob, K.I.; McDowell, D.L. Nucleation of Dislocations from [0 0 1] Bicrystal Interfaces in Aluminum. Acta Mater. 2005, 53, 3579–3589. [Google Scholar] [CrossRef]
- Spearot, D.E.; Tschopp, M.A.; Jacob, K.I.; McDowell, D.L. Tensile Strength of <1 0 0> and <1 1 0> Tilt Bicrystal Copper Interfaces. Acta Mater. 2007, 55, 705–714. [Google Scholar] [CrossRef]
- Cui, C.; Yu, Q.; Wang, W.; Xu, W.; Chen, L. Molecular Dynamics Study on Tensile Strength of Twist Grain Boundary Structures under Uniaxial Tension in Copper. Vacuum 2021, 184, 109874. [Google Scholar] [CrossRef]
- Kotzurek, J.A.; Hofmann, M.; Simic, S.; Pölt, P.; Hohenwarter, A.; Pippan, R.; Sprengel, W.; Würschum, R. Internal Stress and Defect-Related Free Volume in Submicrocrystalline Ni Studied by Neutron Diffraction and Difference Dilatometry. Philos. Mag. Lett. 2017, 97, 450–458. [Google Scholar] [CrossRef]
- Farkas, D.; Van Petegem, S.; Derlet, P.M.; Van Swygenhoven, H. Dislocation Activity and Nano-Void Formation near Crack Tips in Nanocrystalline Ni. Acta Mater. 2005, 53, 3115–3123. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Tucker, G.J.; McDowell, D.L. Structure and Free Volume of <1 1 0> Symmetric Tilt Grain Boundaries with the E Structural Unit. Acta Mater. 2007, 55, 3959–3969. [Google Scholar] [CrossRef]
- Sun, H.; Singh, C.V. Temperature Dependence of Grain Boundary Excess Free Volume. Scr. Mater. 2020, 178, 71–76. [Google Scholar] [CrossRef]
- Tucker, G.J.; Tschopp, M.A.; McDowell, D.L. Evolution of Structure and Free Volume in Symmetric Tilt Grain Boundaries during Dislocation Nucleation. Acta Mater. 2010, 58, 6464–6473. [Google Scholar] [CrossRef]
- Wang, X.Y.; Gao, N.; Setyawan, W.; Xu, B.; Liu, W.; Wang, Z.G. Effect of Irradiation on Mechanical Properties of Symmetrical Grain Boundaries Investigated by Atomic Simulations. J. Nucl. Mater. 2017, 491, 154–161. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Santoro, A.; Mighell, A.D. Coincidence-site Lattices. Acta Crystallogr. Sect. A 1973, 29, 169–175. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of New Interatomic Potentials Appropriate for Crystalline and Liquid Iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Chaussidon, J.; Fivel, M.; Rodney, D. The Glide of Screw Dislocations in Bcc Fe: Atomistic Static and Dynamic Simulations. Acta Mater. 2006, 54, 3407–3416. [Google Scholar] [CrossRef]
- Gao, N.; Ghoniem, A.; Gao, X.; Luo, P.; Wei, K.F.; Wang, Z.G. Molecular Dynamics Simulation of Cu Atoms Interaction with Symmetrical Grain Boundaries of BCC Fe. J. Nucl. Mater. 2014, 444, 200–205. [Google Scholar] [CrossRef]
- Wang, X.Y.; Gao, N.; Xu, B.; Wang, Y.N.; Shu, G.G.; Li, C.L.; Liu, W. Effect of Irradiation and Irradiation Defects on the Mobility of Σ5 Symmetric Tilt Grain Boundaries in Iron: An Atomistic Study. J. Nucl. Mater. 2018, 510, 568–574. [Google Scholar] [CrossRef]
- Gao, N.; Setyawan, W.; Kurtz, R.J.; Wang, Z. Effects of Applied Strain on Nanoscale Self-Interstitial Cluster Formation in BCC Iron. J. Nucl. Mater. 2017, 493, 62–68. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic Analysis of Local Atomic Structure Combined with 3D Computer Graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Gao, N.; Perez, D.; Lu, G.H.; Wang, Z.G. Molecular Dynamics Study of the Interaction between Nanoscale Interstitial Dislocation Loops and Grain Boundaries in BCC Iron. J. Nucl. Mater. 2018, 498, 378–386. [Google Scholar] [CrossRef]
- Hossain, D.; Tschopp, M.A.; Ward, D.K.; Bouvard, J.L.; Wang, P.; Horstemeyer, M.F. Molecular Dynamics Simulations of Deformation Mechanisms of Amorphous Polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Wang, J.; Janisch, R.; Madsen, G.K.H.; Drautz, R. First-Principles Study of Carbon Segregation in Bcc Iron Symmetrical Tilt Grain Boundaries. Acta Mater. 2016, 115, 259–268. [Google Scholar] [CrossRef]
- Bhattacharya, S.K.; Tanaka, S.; Shiihara, Y.; Kohyama, M. Ab Initio Study of Symmetrical Tilt Grain Boundaries in Bcc Fe: Structural Units, Magnetic Moments, Interfacial Bonding, Local Energy and Local Stress. J. Phys. Condens. Matter 2013, 25, 135004. [Google Scholar] [CrossRef]
- Wang, J.; Madsen, G.K.H.; Drautz, R. Grain Boundaries in Bcc-Fe: A Density-Functional Theory and Tight-Binding Study Grain Boundaries in Bcc-Fe: A Density- Functional Theory and Tight-Binding Study. Model. Simul. Mater. Sci. Eng. 2018, 26, 025008. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Bringa, E.M.; Kang, K.; Ackland, G.J.; Ruestes, C.J.; Urbassek, H.M. Polycrystalline Iron under Compression: Plasticity and Phase Transitions. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 86, 144111. [Google Scholar] [CrossRef]
- Pan, F.; Zhang, Z.S. Magnetic Property of the Face Center Cubic Iron with Different Lattice Parameter in Fe/Pd Multilayers. Phys. B Condens. Matter 2001, 293, 237–243. [Google Scholar] [CrossRef]
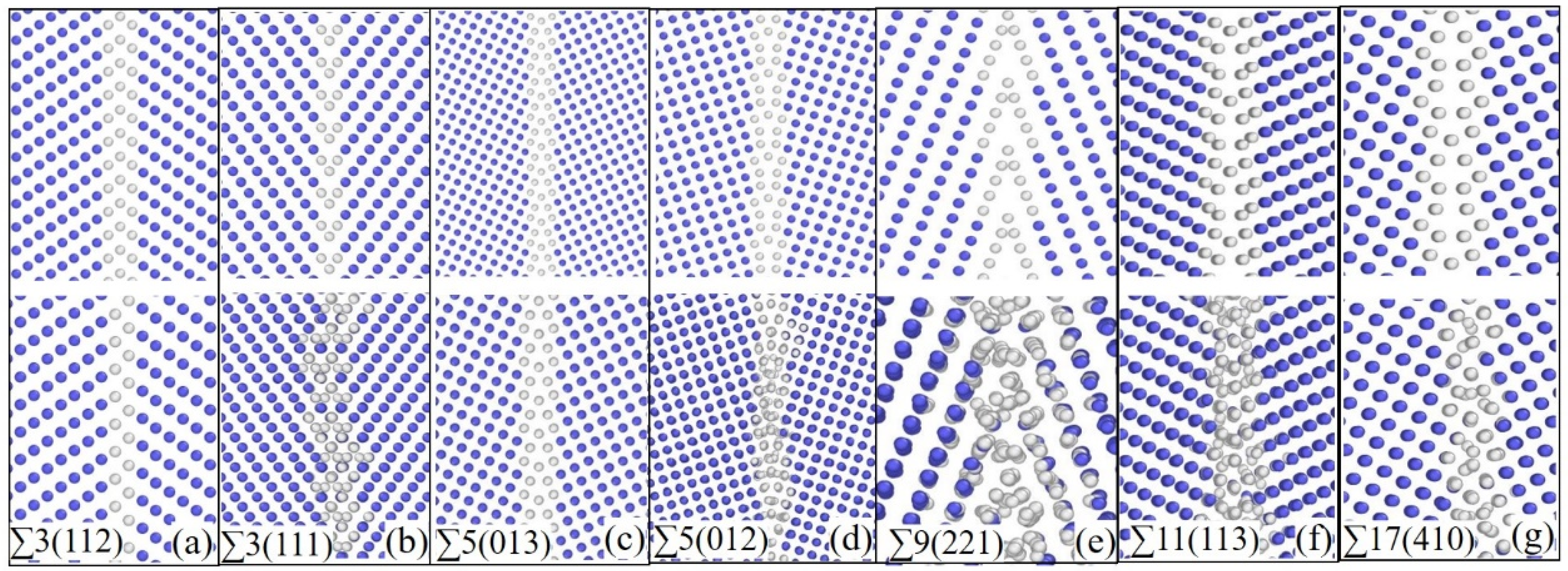
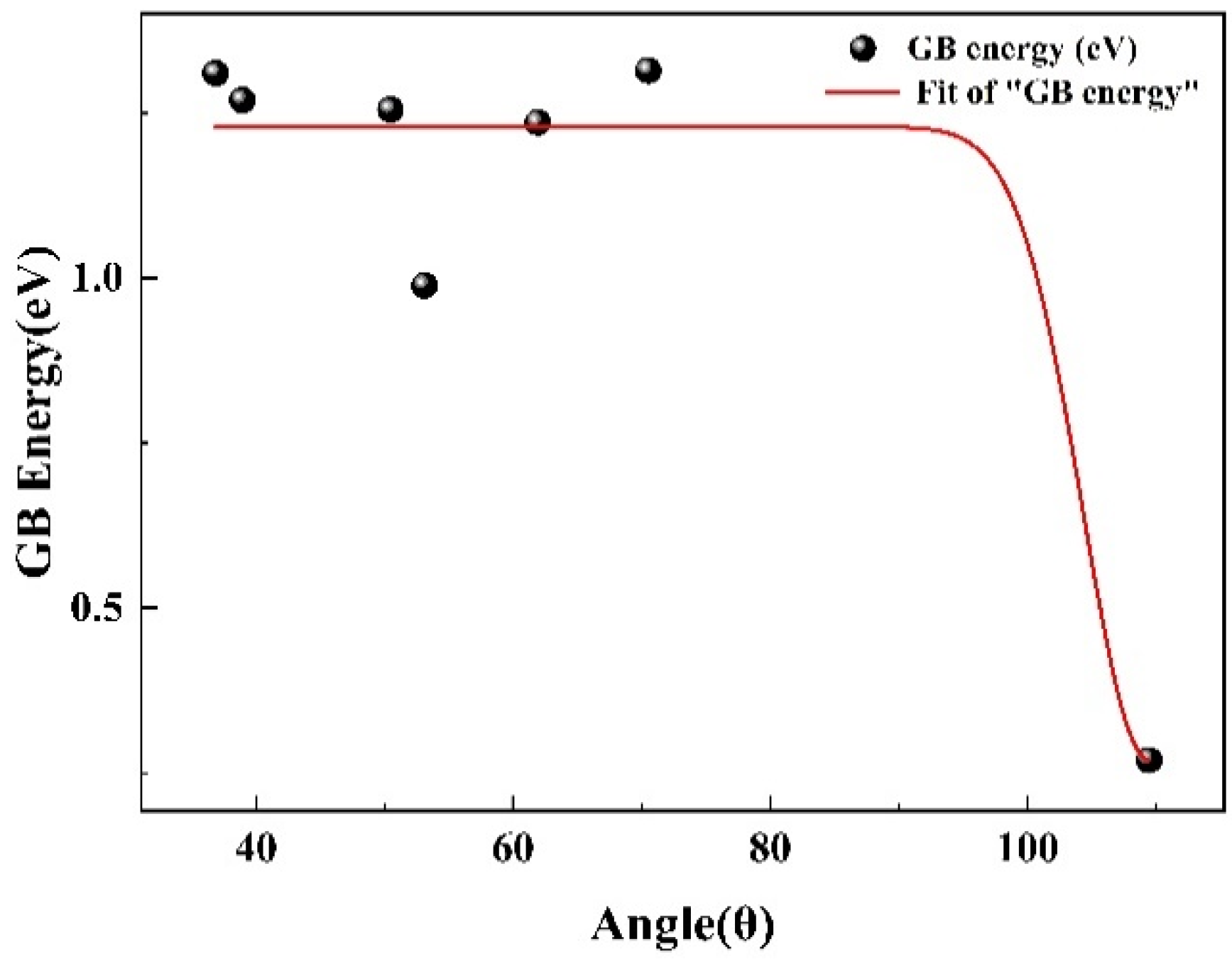
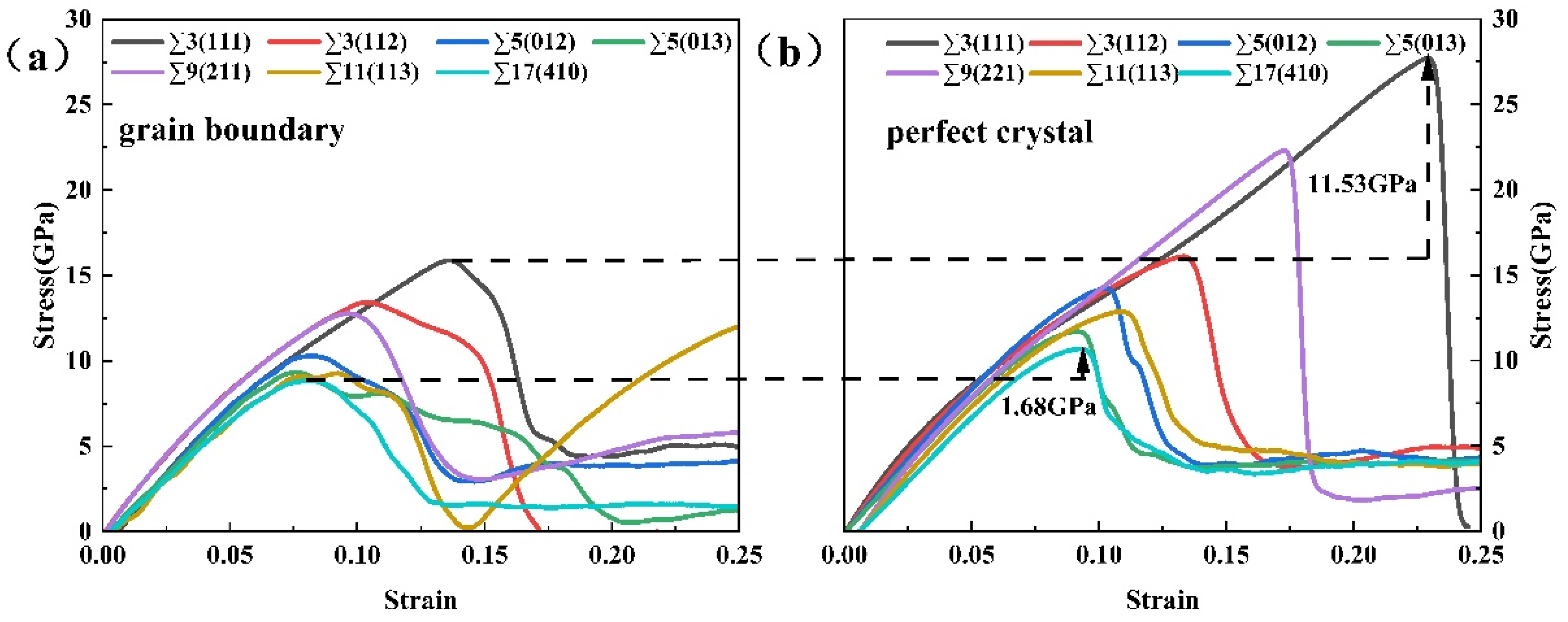



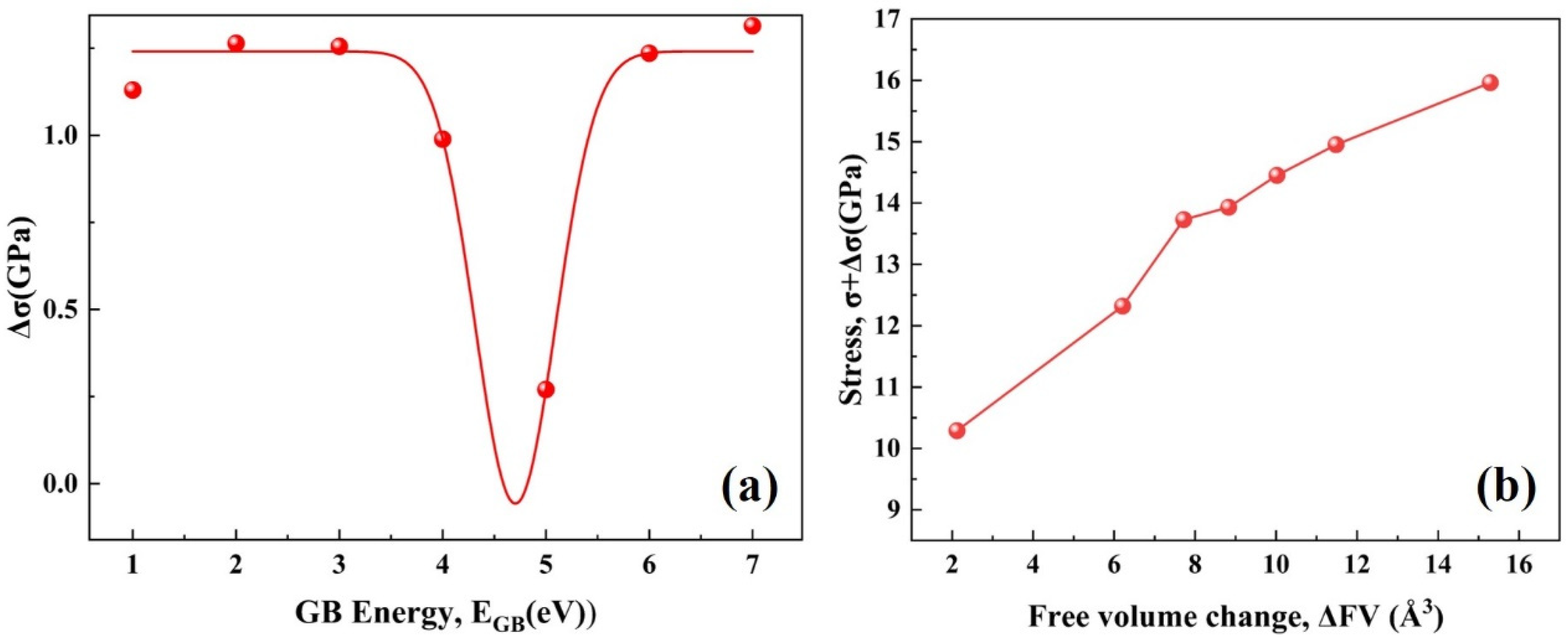
| NO. | GB Plane (hkl) | Sigma (∑) | Simulation Box Length(Å) | Number of Unit Cells along x, y, z and Normal Direction of GB Plane | Number of Atoms |
|---|---|---|---|---|---|
| 1. | (112) | ∑3 | 121.15 × 74.2 × 209.8 | 30 × 30 × 15, Z | 162,000 |
| 2. | (111) | ∑3 | 121.2 × 148.4 × 209.8 | 30 × 30 × 30, Y | 324,000 |
| 3. | (310) | ∑5 | 85.8 × 271.8 × 271.8 | 30 × 30 × 15, Z | 270,000 |
| 4. | (210) | ∑5 | 85.8 × 191.5 × 191.5 | 30 × 30 × 15, Z | 540,000 |
| 5. | (221) | ∑9 | 121.2 × 363.4 × 256.9 | 30 × 30 × 15, Z | 972,000 |
| 6. | (113) | ∑11 | 133.9 × 80.8 × 189.4 | 10×20×20, Z | 176,000 |
| 7. | (410) | ∑17 | 235.4 × 57.2 × 235.4 | 20 × 20 × 10, Z | 272,000 |
| Sigma (∑) | EGBs J/m2 (CG-MD-CG) | EGBs J/m2 (CG) | DFT |
|---|---|---|---|
| ∑3(112) | 0.2703 | 0.3233 | 0.46 [35] |
| ∑3(111) | 1.3144 | 1.3438 | 1.61 [36] |
| ∑5(012) | 1.1301 | 1.6741 | 1.64 [35] |
| ∑5(013) | 0.9889 | 1.0649 | 1.6 [35] |
| ∑9(221) | 1.2639 | 2.3318 | 1.66 [37] |
| ∑11(113) | 1.2551 | 2.4361 | 1.45 [37] |
| ∑17(441) | 1.2356 | 2.5315 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Dong, Y.; Yu, M.; Wang, Z.; Liu, Y.; Gao, N.; Dong, L.; Wang, X. Evolution of Symmetrical Grain Boundaries under External Strain in Iron Investigated by Molecular Dynamics Method. Metals 2022, 12, 1448. https://doi.org/10.3390/met12091448
Ma W, Dong Y, Yu M, Wang Z, Liu Y, Gao N, Dong L, Wang X. Evolution of Symmetrical Grain Boundaries under External Strain in Iron Investigated by Molecular Dynamics Method. Metals. 2022; 12(9):1448. https://doi.org/10.3390/met12091448
Chicago/Turabian StyleMa, Wenxue, Yibin Dong, Miaosen Yu, Ziqiang Wang, Yong Liu, Ning Gao, Limin Dong, and Xuelin Wang. 2022. "Evolution of Symmetrical Grain Boundaries under External Strain in Iron Investigated by Molecular Dynamics Method" Metals 12, no. 9: 1448. https://doi.org/10.3390/met12091448
APA StyleMa, W., Dong, Y., Yu, M., Wang, Z., Liu, Y., Gao, N., Dong, L., & Wang, X. (2022). Evolution of Symmetrical Grain Boundaries under External Strain in Iron Investigated by Molecular Dynamics Method. Metals, 12(9), 1448. https://doi.org/10.3390/met12091448








