A Physically Based Model Predicting the Degradation of Hydrogen on Crack Growth Critical Stress Intensity Factor of Metals
Abstract
:1. Introduction
2. Methodology
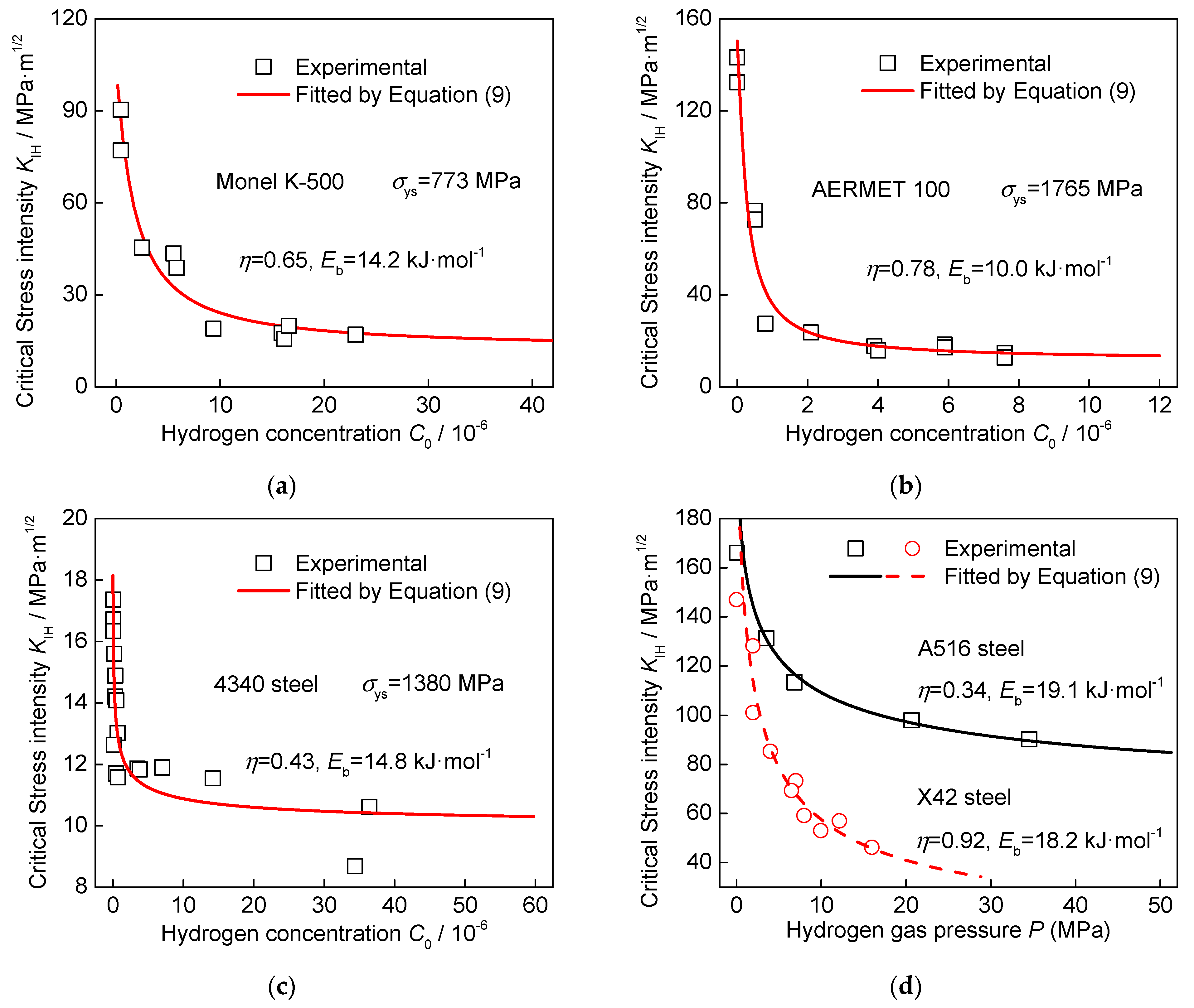
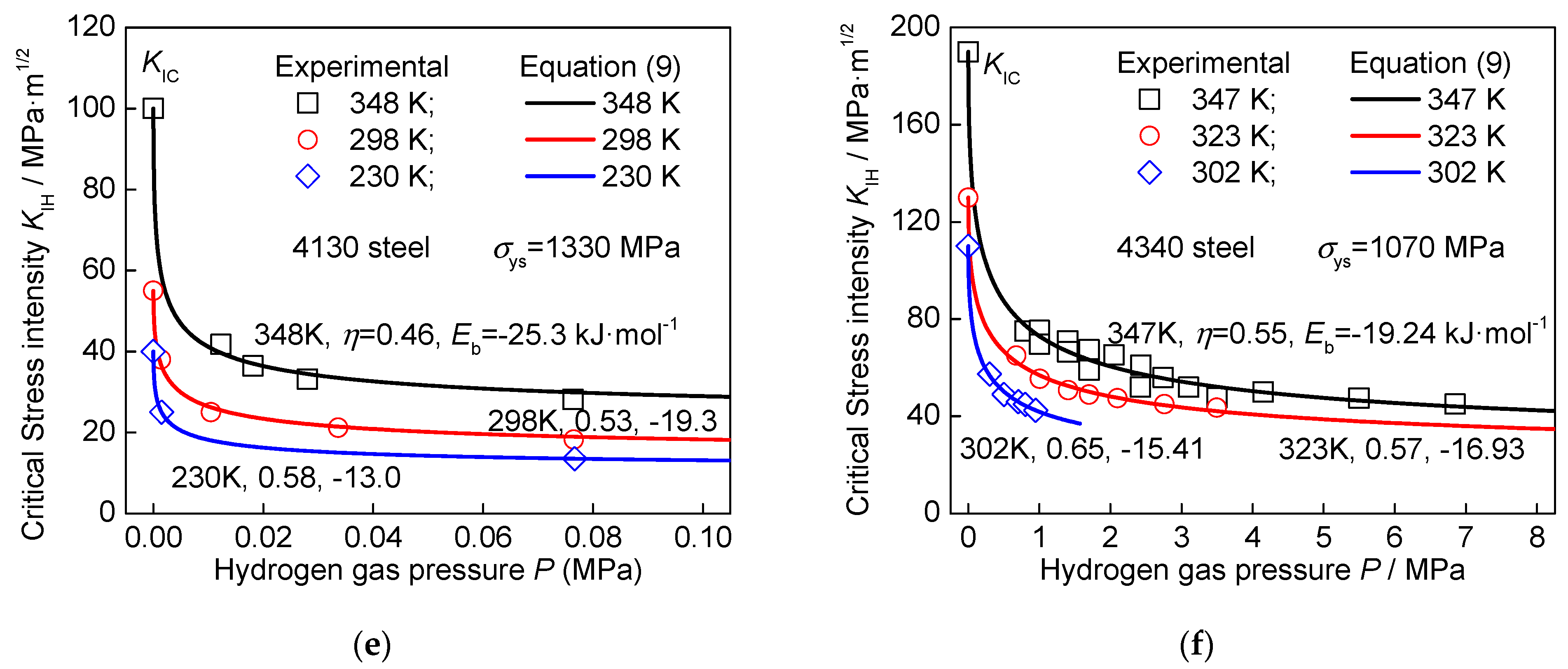
3. Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gerberich, W.W.; Marsh, P.G.; Hoehn, J.W. Hydrogen induced cracking mechanism—Are there critical experiments? In Proceedings of the Fifth International Conference on the Effect of Hydrogen on the Behavior of Materials, Moran, WY, USA, 7 September 1975; The Minerals, Metals, and Materials Society: Warrendale, PA, USA, 1996; p. 539. [Google Scholar]
- Gerberich, W.W. Modeling hydrogen induced damage mechanisms in metals. In Gaseous Hydrogen Embrittlement of Materials in Energy Technologies; Gangloff, R.P., Somerday, B.P., Eds.; Woodhead Publishing Limited: Cambridge, UK, 2012; Volume 2, p. 209. [Google Scholar]
- Gerberich, W.W.; Stauffer, D.D.; Sofronis, P. A coexistent view of hydrogen effects on mechanical behavior of crystals: HELP and HEDE. In Proceedings of the 2008 International Hydrogen Conference—Effects of Hydrogen on Materials, Jackson, WY, USA, 7–10 September 2008; ASM International: Novelty, OH, USA, 2009; p. 38. [Google Scholar]
- Gangloff, R.P. Science-based prognosis to manage structural alloy performance in hydrogen. In Proceedings of the 2008 International Hydrogen Conference—Effects of Hydrogen on Materials, Jackson, WY, USA, 7–10 September 2008; ASM International: Novelty, OH, USA, 2009; p. 1. [Google Scholar]
- Gerberich, W.W.; Chen, Y.T.; John, C.S. A short-time diffusion correlation for hydrogen-induced crack growth kinetics. Metall. Trans. A 1975, 6, 1485–1498. [Google Scholar] [CrossRef]
- Oriani, R.A. A mechanistic theory of hydrogen embrittlement of steels. Ber. Bunsenges. Für. Phys. Chem. 1972, 76, 848–857. [Google Scholar]
- Oriani, R.; Josephic, P. Equilibrium and kinetic studies of the hydrogen-assisted cracking of steel. Acta Metall. 1977, 25, 979–988. [Google Scholar] [CrossRef]
- Akhurst, K.N.; Baker, T.J. The threshold stress intensity for hydrogen-induced crack growth. Metall. Mater. Trans. A 1981, 12, 1059–1070. [Google Scholar] [CrossRef]
- Lee, S.L.; Unger, D.J. A decohesion model of hydrogen assisted cracking. Eng. Fract. Mech. 1988, 31, 647–660. [Google Scholar] [CrossRef]
- Unger, D.J. A mathematical analysis for impending hydrogen assisted crack propagation. Eng. Fract. Mech. 1989, 34, 657–667. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W.A. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 2013, 12, 145–151. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, J.; Jiang, W. A quantitative description on fracture toughness of steels in hydrogen gas. Int. J. Hydrogen Energy 2013, 38, 12503–12508. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, Y.; Yang, C.; Hu, H. Fracture strain model for hydrogen embrittlement based on hydrogen enhanced localized plasticity mechanism. Int. J. Hydrogen Energy 2020, 46, 25541–25554. [Google Scholar] [CrossRef]
- Sofronis, P.; Liang, Y.; Aravas, N. Hydrogen induced shear localization of the plastic flow in metals and alloys. Eur. J. Mech. Solids 2001, 20, 857–872. [Google Scholar] [CrossRef]
- Djukic, M.B.; Bakic, G.M.; Zeravcic, V.S.; Sedmak, A.; Rajicic, B. The synergistic action and interplay of hydrogen embrittlement mechanisms in steels and iron: Localized plasticity and decohesion. Eng. Fract. Mech. 2019, 216, 106528. [Google Scholar] [CrossRef]
- Traidia, A.; Chatzidouros, E.; Jouiad, M. Review of hydrogen-assisted cracking models for application to service lifetime prediction and challenges in the oil and gas industry. Corros. Rev. 2018, 36, 323–347. [Google Scholar] [CrossRef]
- Geng, W.T.; Wang, V.; Li, J.-X.; Ishikawa, N.; Kimizuka, H.; Tsuzaki, K.; Ogata, S. Hydrogen trapping in carbon supersaturated α-iron and its decohesion effect in martensitic steel. Scr. Mater. 2018, 149, 79–83. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Niordson, C.F.; Gangloff, R.P. Strain gradient plasticity-based modeling of hydrogen environment assisted cracking. Acta Mater. 2016, 117, 321–332. [Google Scholar] [CrossRef]
- Thomas, R.L.S.; Scully, J.R.; Gangloff, R.P. Internal hydrogen embrittlement of ultrahigh-strength AERMET 100 steel. Metall. Mater. Trans. A 2003, 34, 327–344. [Google Scholar] [CrossRef]
- Lee, Y.; Gangloff, R.P. Measurement and Modeling of Hydrogen Environment–Assisted Cracking of Ultra-High-Strength Steel. Metall. Mater. Trans. A 2007, 38, 2174–2190. [Google Scholar] [CrossRef]
- Gangloff, R.P.; Ha, H.M.; Burns, J.T.; Scully, J.R. Measurement and Modeling of Hydrogen Environment-Assisted Cracking in Monel K-500. Metall. Mater. Trans. A 2014, 45, 3814–3834. [Google Scholar] [CrossRef]
- Burns, J.T.; Harris, Z.; Dolph, J.D.; Gangloff, R.P. Measurement and Modeling of Hydrogen Environment-Assisted Cracking in a Ni-Cu-Al-Ti Superalloy. Metall. Mater. Trans. A 2016, 47, 990–997. [Google Scholar] [CrossRef]
- Zhang, T.; Chu, W.; Gao, K.; Qiao, L. Study of correlation between hydrogen-induced stress and hydrogen embrittlement. Mater. Sci. Eng. A 2003, 347, 291–299. [Google Scholar] [CrossRef]
- Wang, R. Effects of hydrogen on the fracture toughness of a X70 pipeline steel. Corros. Sci. 2009, 51, 2803–2810. [Google Scholar] [CrossRef]
- Hirth, J.P.; Rice, J.R. On the thermodynamics of adsorption at interfaces as it influences decohesion. Metall. Trans. A 1980, 11, 1501–1511. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.-S. The thermodynamics aspects of hydrogen induced embrittlement. Eng. Fract. Mech. 2001, 68, 647–669. [Google Scholar] [CrossRef]
- Liang, Y.; Sofronis, P. Toward a phenomenological description of hydrogen-induced decohesion at particle/matrix interfaces. J. Mech. Phys. Solids 2003, 51, 1509–1531. [Google Scholar] [CrossRef]
- Novak, P.; Yuan, R.; Somerday, B.; Sofronis, P.; Ritchie, R. A statistical, physical-based, micro-mechanical model of hydrogen-induced intergranular fracture in steel. J. Mech. Phys. Solids 2010, 58, 206–226. [Google Scholar] [CrossRef]
- Jung, S.-P.; Kwon, Y.; Lee, C.S.; Lee, B.-J. Influence of hydrogen on the grain boundary crack propagation in bcc iron: A molecular dynamics simulation. Comp. Mater. Sci. 2018, 149, 424–434. [Google Scholar] [CrossRef]
- Nagao, A.; Dadfarnia, M.; Somerday, B.P.; Sofronis, P.; Ritchie, R.O. Hydrogen-enhanced-plasticity mediated decohesion for hydrogen-induced intergranular and “quasi-cleavage” fracture of lath martensitic steels. J. Mech. Phys. Solids 2018, 112, 403–430. [Google Scholar] [CrossRef]
- Huang, H.; Gerberich, W. Quasi-equilibrium modeling of the toughness transition during semibrittle cleavage. Acta Metall. Mater. 1994, 42, 639–647. [Google Scholar] [CrossRef]
- Marsh, P.; Gerberich, W. A microscopically-shielded Griffith criterion for cleavage in grain oriented silicon steel. Acta Metall. Mater. 1994, 42, 613–619. [Google Scholar] [CrossRef]
- Zielinski, W.; Lii, M.J.; Gerberich, W.W. Crack-tip dislocation emission arrangements for equilibrium—I. In situ TEM observations of Fe–2wt%Si. Acta Metall. Mater. 1992, 40, 2861–2871. [Google Scholar] [CrossRef]
- Jiang, D.; Carter, E.A. First principles assessment of ideal fracture energies of materials with mobile impurities: Implications for hydrogen embrittlement of metals. Acta Mater. 2004, 52, 4801–4807. [Google Scholar] [CrossRef]
- Jensen, I.J.T.; Olden, V.; Løvvik, O.M. Decohesion energy of ∑5(012) grain boundaries in Ni as function of hydrogen content. Metall. Mater. Trans. A 2019, 50, 451–456. [Google Scholar] [CrossRef]
- Hondros, E.D.; Seah, M.P. The theory of grain boundary segregation in terms of surface adsorption analogues. Metall. Trans. A 1977, 8, 1363–1371. [Google Scholar] [CrossRef]
- Serebrinsky, S.; Carter, E.A.; Ortiz, M. A quantum-mechanically informed continuum model of hydrogen embrittlement. J. Mech. Phys. Solids 2004, 52, 2403–2430. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W. A nanoscale mechanism of hydrogen embrittlement in metals. Acta Mater. 2011, 59, 1557–1569. [Google Scholar] [CrossRef]
- Kameda, J. A microscopic model of hydrogen-induced intergranular cracking—I. Equilibrium crack growth. Acta Metall. 1986, 34, 867–882. [Google Scholar] [CrossRef]
- Gerberich, W.W.; Oriani, R.A.; Lji, M.-J.; Chen, X.; Foecke, T. The necessity of both plasticity and brittleness in the fracture thresholds of iron. Philos. Mag. A 1991, 63, 363–376. [Google Scholar] [CrossRef]
- Olden, V.; Thaulow, C.; Johnsen, R.; Østby, E.; Berstad, T. Application of hydrogen influenced cohesive laws in the prediction of hydrogen induced stress cracking in 25%Cr duplex stainless steel. Eng. Fract. Mech. 2008, 75, 2333–2351. [Google Scholar] [CrossRef]
- Cheng, A.; Chen, N.-Z. Fatigue crack growth modelling for pipeline carbon steels under gaseous hydrogen conditions. Int. J. Fatigue 2017, 96, 152–161. [Google Scholar] [CrossRef]
- Symons, D.M. The effect of carbide precipitation on the hydrogen-enhanced fracture behavior of alloy 690. Metall. Mater. Trans. A 1998, 29, 1265–1277. [Google Scholar] [CrossRef]
- Hicks, P.D.; Altstetter, C.J. Hydrogen-enhanced cracking of superalloys. Met. Mater. Trans. A 1992, 23, 237–249. [Google Scholar] [CrossRef]
- Walter, R.J.; Chandler, W.T. Influence of Gaseous Hydrogen on Metals; A Report (NASA-CR-124410) of Marshall Space Flight Center of NASA; NASA: Huntsville, AL, USA, 1973. [Google Scholar]
- Robinson, S.L.; Stoltz, R.E. Toughness losses and fracture behavior of low strength carbon-manganese steels in hydrogen. In Proceedings of the Third International Conference on Effect of Hydrogen on Behavior of Materials; The Metallurgical Society of AIME: Warrendale, PA, USA, 1981; p. 987. [Google Scholar]
- Gutierrez-Solana, F.; Elices, M. High-pressure hydrogen behavior of a pipeline steel. In Proceedings of the First International Conference on Current Solutions to Hydrogen Problems in Steels; ASM International: Novelty, OH, USA, 1982; p. 181. [Google Scholar]
- Nelson, H.G.; Williams, D.P. Quantitative Observations of Hydrogen-Induced, Slow Crack Growth in a Low Alloy Steel; A Report of Ames Research Center of NASA; NASA: Santa Clara, CA, USA, 1977. [Google Scholar]
- Story, G.C. Hydrogen Assisted Cracking of a Low Alloy Steel–Pressure, Temperature and Yield Strength Effects on the Threshold Fracture Toughness. Ph.D. Thesis, University of California-Davis, Davis, CA, USA, 1980. [Google Scholar]
- Kirchheim, R.; Somerday, B.; Sofronis, P. Chemomechanical effects on the separation of interfaces occurring during fracture with emphasis on the hydrogen-iron and hydrogen-nickel system. Acta Mater. 2015, 99, 87–98. [Google Scholar] [CrossRef]
- Ai, J.-H.; Ha, H.M.; Gangloff, R.P.; Scully, J.R. Hydrogen diffusion and trapping in a precipitation-hardened nickel–copper–aluminum alloy Monel K-500 (UNS N05500). Acta Mater. 2013, 61, 3186–3199. [Google Scholar] [CrossRef]
- Li, D.; Gangloff, R.P.; Scully, J.R. Hydrogen trap states in ultrahigh-strength AERMET 100 steel. Metall. Mater. Trans. A 2004, 35, 849–864. [Google Scholar] [CrossRef]
- Barthélémy, H. Effects of pressure and purity on the hydrogen embrittlement of steels. Int. J. Hydrogen Energy 2011, 36, 2750–2758. [Google Scholar] [CrossRef]
- Jokl, M.; Vitek, V.; McMahon, C. A microscopic theory of brittle fracture in deformable solids: A relation between ideal work to fracture and plastic work. Acta Metall. 1980, 28, 1479–1488. [Google Scholar] [CrossRef]



| Parameter | Alloy 690 | Martensitic Steel |
|---|---|---|
| /J·m−2 | 2.28 | 1.95 |
| /J·m−2 | 0.866 | 0.78 |
| /J·m−2 | 3.694 | 3.12 |
| /kJ·mol−1 | −26 | −47.4 |
| /J·mol−1·K−1 | 25 | 25 |
| /kJ·mol−1 | −33.45 | −54.85 |
| /kJ·mol−1 | −96.37 | −95.5 |
| /J·mol−1·K−1 | 15 | 15 |
| /kJ·mol−1 | −100.84 | −99.97 |
| /mol·m−2 | 2.59 × 10−5 | 8.08 × 10−5 |
| /kJ·mol−1 | 12 | / |
| 0.47 | 1.36 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 2 × 10−4 | 0.26 | ||
| /GPa | 200 | 0.3 | |
| 2 × 10−6 | 2.7 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Chen, J.; Wang, Y.; Liu, W.; Wu, W.; Li, X.; Yang, X. A Physically Based Model Predicting the Degradation of Hydrogen on Crack Growth Critical Stress Intensity Factor of Metals. Metals 2022, 12, 1441. https://doi.org/10.3390/met12091441
Huang Y, Chen J, Wang Y, Liu W, Wu W, Li X, Yang X. A Physically Based Model Predicting the Degradation of Hydrogen on Crack Growth Critical Stress Intensity Factor of Metals. Metals. 2022; 12(9):1441. https://doi.org/10.3390/met12091441
Chicago/Turabian StyleHuang, Yuting, Jihan Chen, Yanfei Wang, Wei Liu, Weijie Wu, Xinfeng Li, and Xinyu Yang. 2022. "A Physically Based Model Predicting the Degradation of Hydrogen on Crack Growth Critical Stress Intensity Factor of Metals" Metals 12, no. 9: 1441. https://doi.org/10.3390/met12091441
APA StyleHuang, Y., Chen, J., Wang, Y., Liu, W., Wu, W., Li, X., & Yang, X. (2022). A Physically Based Model Predicting the Degradation of Hydrogen on Crack Growth Critical Stress Intensity Factor of Metals. Metals, 12(9), 1441. https://doi.org/10.3390/met12091441





