Constitutive Modeling on the Ti-6Al-4V Alloy during Air Cooling and Application
Abstract
:1. Introduction
2. Materials and Methods
3. Flow Behavior of Ti-6Al-4V Alloy during Air Cooling
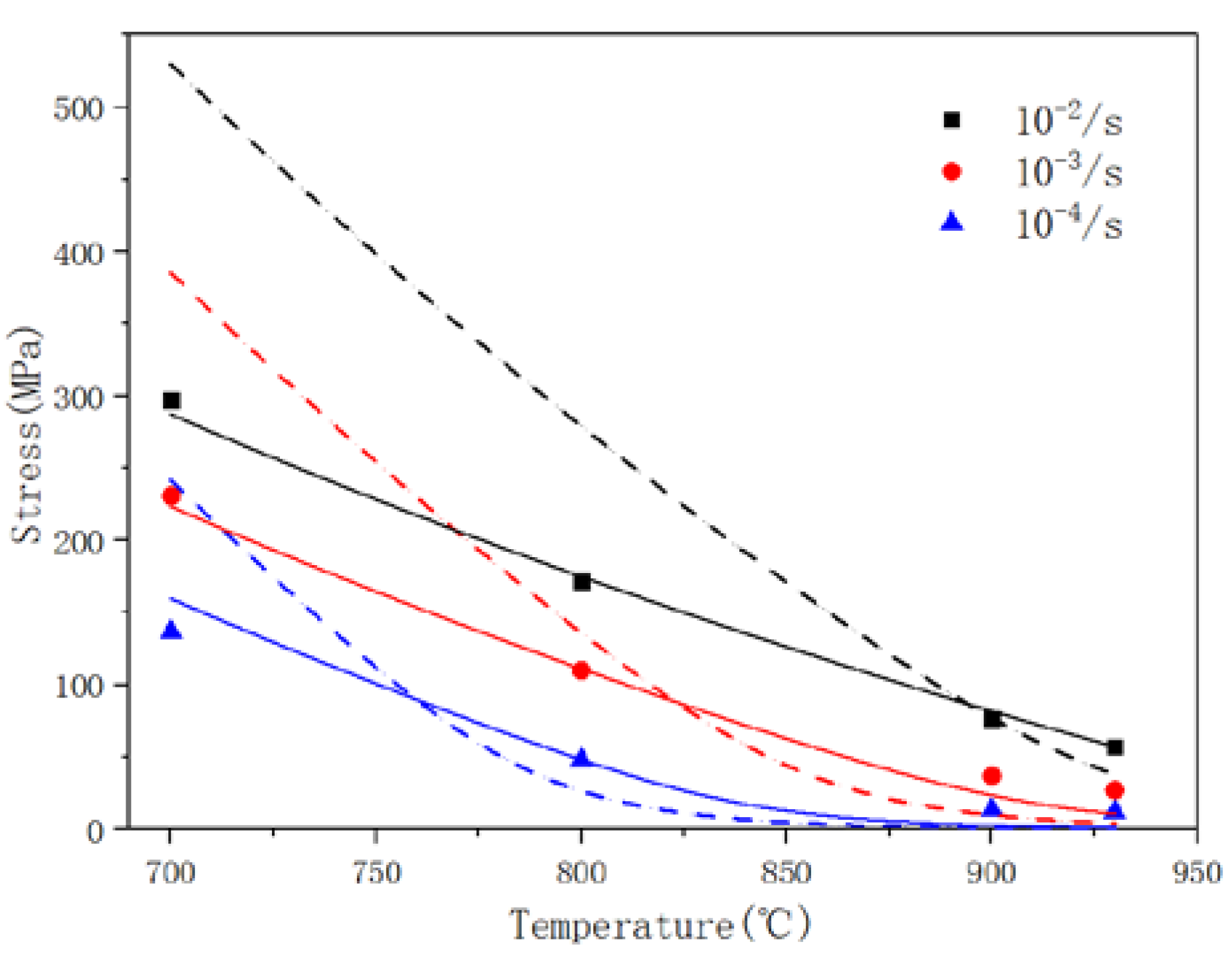
- During the initial stage of deformation, flow stress increased rapidly, which was caused by dislocation multiplication. Dislocations are mainly affected by dislocation multiplication, dynamic recovery (DRV), and dynamic recrystallization (DRX). The latter two are mechanisms of dislocation annihilation. As the deformation progresses, the annihilation mechanism gradually strengthens, gradually weakening the impact of dislocation multiplication.
- For large strains, a stress softening phenomenon appears after the stress reaches a peak. When the strain rate was 10−2/s, such softening behavior was continuous, which may be caused by the effects of voids at high strain rates. Previous research has demonstrated that obvious dynamic recrystallization can occur, resulting in significant void growth [9]. In contrast, the stress was able to maintain a stable state after softening at 10−3/s, which is similar to the SPF process [16,17,18].
- For the low strain rate of 10−4/s, the flow behavior was directly related to the temperature. When T < 900 °C, stress softening also occurred. However, flow stress gradually increased with strain at high temperatures, indicating that the softening mechanism for titanium is not sufficient to eliminate the effects of dislocation multiplication.
4. Constitutive Modeling Based on an Arrhenius Model
4.1. Arrhenius Model
4.2. Determine the Constants of the Constitutive Model
5. Effect of the Strain on Flow Stress
5.1. Strain Hardening Law
5.2. Constitutive Model with Strain Compensation
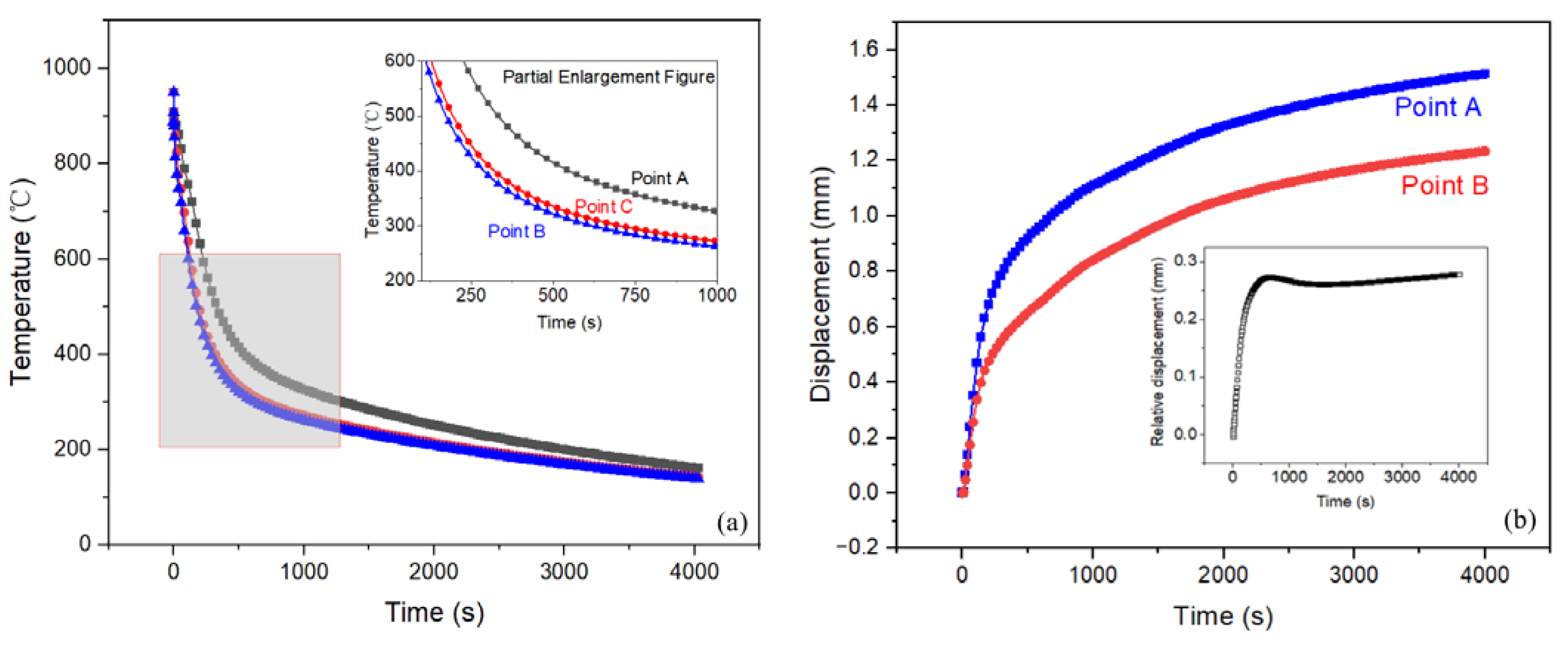
6. Application of the Constitutive Model to a Sandwich Structure
7. Conclusions
- (1)
- Owing to a high cooling rate and a small thickness value, the inner plate might be the first location where damage occurs during the air cooling process;
- (2)
- The engineering strain for the sandwich structure due to the temperature gradient was 0.37%, and distortions in the sandwich structure were caused by the temperature gradient;
- (3)
- The strain stress ratio nh was shown to have a linear relationship with strain, so a strain compensation method based on a linear function is proposed;
- (4)
- Parameter optimization for the Arrhenius model for flow stress was indispensable, since it reduced the mean error from 65% to 16% for the difference between the predicted results and the experimental data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rojas-Arias, N.; Aguilar-Sanchéz, M.; Barrales-Guadarrama, V.R.; Barrales-Guadarrama, R.; Silva, D.D.S.; Medrano-Rivera, L.A. Microstructural and electrical influence of Ti-6Al-4V-modified copper alloy. Mater. Lett. 2021, 285, 129183. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Zhang, W.; Wang, W. A finite-strain thermomechanical model for severe superplastic deformation of Ti-6Al-4V at elevated temperature. J. Alloys Compd. 2019, 787, 1336–1344. [Google Scholar] [CrossRef]
- Picu, R.C.; Majorell, A. Mechanical behavior of Ti-6Al-4V at high and moderate temperatures-Part II: Constitutive modeling. Mater. Sci. Eng. A 2002, 326, 306–316. [Google Scholar] [CrossRef]
- Chuvil’deev, V.N.; Gryaznov, M.Y.; Shotin, S.V.; Kopylov, V.I.; Nokhrin, A.V.; Likhnitskii, C.V.; Murashov, A.A.; Bobrov, A.A.; Tabachkova, N.Y.; Pirozhnikova, O.E. Investigation of superplasticity and dynamic grain growth in ultrafine-grained Al–0.5%Mg–Sc alloys. J. Alloys Compd. 2021, 877, 160099. [Google Scholar] [CrossRef]
- Mosleh, A.O.; Mikhaylovskaya, A.V.; Kotov, A.D.; Kwame, J.S. Experimental, modelling and simulation of an approach for optimizing the superplastic forming of Ti-6%Al-4%V titanium alloy. J. Manuf. Process. 2019, 45, 262–272. [Google Scholar] [CrossRef]
- Sorgente, D.; Lombardi, A.; Coviello, D.; Scintilla, L.D.; Fontana, M. A strain-dependent model for the coefficient of friction in the tool-blank interaction in superplastic forming. J. Manuf. Process. 2022, 73, 791–798. [Google Scholar] [CrossRef]
- Nursyifaulkhair, D.; Park, N.; Baek, E.R.; Kim, S. Influence of cooling rate on volume fraction of α massive phase in a Ti-6Al-4V alloy fabricated using directed energy deposition. Mater. Lett. 2019, 257, 126671. [Google Scholar] [CrossRef]
- Luo, S.; Yao, J.; Zou, G.; Li, J.; Jiang, J.; Yu, F. Transformation characteristics of temperature and phases within Ti-6Al-4V aeroengine drum in hot forging and air cooling procedures. J. Mater. Res. Technol. 2020, 9, 8235–8244. [Google Scholar] [CrossRef]
- Han, X.; Yang, J.; Li, J.; Wu, J. Investigation of the Flow Behavior of Air-Cooling Ti-6Al-4V Alloy after Superplastic Forming. Crystals 2022, 12, 294. [Google Scholar] [CrossRef]
- Wu, J.; Guo, R. Constitutive behavior for quenching of Al-Cu-Mg alloy with consideration of precipitation. J. Eng. Mater. Technol. Trans. ASME 2018, 140, 041009. [Google Scholar] [CrossRef]
- Bodunrin, M.O. Flow stress prediction using hyperbolic-sine Arrhenius constants optimised by simple generalised reduced gradient refinement. J. Mater. Res. Technol. 2020, 9, 2376–2386. [Google Scholar] [CrossRef]
- Yang, J.; Wu, J.; Zhang, Q.; Han, R.; Wang, K. The simple hyperbolic-sine equation for superplastic deformation and parameters optimization. J. Mater. Res. Technol. 2020, 9, 10819–10829. [Google Scholar] [CrossRef]
- Yang, J.; Wu, J.; Zhang, Q.; Ren, Y.; Ruolan, H.; Wang, K. Linear analysis of parameters in Arrhenius model for Ti-6Al-4V at superplastic forming. Eng. Comput. 2020, 38, 2528–2551. [Google Scholar] [CrossRef]
- Alabort, E.; Putman, D.; Reed, R.C. Superplasticity in Ti-6Al-4V: Characterisation, modelling and applications. Acta Mater. 2015, 95, 428–442. [Google Scholar] [CrossRef] [Green Version]
- Yasmeen, T.; Zhao, B.; Zheng, J.H.; Tian, F.; Lin, J.; Jiang, J. The study of flow behavior and governing mechanisms of a titanium alloy during superplastic forming. Mater. Sci. Eng. A 2020, 788, 139482. [Google Scholar] [CrossRef]
- TAYLOR, S.; WEST, G.D.; MOGIRE, E.; TANG, F.; KOTADIA, H.R. Superplastic forming characteristics of AZ41 magnesium alloy. Trans. Nonferrous Met. Soc. China 2021, 31, 648–654. [Google Scholar] [CrossRef]
- Chandrappa, K.; Sumukha, C.S.; Sankarsh, B.B.; Gowda, R. Superplastic forming with diffusion bonding of titanium alloys. Mater. Today Proc. 2019, 27, 2909–2913. [Google Scholar] [CrossRef]
- Yasmeen, T.; Shao, Z.; Zhao, L.; Gao, P.; Lin, J.; Jiang, J. Constitutive modeling for the simulation of the superplastic forming of TA15 titanium alloy. Int. J. Mech. Sci. 2019, 164, 105178. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Hollomon, H.; Zener, C. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Peng, W.; Zeng, W.; Wang, Q.; Yu, H. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013, 51, 95–104. [Google Scholar] [CrossRef]
- Mosleh, A.; Mikhaylovskaya, A.; Kotov, A.; Pourcelot, T.; Aksenov, S.; Kwame, J.; Portnoy, V. Modelling of the superplastic deformation of the near-a titanium alloy (Ti-2.5AL-1.8MN) using arrhenius-type constitutive model and artificial neural network. Metals 2017, 7, 568. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Liu, C.; Guo, Q.; Liu, Y. Variation of activation energy determined by a modified Arrhenius approach: Roles of dynamic recrystallization on the hot deformation of Ni-based superalloy. J. Mater. Sci. Technol. 2021, 72, 162–171. [Google Scholar] [CrossRef]
- Velay, V.; Matsumoto, H.; Vidal, V.; Chiba, A. Behavior modeling and microstructural evolutions of Ti-6Al-4V alloy under hot forming conditions. Int. J. Mech. Sci. 2016, 108–109, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Guo, H.; Shi, Z.; Qin, C.; Zhao, Z. Constitutive equations for high temperature flow stress of TC4-DT alloy incorporating strain, strain rate and temperature. Mater. Des. 2013, 50, 198–206. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, M.; Lei, L.; Huang, X.; Wang, L.; Qin, J.; Lu, W.; Zhang, D. Behavior and modeling of high temperature deformation of an α + β titanium alloy. Mater. Sci. Eng. A 2012, 555, 99–105. [Google Scholar] [CrossRef]
- Khaleel, M.A.; Zbib, H.M.; Nyberg, E.A. Constitutive modeling of deformation and damage in superplastic materials. Int. J. Plast. 2001, 17, 277–296. [Google Scholar] [CrossRef]
- Hu, L.; Lang, M.; Shi, L.; Li, M.; Zhou, T.; Bao, C.; Yang, M. Study on hot deformation behavior of homogenized Mg-8.5Gd-4.5Y-0.8Zn-0.4Zr alloy using a combination of strain-compensated Arrhenius constitutive model and finite element simulation method. J. Magnes. Alloy. 2021. [Google Scholar] [CrossRef]


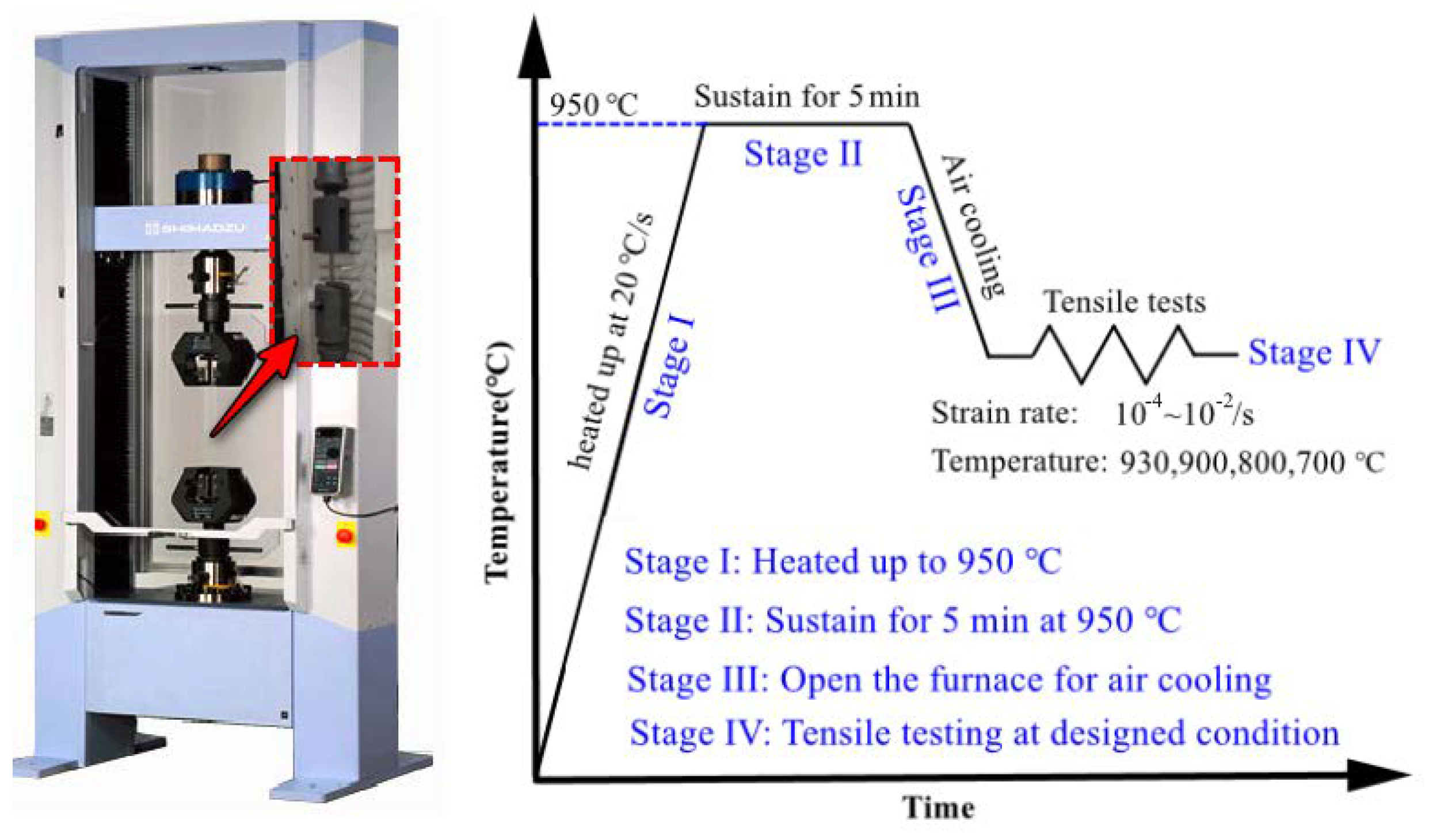
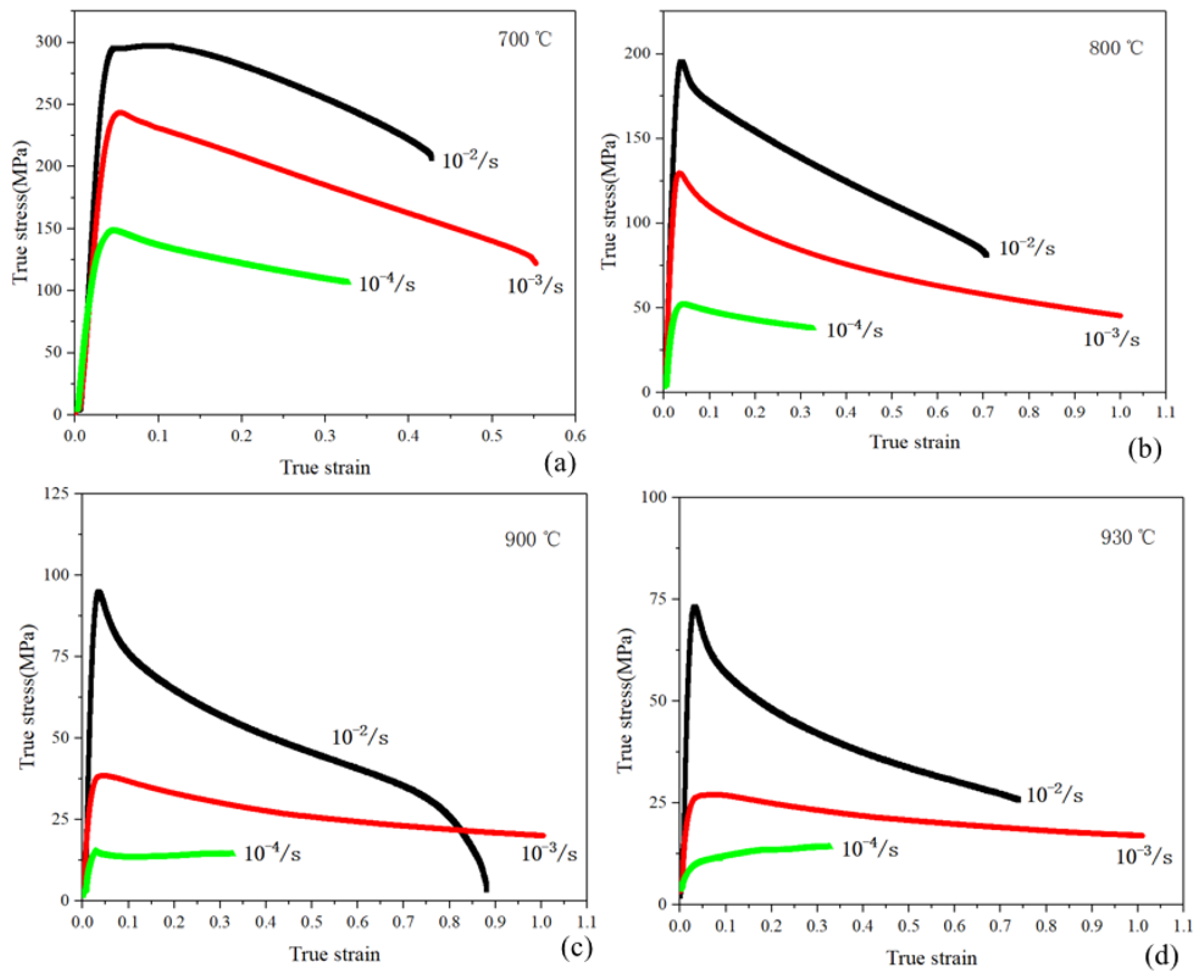

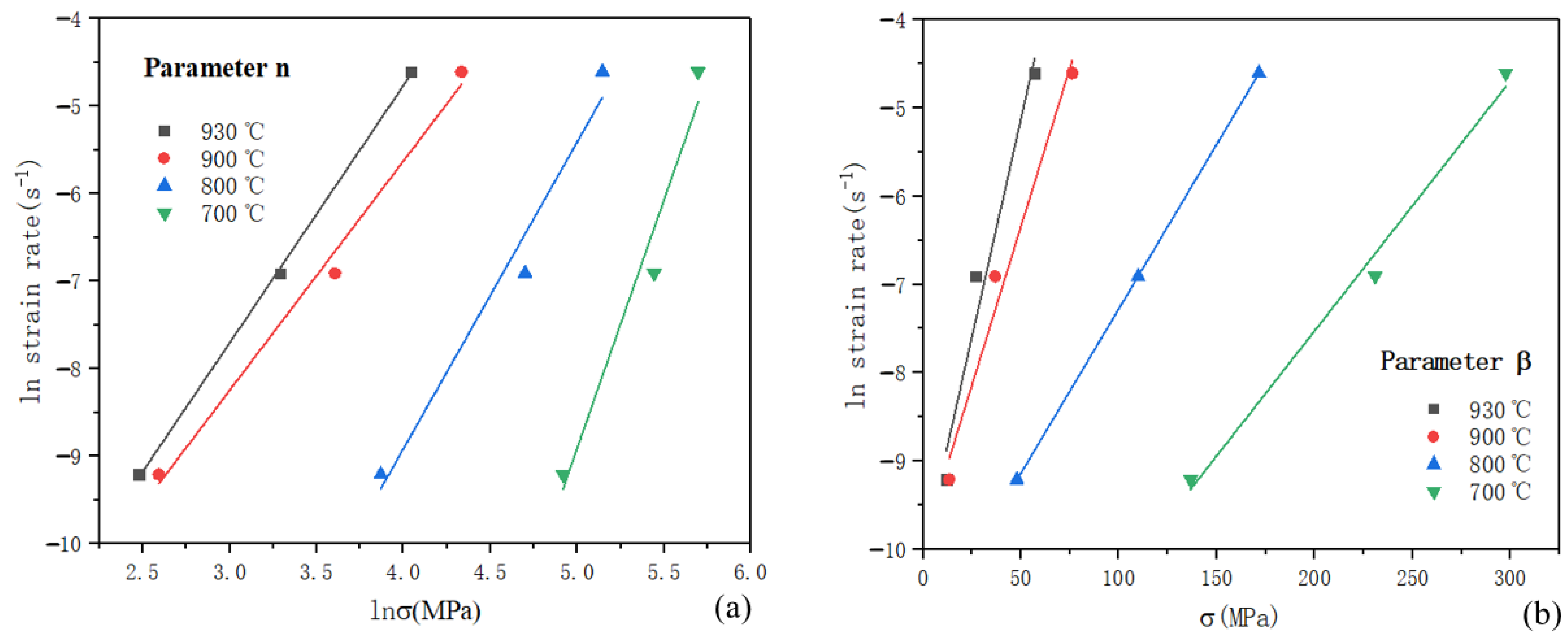

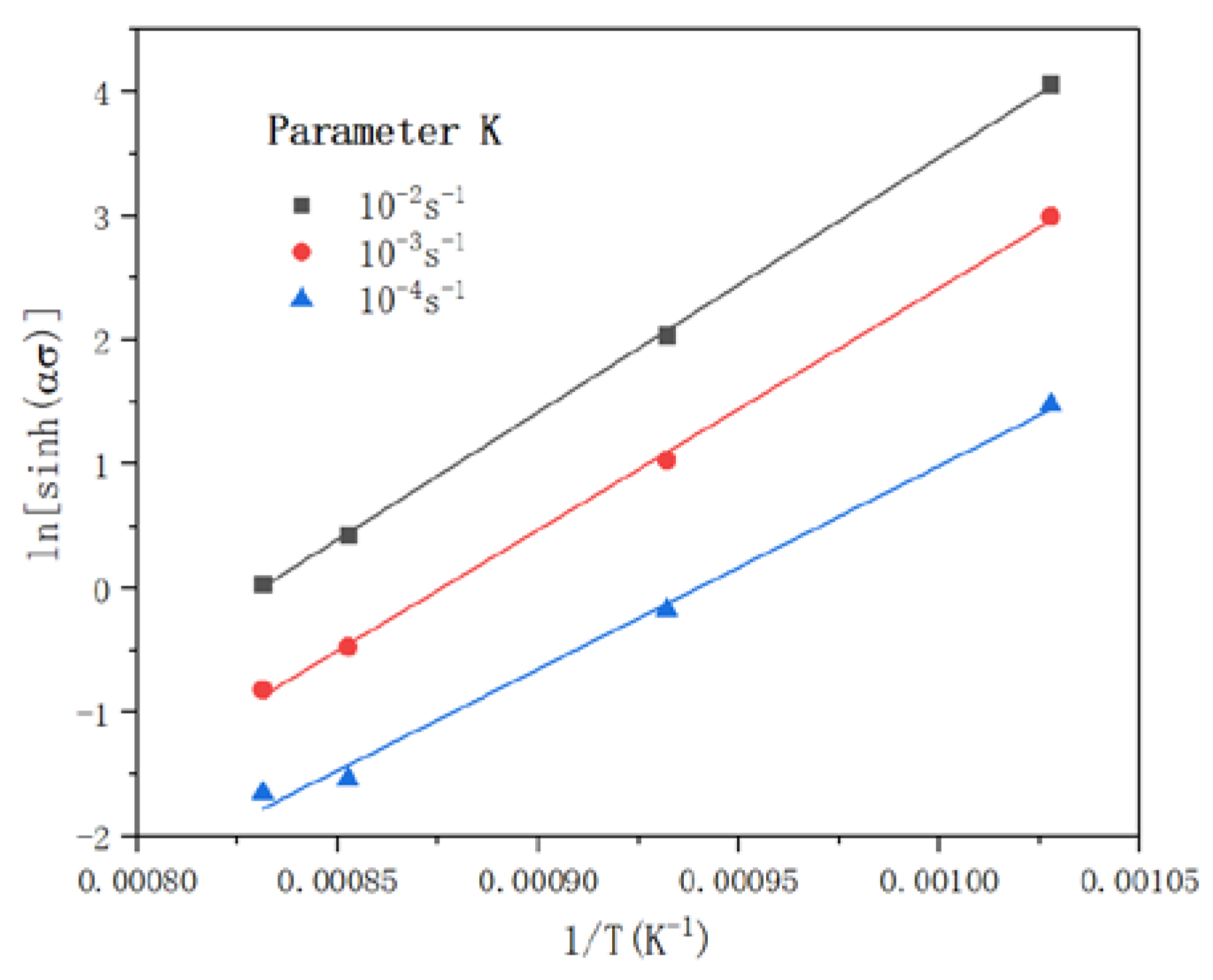
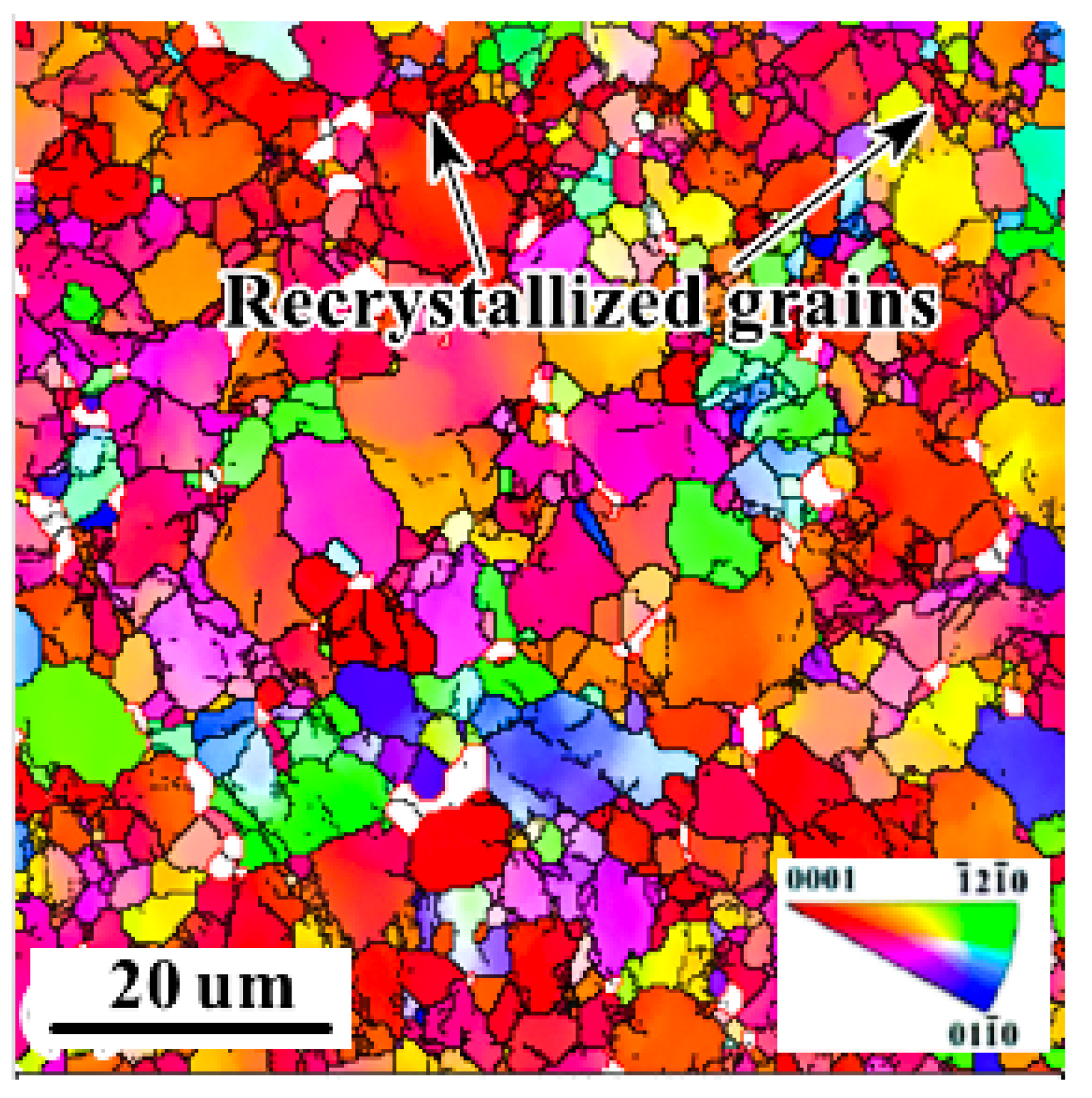




| Nomenclature | Descriptions | Nomenclature | Descriptions |
|---|---|---|---|
| SPF/DB | Superplastic forming/diffusion bonding | True stress | |
| Strain rate | True strain | ||
| Loading force | Initial cross-sectional area | ||
| Initial gauge length | Elongation | ||
| Strain-rate sensitivity parameters | Zener–Hollomon parameter | ||
| Deformation active energy | Temperature | ||
| R | Gas constant | Strain stress ratio |
| Chemistry (wt.%) | Ti | Al | V | C |
|---|---|---|---|---|
| Ti-6Al-4V | 88.31 | 5.59 | 4.85 | 1.25 |
| Temperature (°C) | |||
|---|---|---|---|
| 930 | 56.92 | 26.84 | 11.91 |
| 900 | 76.17 | 36.78 | 13.35 |
| 800 | 171.49 | 109.86 | 47.96 |
| 700 | 297.58 | 230.84 | 136.6 |
| Parameter | 930 °C | 900 °C | 800 °C | 700 °C | Mean Value |
|---|---|---|---|---|---|
| 2.94 | 2.62 | 3.51 | 5.69 | 3.69 | |
| 0.099 | 0.072 | 0.037 | 0.028 | 0.059 | |
| 0.016 | |||||
| Parameter | 930 °C | 900 °C | 800 °C | 700 °C | Mean Value |
|---|---|---|---|---|---|
| 2.72 | 2.33 | 2.07 | 1.76 | 2.22 |
| Parameter | 10−2 s−1 | 10−3 s−1 | 10−4 s−1 | Mean Value |
|---|---|---|---|---|
| 20,534.89 | 19,483.77 | 16,370.95 | 18,796.54 |
| Strain Rate (s−1) | 930 °C | 900 °C | 800 °C | 700 °C |
|---|---|---|---|---|
| 10−2 | 30.03 | 30.05 | 29.79 | 29.30 |
| 10−3 | 29.63 | 29.76 | 29.73 | 29.37 |
| 10−4 | 29.19 | 29.82 | 30.10 | 30.44 |
| Mean value | 29.77 | |||
| 3.69 | 0.059 | 0.016 | 2.22 | 18,796.53 | 347.39 | 29.77 | 8.48 × 1012 |
| Before optimization | 0.016 | 2.22 | 347.39 | 8.48 × 1012 |
| After optimization | 0.036 | 0.44 | 351.93 | 1.11 × 1013 |
| Strain Rate (s−1) | 700 °C | 800 °C | 900 °C | 930 °C | Mean Values |
|---|---|---|---|---|---|
| 10−2 | −0.85 | −0.84 | −0.86 | −0.83 | −0.85 |
| 10−3 | −0.99 | −0.76 | −0.61 | −0.48 | −0.71 |
| 10−4 | −0.71 | −0.59 | 0.12 | 0.54 | −0.16 |
| Strain Rate (s−1) | 700 °C | 800 °C | 900 °C | 930 °C | Mean Values |
|---|---|---|---|---|---|
| 10−2 | 1.10 | 1.07 | 1.04 | 1.03 | 1.06 |
| 10−3 | 1.10 | 1.03 | 1.02 | 1.03 | 1.04 |
| 10−4 | 1.04 | 1.01 | 1.02 | 1.00 | 1.02 |
| Values | −0.15 | −1.59 | 0.0092 | 1.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Yang, J.; Li, J.; Wu, J. Constitutive Modeling on the Ti-6Al-4V Alloy during Air Cooling and Application. Metals 2022, 12, 513. https://doi.org/10.3390/met12030513
Han X, Yang J, Li J, Wu J. Constitutive Modeling on the Ti-6Al-4V Alloy during Air Cooling and Application. Metals. 2022; 12(3):513. https://doi.org/10.3390/met12030513
Chicago/Turabian StyleHan, Xiaoning, Junzhou Yang, Jinshan Li, and Jianjun Wu. 2022. "Constitutive Modeling on the Ti-6Al-4V Alloy during Air Cooling and Application" Metals 12, no. 3: 513. https://doi.org/10.3390/met12030513
APA StyleHan, X., Yang, J., Li, J., & Wu, J. (2022). Constitutive Modeling on the Ti-6Al-4V Alloy during Air Cooling and Application. Metals, 12(3), 513. https://doi.org/10.3390/met12030513






