Influence of Carbon and Oxygen on the Core Structure and Peierls Stress of Screw Dislocation in Molybdenum
Abstract
:1. Introduction
2. Methodology
3. Results and Discussions
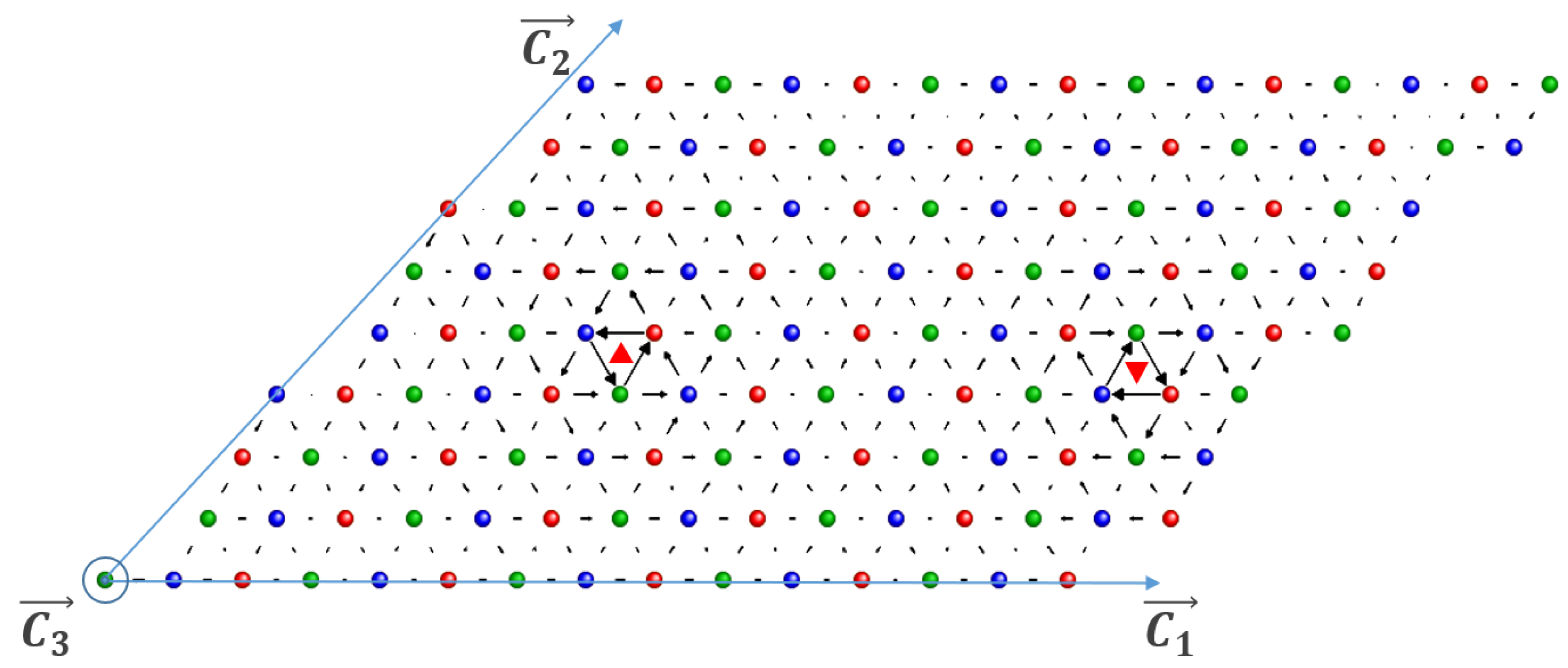
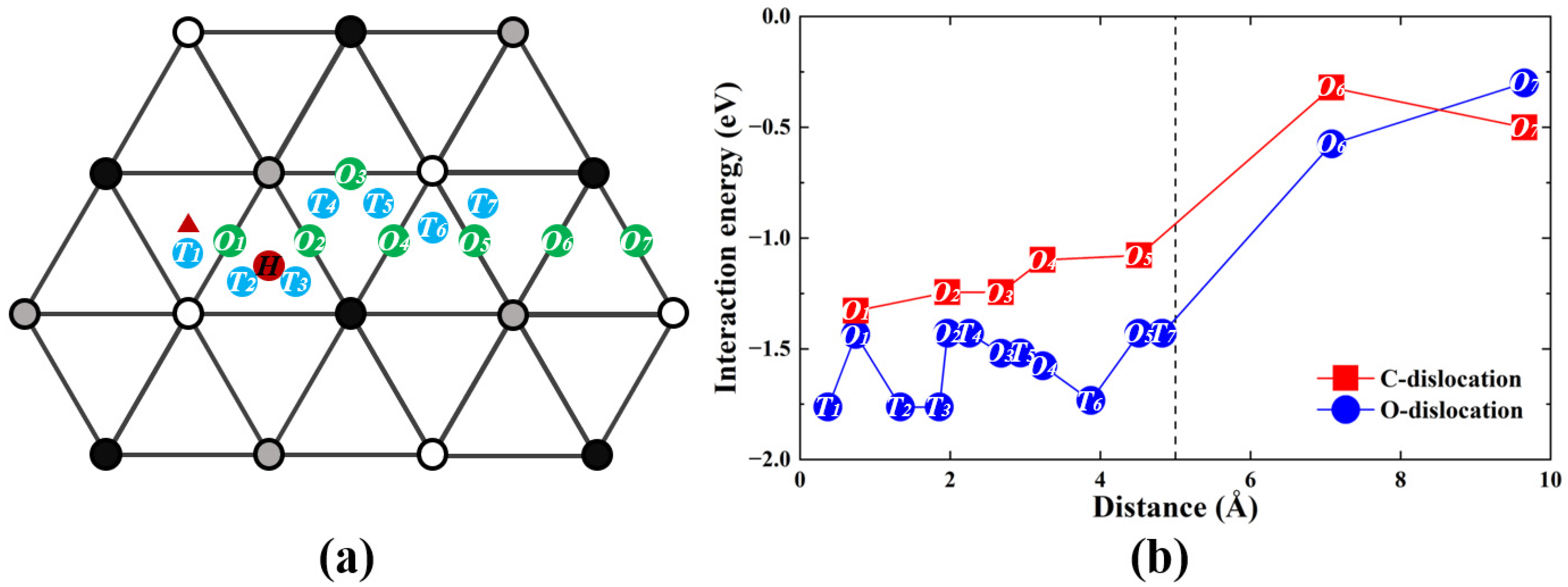
3.1. Interaction of Screw Dislocation with Single C/O Atom
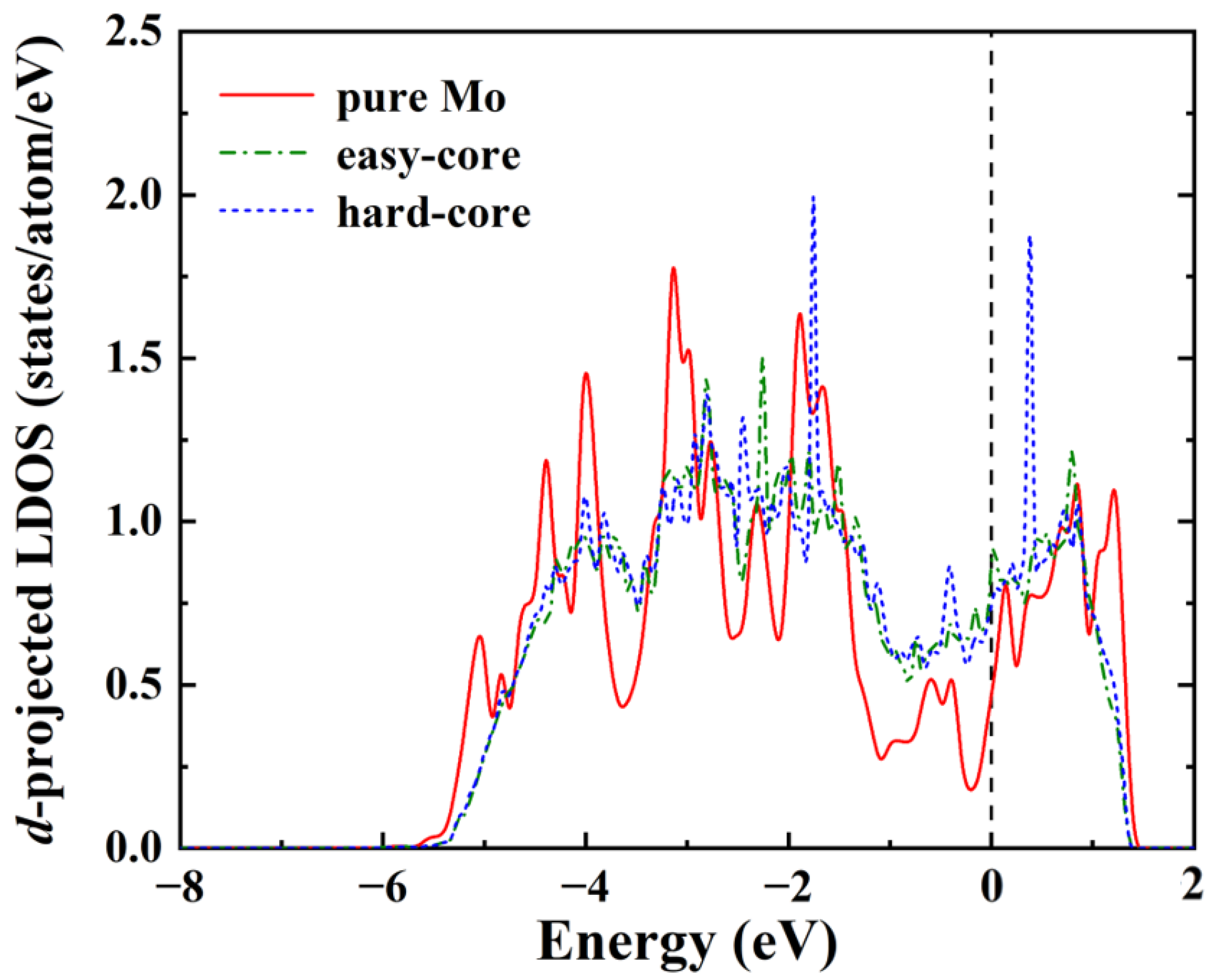
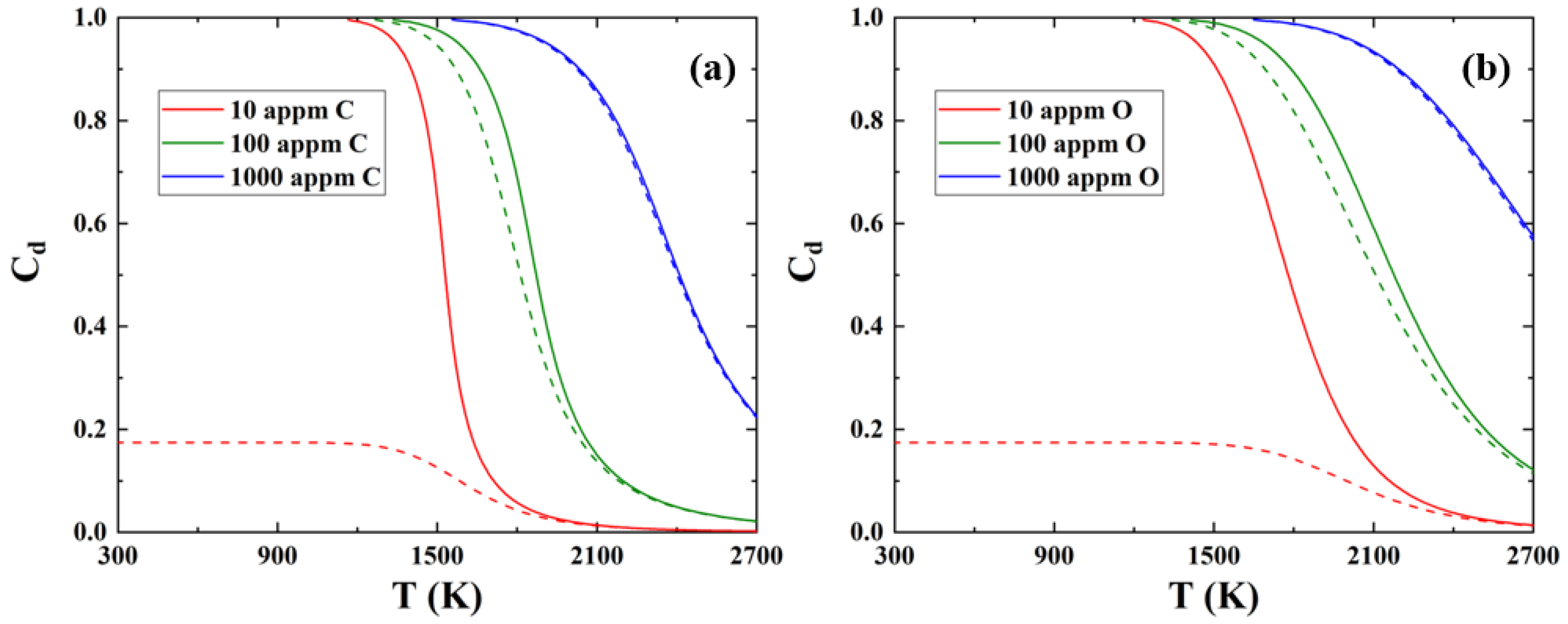
3.2. Segregation of C/O Atoms in the Screw Dislocation
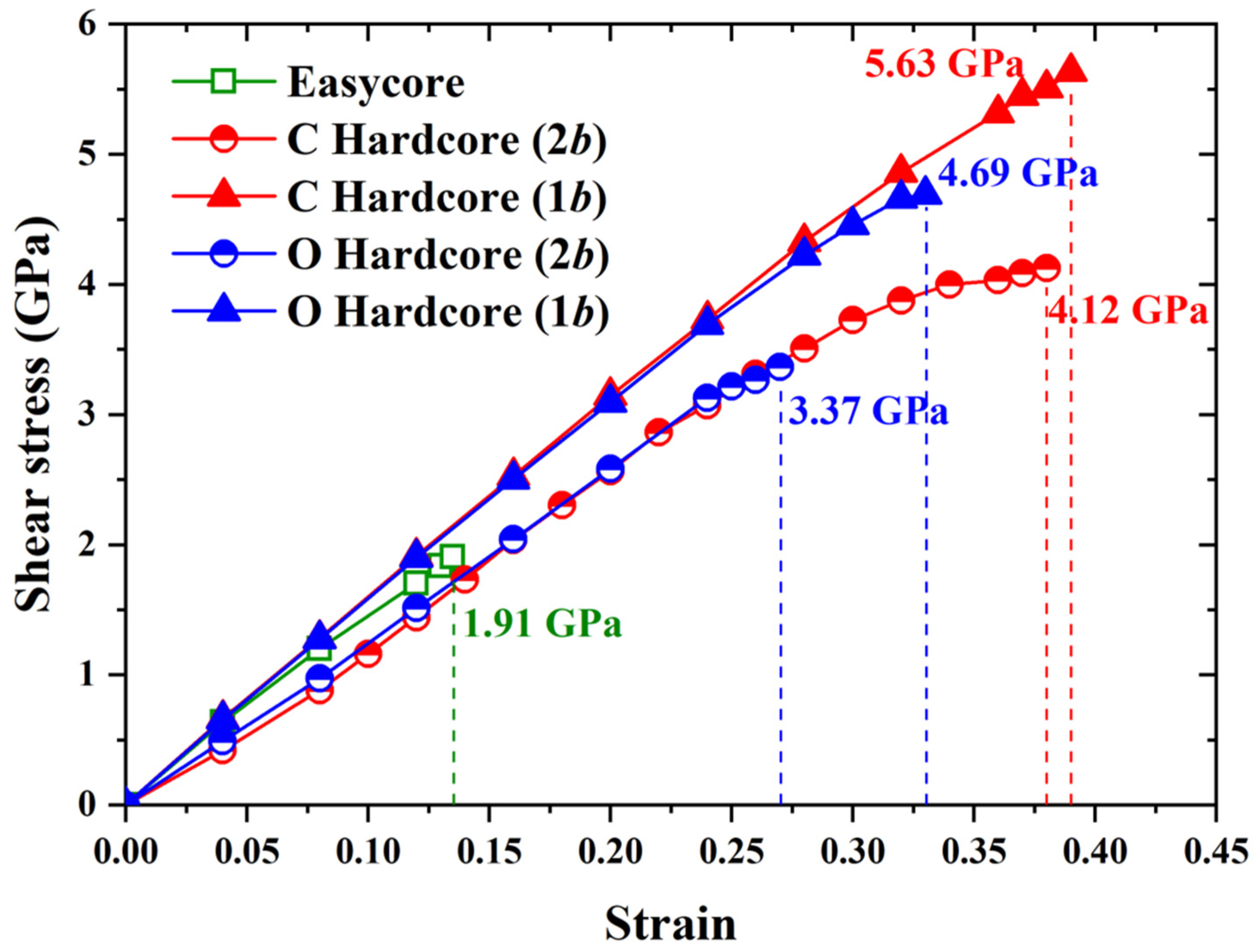
3.3. The Effect of C/O Segregation on the Dislocation Motion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Terrani, K.A. Accident tolerant fuel cladding development: Promise, status, and challenges. J. Nucl. Mater. 2018, 501, 13–30. [Google Scholar] [CrossRef]
- Terrani, K.A.; Zinkle, S.J.; Snead, L.L. Advanced oxidation-resistant iron-based alloys for LWR fuel cladding. J. Nucl. Mater. 2014, 448, 420–435. [Google Scholar] [CrossRef]
- Bachurina, D.; Vorkel, V.; Suchkov, A.; Gurova, J.; Ivannikov, A.; Penyaz, M.; Fedotov, I.; Sevryukov, O.; Kalin, B. Overview of the mechanical properties of tungsten/steel brazed joints for the demo fusion reactor. Metals 2021, 11, 209. [Google Scholar] [CrossRef]
- Christian, J.W. Some surprising features of the plastic deformation of body-centered cubic metals and alloys. Metall. Trans. A 1983, 14, 1237–1256. [Google Scholar] [CrossRef]
- Pande, C.S.; Goswami, R. Dislocation emission and crack dislocation interactions. Metals 2020, 10, 473. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, Í.; Simões, S. Recent Advances in EBSD Characterization of Metals. Metals 2020, 10, 1097. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Weygand, D.; Mrovec, M.; Hochrainer, T.; Gumbsch, P. Multiscale Simulation of Plasticity in bcc Metals. Annu. Rev. Mater. Res. 2015, 45, 369–390. [Google Scholar] [CrossRef]
- Seeger, A. Peierls barriers, kinks, and flow stress: Recent progress. Z. Für Met. 2002, 93, 760–777. [Google Scholar] [CrossRef]
- Gröger, R.; Bailey, A.G.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: I. Atomistic studies of the core structure and glide of 1/2〈1 1 1〉screw dislocations at 0 K. Acta Mater. 2008, 56, 5401–5411. [Google Scholar] [CrossRef]
- Luo, A.; Jacobson, D.L.; Shin, K.S. Solution softening mechanism of iridium and rhenium in tungsten at room temperature. Int. J. Refract. Met. Hard Mater. 1991, 10, 107–114. [Google Scholar] [CrossRef]
- Miao, S.; Xie, Z.; Lin, Y.; Fang, Q.; Tan, J.; Zhao, Y. Mechanical Properties, Thermal Stability and Microstructures of W-Re-ZrC Alloys Fabricated by Spark Plasma Sintering. Metals 2020, 10, 277. [Google Scholar] [CrossRef] [Green Version]
- Caillard, D. An in situ study of hardening and softening of iron by carbon interstitials. Acta Mater. 2011, 59, 4974–4989. [Google Scholar] [CrossRef]
- Yang, P.J.; Li, Q.J.; Tsuru, T.; Ogata, S.; Zhang, J.W.; Sheng, H.W.; Shan, Z.W.; Sha, G.; Han, W.Z.; Li, J.; et al. Mechanism of hardening and damage initiation in oxygen embrittlement of body-centred-cubic niobium. Acta Mater. 2019, 168, 331–342. [Google Scholar] [CrossRef]
- Yang, P.J.; Li, Q.J.; Han, W.Z.; Li, J.; Ma, E. Designing solid solution hardening to retain uniform ductility while quadrupling yield strength. Acta Mater. 2019, 179, 107–118. [Google Scholar] [CrossRef]
- Stephens, J.R. Effects of Interstitial Impurities on the Low-Temperature Tensile Properties of Tungsten; Technical Report NASA TN D-2287; National Aeronautics and Space Administration, Lewis Research Center: Cleveland, OH, USA, 1964. [Google Scholar]
- Xing, H.; Hu, P.; Han, J.; Li, S.; Ge, S.; Hua, X.; Hu, B.; Yang, F.; Wang, K.; Feng, P. Effects of oxygen on microstructure and evolution mechanism of body-centred-cubic molybdenum. Int. J. Refract. Met. Hard Mater. 2022, 103, 105747. [Google Scholar] [CrossRef]
- Ulitchny, M.G.; Gibala, R. The effects of interstitial solute additions on the mechanical properties of niobium and tantalum single crystals. J. Less Common Met. 1973, 33, 105–116. [Google Scholar] [CrossRef]
- Jo, M.G.; Madakashira, P.P.; Suh, J.Y.; Han, H.N. Effect of oxygen and nitrogen on microstructure and mechanical properties of vanadium. Mater. Sci. Eng. A 2016, 675, 92–98. [Google Scholar] [CrossRef]
- Woodward, C.; Rao, S.I. Ab-initio simulation of isolated screw dislocations in bcc Mo and Ta. Philos. Mag. A 2001, 81, 1305–1316. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.-Z.; Chang, J.-P.; Cai, W.; Bulatov, V.V.; Ho, K.-M.; Yip, S. Core energy and Peierls stress of a screw dislocation in bcc molybdenum: A periodic-cell tight-binding study. Phys. Rev. B 2004, 70, 104113. [Google Scholar] [CrossRef] [Green Version]
- Lüthi, B.; Ventelon, L.; Rodney, D.; Willaime, F. Attractive interaction between interstitial solutes and screw dislocations in bcc iron from first principles. Comput. Mater. Sci. 2018, 148, 21–26. [Google Scholar] [CrossRef]
- Lüthi, B.; Ventelon, L.; Elsässer, C.; Rodney, D.; Willaime, F. First principles investigation of carbon-screw dislocation interactions in body-centered cubic metals. Model. Simul. Mater. Sci. Eng. 2017, 25, 084001. [Google Scholar] [CrossRef]
- Hachet, G.; Ventelon, L.; Willaime, F.; Clouet, E. Screw dislocation-carbon interaction in BCC tungsten: An ab initio study. Acta Mater. 2020, 200, 481–489. [Google Scholar] [CrossRef]
- Medvedeva, N.I.; Gornostyrev, Y.N.; Freeman, A.J. Solid solution softening and hardening in the group-V and group-VI bcc transition metals alloys: First principles calculations and atomistic modeling. Phys. Rev. B 2007, 76, 212104. [Google Scholar] [CrossRef]
- Yu, Q.; Qi, L.; Tsuru, T.; Traylor, R.; Rugg, D.; Morris, J.W.; Asta, M.; Chrzan, D.C.; Minor, A.M. Origin of dramatic oxygen solute strengthening effect in titanium. Science 2015, 347, 635–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Marian, J. Direct prediction of the solute softening-to-hardening transition in W-Re alloys using stochastic simulations of screw dislocation motion. Model. Simul. Mater. Sci. Eng. 2018, 26, 045002. [Google Scholar] [CrossRef] [Green Version]
- Ventelon, L.; Lüthi, B.; Clouet, E.; Proville, L.; Legrand, B.; Rodney, D.; Willaime, F. Dislocation core reconstruction induced by carbon segregation in bcc iron. Phys. Rev. B 2015, 91, 220102. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley Sons: New York, NY, USA, 2004. [Google Scholar]
- Trinkle, D.R.; Woodward, C. The Chemistry of Deformation: How Solutes Soften Pure Metals. Science 2005, 310, 1665–1667. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-H.; Zhou, H.-B.; Gao, F.; Lu, G.; Lu, G.-H.; Liu, F. Hydrogen induced dislocation core reconstruction in bcc tungsten. Acta Mater. 2022, 226, 117622. [Google Scholar] [CrossRef]
- Ventelon, L.; Willaime, F. Core structure and Peierls potential of screw dislocations in α-Fe from first principles: Cluster versus dipole approaches. J. Comput. Mater. Des. 2007, 14, 85–94. [Google Scholar] [CrossRef]
- Clouet, E.; Ventelon, L.; Willaime, F. Dislocation Core Energies and Core Fields from First Principles. Phys. Rev. Lett. 2009, 102, 055502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodney, D.; Ventelon, L.; Clouet, E.; Pizzagalli, L.; Willaime, F. Ab initio modeling of dislocation core properties in metals and semiconductors. Acta Mater. 2017, 124, 633–659. [Google Scholar] [CrossRef]
- Ismail-Beigi, S.; Arias, T.A. Ab Initio Study of Screw Dislocations in Mo and Ta: A New Picture of Plasticity in bcc Transition Metals. Phys. Rev. Lett. 2000, 84, 1499–1502. [Google Scholar] [CrossRef] [Green Version]
- Woodward, C.; Rao, S.I. Flexible Ab Initio Boundary Conditions: Simulating Isolated Dislocations in bcc Mo and Ta. Phys. Rev. Lett. 2002, 88, 216402. [Google Scholar] [CrossRef]
- Ventelon, L.; Willaime, F.; Clouet, E.; Rodney, D. Ab initio investigation of the Peierls potential of screw dislocations in bcc Fe and W. Acta Mater. 2013, 61, 3973–3985. [Google Scholar] [CrossRef]
- Itakura, M.; Kaburaki, H.; Yamaguchi, M. First-principles study on the mobility of screw dislocations in bcc iron. Acta Mater. 2012, 60, 3698–3710. [Google Scholar] [CrossRef] [Green Version]
- Dezerald, L.; Ventelon, L.; Clouet, E.; Denoual, C.; Rodney, D.; Willaime, F. Ab initio modeling of the two-dimensional energy landscape of screw dislocations in bcc transition metals. Phys. Rev. B 2014, 89, 024104. [Google Scholar] [CrossRef] [Green Version]
- Scheiber, D.; Pippan, R.; Puschnig, P.; Romaner, L. Ab initio search for cohesion-enhancing impurity elements at grain boundaries in molybdenum and tungsten. Model. Simul. Mater. Sci. Eng. 2016, 24, 085009. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Kimizuka, H.; Kano, T.; Li, J.; Kaburaki, H. First-principles Calculation on Screw Dislocation Core Properties in BCC Molybdenum. J. Earth Simulator 2007, 7, 17–21. [Google Scholar]
- Yang, K.J.; Liu, Y.L.; Liu, Z.L.; Liu, C.; Shao, P.; Zhang, X.; Han, Q.F. Basic physical behavior of impurity carbon in molybdenum for nuclear material: A systematical first-principles simulation. Nucl. Mater. Energy 2021, 28, 101053. [Google Scholar] [CrossRef]
- Hu, Y.-J.; Zhao, G.; Zhang, B.; Yang, C.; Zhang, M.; Liu, Z.-K.; Qian, X.; Qi, L. Local electronic descriptors for solute-defect interactions in bcc refractory metals. Nat. Commun. 2019, 10, 4484. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.-Y.; Li, Y.-H.; Zhou, H.-B.; Li, Z.-Z.; Cheng, L.; Lu, G.-H. Characterization of the energetics and configurations of hydrogen in vacancy clusters in tungsten. Nucl. Fusion 2019, 59, 106032. [Google Scholar] [CrossRef]
- Li, Y.H.; Zhou, H.B.; Liang, L.; Gao, N.; Deng, H.; Gao, F.; Lu, G.; Lu, G.H. Transition from ductilizing to hardening in tungsten: The dependence on rhenium distribution. Acta Mater. 2019, 181, 110–123. [Google Scholar] [CrossRef]
- Tréglia, G.; Legrand, B.; Ducastelle, F.; Saúl, A.; Gallis, C.; Meunier, I.; Mottet, C.; Senhaji, A. Alloy surfaces: Segregation, reconstruction and phase transitions. Comput. Mater. Sci. 1999, 15, 196–235. [Google Scholar] [CrossRef]
- Tsuru, T.; Suzudo, T. First-principles calculations of interaction between solutes and dislocations in tungsten. Nucl. Mater. Energy 2018, 16, 221–225. [Google Scholar] [CrossRef]
- Seeger, A.; Veyssiere, P.; Kubin, L.P.; Castaing, J. Dislocations 1984; CNRS: Paris, France, 1984. [Google Scholar]
- Brunner, D. Comparison of Flow-Stress Measurements on High-Purity Tungsten Single Crystals with the Kink-Pair Theory. Mater. Trans. JIM 2000, 41, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Dudarev, S.L.; Ma, P.-W. Elastic fields, dipole tensors, and interaction between self-interstitial atom defects in bcc transition metals. Phys. Rev. Mater. 2018, 2, 033602. [Google Scholar] [CrossRef]
- Li, H.; Draxl, C.; Wurster, S.; Pippan, R.; Romaner, L. Impact of d-band filling on the dislocation properties of bcc transition metals: The case of tantalum-tungsten alloys investigated by density-functional theory. Phys. Rev. B 2017, 95, 094114. [Google Scholar] [CrossRef]
- Hollang, L.; Hommel, M.; Seeger, A. The Flow Stress of Ultra-High-Purity Molybdenum Single Crystals. Phys. Status Solidi 1997, 160, 329–354. [Google Scholar] [CrossRef]
- Dezerald, L.; Proville, L.; Ventelon, L.; Willaime, F.; Rodney, D. First-principles prediction of kink-pair activation enthalpy on screw dislocations in bcc transition metals: V, Nb, Ta, Mo, W, and Fe. Phys. Rev. B 2015, 91, 094105. [Google Scholar] [CrossRef] [Green Version]

| Configuration | Distance | Voronoi Volume | ||||
|---|---|---|---|---|---|---|
| C | Bulk | 0.46 | 1.66 | −1.19 | 1.57/1.97 | 7.79/9.29 |
| SD | −0.86 | 0.63 | −1.49 | 1.60/2.15 | 8.73/9.95 | |
| O | Bulk | −0.59 | 1.33 | −1.92 | 1.76/1.98 | 7.97/10.38 |
| SD | −2.36 | 0.66 | −3.02 | 1.78/2.16 | 8.73/10.15 | |
| Configuration | ||||
|---|---|---|---|---|
| Pure SD | 1.18 | 2.47 | 1.91 | 1.18 |
| SD + 1C | 0.46 | 2.20 | 4.12 | 1.65 |
| SD + 2C | −0.45 | 1.87 | 5.63 | 1.77 |
| SD + 1O | 0.30 | 2.15 | 3.37 | 1.47 |
| SD + 2O | −0.66 | 1.79 | 4.69 | 1.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-Q.; Li, Y.-H.; Lu, G.-H.; Zhou, H.-B. Influence of Carbon and Oxygen on the Core Structure and Peierls Stress of Screw Dislocation in Molybdenum. Metals 2022, 12, 507. https://doi.org/10.3390/met12030507
Wang Z-Q, Li Y-H, Lu G-H, Zhou H-B. Influence of Carbon and Oxygen on the Core Structure and Peierls Stress of Screw Dislocation in Molybdenum. Metals. 2022; 12(3):507. https://doi.org/10.3390/met12030507
Chicago/Turabian StyleWang, Zi-Qi, Yu-Hao Li, Guang-Hong Lu, and Hong-Bo Zhou. 2022. "Influence of Carbon and Oxygen on the Core Structure and Peierls Stress of Screw Dislocation in Molybdenum" Metals 12, no. 3: 507. https://doi.org/10.3390/met12030507
APA StyleWang, Z.-Q., Li, Y.-H., Lu, G.-H., & Zhou, H.-B. (2022). Influence of Carbon and Oxygen on the Core Structure and Peierls Stress of Screw Dislocation in Molybdenum. Metals, 12(3), 507. https://doi.org/10.3390/met12030507







