Machine-Learning-Based Model of Elastic—Plastic Deformation of Copper for Application to Shock Wave Problem
Abstract
:1. Introduction
2. Materials and Methods
2.1. MD Simulations of Uniform Axisymmetric Deformation
2.2. Training of ANNs for Tensor Equation of State and Structural Transformations
2.3. Dislocation Plasticity Model and Parameter Fitting by Bayesian Algorithm
2.4. Application to Plane Shock Wave
3. Results
3.1. Results of MD Simulations
3.2. Results of ANN Training
3.3. Results of Bayesian Parameterization of Dislocation Plasticity Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Cu.TEOS1.ANNp | Cu.DISL1.ANNp | Cu.VOID1.ANNp | Cu.BCC1.ANNp |
|---|---|---|---|---|
| Number of inputs | 3 | |||
| Inputs | ||||
| Number of outputs | 6 | 1 | 1 | 1 |
| Outputs | ||||
References
- Gurrutxaga-Lerma, B.; Shehadeh, M.A.; Balint, D.S.; Dini, D.; Chen, L.; Eakins, D.E. The effect of temperature on the elastic precursor decay in shock loaded FCC aluminium and BCC iron. Int. J. Plast. 2017, 96, 135–155. [Google Scholar] [CrossRef]
- Kanel, G.I.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V. Effects of temperature on the flow stress of aluminum in shock waves and rarefaction waves. J. Appl. Phys. 2020, 127, 035901. [Google Scholar] [CrossRef]
- Kanel, G.I.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V. Effects of temperature and strain on the resistance to high-rate deformation of copper in shock waves. J. Appl. Phys. 2020, 128, 115901. [Google Scholar] [CrossRef]
- Savinykh, A.S.; Kanel, G.I.; Garkushin, G.V.; Razorenov, S.V. Resistance to high-rate deformation and fracture of lead at normal and elevated temperatures in the sub-microsecond time range. J. Appl. Phys. 2020, 128, 025902. [Google Scholar] [CrossRef]
- Kanel, G.I.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V. High-rate deformation of titanium in shock waves at normal and elevated temperatures. J. Exp. Theor. Phys. 2021, 132, 438–445. [Google Scholar] [CrossRef]
- Saveleva, N.V.; Bayandin, Y.V.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V.; Naimark, O.B. The formation of elastoplastic fronts and spall fracture in AMg6 alloy under shock-wave loading. Tech. Phys. Lett. 2018, 44, 823–826. [Google Scholar] [CrossRef]
- Brodova, I.G.; Petrova, A.N.; Shirinkina, I.G.; Rasposienko, D.Y.; Yolshina, L.A.; Muradymov, R.V.; Razorenov, S.V.; Shorokhov, E.V. Mechanical properties of submicrocrystalline aluminium matrix composites reinforced by “in situ” graphene through severe plastic deformation processes. J. Alloy. Compd. 2021, 859, 158387. [Google Scholar] [CrossRef]
- Ivanov, K.V.; Razorenov, S.V.; Garkushin, G.V. Investigation of structure and mechanical properties under quasi-static and planar impact loading of aluminum composite reinforced with Al2O3 nanoparticles of different shape. Mater. Today Commun. 2021, 29, 102942. [Google Scholar] [CrossRef]
- Klimova-Korsmik, O.; Turichin, G.; Mendagaliyev, R.; Razorenov, S.; Garkushin, G.; Savinykh, A.; Korsmik, R. High-strain deformation and spallation strength of 09CrNi2MoCu steel obtained by direct laser deposition. Metals 2021, 11, 1305. [Google Scholar] [CrossRef]
- Promakhov, V.; Schulz, N.; Vorozhtsov, A.; Savinykh, A.; Garkushin, G.; Razorenov, S.; Klimova-Korsmik, O. The strength of inconel 625, manufactured by the method of direct laser deposition under sub-microsecond load duration. Metals 2021, 11, 1796. [Google Scholar] [CrossRef]
- Khishchenko, K.V.; Mayer, A.E. High- and low-entropy layers in solids behind shock and ramp compression waves. Int. J. Mech. Sci. 2021, 189, 105971. [Google Scholar] [CrossRef]
- Moshe, E.; Eliezer, S.; Dekel, E.; Ludmirsky, A.; Henis, Z.; Werdiger, M.; Goldberg, I.B.; Eliaz, N.; Elieser, D. An increase of the spall strength in aluminum, copper, and Metglas at strain rates larger than 107 s−1. J. Appl. Phys. 1998, 83, 4004. [Google Scholar] [CrossRef] [Green Version]
- Krasyuk, I.K.; Pashinin, P.P.; Semenov, A.Y.; Khishchenko, K.V.; Fortov, V.E. Study of extreme states of matter at high energy densities and high strain rates with powerful lasers. Laser Phys. 2016, 26, 094001. [Google Scholar] [CrossRef] [Green Version]
- Ashitkov, S.I.; Komarov, P.S.; Struleva, E.V.; Agranat, M.B.; Kanel, G.I. Mechanical and optical properties of vanadium under shock picosecond loads. JETP Lett. 2015, 101, 276–281. [Google Scholar] [CrossRef]
- Kanel, G.I.; Zaretsky, E.B.; Razorenov, S.V.; Ashitkov, S.I.; Fortov, V.E. Unusual plasticity and strength of metals at ultra-short load durations. Phys. Uspekhi 2017, 60, 490–508. [Google Scholar] [CrossRef] [Green Version]
- Zuanetti, B.; McGrane, S.D.; Bolme, C.A.; Prakash, V. Measurement of elastic precursor decay in pre-heated aluminum films under ultra-fast laser generated shocks. J. Appl. Phys. 2018, 123, 195104. [Google Scholar] [CrossRef] [Green Version]
- Murzov, S.; Ashitkov, S.; Struleva, E.; Komarov, P.; Zhakhovsky, V.; Khokhlov, V.; Inogamov, N. Elastoplastic and polymorphic transformations of iron at ultra-high strain rates in laser-driven shock waves. J. Appl. Phys. 2021, 130, 245902. [Google Scholar] [CrossRef]
- Shao, J.-L.; Guo, X.-X.; Lu, G.; He, W.; Xin, J. Influence of shear wave on the HCP nucleation in BCC iron under oblique shock conditions. Mech. Mater. 2021, 158, 103878. [Google Scholar] [CrossRef]
- Jiang, D.-D.; Shao, J.-L.; Wu, B.; Wang, P.; He, A.-M. Sudden change of spall strength induced by shock defects based on atomistic simulation of single crystal aluminum. Scr. Mater. 2022, 210, 114474. [Google Scholar] [CrossRef]
- Wang, J.-N.; Wu, B.; Wu, F.-C.; Wang, P.; He, A.-M.; Wu, H.-A. Spall and recompression processes with double shock loading of polycrystalline copper. Mech. Mater. 2022, 165, 104194. [Google Scholar] [CrossRef]
- Austin, R.A.; McDowell, D.L. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. Int. J. Plast. 2011, 27, 1–24. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Yalovets, A.P. Dislocation based high-rate plasticity model and its application to plate-impact and ultra short electron irradiation simulations. Int. J. Plast. 2011, 27, 1294–1308. [Google Scholar] [CrossRef]
- Lloyd, J.T.; Clayton, J.D.; Austin, R.A.; McDowell, D.L. Plane wave simulation of elastic-viscoplastic single crystals. J. Mech. Phys. Solids 2014, 69, 14–32. [Google Scholar] [CrossRef]
- Zuanetti, B.; Luscher, D.J.; Ramos, K.; Bolme, C. Unraveling the implications of finite specimen size on the interpretation of dynamic experiments for polycrystalline aluminum through direct numerical simulations. Int. J. Plast. 2021, 145, 103080. [Google Scholar] [CrossRef]
- Gurrutxaga–Lerma, B.; Verschueren, J.; Sutton, A.P.; Dini, D. The mechanics and physics of high-speed dislocations: A critical review. Int. Mater. Rev. 2021, 66, 215–255. [Google Scholar] [CrossRef]
- Shen, Y.; Spearot, D.E. Mobility of dislocations in FeNiCrCoCu high entropy alloys. Modell. Simul. Mater. Sci. Eng. 2021, 29, 085017. [Google Scholar] [CrossRef]
- Bryukhanov, I.A.; Emelyanov, V.A. Shear stress relaxation through the motion of edge dislocations in Cu and Cu–Ni solid solution: A molecular dynamics and discrete dislocation study. Comput. Mater. Sci. 2022, 201, 110885. [Google Scholar] [CrossRef]
- Esteban-Manzanares, G.; Bellón, B.; Martínez, E.; Papadimitriou, I.; LLorca, J. Strengthening of Al–Cu alloys by Guinier–Preston zones: Predictions from atomistic simulations. J. Mech. Phys. Solids 2019, 132, 103675. [Google Scholar] [CrossRef] [Green Version]
- Rajput, A.; Paul, S.K. Effect of soft and hard inclusions in tensile deformation and damage mechanism of Aluminum: A molecular dynamics study. J. Alloy. Compd. 2021, 869, 159213. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V.; Gazizov, M.R. Influence of θ’ phase cutting on precipitate hardening of Al–Cu alloy during prolonged plastic deformation: Molecular dynamics and continuum modeling. Appl. Sci. 2021, 11, 4906. [Google Scholar] [CrossRef]
- Shang, H.; Wu, P.; Lou, Y.; Wang, J.; Chen, Q. Machine learning-based modeling of the coupling effect of strain rate and temperature on strain hardening for 5182-O aluminum alloy. J. Mater. Process. Technol. 2022, 302, 117501. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Bonatti, C.; Mohr, D. Counterexample-trained neural network model of rate and temperature dependent hardening with dynamic strain aging. Int. J. Plast. 2022, 151, 103218. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. On the importance of self-consistency in recurrent neural network models representing elasto-plastic solids. J. Mech. Phys. Solids. 2022, 158, 104697. [Google Scholar] [CrossRef]
- Gracheva, N.A.; Lekanov, M.V.; Mayer, A.E.; Fomin, E.V. Application of neural networks for modeling shock-wave processes in aluminum. Mech. Solids 2021, 56, 326–342. [Google Scholar] [CrossRef]
- Mayer, A.E.; Krasnikov, V.S.; Pogorelko, V.V. Homogeneous nucleation of dislocations in copper: Theory and approximate description based on molecular dynamics and artificial neural networks. Comput. Mater. Sci. 2022, 206, 111266. [Google Scholar] [CrossRef]
- Ma, K.; Chen, J.; Dongare, A.M. Role of pre-existing dislocations on the shock compression and spall behavior in single-crystal copper at atomic scales. J. Appl. Phys. 2021, 129, 175901. [Google Scholar] [CrossRef]
- Wang, S.; Pan, H.; Wang, X.; Yin, J.; Hu, X.; Xu, W.; Wang, P. Atomic insights into the quasi-elastic response in shock reloading of shocked metals. Results Phys. 2021, 31, 104954. [Google Scholar] [CrossRef]
- Bryukhanov, I.A. Atomistic simulation of the shock wave in copper single crystals with pre-existing dislocation network. Int. J. Plast. 2022, 151, 103171. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef] [Green Version]
- Mase, G.E. Theory and Problems of Continuum Mechanics; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogata, S.; Li, J.; Yip, S. Ideal pure shear strength of aluminum and copper. Science 2002, 298, 807–811. [Google Scholar] [CrossRef] [Green Version]
- Mayer, A.E.; Krasnikov, V.S.; Pogorelko, V.V. Dislocation nucleation in Al single crystal at shear parallel to (111) plane: Molecular dynamics simulations and nucleation theory with artificial neural networks. Int. J. Plast. 2021, 139, 102953. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; SchiØtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Stukowski, A. Computational analysis methods in atomistic modeling of crystals. JOM 2014, 66, 399–407. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [Green Version]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef] [Green Version]
- Greeff, C.W.; Boettger, J.C.; Graf, M.J.; Johnson, J.D. Theoretical investigation of the Cu EOS standard. J. Phys. Chem. Solids 2006, 67, 2033–2040. [Google Scholar] [CrossRef]
- Popova, T.V.; Mayer, A.E.; Khishchenko, K.V. Evolution of shock compression pulses in polymethylmethacrylate and aluminum. J. Appl. Phys. 2018, 123, 235902. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J.; Yoon, J.W.; Nambori, R. Strain rate effect of high purity aluminum single crystals: Experiments and simulations. Int. J. Plast. 2015, 67, 39–52. [Google Scholar] [CrossRef]
- Nguyen, T.; Luscher, D.J.; Wilkerson, J.W. A dislocation-based crystal plasticity framework for dynamic ductile failure of single crystals. J. Mech. Phys. Solids 2017, 108, 1–29. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J. A deformation mechanism based crystal plasticity model of ultrafine-grained/nanocrystalline FCC polycrystals. Int. J. Plast. 2016, 86, 56–69. [Google Scholar] [CrossRef]
- Selyutina, N.; Borodin, E.N.; Petrov, Y.; Mayer, A.E. The definition of characteristic times of plastic relaxation by dislocation slip and grain boundary sliding in copper and nickel. Int. J. Plast. 2016, 82, 97–111. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Nguyen, T.; Fensin, S.J.; Luscher, D.J. Dynamic crystal plasticity modeling of single crystal tantalum and validation using Taylor cylinder impact tests. Int. J. Plast. 2021, 139, 102940. [Google Scholar] [CrossRef]
- Mayer, A.E. Micromechanical model of nanoparticle compaction and shock waves in metal powders. Int. J. Plast. 2021, 147, 103102. [Google Scholar] [CrossRef]
- Kuropatenko, V.F. New models of continuum mechanics. J. Eng. Phys. 2011, 84, 77–99. [Google Scholar] [CrossRef]
- VonNeumann, J.; Richtmyer, R.D. A Method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 1950, 21, 232–237. [Google Scholar] [CrossRef]
- Kuropatenko, V.F. On a difference method for the calculation of shock waves. USSR Comput. Math. Math. Phys. 1963, 3, 268–273. [Google Scholar] [CrossRef]
- Yalovets, A.P. Calculation of flows of a medium induced by high-power beams of charged particles. J. Appl. Mech. Tech. Phys. 1997, 38, 137–150. [Google Scholar] [CrossRef]
- Mayer, A.E.; Mayer, P.N. Evolution of pore ensemble in solid and molten aluminum under dynamic tensile fracture: Molecular dynamics simulations and mechanical models. Int. J. Mech. Sci. 2019, 157–158, 816–832. [Google Scholar] [CrossRef]
- Mayer, A.E.; Mayer, P.N. Strain rate dependence of spall strength for solid and molten lead and tin. Int. J. Fract. 2020, 222, 171–195. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Initial stage of fracture of aluminum with ideal and defect lattice. J. Phys. Conf. Ser. 2015, 653, 012094. [Google Scholar] [CrossRef]
- Moshe, E.; Eliezer, S.; Henis, Z.; Werdiger, M.; Dekel, E.; Horovitz, Y.; Maman, S.; Goldberg, I.B.; Eliezer, D. Experimental measurements of the strength of metals approaching the theoretical limit predicted by the equation of state. Appl. Phys. Let. 2000, 76, 1555. [Google Scholar] [CrossRef]
- Werdiger, M.; Eliezer, S.; Moshe, E.; Henis, Z.; Dekel, E.; Horovitz, Y.; Arad, B. Al and Cu dynamic strength at a strain rate of 5*108 s–1. AIP Conf. Proc. 2002, 620, 583. [Google Scholar] [CrossRef]
- Sharma, S.M.; Turneaure, S.J.; Winey, J.M.; Gupta, Y.M. Transformation of shock-compressed copper to the body-centered-cubic structure at 180 GPa. Phys. Rev. B 2020, 102, 020103. [Google Scholar] [CrossRef]
- Fratanduono, D.E.; Smith, R.F.; Ali, S.J.; Braun, D.G.; Fernandez-Pañella, A.; Zhang, S.; Kraus, R.G.; Coppari, F.; McNaney, J.M.; Marshall, M.C.; et al. Probing the solid phase of noble metal copper at terapascal conditions. Phys. Rev. Lett. 2020, 124, 015701. [Google Scholar] [CrossRef]
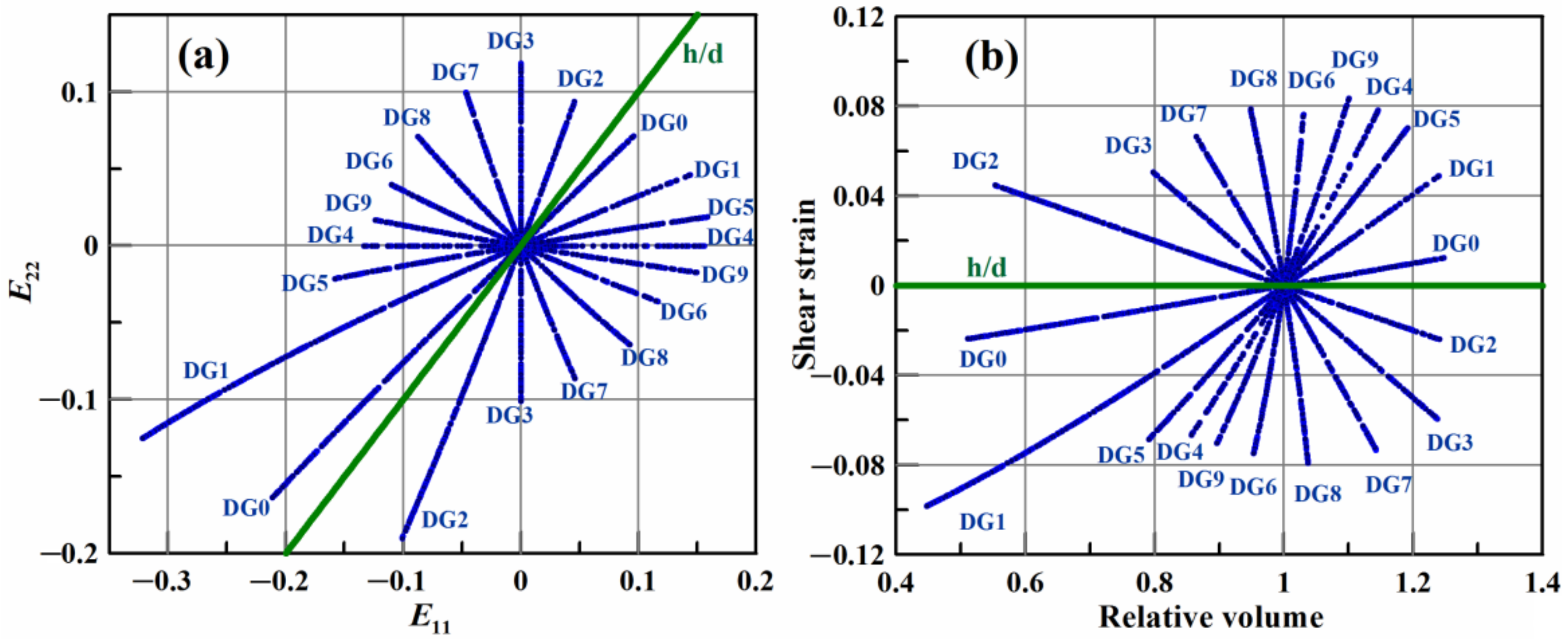

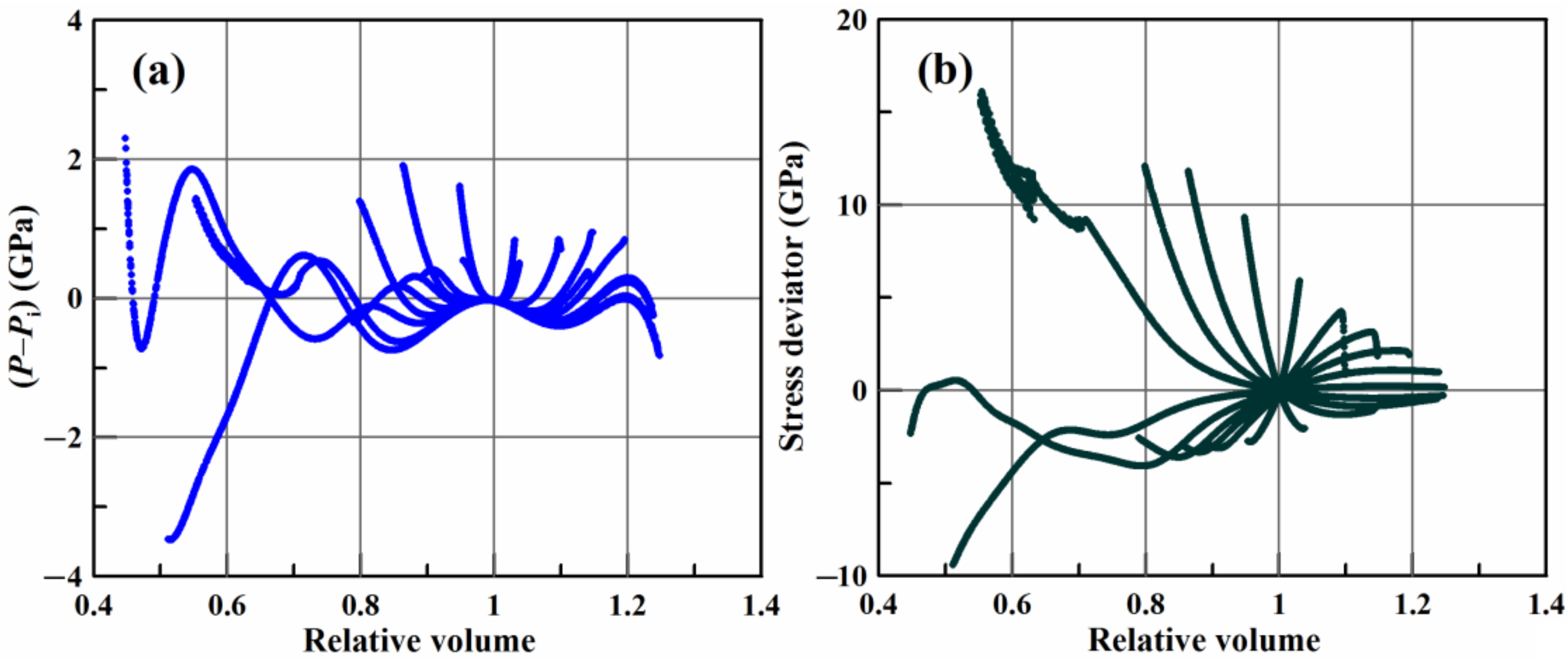
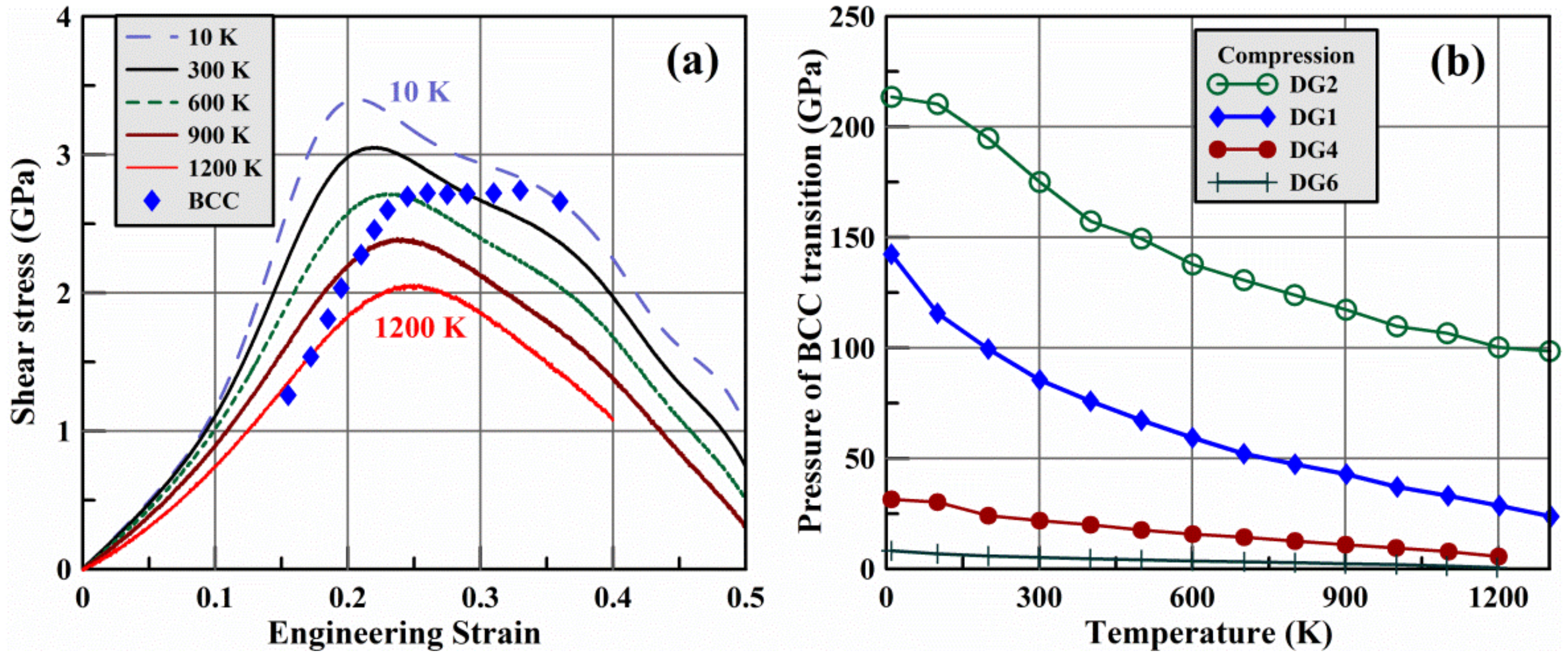

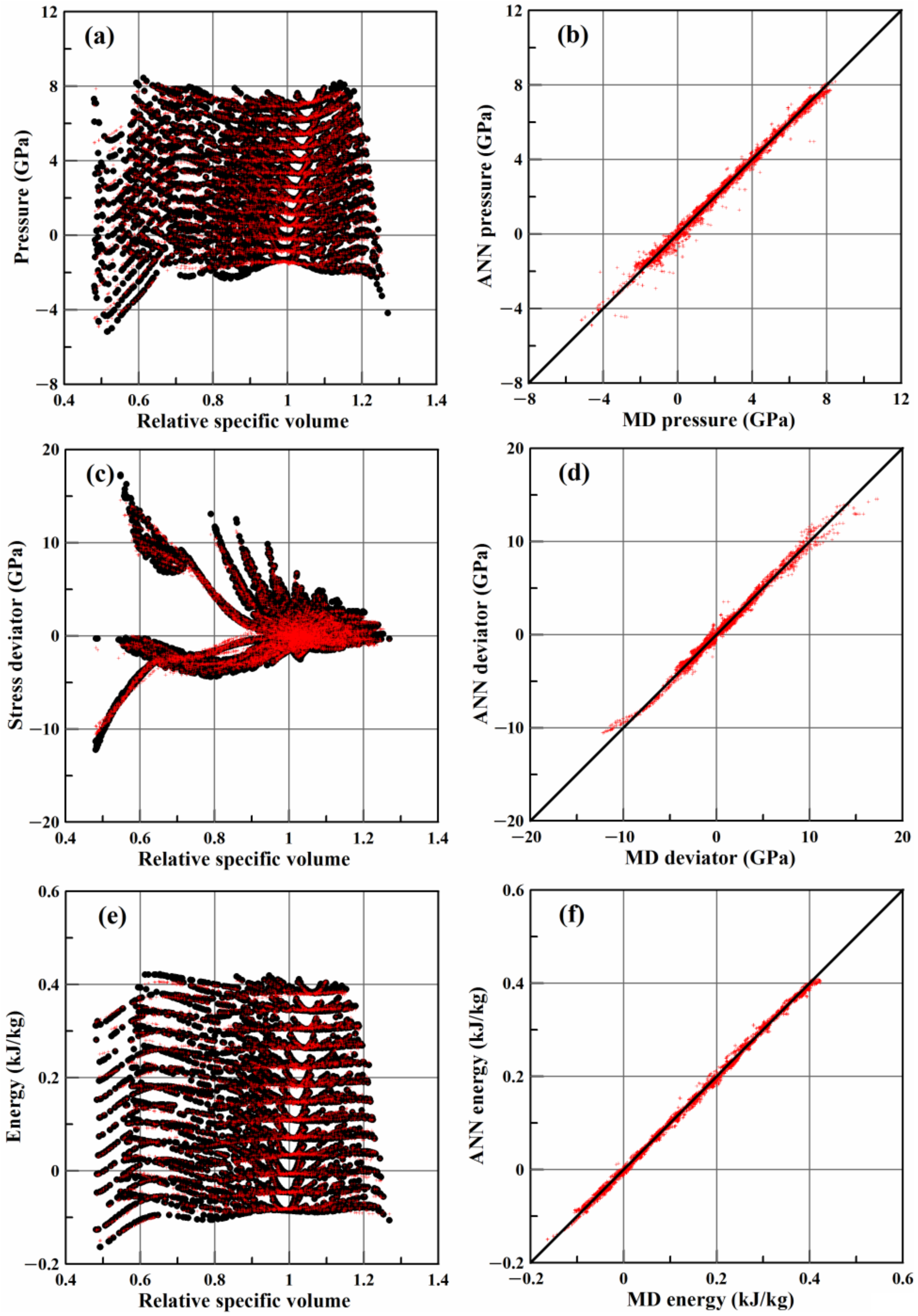
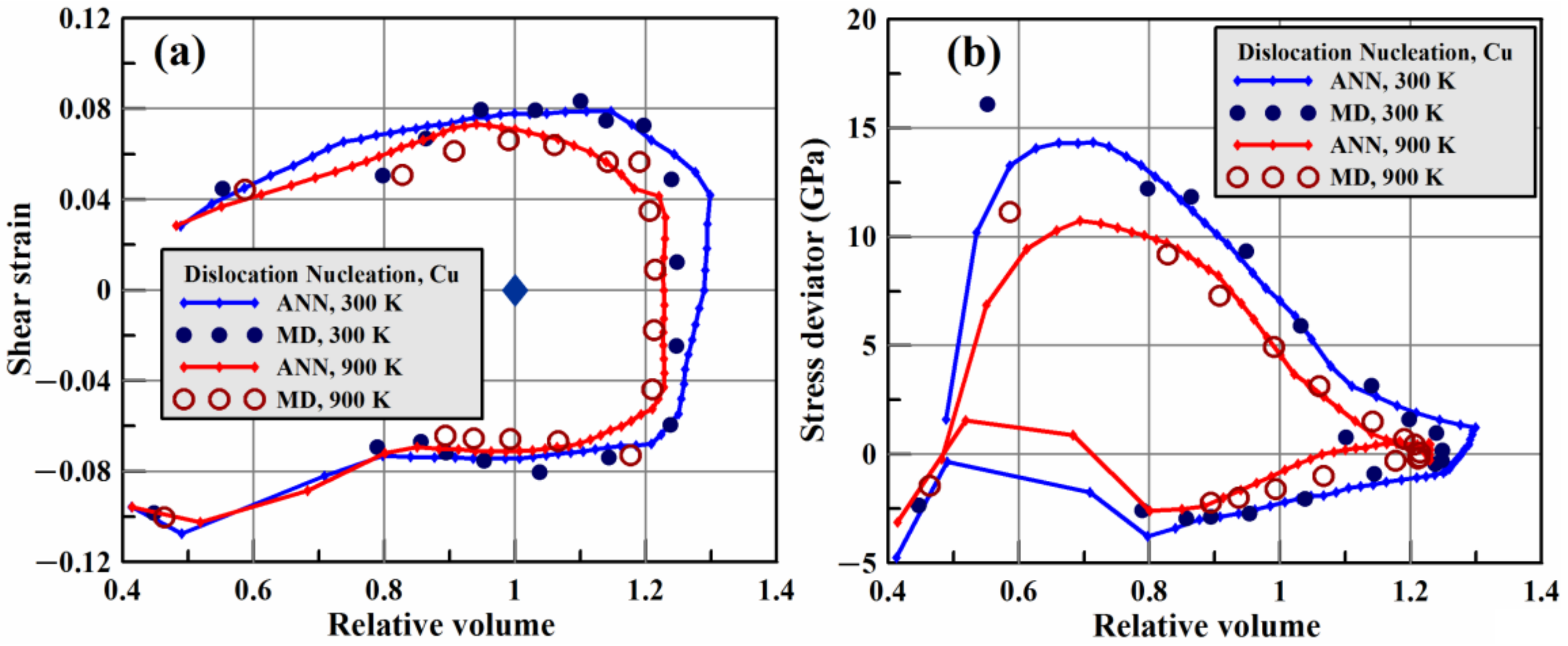
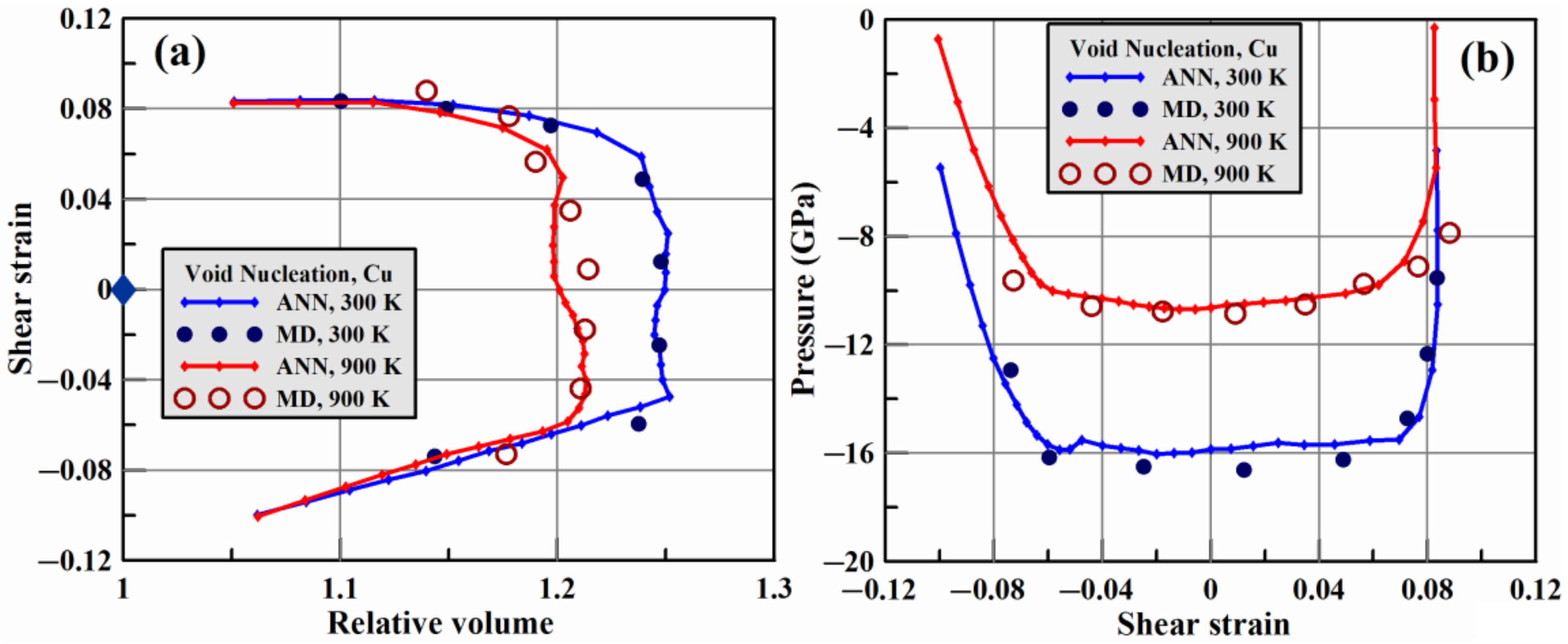
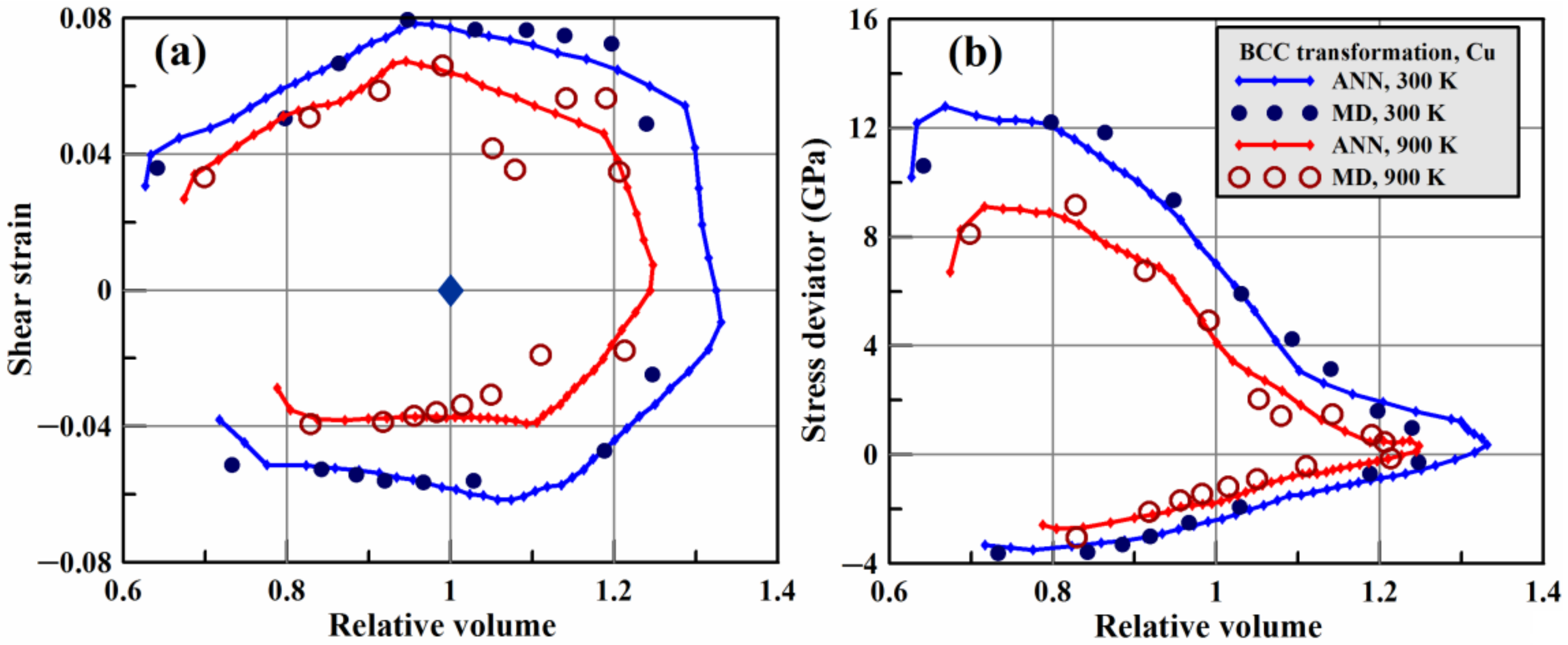
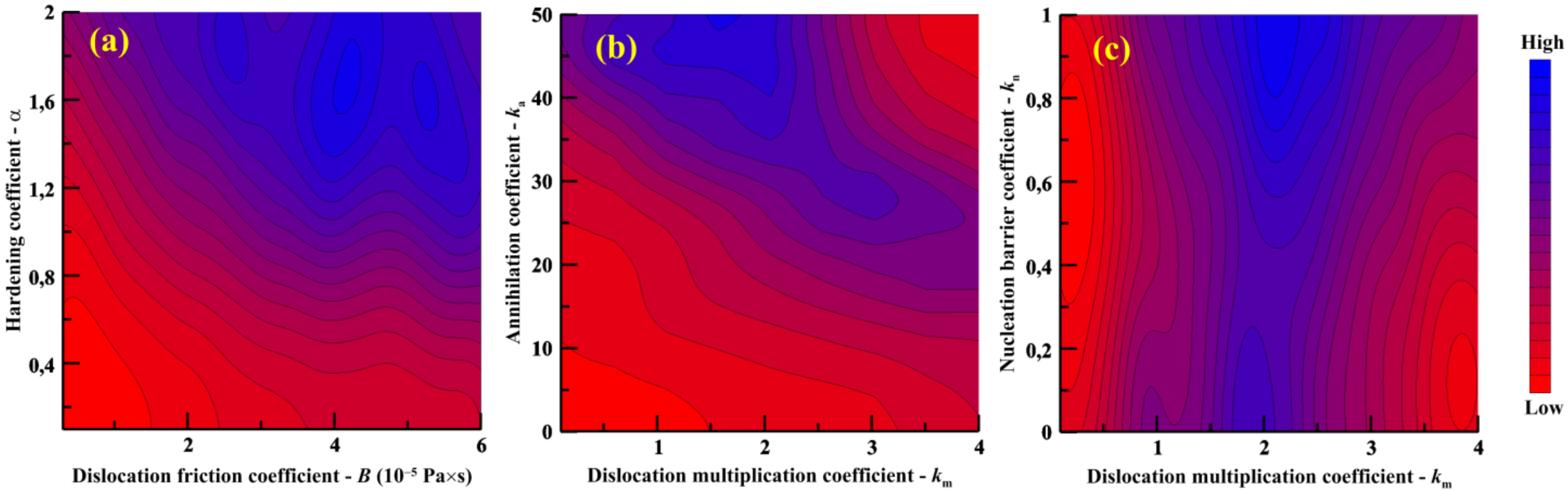
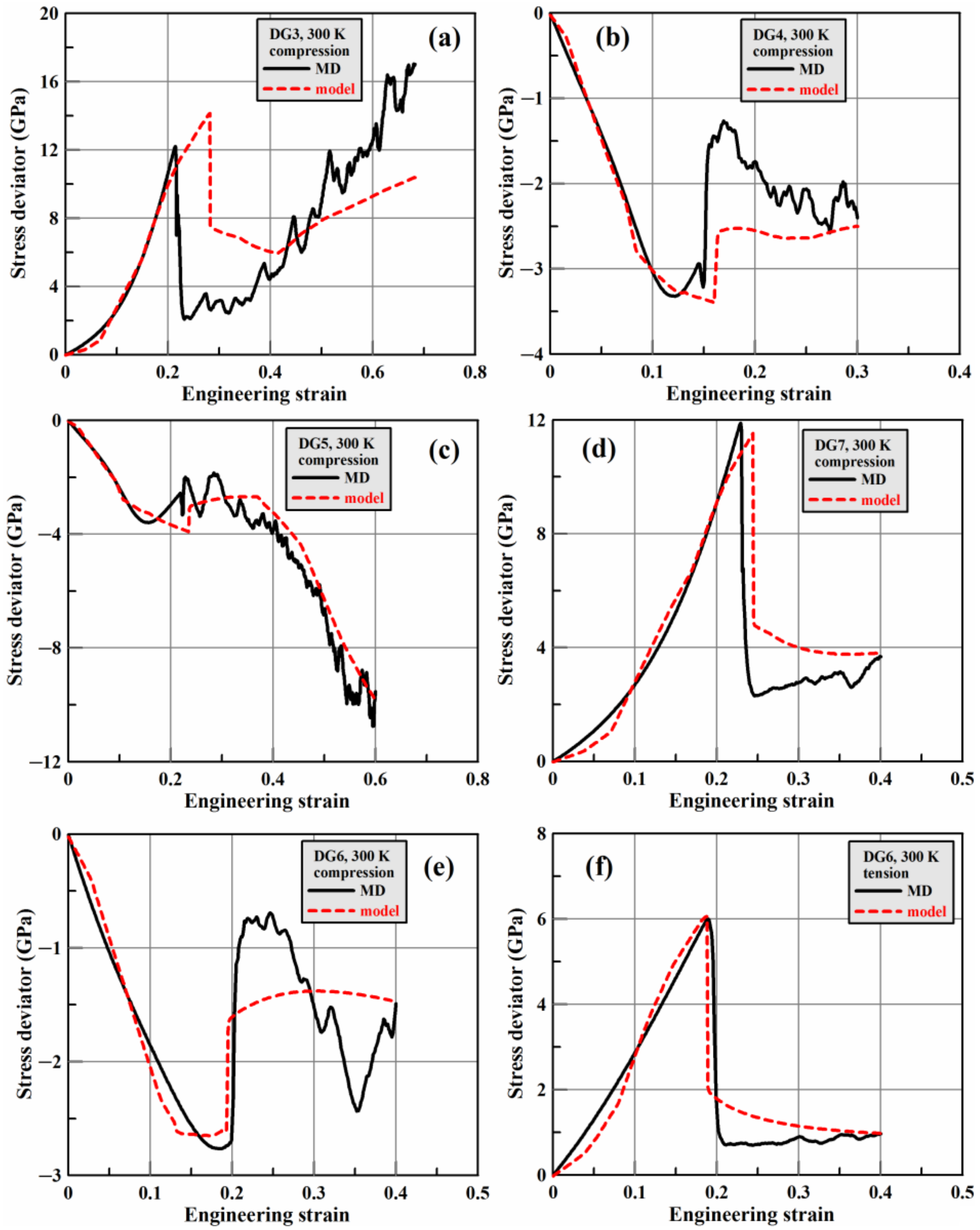

| Identifier | Axial Strain Rate (ns−1) | Transverse Strain Rate (ns−1) |
|---|---|---|
| DG0 | 0.4 | 0.3 |
| DG1 | 0.6 | 0.2 |
| DG2 | 0.2 | 0.4 |
| DG3 | 0 | 0.5 |
| DG4 | 1 | 0 |
| DG5 | 0.8 | 0.1 |
| DG6 | 0.6 | −0.2 |
| DG7 | 0.2 | −0.4 |
| DG8 | 0.4 | −0.3 |
| DG9 | 0.8 | −0.1 |
| Parameter | Value |
|---|---|
| 1.88 × 10−5 Pa × s | |
| 1.56 | |
| 1.4 | |
| 0.3 | |
| 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayer, A.E.; Lekanov, M.V.; Grachyova, N.A.; Fomin, E.V. Machine-Learning-Based Model of Elastic—Plastic Deformation of Copper for Application to Shock Wave Problem. Metals 2022, 12, 402. https://doi.org/10.3390/met12030402
Mayer AE, Lekanov MV, Grachyova NA, Fomin EV. Machine-Learning-Based Model of Elastic—Plastic Deformation of Copper for Application to Shock Wave Problem. Metals. 2022; 12(3):402. https://doi.org/10.3390/met12030402
Chicago/Turabian StyleMayer, Alexander E., Mikhail V. Lekanov, Natalya A. Grachyova, and Eugeniy V. Fomin. 2022. "Machine-Learning-Based Model of Elastic—Plastic Deformation of Copper for Application to Shock Wave Problem" Metals 12, no. 3: 402. https://doi.org/10.3390/met12030402
APA StyleMayer, A. E., Lekanov, M. V., Grachyova, N. A., & Fomin, E. V. (2022). Machine-Learning-Based Model of Elastic—Plastic Deformation of Copper for Application to Shock Wave Problem. Metals, 12(3), 402. https://doi.org/10.3390/met12030402






