Abstract
The deformation behavior of aluminum single crystals subjected to compression along the [100] and [110] directions is numerically examined in terms of crystal plasticity. A constitutive model taking into account slip geometry in face-centered cubic crystals is developed using experimental data for the single-crystal samples with lateral sides coplanar to certain crystal planes. Two sets of calculations are performed using ABAQUS/Explicit to examine the features of plastic strain evolution in perfectly plastic and strain-hardened crystals. Special attention is given to the discussion of mechanical aspects of crystal fragmentation. Several distinct deformation stages are revealed in the calculations. In the first stage, narrow solitary fronts of plastic deformation are alternately formed near the top or bottom surfaces and then propagate towards opposite ends to save the symmetry of the crystal shape. The strain rate within the fronts is an order of magnitude higher than the average strain rate. The first stage lasts longer in the strain-hardened crystals, eventually giving way to an intermediate stage of multiple slips in different crystal parts. Finally, the crystal shape becomes asymmetrical, but no pronounced macroscopic strain localization has been revealed at any deformation stage. The second stage in perfectly plastic crystals relates to abrupt strain localization within a through-thickness band-shaped region, accompanied by macroscale crystal fragmentation. Stress analysis has shown that pure compression took place only in the first deformation stage. Once the crystal shape has lost its symmetry, the compressive stress in some regions progressively decreases to zero and eventually turns tensile.
1. Introduction
Although most metallic materials have a polycrystalline structure, single-crystal research plays a crucial role in understanding the basic deformation mechanisms operating at different length scales. New knowledge of the inelastic deformation gives rise to the development of physically based constitutive models, experimental methods, and, consequently, physically sound deformation theories, which is of great importance for predicting the deformation and fracture of real materials. Based on advanced experimental techniques, modeling provides a bridge between the microstructure characterization, mechanical properties, and deformation response. It is highlighted that analyzing the strain-induced relief with experimental techniques alone cannot provide us with an unambiguous interpretation of shear patterns in the bulk of a single crystal [1]. Moreover, the contributions of individual factors that are difficult to evaluate experimentally can be analyzed numerically using model representations.
The mechanical behavior of a single crystal lays the groundwork for the numerical description of the co-deformation of multiple microstructure elements in a polycrystalline aggregate. Several basic theories proposed to quantitatively describe the elasto-plastic deformation of polycrystalline metals were formulated based on the generalization of a large number of experiments on single crystals [2,3,4,5,6]. The most common strictly crystallographic schemes were proposed by Sachs [4], Taylor [5], and Bishop and Hill [6]. The Sachs model assumes that each grain of a polycrystal is found in the same stress state, whereas Taylor–Bishop–Hill theories follow this assumption in a somewhat opposite manner, treating plasticity from strain homogeneity. It is worth noting, however, that due to the rough estimation of the overall material properties, these models are not reliable for complex nonlinear structures despite the modifications proposed in many of them [7,8,9].
Two-dimensional studies of the tensile behavior of a single crystal were pioneered by Peirce et al. [10]; they performed the first crystal plasticity (CP) finite element (FE) simulations, while Becker et al. [11] were the first to employ the CP finite element method (FEM) in 3D, considering 12 slip systems of a face-centered cubic (FCC) single crystal subjected to channel-die deformation. Now, a number of plasticity models are available ranging from simple Sachs and Taylor models and their modifications [2,3,4,5,6,7,8,9] to multiscale approaches, involving, e.g., an atomistically informed flow rule incorporated into a CP constitutive model [12,13,14]. These models enable research on the inelastic deformation mechanisms and processes that are hard to see in the experiments.
Numerical investigations on single crystals under loading may be divided into two groups. A large group of studies aims to calibrate material parameters and validate the computational models employed for the analysis of loaded polycrystals [15,16,17,18]. Another group develops new constitutive models and focuses on gaining valuable insights into basic deformation mechanisms [9,10,11,12,13,14].
Senas [14] compared the static and dynamic properties of screw dislocations for tungsten, undertaking extensive atomistic simulations, and concluded that a purely static consideration of the dislocation core was insufficient for predicting the dislocation dynamics. As the dislocation mobility functions obtained were found to be unsuitable in a larger-scale CP model due to high strain rates commonly found in molecular dynamics techniques, the constitutive information was obtained from kinetic Monte Carlo simulations or analytically. The multiscale approach proposed by Cereceda et al. [12] incorporates a comprehensive treatment of non-Schmid effects (twinning/anti-twinning asymmetry plus the effects due to non-glide stress components), a flow rule relying on the thermally activated screw dislocation mobility, and the usage of interatomic potentials for computing free parameters in a standard rate-dependent finite-deformation non-associated CP model. Forest and Rubin [19] have offered a new rate-independent CP model incorporating multi-criterion formulation, exact strain rate independence, the absence of a consistency condition, and smooth elasto-plastic transition. They have validated the model, simulating the cyclic behavior of pure copper and nickel-based superalloy single crystals.
Considerable attention has been paid to FCC single crystals. Roters et al. [20] examined strain localization in an Al single crystal under simple shear experimentally and numerically. Khan et al. [21] studied the strain rate and orientation effects on the deformation response of aluminum single crystals under uniaxial compression using a one-element CPFEM. Employing an elastoviscoplastic CPFE model, Trusov et al. [22] demonstrated that a homogeneous single crystal subjected to uniaxial compression was divided into subvolumes characterized by different plastic shear rate intensities and lattice orientations. Considering 3D single crystals of different initial orientations, Schacht et al. [23] showed that the growth and deformation of voids were closely related to crystal orientation. Recently, Wang et al. [24] simulated substructure formation in a multi-pass rolled aluminum single crystal at the micro- and macroscales using a submodeling technique.
To a large extent, the renewed interest in this kind of research is kindled by the development of advanced manufacturing techniques producing metallic and/or composite components characterized by a complex hierarchical microstructure. For instance, additively manufactured aluminum alloys are characterized by much more pronounced structural inhomogeneity and anisotropy of the physical and mechanical properties than the traditional cast alloys of the same composition [25,26]. Friction stir welding creates different microstructural zones in a processed material, including a quasi-uniform distribution of grains in the base metal and a complex texture in the weld nugget and in the adjacent regions with characteristic interfaces between intermixing zones [27,28]. Another example is provided by surface-modified metals where a specific microstructure formed in the surface layers suppresses or intensifies certain deformation mechanisms operating at the micro- and mesoscales and thus affects the overall material response [29]. As a matter of fact, in all cases considered, we have a new composite material whose deformation behavior is controlled by its complex hierarchical microstructure. An accurate prediction of the deformation behavior of advanced materials requires incorporating the deformation mechanisms developing at low scales. In this context, there is stringent demand for experimental and numerical studies of single crystals, which are elementary structural units of most polycrystalline metals.
While extensive numerical data on FCC single crystals have been attained so far, there are still issues that have not been appropriately addressed in the simulations. Of particular interest are coupled effects of crystal orientation and strain hardening on the evolution of inhomogeneous stress and strain fields resulting in crystal fragmentation at micro- and macroscales. CPFEM analysis is a powerful tool to gain this kind of data, although at high computational costs. Researchers commonly have to find a compromise between the high mesh resolution and sufficiently small strain increments to reproduce the fragmentation process with reasonable details. The problem is even more challenging for a simultaneous description of micro- and macroscale deformation [24]. An effective way to reduce computational costs is the simulation of quasistatic deformation in terms of explicit dynamics. Each increment of the explicit calculation is computationally much cheaper than that of the implicit solution. Another valuable opportunity the dynamic simulations offer is reproducing the crystal deformation with a high temporal resolution.
In this contribution, we employ the dynamic approach to investigate the fragmentation of aluminum single crystals under compression. The CPFEM calculations are performed for four specific crystal orientations with the compression applied along the [001] or [110] directions similarly to the experiments. The experiments on aluminum single crystals providing the background for numerical modeling are reviewed in Section 2. The CPFE models and their numerical implementation are discussed in Section 3. Section 4 is organized into two subsections where calculation results for aluminum single crystals with and without strain hardening are presented. Along with an experimentally based model of a strain-hardened crystal realistically reproducing the deformation behavior, a perfect plasticity model is used to artificially enforce plastic strain localization. The comparison of the two models enables separating the strain-hardening effects on the development of plastic deformation, which cannot be attained experimentally. Finally, the stress analysis related to crystal fragmentation is presented in Section 5.
2. Experimental
Bryhni Dæhli et al. [30] highlighted the inherent anisotropy of single crystals due to the discrete nature of the plastic slip. The extensive literature reveals a tendency of loaded single crystals towards strain localization and fragmentation [10,11,17,20,22,24,31,32,33,34,35,36]. The former is related to the crystal’s ability to accumulate slip in narrow band-like zones whose orientation is independent of the crystal lattice orientation [10,11,36,37,38,39,40]. This kind of plastic instability referred to as non-crystallographic shear banding is particularly pronounced in FCC crystals with low stacking fault energy [39,40]. The crystal fragmentation is related to the tendency of plastic deformation in different regions of an initially homogeneous crystal to proceed in different ways, resulting in the formation of specific zones with different sets of active slip systems. This phenomenon is most clearly observed in single crystals with relatively high stacking fault energy under compressive loading [24,31,32,33,34,41]. Basson and Driver [42] and Petryk and Kursa [43] distinguished deformation banding as a specific mode of single-crystal deformation. In contrast to localized shear bands, the deformation bands covered the entire crystal, with the crystal lattice within the bands being rotated relative to the rest of the material.
Numerous experimental data on aluminum single crystals under compression are presented in a series of publications [11,21,31,33,34,37,41,42,44,45,46]. Let us briefly review the experimental results taken as a basis for constructing the numerical model; the experimental procedure is detailed elsewhere [31,32,33,34].
Aluminum single crystals were grown using the Bridgeman method. Their orientations were controlled by backscattering patterns to the accuracy of 2 degrees on an IRIS-3 XRD instrument (Moscow, Russia). The samples of 3 × 3 × 6 mm3 were compressed at a constant strain rate of 3·10−4 s−1 at room temperature on an Instron ElektroPuls E100000 universal testing machine (Instron, Norwood, MA, USA), with the compression axis aligned with the [001] or [110] crystal directions found within the corners of the standard stereographic triangle. Two sets of experiments were performed in the former case, where the sample’s lateral faces were parallel to the (100) and (010) or (110) and crystal planes. In the latter case, the opposite lateral faces were coplanar to the and (001) planes or and planes, respectively. The four sets of experimental schemes (hereinafter referred to as Orientations I–IV) are listed in Table 1 and shown schematically in Figure 1a,d and Figure 2a,d.

Table 1.
Single-crystal geometry.
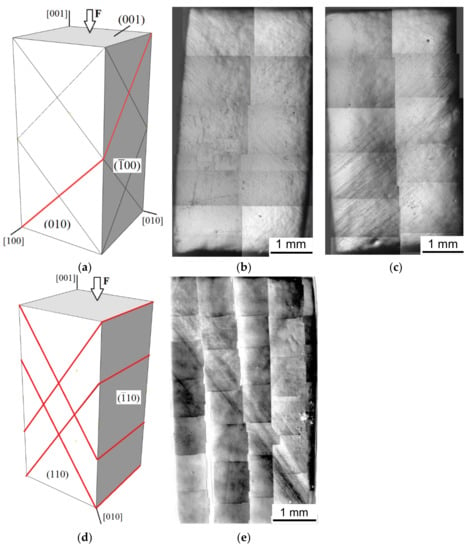
Figure 1.
Single crystals with the {100} (a–c) and {110} (d,e) lateral faces compressed along the [001] direction: crystallographic schemes of {111} slip planes and lines of their intersection with crystal surface (a,d); optical images of crystal lateral faces coplanar with the {100} planes at a strain of 0.07 (b,c) and with the (110) plane at a strain of 0.05 (e).

Figure 2.
Single crystals with the and (001) (a–c) or and lateral faces (d–f) compressed along the [110] direction: Crystallographic schemes of slip planes and directions (a,d) and optical images of the (b), (001) (c), (e), (f) lateral faces at ε = 0.06.
Figure 1a–c presents the results for a single crystal compressed along an axis of symmetry of the fourth order, [001]; its lateral faces also have a cubic orientation (Orientation I). Single crystals of FCC metals and alloys in the chosen orientation have the highest symmetry among all possible combinations of orientations of the loading axis and single-crystal faces.
Figure 1a shows the lines of intersection of the {111} slip planes with the surface of a [001] single crystal with the {100} lateral faces. Analytically, eight of twelve slip systems possessing the same Schmid factor equal to 0.408 should become simultaneously active under the same stress. The other four slip systems possessing a zero Schmid factor remain inactive under this kind of loading. In a single crystal with Orientation I, four close-packed slip planes intersect with vertical faces along two mutually perpendicular lines coinciding with close-packed slip directions. Due to the symmetry of the octahedral slip systems with respect to the [001] loading axis, the intersection of the {111} planes with the lateral faces of the sample should lead to the formation of the same sets of slip bands on all four faces, with each set forming an angle of 45° with a corresponding face.
The corresponding experimental images of the deformation relief on the lateral faces of the single crystal with Orientation I are presented in Figure 1b,c. A pack of slip bands clearly observed in Figure 1b,c are typical elements of the strain-induced relief seen on the two adjacent crystal faces. An analysis of slip band patterns on the free surfaces of the single crystal compressed to a strain of 0.07 showed that, as expected, two sets of slip bands are formed on each lateral face and are closely oriented to the intersections of the {111} planes with the faces. However, a nonhomogeneous deformation breaks the expected symmetry of the slip band patterns observed on the crystal sides. As can be seen from Figure 1b,c, slip bands of one set are more often observed on the face. In other words, compression of a highly symmetric single crystal is accompanied by strain asymmetry clearly observed in the morphology of the deformation relief.
Orientation II is formed by the rotation of the crystal frame by 45° relative to the loading axis (Figure 1d). As in the previous case, this orientation is characterized by eight equally loaded octahedral slip systems. Figure 1d schematically shows the traces of the slip planes on the {110} crystal surfaces of the [001] sample.
If the deformation were homogeneous, one would expect the formation of uniformly distributed horizontal and intersecting slip bands on the lateral faces of the sample. However, despite the high symmetry of the single crystal relative to the loading axis, one of the two intersecting macroscopic bands of localized strain seen on the (110) lateral face is much more pronounced than the other (Figure 1e) [32,34,41]. The former has a higher density of slip bands than the latter, and both appear as macroscopic bands of localized deformation. There is also a third set of slip bands localized predominantly in the top and bottom parts of the {110} faces. Note that, once appeared, the strain asymmetry is clearly observed in the morphology of strain-induced relief: One band of localized deformation hinders the development of the others.
Figure 2a presents the crystallographic scheme for the single crystal with the [110] compression axis and the and (001) lateral faces (Orientation III). The corresponding deformation patterns formed on two adjacent lateral faces at a strain of ε = 0.06 are shown in Figure 2b,c. Theoretical estimates suggest that the slip occurs on the equally loaded (111) and planes, both characterized by two active slip directions. As a result, the deformation of a single crystal of this orientation is fully ensured by four active slip systems.
Following the schematics in Figure 2a, the active planes come up to the lateral faces of the sample in the form of intersecting slip bands tilted at an angle to the loading axis, while the traces of the {111} planes on the (001) faces are horizontal. Thus, the slip bands observed in the surface images in Figure 2b,c are mostly formed by slip on the (111) and slip planes. Theoretically, two equivalent systems of intersecting slip bands are to form on the faces. However, an asymmetric deformation pattern observed on the crystal faces (Figure 2b) suggests that the slip systems at work in different crystal parts are no longer equally loaded. Notably, two sets of slip bands originating near the top and bottom corners intersect at an angle, bordering the weakly deformed regions in the vicinity of punches. Logically, it is the stress concentration in the vicinity of the punches that causes this kind of nonuniform deformation.
The optical images in Figure 2e,f show slip band patterns on the faces of a single crystal with Orientation IV at ε = 0.06. Similar to Orientation III, there is macroscopic fragmentation of the sample. The fragmentation morphology correlates with the theoretical predictions of the slip evidence on the crystal surface (cf. Figure 2d,e). However, the rotation of the crystal frame about the [110] axis to change the orientation from III to IV results in a pronounced asymmetry of the slip band pattern. The asymmetric pattern is well defined on the crystal face, where the slip planes emerge onto the surface (Figure 2e). This allows us to conclude that the slip system is active, where the slip direction is parallel to the faces. Accordingly, no localized slip bands caused by the slip in this slip system are identified on the face (Figure 2f). In other words, in those parts of the single crystal where the slip is active on one family of octahedral planes, it is weak on the conjugate family. In the family of the (111) slip planes, slip predominantly occurs on the slip system. The shear bands caused by this kind of slip prevail on the face (Figure 2f), where they are nearly uniformly distributed. However, a slightly higher density of slip bands is observed near the sample corners, which could be caused by geometrically induced stress concentrations in the vicinity of the punches.
3. Numerical Model
3.1. Boundary-Value Problem, Geometry, and Loading Conditions
Finite element simulations were performed for model single crystals of the same geometry and orientations as those of the experimental samples. A 3 × 6 × 3 mm3 rectangular geometrical model (Figure 3a) was approximated by a regular mesh consisting of 432,000 hexahedral elements (C3D8R).
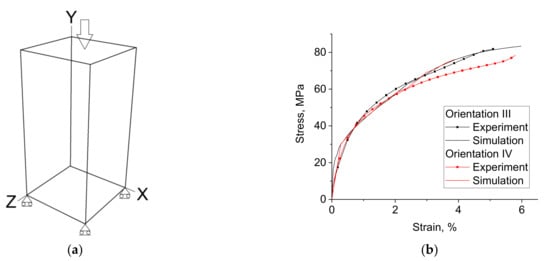
Figure 3.
Schematic of a FE model with the applied boundary conditions (a) and stress–strain curves for single crystals with lateral faces (Orientation III) and (Orientation IV) compressed along [110] direction (b).
The boundary-value problem (BVP) was solved numerically in a dynamic formulation [47,48,49] to study the evolution of the stress–strain fields in the single crystals under compression. Formulated in a strong form, the BVP includes the governing equations of mass and momentum conservation
completed by kinematic relations
and constitutive equations in the form of Hooke’s law
where is the displacement vector, is the relative volume, and are the initial and current mass density values, and are the stress and strain rate tensor components, and are the elastic and plastic strain rate tensors, and is the matrix of elastic moduli. The upper dot denotes a time derivative, and the Einstein notation is used for repeated indices.
The kinematic boundary conditions were set on the model top surface ST to simulate compression along the Y-axis (Figure 3a)
where is the loading velocity. In order to eliminate wave effects unphysical for quasistatic processes, the loading velocity was linearly increased up to its peak value and then kept constant. The surface displacements on the model bottom surface SB were constrained in the Y-direction
and were not constrained in the two other directions. The model lateral faces SL were free of any external load
where is the surface normal.
3.2. Constitutive Model
It is reasonable to describe the elasto-plastic behavior of aluminum single crystals in terms of crystal plasticity to consider mechanical anisotropy attributed to the crystal structure. Let us formulate the CP constitutive equations relative to a local frame with the axes coinciding with the [100], [010], and [001] crystal directions.
Taking into account the decomposition of the strain rate tensor into elastic and plastic components (Equation (3)), Hooke’s law (4) takes the form
where is related to the velocity vector by kinematic Equation (3). Due to the symmetry inherent in the FCC crystal lattice, has twelve non-zero components, with three of them being independent.
In the CP framework, the plastic strain under external load is thought to be realized by means of shear deformation due to a slip of close-packed atomic planes along each other. The components of the plastic strain rate tensor are related to the shear strain rate in the active slip systems by the geometrical equations
where and are the components of slip direction and slip plane normal vectors determining the orientation of the slip system α in the crystal frame. Twelve <111>{110} slip systems are potentially active in the FCC crystals. The shear strain rate for all slip systems follows a power law
where the reference shear strain rate and the exponent are the parameters controlling the strain rate sensitivity. A slip system is assumed to be active when the resolved shear stress is equal to or greater than the critical resolved shear stress (CRSS) . Of primary importance is the CRSS description with a proper account of the strengthening mechanisms. A large number of phenomenological and physically based CRSS models are reported for aluminum alloys (see, e.g., [17]). The more effects are taken into account, the more fitting and physically based parameters have to be determined. Moreover, iterative methods employed in CP calculations additionally increase the computational costs. Therefore, it is reasonable to use simplified constitutive models with a reduced number of parameters where possible. In this paper, an isotropic hardening of aluminum single crystals is calculated as
where is the initial CRSS value, the same for all slip systems, and the second term of the sum describes the strain hardening as
where a1, a2, b1, and b2 are chosen to fit the experimental stress–strain curves (Figure 3b). The model parameters and material constants used in the simulations are C1111 = 108 GPa, C1122 = 61 GPa, C2323 = 28 GPa, = 2 MPa, a1 = 73 MPa, a2 = 0.07, b1 = 16 MPa, and b2 = 0.002 [50]. In perfect plasticity calculations, was set to zero and = 30 MPa.
3.3. Numerical Implementation
The BVP problem (1)–(7) is solved numerically using an ABAQUS/Explicit FE software package (Dassault Systèmes, Velizi, France), where the constitutive model (8)–(12) is implemented through a VUMAT User Subroutine. ABAQUS software is widely employed for numerical research of aluminum single crystals, including the analysis of hardness anisotropy [51], deformation behavior in simple compression [22] and multi-pass rolling [24], the validation of new CP lattice particle method [52], etc., although for the most part the static formulation of BVPs is considered.
The governing Equations (1)–(3) and boundary conditions (5)–(7) are formulated with respect to the sample frame, while the constitutive Equations (8)–(12) are written relative to the crystal frame associated with [100], [010], and [001] crystal directions [26,49]. The advantage of numerical implementation in ABAQUS/Explicit is that the tensor and vector components are automatically rotated from the global to the local coordinate system before they are imported to VUMAT and vice versa after the constitutive behavior is calculated. The stress change due to a rigid rotation is eliminated through the Naghdi–Green derivative.
The time step is chosen to satisfy the Courant–Friedrichs–Lewy condition Δt = kC⋅hmin/Cl, where hmin is the minimum step of the mesh, Cl is the longitudinal velocity of sound, and kC is the Courant ratio. The stability condition implies that an elastic wave within one time step would not cover the distance longer than the minimum mesh step.
A simultaneous solution of Equations (8)–(12) at each time increment calls for an iterative procedure. We employed the method of simple iterations, which provided fast solution convergence with reasonable accuracy. An important condition for the dynamic and static solutions to converge is the use of rate-independent constitutive models in dynamic simulations, where load velocities are artificially increased. The strain-rate sensitivity parameters and appearing in Equation (10) were chosen to meet this requirement.
A material is assumed to be quasi-rate-independent for large values [47], which may, however, have an adverse effect on the iteration convergence. Based on the results for various strain rates [49], the value was set 10. Test calculations showed that for = 10 the strain rate sensitivity was effectively eliminated in the range of strain rates up to 103 s–1.
The reference shear strain rate was calculated individually for each finite element as , where is the local equivalent strain rate and [26,49]. Keeping in mind that the strain rate in the strain localization regions can deviate from the average value by several orders of magnitude, the equation for ensures a sufficient shear strain rate in any region to fit plastic strain.
4. Calculation Results
4.1. Perfect Plasticity
It is known from experimental observations that aluminum single crystals possessing high stacking fault energy do not exhibit strong localization at a low strain but demonstrate rather diffuse necking [31,32,33,34]. In order to artificially enforce plastic strain localization, we began with the analysis of single-crystal deformation in terms of perfect plasticity. While the perfect plasticity behavior is rather unrealistic for FCC metals, this study is useful in validating the numerical model. Particularly, the yield stress values and geometrical features of slip in crystals with different orientations can be directly compared to analytical estimates. Moreover, perfect plasticity simulations enable separating the effects of strain hardening on the plastic strain localization, which is impossible to perform experimentally.
The yield stresses initiating slip in the single crystals with Orientations I–IV (Table 1) were compared with analytical values obtained from Schmid’s law:
where and represent the angles between the compression axis and the slip plane normal vector and the slip direction vector, respectively.
In the model crystals, the octahedral slip systems are characterized by the same set of and . All potentially active slip systems are equally loaded and, thus, expected to be simultaneously involved in plastic deformation at the same level of applied stress. Table 2 compares the stresses initiating slip in the model single crystals with different orientations with the analytical estimates obtained by Equation (13) with = 30 MPa. The value of ⟨⟩ is calculated as von Mises stresses averaged over the computational volume. The discrepancy between the analytical and calculated values of the yield stresses does not exceed 2%, which validates the model and its numerical implementation.

Table 2.
Analytical and calculated yield stresses in aluminum single crystals with different orientations.
Recall that Orientations I and II are identical in terms of the slip system activation since they are obtained from one another by rotating the crystal frame around the [001] axis by an angle of 45°. Since the compression axis coincides with the [001] direction, angles and in Equation (13) and the set of potentially active slip systems remain unchanged after rotation. However, orientations of the slip systems with respect to the crystal faces change, thus affecting the nonuniform deformation patterns formed on the crystal faces due to their intersection with the active slip planes. Similarly, Orientations III and IV are identical to each other in terms of the slip system activation, while anticipated slip band patterns on the crystal faces would be different. Active slip systems of all orientations are characterized by the same Schmid factor, while the number of potentially active slip systems in the crystals loaded along the [001] axis is two times larger than that in the crystals loaded along the [110] direction.
In the absence of strain hardening, equivalent plastic strain fields demonstrate abrupt localization in narrow through-thickness band regions (Figure 4 and Figure 5). Generally, plastic strain instability obtained in calculations in the form of strain localization can result from different kinds of nonlinearity, i.e., a mathematical nonlinearity of constitutive equations, geometrical features (notches, holes, variable cross-section, etc.), interface asperities, microstructural inhomogeneity, nonuniform loading conditions, and so on. The instability of plastic flow in CPFEM simulations has been thoroughly discussed by many researchers [10,20,26,39,53,54].
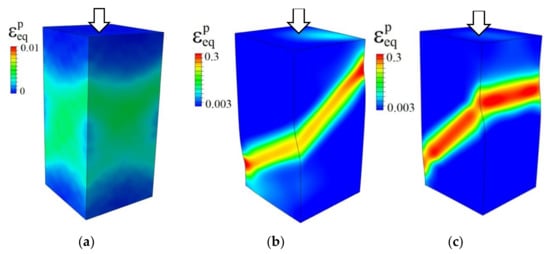
Figure 4.
Equivalent plastic strain fields in model single crystals with {100} (a,b) and {110} lateral faces (c) compressed along the [001] axis up to a strain of 0.003 (a) and 0.05 (b,c).
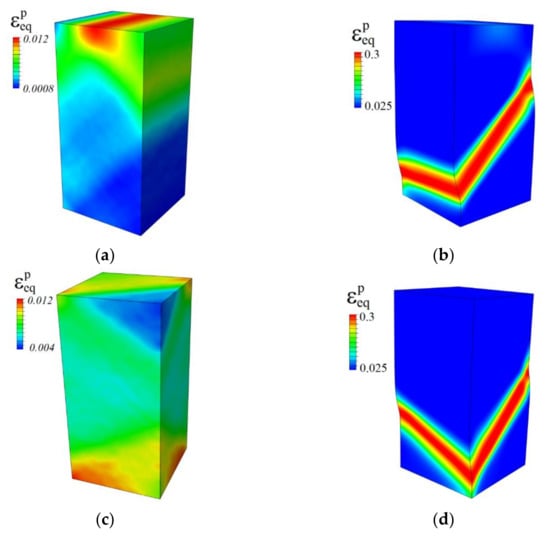
Figure 5.
Equivalent plastic strain fields in model single crystals with the and (001) (the crystal view in (b) is rotated by 90° with respect to (a)) (a,b) and and lateral faces (c,d) compressed along the [110] axis up to a strain of 0.0035 (a,c) and 0.06 (b,d).
Let us analyze plastic strain patterns in the crystals loaded along the [001] axis (Figure 4). The specimen regions adjacent to the top and bottom surfaces and located in the middle part of the crystal are loaded in different ways, which gives rise to the crystal fragmentation into several parts moving relative to each other under compression. The symmetry of potentially active slip systems with respect to the axis of loading would lead to the same symmetrical plastic strain patterns observed on the crystal lateral faces. However, the calculation results show that this is true at the onset of plastic deformation only, which is illustrated for the crystal with {100} faces in Figure 4a. On further loading, plastic deformation develops nonuniformly, breaking the symmetry of the strain patterns and leading to rapid crystal fragmentation. Further plastic deformation mostly localizes within narrow through-thickness regions evident on the surface as macroscopic bands of localized plastic strain (Figure 4b,c). We believe that this is the dynamic formulation of the BVP that enables reproducing the nonsymmetrical mode of single-crystal fragmentation, much similar to the experimental evidence, while the static problem ensures a symmetrical solution to the plastic strain distributions [22]. The wave effects unavoidable in dynamic simulations give rise to small perturbations of the local stress, strain, and kinematic fields. Being neglected in the macroscopic sense, these local perturbations break the symmetry of the stress–strain fields. Once a primary band-like region of strain localization is formed, further plastic deformation develops there in an abrupt manner.
The orientations of the macroscopic bands of localized strain coincide with the traces of one of the active slip planes on the crystal faces. Particularly, in the crystal with {100} faces, the macroscopic bands seen on two adjacent lateral sides are tilted at an angle to the loading axis as it is predicted theoretically and observed experimentally (cf. Figure 1a–c and Figure 4b). Accordingly, the localized strain regions in the crystal with {110} faces are formed at an angle to the loading axis on two opposite sides and lie horizontally on two other sides (cf. Figure 1d,e and Figure 4c). The same band pattern was observed in compressed [001] Ni3Fe alloy single crystals with {110} lateral faces by Kunitsyna et al. [55].
While similar conclusions are generally made for crystals loaded along the [110] axis, some distinct features of strain localization should be mentioned. The equivalent plastic strain distributions calculated for the two crystals are shown in Figure 5 for two degrees of compressive strains. In order to show the deformed crystal shape in a better way, the view in Figure 5b is rotated by an angle of 90 degrees relative to that in Figure 5a. Theoretically, the strain patterns have to be similar on the opposite faces characterized by the same crystallographic orientations and differ on the adjacent sides coplanar with different crystal planes. Anticipated slip distributions on the and (001) crystal faces would be symmetrical relative to the loading axis, which is observed in the onset of plastic strain (Figure 5a). The symmetry, however, is violated shortly after the plastic strain begins, followed by rapid strain localization as it is in the crystals with the [001] loading axis. Again, the orientation of the band of localized plastic strain coincides with the lines of the surface intersection with one of the active slip planes. In accordance with theoretical predictions, the band lies horizontally on the (001) faces and is tilted at an angle on the face (cf. Figure 2 and Figure 5).
A change in the orientation from III to IV leads to a pronounced asymmetry of the strain distributions already in the initial stage of plastic deformation (Figure 5c). In contrast to case III, four potentially active slip systems, remaining equally loaded, intersect each other and the crystal faces asymmetrically about the loading axis. Now, the bands seen on all lateral faces are tilted at a certain angle to the axis of compression (Figure 5d).
Summarizing the results calculated in terms of perfect plasticity, we can distinguish two stages of plastic deformation common for all crystal orientations. These stages are most clearly evident on the evolution of strain-rate patterns illustrated in Figure 6 for the crystal with {100} faces. The equivalent strain-rate fields in Figure 6 are normalized to the strain rate provided by the boundary conditions. It is worth noting that the strain rate in the plastic fronts is an order of magnitude higher than the average value. In the first stage (Figure 6a–d), the deformation develops in a macroscopically quasi-uniform manner where different crystal regions are subsequently involved in plastic deformation to save the symmetry of the crystal shape. Several slip systems at work in the plastically deformed regions make roughly equal contributions to accommodate the strain. The second stage of macroscopically localized deformation comes to play shortly after the first stage. The transition from the first to the second stage is illustrated in Figure 6e–h. The formation of a through-thickness band-like region of localized strain is accompanied by strong perturbations of the strain-rate field (Figure 6g). Further plastic deformation is mainly localized within a narrow layer covering the entire crystal section and seen as bands on the crystal surface. The band orientations specific for each crystal geometry coincide with the traces of one of the active slip systems on the crystal faces.
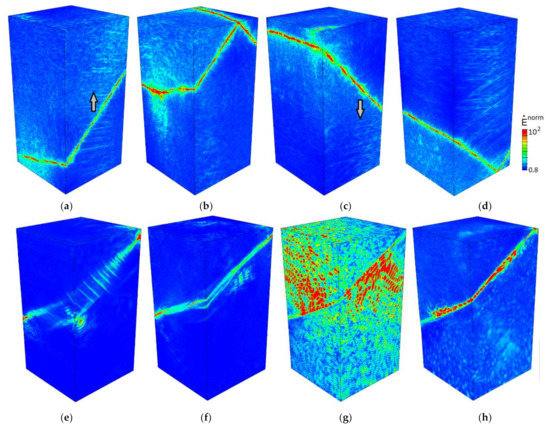
Figure 6.
Normalized equivalent strain rates in a perfectly plastic single crystal with the {100} lateral faces compressed along the [001] axis for compressive strains of 0.008 (a), 0.009 (b), 0.01 (c), 0.011 (d), 0.038 (e), 0.039 (f), 0.04 (g), and 0.044 (h). Video S1 is available online in Supplementary Materials.
Additional series of calculations are performed to evaluate the mesh sensitivity that is a commonly discussed issue in CPFEM simulations of strain localization (see, e.g., [10,47,56]). Needleman [56] showed that the strain localization patterns obtained in rate-independent CPFEM simulations were rather sensitive to the mesh resolution. Harewood and McHugh [47] reported that the rate-dependent CP models were able to provide mesh-independent localization patterns in single-crystal models approximated with sufficiently detailed meshes. Generally, researchers have to find a compromise between the solution’s accuracy and high computational costs.
The mesh sensitivity effect was estimated on the example of a single crystal with Orientation I approximated by the 30 × 60 × 30, 60 × 120 × 60, 100 × 200 × 100, 150 × 300 × 150, and 200 × 400 × 200 meshes. Localization patterns obtained for four different meshes are shown in Figure 7. Their comparison suggests a qualitative similarity. In all models, plastic deformation developed in a similar way, exhibiting two stages. The orientation of macroscopic bands of localized deformation was nearly mesh-independent for all models (Figure 7a–d), and their width was weakly affected by the mesh resolution for the meshes finer than 60 × 120 × 60 (Figure 7b–d). However, the mesh density still influenced the transition from the first stage of plastic deformation to the second one: The finer the mesh, the later the macroscopic localization took place. Respectively, lower strain in the localization region was accumulated in the model approximated by the finest mesh (Figure 7d).
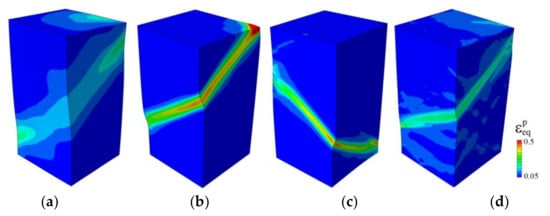
Figure 7.
Equivalent plastic strain fields in the {100} single crystal models approximated by 30 × 60 × 30 (a), 60 × 120 × 60 (b), 100 × 200 × 100 (c), and 150 × 300 × 150 meshes (d) for the compression strain of 0.05.
4.2. Strain-Hardening Effects
In order to study the strain-hardening effects on the plastic strain localization and crystal fragmentation, a series of calculations are performed for single crystals with Orientations I–IV, using the strain-hardening function given by Equation (12).
As in the perfect plasticity case, several stages of plastic deformation, common for all crystal orientations, can be distinguished. The first stage in the strain-hardened crystal where plastic deformation develops in a quasi-uniform manner is similar to that in the perfect plasticity case, though lasts longer. In this stage, different crystal regions are alternatively involved in plastic deformation. Octahedral slip systems become active one by one, and their activation in different crystal parts occurs in switching mode. Due to the strain hardening in the active slip system, the critical stress necessary to maintain the slip increases. As a result, the slip system may become inactive in this region for a while. Further plastic deformation may occur due to the slip intensification in another crystal region to accommodate the plastic deformation of the crystal. Thus, plastic deformation in the strain-hardened crystal propagates as a front back and forth from the top to bottom loading surfaces (see video S2, available online in Supplementary Materials). This conclusion is illustrated in Figure 8 for the crystal with Orientation IV where the strain rate and equivalent plastic strain fields are presented for subsequent loading steps and in Figure 9a for Orientation II by the strain rate field at a compressive strain of 0.005.
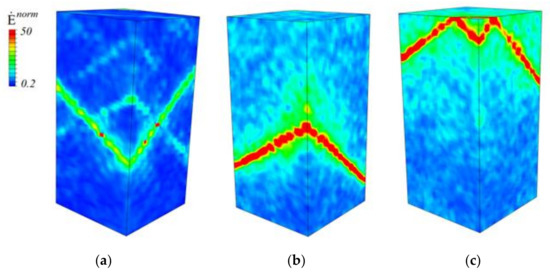
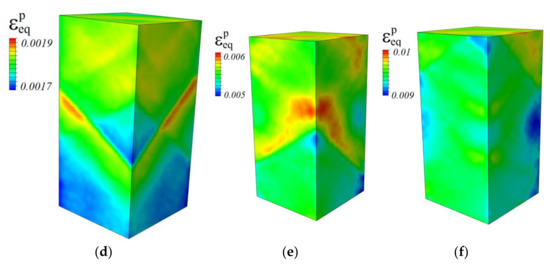
Figure 8.
Normalized strain rate (a–c) and equivalent plastic strain fields (d–f) in the crystal with and lateral faces in the initial stage of compression along the [110] axis for compressive strains of 0.002 (a,d), 0.005 (b,e), and 0.008 (c,f).
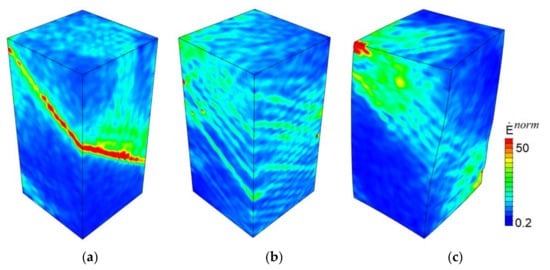
Figure 9.
Normalized strain rates in a single crystal with the {110} lateral faces compressed along the [001] axis in three stages of plastic deformation for compressive strains of 0.005 (a), 0.02 (b), and 0.06 (c). Video S3 is available online in Supplementary Materials.
In contrast to the perfect plasticity case, an intermediate stage preceding macroscopic strain localization can be distinguished in the strain-hardened crystals. This stage is characterized by multiple slips developing simultaneously in several crystal regions. As an illustration, the normalized strain-rate fields corresponding to the intermediate stage are shown in Figure 9b for the single crystal compressed along the [001] axis. In this stage, the crystal still saves its symmetrical shape about the loading axis.
The final deformation stage is associated with the macroscale crystal fragmentation into several parts (Figure 9c). However, the strain localization in all strain-hardened crystals is much less pronounced than in those calculated with perfect plasticity model. The regions adjacent to crystal edges are more involved in plastic deformation than the central part in contrast to the perfect plasticity case where the narrow through-thickness bands of localized strain are formed. This is clearly seen in Figure 10, where isosurfaces of the equivalent plastic strain fields obtained in terms of perfect plasticity and strain-hardening models are compared for the crystals loaded along the [001] direction. This result is consistent with the experimental data [41,57] and simulation results obtained using molecular dynamics [1]. A common conclusion is that strain hardening reduces the material’s ability of plastic strain localization in all stages of loading. Overall, the results obtained support the experimental conclusion drawn in [41] that the shape of macrofragmentation elements is uniquely determined by the mutual orientation of the loading axis and single crystal faces.
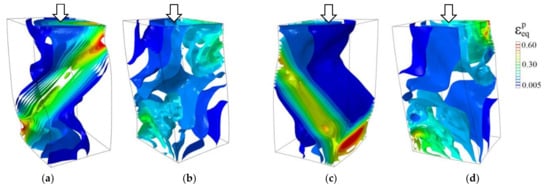
Figure 10.
Isosurfaces of equivalent plastic strains in perfectly plastic (a,c) and strain-hardened single crystals (b,d) with the {100} (a,b) and {110} lateral faces (c,d) under compression along the [100] direction at a strain of 0.05.
5. Discussion
The phenomenon of single-crystal fragmentation is widely discussed among researchers, with many experimental examples presented in the literature. Wonsiewicz and Chin [35] found that an FCC single crystal with a {111}<112> orientation subjected to constrained compression undergoes fragmentation about the transverse direction. The same tendency was characteristic of single crystals with a Cube orientation [36,37,42,45,46], where fragmentation about the transverse direction was complemented with a set of quasi-periodic bands lying along the normal direction [45]. This behavior was reported to be typical of the high-symmetry Cube orientation due to its instability under compression at room temperature [42].
Teplyakova and Kozlov [44] revealed key elements of macrolocalization, including shear, bending-torsion, and rotation fragments. Each fragment was associated with a specific surface pattern where plastic strain manifested itself as shear bands, thin folds parallel to the shear bands, deformation bands, or bending regions [31]. On further loading, some fragments tended to form larger groups belonging to mesoscale phenomena. Apparently, the larger the deformation element size, the larger the scale of strain localization [31].
Lychagin et al. [58] showed for nickel single crystals compressed along the direction that the largest strain occurs at the deformation band junctions rather than within the bands themselves. Prior to the formation of deformation bands, a set of rectilinear shear bands appeared in the regions of the highest stress concentration at the beginning of plastic deformation. On further loading, the deformation bands originating near the primary stress concentrators were united into a larger set of similarly oriented bands, resulting in crystal fragmentation at a larger scale.
Among the main factors of crystal fragmentation, Alfyorova and Lychagin [57] and Lychagin [32] noted (1) different stress states realized in different regions of the loaded crystal, (2) geometrically induced stress concentrations near the rectangular-shaped crystal edges, and (3) the slip ability to emerge onto the crystal faces.
Let us support these assumptions numerically on the example of perfectly plastic crystals where localization patterns are not affected by strain hardening (Figure 11 and Figure 12). In the elastic stage of loading, crystals of all orientations demonstrate nearly homogeneous stress and strain distributions symmetrical about the axis of compression. Let us analyze the evolution of the stress tensor component associated with the load direction, which makes the largest contribution to the material’s resistance to compression. In the elastic stage, this stress is negative all over the crystal volume, which means that all regions undergo compression along the loading axis. Once plastic deformation comes to play, the symmetry is rapidly violated due to strain localization. In the first stage of plasticity, the stresses still increase throughout the crystal volume, but it changes once the crystal shape has lost its symmetry. On further loading, the stresses continue increasing in some regions but start to decrease in others, reaching to zero and then increasing to positive values, as seen in Figure 11. The stress values in Figure 11 are normalized to the yield stress (see Table 2).
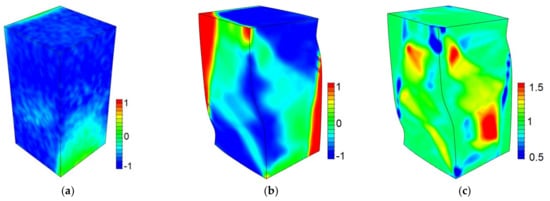
Figure 11.
Normalized stress fields in the single crystal with the {100} faces under compression along the [001] axis: at strains of 0.005 (a) and 0.05 (b) and von Mises stress at a strain of 0.05 (c).
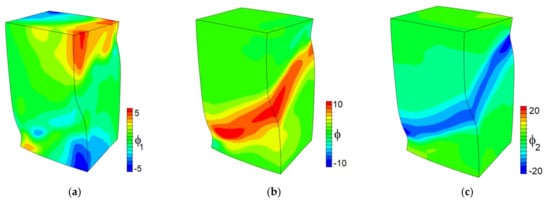
Figure 12.
Distributions of Euler angles ϕ1 (a), ϕ (b), and ϕ2 (c) in the single crystal with {100} faces under compression along the [001] axis at a strain of 0.05.
At the end of compression, the positive (tensile) and negative (compressive) stresses occupy comparable regions. It is not surprising that the highest stresses take place near the crystal edges adjacent to the loaded surfaces. It is noticeable that all stress components in the stage of macrolocalization demonstrate quasi-symmetrical distributions about the load direction, thus bringing the crystal to a balance. Accordingly, the equivalent stress demonstrates an inhomogeneous distribution with the unloaded (red) and overloaded (blue) regions with respect to the average level (green regions in Figure 11c).
In accordance with the experimental observations [37,46,59] and theoretical predictions [17,32,60], the macroscale plastic strain localization in all single crystals is accompanied by relative shifts and rotations of crystal fragments. Analyzing the CPFEM simulation results, Trusov et al. [22] highlight that due to inhomogeneous lattice rotation, the lattice of a single crystal becomes curved in some regions. Let us analyze the contribution of rotation in terms of Euler (Bunge) angles. The Euler angles define three successive rotations bringing the crystal frame to the sample frame. Representative Euler angle distributions in the developed stage of strain localization are shown in Figure 12. The distributions are strongly inhomogeneous, with the highest amount of rotation taking place within the macroscopic localized band, where ϕ and ϕ2 angles deviate from their initial values in the undeformed crystal up to 10 and 20 degrees, respectively. These results are consistent with experimental observations for FCC single crystals under compression reported by Ha and Kim [37], Han et al. [59], and Wert et al. [46] and CPFEM calculations presented by Kuroda [60] and Roters et al. [17].
6. Conclusions
The mechanical aspects of plastic strain localization and fragmentation in FCC single crystals under compression have been addressed in the present study. Experimental data for aluminum single crystals compressed along the [001] and [110] directions were used to construct a numerical model in terms of crystal plasticity. Two series of crystal plasticity finite element simulations have been performed for perfectly plastic and strain-hardened crystals to estimate the strain-hardening effects on the development of strain localization.
The calculations have shown that the development of plastic deformation in single crystals is characterized by staging. Two distinct stages of plastic deformation were identified for perfectly plastic single crystals. In the first stage, deformation developed in a macroscopically quasi-uniform manner where different crystal regions were subsequently involved in plastic deformation to save the symmetry of the crystal shape. In this stage, narrow solitary fronts of plastic deformation propagated back and forth between the top and bottom punches. The strain rate in the plastic fronts was an order of magnitude higher than the average strain rate. The second stage was associated with the abrupt localization of plastic strain within a through-thickness band region. Subsequent plastic deformation was accompanied by the relative shift and rotation of crystal fragments, with the highest amount of rotation observed within the region of localized strain. The transition from the first stage of solitary front propagation to the second stage of macrolocalization was accompanied by strong perturbations of the strain rate fields. In all perfectly plastic crystals, orientations of the macroscopic bands of localized deformation coincided with the traces of one of the active slip systems on the crystal faces.
In the strain-hardened crystals, three stages of plastic deformation were revealed. The first stage, associated with the propagation of solitary fronts of localized deformation, lasted longer than in perfectly plastic crystals, eventually giving way to an intermediate stage related to the formation of multiple plastic fronts in different crystal parts. In both deformation stages, the crystal shape maintained its symmetry about the compression axis and became asymmetrical at the final stage, where macroscale crystal fragmentation occurred. However, there was no evidence of pronounced strain localization in all deformation stages, much like in the experiments.
Stress analysis for a perfectly plastic crystal showed that the specimen underwent pure compression only in the first deformation stage. Once the crystal shape had lost its symmetry, the compressive stress in some regions progressively decreased to zero and then increased to positive values corresponding to tensile loading. In the final stage, the tensile and compressive stresses occupied comparable areas, with the highest stresses taking place near the crystal edges adjacent to the loaded surfaces.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/met12030397/s1, Video S1: Evolution of the normalized equivalent strain rate in a perfectly plastic single crystal with the {100} lateral faces compressed along the [001] axis, “ESM_0.avi”; Video S2: Plastic strain rate evolution in a strain-hardened single crystal with the and lateral faces compressed along the [110] axis, “ESM_2.avi”; Video S3: Evolution of the normalized equivalent strain rate in a strain-hardened single crystal with the {110} lateral faces compressed along the [001] axis.
Author Contributions
Conceptualization, V.R. and O.Z.; methodology, V.R., R.B. and D.L.; software, V.R. and E.D.; investigation, V.R., D.L. and E.E.; resources, D.L.; writing—original draft preparation, O.Z. and V.R.; writing—review and editing, O.Z. and V.R.; visualization, V.R., O.Z. and D.L.; supervision, V.R.; project administration, V.R.; funding acquisition, V.R. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was performed according to the Government research assignment for ISPMS SB RAS, project FWRW-2021-0002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lychagin, D.V.; Dmitriev, A.I.; Nikonov, A.Y.; Alfyorova, E.A. Crystallographic and Geometric Factors in the Shear Development in <001> FCC Single Crystals: Molecular Dynamics Simulation and Experimental Study. Crystals 2020, 10, 666. [Google Scholar] [CrossRef]
- Honeycomb, R.W.K. The Plastic Deformation of Metals; Edward Arnold: London, UK, 1968. [Google Scholar]
- Rice, J.R. Inelastic Constitutive Relations for Solids: An Internal-Variable Theory and Its Application to Metal Plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Sachs, G. Zur Ableitung einer Fließbedingung. Z. Des Ver. Dtsch. Ing. 1928, 72, 734–736. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Bishop, J.F.W.; Hill, R. A Theory of the Plastic Distortion of a Polycrystalline Aggregate under Combined Stresses. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 414–427. [Google Scholar] [CrossRef]
- Leffers, T. A Modified Sachs Approach to the Plastic Deformation of Polycrystals as a Realistic Alternative to the Taylor Model. In Strength of Metals and Alloys: Proceedings of the 5th International Conference; Pergamon Press: Oxford, UK, 1979; pp. 769–774. [Google Scholar] [CrossRef]
- van Houtte, P. On the Equivalence of the Relaxed Taylor Theory and the Bishop-Hill Theory for Partially Constrained Plastic Deformation of Crystals. Mater. Sci. Eng. 1982, 55, 69–77. [Google Scholar] [CrossRef]
- Kocks, U.F.; Chandra, H. Slip Geometry in Partially Constrained Deformation. Acta Metall. 1982, 30, 695–709. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An Analysis of Nonuniform and Localized Deformation in Ductile Single Crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Becker, R.; Butler, J.F.; Hu, H.; Lalli, L.A. Analysis of an Aluminum Single Crystal with Unstable Initial Orientation (001) [110] in Channel Die Compression. Metall. Trans. A 1991, 22, 45–58. [Google Scholar] [CrossRef]
- Cereceda, D.; Diehl, M.; Roters, F.; Raabe, D.; Perlado, J.M.; Marian, J. Unraveling the Temperature Dependence of the Yield Strength in Single-Crystal Tungsten Using Atomistically-Informed Crystal Plasticity Calculations. Int. J. Plast. 2016, 78, 242–265. [Google Scholar] [CrossRef] [Green Version]
- Ryś, M.; Petryk, H. Gradient Crystal Plasticity Models with a Natural Length Scale in the Hardening Law. Int. J. Plast. 2018, 111, 168–187. [Google Scholar] [CrossRef]
- Senas, D.C. Multiscale Modeling of the Plastic Behaviour in Single Crystal Tungsten: From Atomistic to Crystal Plasticity Simulations. Ph.D. Thesis, Polytechnic University of Madrid, Madrid, Spain, 2015. [Google Scholar]
- Emelianova, E.S.; Romanova, V.A.; Balokhonov, R.R.; Pisarev, M.; Zinovieva, O.S. A Numerical Study of the Contribution of Different Slip Systems to the Deformation Response of Polycrystalline Titanium. Phys. Mesomech. 2021, 24, 166–177. [Google Scholar] [CrossRef]
- Jalili, M.; Soltani, B. Investigation the Micromechanisms of Strain Localization Formation in AZ31 Mg Alloy: A Mesoscale 3D Full-Field Crystal Plasticity Computational Homogenization Study. Eur. J. Mech.-A/Solids 2020, 80, 103903. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Zhao, Z.; Ramesh, M.; Raabe, D.; Cuitiño, A.M.; Radovitzky, R. Investigation of Three-Dimensional Aspects of Grain-Scale Plastic Surface Deformation of an Aluminum Oligocrystal. Int. J. Plast. 2008, 24, 2278–2297. [Google Scholar] [CrossRef]
- Forest, S.; Rubin, M.B. A Rate-Independent Crystal Plasticity Model with a Smooth Elastic–Plastic Transition and No Slip Indeterminacy. Eur. J. Mech.-A/Solids 2016, 55, 278–288. [Google Scholar] [CrossRef]
- Roters, F.; Wang, Y.; Kuo, J.C.; Raabe, D. Comparison of Single Crystal Simple Shear Deformation Experiments with Crystal Plasticity Finite Element Simulations. Adv. Eng. Mater. 2004, 6, 653–656. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J.; Yoon, J.W.; Nambori, R. Strain Rate Effect of High Purity Aluminum Single Crystals: Experiments and Simulations. Int. J. Plast. 2015, 67, 39–52. [Google Scholar] [CrossRef]
- Trusov, P.V.; Yanz, A.Y.; Teplyakova, L.A. Direct Crystal Elastoviscoplasticity Model: An Application to the Study of Single Crystal Deformation. Phys. Mesomech. 2019, 22, 275–286. [Google Scholar] [CrossRef]
- Schacht, T.; Untermann, N.; Steck, E. The Influence of Crystallographic Orientation on the Deformation Behaviour of Single Crystals Containing Microvoids. Int. J. Plast. 2003, 19, 1605–1626. [Google Scholar] [CrossRef]
- Wang, H.; Lu, C.; Tieu, K.; Liu, Y. A Crystal Plasticity FE Study of Macro- and Micro-Subdivision in Aluminium Single Crystals {001}<110> Multi-Pass Rolled to a High Reduction. J. Mater. Sci. Technol. 2021, 76, 231–246. [Google Scholar] [CrossRef]
- Romanova, V.; Zinovieva, O.; Balokhonov, R.; Dymnich, E.; Moskvichev, E.; Filippov, A.; Lychagin, D. Effects of the Grain Shape and Crystallographic Texture on the Grain-Scale Mechanical Behavior of Additively Manufactured Aluminum Alloys. Addit. Manuf. 2021, 48, 102415. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Zinovieva, O.; Emelianova, E.; Dymnich, E.; Pisarev, M.; Zinoviev, A. Micromechanical Simulations of Additively Manufactured Aluminum Alloys. Comput. Struct. 2021, 244, 106412. [Google Scholar] [CrossRef]
- Jayaprakash, S.; Siva Chandran, S.; Sathish, T.; Gugulothu, B.; Ramesh, R.; Sudhakar, M.; Subbiah, R. Effect of Tool Profile Influence in Dissimilar Friction Stir Welding of Aluminium Alloys (AA5083 and AA7068). Adv. Mater. Sci. Eng. 2021, 2021, 7387296. [Google Scholar] [CrossRef]
- Balokhonov, R.; Romanova, V.; Batukhtina, E.; Martynov, S.; Zinoviev, A.; Zinovieva, O. A Mesomechanical Analysis of the Stress–Strain Localisation in Friction Stir Welds of Polycrystalline Aluminium Alloys. Meccanica 2016, 51, 319–328. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Zinovieva, O. A Micromechanical Analysis of Deformation-Induced Surface Roughening in Surface-Modified Polycrystalline Materials. Meccanica 2016, 51, 359–370. [Google Scholar] [CrossRef]
- Bryhni Dæhli, L.E.; Faleskog, J.; Børvik, T.; Hopperstad, O.S. Unit Cell Simulations and Porous Plasticity Modelling for Strongly Anisotropic FCC Metals. Eur. J. Mech.-A/Solids 2017, 65, 360–383. [Google Scholar] [CrossRef]
- Teplyakova, L.A.; Bespalova, I.V.; Lychagin, D.V. Spatial Organization of Deformation in Aluminum [1ī2] Single Crystals in Compression. Phys. Mesomech. 2009, 12, 166–174. [Google Scholar] [CrossRef]
- Lychagin, D.V. Fragmentation of Plastically Deformed FCC Metallic Materials. Phys. Mesomech. 2006, 9, 95–105. [Google Scholar]
- Teplyakova, L.A.; Bespalova, I.V.; Lychagin, D.V. Laws of Deformation Macrolocalization in Aluminum Single Crystals with the Orientation of the Compression Axis [110]. Phys. Mesomech. 2004, 7, 63–78. [Google Scholar]
- Teplyakova, L.A.; Lychagin, D.V.; Kozlov, E.V. Shear Localization in Deformed Al Single Crystals with a Compression Axis Orientation [001]. Phys. Mesomech. 2003, 6, 19. [Google Scholar]
- Wonsiewicz, B.C.; Chin, G.Y. Inhomogeneity of Plastic Flow in Constrained Deformation. Metall. Trans. 1970, 1, 57–61. [Google Scholar] [CrossRef]
- Magid, K.R.; Florando, J.N.; Lassila, D.H.; Leblanc, M.M.; Tamura, N.; Morris, J.W., Jr. Mapping Mesoscale Heterogeneity in the Plastic Deformation of a Copper Single Crystal. Philos. Mag. 2009, 89, 77–107. [Google Scholar] [CrossRef] [Green Version]
- Ha, S.; Kim, K.T. Heterogeneous Deformation of Al Single Crystal: Experiments and FInite Element Analysis. Math. Mech. Solids 2011, 16, 652–661. [Google Scholar] [CrossRef]
- Lychagin, D.V.; Tarasov, S.Y.; Chumaevskii, A.V.; Alfyorova, E.A. Macrosegmentation and Strain Hardening Stages in Copper Single Crystals under Compression. Int. J. Plast. 2015, 69, 36–53. [Google Scholar] [CrossRef]
- Paul, H.; Maurice, C.; Driver, J.H. Microstructure and Microtexture Evolution during Strain Path Changes of an Initially Stable Cu Single Crystal. Acta Mater. 2010, 58, 2799–2813. [Google Scholar] [CrossRef]
- Jia, N.; Eisenlohr, P.; Roters, F.; Raabe, D.; Zhao, X. Orientation Dependence of Shear Banding in Face-Centered-Cubic Single Crystals. Acta Mater. 2012, 60, 3415–3434. [Google Scholar] [CrossRef]
- Lychagin, D.V.; Teplyakova, L.A. The Primary Macrofragmentation of Shear in Compressed Aluminum Single Crystals. Tech. Phys. Lett. 2003, 29, 516–518. [Google Scholar] [CrossRef]
- Basson, F.; Driver, J.H. Deformation Banding Mechanisms during Plane Strain Compression of Cube-Oriented f.c.c. Crystals. Acta Mater. 2000, 48, 2101–2115. [Google Scholar] [CrossRef]
- Petryk, H.; Kursa, M. The Energy Criterion for Deformation Banding in Ductile Single Crystals. J. Mech. Phys. Solids 2013, 61, 1854–1875. [Google Scholar] [CrossRef]
- Teplyakova, L.A.; Kozlov, E.V. Formation of Scale Structural Levels of Plastic Deformation Localization in Metal Single Crystals. I. Macrolevel. Phys. Mesomech. 2006, 9, 53–62. [Google Scholar]
- Akef, A.; Driver, J.H. Orientation Splitting of Cube-Oriented Face-Centred Cubic Crystals in Plane Strain Compression. Mater. Sci. Eng. A 1991, 132, 245–255. [Google Scholar] [CrossRef]
- Wert, J.A.; Liu, Q.; Hansen, N. Dislocation Boundary Formation in a Cold-Rolled Cube-Oriented Al Single Crystal. Acta Mater. 1997, 45, 2565–2576. [Google Scholar] [CrossRef]
- Harewood, F.J.; McHugh, P.E. Investigation of Finite Element Mesh Independence in Rate Dependent Materials. Comput. Mater. Sci. 2006, 37, 442–453. [Google Scholar] [CrossRef]
- Romanova, V.A.; Balokhonov, R.R.; Batukhtina, E.E.; Emelianova, E.S.; Sergeev, M.V. On the Solution of Quasi-Static Micro- and Mesomechanical Problems in a Dynamic Formulation. Phys. Mesomech. 2019, 22, 296–306. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Emelianova, E.; Zinovieva, O.; Zinoviev, A. Microstructure-Based Simulations of Quasistatic Deformation Using an Explicit Dynamic Approach. Facta Univ. Ser. Mech. Eng. 2019, 17, 243–254. [Google Scholar] [CrossRef]
- Brandes, E.A.; Brook, G.B. (Eds.) Smithells Metals Reference Book, 7th ed.; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar]
- Zecevic, M.; Cawkwell, M.J.; Ramos, K.J.; Luscher, D.J. Simulating Knoop Hardness Anisotropy of Aluminum and β-HMX with a Crystal Plasticity Finite Element Model. Int. J. Plast. 2021, 144, 103045. [Google Scholar] [CrossRef]
- Meng, C.; Wei, H.; Chen, H.; Liu, Y. Modeling Plasticity of Cubic Crystals Using a Nonlocal Lattice Particle Method. Comput. Methods Appl. Mech. Eng. 2021, 385, 114069. [Google Scholar] [CrossRef]
- Polyanskiy, V.A.; Belyaev, A.K.; Grishchenko, A.I.; Lobachev, A.M.; Modestov, V.S.; Pivkov, A.V.; Tretyakov, D.A.; Shtukin, L.V.; Semenov, A.S.; Yakovlev, Y.A. Finite Element Simulation of Chessboard Strain Localization in View of Statistical Spreads in Polycrystal Grain Parameters. Phys. Mesomech. 2019, 22, 188–194. [Google Scholar] [CrossRef]
- Petryk, H. General Conditions for Uniqueness in Materials with Multiple Mechanisms of Inelastic Deformation. J. Mech. Phys. Solids 2000, 48, 367–396. [Google Scholar] [CrossRef]
- Kunitsyna, T.S.; Teplyakova, L.A.; Potekaev, A.I.; Starenchenko, V.A. Macro-Scale Localized Shear Strain Affected by Configuration of [001]-oriented Single Crystals of Ni3Fe Alloy. Russ. Phys. J. 2019, 61, 2253–2257. [Google Scholar] [CrossRef]
- Needleman, A. Material Rate Dependence and Mesh Sensitivity in Localization Problems. Comput. Methods Appl. Mech. Eng. 1988, 67, 69–85. [Google Scholar] [CrossRef]
- Alfyorova, E.A.; Lychagin, D.V. Self-Organization of Plastic Deformation and Deformation Relief in FCC Single Crystals. Mech. Mater. 2018, 117, 202–213. [Google Scholar] [CrossRef]
- Lychagin, D.V.; Alfyorova, E.A.; Starenchenko, V.A. Effect of Crystallogeometric States on the Development of Macrobands and Deformation Inhomogeneity in [111] Nickel Single Crystals. Phys. Mesomech. 2011, 14, 66–78. [Google Scholar] [CrossRef]
- Han, J.H.; Kim, D.I.; Jee, K.K.; Oh, K.H. Evolution of Crystallographic Orientations in an Aluminum Single Crystal during Tensile Deformation. Mater. Sci. Eng. A 2004, 387–389, 60–63. [Google Scholar] [CrossRef]
- Kuroda, M. Higher-Order Gradient Effects in Micropillar Compression. Acta Mater. 2013, 61, 2283–2297. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).