Structural Materials Durability Statistical Assessment Taking into Account Threshold Sensitivity
Abstract
1. Introduction
- Are there threshold sensitivity measures for statistical distribution in the analysis of mechanical properties of materials?
- Have threshold sensitivity measures for the statistical distribution been used in the statistical processing of low-cycle fatigue tests?
- Can threshold sensitivity measures for the statistical distribution be applied successfully to processing of the results of the tests of mechanical properties of materials?
2. Materials and Methods
2.1. Experiment and Materials
2.2. Review of Sensitivity Calculation Methods
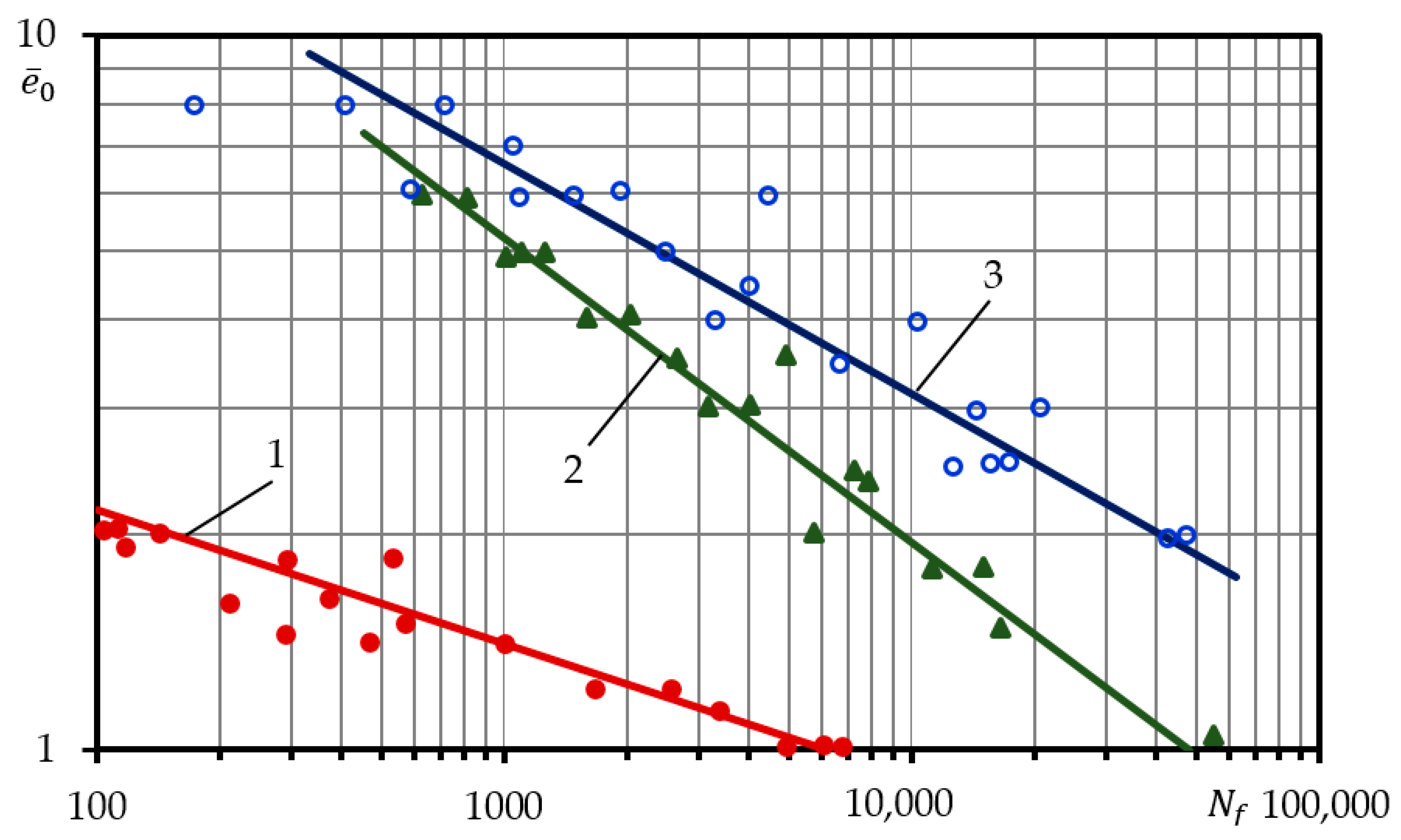
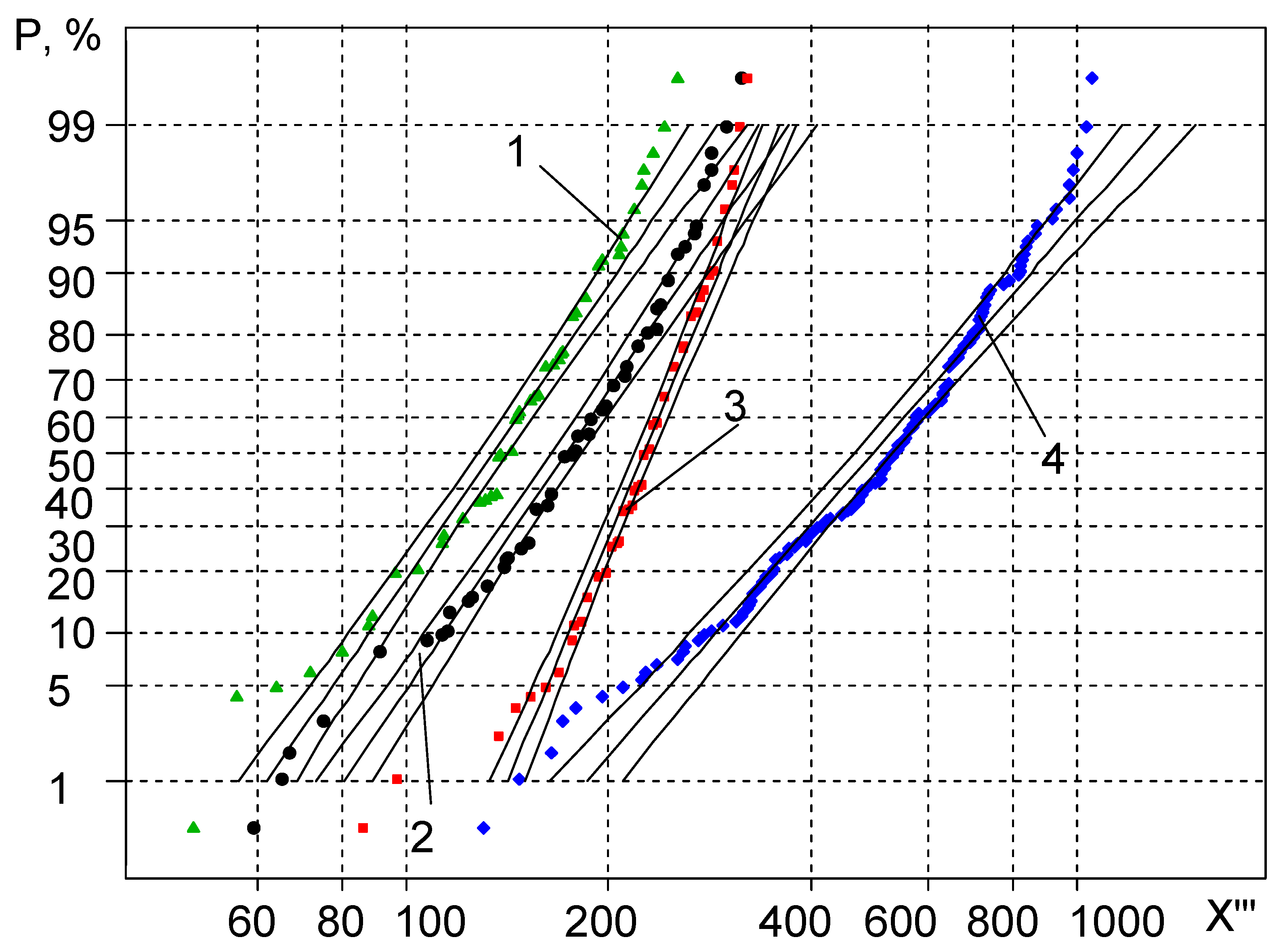
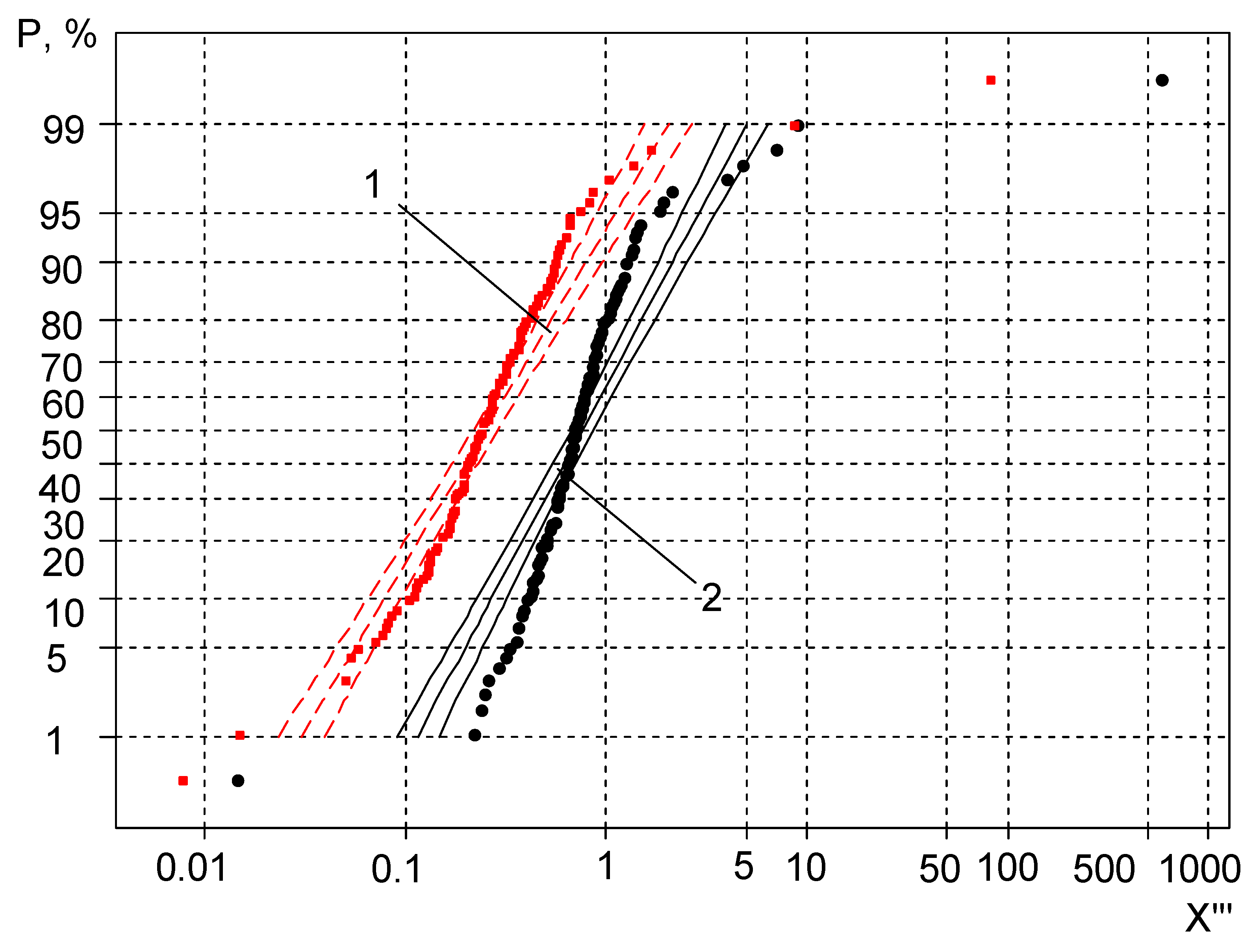
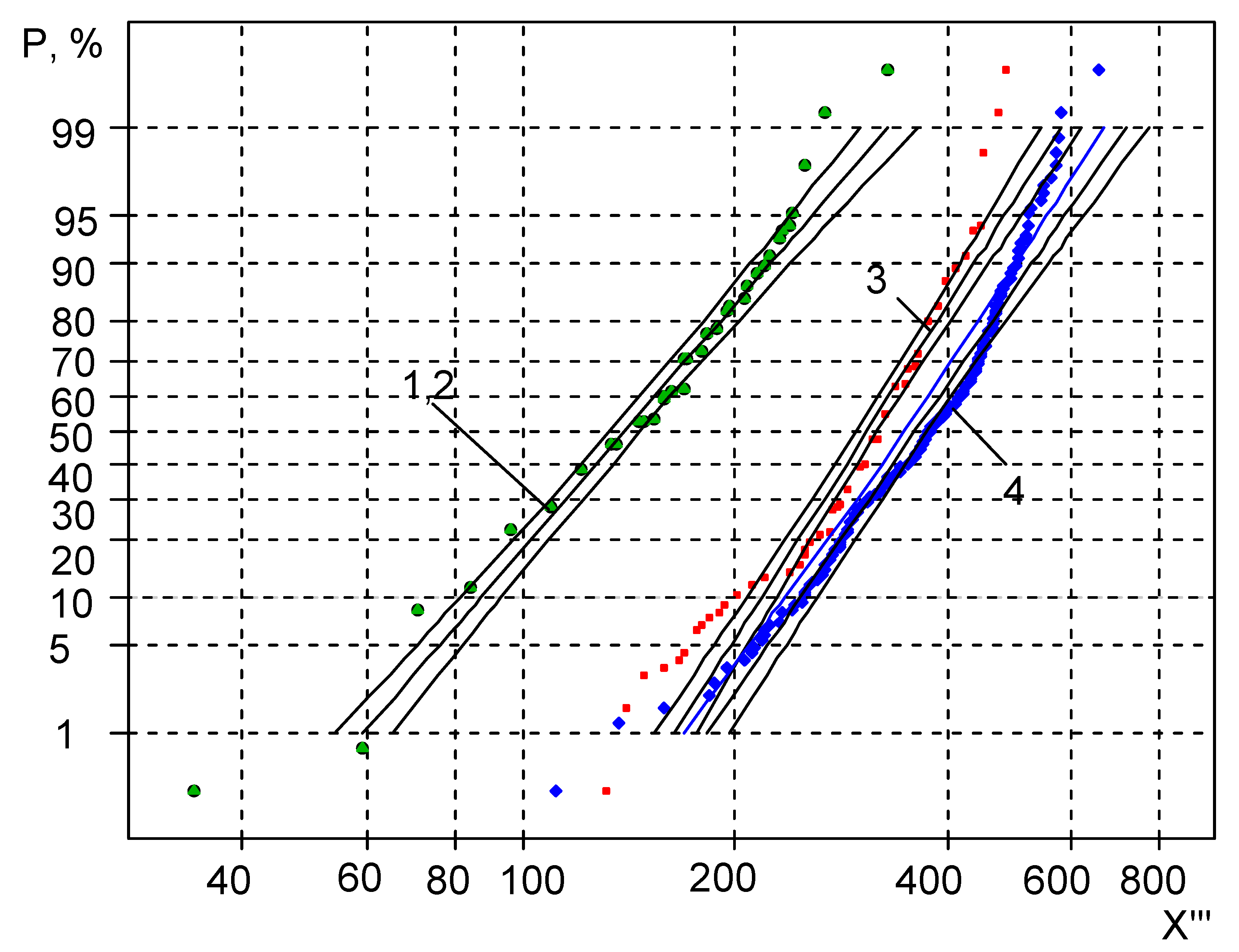
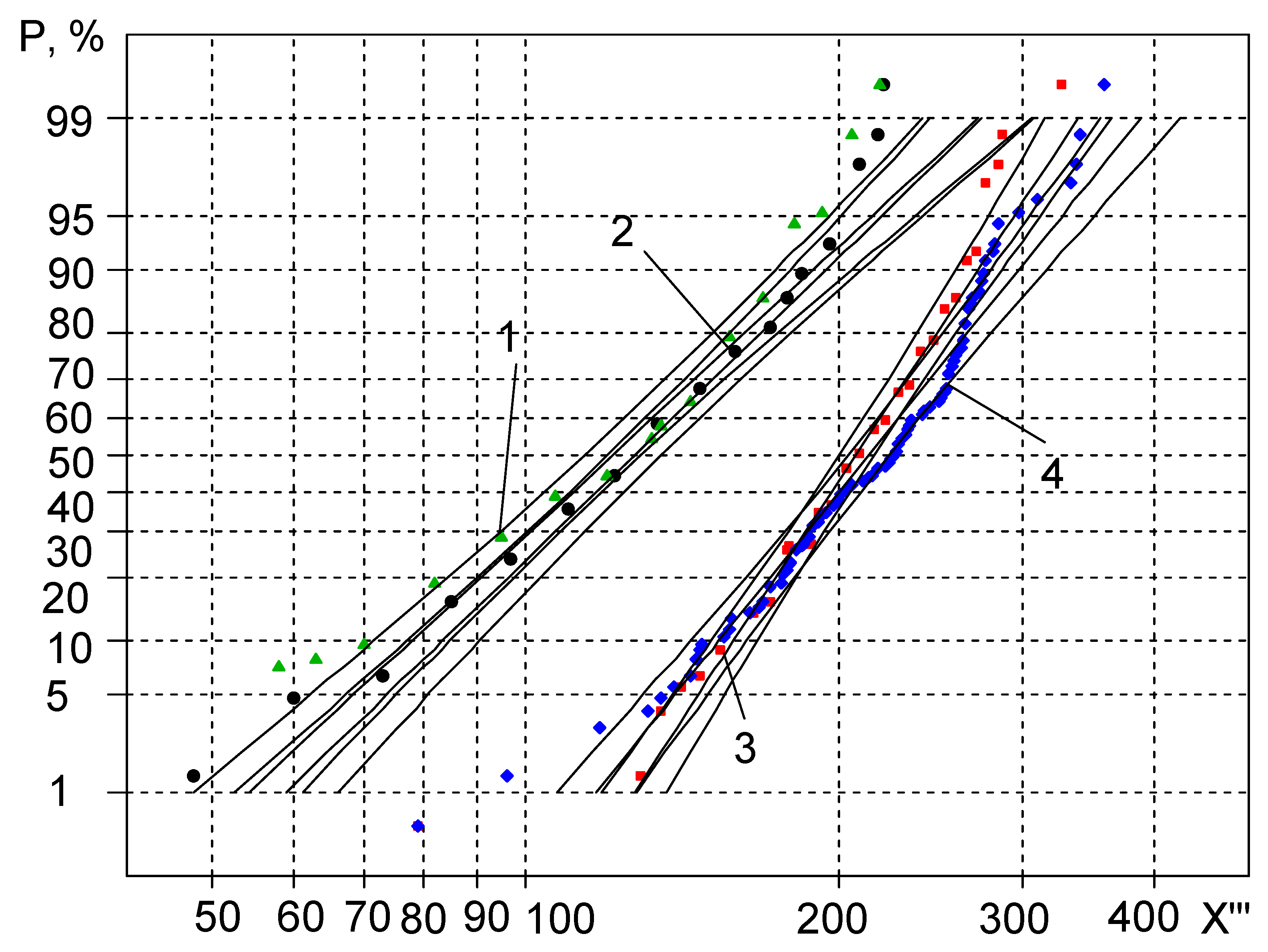
2.3. Application of Sensitivity Threshold to Statistical Calculations of High-Cycle Fatigue
- the scattering of the experimental points has been reduced;
- the statistical distribution curves have become closer to being straight;
- the coefficient of skewness has approached zero, which is characteristic of the normal and logarithmic-normal random measure distribution laws;
- the use of a small number of specimens for the tests results in the errors of calculation of the sensitivity threshold.
2.4. Description of the Mathematical Model Function and Algorithms
- Calculation of lower sensitivity threshold N0 of statistical distribution under approximation method following the selection of lower sensitivity threshold Nk of statistical distribution.
- Provides values of Equation (8) for possible solutions of N0 and Nk.
- Calculates new random measure for each mechanical property.
- Calculates failure probability P for each specimen.
- Calculates statistical parameters , σ, σ2, S, V, and Ex of the distribution for mechanical properties of the analysed structural materials.
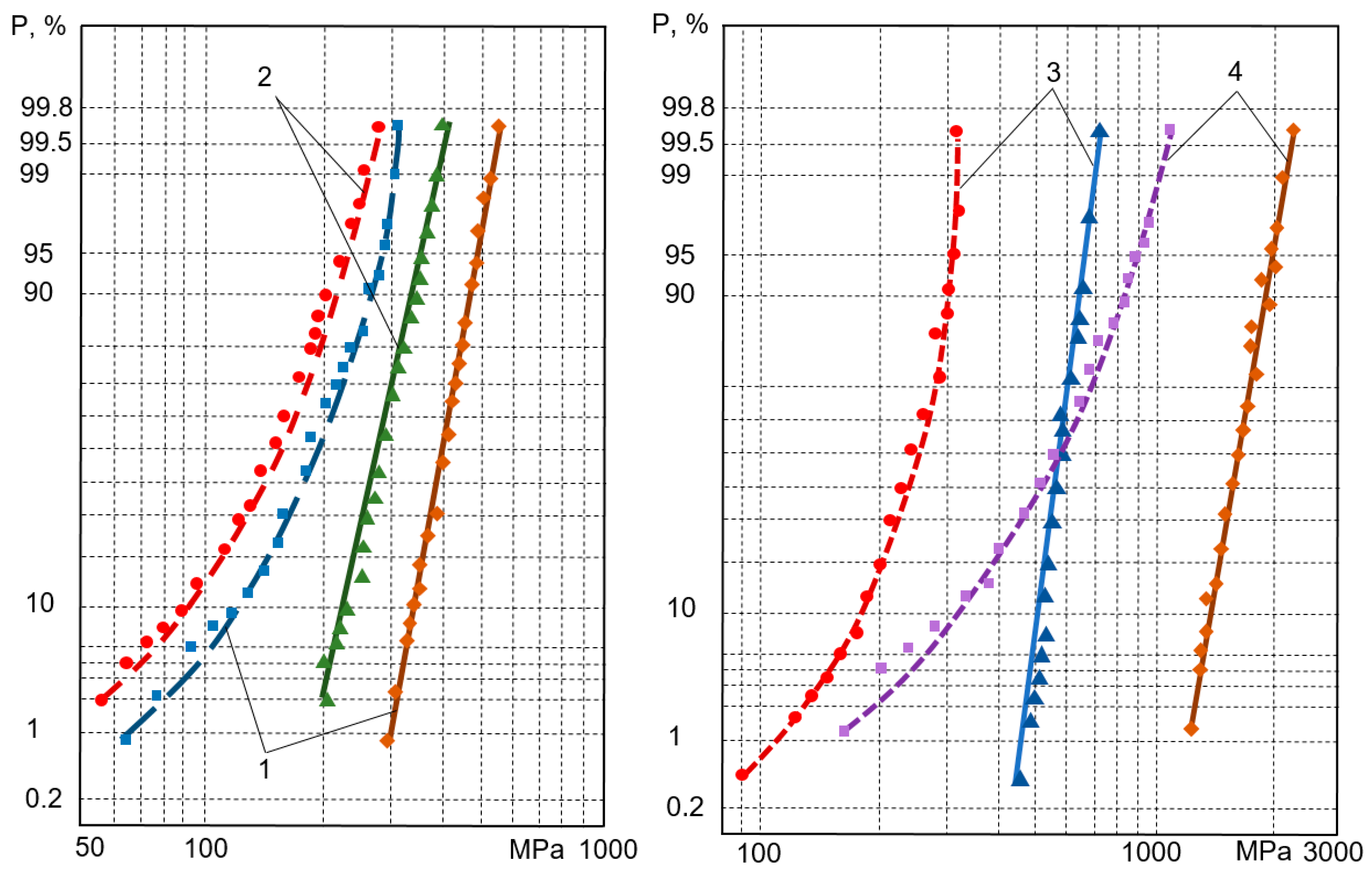
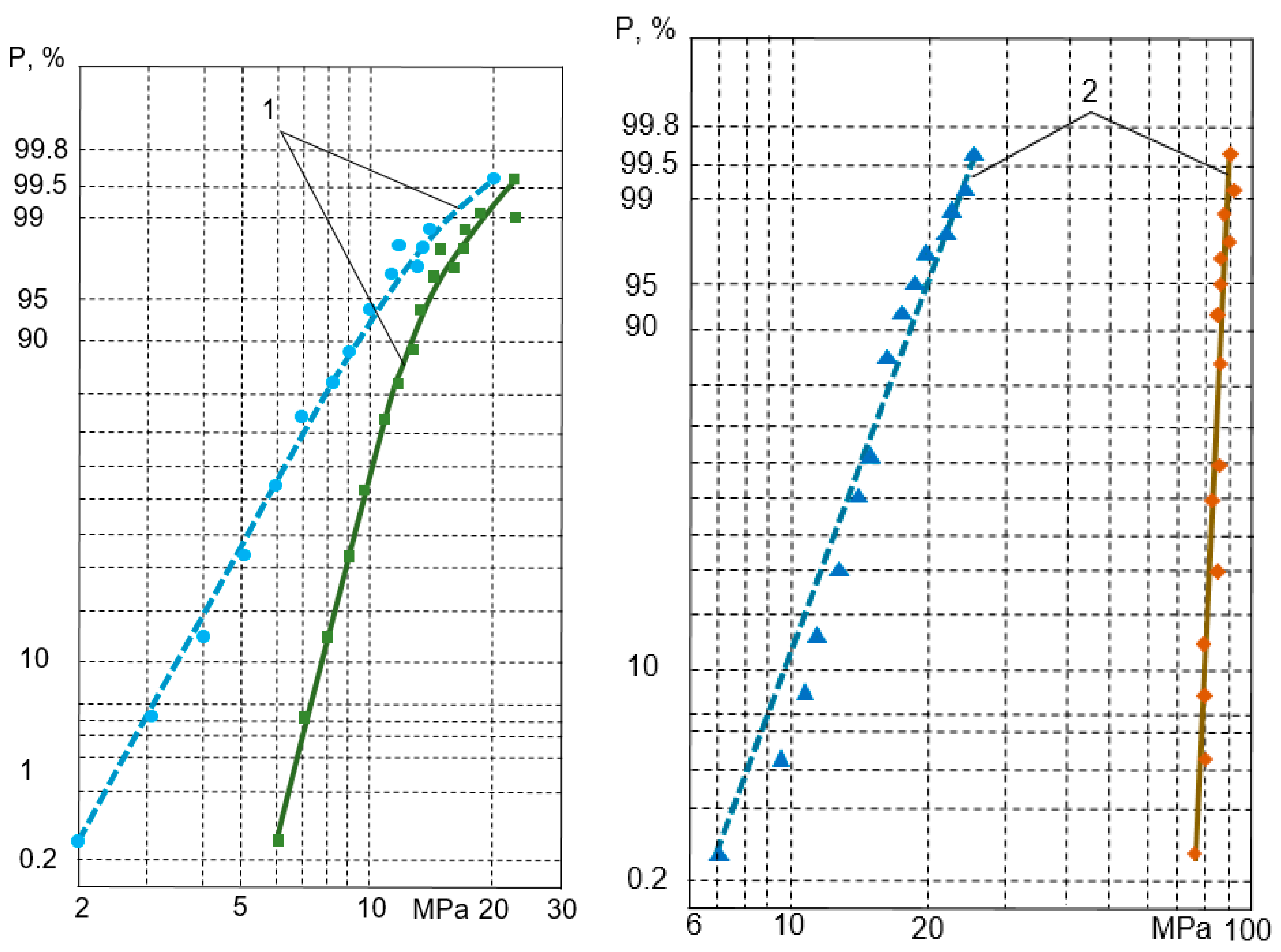
3. Results and Discussion
4. Conclusions
- Analysis of the graphical representation of the distribution in the probabilistic plot shows that the distribution curves for the random variable X″ are more skewed due to the higher variance. The lower part of the distribution curves for size X′ is more downward skewed. This slightly contradicts the statements in the references that, using a sensitivity threshold, the plots of the statistical distributions must be very close to straight lines. This flattening of the curves can be explained by the value of the sensitivity threshold being very close in value to the first members of the X′ variation series. As a result, the first components of X″ are closer to zero, which causes the curves to flatten.
- Application of the sensitivity threshold measure has led to decrease in the coefficient of skewness down to zero; however, the results have not corresponded to the hypothetical straight-line, unlike expected. This demonstrates that, application of the sensitivity threshold would be unreasonable.
- In the calculation of the statistical characteristics of the Weibull distribution, the coefficient of skewness Sk for the variable measures X′ and X″, the difference between the values is small. This suggests that the Weibull’s distribution is not characteristic of measure X′.
- The minimum number of elements of rank order, which still allows a reliable calculation of the sensitivity threshold measure N0, was different for each material and did not depend directly on the initial number of elements.
- Sensitivity thresholds N0 and Nk cannot be used for the description of the statistical distribution of mechanical characteristics skewness, coefficient of variation, and kurtosis develop values that are fairly distant from zero, supporting the fact that the statistical distribution moves further from the norm rather than approximating it.
- During analysis of the statistical distribution curves for mechanical properties, it has been observed that the application of sensitivity thresholds N0 and Nk within the ranges of the average probabilities of statistical distribution has led to a fairly good straight line approximation of the curves, while the curves tend to bend downward and upward in the case of low and high probability values and develop the primal form.
- The estimated values of the random variable X‴ (the approximate part of the straight line) belong to the range of 40–60% probability values, allowing 50% acceptance probability values of the random variables to perform further low cycle fatigue calculations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| b | slope of the straight line corresponding to mean square deviation σ; |
| epr | proportional limit strain (%); |
| strain of initial (0 semi-cycle) loading normalized to proportional limit strain (%); | |
| Ex | kurtosis; |
| F(N) | distribution function; |
| F′(N) | distribution function derivative; |
| i = 1 … ni | specimen ranks in the rank order; |
| h1, h2, h3 | initial moments of distribution; |
| L | likelihood function; |
| m3 | the third central moment of statistical distribution; |
| n | number of specimens; |
| ni | number of values within the j–th interval j = 1...e, e—number of intervals |
| N | number of cycles; |
| N0 | number of cycles bottom threshold sensitivity value; |
| Nf | number of cycles to failure; |
| Nk | number of cycles top threshold sensitivity value; |
| P | probability; |
| Q | sums of mean square deviations; |
| R | variation interval; |
| S | skewness; |
| Sk | cyclic stress of k semi-cycle (MPa); |
| V | coefficient of variation; |
| x | variable; |
| xj | j–th interval mean value; |
| arithmetic mean; | |
| X′, X″, X‴ | random measure value; |
| z | normal distribution quantile; |
| zp | normalized random measure; |
| Greek symbols | |
| ψ | percent area reduction (%); |
| ψu | percent area reduction at failure (%) |
| σ | statistical distribution standard deviation; |
| σ2 | dispersion; |
| σpr | proportional limit stress (MPa); |
| σy | yield strength (MPa); |
| σys | elastic limit or yield strength, the stress at which 0.2% plastic strain occurs (MPa); |
| σu | ultimate tensile stress (MPa); |
References
- Makhutov, N.A. Structural Durability, Resource and Tech. Safety; Nauka: Novosibirsk, Russia, 2005; Volume 1. (In Russian) [Google Scholar]
- Makhutov, N.A. Structural Durability, Resource and Tech. Safety; Nauka: Novosibirsk, Russia, 2005; Volume 2. (In Russian) [Google Scholar]
- Zhu, S.-P.; Huang, H.-Z.; Smith, R.; Ontiveros, V.; He, L.-P.; Modarres, M. Bayesian framework for probabilistic low cycle fatigue life prediction and uncertainty modeling of aircraft turbine disk alloys. Probabilistic Eng. Mech. 2013, 34, 114–122. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Huang, H.-Z.; Peng, W.; Wang, H.-K.; Mahadevan, S. Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Heyraud, H.; Robert, C.; Mareau, C.; Bellett, D.; Morel, F.; Belhomme, N.; Dore, O. A two-scale finite element model for the fatigue design of large welded structures. Eng. Fail. Anal. 2021, 124, 105280. [Google Scholar] [CrossRef]
- Burger, M.; Dreßler, K.; Speckert, M. Load assumption process for durability design using new data sources and data analytics. Int. J. Fatigue 2021, 145, 106116. [Google Scholar] [CrossRef]
- Gadolina, I.V.; Makhutov, N.A.; Erpalov, A.V. Varied approaches to loading assessment in fatigue studies. Int. J. Fatigue 2021, 144, 106035. [Google Scholar] [CrossRef] [PubMed]
- Weibull, W. Fatigue Testing and Analysis of Results; Pergamon Press: New York, NY, USA, 1961; Available online: https://books.google.lt/books?hl=lt&lr=&id=YM4gBQAAQBAJ&oi=fnd&pg=PP1&dq=Weibull,+W.+Fatigue+Testing+and+Analysis+of+Results&ots=VIVGA6VzJY&sig=UsrDkGvsP8go6hPS6IuYK3q9-H0&redir_esc=y#v=onepage&q=Weibull%2C%20W.%20Fatigue%20Testing%20and%20Analysis%20of%20Results&f=false (accessed on 20 December 2021).
- Weibull, W.; Rockey, K.C. Fatigue Testing and Analysis of Results. J. Appl. Mech. 1962, 29, 607. [Google Scholar] [CrossRef]
- Freudenthal, A.M.; Gumbel, E.J. On the statistical interpretation of fatigue tests. Proc. R. Soc. Lond. Ser. A 1953, 216, 309–332. [Google Scholar] [CrossRef]
- Freudenthal, A.M.; Gumbel, E.J. Physical and Statistical Aspects of Fatigue. Adv. Appl. Mech. 1956, 4, 117–158. [Google Scholar] [CrossRef]
- Iida, K.; Inoue, H. Evaluation of low cycle fatigue design curve based on life distribution shape. J. Soc. Nav. Archit. Jpn. 1973, 133, 235–247. [Google Scholar] [CrossRef]
- Serensen, S.V.; Shneiderovich, R.M. Deformations and rupture criteria under low-cycles fatigue. Exp. Mech. 1966, 6, 587–592. [Google Scholar] [CrossRef]
- Serensen, S.V.; Kogayev, V.P.; Shneiderovich, R.M. Load Carrying Ability and Strength Evaluation of Machine Components, 3rd ed.; Mashinostroeniya: Moscow, Russia, 1975; pp. 255–311. (In Russian) [Google Scholar]
- Stepnov, M.N. Statistical Methods for Computation of the Results of Mechanical Experiments, Mechanical Engineering; Mashinostroeniya: Moscow, Russia, 2005. (In Russian) [Google Scholar]
- Jiang, Z.; Han, Z.; Li, M. A probabilistic model for low-cycle fatigue crack initiation under variable load cycles. Int. J. Fatigue 2022, 155, 106528. [Google Scholar] [CrossRef]
- Makhutov, N.A.; Panov, A.N.; Yudina, O.N. The development of models of risk assessment complex transport systems. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Proceedings of the V International Scientific Conference, Survivability and Structural Material Science (SSMS 2020), Moscow, Russia, 27–29 October 2020; Institute of Physics Publishing (IOP): Moscow, Russia, 2020; Volume 1023. Available online: https://scholar.google.lt/scholar?hl=lt&as_sdt=0%2C5&q=The+development+of+models+of+risk+assessment+complex+transport+systems&btnG= (accessed on 22 December 2021).
- Tomaszewski, T.; Strzelecki, P.; Mazurkiewicz, A.; Musiał, J. Probabilistic estimation of fatigue strength for axial and bending loading in high-cycle fatigue. Materials 2020, 13, 1148. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-K.; Chen, S.; Zhu, S.-P.; Ding Liao, D.; Gao, J.-W. Probabilistic fatigue life prediction of notched components using strain energy density approach. Eng. Fail. Anal. 2021, 124, 105375. [Google Scholar] [CrossRef]
- Strzelecki, P. Determination of fatigue life for low probability of failure for different stress levels using 3-parameter Weibull distribution. Int. J. Fatigue 2021, 145, 106080. [Google Scholar] [CrossRef]
- Correia, J.; Apetre, N.; Arcari, A.; Jesus, A.D.; Muñiz-Calvente, M.; Calçada, R.; Berto, F.; Fernández-Canteli, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Angulo, S.C.; Silva, N.V.; Lange, D.A.; Tavares, L.M. Probability distributions of mechanical properties of natural aggregates using a simple method. Constr. Build. Mater. 2020, 233, 117269. [Google Scholar] [CrossRef]
- Matvienko, Y.G.; Kuzmin, D.A.; Reznikov, D.O.; Potapov, V.V. Assessment of the Probability of Fatigue Fracture of Structural Components with Accounting for the Statistical Scatter of Mechanical Properties of the Material and the Residual Defectness. J. Mach. Manuf. Reliab. 2021, 50, 302–311. [Google Scholar] [CrossRef]
- Guo, S.; Liu, R.; Jiang, X.; Zhang, H.; Zhang, D.; Wang, J.; Pan, F. Statistical Analysis on the Mechanical Properties of Magnesium Alloys. Materials 2017, 10, 1271. [Google Scholar] [CrossRef] [PubMed]
- Skejić, D.; Dokšanović, T.; Čudina, I.; Mazzolani, F.M. The Basis for Reliability-Based Mechanical Properties of Structural Aluminium Alloys. Appl. Sci. 2021, 11, 4485. [Google Scholar] [CrossRef]
- Armentani, E.; Greco, A.; De Luca, A.; Sepe, R. Probabilistic Analysis of Fatigue Behavior of Single Lap Riveted Joints. Appl. Sci. 2020, 10, 3379. [Google Scholar] [CrossRef]
- Narayanan, G. Probabilistic fatigue model for cast alloys of aero engine applications. Int. J. Struct. Integr. 2021, 12, 454–469. [Google Scholar] [CrossRef]
- Makhutov, N.A.; Zatsarinny, V.V.; Reznikov, D.O. Fatigue prediction on the basis of analysis of probabilistic mechanical properties. AIP Conf. Proc. 2020, 2315, 40025. [Google Scholar] [CrossRef]
- Daunys, M.; Šniuolis, R. Statistical evaluation of low cycle loading curves parameters for structural materials by mechanical characteristics. Nucl. Eng. Des. 2006, 236, 13. [Google Scholar] [CrossRef]
- Daunys, M.; Šniuolis, R.; Stulpinaite, A. Evaluation of cyclic instability by mechanical properties for structural materials. Mechanics 2012, 18, 280–284. [Google Scholar] [CrossRef][Green Version]
- Raslavičius, L.; Bazaras, Ž.; Lukoševičius, V.; Vilkauskas, A.; Česnavičius, R. Statistical investigation of the weld joint efficiencies in the repaired WWER pressure vessel. Int. J. Press. Vessel. Pip. 2021, 189, 104271. [Google Scholar] [CrossRef]
- Bazaras, Z. Analysis of probabilistic low cycle fatigue design curves at strain cycling. Indian J. Eng. Mater. Sci. 2005, 12, 411–418. Available online: https://scholar.google.lt/scholar?hl=lt&as_sdt=0%2C5&q=Bazaras%2C+Z.+2005.+Analysis+of+probabilistic+low+cycle+fatigue+design+curves+at+strain+cycling%2C+Indian+Journal+of+Engineering+%26+Material+Sciences+2%3A+411-418.&btnG= (accessed on 22 December 2021).
- Daunys, M.; Bazaras, Z.; Timofeev, B.T. Low cycle fatigue of materials in nuclear industry. Mechanics 2008, 73, 12–17. Available online: https://scholar.google.lt/scholar?hl=lt&as_sdt=0%2C5&q=28.%09Daunys%2C+M.%3B+Bazaras%2C+Z.%3B+Timofeev%2C+B.+T.+Low+cycle+fatigue+of+materials+in+nuclear+industry&btnG= (accessed on 22 December 2021).
- Giannella, V. Stochastic approach to fatigue crack-growth simulation for a railway axle under input data variability. Int. J. Fatigue 2021, 144, 106044. [Google Scholar] [CrossRef]
- Giannella, V.; Sepe, R.; Borrelli, A.; De Michele, G.; Armentani, E. Numerical investigation on the fracture failure of a railway axle. Eng. Fail. Anal. 2021, 129, 105680. [Google Scholar] [CrossRef]
- Giannella, V.; Perrella, M.; Citarella, R. Efficient FEM-DBEM coupled approach for crack propagation simulations. Theor. Appl. Fract. Mech. 2017, 91, 76–85. [Google Scholar] [CrossRef]
- Salari, M. Fatigue crack growth reliability analysis under random loading. Int. J. Struct. Integr. 2020, 11, 157–168. [Google Scholar] [CrossRef]
- Stepnov, M.N.; Giacintov, E.V. Fatigue of Light Structural Alloys; Mashinostroeniya: Moscow, Russia, 1973; pp. 8–22. (In Russian) [Google Scholar]
- Ulbrich, D.; Selech, J.; Kowalczyk, J.; Jóźwiak, J.; Durczak, K.; Gil, L.; Pieniak, D.; Paczkowska, M.; Przystupa, K. Reliability Analysis for Unrepairable Automotive Components. Materials 2021, 14, 7014. [Google Scholar] [CrossRef] [PubMed]
- Żurek, J.; Małachowski, J.; Ziółkowski, J.; Szkutnik-Rogoż, J. Reliability Analysis of Technical Means of Transport. Appl. Sci. 2020, 10, 3016. [Google Scholar] [CrossRef]
- Ballo, F.; Comolli, F.; Gobbi, M.; Mastinu, G. Motorcycle Structural Fatigue Monitoring Using Smart Wheels. Vehicles 2020, 2, 648–674. [Google Scholar] [CrossRef]
- Lukoševičius, V.; Makaras, R.; Rutka, A.; Keršys, R.; Dargužis, A.; Skvireckas, R. Investigation of Vehicle Stability with Consideration of Suspension Performance. Appl. Sci. 2021, 11, 9778. [Google Scholar] [CrossRef]
- GOST 25502-79 Standard; Strength Analysis and Testing in Machine Building. Methods of Metals Mechanical Testing. Methods of Fatigue Testing; Standardinform: Moscow, Russia, 1993.
- GOST 22015-76 Standard; Quality of Product. Regulation and Statistical Quality Evaluation of Metal. Materials and Products on Speed-torque Characteristics; Standardinform: Moscow, Russia, 2010.
- EN ISO 6892-1:2016; Metallic Materials—Tensile Testing—Part. 1: Method of Test. at Room Temperature; International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- Regularities and Norms in Nuclear Power Engineering (PNAE) No. G-7-002-89; Rules of Equipment and Pipelines Strength Calculation of Nuclear Power Plant; Energoatomizdat: Moscow, Russia, 1989.
- Daunys, M. Cycle Strength and Durability of Structures; Technologija: Kaunas, Lithuania, 2005. (In Lithuanian) [Google Scholar]
- Severini, T.A. Likelihood Methods in Statistics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
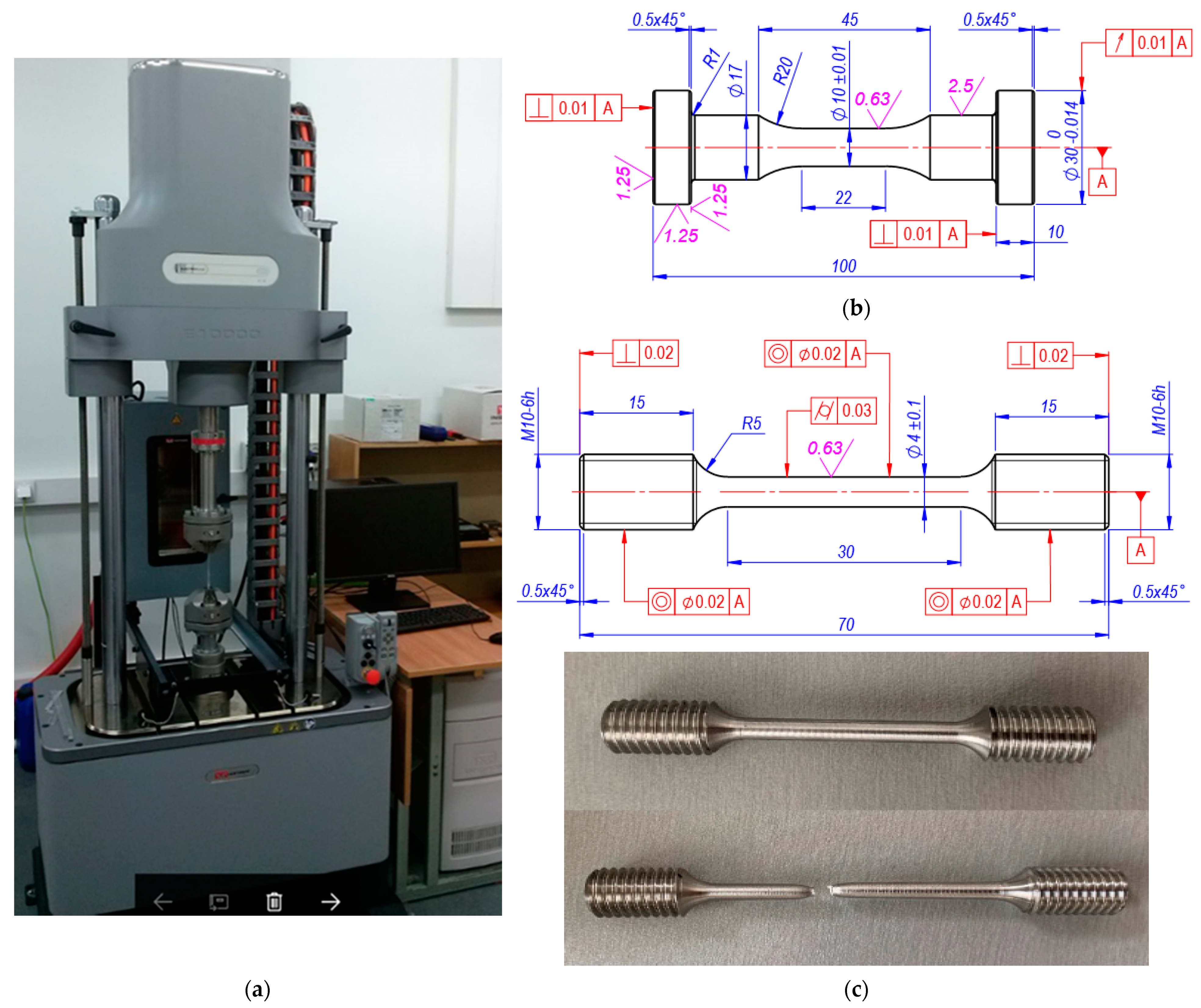
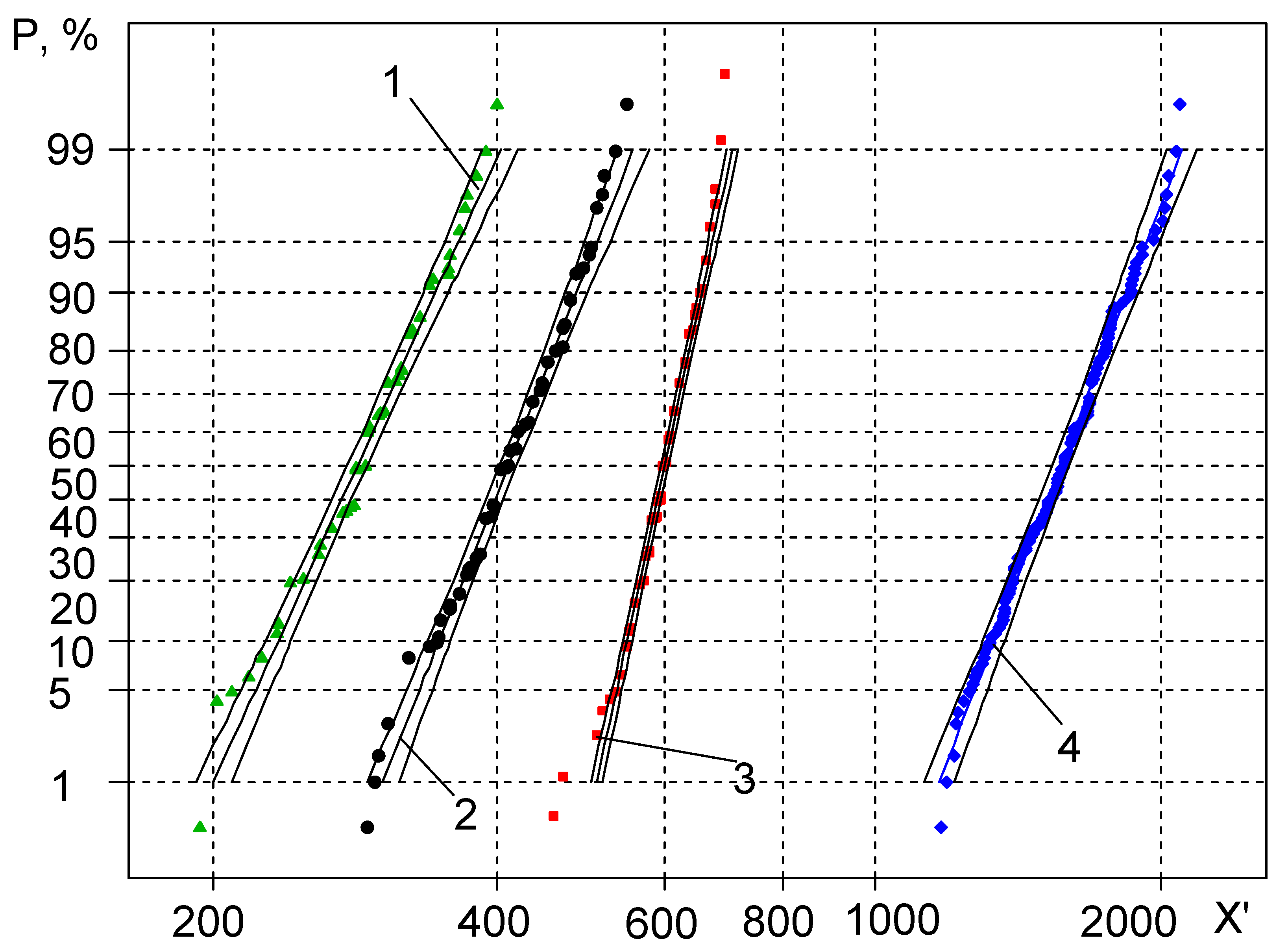
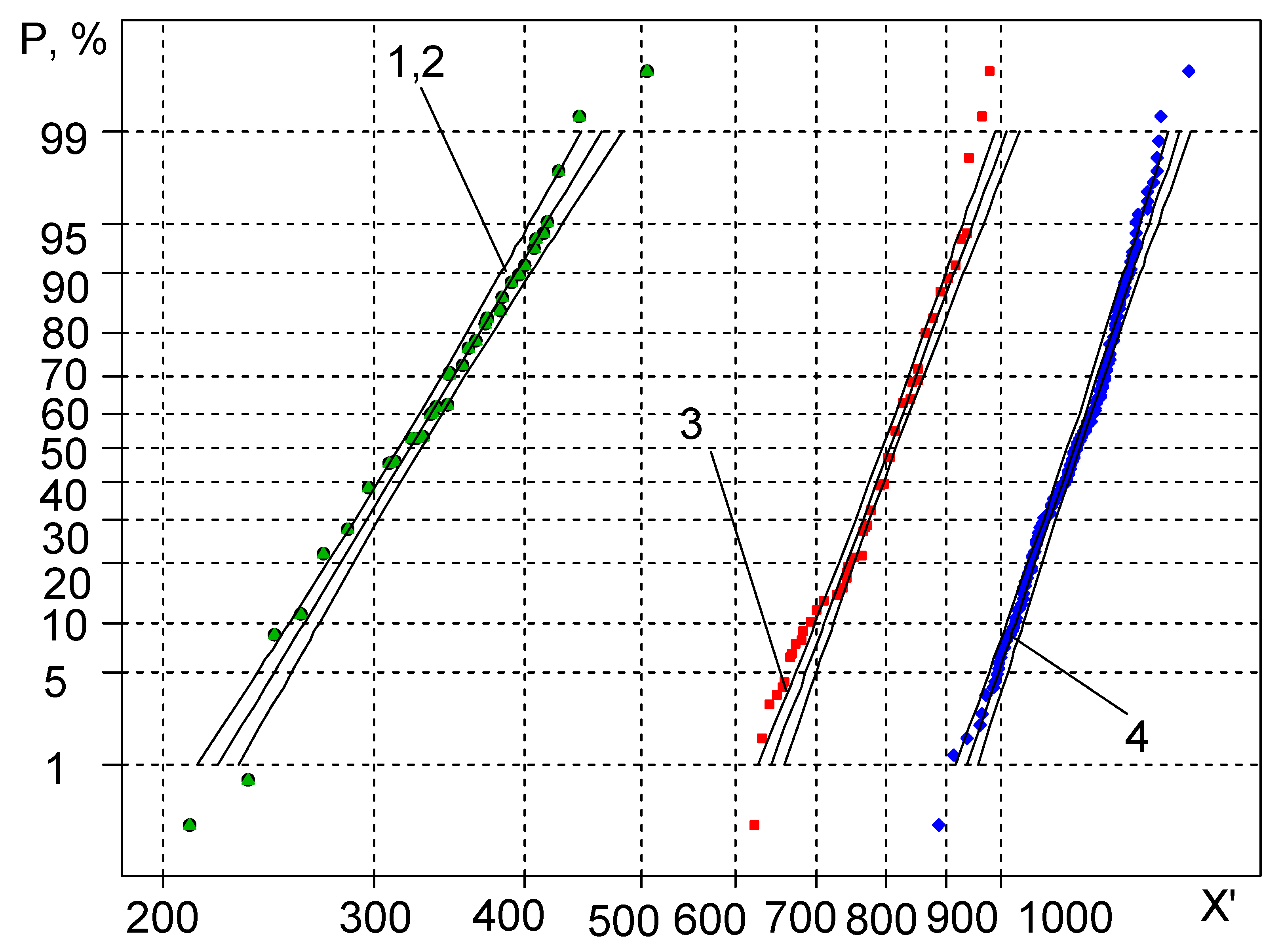
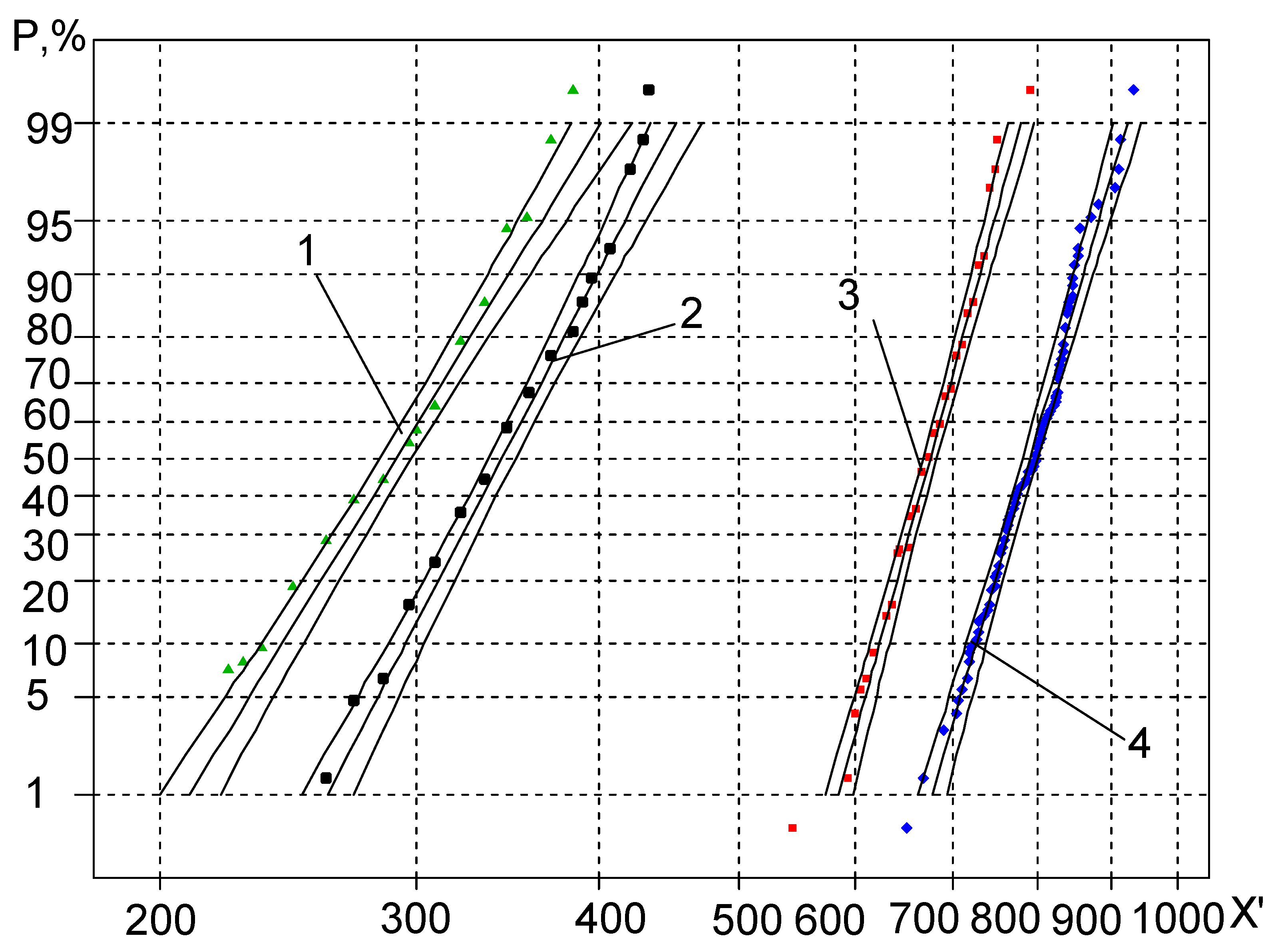
| Material | C | Si | Mn | Cr | Ni | Mo | V | S | P | Mg | Cu | Al |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | ||||||||||||
| 15Cr2MoVA (GOST 5632-2014) | 0.18 | 0.27 | 0.43 | 2.7 | 0.17 | 0.67 | 0.30 | 0.019 | 0.013 | - | - | - |
| C45 (GOST 1050-2013) | 0.46 | 0.28 | 0.63 | 0.18 | 0.22 | - | - | 0.038 | 0.035 | - | - | - |
| D16T1 (GOST 4784-97) | - | - | 0.70 | - | - | - | - | - | - | 1.6 | 4.5 | 9.32 |
| Material | epr | σpr | σys | σu | Sk | ψ |
|---|---|---|---|---|---|---|
| % | MPa | % | ||||
| 15Cr2MoVA (GOST 5632-2014) | 0.200 | 280 | 400 | 580 | 1560 | 80 |
| C45 (GOST 1050-2013) | 0.260 | 340 | 340 | 800 | 1150 | 39 |
| D16T1 (GOST 4784-97) | 0.600 | 290 | 350 | 680 | 780 | 14 |
| Material | Number of Specimens, pcs. | |
|---|---|---|
| 15Cr2MoVA | 1.8 | 40 |
| 3.0 | 80 | |
| 5.0 | 40 | |
| C45 | 2.5 | 60 |
| 4.0 | 100 | |
| 6.0 | 60 | |
| D16T1 | 1.0 | 20 |
| 1.5 | 80 | |
| 2.0 | 20 |
| Mechanical Property | Material | N0 | Nk |
|---|---|---|---|
| σpr, MPa | 15Cr2MoVA C45 D16T1 | 184.0 | 410.0 |
| 206.0 | 510.0 | ||
| 201.8 | 390.0 | ||
| σy, Mpa | 15Cr2MoVA C45 D16T1 | 276.4 | 550.0 |
| 206.0 | 510.0 | ||
| 245.6 | 440.0 | ||
| σu, Mpa | 15Cr2MoVA VA 45 D16T1 | 445.1 | 700.0 |
| 594.8 | 1000.0 | ||
| 535.4 | 800.0 | ||
| Sk, Mpa | 15Cr2MoVA C45 D16T1 | 1153.5 | 2110.0 |
| 874.0 | 1450.0 | ||
| 641.7 | 945.0 | ||
| ψ, % | 15Cr2MoVA C45 D16T1 | 72.4 | 91.0 |
| 29.2 | 55.0 | ||
| 9.1 | 24.0 | ||
| ψu, % | 15Cr2MoVA C45 D16T1 | 5.8 | 25.3 |
| 9.1 | 35.0 | ||
| 10.5 | 15.0 |
| Mechanical Property | Material | Distribution Law | |||||
|---|---|---|---|---|---|---|---|
| Normal | Logarithmic-Normal | Weibull’s | |||||
| X′ | X″ | X′ | X″ | X′ | X″ | ||
| σpr, MPa | 15Cr2MoVA C45 D16T1 | 0.07647 | 0.000038 | −0.3199 | −0.000411 | 0.07793 | 0.07793 |
| 0.41101 | 0.000127 | 0.05815 | −0.000137 | 0.416676 | 0.416682 | ||
| −0.09905 | −0.000008 | −0.2426 | −0.000448 | −0.10158 | −0.010158 | ||
| σy, Mpa | 15Cr2MoVA C45 D16T1 | 0.005413 | 0.000003 | −0.3164 | −0.000427 | 0.005516 | 0.005502 |
| 0.41101 | 0.000127 | 0.05815 | −0.000137 | 0.416676 | 0.416682 | ||
| 0.1197 | 0.000092 | −0.1258 | −0.000489 | 0.122715 | 0.122706 | ||
| σu, Mpa | 15Cr2MoVA C45 D16T1 | −0.3332 | −0.000166 | −0.6145 | −0.000658 | −0.3396 | −0.3396 |
| −0.322 | −0.000099 | −0.5682 | −0.000316 | −0.326442 | −0.32643 | ||
| −0.1403 | −0.000108 | −0.3343 | −0.000743 | −0.143851 | −0.143855 | ||
| Sk, Mpa | 15Cr2MoVA C45 D16T1 | 0.2425 | 0.000121 | −0.05469 | −0.000387 | 0.247175 | 0.247177 |
| −0.1088 | −0.000034 | −0.307 | −0.000274 | −0.110319 | −0.110327 | ||
| −0.06094 | −0.000047 | −0.2495 | −0.000671 | −0.062491 | −0.062505 | ||
| ψ, % | 15Cr2MoVA C45 D16T1 | 1.096878 | 0.000547 | 0.901323 | −0.000013 | 1.436741 | 1.117773 |
| 0.224567 | 0.000069 | 0.021761 | −0.000081 | 0.227662 | 0.227669 | ||
| 0.528782 | 0.000407 | 0.161176 | −0.000074 | 0.542263 | 0.542267 | ||
| ψu, % | 15Cr2MoVA C45 D16T1 | 2.37809 | 0.001186 | 0.916574 | 0.000106 | 2.638781 | 2.423339 |
| 1.445826 | 0.000446 | 0.24641 | 0.000011 | 2.219523 | 1.465758 | ||
| 0.071902 | 0.000055 | −0.177563 | −0.000287 | 0.246678 | 0.073743 | ||
| Property | Material | σ | D | S | V | Ex | |
|---|---|---|---|---|---|---|---|
| σpr, MPa | 15Cr2MoVA | 0.0145 | 0.4154 | 0.1726 | −0.8310 | −2.0004 | 1.2513 |
| C45 | 0.0109 | 0.4380 | 0.1918 | −1.0160 | −2.3199 | 1.8201 | |
| D16T1 | 0.0193 | 0.4575 | 0.2093 | −0.1727 | −0.3776 | 0.2053 | |
| σy, Mpa | 15Cr2MoVA | 0.0169 | 0.4411 | 0.1946 | 0.7756 | 1.7582 | 5.0906 |
| C45 | 0.0109 | 0.4380 | 0.1918 | −1.0160 | −2.3199 | 1.8201 | |
| D16T1 | 0.0199 | 0.4541 | 0.2062 | 0.4916 | 1.0824 | 0.6362 | |
| σu, Mpa | 15Cr2MoVA | 0.0165 | 0.4332 | 0.1877 | 1.3853 | 3.1976 | 1.7565 |
| C45 | 0.0117 | 0.4020 | 0.1616 | 0.0496 | 0.1233 | 0.5252 | |
| D16T1 | 0.0192 | 0.3350 | 0.1122 | 0.2878 | 0.8591 | 4.6627 | |
| Sk, Mpa | 115Cr2MoVA | 0.0159 | 0.5068 | 0.2568 | −0.1880 | −0.3709 | 2.0149 |
| C45 | 0.0113 | 0.3651 | 0.1333 | −0.5566 | −1.5247 | 2.7141 | |
| D16T1 | 0.0188 | 0.3666 | 0.1344 | −0.2374 | −0.6476 | 2.9361 | |
| ψ, % | 15Cr2MoVA | 0.0137 | 0.3307 | 0.1093 | −1.1230 | −3.3962 | 6.4751 |
| C45 | 0.0111 | 0.4228 | 0.1787 | −0.7040 | −1.6650 | 0.1065 | |
| D16T1 | 0.0158 | 0.4902 | 0.2403 | −1.5768 | −3.2166 | 0.4385 | |
| ψu, % | 15Cr2MoVA | 0.0134 | 0.7288 | 0.5312 | −1.1051 | −1.5163 | −0.7647 |
| C45 | 0.0081 | 0.7878 | 0.6206 | −1.3378 | −1.6983 | −0.8945 | |
| D16T1 | 0.0191 | 0.3477 | 0.1209 | 0.1802 | 0.5183 | 4.2422 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazaras, Ž.; Lukoševičius, V.; Bazaraitė, E. Structural Materials Durability Statistical Assessment Taking into Account Threshold Sensitivity. Metals 2022, 12, 175. https://doi.org/10.3390/met12020175
Bazaras Ž, Lukoševičius V, Bazaraitė E. Structural Materials Durability Statistical Assessment Taking into Account Threshold Sensitivity. Metals. 2022; 12(2):175. https://doi.org/10.3390/met12020175
Chicago/Turabian StyleBazaras, Žilvinas, Vaidas Lukoševičius, and Eglė Bazaraitė. 2022. "Structural Materials Durability Statistical Assessment Taking into Account Threshold Sensitivity" Metals 12, no. 2: 175. https://doi.org/10.3390/met12020175
APA StyleBazaras, Ž., Lukoševičius, V., & Bazaraitė, E. (2022). Structural Materials Durability Statistical Assessment Taking into Account Threshold Sensitivity. Metals, 12(2), 175. https://doi.org/10.3390/met12020175






