The Influence of the Degree of Tension and Compression of Aluminum on the Indentation Size Effect (ISE)

Abstract

The presented work deals with the relationship between the degree of cold plastic deformation (up to 84.5% in the tensile test and up to 83.5% in compression) and the parameters of the Indentation Size Effect (ISE). The tested material was 99.5% aluminum. Testers Hanemann (Carl Zeiss, Jena, Germany) and LECO 100 (LECO Corporation, St. Joseph, MI, USA), were used for the measurement of micro- and tester Agilent G200 (Agilent Technologies, Santa Clara, CA, USA) for nano-hardness; which was used to determine the inhomogeneity of deformation. Applied loads in the micro-hardness test ranged between 0.09807 N to 0.9807 N. The influence of the load and degree of the on micro-hardness and at the same time on the ISE, expressed by Meyer’s index n is significant. The influence of the load on the parameters of ISE was also evaluated by Meyer’s index n, PSR method, and Hays–Kendall approach. In the undeformed sample, Meyer’s index is close to 2, with the increase in the degree of tensile deformation increasing its “normal” character (n < 2), and with the increase in the degree of compressive deformation increasing its “reverse” character (n > 2).

1. Introduction

The micro-hardness test is a way how to determine the mechanical properties of a small parts of materials. Several authors, such as Sangwal et al. [1] found that the principle of the Vickers micro-hardness method is identical to the (macro) hardness test, except for a test load lower than 1.691 N (200 g). The micro-hardness can be applied on thin layers of materials, and also to identify the phases in metallography. The independence of the (macro)hardness on the applied load is an advantage of the Vickers test. The form of the Vickers indentation is geometrically similar at all test loads. It is therefore expected that the value of the hardness is constant as long as the tested sample is reasonably homogeneous.

The measured hardness is usually high if a very low load is applied; if a high load is used, the measured hardness decreases. This phenomenon is called a “normal” indentation size effect (ISE). According to Gong et al. [2], measuring the hardness to characterize materials may result in some unreliable conclusions.

As demonstrated by Tabor [3], the ambiguity in the measurement of small indentations, especially if pile-up or sink-in effects are present, may result in over- or underestimation of the diagonals’ length. Gubicza et al. [4] concluded that the existence of ISE can be questioned if it is not possible to guarantee a reliable measurement of the diagonals of the indentations. Similarly, Strand and Jakab-Farkas [5] consider the biggest source of error to be the measurement of indentations. Most operators can measure indentations with a length accuracy of ±0.5 μm. If the diagonal falls below 20 μm, this inaccuracy can have a significant impact.

In the works of Golanet [6], Rayar et al. [7], Kumar et al. [8], Dusza and Stern [9], and Michels et al. [10], there are many examples that point to the fact that “normal” ISE occurs in brittle materials like glass, semiconductors, sintered materials, ceramics ware or organic crystals. Kathavate et al. [11] studied the ISE of piezoelectric relax or ferroelectric material (PMN-PT). They found that different domain configurations are achieved by selectively annealing, and also affect the values of Meyer’s index. The critical analysis of nanoindentation data reveals that the PSR model provides a satisfactory understanding of the genesis of RISE and ISE considering the elastic resistance of test material and frictional resistance at the indenter facet/test material. Meyer index values for Composite A356 + 6%FA subjected to ECAP (n ranged between 1.9112 and 2.3321), where the cast composite shows normal ISE, while samples machined with ECAP show reverse ISE-RISE, were published by Muslić et al. [12]. Liu et al. [13] confirmed the influence of the crystallographic orientation of germanium single crystals on ISE, as did Şahin et al. [14] for tin and Petrik et al. [15] for copper. As [16,17,18] prove in their work, the parameters describing ISE are also affected by the method of sample preparation, especially the final surface roughness on which the micro-hardness is measured. Roughness was not measured on the samples used in the presented measurement. Given the standard preparation by pre-measuring the hardness as well as the mirror finish surface of all samples without scratches, we can assume that the potential effect of roughness on the ISE parameters is equal to all samples.

A reverse (inverse, RISE) type of ISE exists, in contrast to “normal” ISE. In the reverse ISE, the apparent micro-hardness increases with increasing testing load. It mostly takes place in materials with plastic deformation. As shown by Sangwal [19], reverse ISE can be explained by the existence of a distorted zone near the sample—indenter (crystal-medium) interface, the vibration existence of the indenter, the applied energy loss around the indentation, and generation of the cracks.

In the literature, many examples exist, which reveal that the “normal” ISE occurs in brittle materials. On the other hand, the literature is rare on reverse ISE. It mainly concerns reporting for materials passing plastic deformation [1].

The ground of the ISE is still a topic of debate. It may occur by the testing equipment (the applied load, the measurement device of indentation diagonals [1,2,19]), inner properties of the testing material (load to initiate plastic deformation, indentation elastic recovery, work hardening during indentation, and elastic resistance of the materials [1,19,20], the method tested sample preparation (grinding, polishing, and the resulting residual stress), and possibly other factors (indenter/sample friction, lubrication, and also corrosion) [2,21].

The purpose of this paper is to evaluate the influence of the degree/amount of cold plastic deformation (tensile test and compression or upsetting test, thus deformation by tension and pressure) and used load on the micro-hardness and character of the ISE.

2. Materials and Methods

“Commercially pure” aluminum was used as the experimental material. It is a malleable alloy that is formed by rolling, pressing, forging, and other operations. It is widely used in various branches of industry, especially as a conductor in electrical engineering. As an experimental material, it was used primarily for single-phase structure and deformation strengthening by cold working. 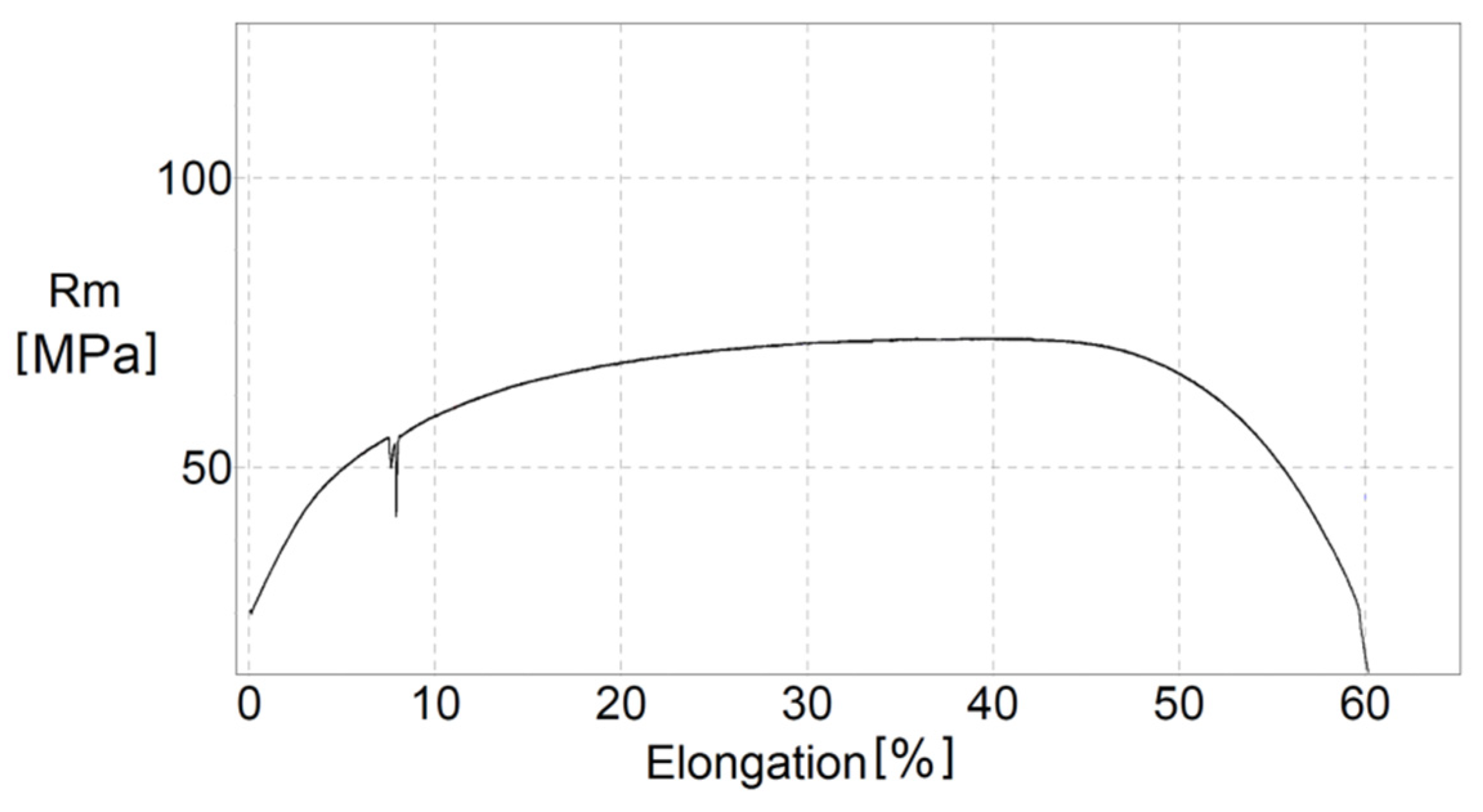The authors were somewhat inspired by the contribution [22], in which the authors, unfortunately, did not use the measurement of hardness. The tested material is 99.5% aluminum (more detail in the standards STN 42 4004 or EN AW 1350) in the form of a rod with a diameter ∅ of 9 mm. The presence of secondary (Fe, Mn, Cu, Cr, Mo, Pb, Si, V, Sn, Zn in the range from 0.1–0.01%) and trace (Ag, Ti in the range from 0.01–0.00001%) elements was determined by semi-quantitative spectral analysis by the spectrograph PGS-2. The rod was annealed for an hour at a temperature of 400 °C and slowly cooled in the furnace to ensure the homogeneity of the structure and to remove stress. After heat treatment, two tensile test samples and cylinders (15 mm × ∅ 9 mm) for compression (upset) test were turned. The tester 200 kN Zwick-Extensometer was used for both tests. For the tensile test, the mean strain rate ${\mathsf{\epsilon }}_{\mathrm{L}\mathrm{c}}=0.0004 {\mathrm{s}}^{-1}$. The ultimate tensile strength UTS is 73 MPa, yield tensile strength YS 25 MPa, elongation TE 59.7%, and reduction of the area/contraction Z is 90.7%. The stress-strain curve is shown in Figure 1. Relative expanded uncertainty U_rel (k = 2) is 1.82% for YS and UTS and less than 1% for TE and Z. The micro-hardness was measured on a longer part of the fractured tensile piece, as shown in Figure 2, and cut in the longitudinal axis by a water-cooled diamond saw. The method used for the measurement of micro-hardness is described in more detail in [23]; some results are shown below for comparison.

The parameters of the tensile test are in

Table 1. Results of the tensile test: the reduction of the area Z (%), values of the micro-hardness and average micro-hardness $\overline{\mathit{H}\mathit{V}}$, and the speed of the indenter. Area Z7 is the head and area Z1 is the neck of the tensile test sample.

Area	Z (%)	HV0.01	HV0.025	HV0.05	HV0.1	$\overline{\mathit{H}\mathit{V}}$	v (μm s−1)
Z7	0	32.32	29.92	28.81	28.30	29.84	1.77
Z6	−14.7	33.17	35.47	34.46	34.04	34.28	2.10
Z5	−17.2	34.13	35.25	34.13	33.46	34.24	2.30
Z4	−19.1	36.32	34.59	33.64	33.52	34.52	2.55
Z3	−28.6	39.11	36.61	35.58	34.88	36.54	2.44
Z2	−53.1	43.26	38.92	38.42	37.80	39.60	2.47
Z1	−84.5	44.67	45.53	44.75	42.62	44.39	2.31

and of the compression are given in

Table 2. Parameters of compression: the degree (amount) of the deformation ε (%), degree of the proportional lateral (transverse) extension φ (%), strain rate $\dot{\phi }$ (s⁻¹), values of the micro-hardness and average micro-hardness $\overline{\mathit{H}\mathit{V}}$, and speed of the indenter for load 0.49035 N.

Sample	ε (%)	φ (%)	$\dot{\mathit{\phi }}$	HV0.01	HV0.025	HV0.05	HV0.1	$\overline{\mathit{H}\mathit{V}}$	v (μm s−1)
Initial state (1)	0.0	0.0	0.000	26.57	28.68	29.24	26.62	27.78	2.349
Initial state (2)	0.0	0.0	0.000	26.00	28.17	26.95	24.96	26.52	2.171
ε1	5.8	6.6	0.029	29.54	31.50	30.50	29.15	30.17	1.914
ε2	16.2	21.9	0.038	31.60	34.86	32.63	35.12	33.55	1.588
ε3	27.2	41.5	0.064	34.89	37.06	38.85	39.06	37.46	1.760
ε4	35.8	63.5	0.025	33.88	40.32	39.95	39.63	38.44	2.540
ε5	46.2	100.2	-	35.12	41.51	42.53	42.53	40.42	1.852
ε6	56.1	119.7	0.056	38.43	45.37	44.70	45.93	43.61	1.863
ε7	65.4	199.4	0.071	36.63	44.39	47.56	45.12	43.43	1.769
ε8	73.1	306.3	0.049	38.25	43.25	45.66	46.70	43.46	1.399
ε9	75.1	346.9	0.094	37.27	45.12	47.91	46.45	44.19	1.759
ε10	76.5	370.6	0.092	37.64	46.87	48.73	47.83	45.27	1.761
ε11	83.5	499.7	-	42.25	48.99	49.50	48.18	47.23	2.466

⁽¹⁾ The cut parallel with the axis; ⁽²⁾ the cut perpendicular to the axis.

. The micro-hardness of the fractured tensile sample was measured with tester LECO 100 in individual areas between the neck (Z1) and the head (Z7). The relationship between the local reduction of the area and micro-hardness is shown in Table 1.

The degree of the deformation ε (%) in the compression is a change in height, and the degree of the extension φ (%) is a change in the diameter. The samples were deformed without the lubricant. The accuracy in measurement of the dimensions was 0.001 mm. The deformed samples were cut parallel to the vertical axis at the maximum diameter with a water-cooled diamond saw; the starting, undeformed state was cut in planes both parallel and perpendicular to its axis.

Cut samples were fixed in the resin (dentacryl). For grinding silicon papers in sequence 80…3000ANSI/CAMI with water-cooling were used. The metallographic surface was polished with the water suspension of Al₂O₃ to a mirror finish. A water solution of 0.5% HF was used as the etching agent. The purpose of etching was to make visible hard intermetallic phases, firstly Al-Fe and Al-Fe-Mn. When measuring the micro-hardness, the area of their occurrence was missed.

For the nanoindentation testing, the sectioned pure aluminum rolls after different deformations were prepared using the fixation technique by cold resin, and then they were ground and polished—flat.

The nanoindentation measurement of the local hardness on the surface of the investigated sample was carried out with Agilent G200 indenter (Agilent Technologies, Inc., Chandler, AZ, USA) with a Berkovich tip perpendicular to the cutting surface mapping the matrix of points with 150 μm spacing. Single loading–unloading indentation was used. The indentation depth-controlled method was used with a maximum depth of 2000 nm was used in all cases.

The micro-hardness of compressed cylinders was measured with tester Hanemann, type Mod D32, part of the optical microscope Neophot-32. The tester’s optics enabled a magnification of 480×. The value of the smallest division of the scale (discrimination) of the device measuring indentations is 0.000313 mm. It ranged between 1.1% and 3.1% of the average diagonal, depending on the used load.

A reference block, –CRM (certified reference material) with specified hardness H_c = 195 HV0.05 and standard uncertainty u = 4.0 HV0.05, was used for the calibration of the tester.

According to the results of the calibration (repeatability r_rel, error of tester E_rel, and relative expanded uncertainty of calibration U_rel), which was done before each measurement, both testers meet the conditions of the standard ISO 6507-2 [24].

3. Results

The nano-hardness of the initial (starting, undeformed) state (the cut perpendicular to the axis), was measured in the axis of the sample over an area of 1.4 mm × 1.4 mm. The purpose was to evaluate the influence of the applied annealing process on the inhomogeneous distribution of hardness. As can be seen in Figure 3, the difference in the nano-hardness is insignificant (between 0.380 and 0.436 GPa ≈ 38.0 and 43.6 HV).

The change of the nano-hardness of sample ε₆, in % (relative change of hardness obtained on the compressed samples in comparison with samples in the initial state without compression), can be seen in Figure 4. The deformation is not homogeneous. At the bottom of the image can be seen an area with low deformation at the sample-anvil (die) contact. By contrast, the deformation in the upper part of the figure is significantly higher, and the arm of the X shape area or the “forging cross” is displayed.

The nano-hardness of sample ε₁₀ was measured to determine the influence of deformation on its value. Since the symmetrical distribution of deformation inhomogeneity is assumed, nano-hardness was measured only on half of the sample. In Figure 5, the measured area is marked as J. Figure 6 displays the change of the nano-hardness (in %), and inhomogeneous deformation is manifested by the formation of regions with different nano-hardness values. This fact was a guide for identifying areas for measuring the micro-hardness and determining its impact on ISE parameters.

One operator measured the micro-hardness according to ISO 6507-1:2004 [25]. The applied loads P were 0.09807 N (10 g), 0.24518 N (25 g), 0.49035 N (50 g), and 0.9807 N (100 g). The duration of the load was 15 seconds. The values of the mean speed of the indenter’s penetration (v, in μm s⁻¹) into the volume of the sample at the load 0.49035 N are in Table 2. The calculation of the speed is described in [23].

First, an indentation of the load 50 g (0.49035 N) was applied. The indentations at the other loads were carried out; the distance between particular indentations meets the requirements of the standard ISO 6507-1 [25]. At a distance of 1 mm, a further indentation was made at a load of 0.49035 N and indentations around it at other loads. The process was repeated until the opposite side of the sample was reached. Thus, the number of indentations was not the same and it increased with the degree (amount) of deformation and thus the sample diameter. For example, the arrangement of the indentations in the band is shown in detail in Figure 7 (sample ε₁₀, area F in Figure 5; the figure is illustrative to display the size of the indentations at different loads. Indentations whose dimensions were used to evaluate the ISE were at distances corresponding to the requirements of the standard).

For the compressed samples, the values of the relative expanded uncertainty U_rel of the micro-hardness range between 29.4% and 61.7%. Its value is overestimated by the used CRM (iron) with a micro-hardness significantly higher than the hardness of the measured samples. Therefore, these values should only be considered indicative. The relationship (correlation) between the degree of deformation ε, and the uncertainty is strong (r² = −0.9049), and the uncertainty decreases with increasing deformation.

The result of the micro-hardness measurement of compressed samples is “clusters” of 32–92 (depending on the degree of deformation) indentations for individual compressed samples. The average values of micro-hardness (HV) of each of the clusters, and the micro-hardness at individual loads are in Table 1 for the fractured tensile piece, and in Table 2 for compressed samples.

The influence of the local reduction of the area, load, and micro-hardness for compressed samples are shown in Figure 8.

Anomalies in (Figure 8) may be due to inhomogeneous deformation during the compression; the inhomogeneity is also increased by the absence of lubricant between the dies and the top or bottom contact face. They can also arise as a result of the presence of intermetallic phases, similar to tensile pieces [23].

The result of the inhomogeneity of the deformation was the formation of three areas: an area without deformation at the sample-anvil (die) contact (above the top or the bottom contact face area H in

Table 3. Sample ε₁₀. The values of Meyer’s index n, average micro-hardness $\overline{x}$, the standard deviation of the hardness SD, and the number of the indentations N, the average micro-hardness at all four loads $\overline{\mathit{H}\mathit{V}}$, and for the load 0.49035 N.

Sample		$\overline{\mathit{H}\mathit{V}}$				HV0.05
		n	$\overline{\mathit{x}}$	SD	N	$\overline{\mathit{x}}$	SD	N
A	periphery (edge)	2.08	43.6	2.88	20	42.4	1.35	5
B	band: top-bottom contact face, periphery (1)	-	-	-	-	45.6	2.71	18
C	band: top-bottom contact face, centre (1)	-	-	-	-	46.3	1.21	8
D	the center 1	2.11	43.9	3.05	20	46.5	1.32	5
E	the centrr 2	2.04	41.0	4.33	20	47.8	0.77	5
F	band: periphery (edge, side) - periphery	2.22	45.3	5.32	64	48.7	3.54	19
G	top contact face, low deformation	2.14	42.1	2.85	20	43.3	2.55	5
H	Bottom contact face, low deformation	2.20	42.7	7.63	20	43.3	2.55	5
I	Bottom contact face, high deformation	2.17	48.6	4.65	20	49.9	1.95	5
J	The area of nano-hardness measurement

⁽¹⁾ Only load 0.49035 N (50 g) was applied.

, Figure 5), a slightly deformed area along the maximum circumference (edges, peripheries, sides of the sample—area A in Table 5, Figure 4), and maximum deformed X shape area—the axisymmetric heterogeneity (barreling, zones of heterogeneity or the “forging cross”; D, E, and the first area I in Table 5, Figure 4).

The relationship between the inhomogeneity of the deformation and the measured values of nano- and micro-hardness is demonstrated in sample ε₁₀. As expected, the locally increased degree of deformation was manifested by an increase in nano-hardness, Figure 6, in the lower left, corresponding to the area I, Figure 5. To investigate the influence of the local deformation (given by the area of the sample), the micro-hardness and the characteristics of ISE, the micro-hardness was measured in bands or in clusters (5 indentations per load, a total of 20 indentations per cluster).

The local degree of deformation could not be accurately measured. The use of the deformation of the originally equiaxed grains to determine the local deformation did not meet expectations. Even the deep etching did not make the grain boundaries clear enough. The selection of sites of the clusters or bands (A–I) was made based on the values of nano-hardness. The position of the clusters and bands is shown in Figure 5 and the description in Table 3, also with the values of the number of the indentations N, average micro-hardness, and Meyer’s indices n.

The statistical significance of the micro-hardness measured in individual areas (A–J) of sample ε₁₀ was obtained by unpaired t-test. It is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment has an effect on the population of interest, or whether two groups are different from one another. If the value of p < α (significance level α = 0.05), the difference between average hardness is statistically significant (these values are in italics in

Table 4. The statistical significance of the micro-hardness measured in individual areas of sample ε₁₀ was obtained by t-test for the micro-hardness at all four loads $\overline{\mathit{H}\mathit{V}}$ and the load 0.49035 N (50 g).

t-Test	HV0.05
	A	B	C	D	E	F	G	H
I	0.0001	0.0038	0.0015	0.0166	0.0158	0.4964	0.0018	0.0017
H	0.0275	0.3834	0.0453	0.0651	0.0012	0.0171	0.4002	-
G	0.5053	0.064	0.0163	0.0397	0.0142	0.0042	-	-
F	0.0005	0.0052	0.0649	0.1769	0.302	-	-	-
E	0.0001	0.2766	0.2223	0.4285	-	-	-	-
D	0.0008	0.5244	0.7635	-	-	-	-	-
C	0.0001	0.5573	-	-	-	-	-	-
B	0.093	-	-	-	-	-		-
	$\overline{\mathit{H}\mathit{V}}$
t-Test	A	B	C	D	E	F	G	H
I	0.0002	-	-	0.0006	0.0001	0.0005	0.0001	0.0003
H	0.5209	-	-	0.3352	0.2406	0.0013	0.6305	-
G	0.136	-	-	0.0613	0.3486	0.0001	-	-
F	0.1076	-	-	0.2033	0.0008	-	-	-
E	0.0395	-	-	0.0191	-	-	-	-
D	0.6569	-	-	-	-	-	-	-

).

For the detection of outlier values Grubb’s test (significance level α = 0.05) was used. Statistical outliers indicate the measurement process that suffers from special disturbances and is out of statistical control. The Anderson – Darling test was applied to determine the normality of a “cluster” of measured values; the values in all “clusters” have normal distribution without outliers.

Meyer’s power law and proportional specimen resistance (PSR) are most often used to determine ISE characteristics [20]:

Meyer’s Law can be expressed using Equation (1):

$$\mathrm{P}={ \mathrm{Ad}}^{\mathrm{n}}$$

(1)

The parameters n and A are determined by exponential curve fitting to indentation diagonal d (mm) versus applied load P (N) or n and A_ln are determined by straight line fitting to ln (d) versus ln (P). The value d is the average value of the diagonals of all indentations in the band, done at one load. Meyer’s index n or work hardening coefficient is the slope, and coefficient A_ln is the y-intercept of the line. This relationship was derived for the ball indenter but it has become common practice to apply Tabor’s interpretation of the strain-hardening by pyramidal indenter and to derive a “work-hardening index” [26]. The index n > 2 was used for reverse ISE, n < 2 was used for “normal” ISE. If n = 2, the micro-hardness is independent of the load and is given by Kick’s law.

The values of n and A_ln are in

Table 5. The parameters of ISE.

Sample	ε (%)	n	Aln	a1	a2	c0	c1	c2	W	A1	a1/a2	c1/c2
Initial state (1)	0.0	2.01	5.019	0.313	140	−0.113	5.395	92	0.018	140	0.0022	0.0583
Initial state (2)	0.0	1.958	4.813	0.618	127	−0.086	4.421	92	0.024	130	0.0049	0.0481
ε1	5.8	1.984	5.020	0.348	151	−0.054	2.938	126	0.013	153	0.0023	0.0234
ε2	16.2	2.071	5.401	−0.539	190	0.060	−3.547	222	−0.015	187	−0.0028	−0.0160
ε3	27.2	2.105	5.618	−0.734	217	−0.019	0.261	206	−0.013	208	−0.0034	0.0013
ε4	35.8	2.131	5.733	−0.648	221	−0.066	2.894	181	−0.007	212	−0.0029	0.0160
ε5	46.2	2.179	5.937	−1.089	244	−0.064	2.378	203	−0.016	229	−0.0045	0.0117
ε6	56.1	2.149	5.925	−0.978	259	−0.023	0.392	242	−0.016	246	−0.0038	0.0016
ε7	65.4	2.2	6.087	−1.055	2601	−0.146	7.004	165	−0.009	243	−0.0040	0.0425
ε8	73.1	2.192	6.058	−1.454	270	−0.025	−0.042	253	−0.026	253	−0.0054	−0.0002
ε9	75.1	2.21	6.134	−1.223	269	−0.121	5.518	188	−0.015	251	−0.0045	0.0293
ε10	76.5	2.22	6.197	−1.326	279	−0.110	4.924	202	−0.016	259	−0.0048	0.0244
ε11	83.5	2.115	5.897	−0.568	267	−0.079	4.088	209	−0.003	256	−0.0021	0.0196

⁽¹⁾ The cut parallel to the axis; ⁽²⁾ the cut perpendicular to the axis.

. The relationship between deformation (Z for tensile test and ε for compressed samples) and Meyer’s index n is in Figure 9. The ISE character (nature) changes from neutral (n = 2) to reverse for compressed samples and to “normal” for tensile test sample with an increase of deformation. As the deformation increases, the absolute value of the size of n also increases. The relationship between the amount of plastic deformation and Meyer’s index n is described by the polynomial 3rd degree with a strong correlation (Pearson’s coefficient r² = 0.8947; the coefficient of determination r² = 0.9291).

The dependence of the value of Meyer’s index on the position of the indentations and the degree of deformation for (a) the tensile piece and (b) the compressed samples can be seen in Figure 10. In the case of a tensile piece and compressed samples, the values of the micro-hardness of the indentations in the bands were used to calculate the n index. In the case of the tensile sample, the indices are evaluated also in the bands, as shown in Figure 2. The index was calculated from the values of the diagonals of the four nearest indents, the first of which was made at a load of 0.9807 N, the second 0.49035 N, the third 0.24518 N, and the fourth 0.09807 N.

The resistance model of Li and Bradt about proportional specimen PSR is considered a modified way of the Hays/Kendall coming nearer to the ISE [2]. Many authors as [1,2,20,27,28] have proposed that the ISE can be expressed by the Equation (2):

$$\mathrm{P}={ \mathrm{a}}_1\mathrm{d}+{ \mathrm{a}}_2{\mathrm{d}}^2$$

(2)

As stated by Li and Bradt [21,27], parameter a₁ (N mm⁻¹) is related to the elastic, and a₂ (N mm⁻²) is related to the plastic properties of the material. We calculate both parameters using Equation (2). Both parameters can be obtained from the plots of P/d (N mm⁻¹) against d (mm).

$$\mathrm{P}={\mathrm{c}}_0+{\mathrm{c}}_1\mathrm{d}+{\mathrm{c}}_2{\mathrm{d}}^2.$$

(3)

Equation (3) can be regarded as a modified form of the PSR model. Parameter c₀ (N) is associated with residual surface stress, parameter c₁ (N mm⁻¹) is related to the elasticity, and parameter c₂ (N mm⁻²) is related to the plastic properties of the material. Values of parameters can be obtained from the quadratic regressions of P (N) against d (mm), using Equation (5). Parameters c₁ and c₂ correspond to parameters a₁ and a₂ obtained by Hays/Kendall approach [1,2].

Parameter a₁ characterizes the load dependence of micro-hardness and describes the ISE in the PSR model. It consists of two components: the elastic resistance of the test sample and the friction resistance developed at the indenter facet/sample interface [1,20]. The harder material with a higher Young’s modulus has a higher value of a₁ [29]. The parameter a₂ is related to load-independent micro-hardness, the “true hardness” HPSR, calculated by Equation (4) [30].

$${\mathrm{H}}_{\mathrm{PSRa}2}=0.1891{ \ast \mathrm{a}}_2$$

(4)

The measure of the residual stress, the result of mechanical processing (preparation of the metallographic surface), is ratio c₁/c₂. According to [1,2], a relationship between c₀ and the ratio c₁/c₂ expressed by a linear dependence, is assumed. This fact confirms Figure 11 for obtained data. The values of the parameters calculated using modified PSR are in Table 5.

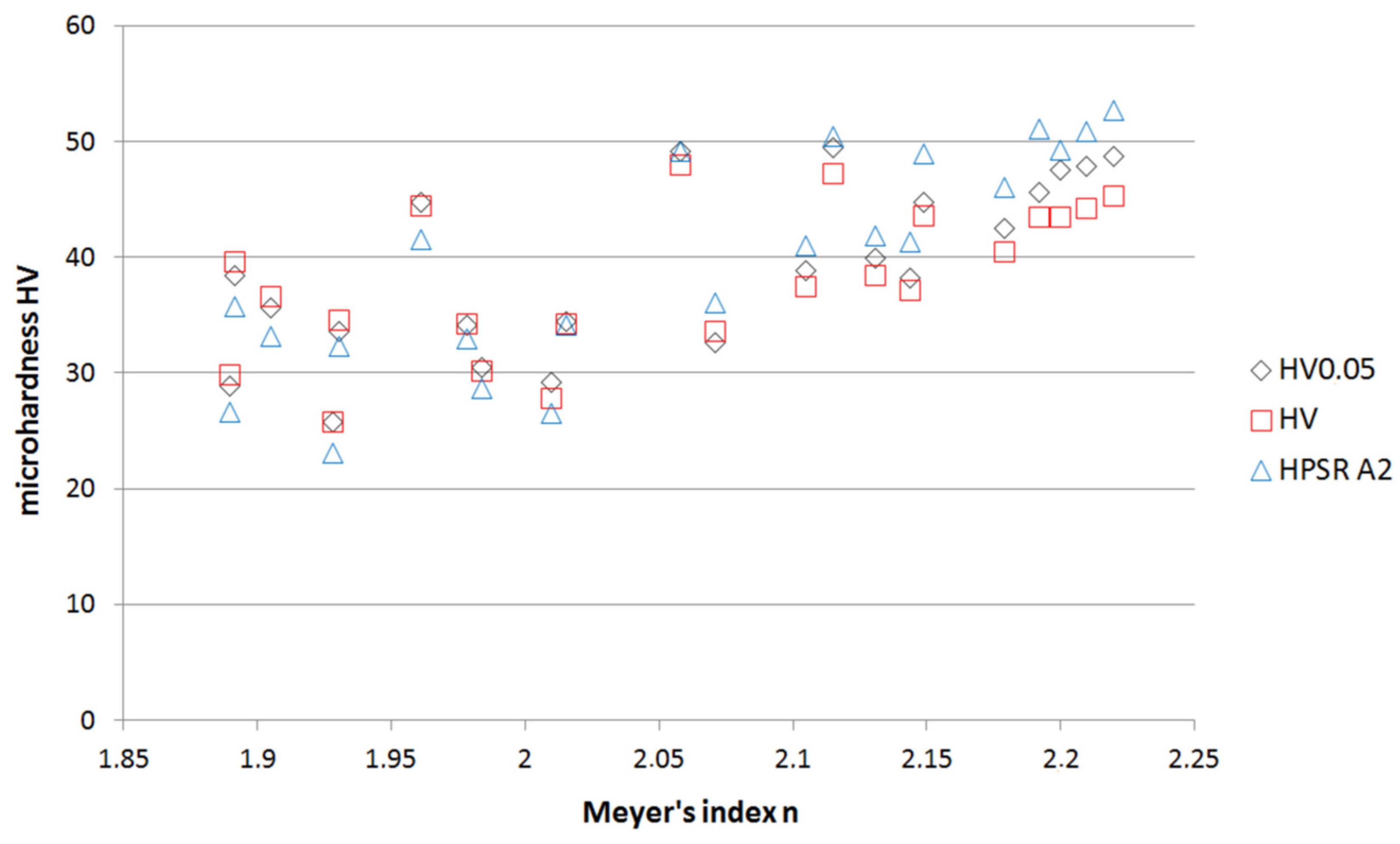
The value of Meyer’s index n increases with increasing micro-hardness, as shown in Figure 12, for both tensile and pressure deformations. A similar ratio between the micro-hardness and Meyer’s index n was observed for iron-based CRMs with micro-hardness between 195 and 519 HV0.05, heat-treated carbon steel, aluminum alloy EN 6082, and technically pure metals (Al, Zn, Cu, Fe, Ni, Co), all with reverse ISE [31,32]. The mentioned samples were not deformed, except for surface treatment by grinding and polishing. The “true hardness” by analogy to a₂ can be calculated as H_PSRc2 using c₂ instead of a₂ in Equation (4).

Test load W (N) is the load necessary to initiate plastic deformation with a visible indentation; only elastic deformation occurs below it. In that event, the load dependence of hardness is expressed by Equation (5):

$$\mathrm{P}= \mathrm{W}+{ \mathrm{A}}_1{\mathrm{d}}^2$$

(5)

Parameter A₁ (N mm⁻²) is independent of load. W and A₁ may be obtained from the regressions of P (N) against d² (mm) [1], their values are in Table 5.

By analogy to a₂, the “true hardness” H_PSRA₁ can be calculated by Equation (4). The values of “true hardness” are in

Table 6. The values of “true hardness”.

Sample	HPSRa2	HPSRc2	HPSRA1
Initial state (1)	27	17	26
Initial state (2)	24	17	25
ε1	29	24	29
ε2	36	42	35
ε3	41	39	39
ε4	42	34	40
ε5	46	38	43
ε6	49	46	47
ε7	49	31	46
ε8	51	48	48
ε9	51	36	47
ε10	53	38	49
ε11	50	39	48

⁽¹⁾ The cut parallel to the axis; ⁽²⁾ the cut perpendicular to the axis.

.

4. Discussion

For the tensile sample, the residual surface stress, expressed by parameter c₀, increases with increasing the reduction of area (Z). The ratio c₁/c₂ is the measure of stress, a result of mechanical processing. The whole tensile sample was cut, ground, and polished under the same conditions: the whole metallographic surface of the sample was finalized in the same way. The relationship between the characteristics found in the tensile sample is detailed in the paper [23].

As the deformation increases, the value of the c₁/c₂ ratio of compressed samples tends to increase. There are significant differences between the individual samples. The conditions of preparation of these samples (cutting, grinding, and polishing) may have been slightly different. Each sample was processed individually. This fact may further affect the interaction between stress from these sources and stress from deformation.

Hays and Kendall defined the parameter W as a minimum load necessary to initiate plastic deformation, therefore creating a visible indentation. However, visible indentations) were created with the load 0.009807 N (1 g), which is less than some calculated values of parameter W listed in Table 5. This phenomenon has been observed in both tensile [23] and compressed samples. This fact does not conform to the definition of parameter W. It would be appropriate to focus the research on this problem in the future.

As can be concluded from the relevant professional articles, indirect calibration of micro-hardness testers is not a routine matter even now. Even if the calibration was carried out, its results are usually not mentioned in the articles. The uncertainty of the measured values of micro-hardness can be determined only by calibration. However, the uncertainty can significantly affect the character of ISE. It is possible that “normal” and reverse ISE are simultaneously the result of the same input values if the uncertainty is taken into account (with a coverage factor k = 2. and the probability of 95.45%) [32].

The uncertainty in the case of measurement of small or irregular indentations, particularly if pile-up or sink-in effects are present, or in the case of low contrast between the indentation and the surface of the sample can lead to over- or underestimation of diagonal dimension [31]. Vickers’ method employs manual measurement of the diagonal significant source of errors. This fact is the result of the operator’s subjective decision in determining the indentation edge as well as his/her eye strain as a result of the prolonged measurement [32].

Meyer’s index n of annealed aluminum (99.999%) measured by Hanemann ranged between 2.0288 and 2.1822 [33]. Tabor [3] lists values of Meyer’s index which lie between 2 for fully work-hardened metals and about 2.6 for annealed metals.

For the deformation test in pressure, the multiple linear regression was used (EXCEL → LINEST program) for the study of the simultaneous effect of several factors on the micro-hardness values and Meyer’s index n:

• Simultaneous influence of the deformation (ε) and speed of the indenter (v) on micro-hardness HV0.05, calculated by Equation (6).
• Simultaneous influence of the deformation (ε) and the speed of the indenter (v) on Meyer index n, calculated by Equation (7).
• Simultaneous influence of the deformation (ε), speed of the indenter (v), and micro-hardness HV0.05 on Meyer’s, calculated by Equation (7).

The values from Table 2 (the degree /amount of the deformation ε (%), HV0.05, and the speed of the indenter for the load 0.49035 N) and Table 5 (Meyer’s index n) were used as input data for the calculation of Equations (6) and (7); calculated coefficients of regression and coefficients expressing the quality of correlation are shown in

Table 7. Calculated coefficients of regression and coefficients expressing the quality of correlation.

Num.	a (ε)	b (v)	c (HV0.05)	d Constant	Equation	r2
1.	0.21726	−3.45689	-	37.9086	(6)	97.3
2.	0.00207	−0.07597	-	2.1870	(7)	95.8
3.	0.00106	−0.05999	0.00462	2.0118	(7)	96.2

.

$$\mathrm{HV}0.05= \mathrm{d}+\left(\mathrm{a} \ast \mathsf{\epsilon }\right)+\left(\mathrm{b} \ast \mathrm{v}\right)$$

(6)

$$\mathrm{n}= \mathrm{d}+\left(\mathrm{a} \ast \mathrm{v}\right)+\left(\mathrm{b} \ast \mathrm{v}\right)+\left(\mathrm{c} \ast \mathrm{HV}0.05\right)$$

(7)

The value of the determination coefficient r² = 0.973 for Equation (6) and (0.958 and 0.962 for Equation (7), respectively. They indicate a strong relationship between considered input factors and micro-hardness or Meyer’s index n. It means that 97.3% (95.8 and 96.2%) of the variation of the micro-hardness or n can be explained by the effect of these factors [34,35].

5. Conclusions

• Research was conducted on 99.5% of aluminum deformed in cold-formed tensile and pressure tests.
• Non-homogeneous deformation in the volume of the sample was found in the deformation in pressure (compression/upsetting deformation), which affects both the nano- and micro-hardness values.
• Correlation was found in both the tensile and pressure tests between the degree of deformation and Meyer’s index (n).
• In the undeformed sample, the value of Meyer’s index is close to 2, with the increase in the degree of tensile deformation increasing its “normal” character (values less than 2), and with the increase in the degree of compressive deformation increasing its “reverse” character (values greater than 2).
• As can be seen from the above results, the size and nature of the ISE affect the micro-hardness value. If this is not taken into account, the measured micro-hardness values can be misleading. For this reason, we recommend using the above methodology to calculate “true hardness”.