Micro-Scale Flow Excitation under Imposition of Uniform Magnetic Field and Electrical Current
Abstract
1. Introduction
2. Experimental Methods
3. Results and Discussion
3.1. Concentration Measurement Results
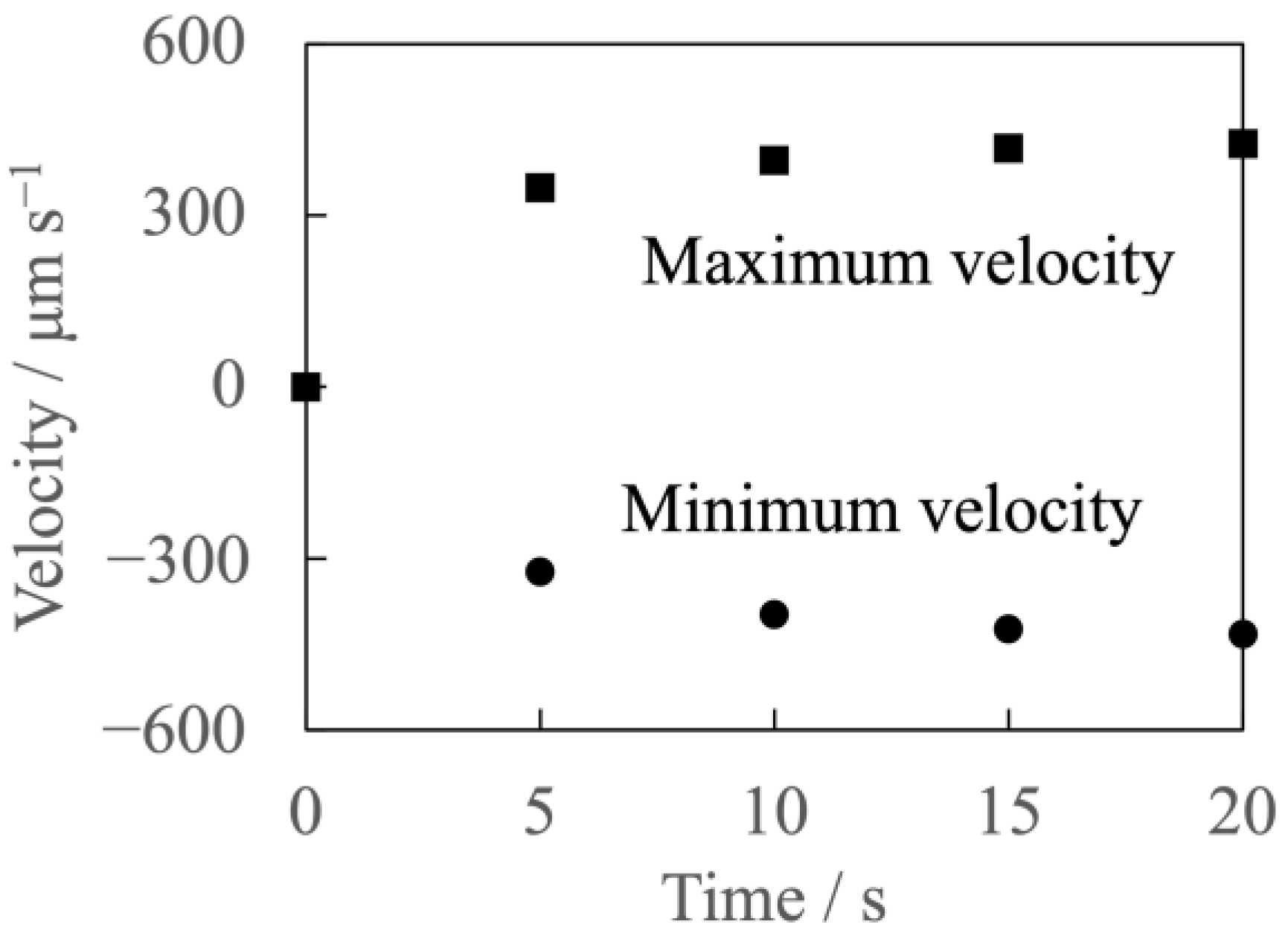
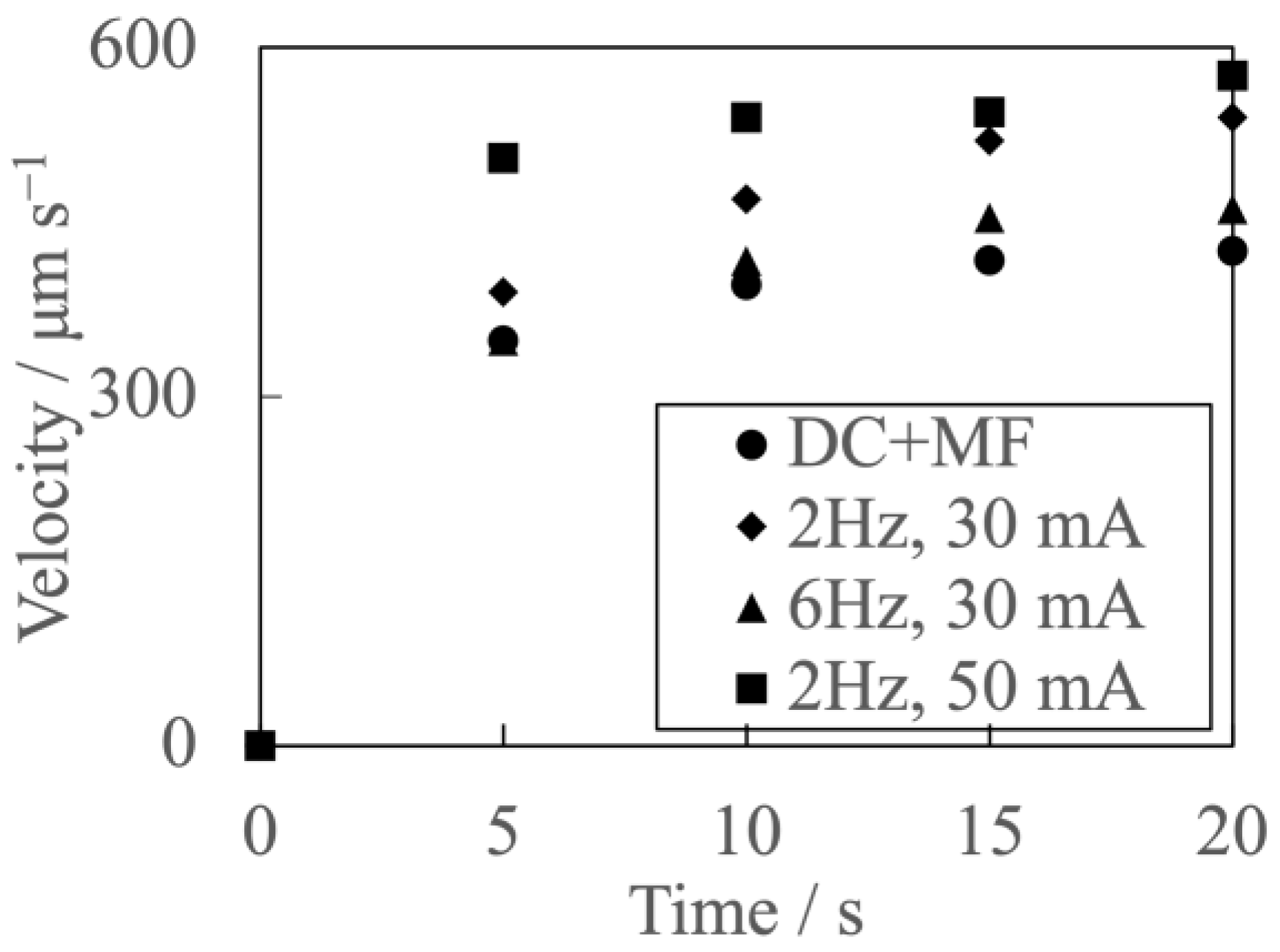
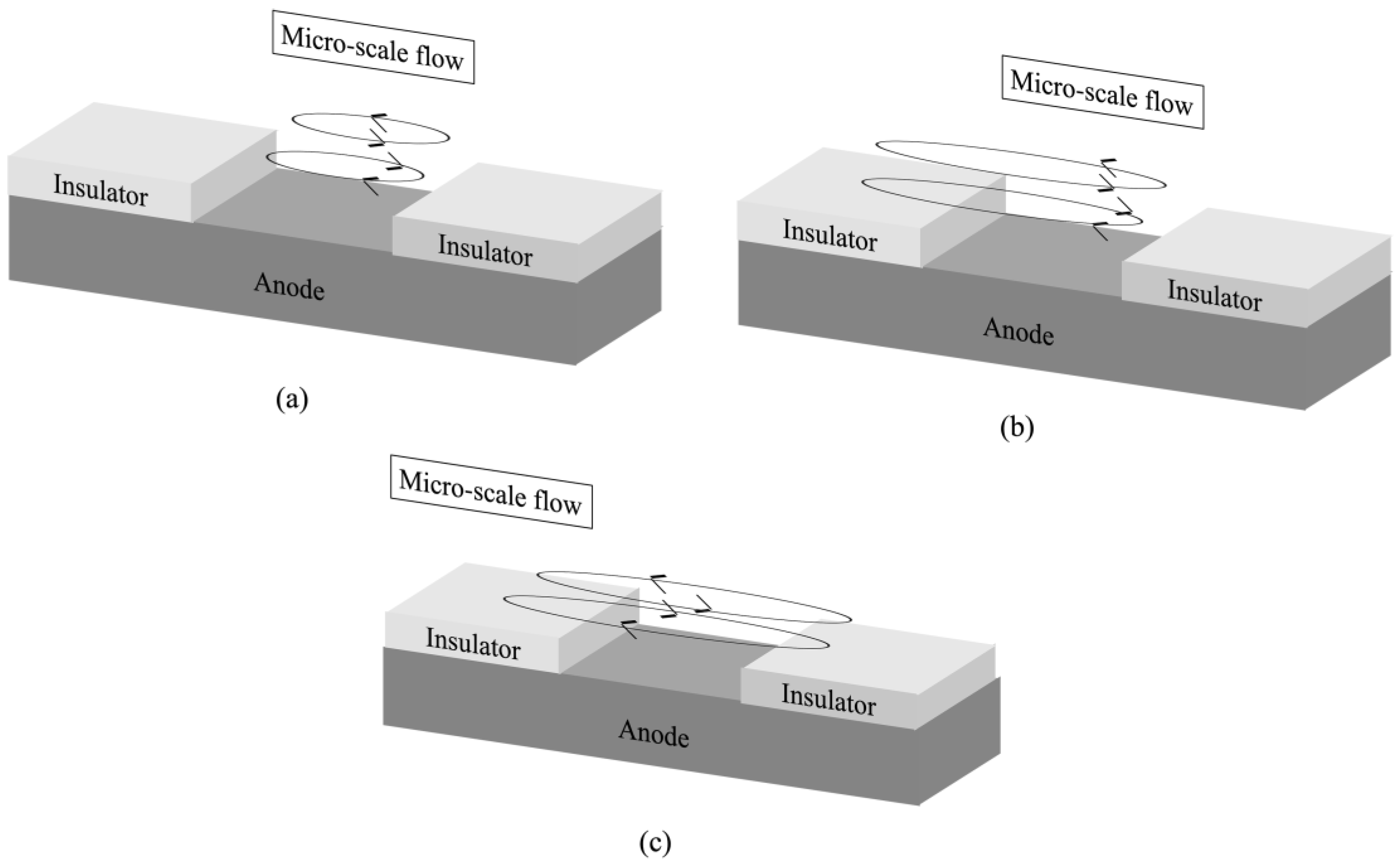
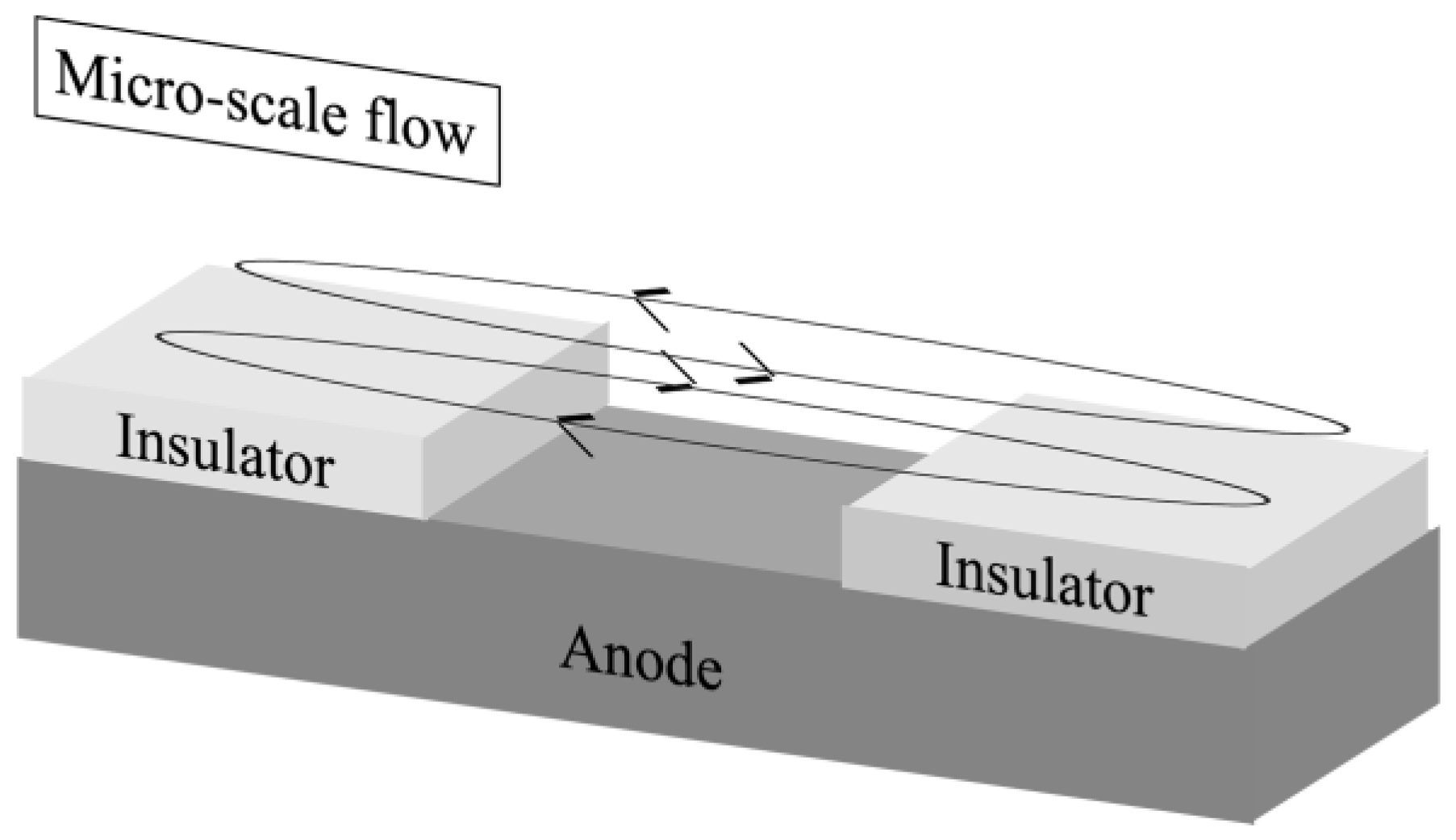
3.2. Velocity Measurement Results and Liquid Flow Pattern Observation Results
4. Conclusions
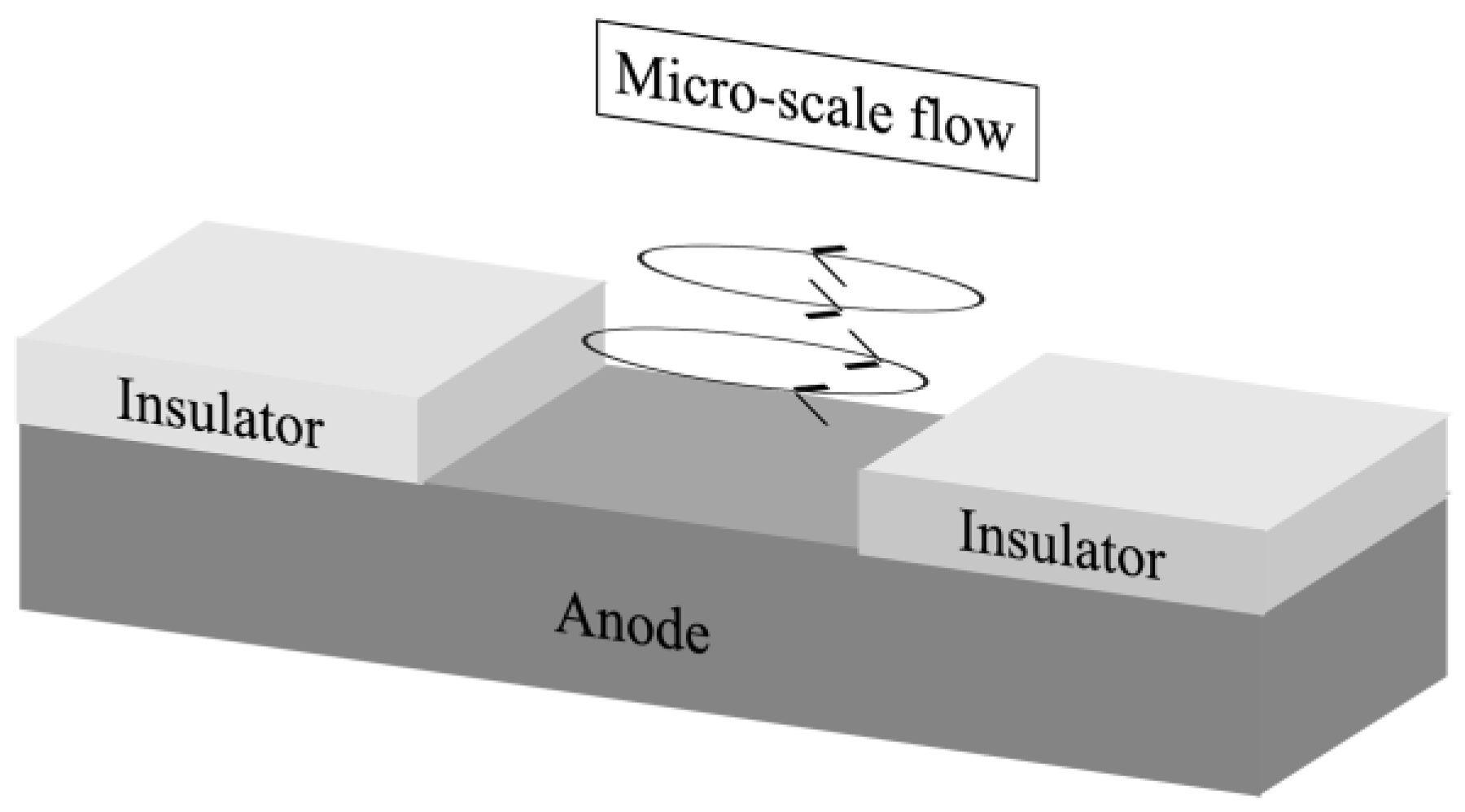
- Only the micro-scale flow was observed near the anode surface under the experimental conditions with the current and the uniform magnetic field superimposition.
- By superimposing the modulated current with the uniform magnetic field, the micro-scale flow excitation was enhanced compared to that under the superimposition of the DC current and the uniform magnetic field.
- The decrease in modulated current frequency or the increase in modulated current amplitude enhanced the micro-scale flow excitation.
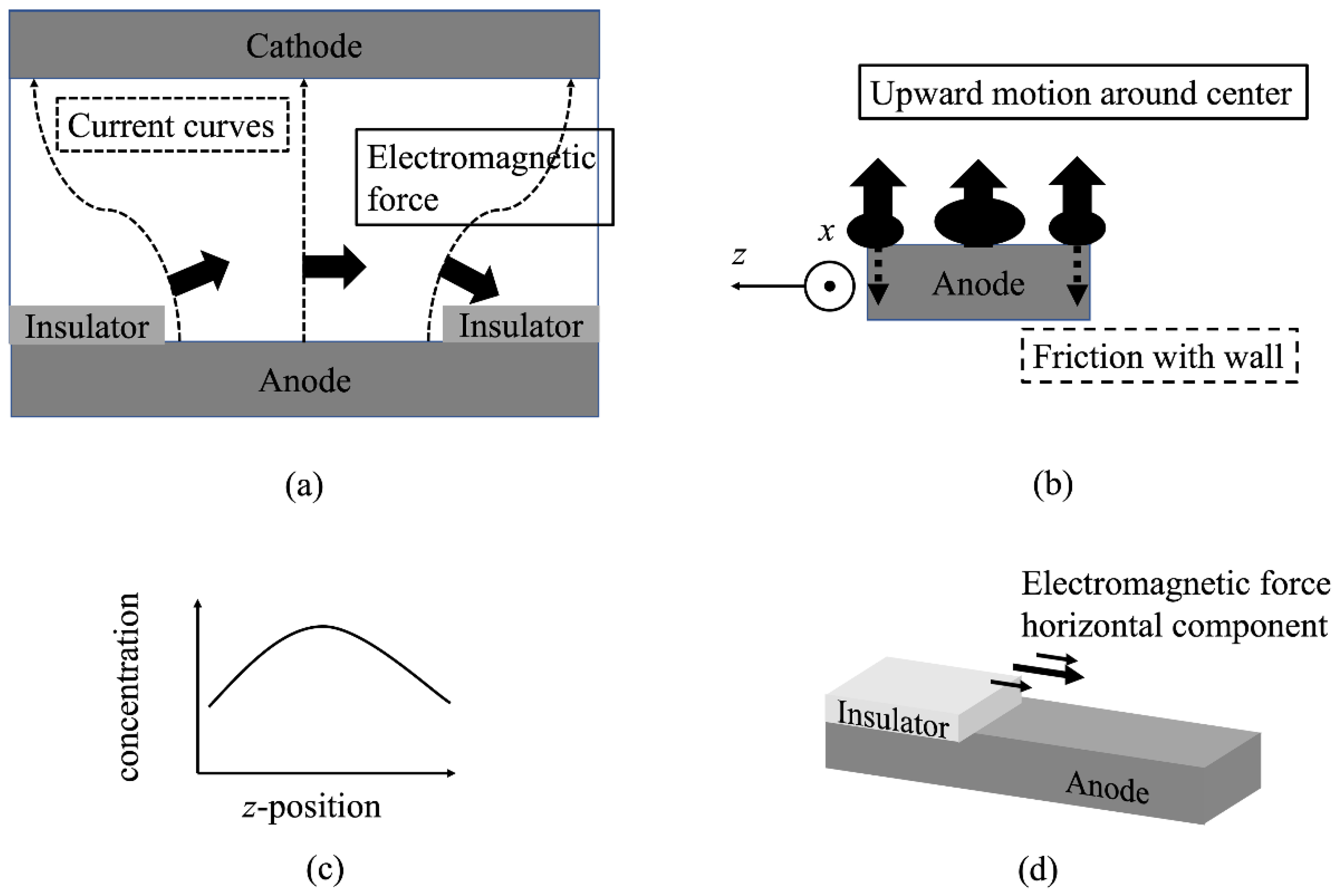
- The mechanism of micro-scale flow excitation was clarified. That is, the driving force for the micro-scale flow excitation was the non-uniform electromagnetic force distribution in the z-direction caused by the non-uniform current distribution and the positive relationship between the Cu2+ concentration and the electrical conductivity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| A | constant (mol/m3 or mol/L) |
| B | magnetic field intensity (T) |
| c0 | initial concentration (mol/m3 or mol/L) |
| c | concentration (mol/m3 or mol/L) |
| D | diffusion coefficient (m2/s) |
| F | Faraday’s constant (A·s/mol) |
| I1 | brightness of the objective liquid (-) |
| I2 | brightness of a standard liquid (-) |
| J | current density (A/m2) |
| l | optical path length (m) |
| Sc | Schmidt number (-) |
| t | time (s) |
| x, y, z | cartesian coordinates (m) |
| molar absorption coefficient [(m2/mol or L/(mol·m)] | |
| v | kinematic viscosity (m2/s) |
References
- Wen, C.Y. Noncatalytic heterogeneous solid-fluid reaction models. J. Ind. Eng. Chem. 1968, 60, 34–54. [Google Scholar] [CrossRef]
- Iwai, K.; Yokota, T.; Maruyama, A.; Yamada, T. Oscillating Electromagnetic Force Effect on Concentration Distribution near Liquid Solid Interface. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 012051. [Google Scholar] [CrossRef]
- Frank, C.W. The Kinetics of Electrode Reactions: Part II—Mass transfer and mixed control. J. Ind. Eng. Chem. 1992, 70, 95–99. [Google Scholar]
- Madden, J.D.; Hunter, I.W. Three-dimensional microfabrication by localized electrochemical deposition. J. Microelectromech. Sys. 1996, 5, 24–32. [Google Scholar] [CrossRef]
- Jaiswal, D.K.; Kumar, A.; Yadav, R.R. Analytical Solution to the One-Dimensional Advection-Diffusion Equation with Temporally Dependent Coefficients. J. Water Resour. Prot. 2011, 3, 76–84. [Google Scholar] [CrossRef]
- Stocker, T. Introduction to Climate Modelling, 1st ed.; Springer: Berlin, Germany, 2011; p. 57. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2007; p. 621. [Google Scholar]
- Umezawa, K.; Matsunaga, H.; Tonomura, R.; Furugaki, I. The influence of operating condition on dephosphorization and desulphurization reactions of hot metal with lime-based flux. Tetsu-to-Hagane 1983, 15, 1810–1817. [Google Scholar] [CrossRef] [PubMed]
- Panneerselvam, R.; Savithri, S.; Surender, G.D. CFD modeling of gas–liquid–solid mechanically agitated contactor. Chem. Eng. Res. Des. 2008, 86, 1331–1344. [Google Scholar] [CrossRef]
- Ilegbusi, O.J. The role of gas plumes in agitation and mass transfer in metallurgical systems. Steel Res. 1994, 65, 534–540. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Choi, H.Y. Heat, Mass and Momentum Transfer, 1st ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1963; p. 25. [Google Scholar]
- Streeter, V.L. Fluid Mechanics, 2nd ed.; McGRAW-Hill Book Company, Inc.: New York, NY, USA, 1958; p. 3. [Google Scholar]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E.; Rorrer, G.L. Fundamentals of Momentum, Heat, and Mass Transfer, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; p. 519. [Google Scholar]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the Values for the Turbulent Schmidt Number in Environmental Flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef]
- Yokota, T.; Maruyama, A.; Yamada, T.; Iwai, K. Direct observation of concentration boundary layer formed in the vicinity of anode electrode under imposition of vibrating electromagnetic force. Tetsu-to-Hagane 2016, 102, 119–126. [Google Scholar] [CrossRef]
- Yokota, T.; Maruyama, A.; Yamada, T.; Iwai, K. Decrease of concentration boundary layer thickness by using vibrating electromagnetic force. J. Japan. Inst. Met. Mater. 2017, 81, 516–521. [Google Scholar] [CrossRef]
- Xu, G.; Iwai, K. Solute concentration distribution in the vicinity of solid-liquid interface under the imposition of a time-varying force. ISIJ Int. 2022, 62, 1389–1395. [Google Scholar] [CrossRef]
- Moon, K.H.; Shin, H.K.; Kin, B.J.; Chung, J.Y.; Hwang, Y.S.; Yoon, J.K. Flow control of molten steel by electromagnetic brake in the continuous casting mold. ISIJ Int. 1996, 36, S201–S203. [Google Scholar] [CrossRef] [PubMed]
- Moffatt, H.K. Electromagnetic stirring. Phys. Fluids A 1991, 3, 1336–1343. [Google Scholar] [CrossRef]
- Swinehart, D.F. The Beer-Lambert law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Mutschke, H.; Popp, J. Employing theories far beyond their limits—The case of the (Boguer-) beer–lambert law. Chem. Phys. Chem. 2016, 17, 1948–1955. [Google Scholar] [CrossRef] [PubMed]
- Kanani, N. Electroplating-Basic Principles, Processes and Practice, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 99–105. [Google Scholar]
- Price, D.C.; Davenport, W.G. Densities, electrical conductivities and viscosities of CuSO4/H2SO4 solutions in the range of modern electrorefining and electrowinning electrolytes. Metall. Mater. Trans. B 1980, 11, 159–163. [Google Scholar] [CrossRef]
- The Chemical Society of Japan. Handbook of Chemistry, Basics II, 3rd ed.; Maruzen: Tokyo, Japan, 1984; p. 453. [Google Scholar]
- Fueki, K. Handbook of Electrochemistry, 4th ed.; Maruzen: Tokyo, Japan, 1985; p. 158. [Google Scholar]
- Emanuel, A.; Olander, D.R. Diffusion Coefficients of Copper Sulfate in Water and Water in n-Butyl Alcohol. J. Chem. Eng. Data 1963, 8, 31–32. [Google Scholar] [CrossRef]
- Eversole, W.G.; Kindsvater, H.M.; Peterson, J.D. The Diffusion Coefficient of Cupric Sulfate from 0.0 to 0.35 Molar at 25 °C. J. Phys. Chem. 1942, 3, 370–375. [Google Scholar] [CrossRef]
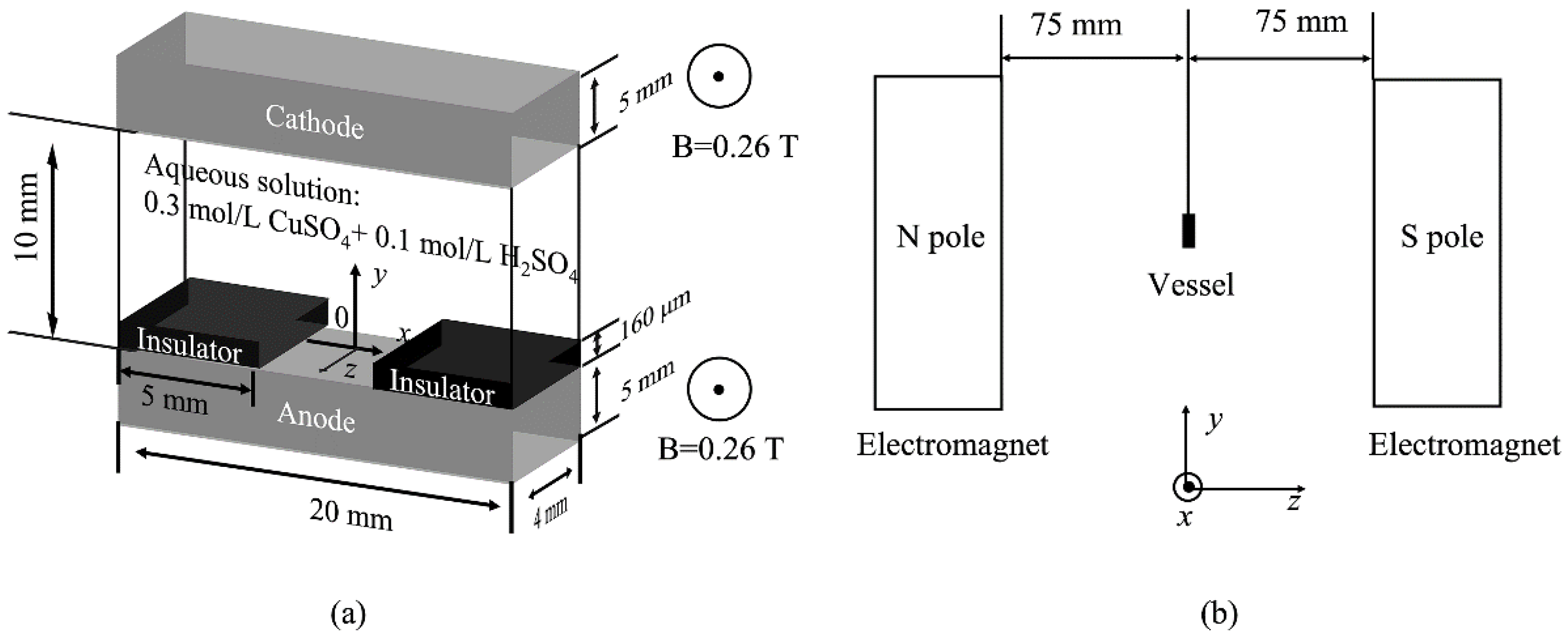

| Experimental Condition Abbreviation | DC Current Intensity (mA) | AC Current Amplitude (mA) | AC Current Frequency (Hz) | Magnetic Field Intensity near Anode (T) | Magnetic Field Intensity near Cathode (T) | |
|---|---|---|---|---|---|---|
| 1 | DC condition | 25 | 0 | none | 0 | 0 |
| 2 | DC + MF condition | 25 | 0 | none | 0.26 | 0.26 |
| 3 | 2 Hz, 30 mA condition | 25 | 30 | 2 | 0.26 | 0.26 |
| 4 | 6 Hz, 30 mA condition | 25 | 30 | 6 | 0.26 | 0.26 |
| 5 | 2 Hz, 50 mA condition | 25 | 50 | 2 | 0.26 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Iwai, K. Micro-Scale Flow Excitation under Imposition of Uniform Magnetic Field and Electrical Current. Metals 2022, 12, 2034. https://doi.org/10.3390/met12122034
Xu G, Iwai K. Micro-Scale Flow Excitation under Imposition of Uniform Magnetic Field and Electrical Current. Metals. 2022; 12(12):2034. https://doi.org/10.3390/met12122034
Chicago/Turabian StyleXu, Guangye, and Kazuhiko Iwai. 2022. "Micro-Scale Flow Excitation under Imposition of Uniform Magnetic Field and Electrical Current" Metals 12, no. 12: 2034. https://doi.org/10.3390/met12122034
APA StyleXu, G., & Iwai, K. (2022). Micro-Scale Flow Excitation under Imposition of Uniform Magnetic Field and Electrical Current. Metals, 12(12), 2034. https://doi.org/10.3390/met12122034





