The Alloying Strategy to Tailor the Mechanical Properties of θ-Al13Fe4 Phase in Al-Mg-Fe Alloy by First-Principles Calculations
Abstract
1. Introduction
2. Experiments Methods and Details of Calculations
2.1. Experimental Methods
2.2. Calculation Details
3. Results and Discussions
3.1. Determination of Composition and Crystal Structure of Al13Fe4 Phase
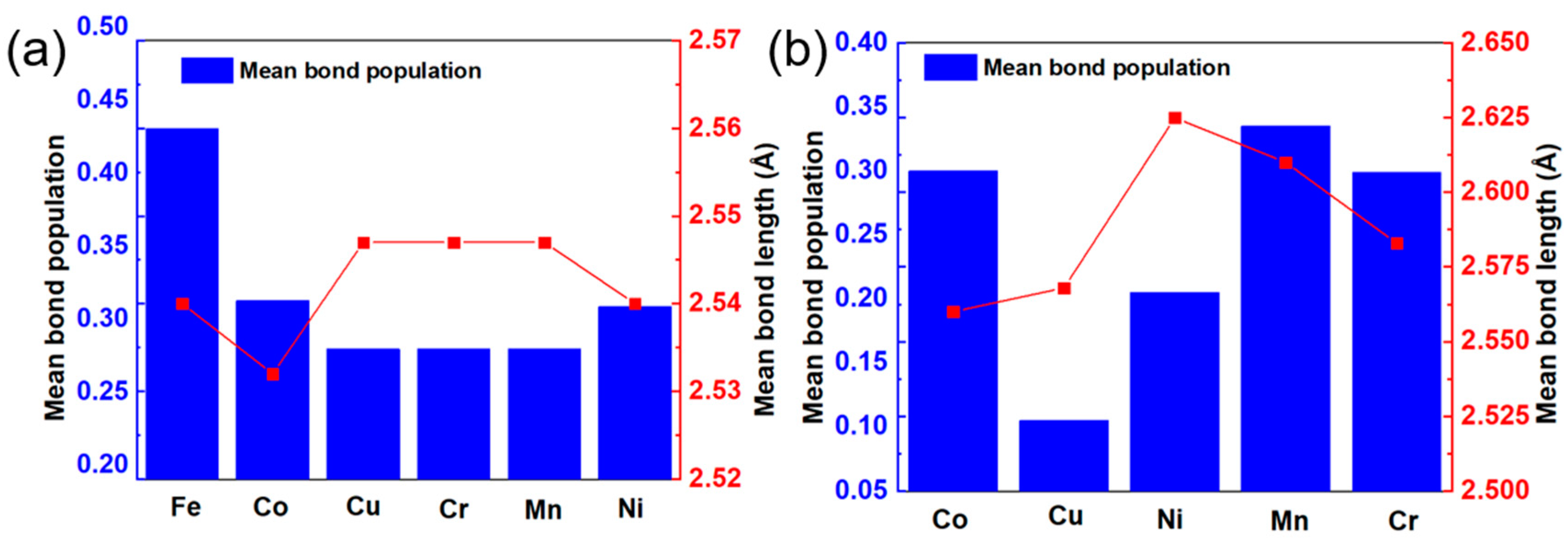
3.2. Stability and Electronic Structure of Al13(Fe,M)4
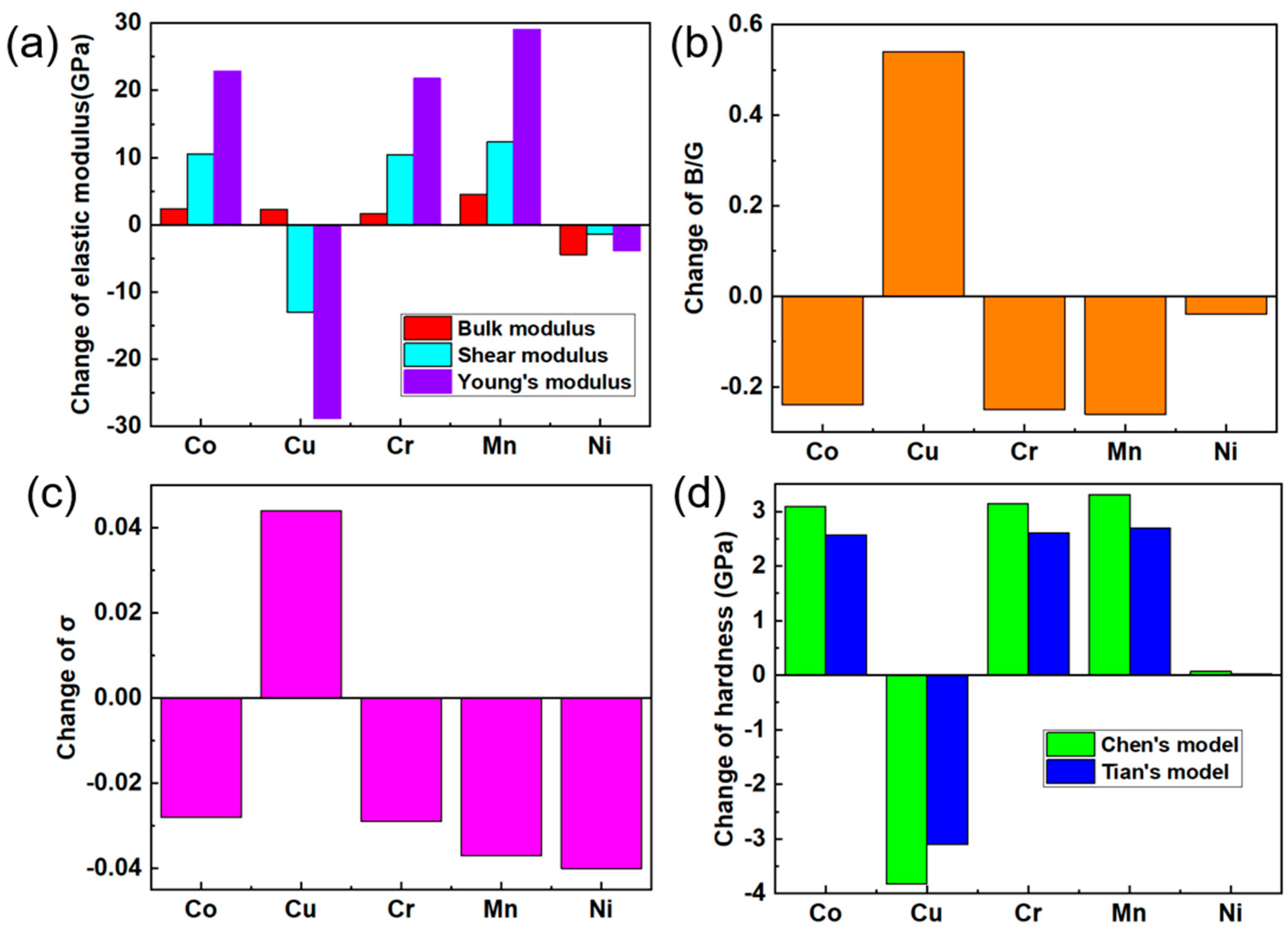
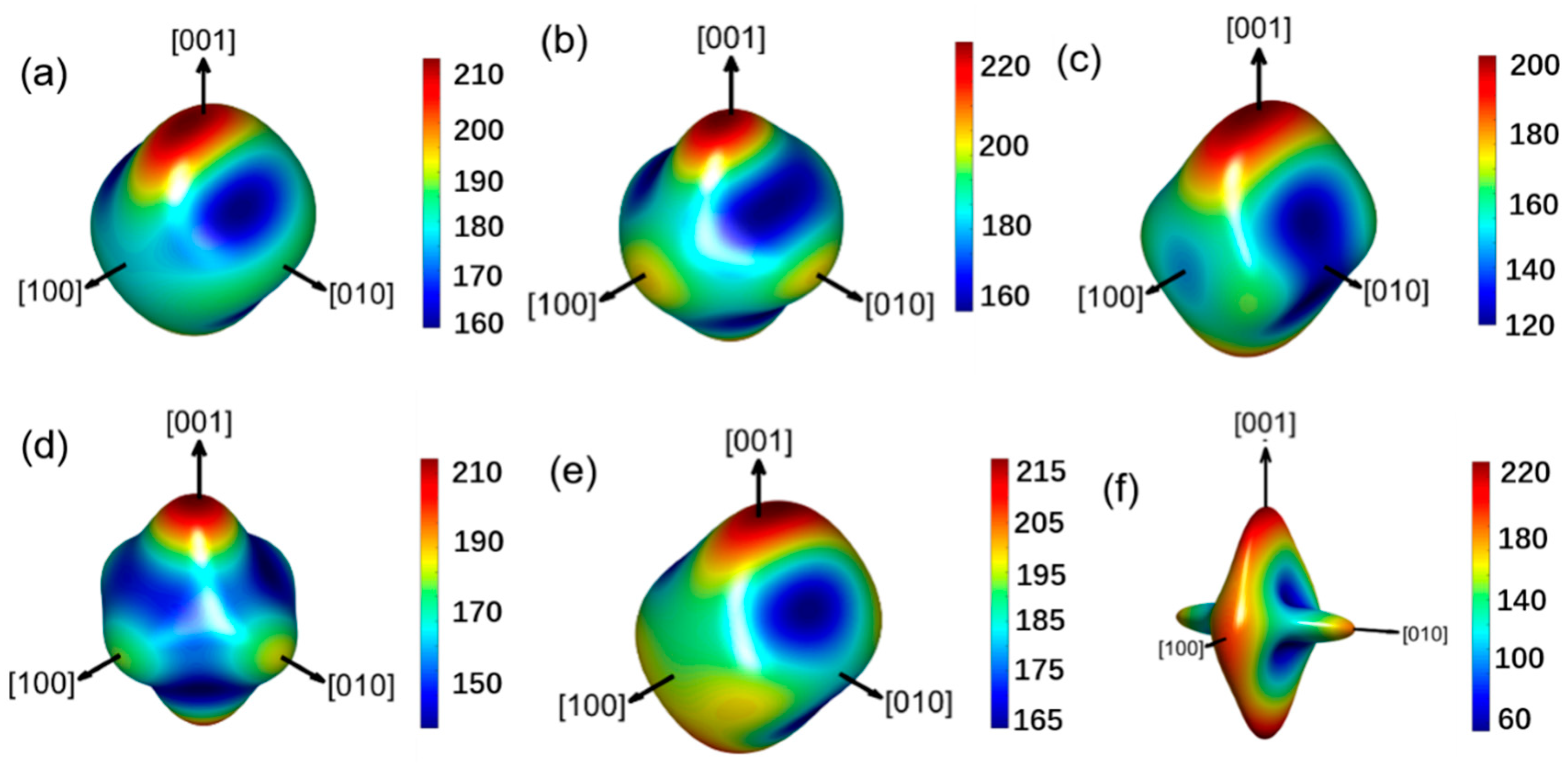
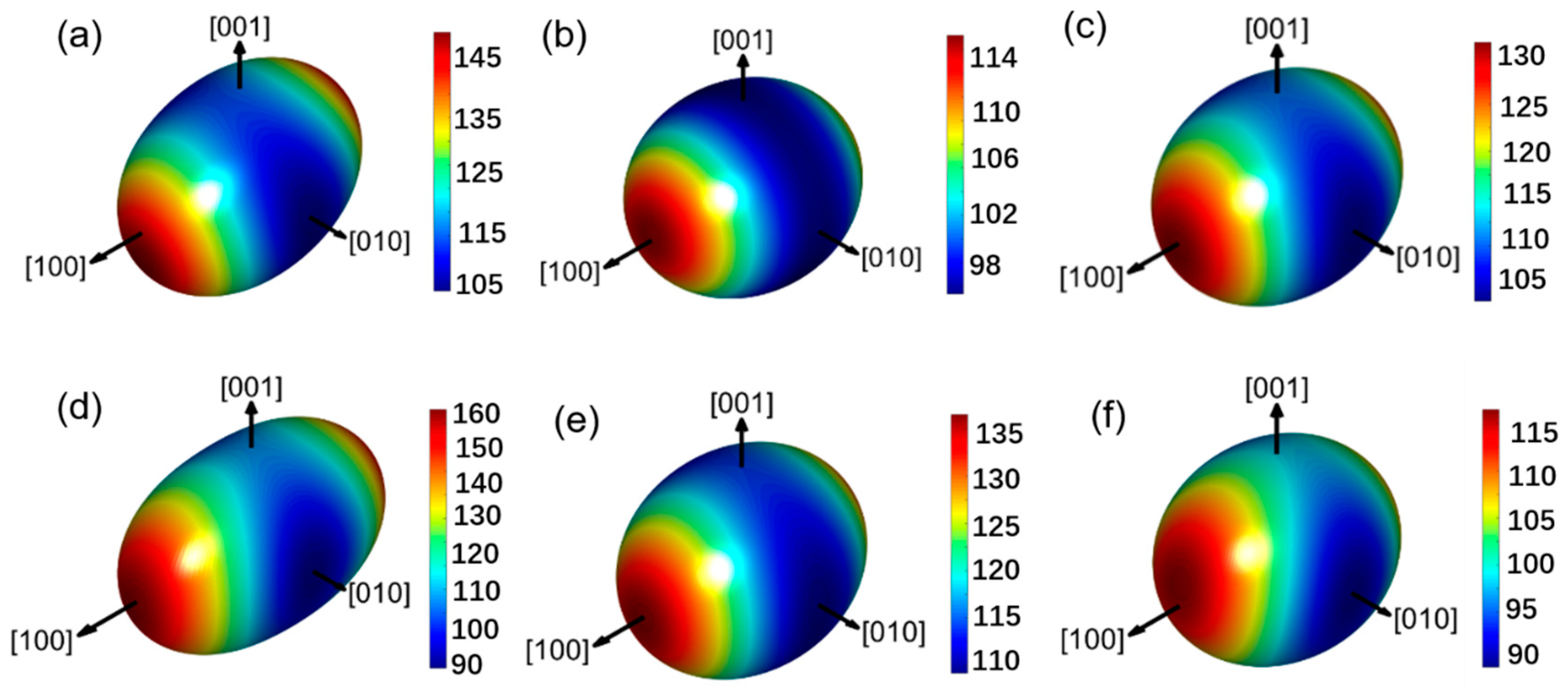
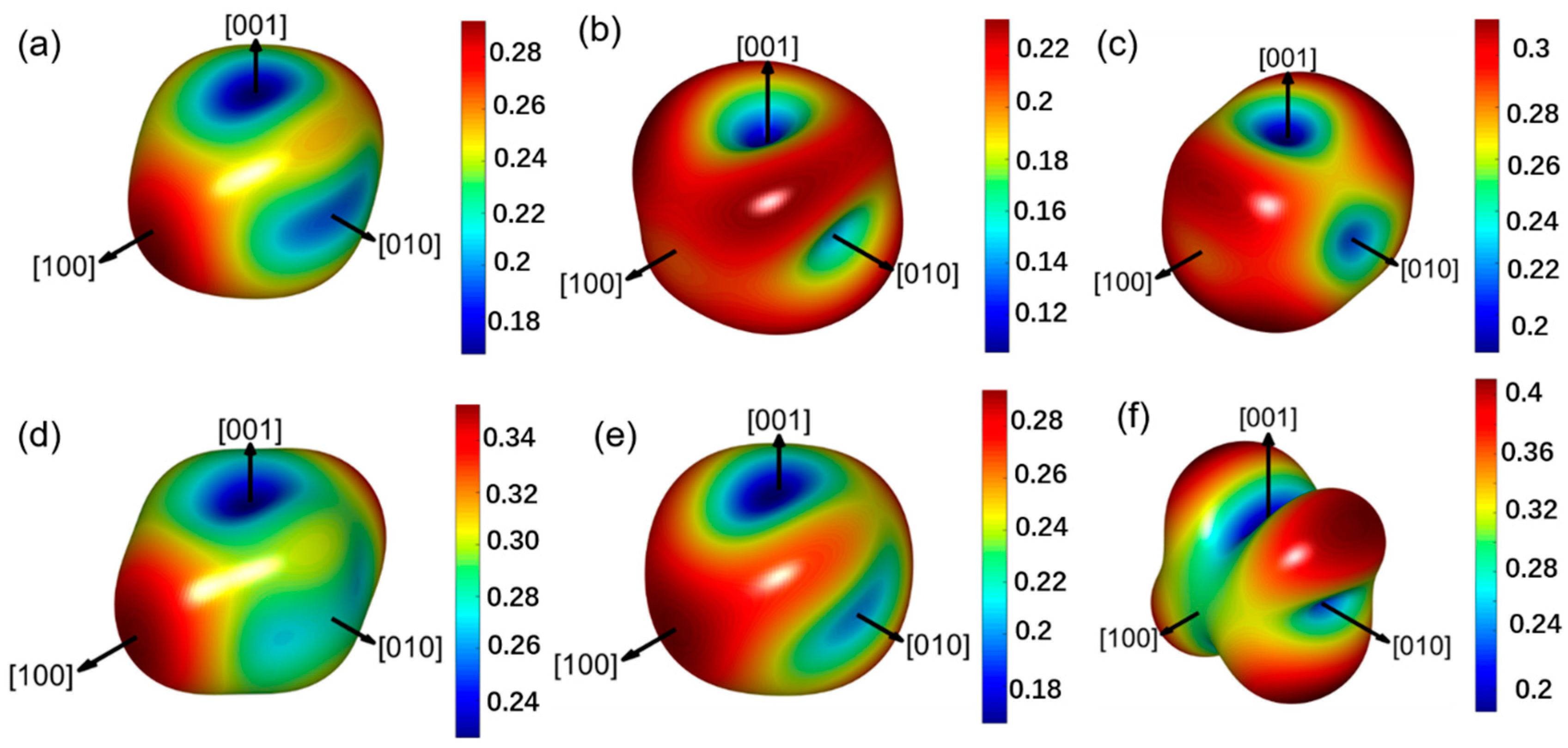
3.3. Mechanical Properties and Anisotropy
C11 + C22 + C33 + 2 (C12 + C13 + C23) > 0;
C11 + 2C12 > 0; (C44C66 − C462) > 0;
C22 (C33C55 − C352) + 2C23C25C35 − C232C35 − C252C33 > 0;
2 [C15C25 (C33C12 − C13C23) + C15C35 (C22C13 − C12C23) + C25C35 (C11C23 − C12C13)] − [C152 (C11C22 − C122) + C55 (C11C22C33 − C232C11 − C132C22 − C122C33 + C12C13C23)] > 0
4. Conclusions
- (1)
- The substitution of Fe by M (M = Co, Cr, Cu, Mn, and Ni) in Al13Fe4 is energetically favourable at 0 K due to the negative mixing enthalpy and cohesive energy.
- (2)
- With the doping of Co, Cr, and Mn, the Young’s modulus values are increased to 181.25, 180.82, and 187.48 GPa, the hardness values are increased to 10.9, 10.95, and 11.12 GPa, owing to the formation of stronger Al-Co, Al-Cr, and Al-Mn chemical bonds, the existence of which is validated by electronic structure calculation conducted in this study.
- (3)
- Co, Cr, and Mn are potential candidate elements for the mechanical optimization of Al13Fe4 for the simultaneous improvement of mechanical modulus, hardness, and fracture toughness (KIC from 1.34 to 1.46, 1.45, and 1.49).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stefániay, V.; Griger, A.; Turmezey, T. Intermetallic phases in the aluminium-side corner of the AlFeSi-alloy system. J. Mater. Sci. 1987, 22, 539–546. [Google Scholar] [CrossRef]
- Rømming, C.; Hansen, V.; Gjønnes, J. Crystal structure of β-Al4.5FeSi. Acta Crystallogr. Sect. B Struct. Sci. 1994, 50, 307–312. [Google Scholar] [CrossRef]
- Que, Z.; Mendis, C.L. Heterogeneous nucleation and phase transformation of Fe-rich intermetallic compounds in Al–Mg–Si alloys. J. Alloys Compd. 2020, 836, 155515. [Google Scholar] [CrossRef]
- Zhu, X.; Blake, P.; Dou, K.; Ji, S. Strengthening die-cast Al-Mg and Al-Mg-Mn alloys with Fe as a beneficial element. Mater. Sci. Eng. A 2018, 732, 240–250. [Google Scholar] [CrossRef]
- Cai, B.; Kao, A.; Lee, P.; Boller, E.; Basevi, H.; Phillion, A.; Leonardis, A.; Pericleous, K. Growth of β intermetallic in an Al-Cu-Si alloy during directional solidification via machine learned 4D quantification. Scr. Mater. 2019, 165, 29–33. [Google Scholar] [CrossRef]
- Puncreobutr, C.; Lee, P.; Kareh, K.; Connolley, T.; Fife, J.; Phillion, A. Influence of Fe-rich intermetallics on solidification defects in Al–Si–Cu alloys. Acta Mater. 2014, 68, 42–51. [Google Scholar] [CrossRef]
- Terzi, S.; Taylor, J.A.; Cho, Y.; Salvo, L.; Suéry, M.; Boller, E.; Dahle, A.K. Nucleation and growth dynamics of the α-Al/β-Al5FeSi eutectic in a complex Al-Si-Cu-Fe alloy. In Proceeding of the 12th International Conference on Alu-minium Alloys, Yokohama, Japan, 5–9 September 2010; pp. 1273–1278. [Google Scholar]
- Ferraro, S.; Timelli, G. Influence of Sludge Particles on the Tensile Properties of Die-Cast Secondary Aluminum Alloys. Met. Mater. Trans. A 2014, 46, 1022–1034. [Google Scholar] [CrossRef]
- Gao, T.; Hu, K.; Wang, L.; Zhang, B.; Liu, X. Morphological evolution and strengthening behavior of α-Al(Fe,Mn)Si in Al–6Si–2Fe–xMn alloys. Results Phys. 2017, 7, 1051–1054. [Google Scholar] [CrossRef]
- Becker, H.; Bergh, T.; Vullum, P.; Leineweber, A.; Li, Y. Effect of Mn and cooling rates on α-, β- and δ-Al–Fe–Si intermetallic phase formation in a secondary Al–Si alloy. Materialia 2018, 5, 100198. [Google Scholar] [CrossRef]
- Zhenming, X.; Tianxiao, L.; Yaohe, Z. Elimination of Fe in Al-Si cast alloy scrap by electromagnetic filtration. J. Mater. Sci. 2003, 38, 4557–4565. [Google Scholar] [CrossRef]
- Rajabi, M.; Vahidi, M.; Simchi, A. Microstructural evolution of Al-20Si-5Fe alloy during rapid solidification and hot consoli-dation. Rare Metals 2009, 28, 639–645. [Google Scholar] [CrossRef]
- Seifeddine, S.; Johansson, S.; Svensson, I.L. The influence of cooling rate and manganese content on the β-Al5FeSi phase formation and mechanical properties of Al–Si-based alloys. Mater. Sci. Eng. A 2008, 490, 385–390. [Google Scholar] [CrossRef]
- Ferreira, T.; Vidilli, A.L.; Zepon, G.; Kiminami, C.S.; Botta, W.J. Bolfarini, Strong and ductile recycled Al-7Si-3Cu-1Fe alloy: Controlling the morphology of quasicrystal approximant α-phase by Mn and V addition. J. Alloys Compd. 2021, 888, 161508. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Song, D.F.; Wang, H.L.; Jia, Y.W.; Lin, B.; Tang, Y.; Tang, Y.; Shu, D.; Sun, Z.Z.; Fu, Y.N.; et al. Revealing the influence of Fe on Fe-rich phases formation and mechanical properties of cast Al-Mg-Mn-Fe alloys. J. Alloys Compd. 2022, 901, 163666. [Google Scholar] [CrossRef]
- Fang, C.M.; Que, Z.P.; Dinsdale, A.; Fan, Z. Si solution in θ-Al13Fe4 from first-principles. Intermetallics 2020, 126, 106939. [Google Scholar] [CrossRef]
- Chong, X.; Palma, J.P.S.; Wang, Y.; Shang, S.-L.; Drymiotis, F.; Ravi, V.A.; Star, K.E.; Fleurial, J.-P.; Liu, Z.-K. Thermodynamic properties of the Yb-Sb system predicted from first-principles calculations. Acta Mater. 2021, 217, 117169. [Google Scholar] [CrossRef]
- Popcevic, P.; Smontara, A.; Ivkov, J.; Wencka, M.; Komelj, M.; Vrtnik, S.; Bobnar, M.; Jaglicic, Z.; Bauer, B.; Gille, P.; et al. Anisotropic physical properties of the Al13Fe4 complex intermetallic and its ternary derivative Al13(Fe,Ni)4. Phys. Rev. B 2010, 81, 184203. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Zhou, Y.; Chong, X.; Li, X.; Zhang, H.; Nagaumi, H. Exploring crystal structures, stability and mechanical properties of Fe, Mn-containing intermetallics in Al-Si Alloy by experiments and first-principles calculations. J. Alloys Compd. 2021, 876, 160022. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, Z.J.; Zhang, P.Z.; Wei, D.B.; Luo, X.X.; Xue, F. Effect of Alloying Elements V, Cr and Ni on the Electronic Structure and Mechanical Properties of FeAl from First-Principles Calculation. Adv. Mater. Res. 2014, 887–888, 378–383. [Google Scholar] [CrossRef]
- Chong, X.; Hu, M.; Wu, P.; Shan, Q.; Jiang, Y.H.; Li, Z.L.; Feng, J. Tailoring the anisotropic mechanical properties of hexagonal M7X3 (M=Fe, Cr, W, Mo; X=C, B) by multialloying. Acta Mater. 2019, 169, 193–208. [Google Scholar] [CrossRef]
- Chong, X.; Guan, P.; Hu, M.; Jiang, Y.H.; Li, Z.L.; Feng, J. Exploring accurate structure, composition and thermophysical properties of η carbides in 17.90 wt% W-4.15 wt% Cr-1.10 wt% V-0.69 wt% C steel. Scr. Mater. 2018, 154, 149–153. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, Y.; Li, Z.; Chong, X.; Feng, J. Balance between strength and ductility of dilute Fe2B by high-throughput first-principles calculations. Ceram. Int. 2020, 47, 4758–4768. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Wei, X.; Chen, Z.; Zhong, J.; Wang, L.; Yang, W.; Wang, Y. Effect of alloying elements on mechanical, electronic and magnetic properties of Fe2B by first-principles investigations. Comput. Mater. Sci. 2018, 147, 322–330. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Shang, S.; Wang, Y.; Liu, Z.-K. First-principles elastic constants of α- and θ-Al2O3. Appl. Phys. Lett. 2007, 90, 101909. [Google Scholar] [CrossRef]
- Wu, Z.-J.; Zhao, E.-J.; Xiang, H.-P.; Hao, X.-F.; Liu, X.-J.; Meng, J. Crystal structures and elastic properties of superhardIrN2andIrN3from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Gueneau, C.; Servant, C.; D’Yvoire, F.; Rodier, N. FeAl3Si2. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1995, 51, 177–179. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Yamanaka, T.; Matsui, M. Molecular dynamics study of pressure-induced transformation of quartz-type GeO2. Phys. Chem. Miner. 2000, 27, 149–155. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Zhou, R.; Feng, J. Elastic properties and electronic structures of CrxBy as superhard compounds. J. Alloys Compd. 2014, 610, 684–694. [Google Scholar] [CrossRef]
- Niu, H.; Niu, S.; Oganov, A.R. Simple and accurate model of fracture toughness of solids. J. Appl. Phys. 2019, 125, 065105. [Google Scholar] [CrossRef]
- Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Yang, J. First principle calculations and mechanical properties of the intermetallic compounds in a laser welded steel/aluminum joint. Opt. Laser Technol. 2020, 122, 105875. [Google Scholar] [CrossRef]
- He, L.; Li, Z.; Zhang, J.; Peng, F.; Zhao, S.; Chen, H.; Yan, H.; Yang, T.; Chen, S.; Liu, B.; et al. Softening Al13Fe4 intermetallic compound through Fe-site multi-principal-element doping. Scr. Mater. 2022, 218, 114811. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Hu, M.; Feng, J. Elaborating the phases and mechanical properties of multiphase alloy: Experimental two-dimensional mapping combined with theoretical calculations. Mater. Charact. 2017, 134, 347–353. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Zhou, R.; Feng, J. Multialloying effect on thermophysical properties of Cr7 C3 -type carbides. J. Am. Ceram. Soc. 2017, 100, 1588–1597. [Google Scholar] [CrossRef]
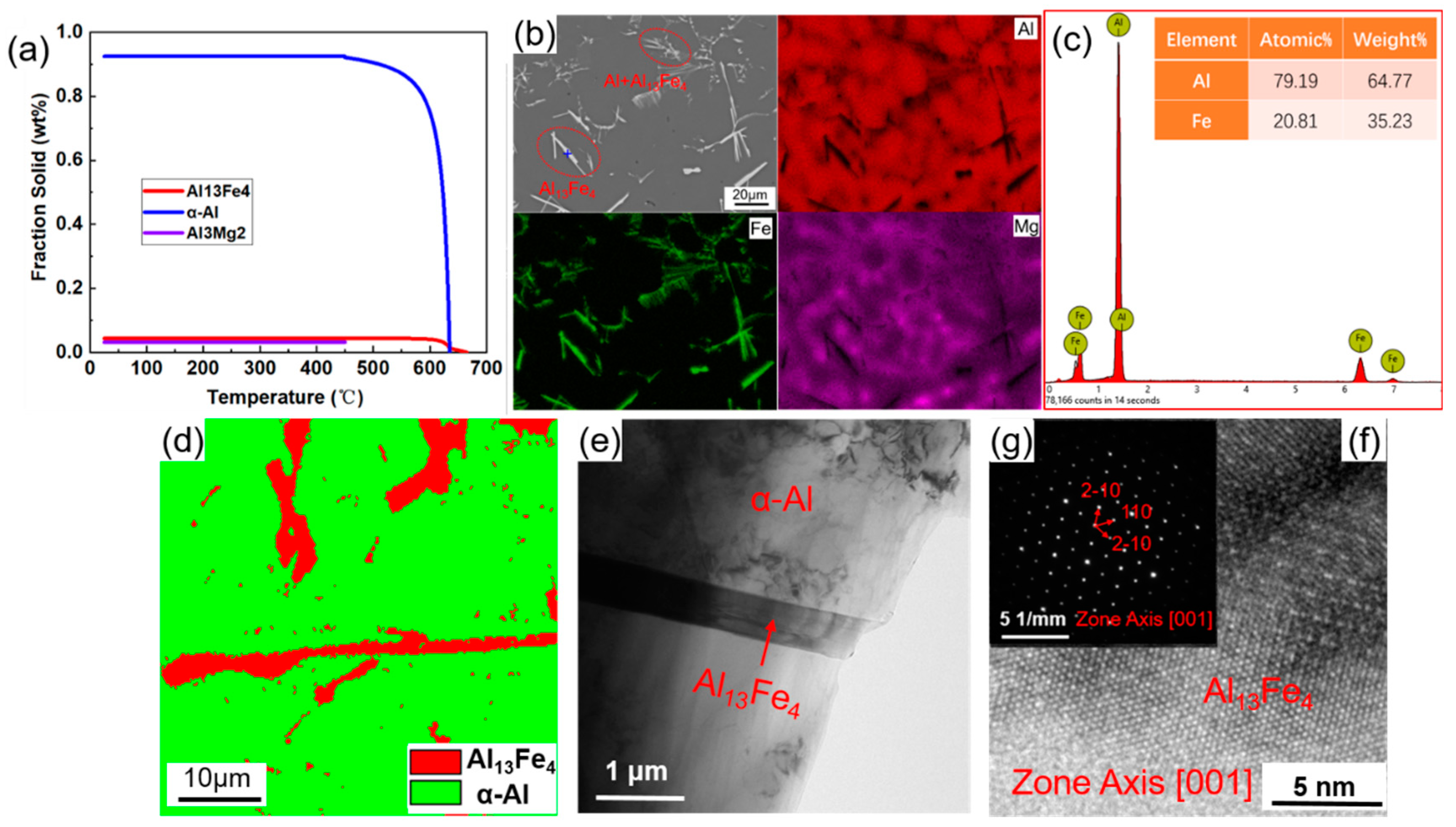
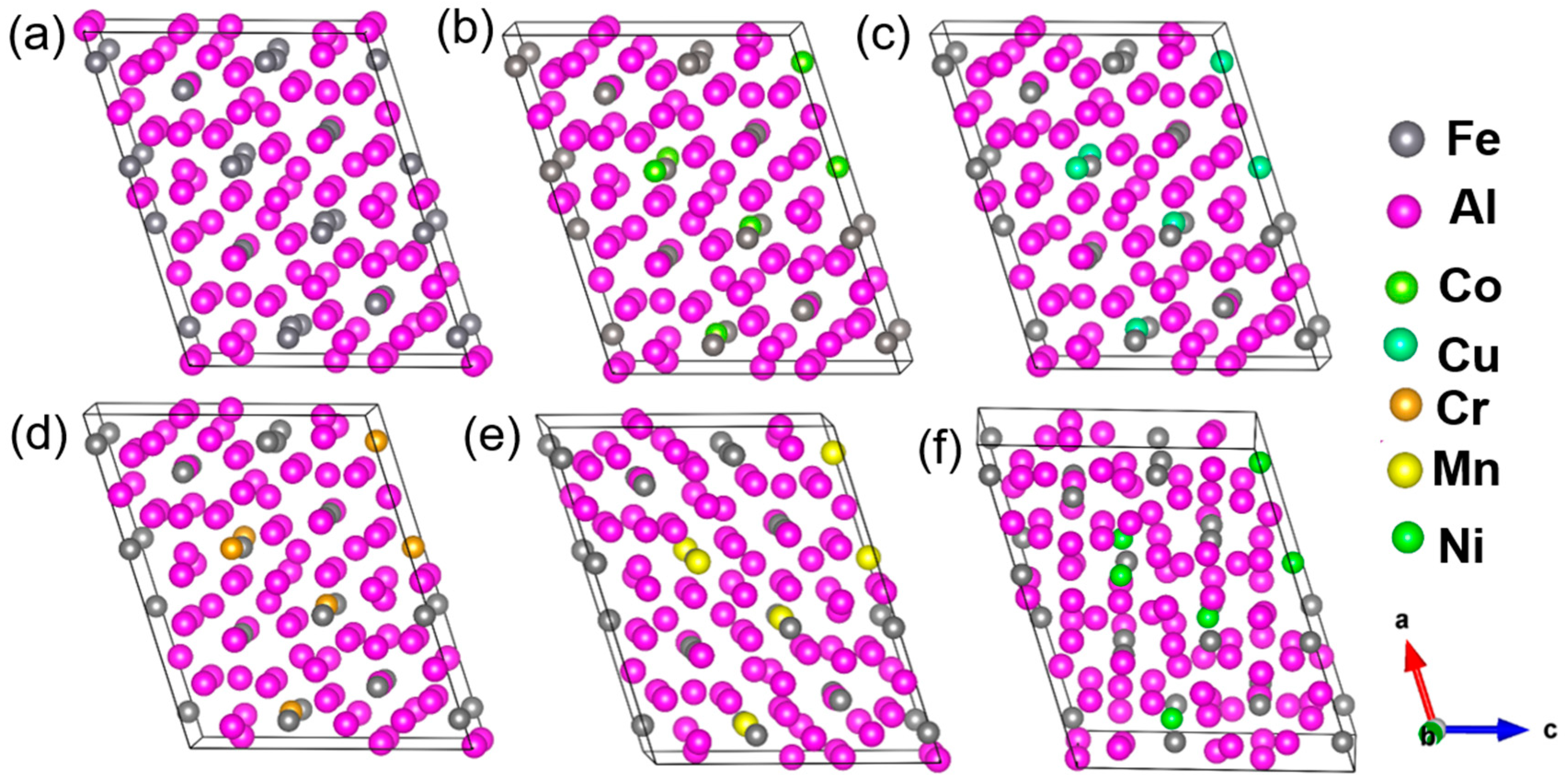
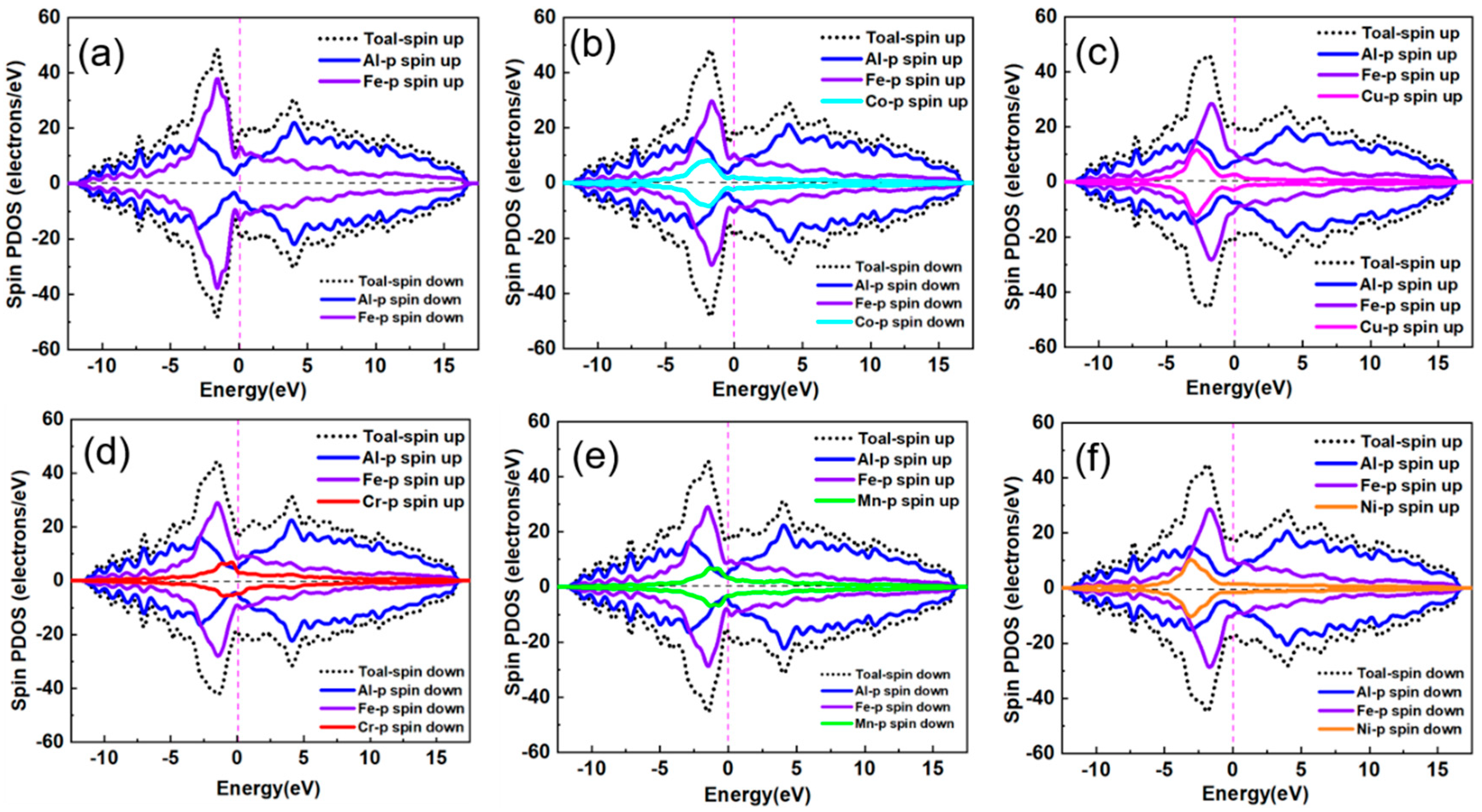
| Mg | Fe | Ti | Cu | Si | Mn | Al |
|---|---|---|---|---|---|---|
| 4.56 | 1.81 | <0.05 | <0.03 | <0.02 | <0.03 | Bal |
| Al13(Fe,M)4 | Atom Coordinates of M | Lattice Constants (Å) | ||||
|---|---|---|---|---|---|---|
| a | b | c | V (Å3) | |||
| Al13Fe4 | M1 (0.098, 0.5, 0.38) M2 (0.414, 0.5, 0.62) M3 (0.59, 0.5, 0.99) M4 (0.43, 0.5, 0.98) | 15.43 | 8.03 | 12.44 | 1542.5 | α = 89.9° β = 107.7° γ = 90.1° |
| Al13(Fe,Co)4 | 15.41 | 8.06 | 12.43 | 1543.7 | ||
| Al13(Fe,Cu)4 | 15.42 | 8.15 | 12.46 | 1566 | ||
| Al13(Fe,Cr)4 | 15.64 | 8.07 | 12.57 | 1586.6 | ||
| Al13(Fe,Mn)4 | 15.5 | 8.04 | 12.5 | 1558.2 | ||
| Al13(Fe,Ni)4 | 15.42 | 8.08 | 12.42 | 1547.6 | ||
| Species | Cohesive Energy (eV/atom) | Mixing Enthalpy (eV/atom) |
|---|---|---|
| Al13Fe4 | −4.69 | −0.28 |
| Al13(Fe,Co)4 | −5.05 | −0.34 |
| Al13(Fe,Cu)4 | −5.04 | −0.39 |
| Al13(Fe,Cr)4 | −4.92 | −0.15 |
| Al13(Fe,Mn)4 | −4.97 | −0.34 |
| Al13(Fe,Ni)4 | −4.98 | −0.3 |
| Species | Cij | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | C15 | C25 | C35 | C46 | |
| Al13Fe4 | 225.7 | 219.4 | 235.2 | 61.52 | 72.6 | 70.6 | 83.2 | 68.3 | 39.8 | −1.74 | −2.9 | 5.8 | −2.1 |
| Al13(Fe,Co)4 | 222.1 | 217.4 | 236.1 | 64.6 | 75.1 | 68.2 | 82.1 | 70.0 | 44.0 | −0.51 | −3.18 | 3.6 | −4.3 |
| Al13(Fe,Cu)4 | 205.9 | 174.2 | 224.8 | 50.4 | 68.8 | 59.51 | 95.4 | 66.3 | 42.6 | −0.42 | −1.71 | 2.2 | −1.3 |
| Al13(Fe,Cr)4 | 218.7 | 213.2 | 235.6 | 57.9 | 50.2 | 52.5 | 81.0 | 67.9 | 40.9 | −1.7 | −2.4 | 3.5 | 4.7 |
| Al13(Fe,Mn)4 | 236.6 | 214.7 | 240.5 | 65.4 | 78.6 | 76.0 | 82.2 | 70.6 | 46.1 | −3.7 | −1.5 | −4.1 | −2.0 |
| Al13(Fe,Ni)4 | 221.3 | 203.9 | 239.6 | 18.4 | 74.0 | 40.9 | 88.8 | 67.9 | 45.6 | −1.75 | −2.53 | 3.1 | 5.2 |
| Species | B | G | E | σ | B/G | HVC | HVT | KIC (MPa·m1/2) |
|---|---|---|---|---|---|---|---|---|
| Al13Fe4 | 116.11 | 62.24 | 158.41 | 0.273 | 1.87 | 7.81 | 8.44 | 1.34 |
| Cal. Al13Fe4 1 | 123 | 76 | 189 | 0.243 | 1.618 | - | - | - |
| Cal. Al13Fe4 2 | 121.886 | 86.942 | 210.723 | 0.211 | 1.40 | - | - | - |
| Al13(Fe,Co)4 | 118.43 | 72.8 | 181.25 | 0.245 | 1.63 | 10.9 | 11.01 | 1.46 |
| Al13(Fe,Cu)4 | 118.42 | 49.17 | 129.58 | 0.317 | 2.41 | 3.98 | 5.34 | 1.20 |
| Al13(Fe,Cr)4 | 117.77 | 72.67 | 180.82 | 0.244 | 1.62 | 10.95 | 11.05 | 1.45 |
| Al13(Fe,Mn)4 | 120.64 | 74.56 | 187.48 | 0.236 | 1.61 | 11.12 | 11.23 | 1.49 |
| Al13(Fe,Ni)4 | 111.68 | 60.87 | 154.53 | 0.269 | 1.83 | 7.88 | 8.46 | 1.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Zhang, H.; Jiang, P.; Lv, Y. The Alloying Strategy to Tailor the Mechanical Properties of θ-Al13Fe4 Phase in Al-Mg-Fe Alloy by First-Principles Calculations. Metals 2022, 12, 1999. https://doi.org/10.3390/met12121999
Liu Q, Zhang H, Jiang P, Lv Y. The Alloying Strategy to Tailor the Mechanical Properties of θ-Al13Fe4 Phase in Al-Mg-Fe Alloy by First-Principles Calculations. Metals. 2022; 12(12):1999. https://doi.org/10.3390/met12121999
Chicago/Turabian StyleLiu, Qianli, Hao Zhang, Peng Jiang, and Yifan Lv. 2022. "The Alloying Strategy to Tailor the Mechanical Properties of θ-Al13Fe4 Phase in Al-Mg-Fe Alloy by First-Principles Calculations" Metals 12, no. 12: 1999. https://doi.org/10.3390/met12121999
APA StyleLiu, Q., Zhang, H., Jiang, P., & Lv, Y. (2022). The Alloying Strategy to Tailor the Mechanical Properties of θ-Al13Fe4 Phase in Al-Mg-Fe Alloy by First-Principles Calculations. Metals, 12(12), 1999. https://doi.org/10.3390/met12121999




