Abstract
In this paper, we review the upper bound method in plasticity with special reference to metal forming processes. We focus on the method itself, solution methods, and restrictions of the upper bound method. Particular upper bound solutions are not considered. The upper bound theorem is formulated using the work function, which is different from conventional proofs. This approach allows for a unified formulation for several types of rigid plastic materials. The solution methods include upper bound elemental techniques, streamline-based methods, and singular solutions. The major restrictions are related to stationary processes and friction laws.
1. Introduction
In the present paper, we review the upper bound method and its application to metal forming processes. The first systematic review on this topic was provided in [1]. The present review encompasses a larger class of constitutive equations and concerns the general approaches and restrictions. Routine particular upper bound solutions are not analyzed, although a few references to such solutions are included to illustrate general approaches.
The paper consists of three main parts. The first part discusses the upper bound theorem based on the work function introduced in [2]. This formulation is not used in textbooks and monographs on plasticity theory. The general theorem applies to several particular work functions. The second part reviews several common methods for constructing kinematically admissible velocity fields involved in the theorem. Most of these methods have been developed and used in the literature for the material model based on the von Mises yield criterion. However, they can be used in conjunction with the formulation of the theorem used in the present paper, which allows for the consideration of much more general yield criteria. The third part addresses the major restrictions of the upper bound method. The emphasis here is on stationary processes and friction, both of which are important for the modeling of metal forming processes.
2. Upper Bound Theorem
2.1. Work Function
Isotropic rigid plastic solids whose yielding is independent of hydrostatic stress are considered. A large class of such solids is defined by the following constitutive equation:
Here, are the components of the deviatoric stress tensor, are the components of the strain rate tensor, and E is the work function introduced in [2]. It is a function of and is supposed to be convex. Therefore,
For any pair and . In the case of incompressible materials, E depends on the deviator of the strain rate tensor.
In what follows, the following summation convention applies. In a quantity containing two repeated suffixes, for example , the summation must be carried out for all values 1, 2, and 3 of both i and j. In a quantity containing one repeated suffix, the summation must be carried out for all values 1, 2, and 3 of this suffix.
Without body forces, the virtual work-rate principle of a continuum reads
Here, the first integral is taken through the volume of a plastic mass and the second over its surface. Also, are the components of the stress tensor, are the surface tractions, and are the components of the velocity vector. If the velocity field satisfies the equation of incompressibility, Equation (3) becomes
A velocity field is said to be kinematically admissible if it satisfies the velocity boundary conditions, and the strain rate tensor is derivable from this field. In the case under consideration, the velocity field should be solenoidal. However, this is unnecessary for plastically compressible materials [3]. In what follows, s, u, and denote the actual deviatoric stress, velocity, and strain rate. The kinematically admissible velocity and strain rate are denoted as u* and , respectively.
Equation (4) is valid for both the actual and kinematically admissible velocity fields. Therefore, it follows from this equation that
Substituting (1) into (2) and integrating through the volume yields
Equations (5) and (6) combine to give
Consider the boundary value problem for a body on whose surface the traction is given on a part and the velocity on the remainder . Since on , Equation (7) becomes
One can rewrite Equation (4) as
The last integral in (8) can be eliminated using (9). As a result,
The left-hand side of this inequality can be calculated for any kinematically admissible velocity field. All the quantities involved on the right-hand side of (10) are actual. In particular, involved in the last integral is known from the boundary conditions. Therefore, the values of involved in this integral can be evaluated for certain functions E and certain boundary value problems.
2.2. Specific Materials
Assume that
where is independent of strain rate and
Also, and is the Kroneker delta. Substituting (11) into (1) yields
It follows from this equation and (12) that
This equation represents the von Mises yield criterion if where is the tensile yield stress. In this case, Equation (11) becomes
And, employing (12), Equation (13) gives
Substituting (15) and (16) into (10) yields
If the material is homogeneous, the tensile yield stress is independent of position. In this case, Equation (17) becomes
The tensile yield stress may be a piece-wise constant function of position, allowing for piece-wise homogeneous materials to be considered. In this case, the first term in (18) is the sum of volume integrals, each of which is taken through the volume where the tensile yield stress is constant.
In many cases, an unknown traction component T is applied over , and the corresponding velocity component U is constant. For such boundary value problems, Equation (18) becomes
Let , , and be the principal strain rates; , , and be the principal components of the deviatoric stress tensor; and , , and be the principal stresses. Assume that
Here, , , and are independent of strain rate. Equation (1) can be referred to the principal axes of stress and strain rates. Substituting (20) into this equation yields
By definition, . Therefore, it follows from (21) that
Consider . Equations (21) and (22) combine to give and
It is straightforward to verify that this equation is equivalent to
If where k is the shear yield stress. Equation (24) represents one of the face regimes of the Tresca yield criterion. In this regime, and is the maximum principal strain rate, . Equation (20) becomes
Moreover,
Substituting (25) and (26) into (10) leads to
The incompressibility equation can be represented as
Since and any kinematically admissible velocity field satisfies the incompressibility equation, Equation (27) transforms to
Further simplifications of this equation are similar to those provided above for the work function (11). The work functions for other piece-wise linear yield criteria [4,5] reduce to (20) and can be found in a similar way to what led to (25).
Assume that
where is independent of strain rate, , and . It follows from (1) and (30) that
where
In the case of uniaxial tension and , and Equation (31) supplies . The work function and equation (31) become
And
Respectively. In the case of pure shear and Then, it follows from (34) that
where is the shear yield stress. Substituting (33) and (34) into (10) yields
Further simplifications of this equation are similar to those provided above for the work function (11).
There are two extreme bounds for all physically reasonable pressure-independent isotropic yield criteria [6]. One of these extreme criteria is usually called the Schmidt–Ishlinskii yield criterion [7]. The other is the Tresca criterion. Assuming that and the criterion proposed in [6] reads
This criterion reduces to the Tresca yield criterion if or . Also, it reduces to the von Mises criterion if or . Equation (33) coincides with (15) if or . Therefore, the von Mises yield criterion is associated with the work function in (33) if or . The yield criterion corresponding to other t-values can be found numerically.
Figure 1 depicts several physically reasonable yield loci in the -space. The loci are shown within the angular sector between the lines and where the inequalities and are satisfied. The three curves between the von Mises and Tresca loci correspond to the yield criterion (37) at , , and .
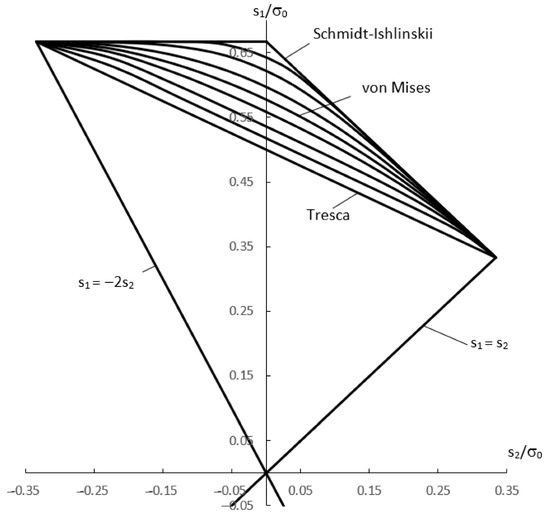
Figure 1.
Several isotropic yield loci.
The considered particular work functions simplify (10) because the first two integrals on its right-hand side are cancelled. It is always so if the work function is a homogeneous function of degree 1. For, Euler’s theorem for homogeneous functions of order 1 reads
Substituting (38) into (10) and using (1) proves the statement above. The most important consequence of this particular form of (10) is that the resulting inequalities, such as (19), allow for an upper bound on unknown tractions to be found for certain boundary conditions. This is not the case for viscoplastic materials.
Assume that
where is independent of strain rate. Substituting (39) into (1) yields the Norton–Hoff law (see, for example, [8,9,10]):
This constitutive equation is often used in superplasticity [11]. It follows from (12) and (40) that
Substituting (39) and (41) into (10) yields
The first integral on the right-hand side involves the actual velocity field and cannot be evaluated. Of course, one can return to (8), which becomes
The functional on the left-hand side should be minimized. This allows for an approximate velocity field to be found. Using this velocity field and the virtual work-rate principle, one can determine an approximate value of the traction in question for certain boundary conditions. However, in contrast to (19), the theorem does not imply that the traction found in this way is an upper bound on its actual value.
Some papers replace the volume integrals in (43) with the plastic work rate dissipated in the volume (for example, [12]). The equation becomes
where the components are calculated using the kinematically admissible velocity field and (40). In general, the significance of and motivation for using this approach are questionable. However, the approach is justified for a class of boundary value problems. Assume that is a traction-free surface. Then, Equations (43) and (44) become
And
Respectively. It is seen from (41) that (45) implies (46). Using (4), one can transform (46) into
If there is one unknown traction component over and the corresponding velocity component is constant, the latter can be taken outside the integral, and the unknown traction can be evaluated.
2.3. Discontinuous Velocity Fields
The velocity field may be discontinuous in the case of perfectly plastic materials. The corresponding functionals for minimization are (17), (29), or (36). Similar functionals exist for other yield criteria. The incompressibility equation demands that the normal velocity must be continuous across velocity discontinuity surfaces. The tangent velocity may be discontinuous, and the amount of its discontinuity is denoted as . Let be the velocity discontinuity surface. The plastic work rate at this surface is determined as
where is the shear yield stress. This work rate should be added to the functionals for minimization. For example, Equation (17) becomes
Equations (29) and (36) should be modified similarly. The yield stresses and are not independent if the yield criterion is specified. In particular,
in the case of the von Mises criterion, Tresca criterion, and criterion (37), respectively. The last equation in (50) shows that the shear yield stress predicted by the yield criterion (37) is smaller than that predicted by the von Mises yield criterion if and . On the other hand, Equation (35) shows that the shear yield stress associated with the work function (33) is larger than that predicted by the von Mises yield criterion if and .
3. Solution Methods
3.1. UBET and TEUBA
Papers [13,14,15] propose an upper bound approach for plane strain problems based on discontinuous kinematically admissible velocity fields consisting of rigid blocks. Since all strain rate components vanish in each rigid block, Equation (49) becomes
These papers also determined an upper bound on the load for several metal forming processes using the proposed approach. Many researchers have further developed this approach, which is now known as the upper bound elemental technique (UBET) and tetrahedral upper bound analysis (TEUBA). The latter is used for solving three-dimensional problems. An overview of UBET and TEUBA is presented in [16]. These methods can be regarded as variants of the finite element method. UBET is also used in conjunction with non-constant velocity fields in blocks [17]. Paper [18] presents such kinematically admissible velocity fields under axial symmetry.
Since UBET is based on discontinuous kinematically admissible velocity fields, the method can only be used in conjunction with rigid perfectly plastic models.
3.2. Stream Functions
Kinematically admissible velocity fields can be conveniently constructed for a class of processes using stream functions. Consider plane strain deformation. Let and be the velocity components referred to Cartesian coordinates . This velocity field can be described as
where is the stream function. It is evident from (52) that the velocity field is solenoidal. The non-zero strain rate components are determined from (52) as
Using these components, one can calculate the work functions involved in the functionals in Section 2.
Using a cylindrical coordinate system in which the circumferential velocity vanishes is usually convenient for solving axisymmetric problems. The velocity field can be described as (for example, [19])
Here, is the radial velocity, is the axial velocity, and is the stream function. The velocity field is solenoidal at any choice of stream functions. The strain rate components are
Using these components, one can calculate the work functions involved in the functionals in Section 2.
Paper [19] combines the UBET and stream function approaches. The stream function approach can also be applied to three-dimensional problems. In this case, Bezier’s curves can be used for describing streamlines [20].
3.3. Singular Velocity Fields
The maximum friction law demands that the friction stress is equal to the shear yield stress at sliding. This law is used under certain conditions at frictional interfaces [21]. The friction surface where the maximum friction law is valid is called the maximum friction surface. In the case of rigid perfectly plastic materials, the actual velocity field is singular near maximum friction surfaces [22]. In particular,
As . Here, z is the Cartesian coordinate normal to the maximum friction surface, is the velocity component tangent to this surface, and and are independent of z. One can choose a kinematically admissible velocity field satisfying (56). An advantage of such a choice is that the stress field generated by this kinematically admissible velocity field and the associated flow rule satisfies the friction law [23,24].
It is seen from (56) that some strain rate components approach infinity or negative infinity near maximum friction surfaces. Therefore, the volume integrals in (17), (29), and (36) are improper. However, they are convergent.
4. Restrictions of the Method
4.1. Stress Fields and Combined Loading
Equation (1) provides only the deviatoric portion of the stress. Therefore, the hydrostatic stress does not enter the formulation, and the stress field cannot be determined using the upper bound theorem. A postprocessing procedure was proposed in [25] to overcome this restriction in the case of rigid perfectly plastic materials.
Equations (15), (27), and (34) each allow for one scalar quantity to be evaluated. In the case of a single loading force, it is the force itself, if the conditions that have led to (19) are satisfied. In the case of combined loading, it may be a combination of several forces. Additional information or assumptions are required to separate these forces (for example, [26,27,28]).
4.2. Stationary Processes
4.2.1. Geometry
The inequality (8) and all the subsequent inequalities following it have been proven for a given configuration of the plastic body. This condition is not satisfied for many stationary metal forming processes, for example, flat rolling with lateral spreading [29], tube sinking [30], and manufacturing composite materials [31,32]. A schematic diagram of a tube sinking process is shown in Figure 2. If the shape of the free surface were known, the inequality above would be valid. However, this shape should be found in solving the problem. A schematic diagram of a bi-metallic extrusion process is shown in Figure 3. The shape of the bi-metallic interface is unknown. Therefore, the distribution of material properties is unknown, and (8) is not valid. The condition above is often ignored in the literature. This issue is discussed in some detail in [33], where a model of ploughing by a pyramidal indenter is considered. The significance of and motivation for using the upper bound theorem to analyze such processes (for example, [34,35,36]) are questionable.
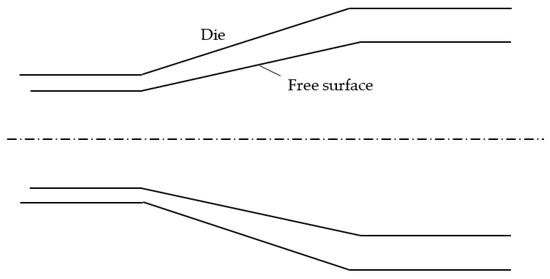
Figure 2.
Schematic diagram of a tube sinking process.
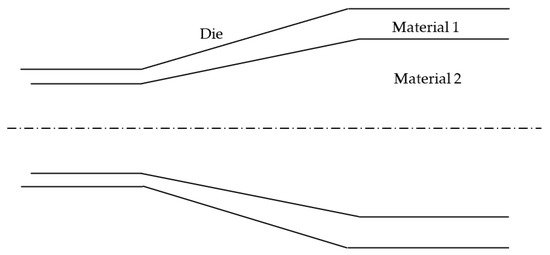
Figure 3.
Schematic diagram of a bi-metallic extrusion process.
4.2.2. Strain Hardening
The distribution of the yield stress is unknown in stationary processes. Therefore, in (17) and other similar inequalities is unknown, and the corresponding integral cannot be evaluated. The significance of and motivation for using the upper bound theorem to analyze such processes (for example, [37,38]) are questionable.
4.3. Non-Stationary Processes
Equation (8) and all the equations following on from (8) are understood to hold incrementally in time. The configuration and properties can be updated after each step of a step-by-step procedure [39]. However, it is worthy of note that the only reliable result from the upper bound theorem is the limit load. In particular, quite different kinematically admissible velocity fields may result in the same limit load. An excellent example is provided in [40]. It is evident that using two different kinematically admissible velocity fields in the step-by-step procedure will lead to different updated configurations and different solutions. The upper bound theorem is not capable of choosing one of these fields.
4.4. Friction
There are several issues related to friction. Some of them can be successfully resolved using trial velocity fields that are not kinematically admissible [41]. This technique is outside the scope of the present paper. Some issues can be resolved by exaggerating the inequality in (8).
Two friction laws are usually used in the modeling of metal forming processes. These are Coulomb’s friction law
and Tresca’s friction law
Here, is the friction stress, is the friction coefficient, is the friction factor, and is the traction component normal to the friction surface. If the equality holds in (57) and (58), then the friction surface belongs to . Consider the second integral on the left-hand side of (8). The integrand involves , which are the actual traction components. One of these components is . Equation (57) does not supply the actual value of this component. Therefore, the integral cannot be evaluated. Equation (58) supplies the actual value of if is constant (i.e., rigid perfectly plastic materials). In this case, the left-hand side of (8) can be calculated for a kinematically admissible velocity field. It is also possible if a step-by-step procedure is used to model a non-stationary process in the case of strain hardening materials (please see Section 4.3). However, the distribution of along the friction surfaces is unknown in the case of stationary processes. Therefore, the upper bound theorem is not valid. Sometimes, kinematically admissible velocity fields are used to calculate the distribution of and then . This method cannot be regarded as the upper bound approach. In the literature, it is sometimes referred to as “an intuitively sound approximation” [42]. In the case of rate-dependent models, such as (39), the actual velocity field is necessary to determine the value of even if a process is non-stationary. Therefore, involved in (8) is unknown, and the corresponding integral cannot be evaluated.
The discussion above assumes that the regime of sliding is operative over the entire friction interface. However, this is not generally true. A generic friction surface is schematically shown in Figure 4. Point A corresponds to the boundary of domains where the material sticks to or slips at the interface. Assume that the regime of sticking occurs over AB. Then, this portion of the friction interface must be regarded as . Consequently, domain AC must be regarded as . Kinematically admissible velocity fields determine another position of point A on the friction interface, for example or . Therefore, the surface integral in (8) cannot be generally evaluated. However, the inequality is valid if is replaced with a surface determined by a kinematically admissible velocity field.
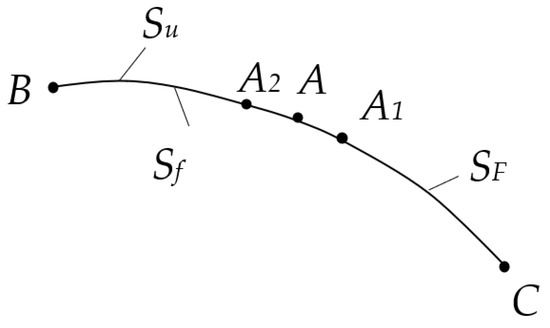
Figure 4.
Possible positions of the boundary between sliding and sticking regions.
Suppose a kinematically admissible velocity field determines a sticking region whose size is smaller than that of the actual sticking region (i.e., the boundary of the domains is at the point ). In this case, the inequality in (8) is exaggerated since no plastic work rate is dissipated between the points and A in the exact solution.
Suppose a kinematically admissible velocity field determines a sticking region whose size is larger than that of the actual sticking region (i.e., the boundary of the domains is at the point ). This is equivalent to the assumption that the kinematically admissible velocity field satisfies the sticking conditions between the points and A, which does not contradict the theorem.
The special case should be treated separately. In the case of strain and viscoplastic materials, the entire friction surface must be regarded as [43,44]. In contrast to the general case noted above, this particular frictional law is compatible with the upper bound formulation [45].
The portion of the surface integral on the left-hand side of (8) related to the friction law can be written as
Here, is the angle between the friction traction and the velocity vector (Figure 5). In the case of plane strain and axisymmetric processes, the directions of and coincide. Therefore, and the integral in (59) can be evaluated. The direction of is unknown in three-dimensional processes. Hence, the integral in (59) cannot be evaluated. However, since , one can replace with −1 in (59), which exaggerates the inequality in (8).
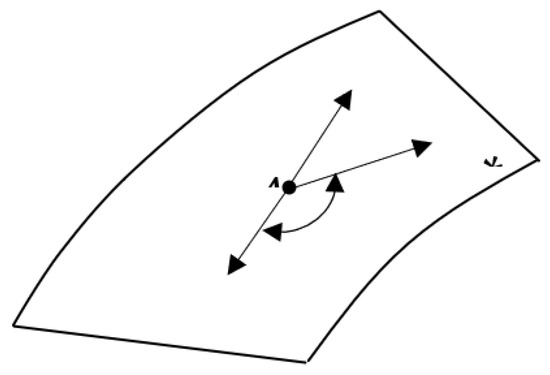
Figure 5.
Orientation of actual and kinematically admissible velocities at a generic point of the friction surface.
5. Discussion
In the present paper, we have discussed the upper bound theorem in plasticity with special reference to metal forming technologies. We have focused on the theorem itself and its advantages and disadvantages for application to metal forming. Particular upper bound solutions have not been considered.
The upper bound theorem for rigid perfectly plastic materials is a convenient and efficient tool for evaluating the limit load. The majority of available solutions are for such constitutive equations. The efficiency of the theorem for applications is significantly reduced for other constitutive equations, which is a consequence of two main factors. One of these factors is the friction law. Among the friction laws widely used in metal forming applications, the only law that results in a constant friction stress is compatible with the theorem. The other factor is that it is usually difficult to construct a continuous kinematically admissible velocity field. Even FE-type methods, such as UBET, use discontinuous fields. The constitutive equations for other rigid perfectly plastic solids do not permit such kinematically admissible velocity fields.
Most available rigid perfectly plastic solutions are for the von Mises yield criterion, including recent publications [46,47,48,49]. It is straightforward to extend these solutions to other yield criteria. In particular, the same kinematically admissible velocity fields can be adopted. Combining these velocity fields and an appropriate functional for minimization, one can investigate the effect of the yield criterion on the limit load and other parameters. However, no attempt has yet been made.
Author Contributions
Conceptualization, S.A.; formal analysis, M.R.; writing—review and editing, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was made possible by grant 20-69-46070 from the Russian Science Foundation.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper has been supported by the RUDN University Strategic Academic Leadership Program.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| k | shear yield stress |
| friction factor | |
| deviatoric stress tensor | |
| deviatoric stress tensor calculated using kinematically admissible velocity fields | |
| , , | principal components of the deviatoric stress tensor |
| surface tractions | |
| velocity components | |
| , | velocity components referred to Cartesian coordinates |
| radial velocity | |
| axial velocity | |
| velocity components tangent to the surface | |
| z | coordinate normal to the maximum friction surface |
| E | work function |
| S | surface of plastic mass |
| velocity discontinuity surface | |
| friction surface | |
| surface over which the traction is given | |
| surface over which the velocity is given | |
| amount of velocity discontinuity | |
| angle between the friction traction and the velocity vector tangent to the friction surface | |
| friction coefficient | |
| strain rate tensor | |
| strain rate tensor calculated using kinematically admissible velocity fields | |
| ξeq | equivalent strain rate |
| , , | principal strain rates |
| maximum principal strain rate | |
| stress tensor | |
| tensile yield stress | |
| ,, | principal stresses |
| traction component normal to the friction surface | |
| friction stress | |
| shear yield stress | |
| stream function | |
| cylindrical coordinate system |
References
- Avitzur, B. Metal Forming: The Application of Limit Analysis. Annu. Rev. Mater. Sci. 1977, 7, 261–300. [Google Scholar] [CrossRef]
- Hill, R. New horizons in the mechanics of solids. J. Mech. Phys. Solids 1956, 5, 66–74. [Google Scholar] [CrossRef]
- Druyanov, B. Technological Mechanics of Porous Bodies; Clarendon Press, Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Billington, E.W. Generalized isotropic yield criterion for incompressible materials. Acta Mech. 1988, 72, 1–20. [Google Scholar] [CrossRef]
- Yu, M. Advances in strength theories for materials under complex stress state in the 20th Century. ASME Appl. Mech. Rev. 2002, 55, 169–218. [Google Scholar] [CrossRef]
- Hosford, W.F. A Generalized Isotropic Yield Criterion. ASME. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Semka, E.V.; Artemov, M.A.; Babkina, Y.N.; Baranovskii, E.S.; Shashkin, A.I. Mathematical modeling of rotating disk states. IOP Conf. Ser. J. Phys. Conf. Ser. 2020, 1479, 012122. [Google Scholar] [CrossRef]
- Lochegnies, D.; Gelin, J.C. A mixed variational formulation for the solution of norton-hoff viscoplastic flows. Comput. Struct. 1997, 65, 177–189. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, Y.; Kong, F.; Wang, X.; Yu, Y. Hot Deformation Behavior and Hot Rolling Properties of a Nano-Y2O3 Addition Near-α Titanium Alloy. Metals 2021, 11, 837. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J.; Rodrigues, C.M.G. Norton-Hoff model for deformation of growing solid shell of thin slab casting in funnel-shape mold. J. Iron Steel Res. Int. 2022, 29, 88–102. [Google Scholar] [CrossRef]
- Chandra, N. Constitutive behavior of superplastic materials. Int. J. Non-Linear Mech. 2002, 37, 461–484. [Google Scholar] [CrossRef]
- Iddan, D.; Tirosh, J.; Pawelskis, O. Strip Rolling of Hardening Rate Sensitive Solids. Ann. CIRP 1986, 35, 151–155. [Google Scholar] [CrossRef]
- Kudo, H. An upper-bound approach to plane-strain forging and extrusion—I. Int. J. Mechan. Sci. 1960, 1, 57–83. [Google Scholar] [CrossRef]
- Kudo, H. An upper-bound approach to plane-strain forging and extrusion—II. Int. J. Mechan. Sci. 1960, 1, 229–252. [Google Scholar] [CrossRef]
- Kudo, H. An upper-bound approach to plane-strain forging and extrusion—III. Int. J. Mechan. Sci. 1960, 1, 366–368. [Google Scholar] [CrossRef]
- Bramley, A.N. UBET and TEUBA: Fast methods for forging simulation and preform design. J. Mater. Process. Technol. 2001, 116, 62–66. [Google Scholar] [CrossRef]
- Ranatunga, V.; Gunasekera, J.S. UBET-based numerical modeling of bulk deformation processes. J. Mater. Eng. Perform. 2006, 15, 47–52. [Google Scholar] [CrossRef]
- Wilson, W.R.D. A simple upper-bound method for axisymmetric metal forming problems. Int. J. Mech. Sci. 1977, 19, 103–112. [Google Scholar] [CrossRef]
- Lin, Y.T.; Wang, J.P. A new upper-bound elemental technique approach. Comput. Struct. 1977, 65, 601–611. [Google Scholar] [CrossRef]
- Abrinia, K.; Fazlirad, A. Investigation of Single Pass Shape Rolling Using an Upper Bound Method. J. Mater. Eng. Perform. 2010, 19, 541–552. [Google Scholar] [CrossRef]
- Lee, C.H.; Altan, T. Influence of Flow Stress and Friction Upon Metal Flow in Upset Forging of Rings and Cylinders. ASME. J. Eng. Ind. 1972, 94, 775–782. [Google Scholar] [CrossRef]
- Alexandrov, S.; Richmond, O. Singular plastic flow fields near surfaces of maximum friction stress. Int. J. Non-Linear Mech. 2011, 36, 1–11. [Google Scholar] [CrossRef]
- Alexandrov, S.; Mishuris, G.; Miszuris, W.; Sliwa, R.E. On the dead-zone formation and limit analysis in axially symmetric extrusion. Int. J. Mech. Sci. 2001, 43, 367–379. [Google Scholar] [CrossRef]
- Alexandrova, N. Analytical treatment of tube drawing with a mandrel. Proc. Inst. Mechan. Eng. Part C J. Mechan. Eng. Sci. 2001, 215, 581–589. [Google Scholar] [CrossRef]
- Azarkhin, A.; Richmond, O. Extension of the Upper Bound Method to Include Estimation of Stresses. ASME J. Appl. Mech. 1991, 58, 493–498. [Google Scholar] [CrossRef]
- De Vathaire, M.; Delamare, F.; Felder, E. An upper bound model of ploughing by a pyramidal indenter. Wear 1981, 66, 55–64. [Google Scholar] [CrossRef]
- Sutcliffe, M.P.F. Surface asperity deformation in metal forming processes. Int. J. Mechan. Sci. 1988, 30, 847–868. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Sheu, S. Real area of contact and boundary friction in metal forming. Int. J. Mechan. Sci. 1988, 30, 475–489. [Google Scholar] [CrossRef]
- Montmitonnet, P. Hot and cold strip rolling processes. Comp. Meth. Appl. Mech. Eng. 2006, 195, 6604–6625. [Google Scholar] [CrossRef]
- Gülseren, B.; Bychkov, O.; Frolov, I.; Schaper, M.; Grydin, O. Sinking of ultra-thick-walled double-layered aluminium tubes. Arch. Met. Mater. 2018, 63, 365–370. [Google Scholar]
- Milenin, A.A.; Berski, S.; Banaszek, G.; Dyja, H. Theoretical analysis and optimisation of parameters in extrusion process of explosive cladded bimetallic rods. J. Mater. Process. Techn. 2004, 157, 208–212. [Google Scholar] [CrossRef]
- Li, X.; Zu, G.; Ding, M.; Mu, Y.; Wang, P. Interfacial microstructure and mechanical properties of Cu/Al clad sheet fabricated by asymmetrical roll bonding and annealing. Mater. Sci. Eng. A 2011, 529, 485–491. [Google Scholar] [CrossRef]
- Azarkhin, A.; Richmond, O. A model of ploughing by a pyramidal indenter—Upper bound method for stress-free surfaces. Wear 1992, 157, 409–418. [Google Scholar] [CrossRef]
- Hartley, C.S. Upper bound analysis of extrusion of axisymmetric, piecewise homogeneous tubes. Int. J. Mechan. Sci. 1973, 15, 651–663. [Google Scholar] [CrossRef]
- Chitkara, N.R.; Aleem, A. Extrusion of axi-symmetric bi-metallic tubes from solid circular billets: Application of a generalised upper bound analysis and some experiments. Int. J. Mechan. Sci. 2001, 43, 2833–2856. [Google Scholar] [CrossRef]
- Haghighat, H.; Asgari, G.R. A generalized spherical velocity field for bi-metallic tube extrusion through dies of any shape. Int. J. Mechan. Sci. 2011, 53, 248–253. [Google Scholar] [CrossRef]
- Rubio, E.M.; Marín, M.; Domingo, R.; Sebastián, M.A. Analysis of plate drawing processes by the upper bound method using theoretical work-hardening materials. Int. J. Adv. Manuf. Technol. 2009, 40, 261–269. [Google Scholar] [CrossRef]
- Pérez, C.J.L.; Luri, R. Upper Bound Analysis of the ECAE Process by Considering Circular Cross-Section and Strain Hardening Materials. ASME. J. Manuf. Sci. Eng. 2010, 132, 041003. [Google Scholar] [CrossRef]
- Huh, H.; Lee, C.-H. Eulerian finite-element modeling of the extrusion process for work-hardening materials with the extended concept of limit analysis. J. Mater. Process. Techn. 1993, 38, 51–61. [Google Scholar] [CrossRef]
- Richmond, O. Plane strain necking of V-notched and un-notched tensile bars. J. Mech. Phys. Solids 1969, 17, 83–90. [Google Scholar] [CrossRef]
- Collins, I.F. The upper bound theorem for rigid/plastic solids generalized to include Coulomb friction. J. Mech. Phys. Solids 1969, 17, 323–338. [Google Scholar] [CrossRef]
- Marques, M.J.M.B.; Martins, P.A.F. A solution to plane strain rolling by the weighted residuals method. Int. J. Mechan. Sci. 1990, 32, 817–827. [Google Scholar] [CrossRef]
- Alexandrov, S.; Alexandrova, N. On the Maximum Friction Law for Rigid/Plastic, Hardening Materials. Meccanica 2000, 35, 393–398. [Google Scholar] [CrossRef]
- Alexandrov, S.; Alexandrova, N. On the Maximum Friction Law in Viscoplasticity. Mech. Time-Depend. Mater. 2000, 4, 99–104. [Google Scholar] [CrossRef]
- Alexandrov, S. An Analysis of the Axisymmetric Compression of Viscous Materials. J. Mater. Proc. Technol. 2000, 105, 278–283. [Google Scholar] [CrossRef]
- Laptev, A.; Perig, A.; Vyal, O. Analysis of Equal Channel Angular Extrusion by Upper Bound Method and Rigid Block Model. Mater. Res. 2014, 17, 359–366. [Google Scholar] [CrossRef]
- Cai, S.-P.; Wang, Z.-J. An analysis for three-dimensional upset forging of elliptical disks and rings based on the upper-bound method. Int. J. Mechan. Sci. 2020, 183, 105835. [Google Scholar] [CrossRef]
- Zhang, X.J.; Li, F.; Wang, Y.; Chen, Z.Y. An analysis for magnesium alloy curvature products formed by staggered extrusion (SE) based on the upper bound method. Int. J. Adv. Manuf. Technol. 2022, 119, 303–313. [Google Scholar] [CrossRef]
- Zhou, W.; Xi, Z. Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model. Metals 2022, 12, 877. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).