Crystal Plasticity Model Analysis of the Effect of Short-Range Order on Strength-Plasticity of Medium Entropy Alloys
Abstract
1. Introduction
2. Crystal Plasticity Framework
2.1. Kinematics of Crystal Plasticity
2.2. Dislocation Slipping
2.3. Deformation Twinning
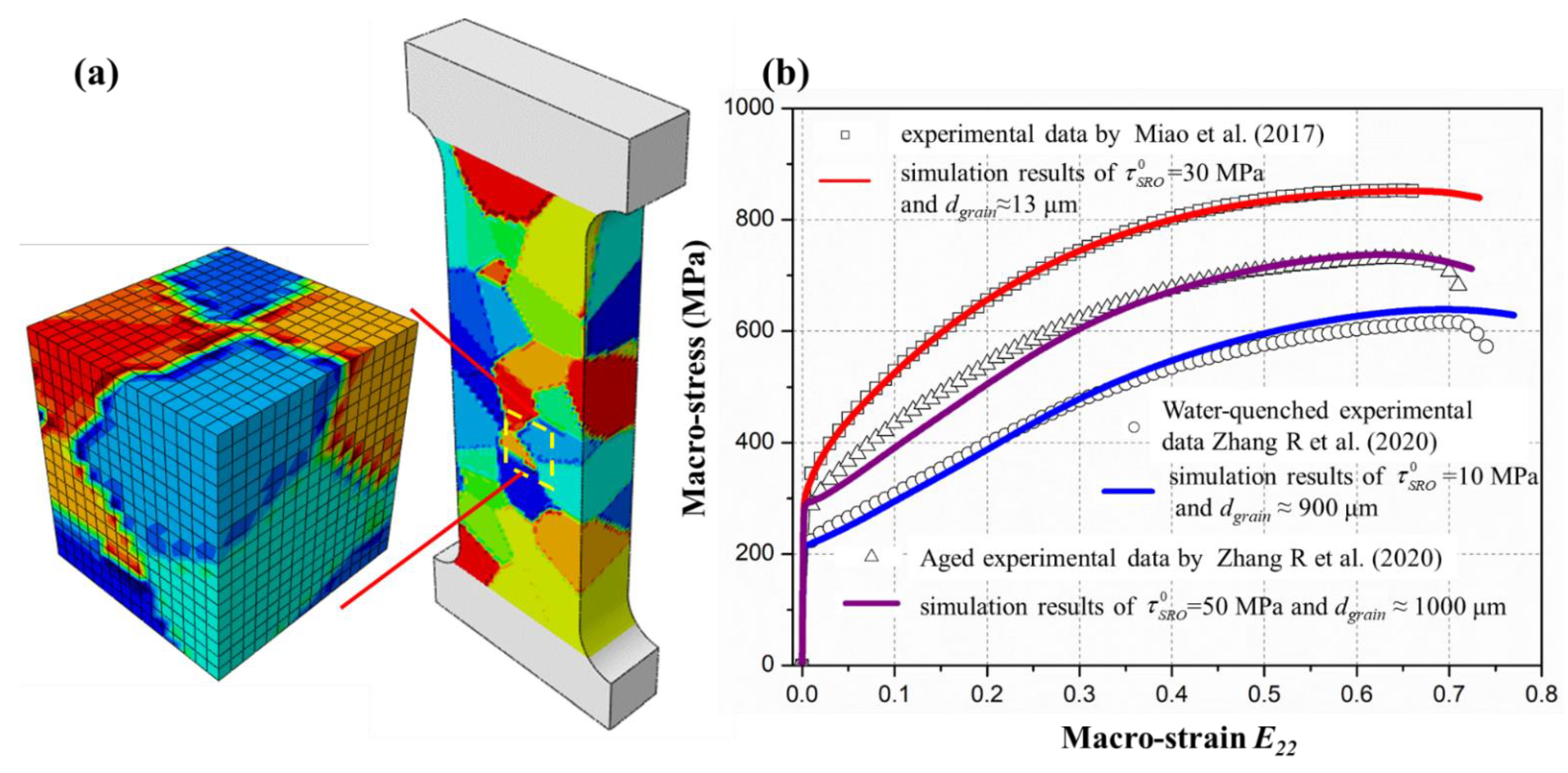
3. Simulations and Validation of the Constitutive Model
3.1. Polycrystalline Finite Element Model
3.2. Parameter Validation
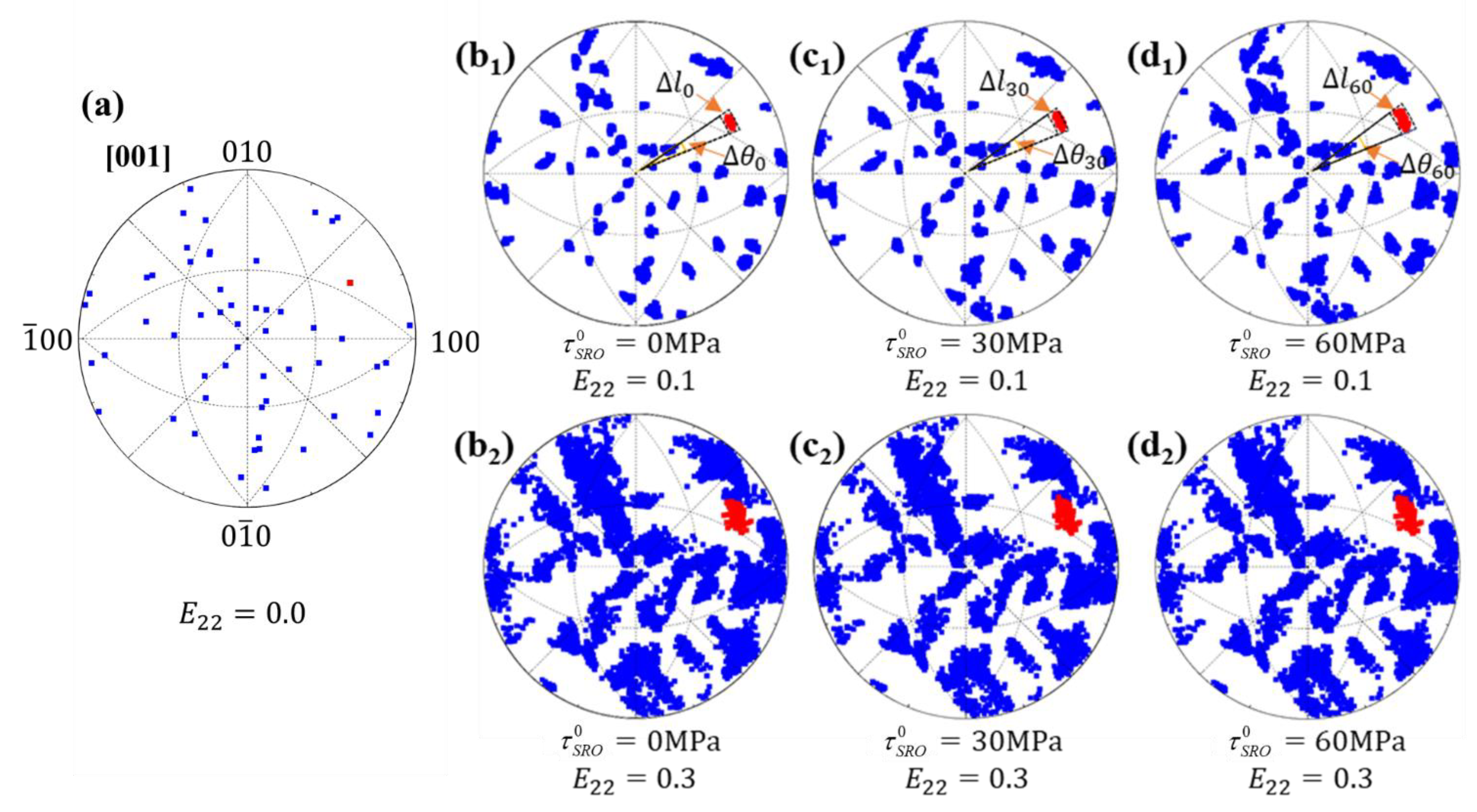
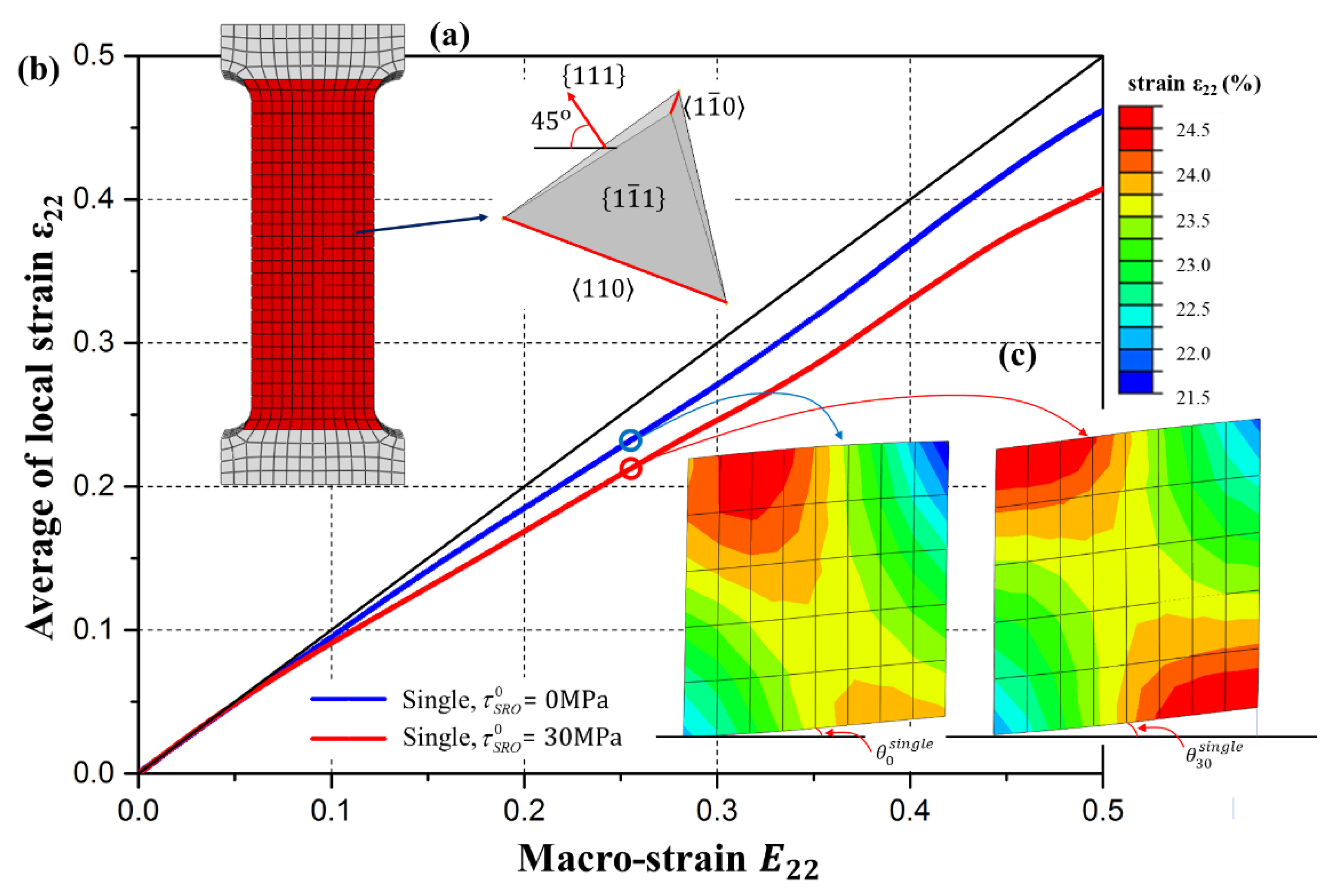
4. Influence of SRO on Deformation Behavior
5. Conclusions
- (1)
- A set of parameters consistent with CoCrNi MEAs was determined and can be used to discuss the influence of various factors on a material’s deformation behavior.
- (2)
- Adjusting the resistance of SRO at a certain range increases both the yield strength and elongation simultaneously, but beyond this range, the yield strength increases but the elongation decreases.
- (3)
- As the resistance of SRO increases, the elongation increases and then decreases, which is attributed to the more intense local rotation with coplanar slip. Local rotation can increase the additional macro strain, while also causing a more intense stress concentration; when the resistance of SRO is low, the additional macro strain dominates the elongation increase; when the resistance is high, the stress concentration dominates the elongation decrease.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Diao, H.Y.; Feng, R.; Dahmen, K.A.; Liaw, P.K. Fundamental deformation behavior in high-entropy alloys: An overview. Curr. Opin. Solid State Mater. Sci. 2017, 21, 252–266. [Google Scholar] [CrossRef]
- Zhang, F.X.; Zhao, S.; Jin, K.; Xue, H.; Velisa, G.; Bei, H.; Huang, R.; Ko, J.Y.P.; Pagan, D.C.; Neuefeind, J.C.; et al. Local Structure and Short-Range Order in a NiCoCr Solid Solution Alloy. Phys. Rev. Lett. 2017, 118, 205501. [Google Scholar] [CrossRef]
- Chen, J.; Liu, T.-W.; Cao, F.-H.; Wang, H.-Y.; Chen, Y.; Dai, L.-H. Deformation Behavior and Microstructure Evolution of CoCrNi Medium-Entropy Alloy Shaped Charge Liners. Metals 2022, 12, 811. [Google Scholar] [CrossRef]
- Liu, X.-F.; Tian, Z.-L.; Zhang, X.-F.; Chen, H.-H.; Liu, T.-W.; Chen, Y.; Wang, Y.-J.; Dai, L.-H. “Self-sharpening” tungsten high-entropy alloy. Acta Mater. 2020, 186, 257–266. [Google Scholar] [CrossRef]
- Xie, Z.-C.; Li, C.; Wang, H.-Y.; Lu, C.; Dai, L.-H. Hydrogen induced slowdown of spallation in high entropy alloy under shock loading. Int. J. Plast. 2021, 139, 102944. [Google Scholar] [CrossRef]
- Ehler, A.; Dhiman, A.; Dillard, T.; Dingreville, R.; Barrick, E.; Kustas, A.; Tomar, V. High-Strain Rate Spall Strength Measurement for CoCrFeMnNi High-Entropy Alloy. Metals 2022, 12, 1482. [Google Scholar] [CrossRef]
- El Batal, O.; Abuzaid, W.; Egilmez, M.; Alkhader, M.; Patriarca, L.; Casati, R. Deformation Rate and Temperature Sensitivity in TWIP/TRIP VCrFeCoNi Multi-Principal Element Alloy. Metals 2022, 12, 1510. [Google Scholar] [CrossRef]
- Semenyuk, A.; Povolyaeva, E.; Sanin, V.; Zherebtsov, S.; Stepanov, N. Effect of Nitrogen Doping on the Structure and Mechanical Properties of the Fe40Mn40Cr10Co10 High-Entropy Alloy. Metals 2022, 12, 1599. [Google Scholar] [CrossRef]
- Bu, Y.Q.; Wang, H.T. Short-range order in multicomponent alloys. Advances in Mechanics Adv. Mech. 2021, 51, 915–919. [Google Scholar] [CrossRef]
- Chen, Z.K.; Li, X.Y. Numerical simulations for microstructure evolution during metal additive manufacturing. Adv. Mech. 2022, 52, 397–409. [Google Scholar] [CrossRef]
- Qiao, Y.; Chen, Y.; Cao, F.-H.; Wang, H.-Y.; Dai, L.-H. Dynamic behavior of CrMnFeCoNi high-entropy alloy in impact tension. Int. J. Impact Eng. 2021, 158, 104008. [Google Scholar] [CrossRef]
- Cao, F.; Chen, Y.; Zhao, S.; Ma, E.; Dai, L. Grain boundary phase transformation in a CrCoNi complex concentrated alloy. Acta Mater. 2021, 209, 116786. [Google Scholar] [CrossRef]
- Cao, F.-H.; Wang, Y.-J.; Dai, L.-H. Novel atomic-scale mechanism of incipient plasticity in a chemically complex CrCoNi medium-entropy alloy associated with inhomogeneity in local chemical environment. Acta Mater. 2020, 194, 283–294. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, Y.; Chen, X.; Fu, X.; Chen, D.; Chen, S.; Gu, L.; Wei, F.; Bei, H.; Gao, Y.; et al. Tuning element distribution, structure and properties by composition in high-entropy alloys. Nature 2019, 574, 223–227. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Q.; Cheng, Z.; Zhu, M.; Zhou, H.; Jiang, P.; Zhou, L.; Xue, Q.; Yuan, F.; Zhu, J.; et al. Direct observation of chemical short-range order in a medium-entropy alloy. Nature 2021, 592, 712–716. [Google Scholar] [CrossRef]
- Ma, E. Unusual dislocation behavior in high-entropy alloys. Scr. Mater. 2020, 181, 127–133. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, S.; Ding, J.; Chong, Y.; Jia, T.; Ophus, C.; Asta, M.; Ritchie, R.O.; Minor, A.M. Short-range order and its impact on the CrCoNi medium-entropy alloy. Nature 2020, 581, 283–287. [Google Scholar] [CrossRef]
- Qiao, J.C.; Zhang, L.T.; Tong, Y.; Lyu, G.J.; Hao, Q.; Tao, K. Mechancial properties of amorphous alloys: In the framework of the microstructure heterogeneity. Adv. Mech. 2022, 52, 117–152. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, P.; Yuan, F.; Wu, X. Chemical medium-range order in a medium-entropy alloy. Nat. Commun. 2022, 13, 1021. [Google Scholar] [CrossRef]
- Li, Q.-J.; Sheng, H.; Ma, E. Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 2019, 10, 3563. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Zong, H.; Ding, X.; Sun, J.; Ma, E. Unusual activated processes controlling dislocation motion in body-centered-cubic high-entropy alloys. Proc. Natl. Acad. Sci. USA 2020, 117, 16199–16206. [Google Scholar] [CrossRef]
- Han, D.; Wang, Z.Y.; Yan, Y.; Shi, F.; Li, X.W. A good strength-ductility match in Cu-Mn alloys with high stacking fault energies: Determinant effect of short range ordering. Scr. Mater. 2017, 133, 59–64. [Google Scholar] [CrossRef]
- Gerold, V.; Karnthaler, H. On the origin of planar slip in fcc alloys. Acta Metall. 1989, 37, 2177–2183. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Han, D.; Li, X.W. A unique two-stage strength-ductility match in low solid-solution hardening Ni-Cr alloys: Decisive role of short range ordering. Scr. Mater. 2020, 178, 269–273. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incroporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard Univ.: Cambridge, UK, 1991. [Google Scholar]
- Orowan, E. Zur Kristallplastizität. I—Tieftemperaturplastizität und Beckersche Formel. Z. Für Phys. 1934, 89, 605–613. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, J.; Wang, Z.; Gan, B.; Zhao, J.; Kang, G.; Zhang, X. Crystal plasticity finite element analysis of gradient nanostructured TWIP steel. Int. J. Plast. 2020, 130, 102703. [Google Scholar] [CrossRef]
- Madec, R.; Devincre, B.; Kubin, L.P.; Hoc, T.; Rodney, D. The Role of Collinear Interaction in Dislocation-Induced Hardening. Science 2003, 301, 1879–1882. [Google Scholar] [CrossRef] [PubMed]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Miao, J.; Slone, C.E.; Smith, T.M.; Niu, C.; Bei, H.; Ghazisaeidi, M.; Pharr, G.M.; Mills, M.J. The evolution of the deformation substructure in a Ni-Co-Cr equiatomic solid solution alloy. Acta Mater. 2017, 132, 35–48. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Reinhart, C.; Hunfeld, J.; Eggeler, G.; George, E.P. Reasons for the superior mechanical properties of medium-entropy CrCoNi compared to high-entropy CrMnFeCoNi. Acta Mater. 2017, 128, 292–303. [Google Scholar] [CrossRef]
- Jin, K.; Gao, Y.F.; Bei, H. Intrinsic properties and strengthening mechanism of monocrystalline Ni-containing ternary concentrated solid solutions. Mater. Sci. Eng. A 2017, 695, 74–79. [Google Scholar] [CrossRef]
- Mridha, S.; Sadeghilaridjani, M.; Mukherjee, S. Activation Volume and Energy for Dislocation Nucleation in Multi-Principal Element Alloys. Metals 2019, 9, 263. [Google Scholar] [CrossRef]


| Symbol | Physical Mean | Value |
|---|---|---|
| Elastic constants | 249, 156, 142 GPa | |
| Solid solution strength | 200 MPa | |
| Total number of slip systems | 12 | |
| Burgers vector | 0.2522 nm | |
| Saturated number of piled-up dislocation | 39 | |
| Mean spacing between slip bands | 223 nm | |
| Hall–Petch coefficient (Converted to resolved shear stress) | ||
| Forest dislocation hardening constant | 0.0488 | |
| The initial dislocation density of the slip system | ||
| Reference velocity for dislocation slip | ||
| The activation energy for dislocation slip | 0.27 eV | |
| The exponent in slip velocity | 0.75, 2.5 | |
| Annihilation distance for dislocations | 1.1 | |
| Interaction coefficient between slip systems | 0.122, 0.122, 0.625, 0.07, 0.137, 0.122 | |
| Total number of twin systems | 12 | |
| , | The width and thickness of twin lamellas | 10 μm, 0.01 μm |
| Maximum twin fraction of twin system | 0.01 | |
| Cross-slip volume | ||
| Twinning transition profile width exponent | 5 | |
| reference twin nucleation rate | 2 s−1 | |
| Interaction coefficient between slip and twin systems | 0.0 (coplanar) 0.042 (cross-slip) | |
| Interaction coefficient between twin systems | 0.0 (coplanar) 0.468 (non-coplanar) | |
| Stacking fault energy | ||
| Dislocation resistance of SRO | 10, 30, 50 MPa | |
| reference strain | 0.25 | |
| Interaction coefficient between slip and degree of SRO | 3 (coplanar) −1 (non-coplanar) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Cao, F.; Chen, Y.; Wang, H.; Dai, L. Crystal Plasticity Model Analysis of the Effect of Short-Range Order on Strength-Plasticity of Medium Entropy Alloys. Metals 2022, 12, 1757. https://doi.org/10.3390/met12101757
Li C, Cao F, Chen Y, Wang H, Dai L. Crystal Plasticity Model Analysis of the Effect of Short-Range Order on Strength-Plasticity of Medium Entropy Alloys. Metals. 2022; 12(10):1757. https://doi.org/10.3390/met12101757
Chicago/Turabian StyleLi, Chen, Fuhua Cao, Yan Chen, Haiying Wang, and Lanhong Dai. 2022. "Crystal Plasticity Model Analysis of the Effect of Short-Range Order on Strength-Plasticity of Medium Entropy Alloys" Metals 12, no. 10: 1757. https://doi.org/10.3390/met12101757
APA StyleLi, C., Cao, F., Chen, Y., Wang, H., & Dai, L. (2022). Crystal Plasticity Model Analysis of the Effect of Short-Range Order on Strength-Plasticity of Medium Entropy Alloys. Metals, 12(10), 1757. https://doi.org/10.3390/met12101757







