Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements
Abstract
1. Introduction
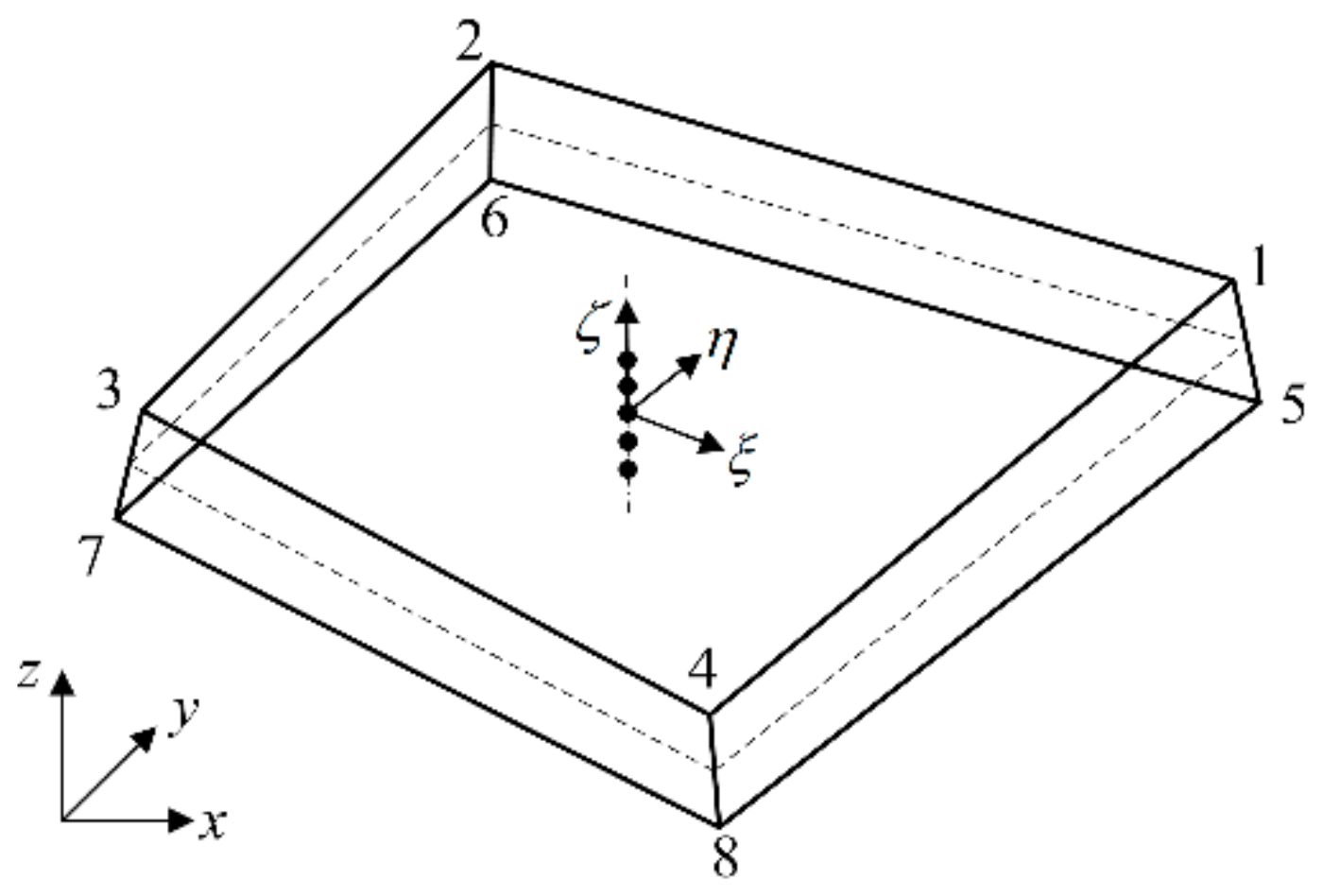
2. Solid-Shell Formulation
2.1. Geometrics and Kinematic
2.2. EAS Method
2.3. ANS Method
2.4. Hourglass Stabilization
3. Central Difference Scheme and Time Step Estimation
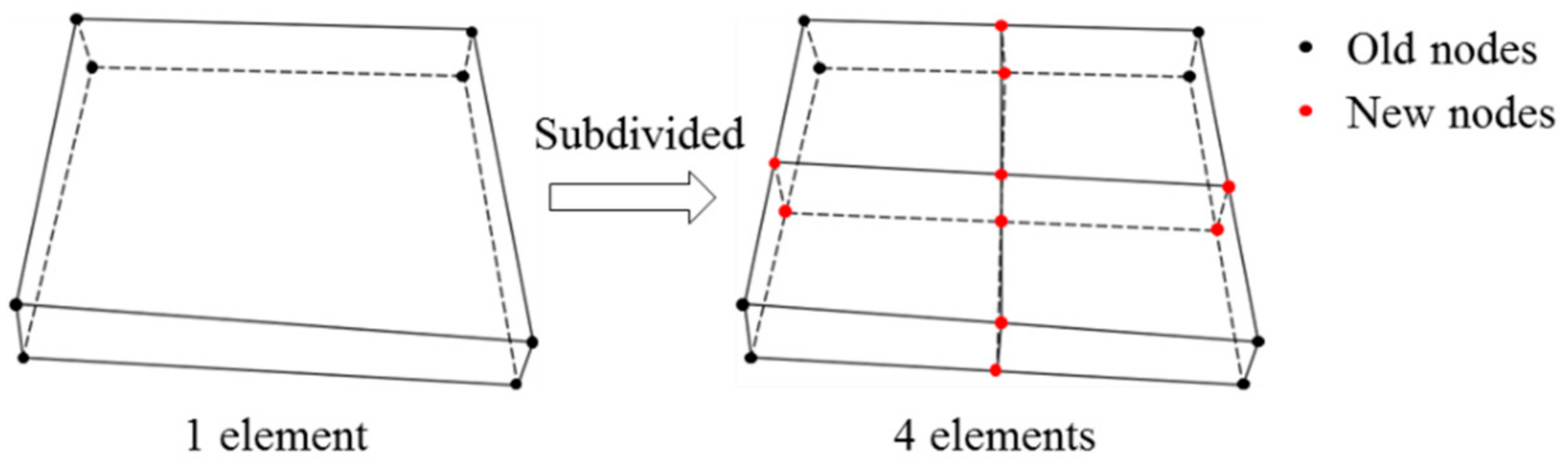
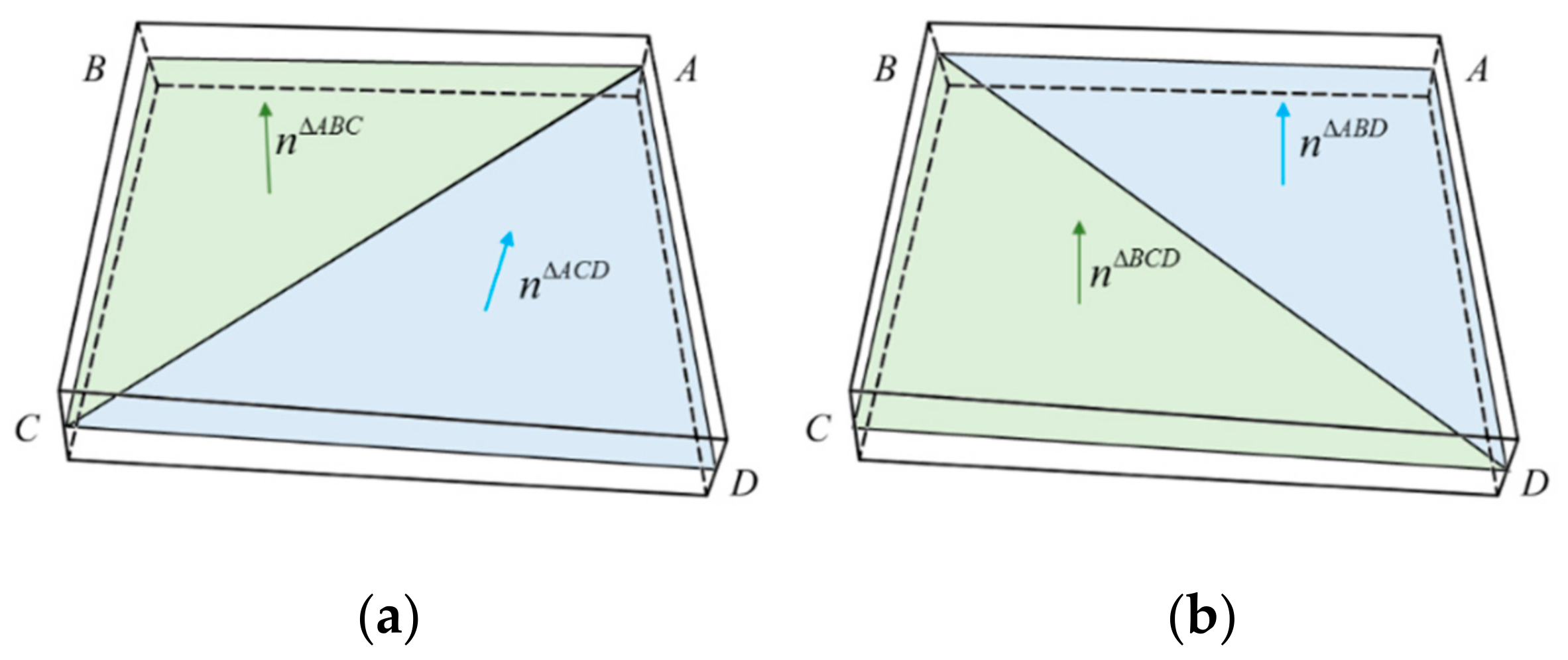
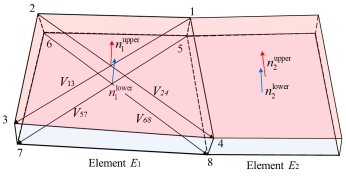
4. Adaptive Mesh Subdivision
5. Material Modeling
5.1. Hill48 Yield Function
5.2. Yld91 Yield Function
5.3. Yld2004-18pYield Function
6. Numerical Examples
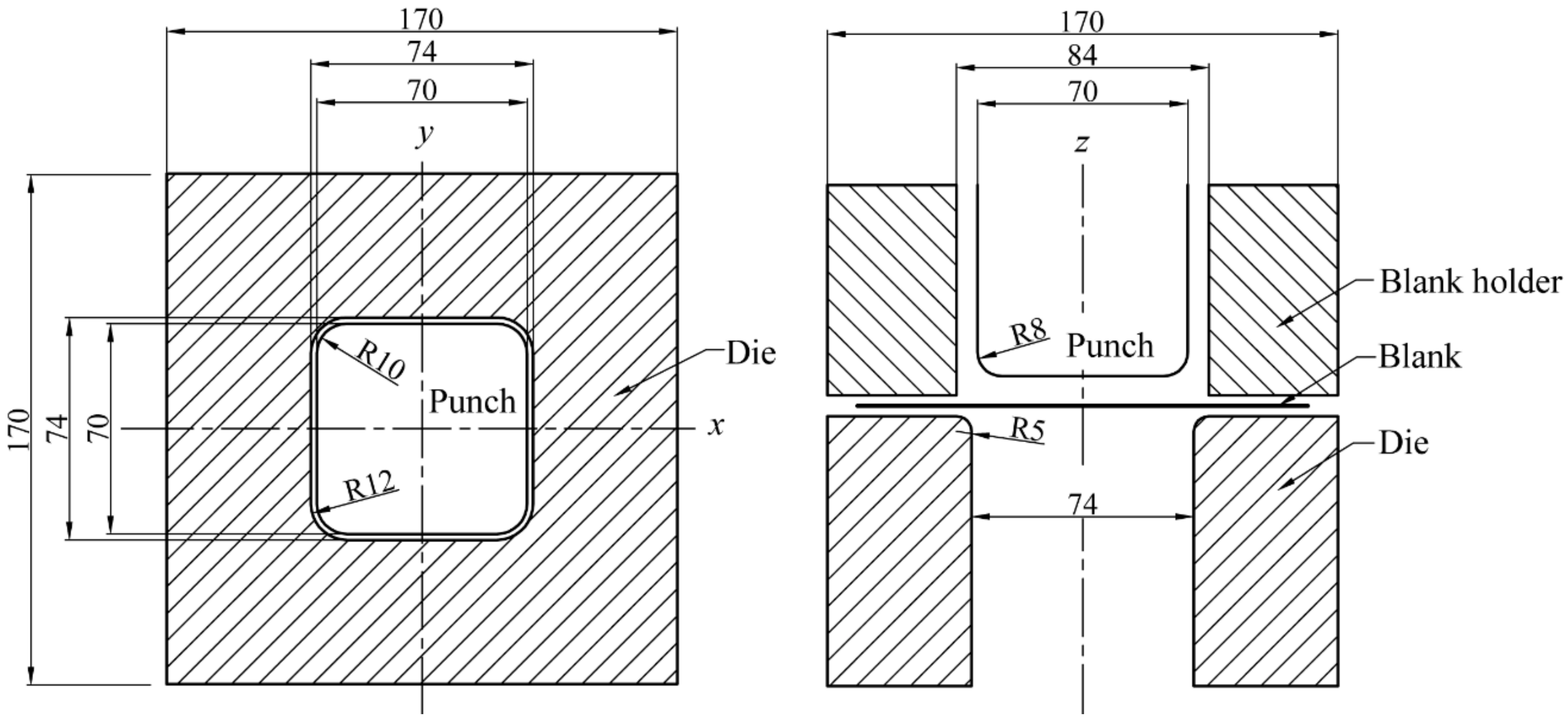
6.1. Deep Drawing of a Square Cup
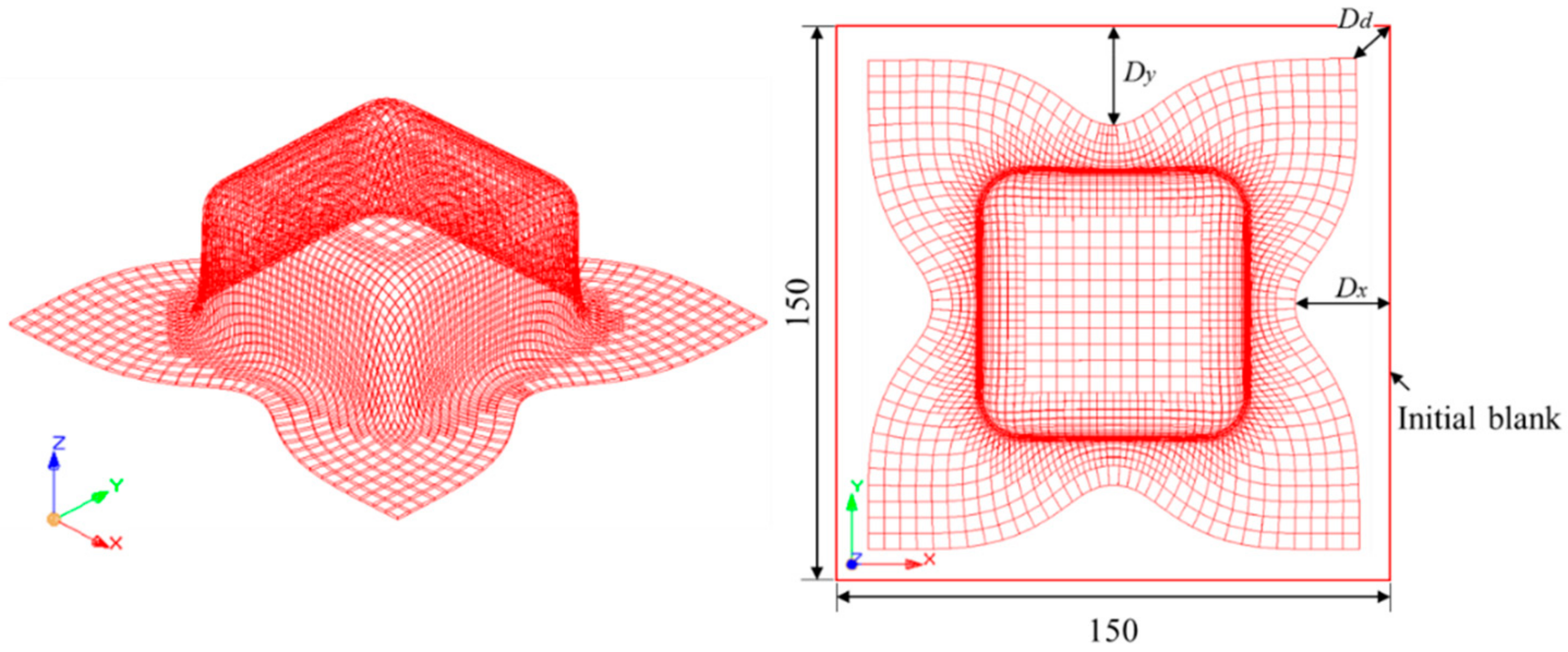
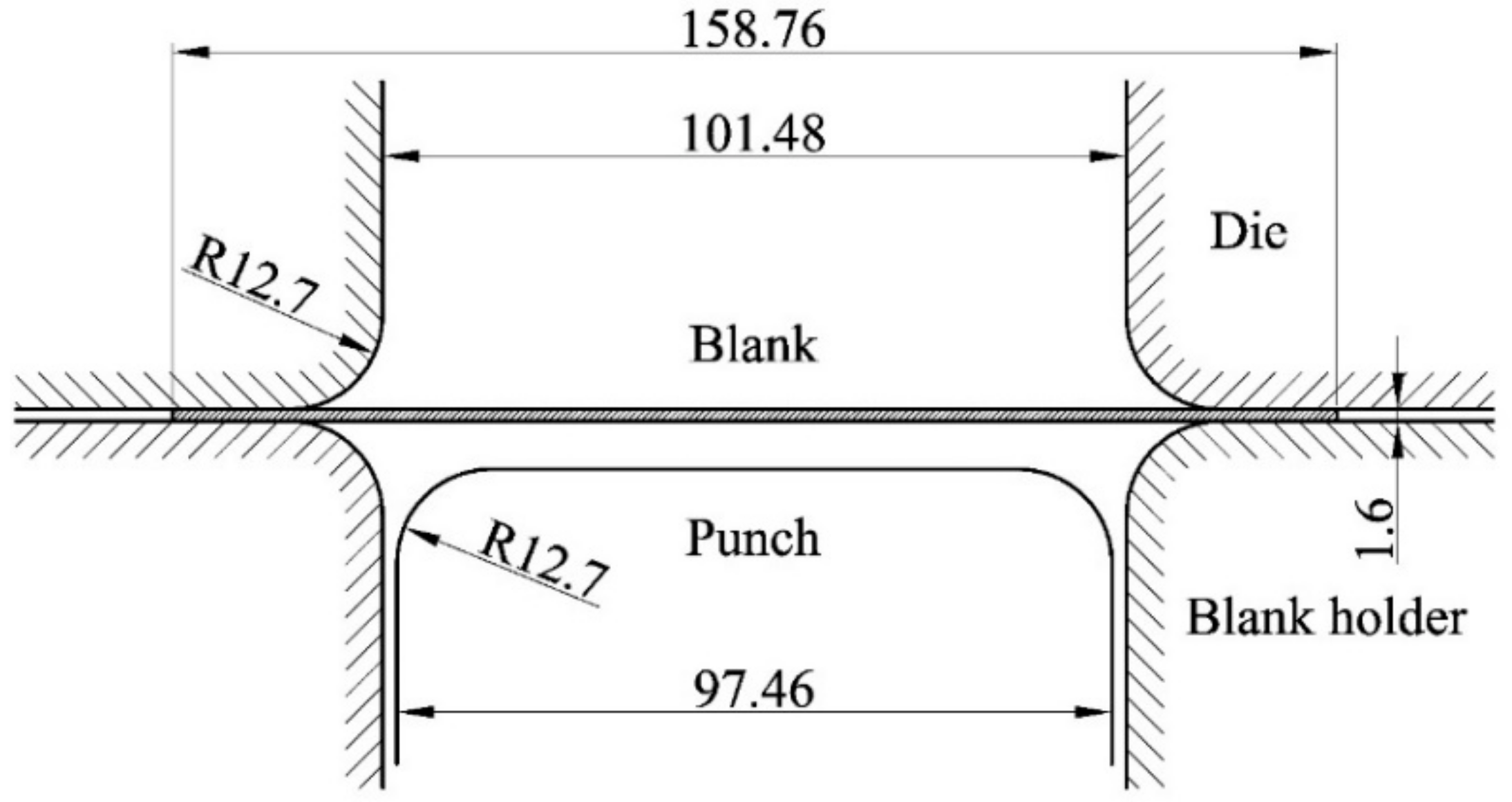
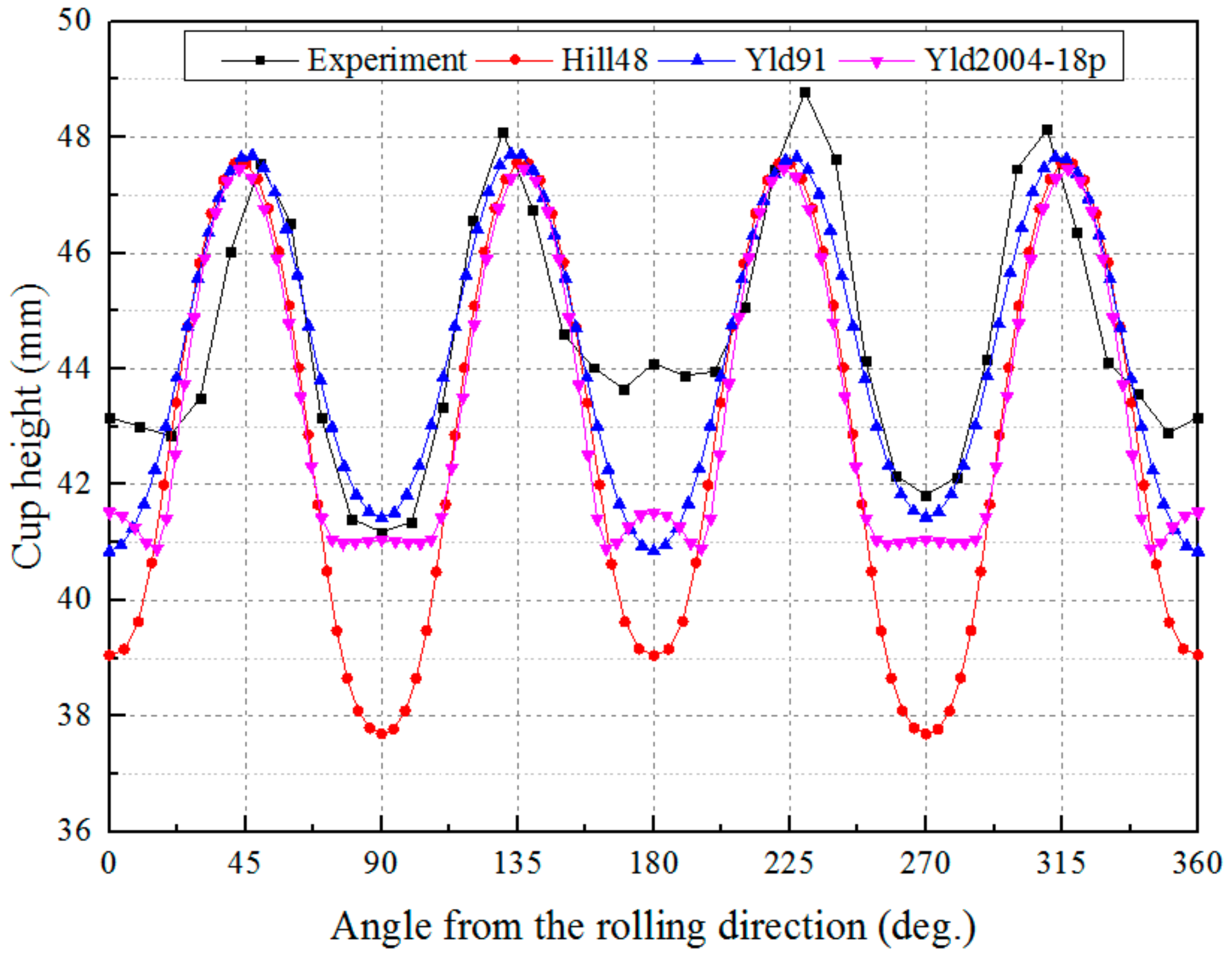
6.2. Earing Prediction for a Cylindrical Cup
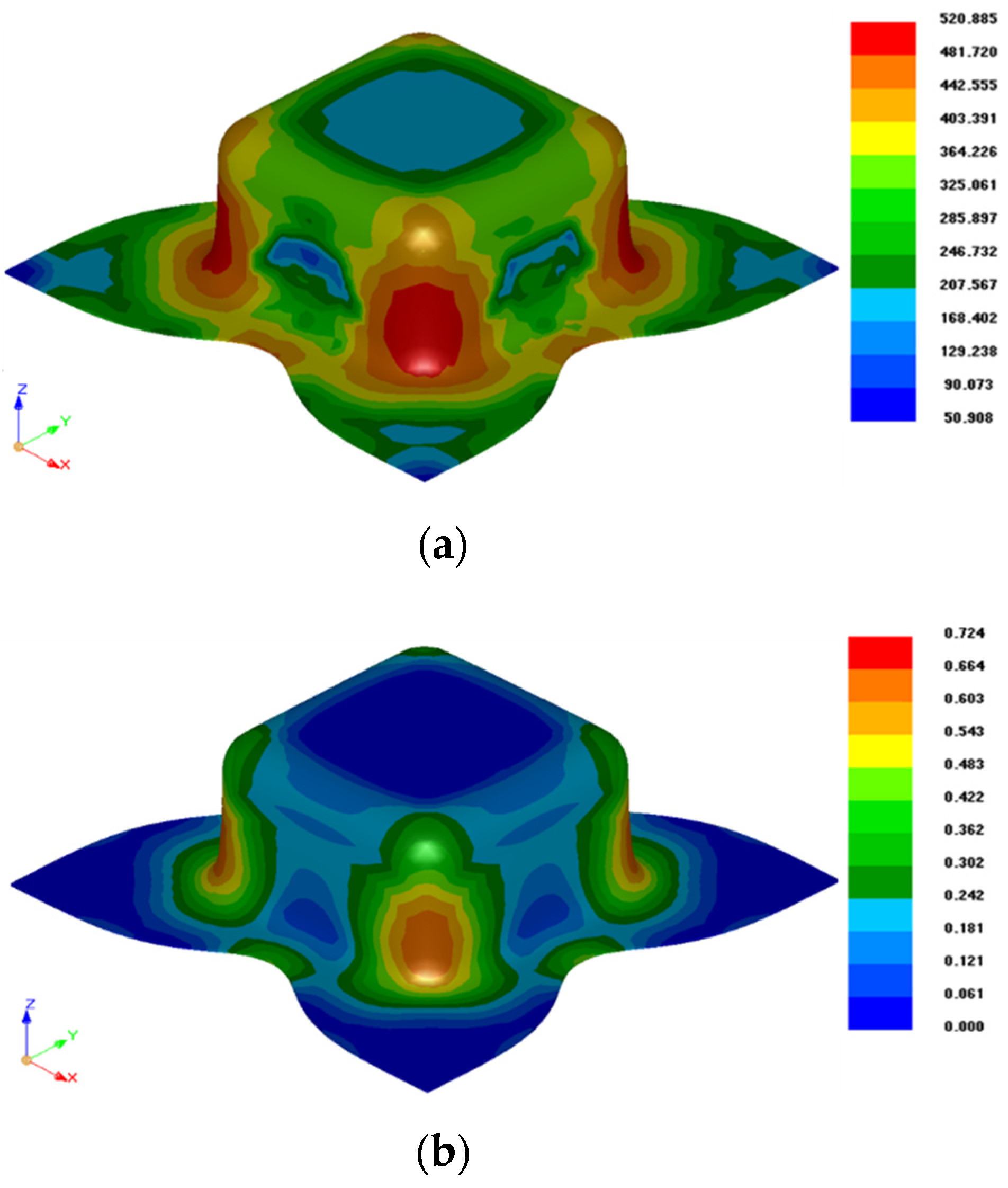
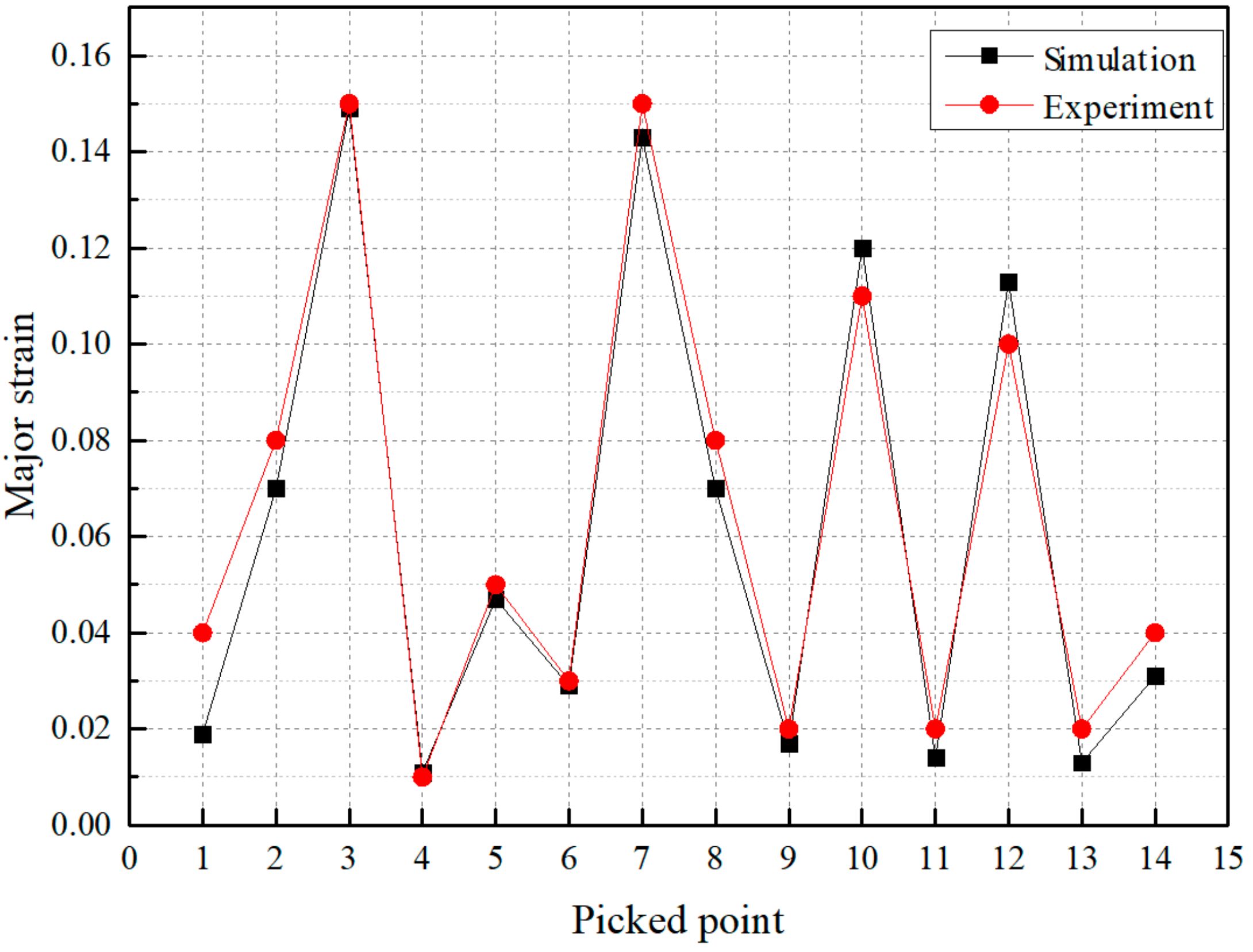
6.3. Drawing of an Automobile Component
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chalal, H.; Abed-Meraim, F. Simulation of structural applications and sheet metal forming processes based on quadratic solid–shell elements with explicit dynamic formulation. Int. J. Appl. Mech. 2019, 11, 1950082. [Google Scholar] [CrossRef]
- Antolin, P.; Kiendl, J.; Pingaro, M.; Reali, A. A simple and effective method based on strain projections to alleviate locking in isogeometric solid shells. Comput. Mech. 2020, 65, 1621–1631. [Google Scholar] [CrossRef]
- Alves De Sousa, R.J.; Cardoso, R.P.R.; Fontes Valente, R.A.; Yoon, J.; Grácio, J.J.; Natal Jorge, R.M. A new one-point quadrature enhanced assumed strain (EAS) solid-shell element with multiple integration points along thickness: Part I—geometrically linear applications. Int. J. Numer. Meth. Eng. 2005, 62, 952–977. [Google Scholar] [CrossRef]
- Simo, J.C.; Rifai, M.S. A class of mixed assumed strain methods and the method of incompatible modes. Int. J. Numer. Meth. Eng. 1990, 29, 1595–1638. [Google Scholar] [CrossRef]
- Su, Z.; Xue, P.; Tang, Y. An improved solid-shell element based on the computational condensation technique. Int. J. Mech. Sci. 2018, 141, 236–244. [Google Scholar] [CrossRef]
- Li, L.M.; Peng, Y.H.; Li, D.Y. A stabilized underintegrated enhanced assumed strain solid-shell element for geometrically nonlinear plate/shell analysis. Finite Elem. Anal. Des. 2011, 47, 511–518. [Google Scholar] [CrossRef]
- Mostafa, M.; Sivaselvan, M.V.; Felippa, C.A. A solid-shell corotational element based on ANDES, ANS and EAS for geometrically nonlinear structural analysis. Int. J. Numer. Meth. Eng. 2013, 95, 145–180. [Google Scholar] [CrossRef]
- Mostafa, M. An improved solid-shell element based on ANS and EAS concepts. Int. J. Numer. Meth. Eng. 2016, 108, 1362–1380. [Google Scholar] [CrossRef]
- Schwarze, M.; Reese, S. A reduced integration solid-shell finite element based on the EAS and the ANS concept—Geometrically linear problems. Int. J. Numer. Meth. Eng. 2009, 80, 1322–1355. [Google Scholar] [CrossRef]
- Cardoso, R.P.R.; Yoon, J.W.; Mahardika, M.; Choudhry, S.; Alves De Sousa, R.J.; Fontes Valente, R.A. Enhanced assumed strain (EAS) and assumed natural strain (ANS) methods for one-point quadrature solid-shell elements. Int. J. Numer. Meth. Eng. 2008, 75, 156–187. [Google Scholar] [CrossRef]
- Norachan, P.; Suthasupradit, S.; Kim, K. A co-rotational 8-node degenerated thin-walled element with assumed natural strain and enhanced assumed strain. Finite Elem. Anal. Des. 2012, 50, 70–85. [Google Scholar] [CrossRef]
- Schwarze, M.; Vladimirov, I.N.; Reese, S. Sheet metal forming and springback simulation by means of a new reduced integration solid-shell finite element technology. Comput. Method. Appl. Mech. Eng. 2011, 200, 454–476. [Google Scholar] [CrossRef]
- Schwarze, M.; Vladimirov, I.N.; Reese, S. A new continuum shell finite element for sheet metal forming applications. Int. J. Mater. Form. 2010, 3, 919–922. [Google Scholar] [CrossRef]
- Parente, M.P.L.; Fontes Valente, R.A.; Natal Jorge, R.M.; Cardoso, R.P.R.; Alves De Sousa, R.J. Sheet metal forming simulation using EAS solid-shell finite elements. Finite Elem. Anal. Des. 2006, 42, 1137–1149. [Google Scholar] [CrossRef]
- Wang, P.; Chalal, H.; Abed-Meraim, F. Quadratic solid–shell elements for nonlinear structural analysis and sheet metal forming simulation. Comput. Mech. 2017, 59, 161–186. [Google Scholar] [CrossRef]
- Mahmoud, M.; Bay, F.; Muñoz, D.P. An efficient multiphysics solid shell based finite element approach for modeling thin sheet metal forming processes. Finite Elem. Anal. Des. 2022, 198, 103645. [Google Scholar] [CrossRef]
- Mattern, S.; Schmied, C.; Schweizerhof, K. Highly efficient solid and solid-shell finite elements with mixed strain–displacement assumptions specifically set up for explicit dynamic simulations using symbolic programming. Comput. Struct. 2015, 154, 210–225. [Google Scholar] [CrossRef]
- Chen, T.C.; Hsu, C.M.; Wang, C.C. The deep drawing of a flanged square hole in thin stainless steel sheet. Metals 2021, 11, 1436. [Google Scholar] [CrossRef]
- Palmieri, M.E.; Lorusso, V.D.; Tricarico, L. Robust optimization and Kriging metamodeling of deep-drawing process to obtain a regulation curve of blank holder force. Metals 2021, 11, 319. [Google Scholar] [CrossRef]
- Xie, Q.; Sze, K.Y.; Zhou, Y.X. Drape simulation using solid-shell elements and adaptive mesh subdivision. Finite Elem. Anal. Des. 2015, 106, 85–102. [Google Scholar] [CrossRef][Green Version]
- de Sena, J.I.V.; Guzmán, C.F.; Duchêne, L.; Habraken, A.M.; Behera, A.K.; Duflou, J.; Valente, R.A.F.; de Sousa, R.J.A. Simulation of a two-slope pyramid made by SPIF using an adaptive remeshing method with solid-shell finite element. Int. J. Mater. Form. 2016, 9, 383–394. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Zhang, Z.; Zhong, W. A new reduced integration solid-shell element based on EAS and ANS with hourglass stabilization. Int. J. Numer. Meth. Eng. 2015, 104, 805–826. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. In Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences; The Royal Society: London, UK, 1948; Volume 193, pp. 281–297. [Google Scholar]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.E.; Brem, J.C.; Dick, R.E. Linear transfomation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Reese, S. A large deformation solid-shell concept based on reduced integration with hourglass stabilization. Int. J. Numer. Meth. Eng. 2007, 69, 1671–1716. [Google Scholar] [CrossRef]
- Recio, D.P.; Jorge, R.M.N.; Dinis, L.M.S. Locking and hourglass phenomena in an element-free Galerkin context: The B-bar method with stabilization and an enhanced strain method. Int. J. Numer. Meth. Eng. 2006, 68, 1329–1357. [Google Scholar] [CrossRef]
- Reese, S.; Rickelt, C. A model-adaptive hanging node concept based on a new non-linear solid-shell formulation. Comput. Methods Appl. Mech. Eng. 2007, 197, 61–79. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Taylor, Z.; Zienkiewicz, O.C. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Oxford, UK, 2013; p. 613. [Google Scholar]
- Dunne, F.; Petrinic, N. Introduction to Computational Plasticity; Oxford University Press: Demand, UK, 2005; pp. 20–23. [Google Scholar]
- Makinouchi, A., Nakamachi, E., Oñate, E., Wagoner, R.H., Eds.; Numisheet 1993. In Proceedings of the 2nd International Conference and Workshop on Numerical Simulation of 3D Sheet Forming Processes—Verification of Simulation with Experiment, Isehara, Japan, 31 August–2 September 1993. [Google Scholar]
- Danckert, J. Experimental investigation of a square-cup deep-drawing process. J. Mater. Process. Technol. 1995, 50, 375–384. [Google Scholar] [CrossRef]
- Yoon, J.; Barlat, F.; Dick, R.; Karabin, M. Prediction of six or eight ears in a drawn cup based on a new anisotropic yield function. Int. J. Plast. 2006, 22, 174–193. [Google Scholar] [CrossRef]
- Alves De Sousa, R.J.; Yoon, J.W.; Cardoso, R.P.R.; Fontes Valente, R.A.; Grácio, J.J. On the use of a reduced enhanced solid-shell (RESS) element for sheet forming simulations. Int. J. Plast. 2007, 23, 490–515. [Google Scholar] [CrossRef]






| Min. experiment | 26.75 | 26.75 | 14.60 |
| Max. experiment | 29.60 | 29.58 | 16.31 |
| 35 × 35 mesh with subdivision | 27.93 | 27.73 | 15.20 |
| 70 × 70 mesh | 29.22 | 29.21 | 16.02 |
| Hill48 r-Values | |||||||||
| 0.2115 | 1.5769 | 0.6923 | |||||||
| Yld91 Coefficients | |||||||||
| 1.0674 | 0.8559 | 1.1296 | 1.2970 | 1.0000 | 1.0000 | 8 | |||
| Yld2004-18p Coefficients | |||||||||
| −0.0698 | 0.9364 | 0.0791 | 1.0030 | 0.5247 | 1.3631 | 0.9543 | 1.0237 | 1.0690 | 8 |
| 0.9811 | 0.4767 | 0.5753 | 0.8668 | 1.1450 | −0.0792 | 1.4046 | 1.0516 | 1.1471 | |
| Experimental Data (MPa) | ||||||
| 99.0 | 100.5 | 102.5 | 98.9 | |||
| Yld91 coefficients | ||||||
| 0.9669 | 1.0342 | 0.9648 | 0.9797 | 1.0000 | 1.0000 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.-M.; Yi, Z.-W.; Liu, Y.-Q.; Tang, X.-F.; Jiang, W.; Li, H.-J. Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements. Metals 2022, 12, 52. https://doi.org/10.3390/met12010052
Li Q-M, Yi Z-W, Liu Y-Q, Tang X-F, Jiang W, Li H-J. Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements. Metals. 2022; 12(1):52. https://doi.org/10.3390/met12010052
Chicago/Turabian StyleLi, Qiao-Min, Zhao-Wei Yi, Yu-Qi Liu, Xue-Feng Tang, Wei Jiang, and Hong-Jun Li. 2022. "Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements" Metals 12, no. 1: 52. https://doi.org/10.3390/met12010052
APA StyleLi, Q.-M., Yi, Z.-W., Liu, Y.-Q., Tang, X.-F., Jiang, W., & Li, H.-J. (2022). Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements. Metals, 12(1), 52. https://doi.org/10.3390/met12010052






