Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Parameters
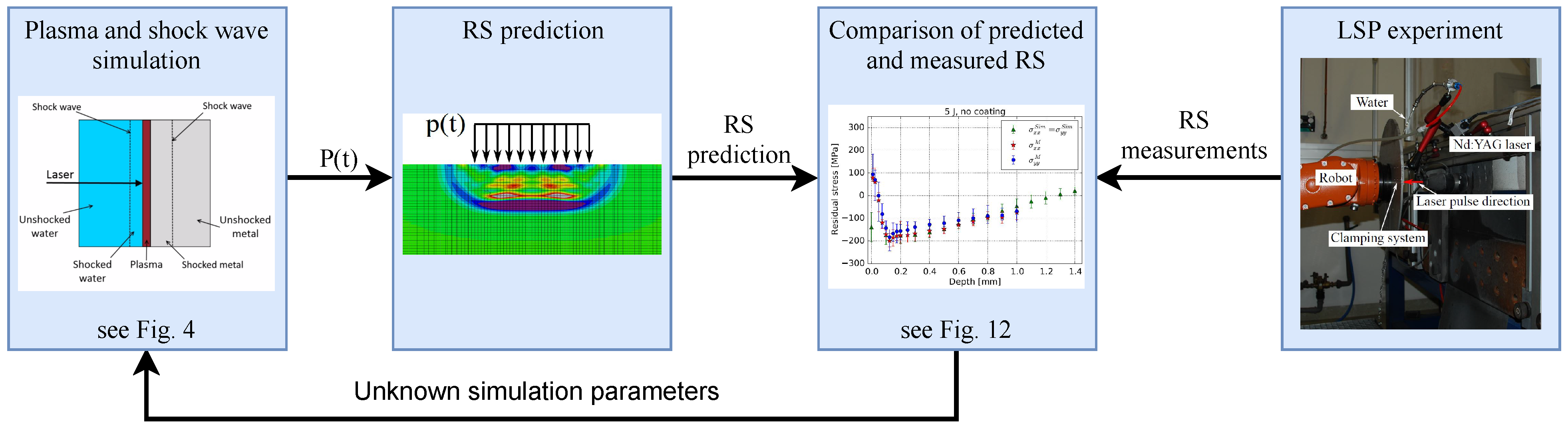
2.2. Simulation Scheme
2.2.1. Global LSP Model
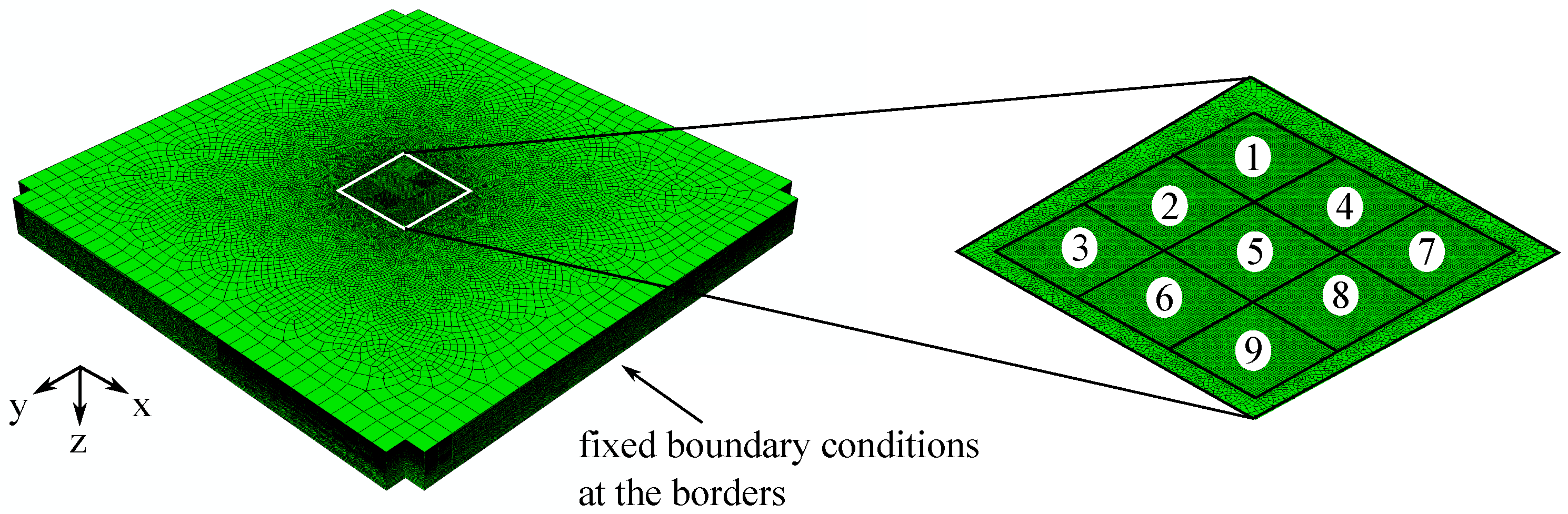
2.2.2. Finite Element Model
2.3. Model Analysis
2.3.1. Sensitivity Study
2.3.2. Residual Stress Prediction
2.3.3. Parameter Identification
3. Results and Discussion
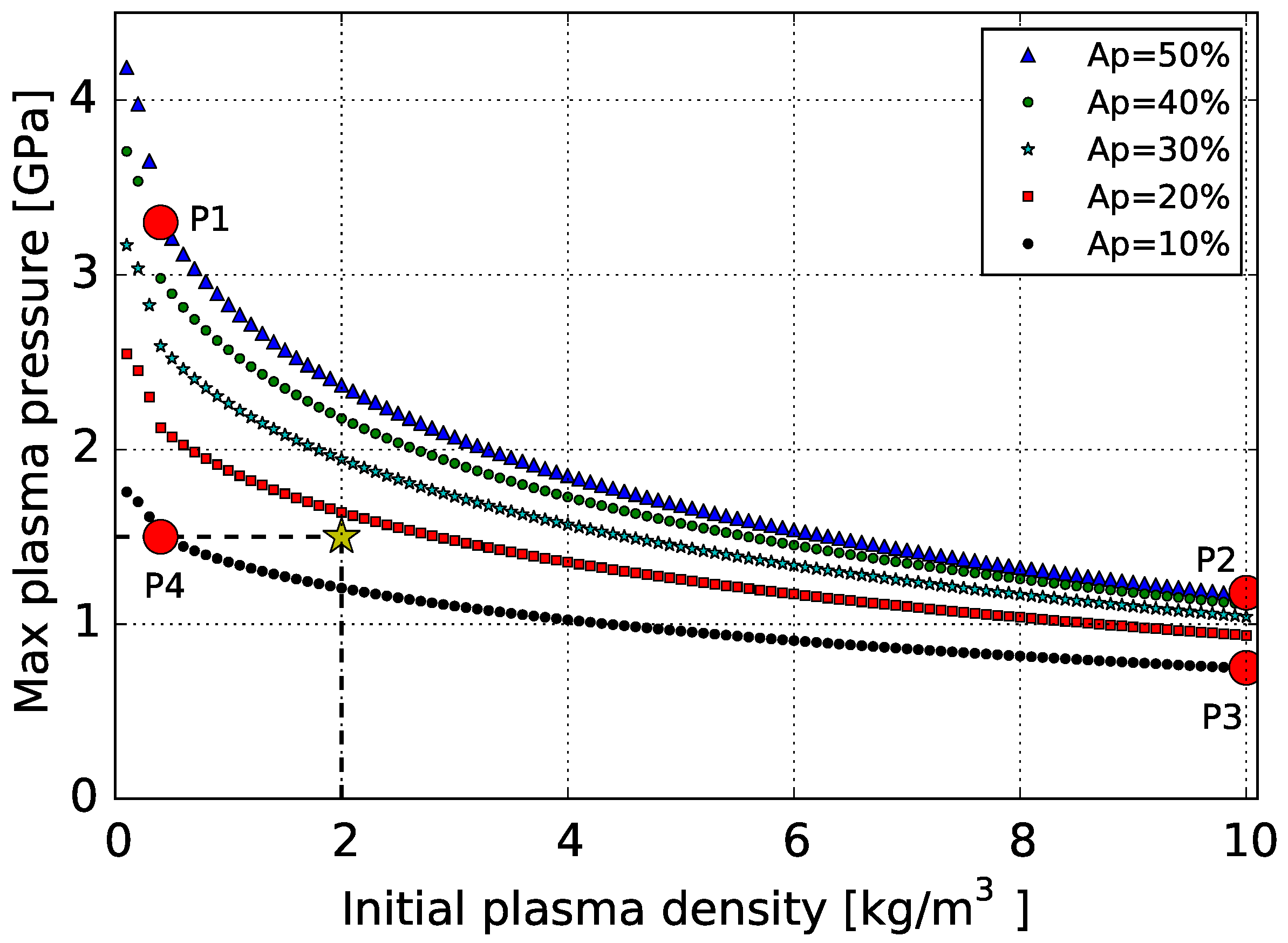
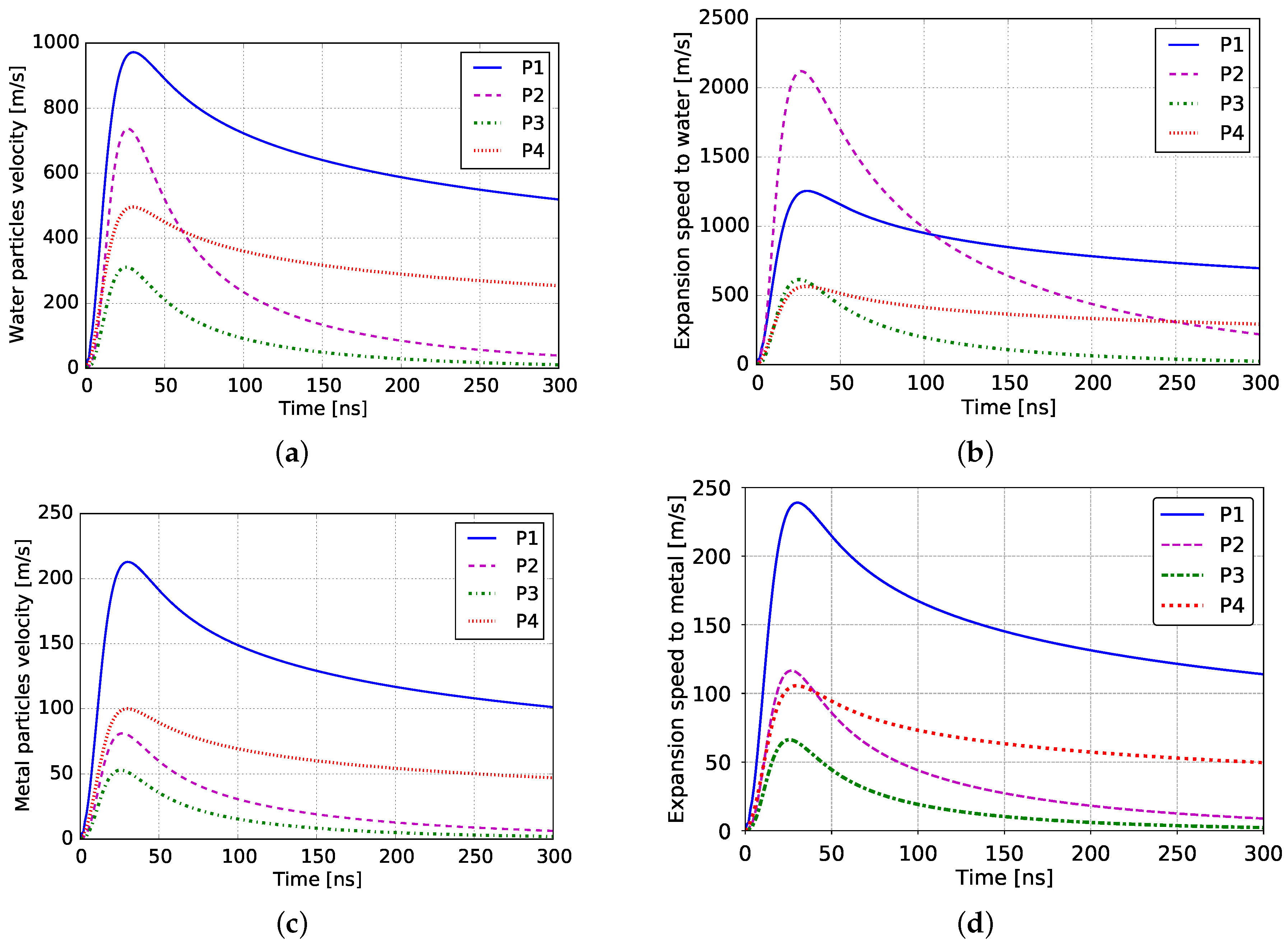
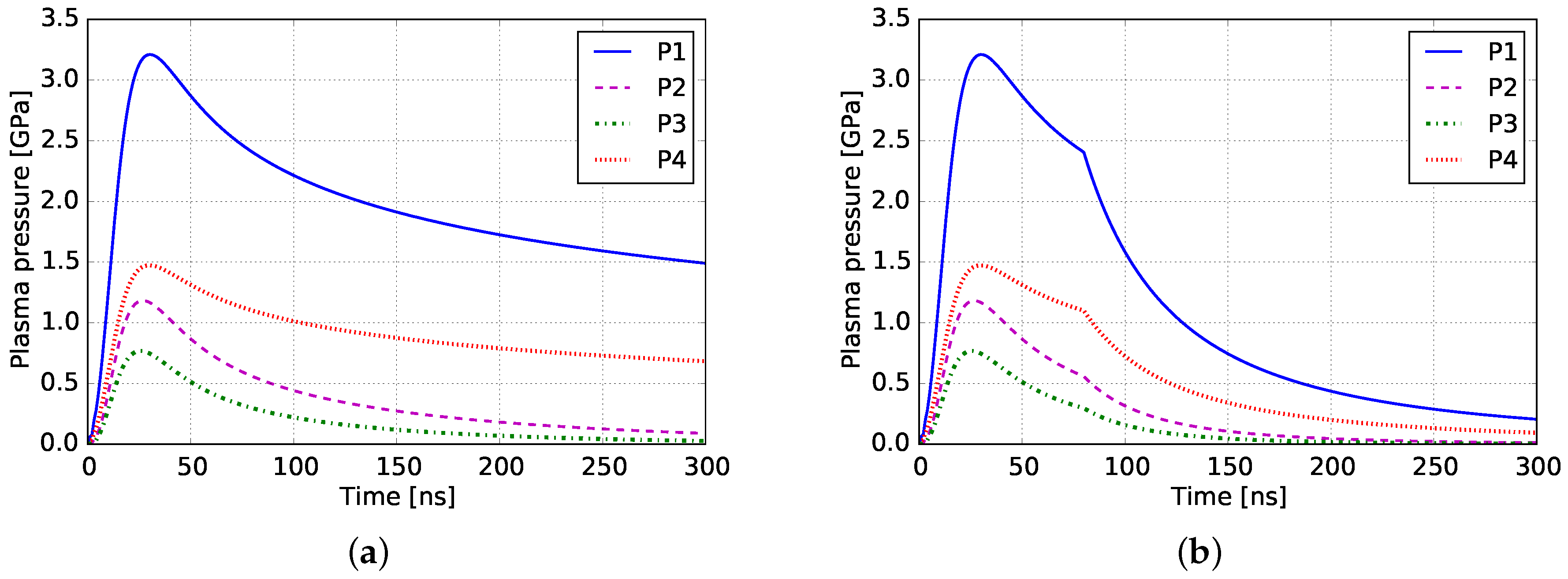
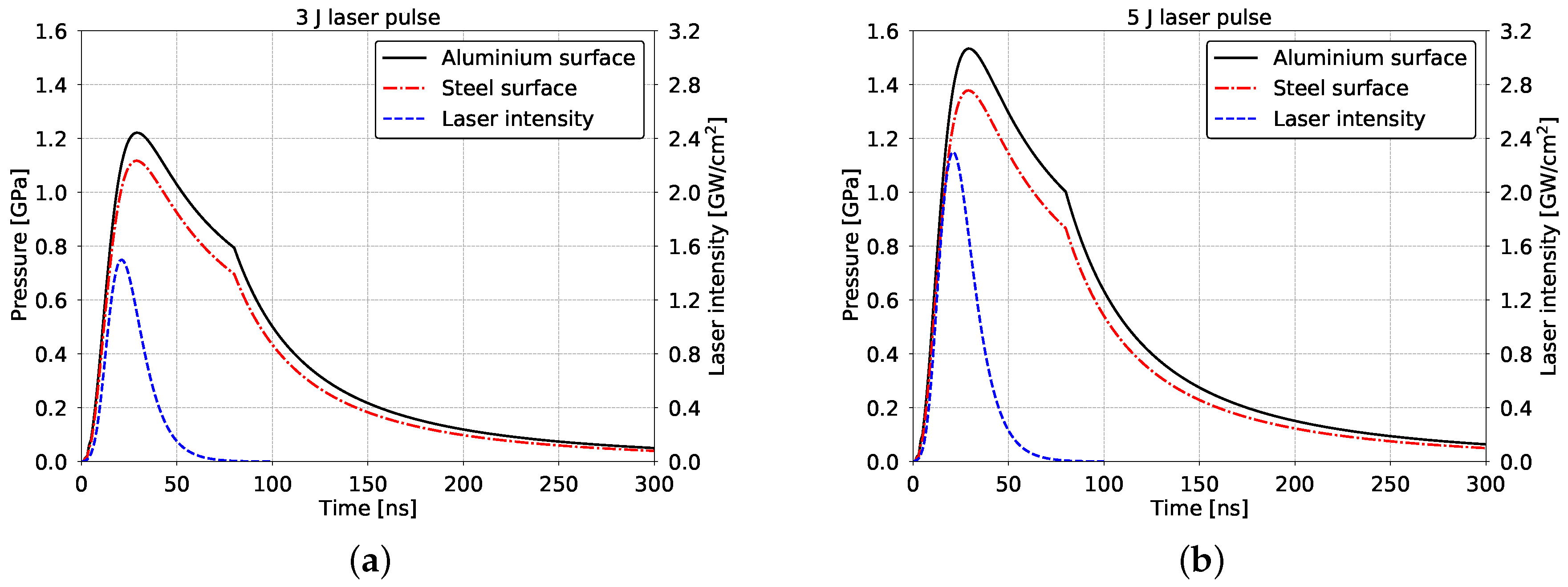
3.1. Pressure Profiles
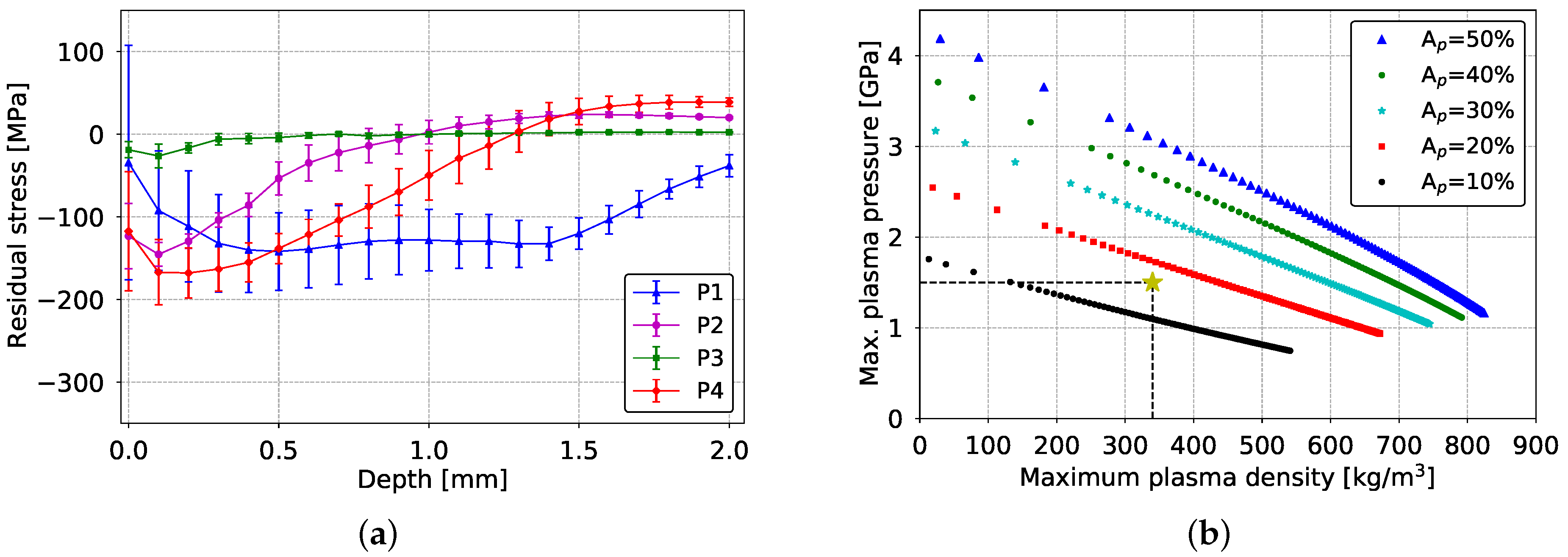
3.2. Residual Stresses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | yield strength |
| coefficient of laser absorption by the plasma | |
| B | strengthening coefficient |
| mass flow | |
| C | rate dependency of the material |
| D | shock wave velocity |
| E | internal energy |
| Young’s modulus | |
| energy exchange through mass flows | |
| kinetic plasma energy | |
| total plasma energy | |
| F | laser focus size |
| I | laser intensity |
| peak of laser intensity | |
| L | plasma thickness |
| P | pressure |
| maximum plasma pressure | |
| Q | specific phase change energy |
| S | empiric parameters, which connect shock and particle velocities |
| T | laser pulse FWHM |
| total pulse duration | |
| U | particles velocity |
| expansion velocity of plasma in metal direction | |
| expansion velocity of plasma in water direction | |
| velocity of sound | |
| work done by plasma | |
| specific heat ratio | |
| plastic strain | |
| plastic strain rate | |
| reference plastic strain rate | |
| Poisson’s ratio | |
| n | strain hardening exponent |
| mass density | |
| maximum plasma density | |
| yield stress | |
| measured residual stress in xx-direction | |
| measured residual stress in yy-direction | |
| calculated residual stress in xx-direction | |
| calculated residual stress in yy-direction | |
| t | time |
| FE | finite element |
| FWHM | full-width-at-half-maximum |
| ICF | inertial confinement fusion |
| LSP | laser shock peening |
| RS | residual stress |
| Subscript ’m’ | metal region |
| Subscript ’0’ | unshocked region |
| Subscript ’p’ | plasma region |
| Subscript ’w’ | water region |
References
- Vilhauer, B.; Bennett, C.R.; Matamoros, A.B.; Rolfe, S.T. Fatigue behavior of welded coverplates treated with Ultrasonic Impact Treatment and bolting. Eng. Struct. 2012, 34, 163–172. [Google Scholar] [CrossRef]
- Hatamleh, O. A comprehensive investigation on the effects of laser and shot peening on fatigue crack growth in friction stir welded AA 2195 joints. Int. J. Fatigue 2009, 31, 974–988. [Google Scholar] [CrossRef]
- Gujba, A.K.; Medraj, M. Laser Peening Process and Its Impact on Materials Properties in Comparison with Shot Peening and Ultrasonic Impact Peening. Materials 2014, 7, 7925–7974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, J.; Jiao, X.; Zhou, C.; Gao, H. Applications of Underwater Laser Peening in Nuclear Power Plant Maintenance. Energy Procedia 2012, 16, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Colon, C.; de Andres-Garcia, M.I.; Moreno-Diaz, C.; Alonso-Medina, A.; Porro, J.A.; Angulo, I.; Ocana, J.L. Experimental Determination of Electronic Density and Temperature in Water-Confined Plasmas Generated by Laser Shock Processing. Metals 2019, 9, 808. [Google Scholar] [CrossRef] [Green Version]
- Radziejewska, J.; Strzelec, M.; Ostrowski, R.; Sarzyński, A. Experimental investigation of shock wave pressure induced by a ns laser pulse under varying confined regimes. Opt. Laser Eng. 2020, 126, 105913. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Berthe, L.; Dubouchet, C. Laser shock processing of materials, physical processes involved and examples of applications. J. Laser Appl. 1996, 8, 135. [Google Scholar] [CrossRef]
- Askaryan, G.A.; Moroz, E.M. Pressure on evaporation of matter in a radiation beam. JETP Lett. 1963, 16, 1638. [Google Scholar]
- White, R.M. Elastic Wave Generation by Electron Bombardment or Electromagnetic Wave Absorption. J. Appl. Phys. 1963, 34, 2123–2124. [Google Scholar] [CrossRef]
- Lindl, J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 1995, 2, 3933–4024. [Google Scholar] [CrossRef] [Green Version]
- Moscicki, T.; Hoffman, J.; Szymanski, Z. Modelling of plasma formation during nanosecond laser ablation. Arch. Mech. 2011, 63, 99–116. [Google Scholar]
- Anderholm, N.C. Laser-generated stress waves. Appl. Phys. Lett. 1970, 16, 113–115. [Google Scholar]
- O’Keefe, J.D.; Skeen, C.H.; York, C.M. Laser-induced deformation modes in thin metal targets. J. Appl. Phys. 1973, 44, 4622–4626. [Google Scholar] [CrossRef]
- Fairand, B.P.; Clauer, A.H.; Jung, R.G.; Wilcox, B.A. Quantitative assessment of laser-induced stress waves generated at confined surfaces. Appl. Phys. Lett. 1974, 25, 431–433. [Google Scholar] [CrossRef]
- Warren, A.W.; Guo, Y.B.; Chen, S.C. Massive parallel laser shock peening: Simulation, analysis, and validation. Int. J. Fatigue 2008, 30, 188–197. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Z.; Hu, J. 3-D FEM simulation of laser shock processing. Surf. Coat. Technol. 2006, 201, 1426–1435. [Google Scholar] [CrossRef]
- Golabi, S.; Vakil, M.R.; Amirsalari, B. Multi-Objective Optimization of Residual Stress and Cost in Laser Shock Peening Process Using Finite Element Analysis and PSO Algorithm. Lasers Manuf. Mater. Process. 2019, 6, 398–423. [Google Scholar] [CrossRef]
- Braisted, W.; Brockman, R. Finite element simulation of laser shock peening. Int. J. Fatigue 1999, 21, 719–724. [Google Scholar] [CrossRef]
- Zhai, P.; Dong, Z.; Miao, R.; Deng, X.; Chen, L. Investigation on the laser-induced shock pressure with condensed matter model. J. Appl. Phys. 2015, 54, 056203. [Google Scholar] [CrossRef]
- Wei, X.L.; Ling, X. Numerical modeling of residual stress induced by laser shock processing. Appl. Surf. Sci. 2014, 301, 557–563. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, Y.J.; Lee, J.W.; Yoo, S.H. Study on effect of time parameters of laser shock peening on residual stresses using FE simulation. J. Mech. Sci. Technol. 2014, 28, 1803–1810. [Google Scholar] [CrossRef]
- Ding, K.; Ye, L. Simulation of multiple laser shock peening of a 35CD4 steel alloy. J. Mater. Process. Technol. 2006, 178, 162–169. [Google Scholar] [CrossRef]
- Yang, C.; Hodgson, P.D.; Liu, Q.; Ye, L. Geometrical effects on residual stresses in 7050-T7451 aluminum alloy rods subject to laser shock peening. J. Mater. Process. Technol. 2008, 201, 303–309. [Google Scholar] [CrossRef]
- Wang, X.; Xia, W.; Wu, X.; Huang, C. Scaling Law in Laser-Induced Shock Effects of NiTi Shape Memory Alloy. Metals 2018, 8, 174. [Google Scholar] [CrossRef]
- Kumar, G.R.; Rajyalakshmi, G. Modelling and multi objective optimization of laser peening process using Taguchi utility concept. IOP Conf. Ser. Mater. Sci. Eng. 2017, 263, 062055. [Google Scholar] [CrossRef]
- Jiang, X.; Yu, X.; Deng, X.; Shao, Y.; Peng, P. Investigation on Laser-Induced Shock Pressure with Condensed Matter Model and Experimental Verification. Exp. Tech. 2019, 43, 161–167. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J.; Ballard, P.; Devaux, D.; Virmont, J. Physical study of laser-produced plasma in confined geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y.C. A self-closed thermal model for laser shock peening under the water confinement regime configuration and comparisons to experiments. J. Appl. Phys. 2005, 97, 113517. [Google Scholar] [CrossRef]
- Morales, M.; Porro, J.A.; Blasco, M.; Molpeceres, C.; Ocana, J.L. Numerical simulation of plasma dynamics in laser shock processing experiments. Appl. Surf. Sci. 2009, 255, 5181–5185. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, Y.L.; Noyan, I.C. Microscale Laser Shock Peening of Thin Films, Part 1: Experiment, Modeling and Simulation. J. Manuf. Sci. Eng. 2004, 126, 10–17. [Google Scholar] [CrossRef]
- Pirri, A.N.; Root, R.G. Plasma Energy Transfer to Metal Surfaces Irradiated by Pulsed Lasers. AIAA J. 1978, 16, 1296–1304. [Google Scholar] [CrossRef]
- Fortunato, A.; Orazi, L.; Cuccolini, G.; Ascari, A. Laser shock peening and warm laser shock peening: Process modeling and pulse shape influence. Proc. SPIE 1978, 8603, 86030G. [Google Scholar]
- Sinha, S. Nanosecond laser ablation of graphite: A thermal model based simulation. J. Laser Appl. 2018, 30, 012008. [Google Scholar] [CrossRef]
- MacFarlane, J.J.; Golovkin, I.E.; Woodruff, P.R. HELIOS-CR—A 1-D radiation-magnetohydrodynamics code with inline atomic kinetics modeling. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 381–397. [Google Scholar] [CrossRef] [Green Version]
- Lyon, S.P.; Johnson, J.D. SESAME: The Los Alamos National Laboratory Equation of State Database; Technical Report, LA-UR-92-3407; Los Alamos National Laboratory: Los Alamos, NM, USA, 1992.
- Bhamare, S.; Ramakrishnan, G.; Mannava, S.R.; Langer, K.; Vasudevan, V.K.; Qian, D. Simulation-based optimization of laser shock peening process for improved bending fatigue life of Ti–6Al–2Sn–4Zr–2Mo alloy. Surf. Coat. Technol. 2013, 232, 464–474. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Merrien, P.; Lieurade, H.P. Laser shock processing of aluminium alloys. Application to high cycle fatigue behaviour. Mater. Sci. Eng. 1996, 210, 102–113. [Google Scholar] [CrossRef]
- Amarchinta, H.K.; Grandhi, R.V.; Clauer, A.H.; Langer, K.; Stargel, D.S. Simulation of residual stress induced by a laser peening process through inverse optimization of material models. J. Mater. Process. Technol. 2010, 210, 1997–2006. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates, and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Langer, K.; Olson, S.; Brockman, R.; Braisted, W.; Spradlin, T.; Fitzpatrick, M.E. High Strain-Rate Material Model Validation for Laser Peening Simulation. J. Eng. 2015, 2015, 150–157. [Google Scholar] [CrossRef]
- Keller, S.; Chupakhin, S.; Staron, P.; Maawad, E.; Kashaev, N.; Klusemann, B. Experimental and numerical investigation of residual stresses in laser shock peened AA2198. J. Mater. Process. Technol. 2018, 255, 294–307. [Google Scholar] [CrossRef]
- Schajer, G.S. Advances in hole-drilling residual stress measurements. Exp. Mech. 2010, 50, 159–168. [Google Scholar] [CrossRef]
- Meyers, M. Shock Waves and High-Strain-Rate Phenomena in Metals; Springer: Boston, MA, USA, 1981; pp. 1033–1049. [Google Scholar]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov (accessed on 1 June 2019).
- Material Property Data. Available online: http://www.matweb.com (accessed on 1 June 2019).
- Liley, P.E. Thermophysical Properties of Fluids. In Mechanical Engineers Handbook: Energy and Power, 3rd ed.; Kutz, M., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; Volume 4, pp. 1–45. [Google Scholar]
- Leitner, M.; Leitner, T.; Schmon, A.; Aziz, K.; Pottlacher, G. Thermophysical Properties of Liquid Aluminum. Metall. Mater. Trans. A 2017, 48, 3036–3045. [Google Scholar] [CrossRef] [Green Version]
- Simons, G.A. Momentum Transfer to a Surface When Irradiated by a High-Power Laser. AIAA J. 1984, 22, 1275–1280. [Google Scholar] [CrossRef]
- Sticchi, M.; Staron, P.; Sano, Y.; Meixer, M.; Klaus, M.; Rebelo-Kornmeier, J.; Huber, N.; Kashaev, N. A parametric study of laser spot size and coverage on the laser shock peening induced residual stress in thin aluminium samples. J. Eng. 2015, 2015, 97–105. [Google Scholar] [CrossRef]
- Ready, J.F. Effects of High-Power Laser Radiation; Academic: London, UK, 1971. [Google Scholar]
- Mahdavi, M.; Ghazizadeh, S.F. Linear absorption mechanisms in laser plasma interactions. J. Appl. Sci. 2012, 12, 12–21. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, Y.L. Modeling and Simulation Improvement in Laser Shock Processing. In Proceedings of the ICALEO 2001 Congress, Jacksonville, FL, USA, 15–18 October 2001; pp. 59–68. [Google Scholar]
- Rubio-Gonzalez, C.; Gomez-Rosas, G.; Ocana, J.; Molpeceres, C.; Banderas, A.; Porro, J.; Morales, M. Effect of an absorbent overlay on the residual stress field induced by laser shock processing on aluminum samples. Appl. Surf. Sci. 2006, 252, 6201–6205. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Ren, X.D.; Zhang, Y.K.; Zhou, J.Z.; Zhang, X.Q. Coating Influence on Residual Stress in Laser Shock Processing. Key Eng. Mater. 2007, 353–358, 1753–1756. [Google Scholar] [CrossRef]
- Kallien, Z.; Keller, S.; Ventzke, V.; Kashaev, N.; Klusemann, B. Effect of laser peening process parameters and sequences on residual stress profiles. Metals 2019, 9, 655. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Water | Aluminum | Steel |
|---|---|---|---|
| Density , | 1000 | 2800 | 7900 |
| Sound velocity [43], m/s | 2393 | 5328 | - |
| Coefficient S [43] | 1.333 | 1.338 | - |
| Specific phase change energy Q [44,45,46,47], | ≈3 | ≈15 | ≈9 |
| Parameter | AA2198-T3 |
|---|---|
| Young’s modulus , GPa | 78 |
| Poisson’s ratio | 0.33 |
| Quasi-static yield strength A, MPa | 310 |
| Strengthening coefficient B, MPa | 1177 |
| Strain hardening exponent n | 0.894 |
| Reference plastic strain rate , s | 1.8 |
| Dynamic strain hardening coefficient C | 0.01 |
| Parameter | Initial Value |
|---|---|
| Expansion velocities and , m/s | 0 |
| Plasma density , kg/m | 0.1–10 |
| Plasma pressure , Pa | |
| Absorption coefficient | 10–50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozdnyakov, V.; Keller, S.; Kashaev, N.; Klusemann, B.; Oberrath, J. Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction. Metals 2022, 12, 107. https://doi.org/10.3390/met12010107
Pozdnyakov V, Keller S, Kashaev N, Klusemann B, Oberrath J. Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction. Metals. 2022; 12(1):107. https://doi.org/10.3390/met12010107
Chicago/Turabian StylePozdnyakov, Vasily, Sören Keller, Nikolai Kashaev, Benjamin Klusemann, and Jens Oberrath. 2022. "Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction" Metals 12, no. 1: 107. https://doi.org/10.3390/met12010107
APA StylePozdnyakov, V., Keller, S., Kashaev, N., Klusemann, B., & Oberrath, J. (2022). Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction. Metals, 12(1), 107. https://doi.org/10.3390/met12010107








