Vibration Characteristics of Hot Rolling Mill Rolls Based on Elastoplastic Hysteretic Deformation
Abstract
1. Introduction
2. Modeling of Dynamic Rolling Force with Hysteresis
2.1. Rolling Force Fp in the Plastic Zone
2.2. Rolling Force Fe in the Elastic Zone
2.3. Total Rolling Force F
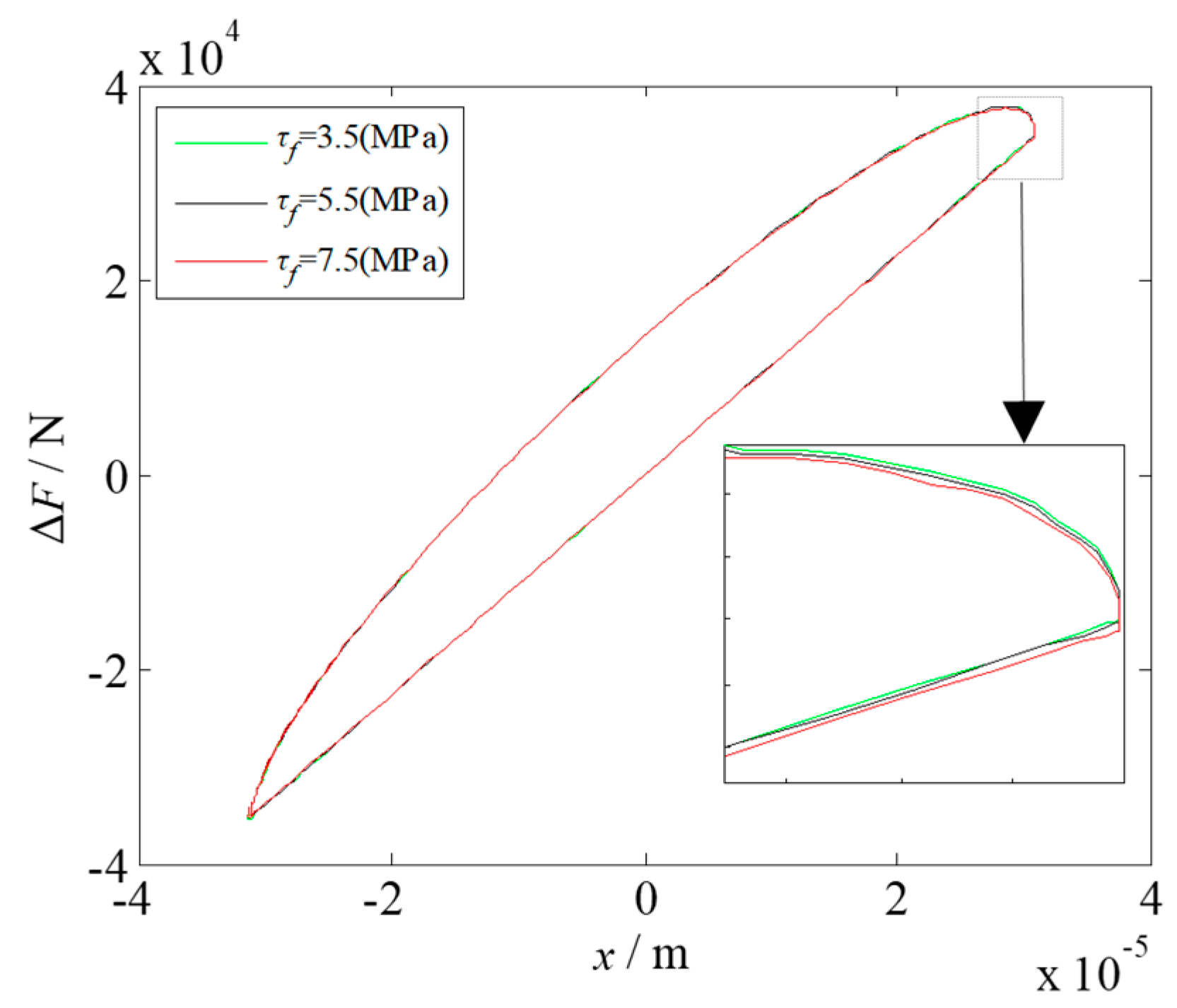
2.4. Effect of Rolling Parameters on Dynamic Rolling Force ΔF
3. Hysteresis Nonlinear Dynamic Modeling of Hot Rolling Mills
4. Amplitude-Frequency Characteristics of the Vertical Vibration System of the Hot Rolling Mill
4.1. Solution of the Subharmonic Resonance Response
4.2. Solution of Internal Resonance Response
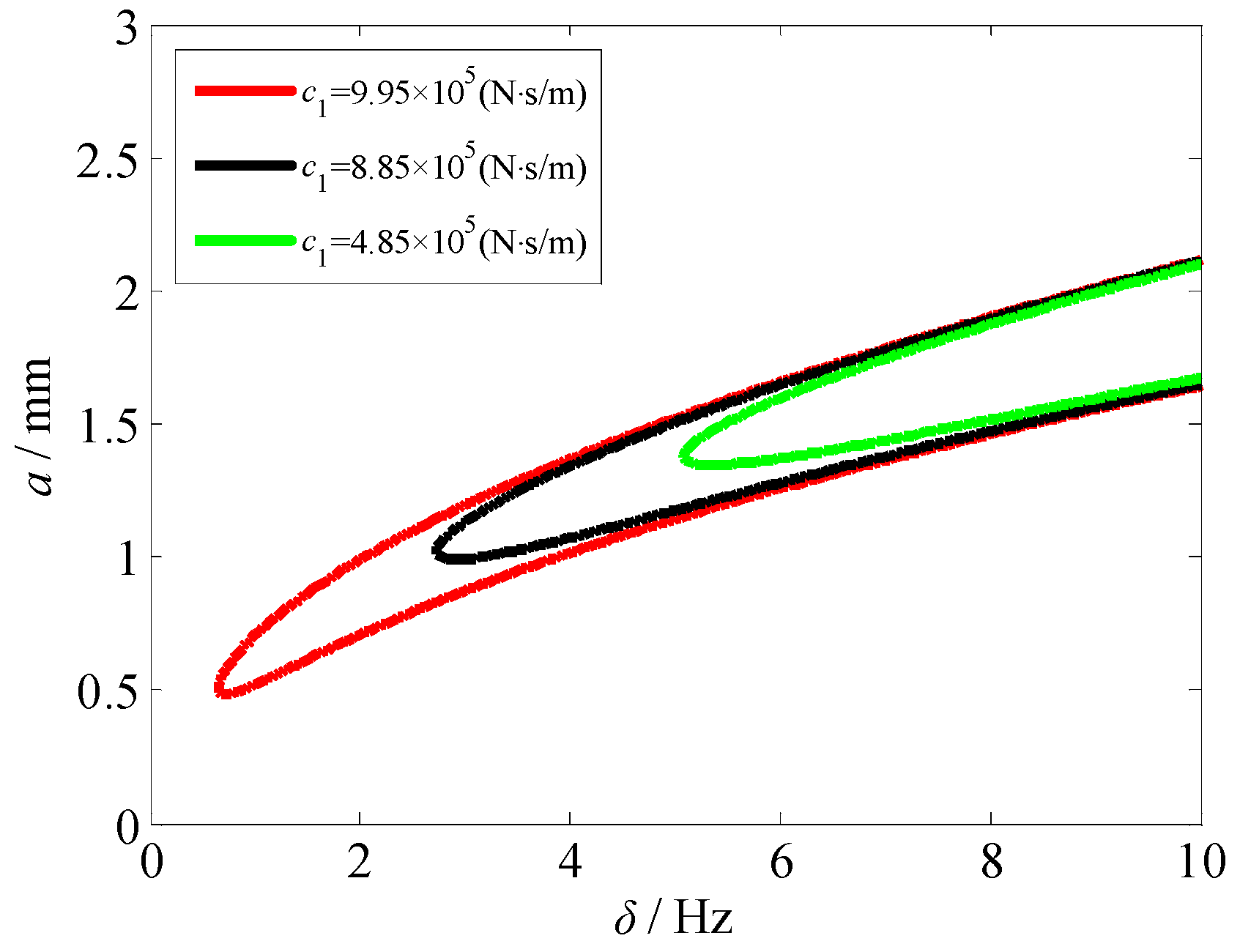
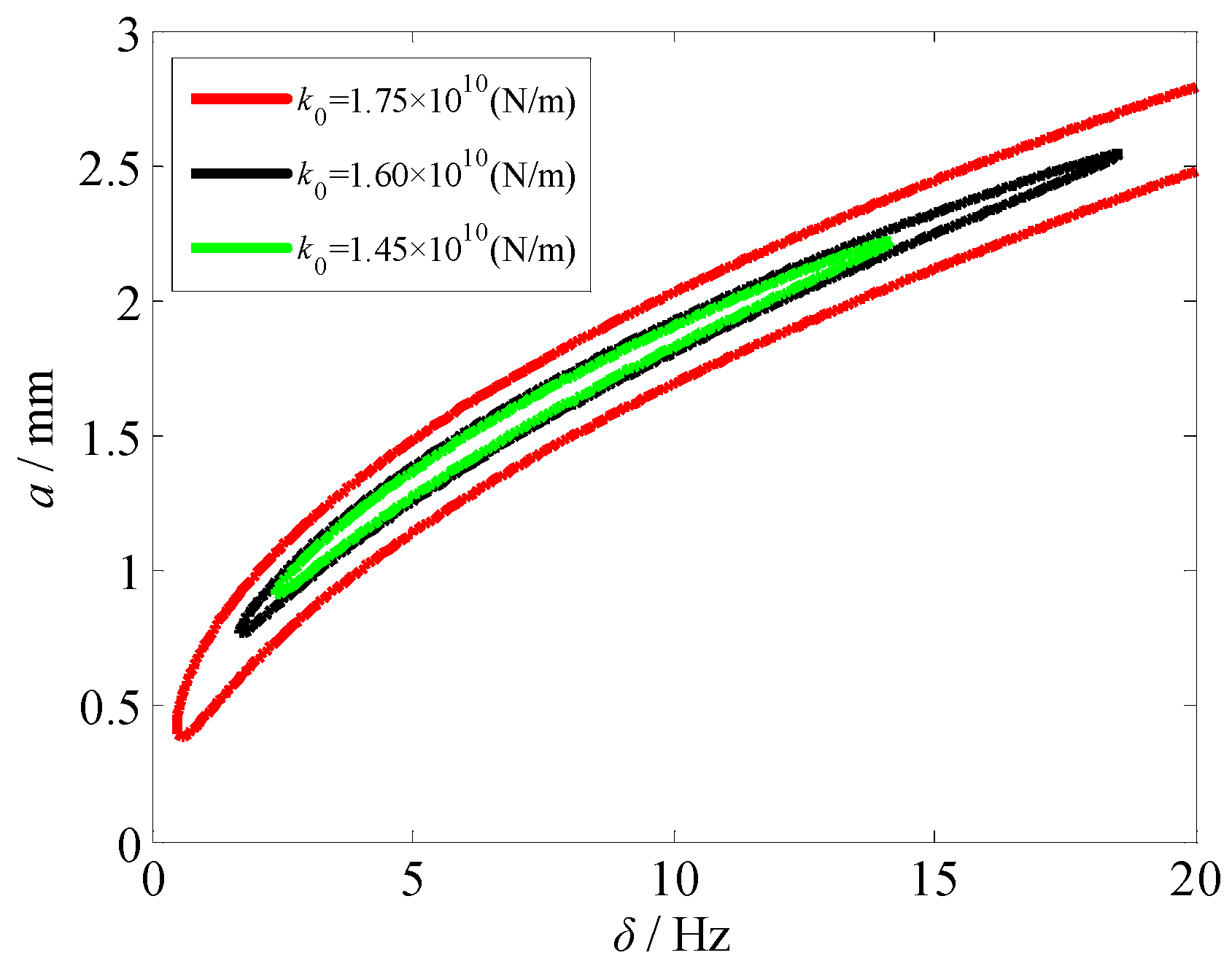
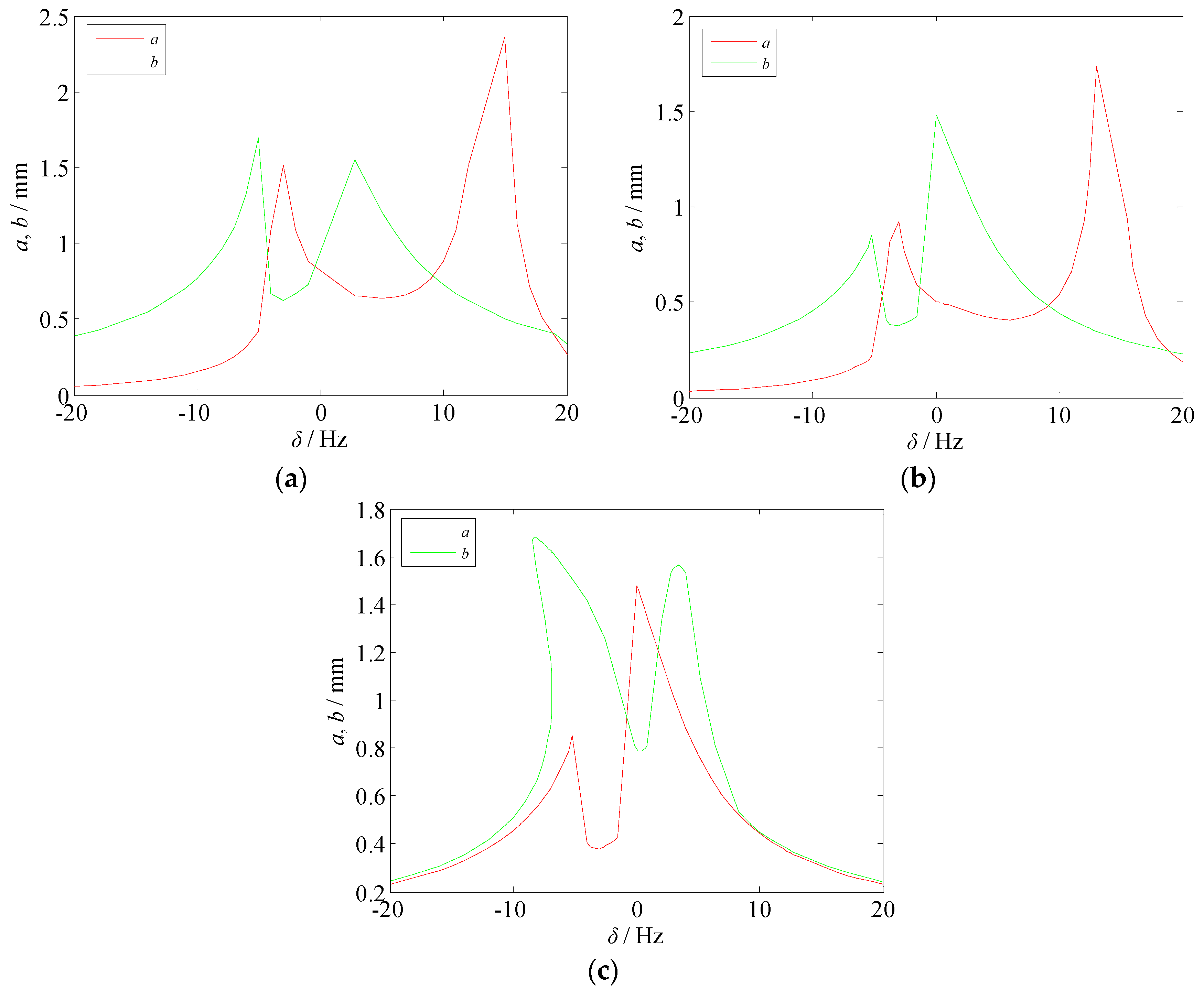
4.3. Amplitude-Frequency Characteristics of the Subharmonic and Internal Resonances of the Rolling Mill Rolls
- When vibration occurs, there will be two vibration regions on the vibration curve of the work and backup rolls. This is because the internal resonance of the rolling mill roll occurs at this time. Moreover, we verified that the resonance relationships ω1 = ω2 + εδ1 and ω = 2ω1 + εδ are correct.
- Comparing the two curves in each image, it can be found that the vibration amplitude of the work and backup rolls alternately increase or decrease, and the vibration energy is constantly exchanged between the work and backup rolls, which is one of the unique phenomena of the internal resonance.
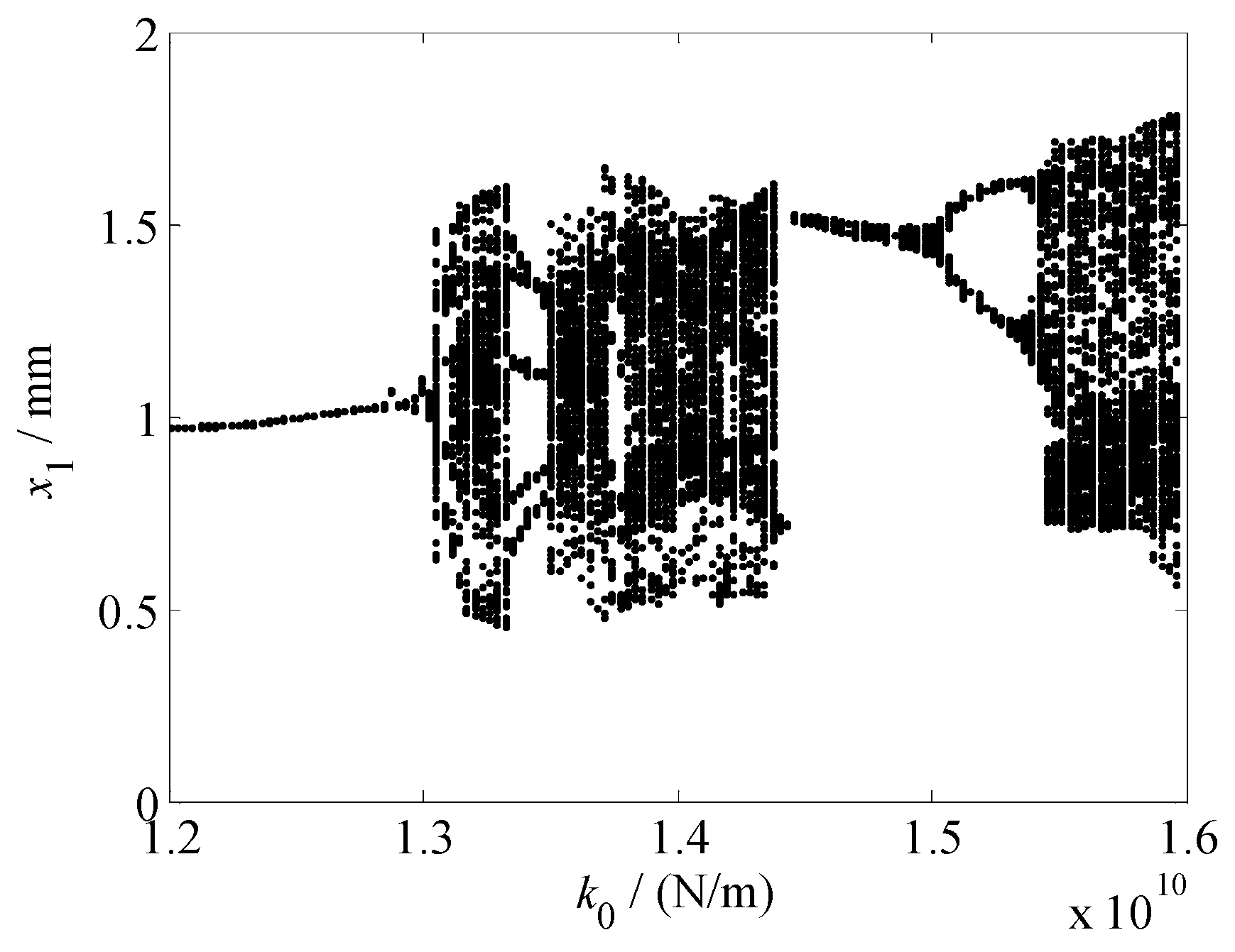
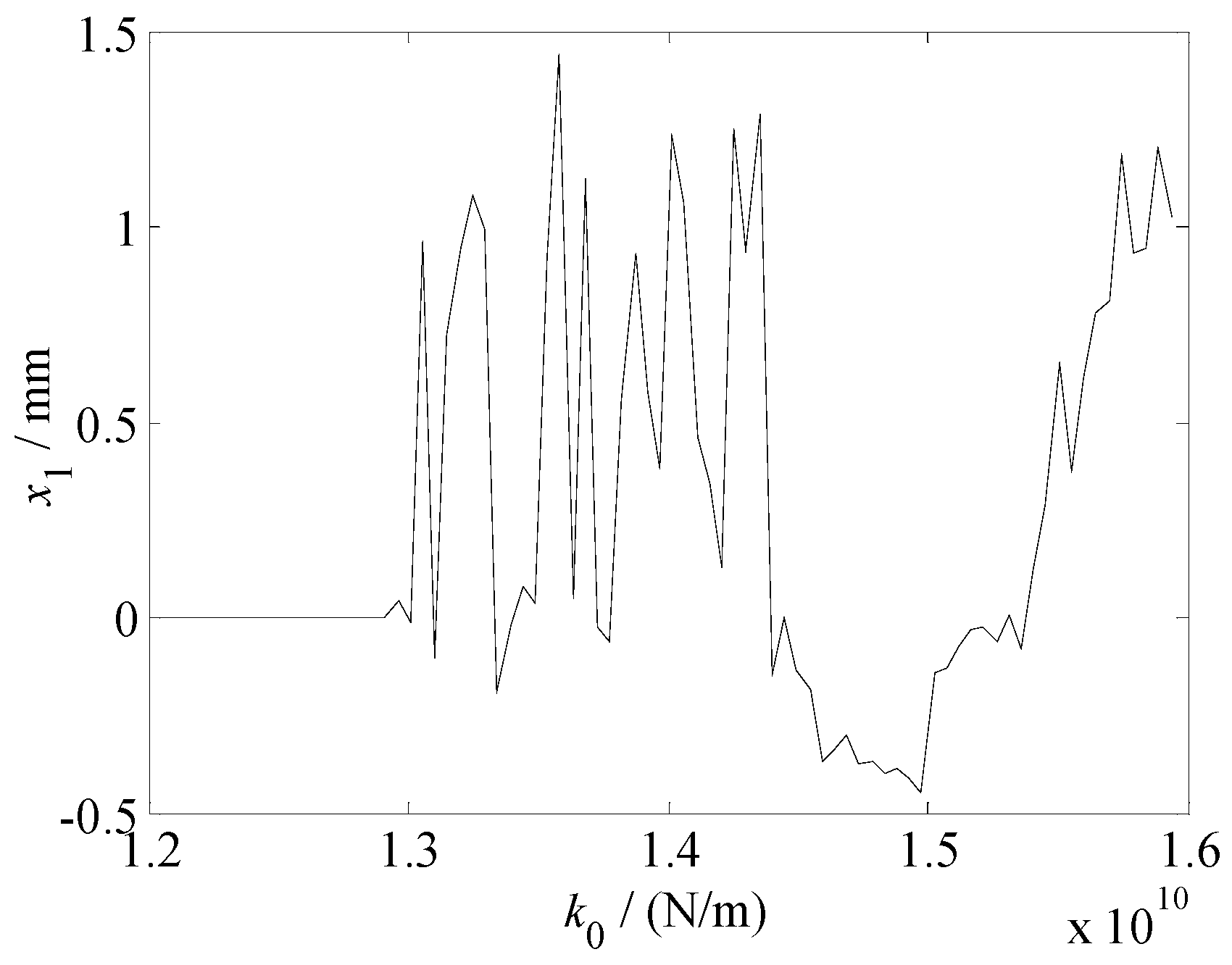
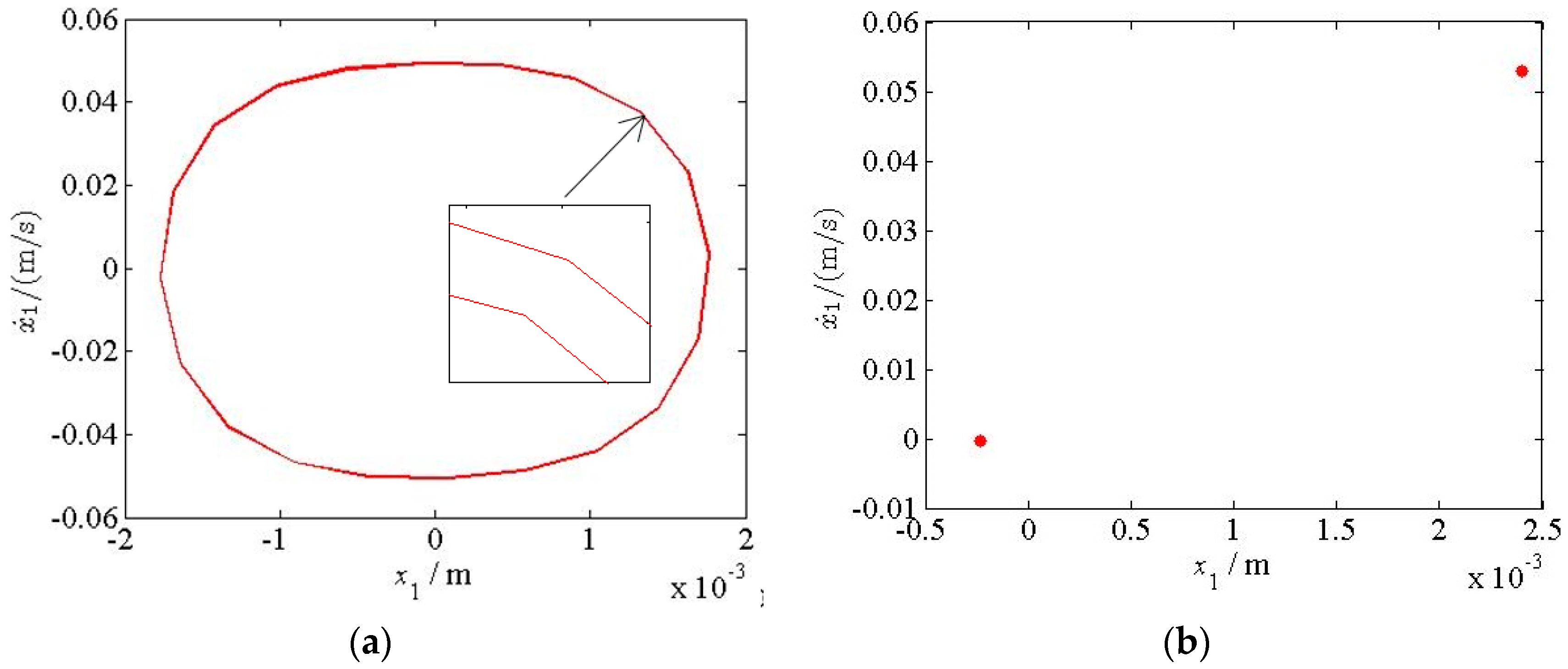
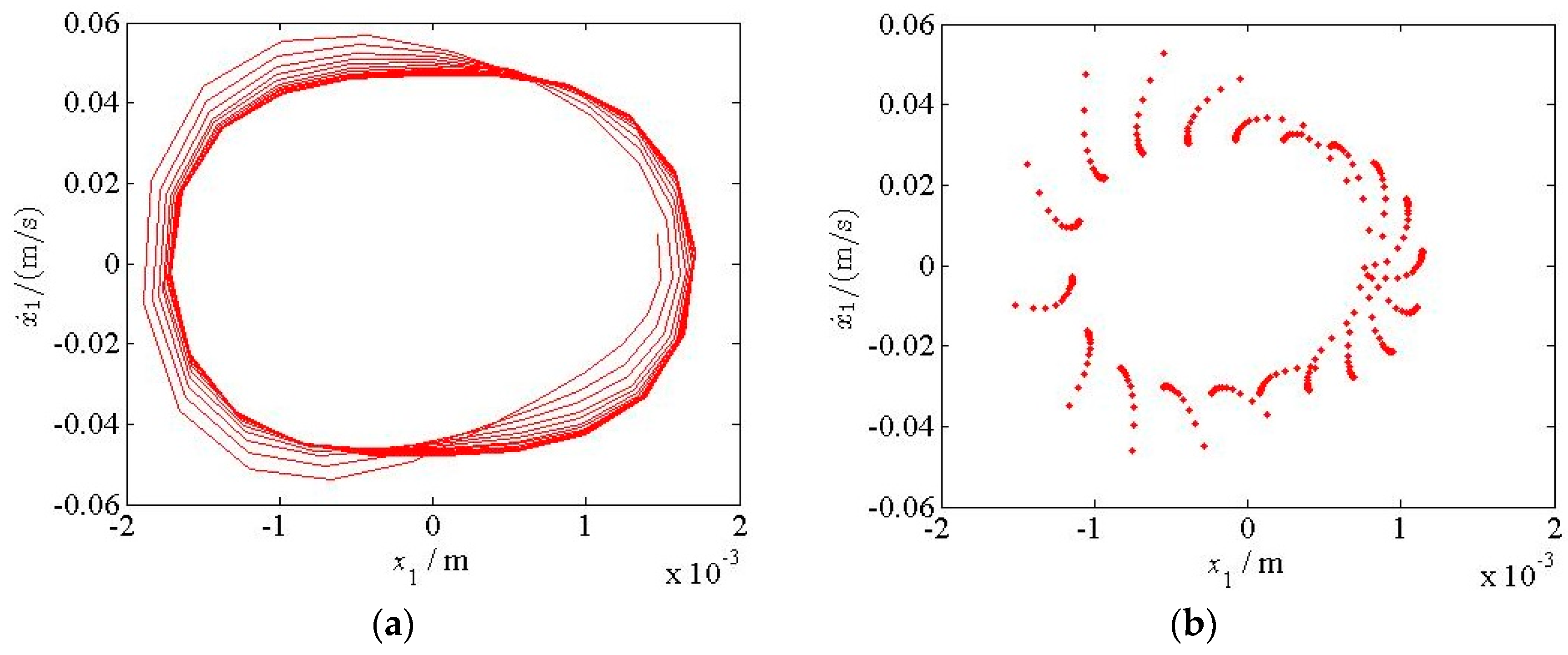
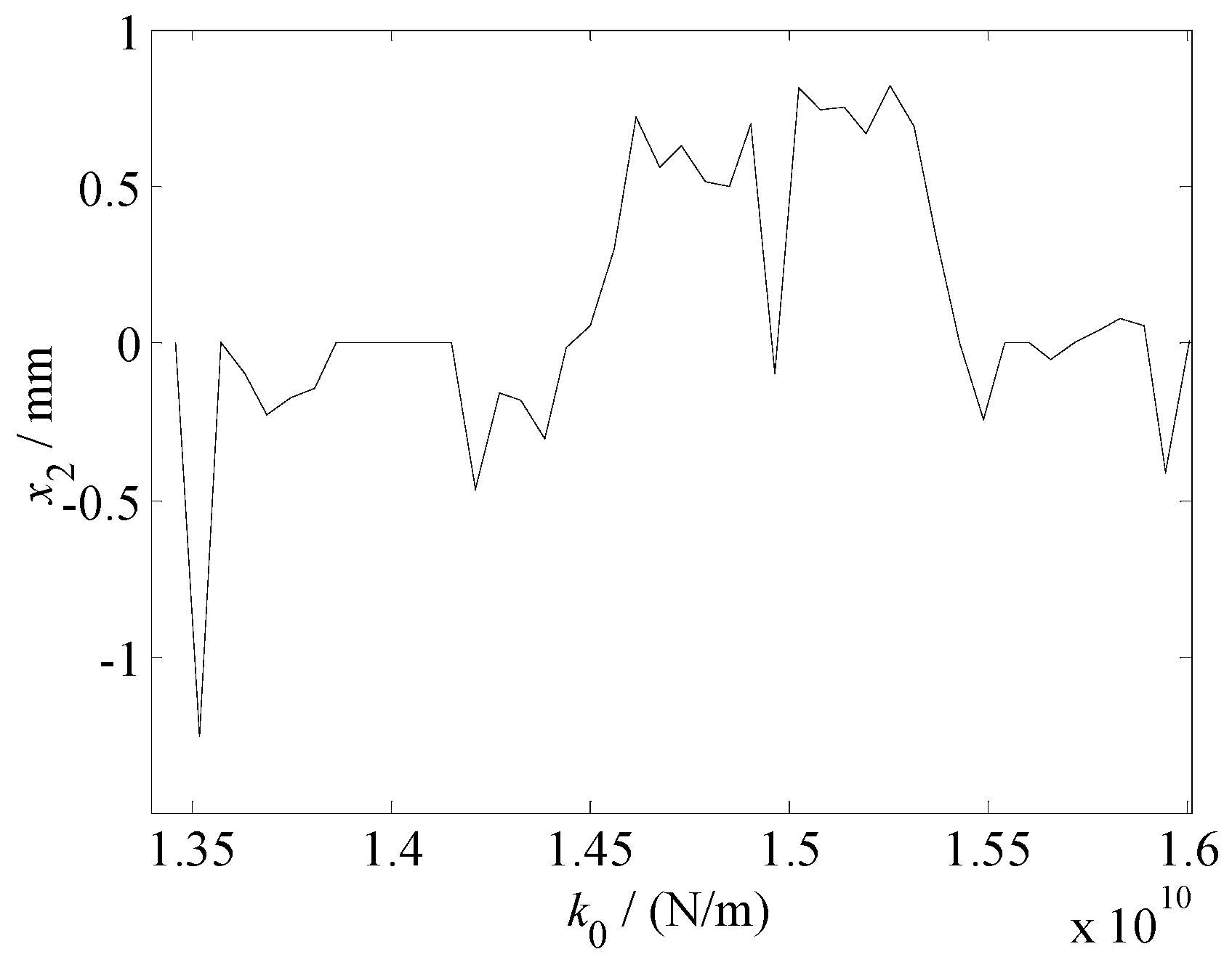
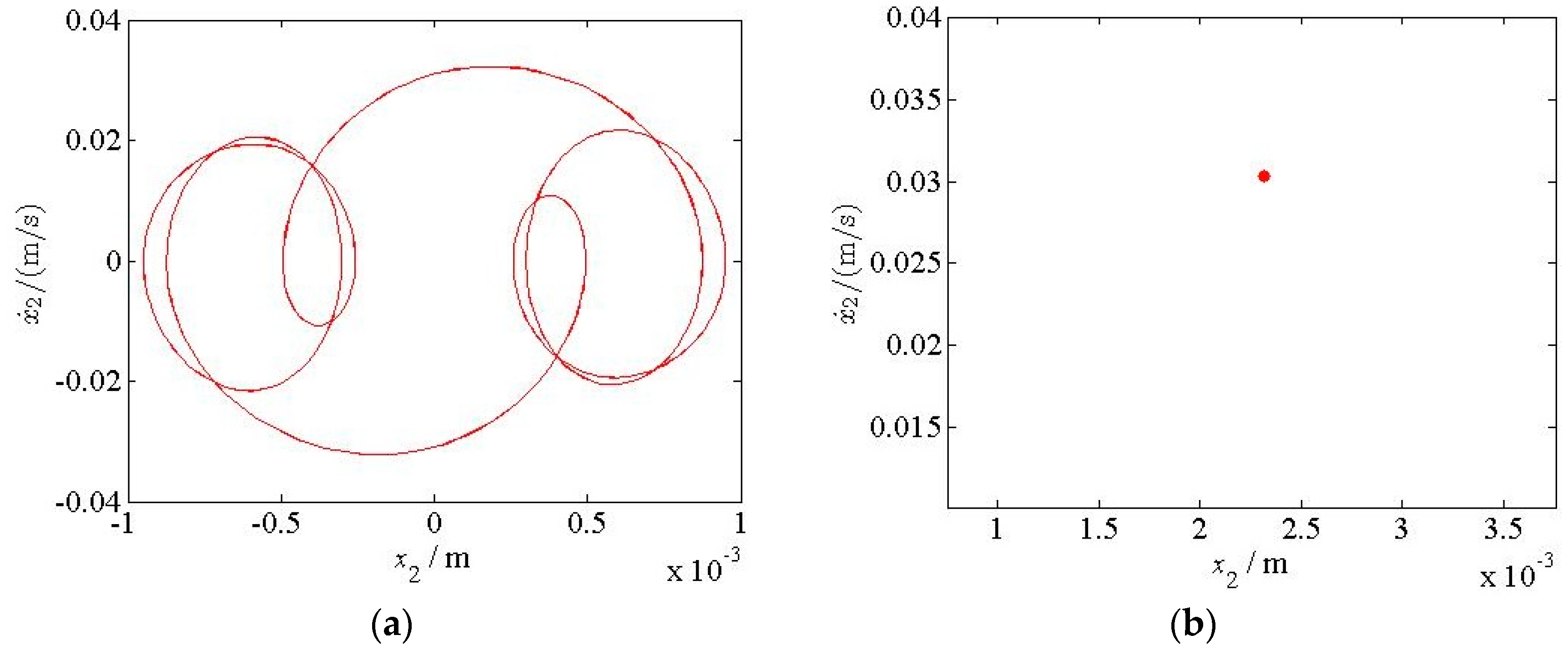
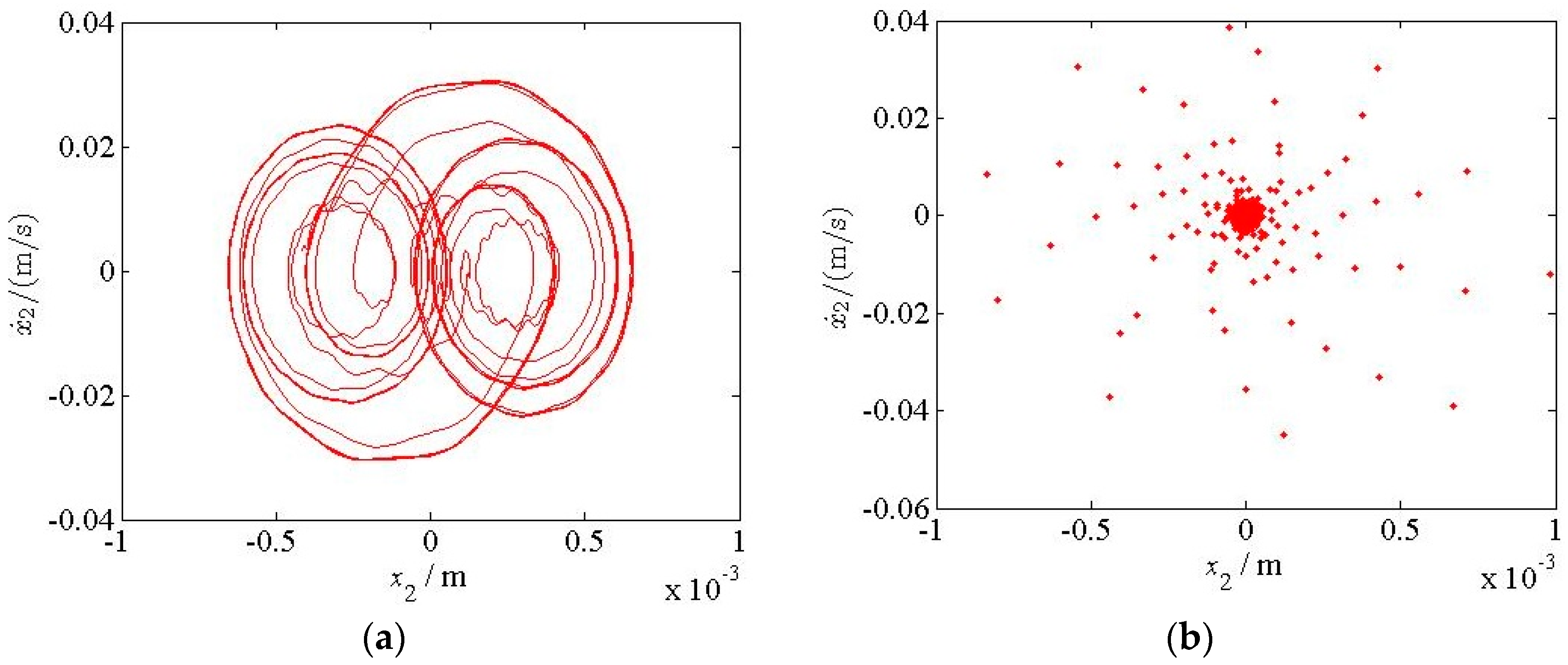
5. Chaotic Characteristics of the Vertical Vibration System of the Hot Rolling Mill
6. Conclusions and Observations
- Considering the influence of the nonlinear deformation of a workpiece undergoing elastoplastic hysteresis in a rolling process, a dynamic rolling force model with the hysteresis effect was established, providing a theoretical basis for studying rolling mill vibration. Based on the actual rolling parameters of a 1780 mm hot rolling mill, the hysteresis characteristics between the dynamic rolling force and the vibration displacement under different rolling parameters were analyzed by conducting simulations. The hysteresis phenomenon of the rolling mill rolls could be weakened gradually by appropriately increasing the rolling speed and reducing the roll radius and entry thickness, whereas the rolling width, front tension, and back tension have little effect on the hysteresis characteristics.
- We analyzed the subharmonic resonance characteristics of the rolling mill rolls by varying the structural damping, parametric stiffness, linear damping term, and nonlinear stiffness term. Measures to restrain the vibration of the rolling mill were provided in terms of the vibration amplitude, resonance area, and vibration curve deviation. Moreover, as evident characteristics of the internal resonance of the rolling mill rolls, the vibration amplitudes of the work and backup rolls increase and decrease alternately, and there is an evident energy exchange process. With the change in the parametric stiffness, the internal resonance system exhibits a jump phenomenon, thus destabilizing the rolling mill vibration system.
- The chaotic vibration characteristics of the work and backup rolls with the change in the parametric stiffness were analyzed and verified using a chaos diagram, maximum Lyapunov exponent, phase trajectory, and Poincare section. The vibration system exhibits periodic, period doubling, and chaotic motions, and it transitions from one form to another, which is one of the reasons for the occurrence of light and dark stripes in the rolled pieces. We also determined the critical value and value range of the parametric stiffness in the presence of chaotic motion, thus providing an effective guidance for adjusting the parametric stiffness between the rolls when the rolling mill vibration is suppressed.
- In the research process, the modeling and theoretical analysis of the traditional rolling mill vibration mechanism simplify many factors in actual production, resulting in a large error between the theoretical analysis and the actual measurement. A single model cannot explain the cause of rolling chatter completely, and it is not capable of generalization. In recent years, machine learning has been widely used in the industrial field, where deep learning can unearth the deep-seated characteristics that affect the vibration of a rolling mill from a large amount of data and can thus effectively solve problems such as high dimensionality, nonlinearity, and high coupling. The follow-up research will use deep learning to address the vibration phenomenon of rolling mills under complex conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| R | Radius of the work roll |
| B | Width of the workpiece |
| H0 | Entry thickness |
| h0 | Exit thickness |
| τf | Front tension |
| τb | Back tension |
| vR | Rotation speed of the roll |
| vy | Vertical reduction speed |
| lc | Horizontal projection length of the contact arc |
| α | Bite angle |
| c1 | Equivalent damping between the upper work roll and the upper backup roll |
| c2 | Equivalent damping between the upper backup roll and the upper beam of the frame |
| c3 | Equivalent damping between the lower work roll and the lower backup roll |
| c4 | Equivalent damping between the lower backup roll and the lower beam of the frame |
| k1 | Equivalent stiffness between the upper work roll and the upper backup roll |
| k2 | Equivalent stiffness between the upper backup roll and the upper beam of the frame |
| k3 | Equivalent stiffness between the lower work roll and the lower backup roll |
| k4 | Equivalent stiffness between the lower backup roll and the lower beam of the frame |
| x1, x2 | Vertical vibration displacement of the upper work roll and upper backup roll |
| x3, x4 | Vertical vibration displacement of the lower work roll and lower backup roll |
| m1, m2 | Equivalent mass of the upper work roll and upper backup roll |
| m3, m4 | Equivalent mass of the lower work roll and lower backup roll |
| a1, a2, a3 | Equivalent stiffness coefficients corresponding of dynamic rolling force |
| b1, b2, b3 | Equivalent damping coefficients corresponding of dynamic rolling force |
| ΔF | Dynamic rolling force variation |
| φm | Included angle at a distance of m from the center line of the work roll |
| k′ | Excitation stiffness |
| t′ | Deformation temperature |
| ω | Excitation frequency |
| ε | Small parameter |
References
- Hu, P.H.; Ehmann, K.F. Stability Analysis of Chatter on a Tandem Rolling Mill. J. Manuf. Process. 2000, 2, 217–224. [Google Scholar] [CrossRef]
- Niziol, J.; Swiatoniowski, A. Numerical Analysis of the Vertical Vibration of Rolling Mill and Their Negative Effect on the Sheet Quality. J. Mater. Process. Tech. 2005, 162, 546–550. [Google Scholar] [CrossRef]
- Yan, X.Q.; Sun, Z.H.; Chen, W.Q. Vibration Control in Thin Slab Hot Strip Mills. Ironmak. Steelmak. 2011, 38, 309–313. [Google Scholar] [CrossRef]
- Efrain, U. Identification and Countermeasures to Resolve Hot Mill Chatter. AISE. Steel. Tech. 2001, 78, 48–52. [Google Scholar]
- Fan, X.B.; Zang, Y.; Jin, K. Rolling Process and Its Influence Analysis on Hot Continuous Rolling Mill Vibration. Appl. Phys. A 2016, 122, 1008. [Google Scholar] [CrossRef]
- Sun, J.L.; Peng, Y.; Liu, H.M. Non-Linear Vibration and Stability of Moving Strip with Time-Dependent Tension in Rolling Process. J. Iron. Steel. Res. Int. 2010, 17, 11–15, 20. [Google Scholar] [CrossRef]
- Valigi, C.M.; Papini, S. Analysis of Chattering Phenomenon in Industrial S6-High Rolling Mill. Diagnostyka 2013, 14, 3–8. [Google Scholar]
- Papini, S.; Valigi, C.M. Analysis of Chattering Phenomenon in Industrial S6-High Rolling Mill. Part II Experimental Study. Diagnostyka 2016, 17, 27–32. [Google Scholar]
- Kozhevnikov, A.; Bolobanova, N.; Simirnov, A. Chatter Prevention in Stands of Continuous Cold Rolling Mills. Metallurgy 2020, 59, 55–58. [Google Scholar]
- Pawelski, O.; Rasp, W.; Zwick, W.; Nettelbeck, H.J.; Steinhoff, K. The Influence of Different Work-Roll Texturing Systems on the Development of Surface Structure in the Temper Rolling Process of Steel Sheet Used in the Automotive Industry. J. Mater. Process. Tech. 1994, 45, 215–222. [Google Scholar] [CrossRef]
- Lackinger, C.V.; Nettelbeck, H.J.; Oemkes, H. The New Yandem Mill at Thyssenkrupp Stahl’s Beeckerwerth Cold Strip. Stahl Und Elsen 2002, 122, 25–32. [Google Scholar]
- Yarita, I.; Furukawa, K.; Seino, Y. An Analysis of Chattering in Cold Rolling of Ultra Thin Gauge Steel Strip. T. ISU 1979, 19, 110. [Google Scholar]
- Youne, M.A.; Shahtout, M.; Damir, M.N. A Parameters Design Approach to Improve Product Quality and Equipment Performance in Hot Rolling. J. Mater. Process. Tech. 2006, 17, 83–92. [Google Scholar] [CrossRef]
- Swiatoniowski, A.; Bar, A. Parametrical Excitement Vibration in Tandem Mills—Mathematical Model and Its Analysis. J. Mater. Process. Tech. 2003, 134, 214–224. [Google Scholar] [CrossRef]
- Zhang, G.M.; Xiao, H.; Wang, C.H. Three-Dimensional Model for Strip Hot Rolling. J. Iron. Steel. Res. Int. 2006, 13, 23–26. [Google Scholar] [CrossRef]
- Fan, X.B.; Zang, Y.; Jin, K. Research on Strip Hysteretic Behavior and Mill Vertical Vibration System Nonlinear Dynamics. Appl. Phys. A 2016, 122, 1–12. [Google Scholar] [CrossRef]
- Sims, R.B. The Calculation of Roll Force and Torque in Hot Rolling Mills. Proc. Inst. Mech. Eng. 1954, 168, 191–200. [Google Scholar] [CrossRef]
- Jia, C.Y.; Shan, X.Y.; Niu, Z.P. High Precision Prediction of Rolling Force Based on Fuzzy and Nerve Method for Cold Tandem Mill. J. Iron. Steel. Res. Int. 2008, 15, 23–27. [Google Scholar] [CrossRef]
- Dong, Y.G.; Zhang, W.Z.; Song, J.F. Theoretical and Experimental Research on Rolling Force for Rail Hot Tolling by Universal Mill. J. Iron. Steel. Res. Int. 2010, 17, 27–32. [Google Scholar] [CrossRef]
- Bagheripoor, M.; Bisadi, H. An Investigation on the Roll Force and Torque Fluctuations During Hot Strip Rolling Process. Prod. Manu. Res. 2014, 2, 128–141. [Google Scholar] [CrossRef]
- Wu, S.L.; Shao, Y.M.; Wang, L.M.; Yuan, Y.L.; Mechefske, C.K. Relationship between Chatter Marks and Rolling Force Fluctuation for Twenty-High Roll Mill. Eng. Fail. Anal. 2015, 55, 87–99. [Google Scholar] [CrossRef]
- Feng, X.W.; Wang, X.C.; Yang, Q.; Sun, J.Q. Analysis of Rate Dependency on Roll Force Calculation During Hot Strip Rolling Based on Karman Equation. Adv. Mech. Eng. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.G.; Guo, Y.F. A Novel Analytical Model for Prediction of Rolling Force in Hot Strip Rolling Based on Tangent Velocity Field and MY Criterion. J. Manu. Process. 2019, 47, 202–210. [Google Scholar] [CrossRef]
- Kazeminezhad, M.; Karimi, T.A. Calculation of the Rolling Pressure Distribution and Force in Wire Flat Rolling Process. J. Mater. Process. Tech. 2006, 171, 253–258. [Google Scholar] [CrossRef]
- Peng, R.R.; Zhang, X.Z.; Shi, P.M. Coupled Vibration Behavior of Hot Rolling Mill Rolls Under Multi-Nonlinear Effects. Shock Vib. 2020, 2020, 6104028. [Google Scholar]
- Zhang, S.H.; Deng, L.; Zhang, Q.Y.; Li, Q.H.; Hou, J.X. Modeling of Rolling Force of Ultra-Heavy Plate Considering the Influence of Deformation Penetration Coefficient. Int. J. Mech. Sci. 2019, 159, 373–381. [Google Scholar] [CrossRef]
- Sun, Y.K. Modelling and Control of Hot Tandem Rolling; Metallurgical Industry Publishing House: Beijing, China, 2002. [Google Scholar]
- Hu, P.H.; Zhao, H.Y.; Ehmann, K.F. Third-Octave-Mode Chatter in Rolling. Part 1: Chatter Model. Proc. Inst. Mech. Eng. Part B J. Eng. Manu. 2006, 220, 1267–1277. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; Wiley-InterScience: New York, NY, USA, 1973. [Google Scholar]
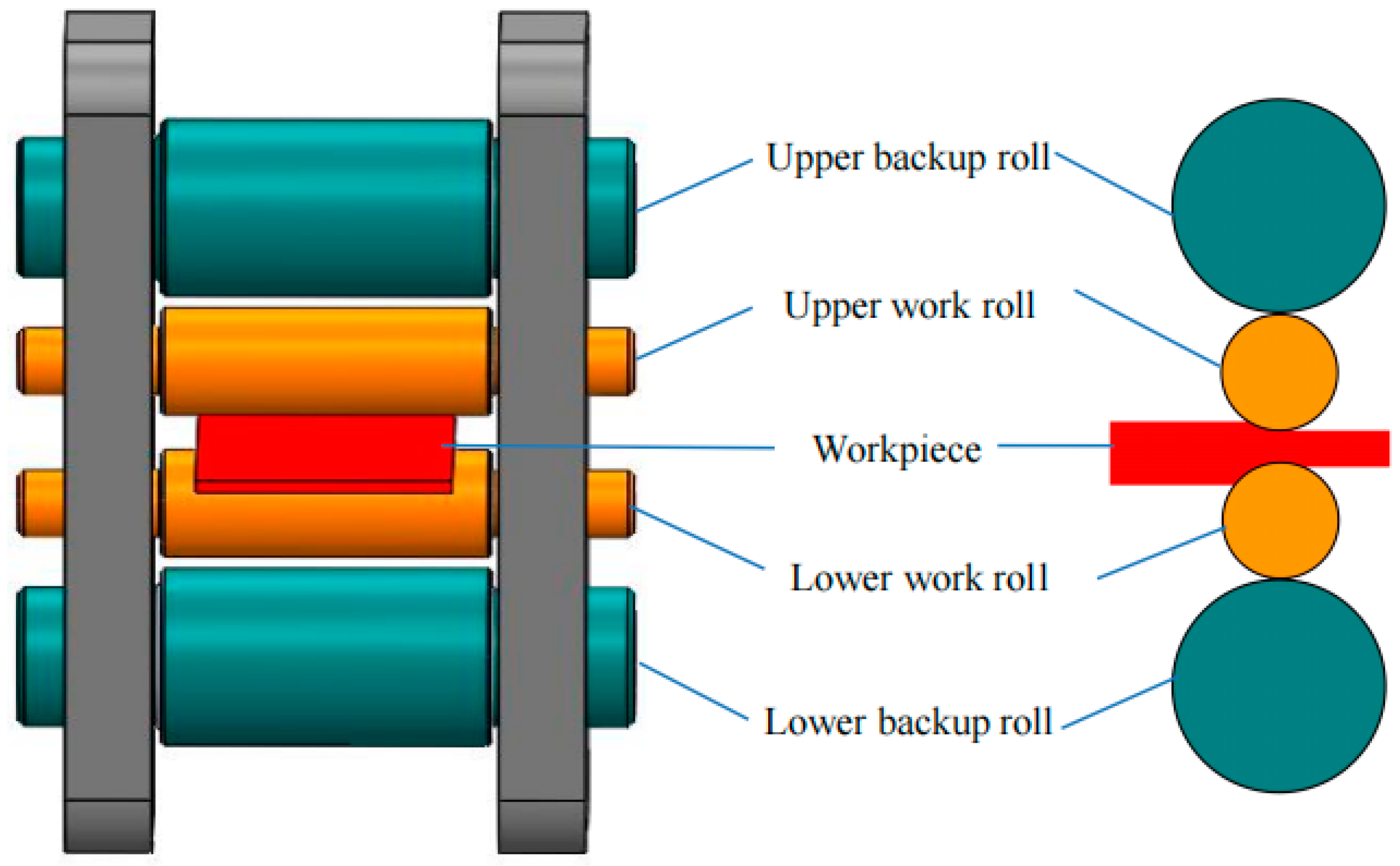


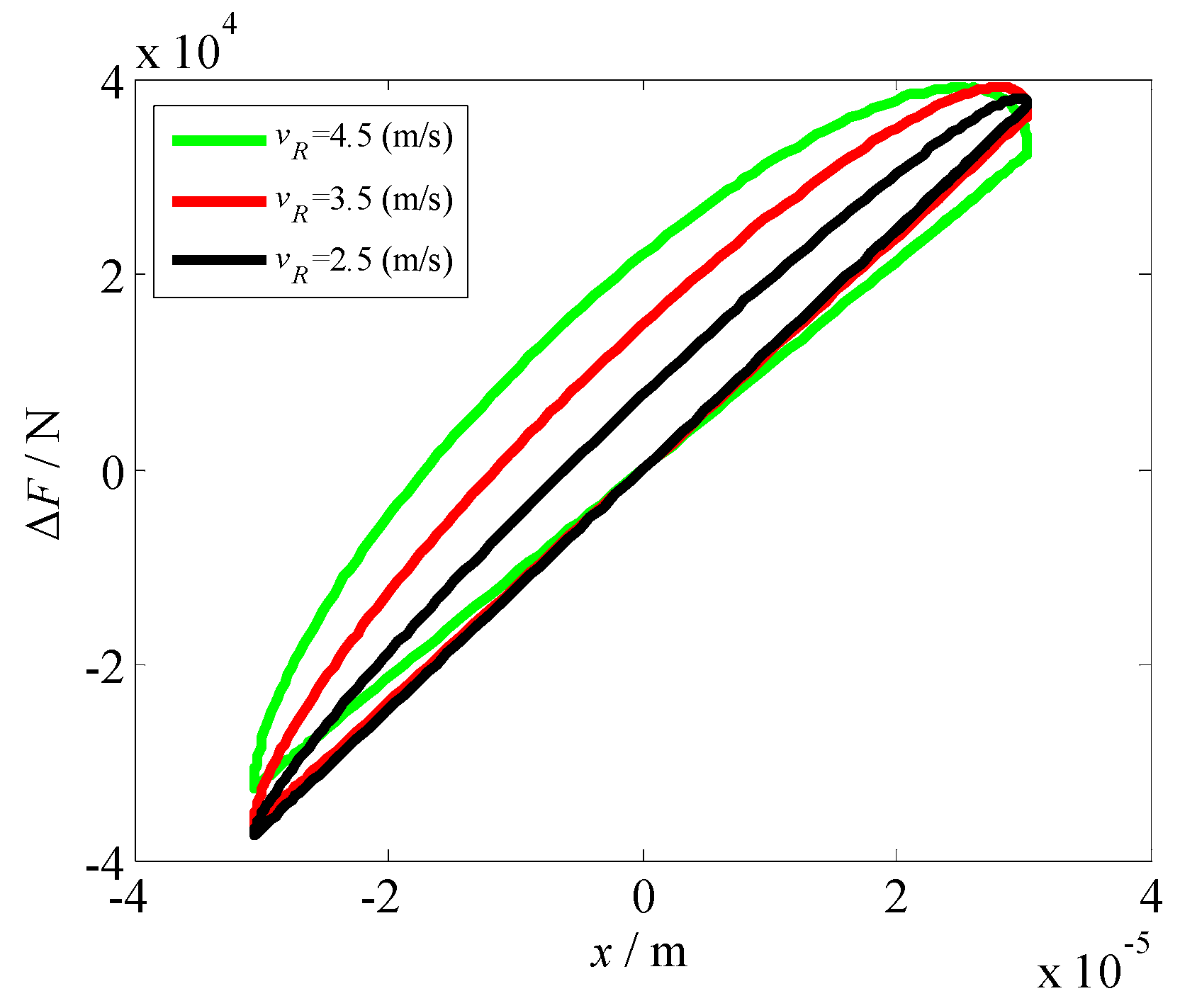
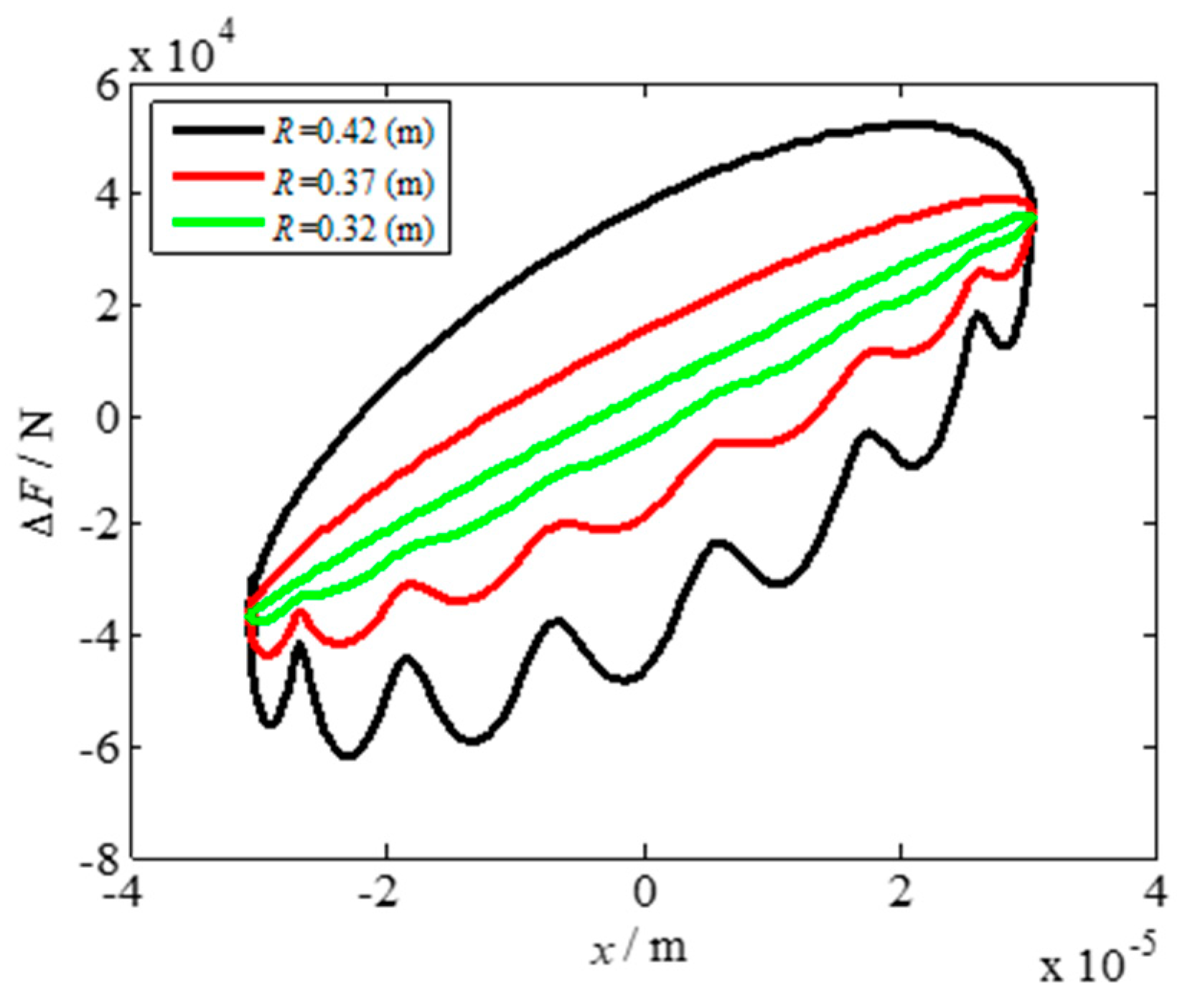

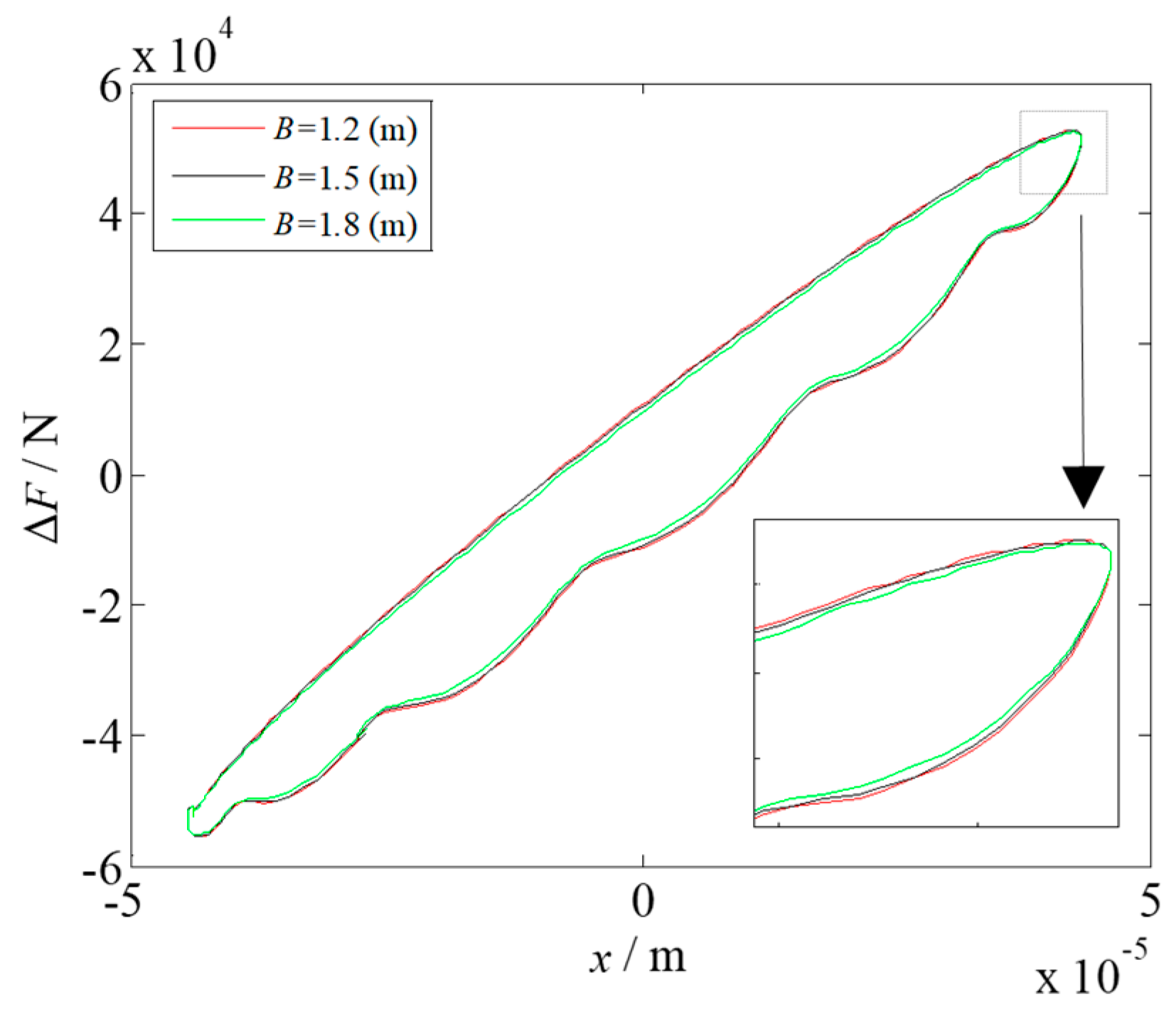

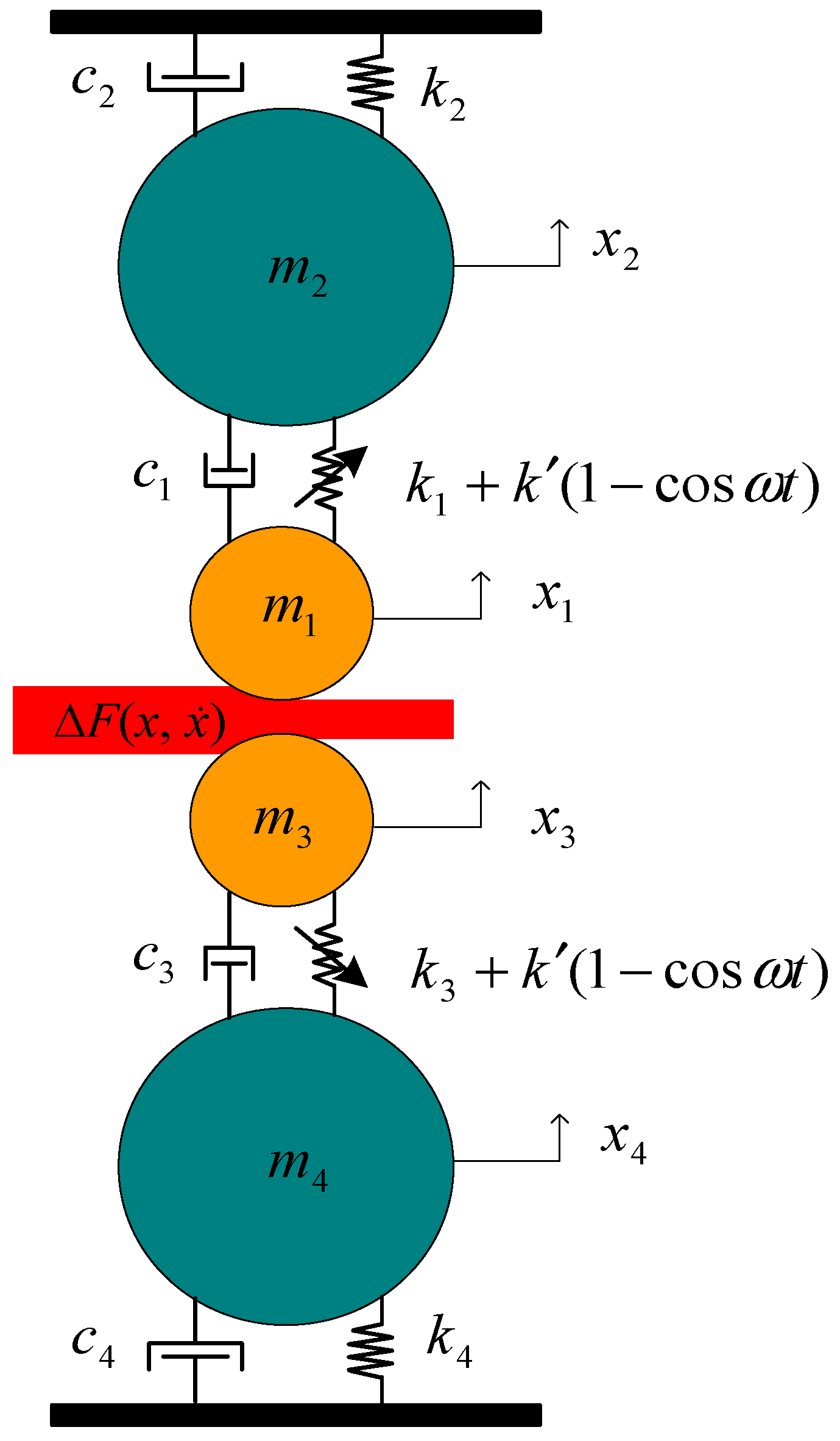




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| B (m) | 1.5 | τb (MPa) | 5.5 |
| R (m) | 0.42 | τf (MPa) | 3.8 |
| vR (m/s) | 2.5 | H0 (m) | 0.0141 |
| t′ (°C) | 996 | h0 (m) | 0.0082 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| a1 (N/m) | −5.96 × 109 | b1 (N·s/m) | −1.23 × 105 |
| a2 (N/m2) | −1.08 × 1011 | b2 (N·s2/m2) | −2027.03 |
| a3 (N/m3) | 2.05 × 1013 | b3 (N·s3/m3) | −46.89 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| m1 (kg) | 1440 | k1 (N/m) | 7.21 × 109 |
| m2 (kg) | 2400 | k2 (N/m) | 9.91 × 1011 |
| c1 (N·s/m) | 8.85 × 105 | k’ (N/m) | 1.6 × 1010 |
| c2 (N·s/m) | 2.0 × 105 | ε | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, R.; Zhang, X.; Shi, P. Vibration Characteristics of Hot Rolling Mill Rolls Based on Elastoplastic Hysteretic Deformation. Metals 2021, 11, 869. https://doi.org/10.3390/met11060869
Peng R, Zhang X, Shi P. Vibration Characteristics of Hot Rolling Mill Rolls Based on Elastoplastic Hysteretic Deformation. Metals. 2021; 11(6):869. https://doi.org/10.3390/met11060869
Chicago/Turabian StylePeng, Rongrong, Xingzhong Zhang, and Peiming Shi. 2021. "Vibration Characteristics of Hot Rolling Mill Rolls Based on Elastoplastic Hysteretic Deformation" Metals 11, no. 6: 869. https://doi.org/10.3390/met11060869
APA StylePeng, R., Zhang, X., & Shi, P. (2021). Vibration Characteristics of Hot Rolling Mill Rolls Based on Elastoplastic Hysteretic Deformation. Metals, 11(6), 869. https://doi.org/10.3390/met11060869






