Deformation Behavior and Microstructural Evolution of Inconel 625 Superalloy during the Hot Compression Process
Abstract
:1. Introduction
2. Experimental Procedure
3. Results and Discussion
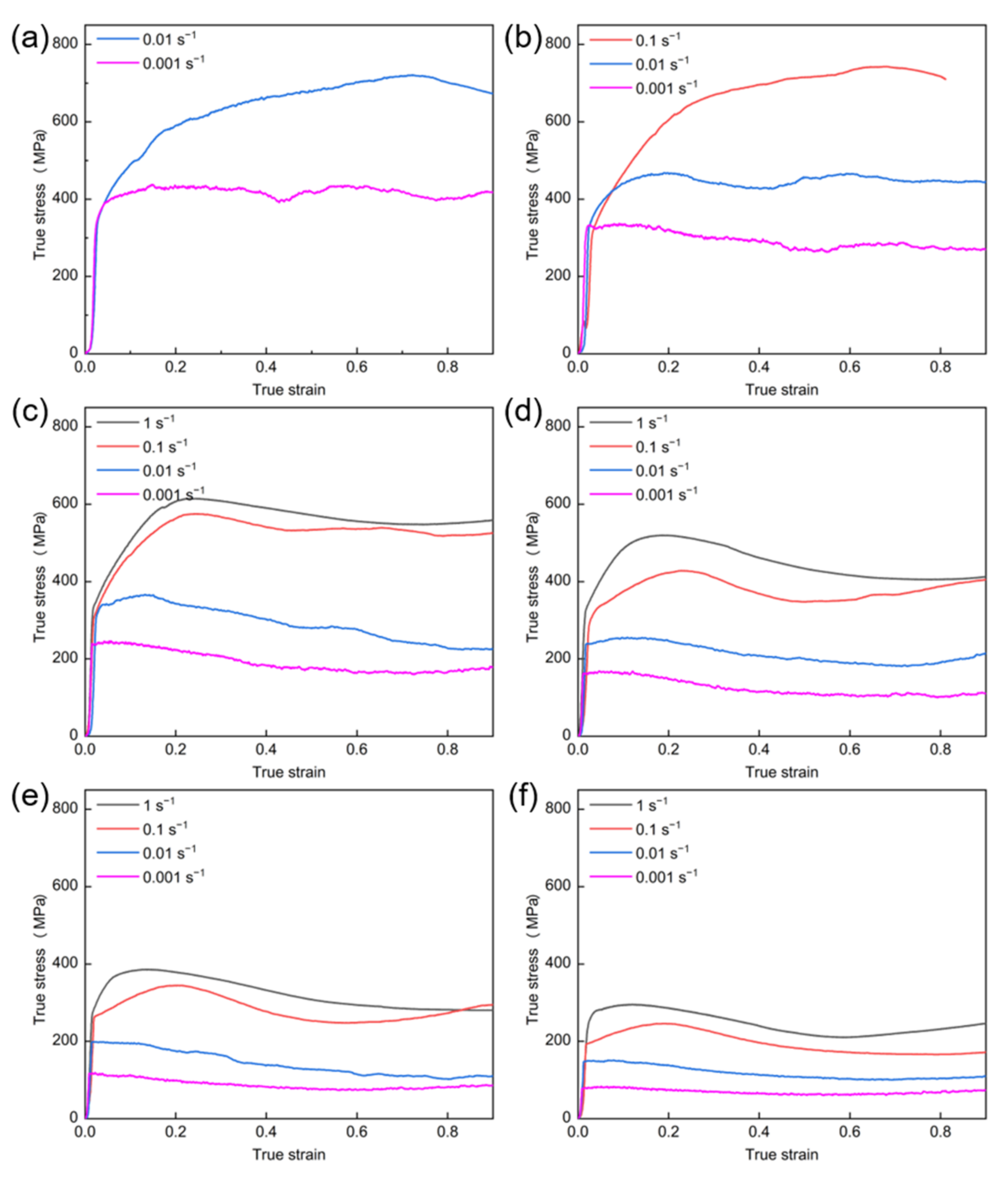
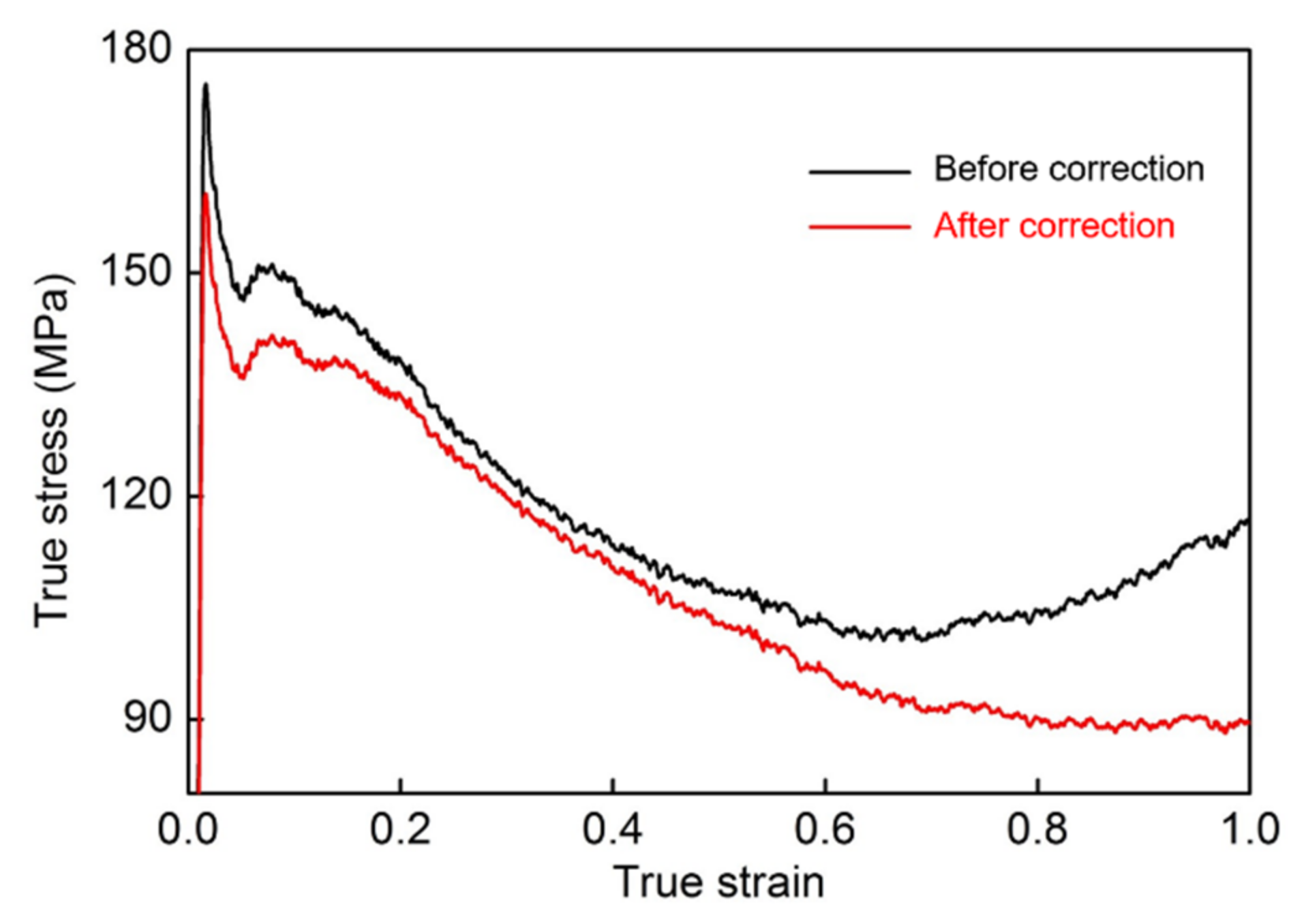
3.1. Deformation Behavior
3.2. Microstructural Evolution during Hot Compression Process
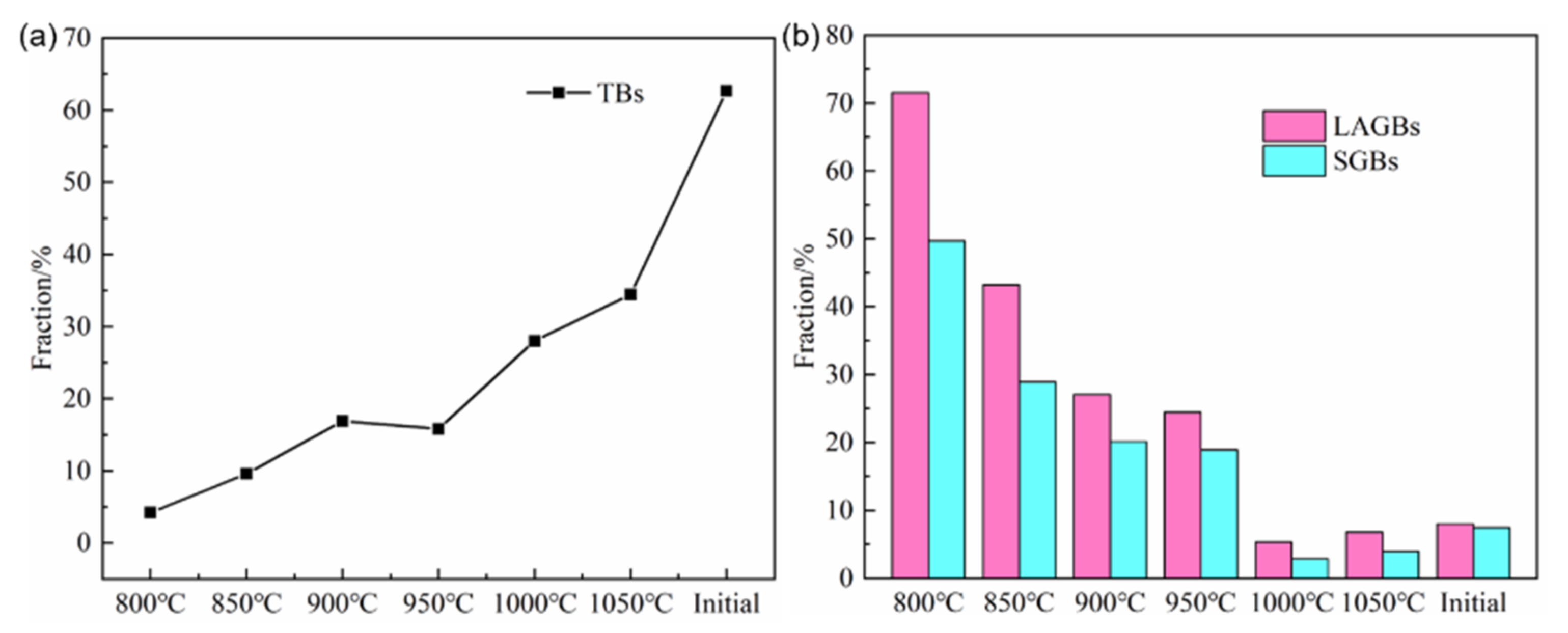
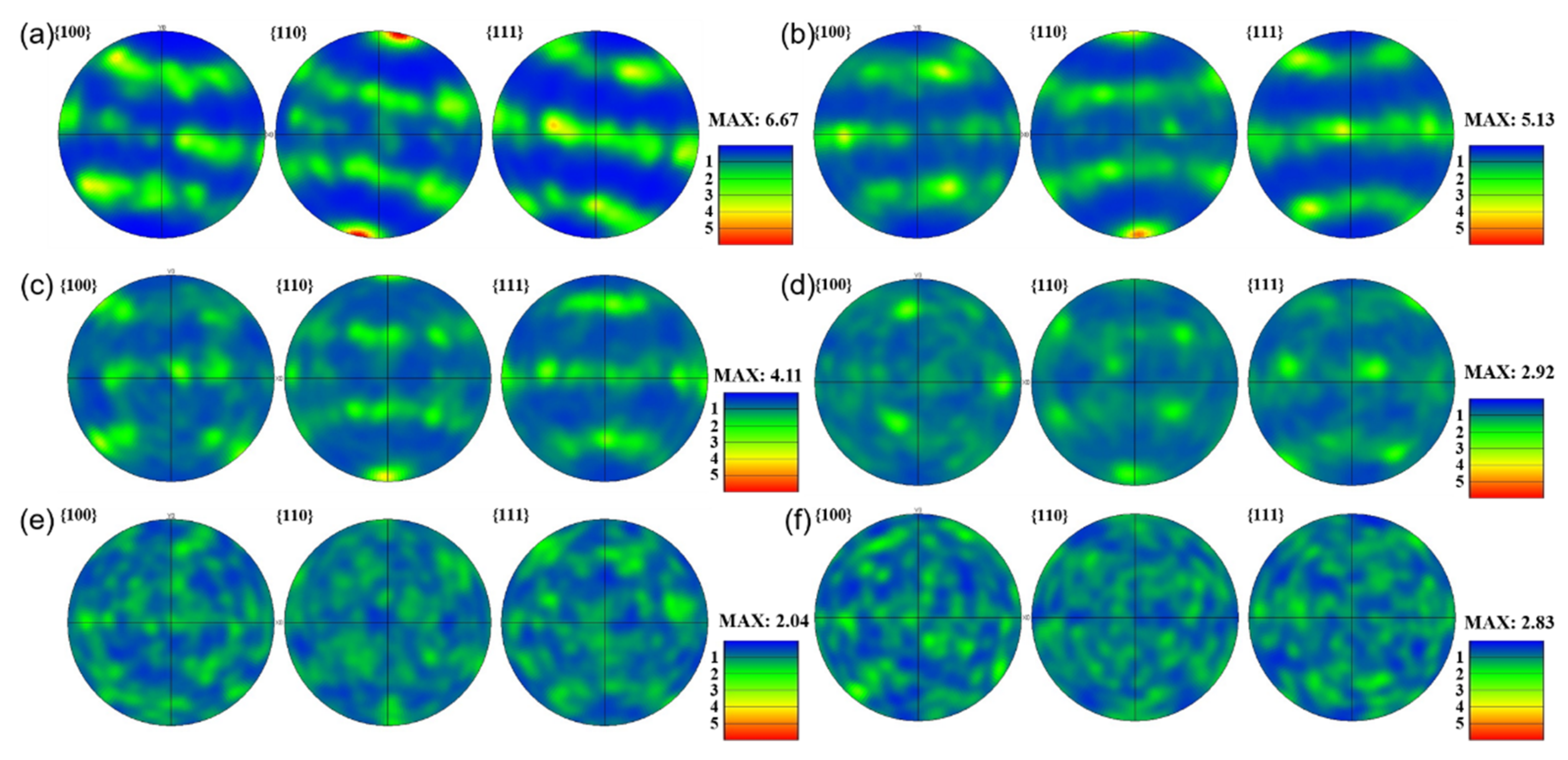
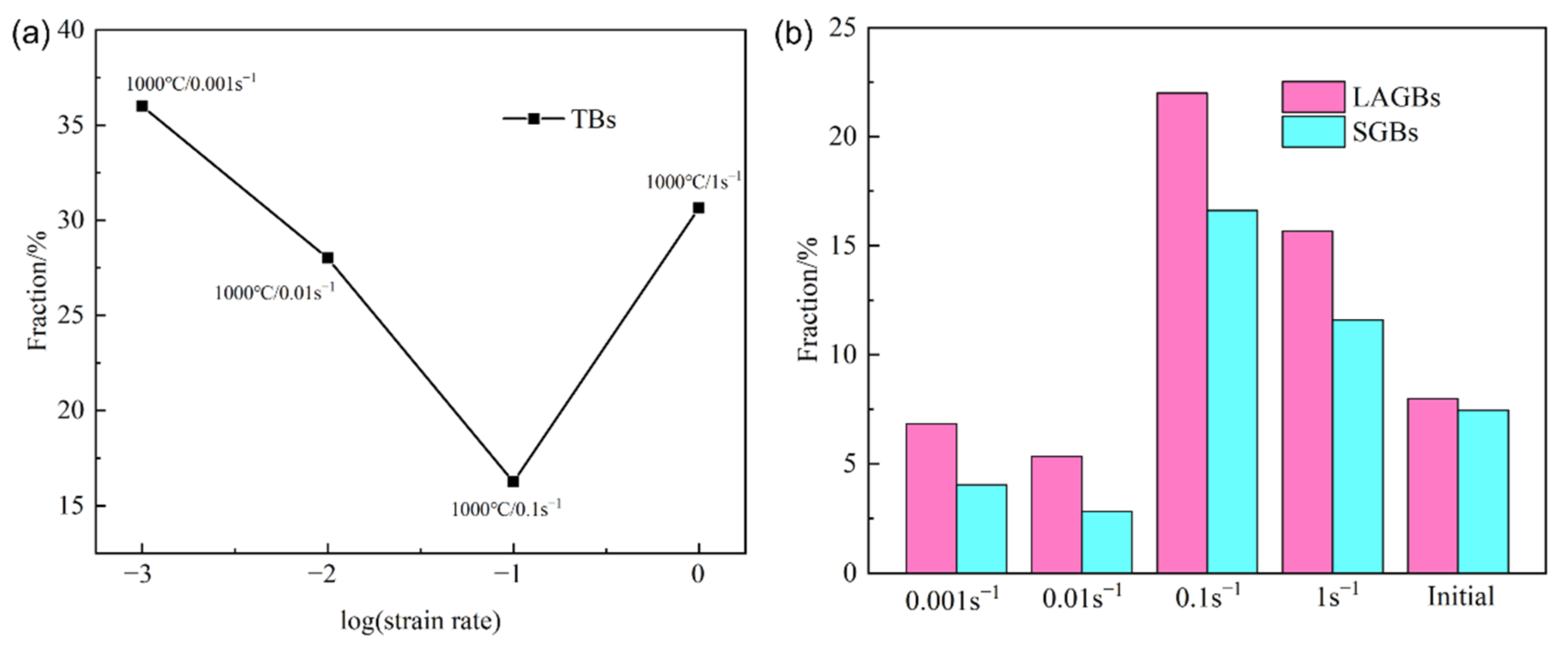
3.2.1. Effects of Deformation Temperature on the Microstructure Evolution
3.2.2. Effects of Strain Rate on the Microstructure
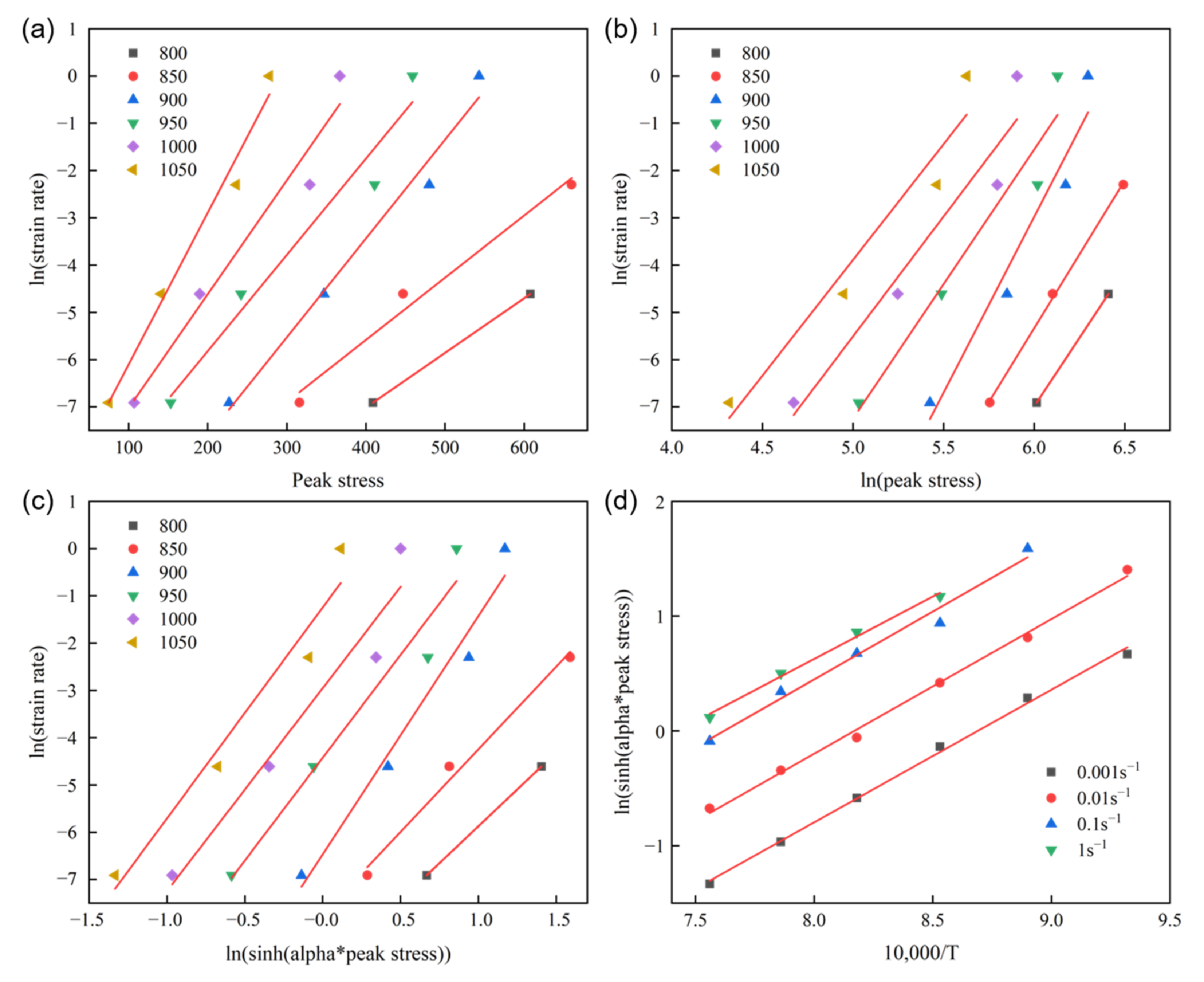
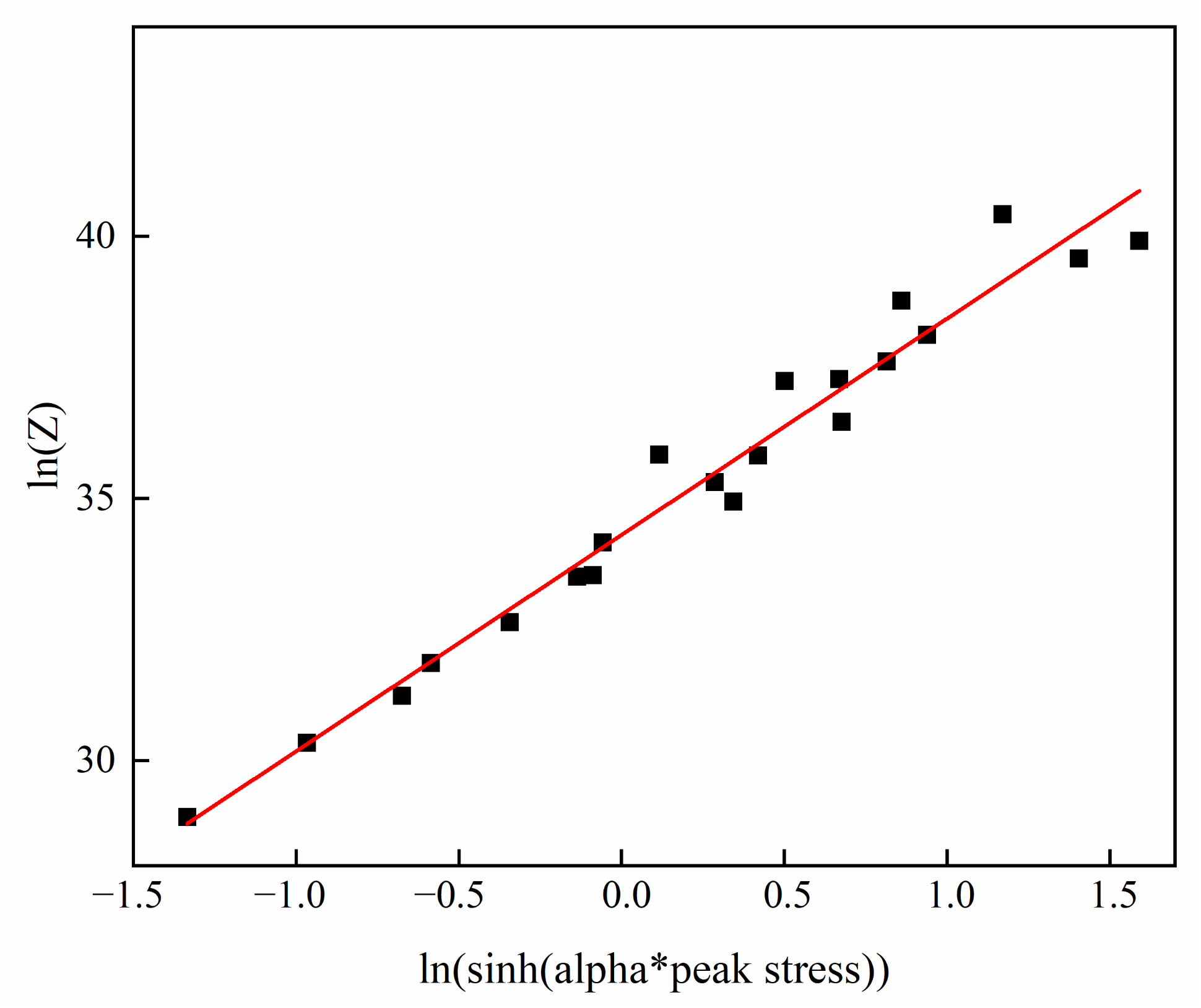
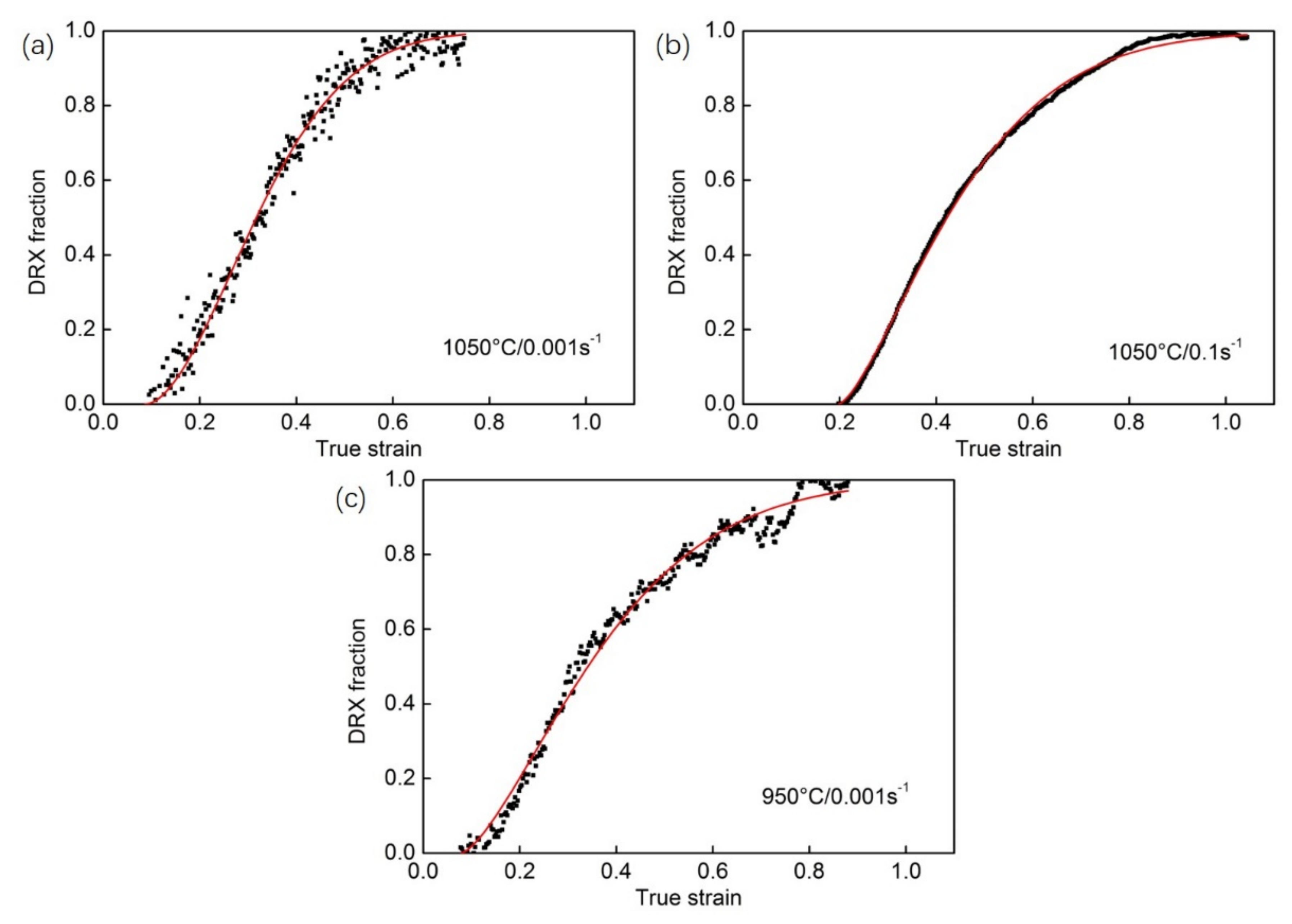
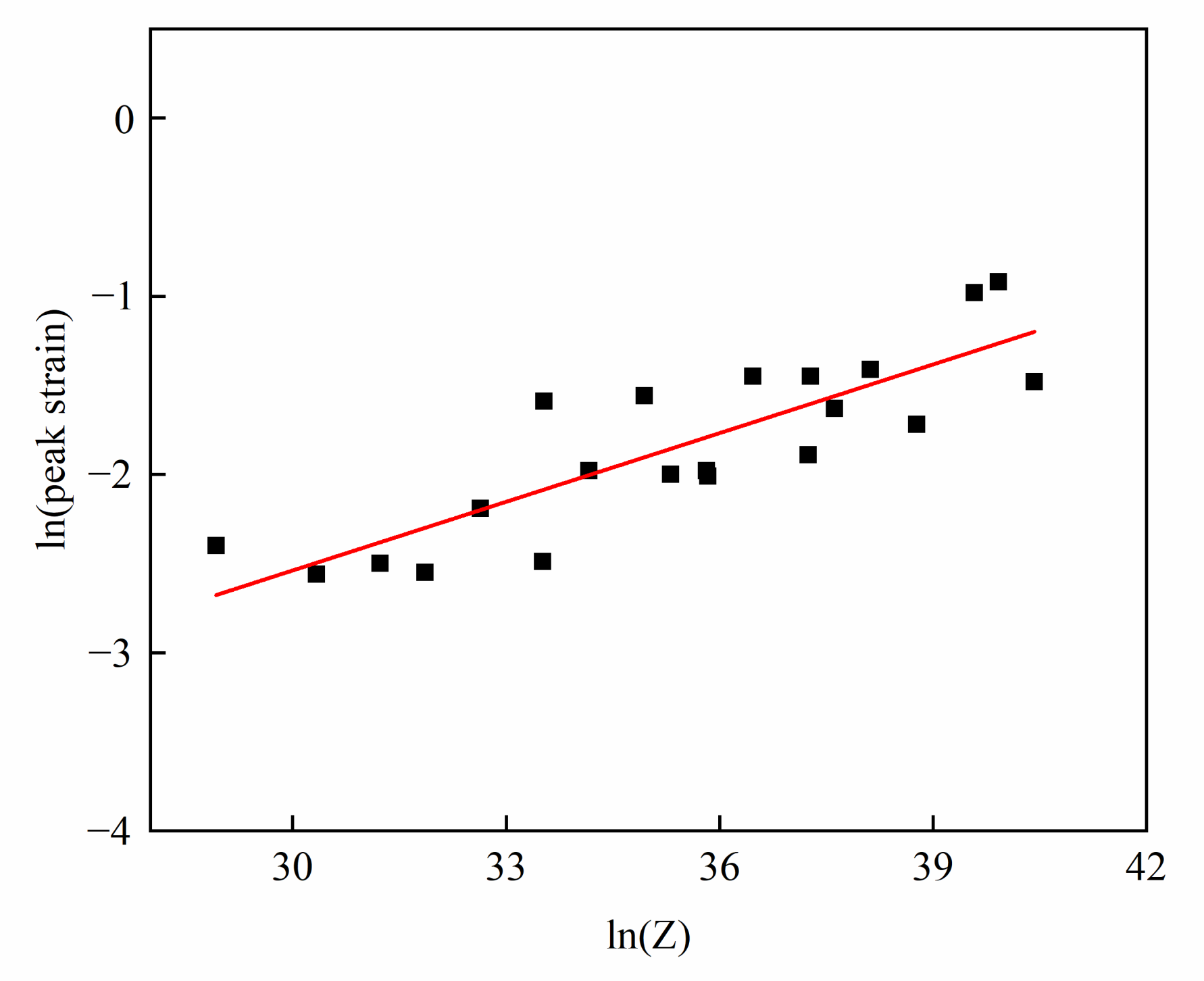
3.3. DRX Kinetics
4. Conclusions
- (1)
- During the uniaxial compression test, a strong <110> texture appears in the microstructure when the temperature is below 950 °C, and the intensity of the texture decreases with the increases of the temperature.
- (2)
- Twin-related DRX occurs in the compressing process. The intensity of twin-related DRX increases with the increases of the temperature. Moreover, the changes of twin morphology may lead to changes in DRX mechanism, and the intensity of cDRX decreases with the increases of the temperature.
- (3)
- With the increases of the temperature or the decreases of the strain rate, the critical strain of DRX decreases, and thereby DRX is promoted.
- (4)
- This work has a strong guiding significance for the hot spinning formation process of superalloys.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.D.; Fan, J.K.; Zhang, P.Z.; Xie, J.; Chen, F.L.; Liu, D.G.; Yuan, R.G.; Tang, B.; Kou, H.C.; Li, J.S. Temperature dependence of deformation behavior, microstructure evolution and fracture mechanism of Inconel 625 superalloy. J. Alloy. Compd. 2021, 869, 159342. [Google Scholar] [CrossRef]
- Yu, L.J.; Marquis, E.A. Precipitation behavior of Alloy 625 and Alloy 625 plus. J. Alloy. Compd. 2019, 811, 151916. [Google Scholar] [CrossRef]
- Nguejio, J.; Szmytka, F.; Hallais, S.; Tanguy, A.; Nardone, S.; Godino Martinez, M. Comparison of microstructure features and mechanical properties for additive manufactured and wrought nickel alloys 625. Mater. Sci. Eng. A 2019, 764, 138214. [Google Scholar] [CrossRef]
- Huebner, J.; Kata, D.; Kusiński, J.; Rutkowski, P.; Lis, J. Microstructure of laser cladded carbide reinforced Inconel 625 alloy for turbine blade application. Ceram. Int. 2017, 43, 8677–8684. [Google Scholar] [CrossRef]
- Wang, Y.F.; Chen, X.Z.; Shen, Q.K.; Su, C.C.; Zhang, Y.P.; Jayalakshmi, S.; Singh, R.A. Effect of magnetic Field on the microstructure and mechanical properties of inconel 625 superalloy fabricated by wire arc additive manufacturing. J. Manuf. Process. 2021, 64, 10–19. [Google Scholar] [CrossRef]
- Tian, Y.; Chekir, N.; Wang, X.; Nommeots-Nomm, A.; Gauvin, R.; Brochu, M. Effect of heat treatments on microstructure evolution and grain morphology of alloy 625 with 0.4 wt.% boron modification fabricated by laser wire deposition. J. Alloy. Compd. 2018, 764, 815–823. [Google Scholar] [CrossRef]
- Li, C.; White, R.; Fang, X.Y.; Weaver, M.; Guo, Y.B. Microstructure evolution characteristics of Inconel 625 alloy from selective laser melting to heat treatment. Mater. Sci. Eng. A 2017, 705, 20–31. [Google Scholar] [CrossRef]
- Evans, N.D.; Maziasz, P.J.; Shingledecker, J.P.; Yamamoto, Y. Microstructure evolution of alloy 625 foil and sheet during creep at 750 °C. Mater. Sci. Eng. A 2008, 498, 412–420. [Google Scholar] [CrossRef]
- Safarzade, A.; Sharifitabar, M.; Shafiee, A.M. Effects of heat treatment on microstructure and mechanical properties of Inconel 625 alloy fabricated by wire arc additive manufacturing process. Trans. Nonferr. Met. Soc. China 2020, 30, 3016–3030. [Google Scholar] [CrossRef]
- Gao, Y.B.; Ding, Y.T.; Chen, J.J.; Xu, J.Y.; Ma, Y.J.; Wang, X.M. Effect of twin boundaries on the microstructure and mechanical properties of Inconel 625 alloy. Mater. Sci. Eng. A 2019, 767, 138361. [Google Scholar] [CrossRef]
- Marchese, G.; Parizia, S.; Rashidi, M.; Saboori, A.; Manfredi, D.; Ugues, D.; Lombardi, M.; Hryha, E.; Biamino, S. The role of texturing and microstructure evolution on the tensile behavior of heat-treated Inconel 625 produced via laser powder bed fusion. Mater. Sci. Eng. A 2020, 769, 138500. [Google Scholar] [CrossRef]
- Parizia, S.; Marchese, G.; Rashidi, M.; Lorusso, M.; Hryha, E.; Manfredi, D.; Biamino, S. Effect of heat treatment on microstructure and oxidation properties of Inconel 625 processed by LPBF. J. Alloy. Compd. 2020, 846, 156418. [Google Scholar] [CrossRef]
- López, B.; Urcola, J.J. Hot deformation characteristics of Inconel 625. Mater. Sci. Technol. 1996, 12, 673–678. [Google Scholar] [CrossRef]
- Sani, S.A.; Arabi, H.; Ebrahimi, G.R. Hot deformation behavior and DRX mechanism in a γ-γ/cobalt-based superalloy. Mater. Sci. Eng. A 2019, 764, 138165. [Google Scholar] [CrossRef]
- Guo, S.L.; Li, D.F.; Guo, Q.M.; Wu, Z.G.; Peng, H.J.; Hu, J. Investigation on hot workability characteristics of Inconel 625 superalloy using processing maps. J. Mater. Sci. 2012, 47, 5867–5878. [Google Scholar] [CrossRef]
- Jia, Z.; Sun, X.; Ji, J.J.; Wang, Y.J.; Wei, B.L.; Yu, L.D. Hot Deformation Behavior and Dynamic Recrystallization Nucleation Mechanisms of Inconel 625 during Hot Compressive Deformation. Adv. Eng. Mater. 2021, 23, 2001048. [Google Scholar] [CrossRef]
- Lizzi, F.; Pradeep, K.; Stanojevic, A.; Sommadossi, S.; Poletti, M.C. Hot Deformation Behavior of a Ni-Based Superalloy with Suppressed Precipitation. Metals 2021, 11, 605. [Google Scholar] [CrossRef]
- Li, D.F.; Guo, Q.M.; Guo, S.L.; Peng, H.J.; Wu, Z.G. The microstructure evolution and nucleation mechanisms of dynamic recrystallization in hot-deformed Inconel 625 superalloy. Mater. Des. 2011, 32, 696–705. [Google Scholar] [CrossRef]
- Hu, Y.L.; Lin, X.; Li, Y.L.; Zhang, S.Y.; Gao, X.H.; Liu, F.G.; Li, X.; Huang, W.D. Plastic deformation behavior and dynamic recrystallization of Inconel 625 superalloy fabricated by directed energy deposition. Mater. Des. 2020, 186, 108359. [Google Scholar] [CrossRef]
- Bonnekoh, C.; Lied, P.; Zaefferer, S.; Jäntsch, U.; Hoffmann, A.; Reiser, J.; Rieth, M. The brittle-to-ductile transition in cold-rolled tungsten sheets: Contributions of grain and subgrain boundaries to the enhanced ductility after pre-deformation. J. Nucl. Mater. 2020, 25, 100769. [Google Scholar] [CrossRef]
- Lang, Y.J.; Cai, Y.H.; Cui, H.; Zhang, J.S. Effect of strain-induced precipitation on the low angle grain boundary in AA7050 aluminum alloy. Mater. Des. 2011, 32, 4241–4246. [Google Scholar] [CrossRef]
- Yang, J.; Luo, J.; Li, X.Y.; Li, M.Q. Evolution mechanisms of recrystallized grains and twins during isothermal compression and subsequent solution treatment of GH4586 superalloy. J. Alloy. Compd. 2021, 850, 156732. [Google Scholar] [CrossRef]
- Wei, D.X.; Koizumi, Y.; Chiba, A. Discontinuous yielding and microstructural evolution of Ti-40 at.% Al alloy compressed in single α-hcp phase region. J. Alloy. Compd. 2017, 693, 1261–1276. [Google Scholar] [CrossRef]
- Xiang, L.; Tang, B.; Xue, X.Y.; Kou, H.C.; Li, J.S. Microstructural characteristics and dynamic recrystallization behavior of β-γ TiAl based alloy during high temperature deformation. Intermetallics 2018, 97, 52–57. [Google Scholar] [CrossRef]
- León-Cázares, F.D.; Monni, F.; Rae, C.M.F. Stress orientation dependence for the propagation of stacking faults and superlattice stacking faults in nickel-based superalloys. Acta Mater. 2020, 199, 209–224. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Wu, Y.T.; Liu, Y.C.; Li, C.; Xia, X.C.; Huang, Y.; Li, H.J.; Wang, H.P. Deformation behavior and processing maps of Ni 3 Al-based superalloy during isothermal hot compression. J. Alloy. Compd. 2017, 712, 687–695. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22. [Google Scholar] [CrossRef]
- Li, J.; Li, F.G.; Cai, J.; Wang, R.T.; Yuan, Z.W.; Ji, G.L. Comparative investigation on the modified Zerilli–Armstrong model and Arrhenius-type model to predict the elevated-temperature flow behaviour of 7050 aluminium alloy. Comput. Mater. Sci. 2013, 71, 56–65. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]


| Ni | Co | Cr | Fe | Mo | Cu | Nb |
| 63.8 | <0.005 | 21.95 | 2.07 | 8.20 | 0.017 | 3.44 |
| Al | Ti | Mn | Si | P | C | S |
| 0.17 | 0.17 | <0.005 | 0.13 | 0.002 | 0.039 | <0.001 |
| Temperature (°C) | 800 | 850 | 900 | 950 | 1000 | 1050 |
|---|---|---|---|---|---|---|
| Strain rate (s−1) | 1 | 0.1 | 0.01 | 0.001 | ||
| Deformation (%) | 65 | |||||
| Temperature (°C) | |||||||
|---|---|---|---|---|---|---|---|
| 800 | 850 | 900 | 950 | 1000 | 1050 | ||
| Strain Rate (s−1) | 0.001 | 409 | 316 | 227 | 153 | 107 | 75 |
| 0.01 | 608 | 447 | 347 | 242 | 190 | 141 | |
| 0.1 | - | 660 | 480 | 411 | 329 | 236 | |
| 1 | - | - | 543 | 459 | 367 | 278 | |
| Temperature (°C) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 800 | 850 | 900 | 950 | 1000 | 1050 | ||||||||
| k | n | k | n | k | n | k | n | k | n | k | n | ||
| Strain Rate (s−1) | 1 | - | - | - | - | - | - | - | - | - | - | 0.19 | 2.3 |
| 0.1 | - | - | - | - | - | - | - | - | 1.03 | 1.6 | 0.59 | 1.4 | |
| 0.01 | - | - | - | - | 0.13 | 1.8 | 0.26 | 1.5 | 0.17 | 1.5 | 0.11 | 1.6 | |
| 0.001 | - | - | - | - | 0.10 | 1.7 | 0.13 | 1.4 | 0.20 | 1.4 | 0.14 | 1.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Li, K.; Tang, B.; Liu, D.; Zhong, H.; Li, J. Deformation Behavior and Microstructural Evolution of Inconel 625 Superalloy during the Hot Compression Process. Metals 2021, 11, 824. https://doi.org/10.3390/met11050824
Chen F, Li K, Tang B, Liu D, Zhong H, Li J. Deformation Behavior and Microstructural Evolution of Inconel 625 Superalloy during the Hot Compression Process. Metals. 2021; 11(5):824. https://doi.org/10.3390/met11050824
Chicago/Turabian StyleChen, Fulong, Kaidi Li, Bin Tang, Degui Liu, Hong Zhong, and Jinshan Li. 2021. "Deformation Behavior and Microstructural Evolution of Inconel 625 Superalloy during the Hot Compression Process" Metals 11, no. 5: 824. https://doi.org/10.3390/met11050824
APA StyleChen, F., Li, K., Tang, B., Liu, D., Zhong, H., & Li, J. (2021). Deformation Behavior and Microstructural Evolution of Inconel 625 Superalloy during the Hot Compression Process. Metals, 11(5), 824. https://doi.org/10.3390/met11050824







