Artificial Neural Networks-Based Prediction of Hardness of Low-Alloy Steels Using Specific Jominy Distance
Abstract
1. Introduction
2. Materials and Data
2.1. Materials
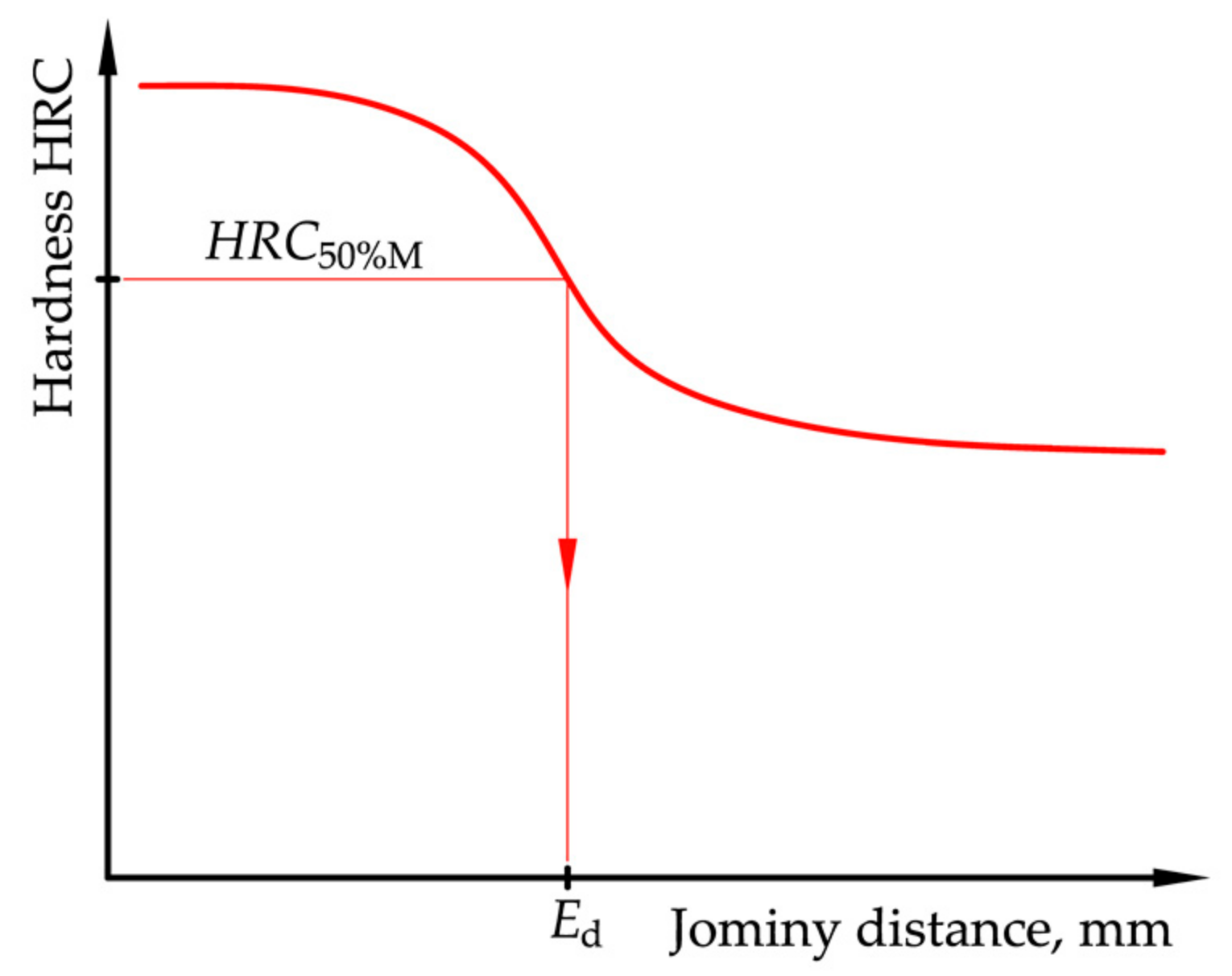
2.2. Input Variables and Data
3. Methods
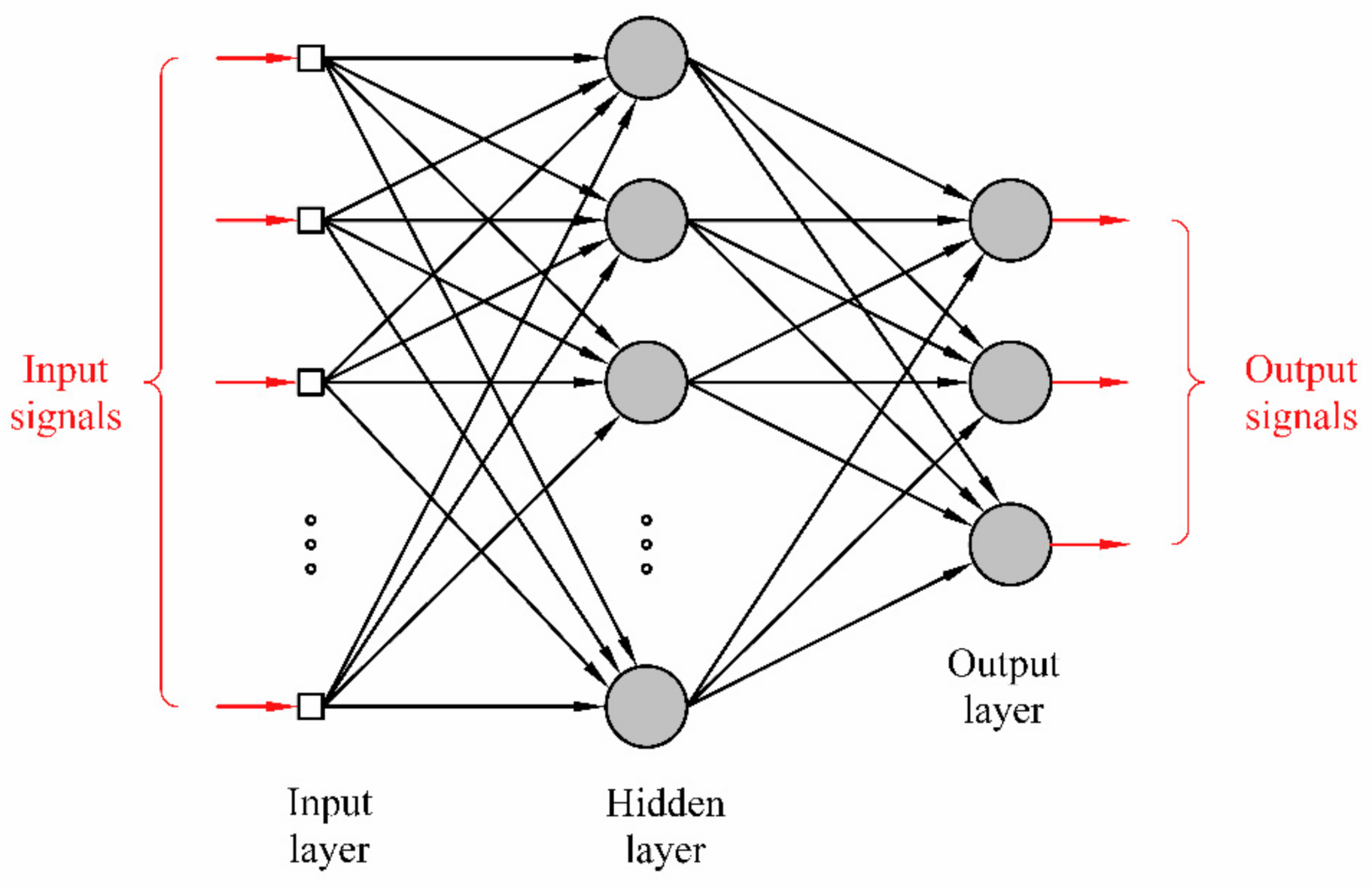
Development of Artificial Neural Networks for Prediction of Total Hardness after Continuous Cooling, HVtot
4. Results
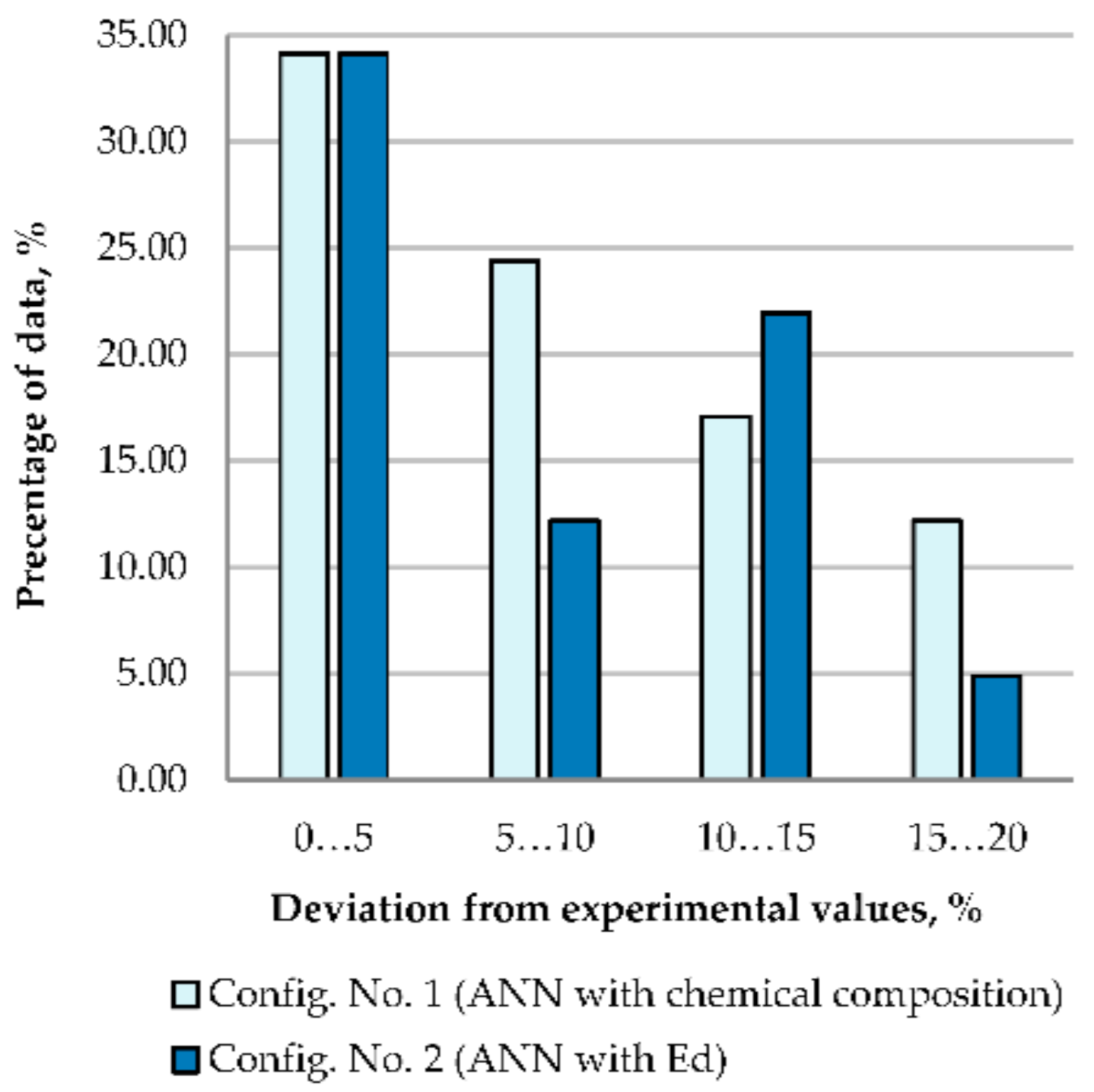
5. Discussion
6. Conclusions
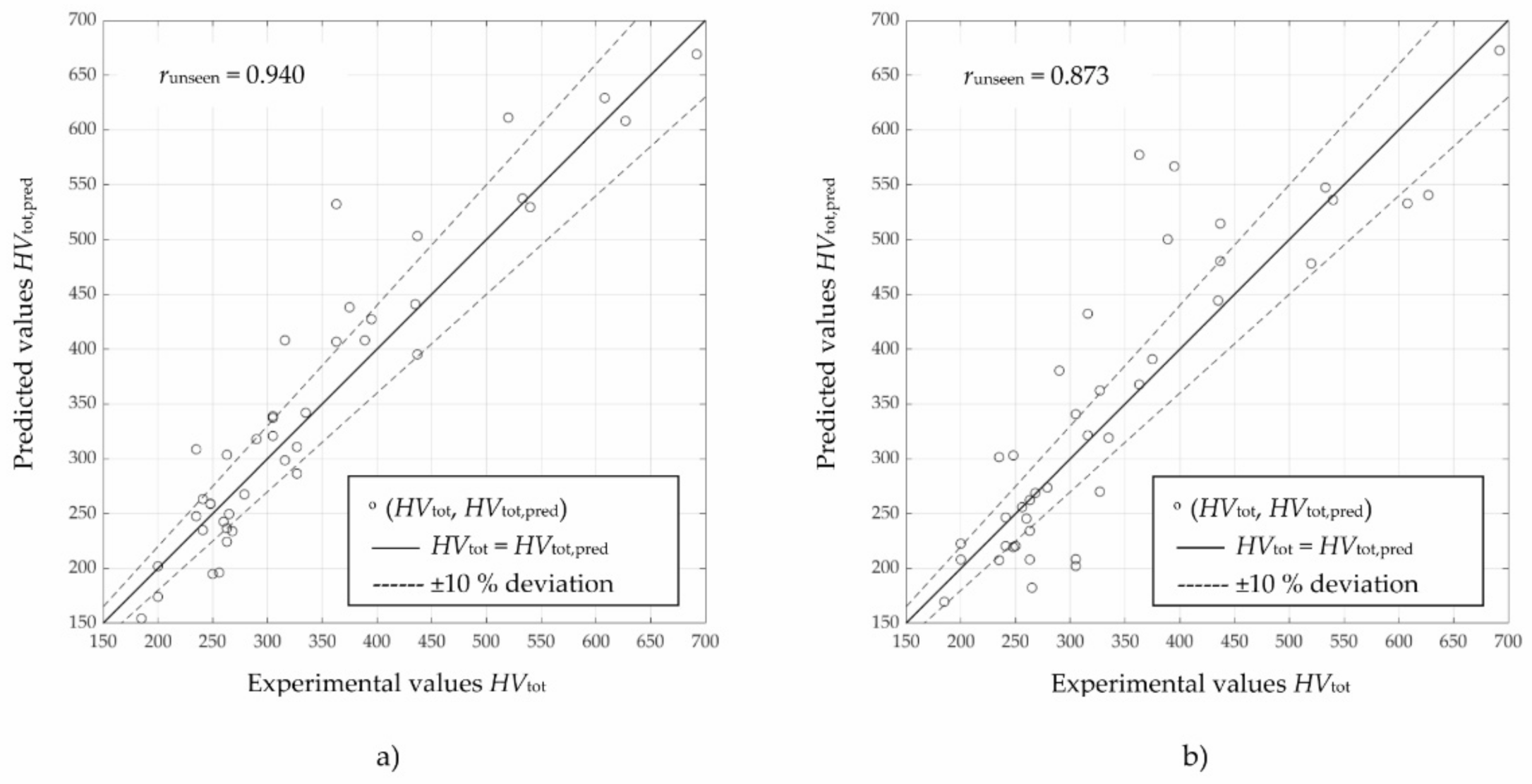
- Both configurations of artificial neural networks show similar performance. ANN using the specific Jominy distance as input variable (runseen = 0.873, RMSEunseen = 67, MAPE = 14.8%) is almost as successful as ANN using main alloying elements (runseen = 0.940, RMSEunseen = 46, MAPE = 10.7%).
- The prediction results indicate that the ANN designs are robust, and that generalization capability of the ANNs, as well as the expected forecasting/prediction are promising.
- The prediction of total hardness of steel can be successfully performed only based on four input variables: the austenitizing temperature, the austenitizing time, the cooling time to 500 °C, and the specific Jominy distance.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbaschian, R. Mechanical Testing. In Characterization of Materials, 1st ed.; Kaufmann, E.N., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 2003; Volumes 1–2, pp. 279–336. [Google Scholar]
- Narazaki, M.; Totten, G.E. Distortion of Heat-Treated Components. In Steel Heat Treatment Handbook: Metallurgy and Technologies, 2nd ed.; Totten, G.E., Ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2007; pp. 607–650. [Google Scholar]
- Şimşir, C.; Gür, C.H. Simulation of Quenching. In Handbook of Thermal Process Modeling of Steels; Gür, C.H., Pan, J., Eds.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2009; pp. 341–425. [Google Scholar]
- Smoljan, B.; Iljkić, D.; Totten, G.E. Mathematical Modeling and Simulation of Hardness of Quenched and Tempered Steel. Metall. Mater. Trans. B 2015, 46, 2666–2673. [Google Scholar] [CrossRef]
- Cahoon, J.R.; Broughton, W.H.; Kutzak, A.R. The determination of yield strength from hardness measurements. Metall. Trans. 1971, 2, 1979–1983. [Google Scholar] [CrossRef]
- Bain, E.C. Functions of the Alloying Elements in Steel; American Society for Metals: Cleveland, OH, USA, 1939. [Google Scholar]
- Krauss, G. Steels: Heat Treatment and Processing Principles, 2nd ed.; ASM International: Materials Park, OH, USA, 1990; pp. 1–16. [Google Scholar]
- Sverdlin, A.V.; Ness, A.R. Fundamental Concepts in Steel Heat Treatment. In Steel Heat Treatment: Metallurgy and Technologies, 2nd ed.; Totten, G.E., Ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2007; pp. 121–164. [Google Scholar]
- Colpaert, H. Metallography of Steel–Interpretation of Structure and the Effects of Processing; ASM International: Materials Park, OH, USA, 2018; pp. 193–352. [Google Scholar]
- Smokvina Hanza, S.; Smoljan, B.; Štic, L.; Hajdek, K. Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite. Metals 2021, 11, 180. [Google Scholar] [CrossRef]
- Liščić, B. Steel Heat Treatment. In Steel Heat Treatment Handbook: Metallurgy and Technologies, 2nd ed.; Totten, G.E., Ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2007; pp. 277–414. [Google Scholar]
- Smoljan, B.; Iljkić, D.; Smokvina Hanza, S.; Jokić, M.; Štic, L.; Borić, A. Mathematical Modeling and Computer Simulation of Steel Quenching. Mater. Perform. Charact. 2019, 8, 17–36. [Google Scholar] [CrossRef]
- Juez-Gil, M.; Erdakov, I.N.; Bustillo, A.; Pimenov, D.Y. A regression-tree multilayer-perceptron hybrid strategy for the prediction of ore crushing-plate lifetimes. J. Adv. Res. 2019, 18, 173–184. [Google Scholar] [CrossRef]
- Wang, S.; Xia, X.; Ye, L.; Yang, B. Automatic Detection and Classification of Steel Surface Defect Using Deep Convolutional Neural Networks. Metals 2021, 11, 388. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Colla, V.; Reyneri, L.M.; Sgarbi, M. Neuro-Wavelet parametric characterization of Jominy profiles of steels. Integr. Comput. Aided Eng. 2000, 7, 217–228. [Google Scholar] [CrossRef]
- Doane, D.V.; Kirkaldy, J.S. (Eds.) Hardenability Concepts with Applications to Steel, Proceedings of a Symposium Held at the Sheraton-Chicago Hotel, October 24–26, 1977; Metallurgical Society of AIME: Warrendale, PA, USA, 1978. [Google Scholar]
- Vermeulen, W.G.; van der Wolk, P.J.; de Weijer, A.P.; van der Zwaag, S. Prediction of Jominy Hardness Profiles of Steels Using Artificial Neural Networks. J. Mater. Eng. Perform. 1996, 5, 57–63. [Google Scholar] [CrossRef]
- Smoljan, B.; Smokvina Hanza, S.; Filetin, T. Prediction of Phase Transformation Using Neural Networks. In Proceedings of the 2nd International Conference Heat Treatment and Surface Engineering in Automotive Applications, Riva del Garda, Italy, 20–22 June 2005. [Google Scholar]
- Smokvina Hanza, S.; Iljkić, D.; Tomašić, N. Modelling of Microstructure Transformation during the steel quenching. In Proceedings of the 4th International PhD Conference on Mechanical Engineering, Pilsen, Czech Republic, 11–13 September 2006. [Google Scholar]
- Chan, B.; Bibby, M.; Holtz, N. Predicting HAZ hardness with artificial neural networks. Can. Metall. Q. 1995, 34, 353–356. [Google Scholar] [CrossRef]
- Dobrzanski, L.A.; Kowalski, M.; Madejski, J. Methodology of the mechanical properties prediction for the metallurgical products from the engineering steels using the artificial intelligence methods. J. Mater. Process. Technol. 2005, 164-165, 1500–1509. [Google Scholar] [CrossRef]
- Kusiak, J.; Kuziak, R. Modelling of microstructure and mechanical properties of steel using the artificial neural network. J. Mater. Process. Technol. 2002, 127, 115–121. [Google Scholar] [CrossRef]
- Yilmaz, M.; Metin Ertunc, H. The prediction of mechanical behavior for steel wires and cord materials using neural networks. Mater. Des. 2007, 28, 599–608. [Google Scholar] [CrossRef]
- Song, R.G.; Zhang, Q.Z. Heat treatment optimization for 7175 aluminum alloy by genetic algorithm. Mater. Sci. Eng. C 2001, 17, 133–137. [Google Scholar] [CrossRef]
- Trzaska, J. Neural networks model for prediction of the hardness of steels cooled from the austenitizing temperature. Arch. Mater. Sci. Eng. 2016, 82, 62–69. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Li, X.; Xie, Z.; Liu, R.; Liu, W.; Zhang, Y.; Xu, Y.; Liu, C. Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals 2020, 10, 234. [Google Scholar] [CrossRef]
- Narayana, P.L.; Kim, J.H.; Maurya, A.K.; Park, C.H.; Hong, J.-K.; Yeom, J.-T.; Reddy, N.S. Modeling Mechanical Properties of 25Cr-20Ni-0.4C Steels over a Wide Range of Temperatures by Neural Networks. Metals 2020, 10, 256. [Google Scholar] [CrossRef]
- Liščić, B. Hardenability. In Steel Heat Treatment Handbook: Metallurgy and Technologies, 2nd ed.; Totten, G.E., Ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2007; pp. 213–276. [Google Scholar]
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Basan, R.; Franulović, M.; Smokvina Hanza, S. Estimation of cyclic stress-strain curves for low-alloy steel from hardness. Metallurgy 2010, 49, 83–86. [Google Scholar]
- Just, E. Hardening and tempering—Influencing steel by hardening. Vdi Ber. 1976, 256, 125–140. (In German) [Google Scholar]
- Rose, A.; Hougardy, H. Atlas zur Wärmebehandlung der Stähle; Verlag Stahleisen: Düsseldorf, Germany, 1972. [Google Scholar]
- Smoljan, B.; Iljkić, D.; Traven, F. Mathematical modelling of mechanical properties of quenched and tempered steel. Int. Heat Treat. Surf. Eng. 2013, 7, 16–22. [Google Scholar] [CrossRef]
- Iljkić, D. A Contribution to the Development of the Mechanical Properties Prediction of Quenched and Tempered Steel and Cast Steel. Ph.D. Thesis, University of Rijeka, Rijeka, Croatia, 2010. (In Croatian). [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design, 2nd ed.; Oklahoma State University: Stillwater, OK, USA, 2014. [Google Scholar]
| Data No. | Designation (DIN) | Chemical Composition, wt. % | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Al | Cr | Cu | Mo | Ni | V | ||
| 1. | Ck15 | 0.15 | 0.22 | 0.41 | 0.021 | 0.024 | <0.005 | 0.06 | 0.15 | - | 0.06 | - |
| 2. | Ck15 1 | 0.30 | 0.29 | 0.39 | 0.012 | 0.026 | 0.003 | 0.12 | 0.215 | - | - | - |
| 3. | 16MnCr5 | 0.16 | 0.22 | 1.12 | 0.030 | 0.008 | 0.015 | 0.99 | - | 0.02 | 0.12 | 0.01 |
| 4. | 15CrNi6 | 0.13 | 0.31 | 0.51 | 0.023 | 0.009 | 0.010 | 1.50 | - | 0.06 | 1.55 | <0.01 |
| 5. | 20MoCr4 1 | 0.28 | 0.30 | 0.66 | 0.018 | 0.011 | 0.049 | 0.56 | 0.18 | 0.44 | 0.15 | - |
| 6. | 20MoCr4 1 | 0.57 | 0.30 | 0.66 | 0.018 | 0.011 | 0.049 | 0.56 | 0.18 | 0.44 | 0.15 | - |
| 7. | 25MoCr4 1 | 0.31 | 0.20 | 0.67 | 0.017 | 0.022 | 0.034 | 0.50 | - | 0.45 | 0.11 | - |
| 8. | 20NiMoCr6 1 | 0.28 | 0.15 | 0.62 | 0.015 | 0.020 | 0.015 | 0.47 | - | 0.48 | 1.58 | - |
| 9. | Ck45 | 0.44 | 0.22 | 0.66 | 0.022 | 0.029 | - | 0.15 | - | - | - | 0.02 |
| 10. | 37MnSi5 | 0.38 | 1.05 | 1.14 | 0.035 | 0.019 | - | 0.23 | - | - | - | 0.02 |
| 11. | 42MnV7 | 0.43 | 0.28 | 1.67 | 0.021 | 0.008 | - | 0.32 | 0.06 | 0.03 | 0.11 | 0.10 |
| 12. | 34Cr4 | 0.35 | 0.23 | 0.65 | 0.026 | 0.013 | - | 1.11 | 0.18 | 0.05 | 0.23 | <0.01 |
| 13. | 34Cr4 | 0.36 | 0.29 | 0.69 | 0.011 | 0.014 | - | 1.09 | 0.12 | 0.07 | 0.08 | 0.01 |
| 14. | 41Cr4 | 0.44 | 0.22 | 0.80 | 0.030 | 0.023 | - | 1.04 | 0.17 | 0.04 | 0.26 | <0.01 |
| 15. | 41Cr4 | 0.41 | 0.25 | 0.71 | 0.031 | 0.024 | - | 1.06 | 0.17 | 0.02 | 0.22 | <0.01 |
| 16. | 36Cr6 | 0.36 | 0.25 | 0.49 | 0.021 | 0.020 | - | 1.54 | 0.16 | 0.03 | 0.21 | <0.01 |
| 17. | 25CrMo4 | 0.22 | 0.25 | 0.64 | 0.010 | 0.011 | - | 0.97 | 0.16 | 0.23 | 0.33 | <0.01 |
| 18. | 34CrMo4 | 0.30 | 0.22 | 0.64 | 0.011 | 0.012 | - | 1.01 | 0.19 | 0.24 | 0.11 | <0.01 |
| 19. | 42CrMo4 | 0.38 | 0.23 | 0.64 | 0.019 | 0.013 | - | 0.99 | 0.17 | 0.16 | 0.08 | <0.01 |
| 20. | 50CrMo4 | 0.50 | 0.32 | 0.80 | 0.017 | 0.022 | - | 1.04 | 0.17 | 0.24 | 0.11 | <0.01 |
| 21. | 50CrMo4 | 0.46 | 0.22 | 0.50 | 0.015 | 0.014 | - | 1.00 | 0.26 | 0.21 | 0.22 | <0.01 |
| 22. | 27MnCrV4 | 0.24 | 0.21 | 1.06 | 0.014 | 0.020 | - | 0.79 | 0.17 | 0.02 | 0.18 | <0.01 |
| 23. | 50CrV4 | 0.55 | 0.22 | 0.98 | 0.017 | 0.013 | - | 1.02 | 0.07 | - | 0.01 | 0.11 |
| 24. | 50CrV4 | 0.47 | 0.35 | 0.82 | 0.035 | 0.015 | - | 1.20 | 0.14 | - | 0.04 | 0.11 |
| Data No. | Variable | Data No. | Variable |
|---|---|---|---|
| 1. | Carbon (C, wt. %) | 6. | Nickel (Ni, wt. %) |
| 2. | Silicon (Si, wt. %) | 7. | Austenitizing temperature (Ta, °C) |
| 3. | Manganese (Mn, wt. %) | 8. | Austenitizing time (ta, min.) |
| 4. | Chromium (Cr, wt. %) | 9. | Cooling time to 500 °C (t500, s) |
| 5. | Molybdenum (Mo, wt. %) | 10. | Specific Jominy distance (Ed, mm) |
| Data No. | C wt. % | Si wt. % | Mn wt. % | Cr wt. % | Mo wt. % | Ni wt. % | Ta °C | ta min | t500 s | Ed mm | HVtot |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 3.0 | 16 | 735 |
| 2. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 8.8 | 16 | 627 |
| 3. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 51.0 | 16 | 279 |
| 4. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 98.0 | 16 | 267 |
| 5. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 296.4 | 16 | 267 |
| 6. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 611.7 | 16 | 263 |
| 7. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 2010.8 | 16 | 235 |
| 8. | 0.38 | 0.23 | 0.64 | 0.99 | 0.16 | 0.08 | 1050 | 10 | 6961.4 | 16 | 245 |
| Variable | Configuration No. 1 | Configuration No. 2 | |
|---|---|---|---|
| Input | Carbon (C, wt. %) | + | |
| Silicon (Si, wt. %) | + | ||
| Manganese (Mn, wt. %) | + | ||
| Chromium (Cr, wt. %) | + | ||
| Molybdenum (Mo, wt. %) | + | ||
| Nickel (Ni, wt. %) | + | ||
| Austenitizing temperature (Ta, °C) | + | + | |
| Austenitizing time (ta, min.) | + | + | |
| Cooling time to 500 °C (t500, s) | + | + | |
| Specific Jominy distance (Ed, mm) | + | ||
| Output | Total hardness after continuous cooling (HVtot, HV) | + | + |
| Configuration No. | Hidden Layer Size H | Training No. | r | RMSE | rtest | RMSEtest |
|---|---|---|---|---|---|---|
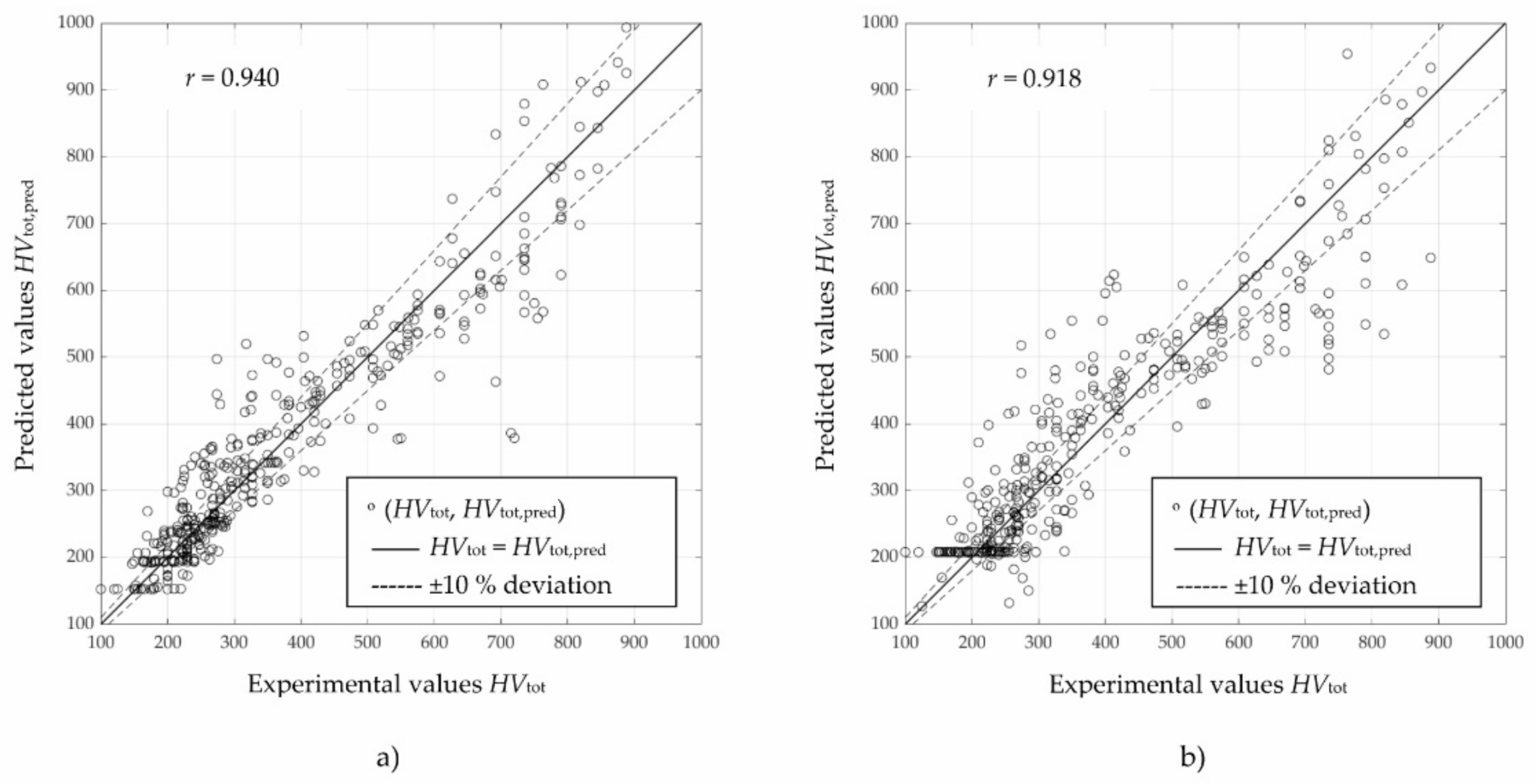
| 1 | 3 | 7 | 0.940 | 65 | 0.911 | 88 |
| 2 | 6 | 3 | 0.918 | 75 | 0.903 | 93 |
| Configuration No. | runseen | RMSEunseen | MAPEunseen, % |
|---|---|---|---|
| 1 | 0.940 | 46 | 10.7 |
| 2 | 0.873 | 67 | 14.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smokvina Hanza, S.; Marohnić, T.; Iljkić, D.; Basan, R. Artificial Neural Networks-Based Prediction of Hardness of Low-Alloy Steels Using Specific Jominy Distance. Metals 2021, 11, 714. https://doi.org/10.3390/met11050714
Smokvina Hanza S, Marohnić T, Iljkić D, Basan R. Artificial Neural Networks-Based Prediction of Hardness of Low-Alloy Steels Using Specific Jominy Distance. Metals. 2021; 11(5):714. https://doi.org/10.3390/met11050714
Chicago/Turabian StyleSmokvina Hanza, Sunčana, Tea Marohnić, Dario Iljkić, and Robert Basan. 2021. "Artificial Neural Networks-Based Prediction of Hardness of Low-Alloy Steels Using Specific Jominy Distance" Metals 11, no. 5: 714. https://doi.org/10.3390/met11050714
APA StyleSmokvina Hanza, S., Marohnić, T., Iljkić, D., & Basan, R. (2021). Artificial Neural Networks-Based Prediction of Hardness of Low-Alloy Steels Using Specific Jominy Distance. Metals, 11(5), 714. https://doi.org/10.3390/met11050714








