Investigation on Analysis Method of Environmental Fatigue Correction Factor of Primary Coolant Metal Materials in LWR Water Environment
Abstract
:1. Introduction
2. EAF Analysis Method and Fen Expression
2.1. EAF Analysis Method
- (1)
- Calculate the fatigue usage factor in the air for the key parts:
- The temperature and pressure transients of the model are calculated one by one, and the envelope curves of the design transient and the actual operation transient should be used for the temperature and pressure transient curves;
- The peak value of stress is selected as the event in fatigue analysis combined with the operation basis earthquake load;
- According to the fatigue calculation method of ASME or RCC-M and the fatigue curve in the air, the fatigue service factor is calculated. The number of each transient should consider the actual operation of the power plant. Assuming that the design life of the nuclear power plant is years and has been in operation for years, the nuclear power plant will apply for extending its life by years. The number of transients that have been in operation for years is the operated number , and the number of T − H + E year transients that have not been operated is of the original design transient numbers NT. Each transient number is the sum of these two parts, namely, .
- (2)
- Compute the for each transient pair in the fatigue analysis.
- (3)
- Apply the to the fatigue usage factor calculated for each transient pair , to determine the cumulative fatigue usage factor considering the effect of the water environment ().where n is the number of transient pairs.
2.2. Fen Expression
3. Transformed Strain Rate of Fen Calculation
3.1. Detailed Method
- (1)
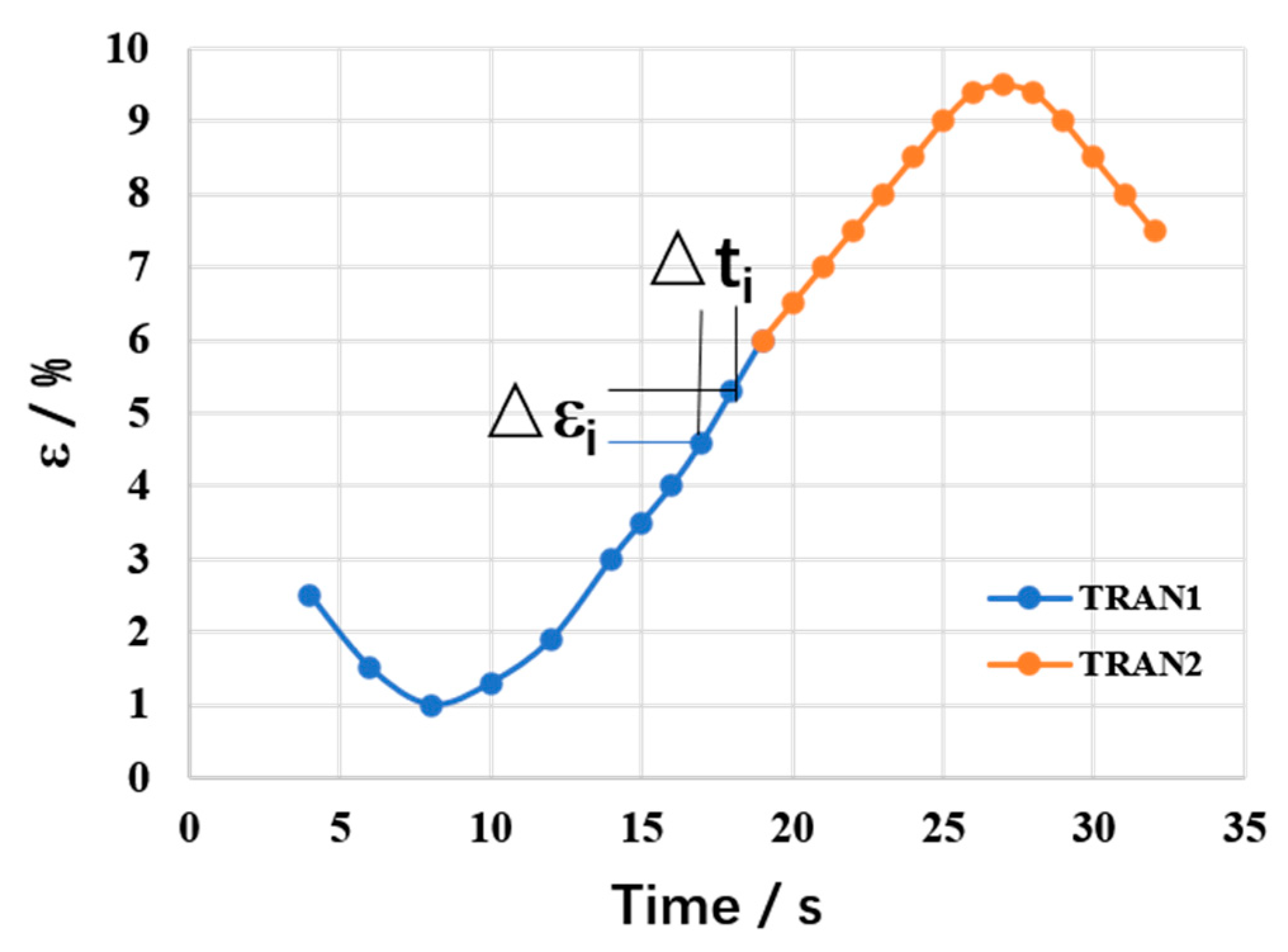
- Calculate the stress range (, , , , , ) between the (i−1)th and the ith time steps on a component basis;
- (2)
- From , , , , and , the principal stress ranges , , and the stress intensity range () can be computed;
- (3)
- A sign is then assigned to the stress intensity range based on the sign of the principal stress range with the largest magnitude, as shown in Equation (15).where is defined as the largest absolute value of the principal stress range (, , ), and Sgn is the corresponding sign.
- (4)
- The strain increment () is then computed so that only increments that are increasingly tensile will be included in the Fen calculation, based on the following equation:where is the elastic–plastic factor, and E is the elastic modulus.
- (1)
- From the stress tensor (, , , , , ), the principal stresses are calculated (, , );
- (2)
- The differences of principal stresses are then calculated,
- (3)
- The signed Tresca stress intensity is then defined as the largest absolute value of , and , with the maximum principal stress corresponding sign;
- (4)
- Lastly, the signed Tresca equivalent strain is obtained by dividing the previously obtained stress by the modulus of elasticity from the stress calculation.
3.2. Simplified Method
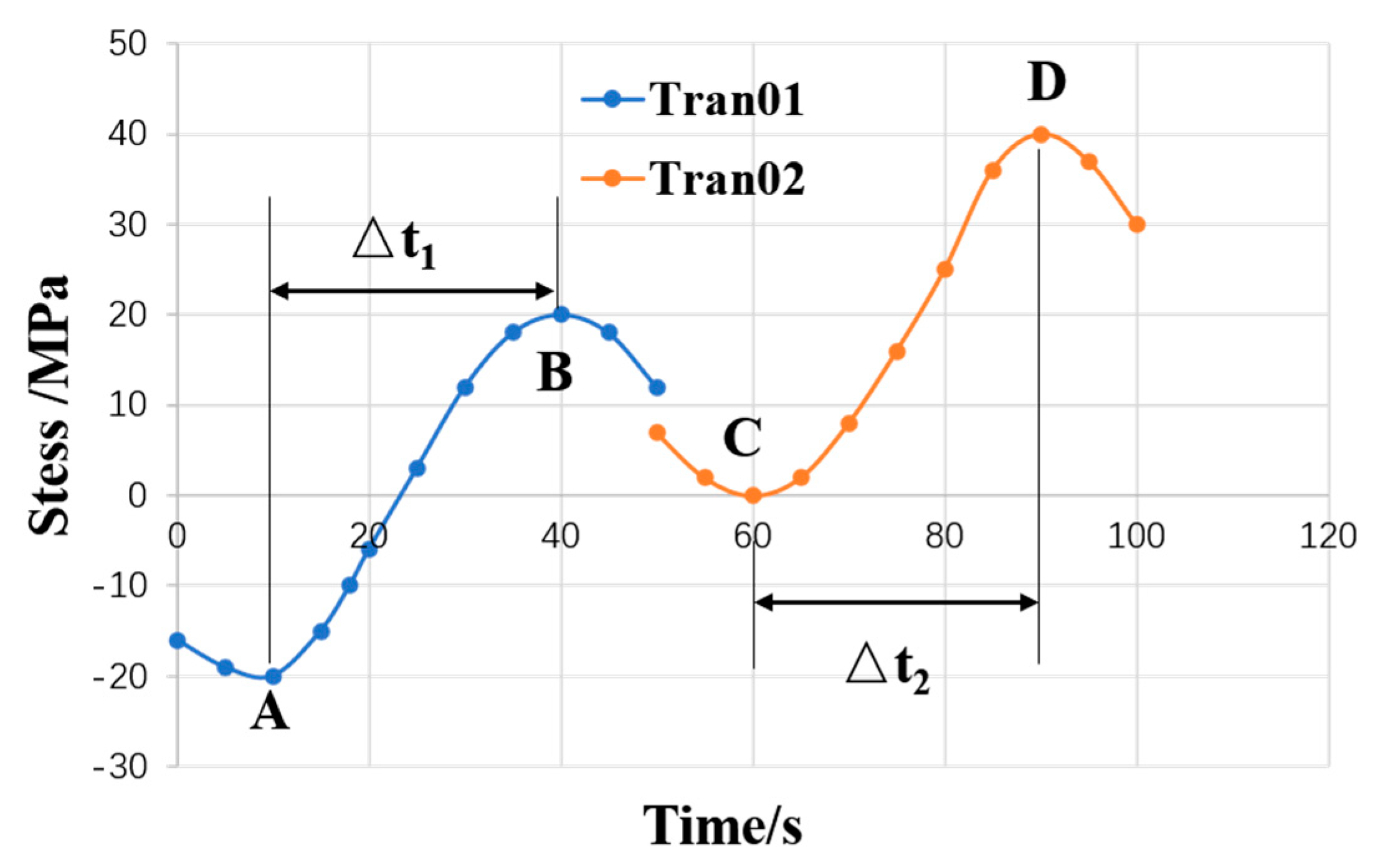
- (1)
- Firstly, in the transient time history, the period when the stress increment is positive is selected to determine the maximum stress and minimum stress , , , , , , , , , , , ;
- (2)
- The stress rates of the six components are determined by dividing the corresponding time increment;
- (3)
- According to the six components of the stress rate tensor, the rate of stress intensity is determined;
- (4)
- The strain rate and strain amplitude are then calculated as
4. The Simple Model Analysis and Comparison
4.1. EPRI Guideline Case
4.2. The Influence of Different Fen Expressions
4.3. The Influence of Different Strain Rate Approaches
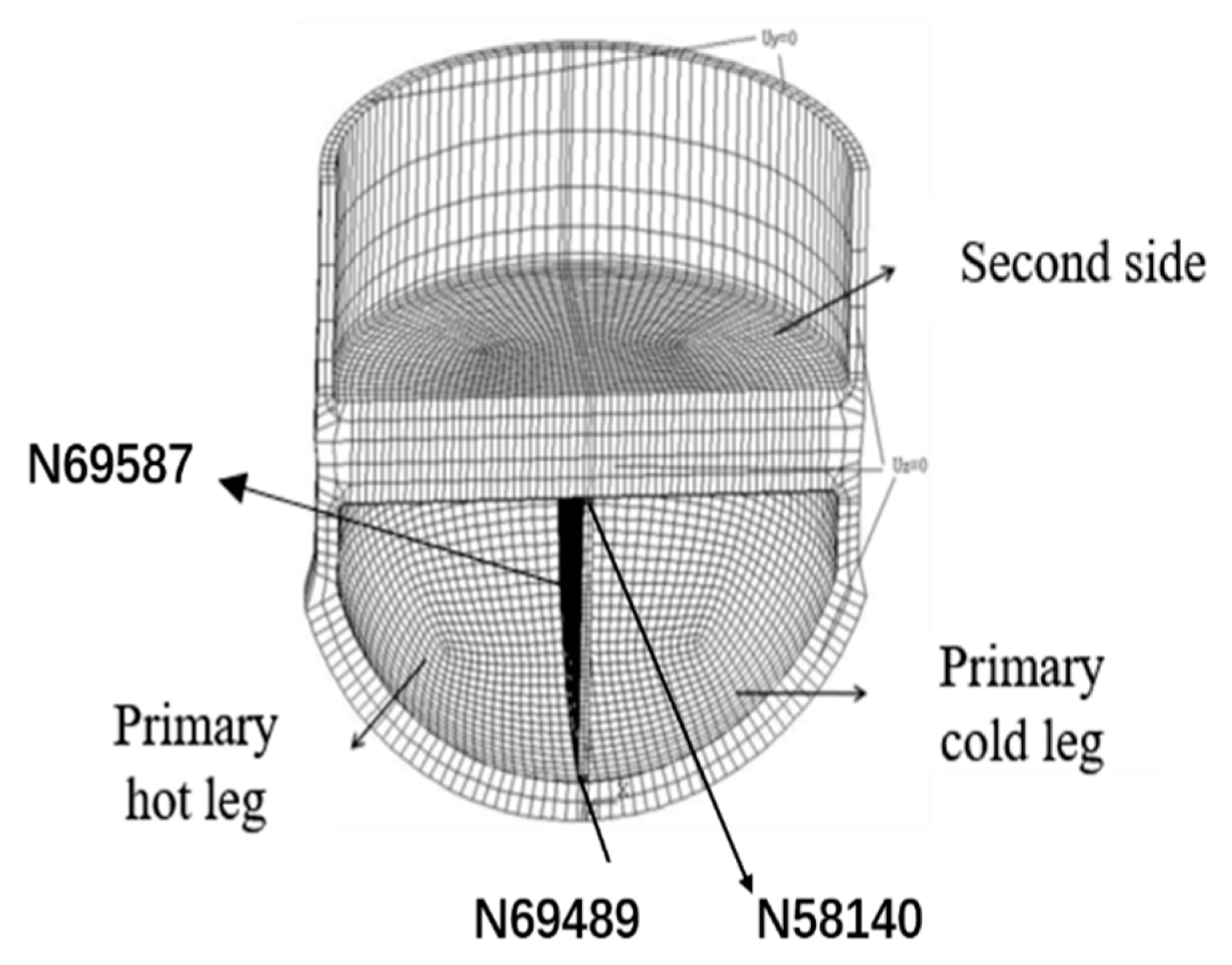
5. Reactor Pressure Vessel and Steam Generator EAF Evaluation
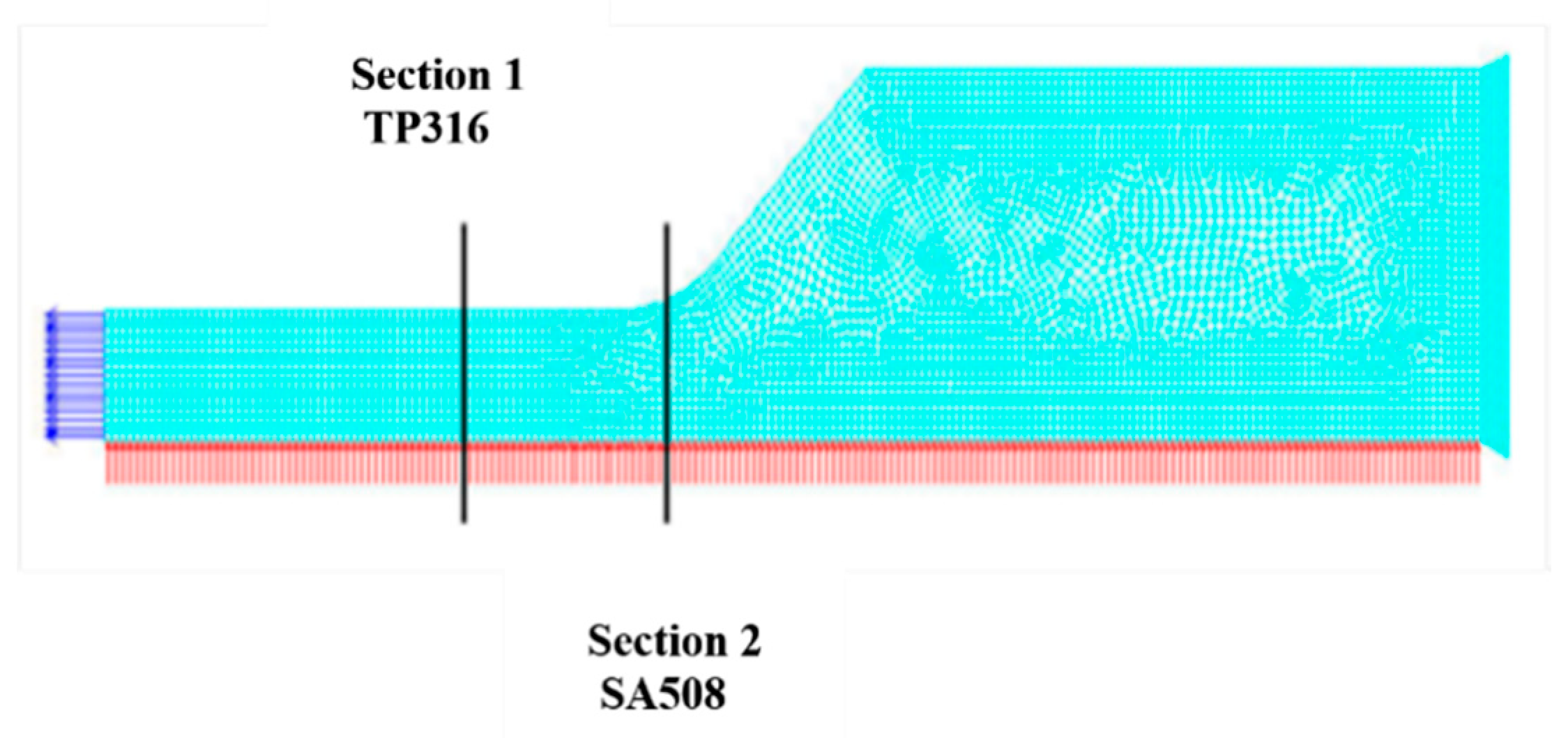
5.1. Environmental Fatigue Calculation of RPV
5.2. Environmental Fatigue Calculation of Steam Generator
6. Summary
- (1)
- By comparing the detailed method with the average strain and conservative method, the detailed strain rate method can more accurately evaluate the environmental fatigue life of the structure and can be applied to the analysis of the metal fatigue time-limit aging of key components in the nuclear power plant;
- (2)
- Compared with Fen expressions of JNES, CR6909 Rev.0 and CR6909 Rev.1, NUREG/CR-6909 Rev.1 has the smallest result and JNES has the largest result, which indicates that JNES in Japan allows a more rigorous assessment of environmental fatigue;
- (3)
- The influence of the Fen expression for low-alloy steel is opposite to that for austenitic stainless steel and nickel-based alloy. The calculation results of version 1 are greater than those of version 0, and the maximum difference increases by 62.6%;
- (4)
- Compared with the GD method, the RPP3 method has a lesser effect on the maximum differences between the austenitic stainless steel and low-alloy steel at the inlet nozzle of the pressure vessel, which are 1.9% and 5.1%, respectively. For the nickel-based alloy of the steam generator’s divider plate, the maximum difference is 16%;
- (5)
- If the fatigue usage factor of austenitic stainless steel in the air is less than 0.065 and that of nickel-based alloy is less than 0.078, the influence of environmental fatigue can be ignored.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Omesh, C.K.; Shack, W.J. Effect of LWR coolant environments on fatigue S-N curves for carbon and low-alloy steel: ANL/ET/CP/89687. In Proceedings of the American Society of Mechanical Engineers (ASME) pressure vessels and piping conference, Montreal, QC, Canada, 21–26 July 1996. [Google Scholar]
- He, Y.; Cao, M.; Yao, W. Overview of LWR environment assisted fatigue issues for primary components and piping of NPPs. Nucl. Eng. Des. 2011, 32, 35–39. [Google Scholar]
- Sun, H.; Wang, C.; Xiong, D. Effect of PWR coolant environment on the fatigue life of reactor equipment materials. Chin. J. Nucl. Sci. Eng. 2014, 34, 482–487. [Google Scholar]
- Shao, X.; Xie, H.; Zhang, L. Analysis of fatigue time limit aging of reactor pressure vessels. Nucl. Eng. Des. 2020, 41, 60–64. [Google Scholar]
- NRC Regulatory Guide 1.207. NRC Guidelines for Evaluating Fatigue Analyses Incorporating the Life Reduction of Metal Components Due to the Effects of the Light-Water Reactor Environment for New Reactors; NRC: North Bethesda, MD, USA, 2007. [Google Scholar]
- Argonne National Laboratory. Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials: NUREG/CR6909 ANL-06/08; Argonne National Laboratory: Lemont, IL, USA, 2007. [Google Scholar]
- Higuchi, M.; Iida, K. Fatigue Strength Correction Factors for Carbon and Low-Alloy Steels in Oxygen-Containing high-Temperature Water. Nucl. Eng. Des. 1991, 129, 293–306. [Google Scholar] [CrossRef]
- Argonne National Laboratory. Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials: NUREG/CR6909 ANL-12/60; Argonne National Laboratory: Lemont, IL, USA, 2018. [Google Scholar]
- Higuchi, M.; Sakaguchi, K. Final proposal of environmental fatigue life correction factor (Fen) for Structural materials in LWR water environment. In Proceedings of the 2007 ASME Pressure Vessels and Piping Division Conference, San Antonio, TX, USA, 22–26 July 2007. [Google Scholar]
- EPRI. Guidelines for Addressing Environmental Effects in Fatigue Usage Calculations; 2012 Technical Report 1025823; EPRI: Palo Alto, CA, USA, 2012. [Google Scholar]
- RCC-M. Design and Construction Rules for Mechanical Components of PWR Nuclear Islands, 2017 Edition Section VI-Probationary Phase Rules RPP3; AFCEN: Paris, France, 2017. [Google Scholar]
- ASME. ASME Boiler and Pressure Vessel Code: 2007 + 2009 Addenda Edition, Section II Materials, Part D—Properties; ASME: New York, NY, USA, 2009. [Google Scholar]

| Transient | Time T/s | Temperature/°C | Heat Transfer/(W·m−2·K−1) | Pressure/MPa | Moment/(kN·m) |
|---|---|---|---|---|---|
| Tran1 N = 20 | 0 | 315.6 | 8831 | 15.513 | −338.97 |
| 5 | 315.6 | 8831 | 15.513 | −338.97 | |
| 205 | 37.8 | 8831 | 6.895 | 112.99 | |
| 100 | 37.8 | 8831 | 6.895 | 112.99 | |
| 1200 | 315.6 | 8831 | 15.513 | −338.97 | |
| 3000 | 315.6 | 8831 | 15.513 | −338.97 | |
| Tran 2 N = 50 | 0 | 260.0 | 8831 | 10.342 | −282.48 |
| 5 | 260.0 | 8831 | 10.342 | −282.48 | |
| 405 | 315.6 | 8831 | 15.513 | 112.99 | |
| 1500 | 315.6 | 8831 | 15.513 | 112.99 | |
| 1900 | 260.0 | 8831 | 13.790 | −282.48 | |
| 2500 | 260.0 | 8831 | 13.790 | −282.48 | |
| Tran 3 N = 20 | 0 | 232.2 | 8831 | 3.103 | −225.98 |
| 5 | 232.2 | 8831 | 3.103 | −225.98 | |
| 14,000 | 21.1 | 8831 | 3.034 | 169.49 | |
| 16,000 | 21.1 | 8831 | 2.758 | 169.49 | |
| 20,000 | 176.7 | 8831 | 2.758 | −225.98 | |
| 24,000 | 176.7 | 8831 | 2.758 | −225.98 |
| Section | Pair | TranA | TranB | Ui | Fen | Fen-GD | Ui·Fen | CUF-water |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0.72676 | 5.0271 | 5.1166 | 3.6535 | 4.3092 |
| 2 | 2 | 2 | 0.16684 | 3.9304 | 3.9854 | 0.65575 | ||
| 3 | 3 | 3 | 0 | 2.7225 | 2.7153 | 0 |
| Section | Pair | Ui | CUF-air | Fen | Ui·Fen | CUF-water | CUF-water-GD |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.6706 | 1.3498 | 4.79 | 3.2115 | 5.7088 | 5.4521 |
| 2 | 0.5580 | 3.87 | 2.1618 | ||||
| 3 | 0.0756 | 2.66 | 0.2010 | ||||
| 4 | 0.0256 | 2.49 | 0.0637 | ||||
| 5 | 0.0154 | 2.71 | 0.0418 | ||||
| 6 | 0.0027 | 6.37 | 0.0173 | ||||
| 7 | 0.0012 | 8.09 | 0.0094 | ||||
| 8 | 0.0002 | 1.00 | 0.0002 | ||||
| 9 | 0.0005 | 4.09 | 0.0022 | ||||
| 2 | 1 | 0.0914 | 0.131 | 11.60 | 1.0594 | 1.2381 | 1.5979 |
| 2 | 0.0349 | 4.51 | 0.1574 | ||||
| 3 | 0.0015 | 6.74 | 0.0102 | ||||
| 4 | 0.0015 | 2.76 | 0.0041 | ||||
| 5 | 0.0011 | 3.53 | 0.0040 | ||||
| 6 | 0.0002 | 4.09 | 0.0008 | ||||
| 7 | 0.0002 | 5.04 | 0.0008 | ||||
| 8 | 0.0001 | 8.61 | 0.0009 | ||||
| 9 | 0.0001 | 8.60 | 0.0005 |
| Transient | NUREG/CR-6909Rev.0 | NUREG/CR-6909Rev.1 | JNES |
|---|---|---|---|
| 1 | 5.0271 | 4.2856 | 7.0267 |
| 2 | 3.9304 | 3.0306 | 5.7055 |
| 3 | 2.7470 | 1.9071 | 4.1400 |
| Transients | Detailed-GD | Detailed-RPP3 | Simplified Method |
|---|---|---|---|
| 1 | 5.0271 | 4.991 | 6.5470 |
| 2 | 3.9304 | 3.874 | 4.9870 |
| 3 | 2.7470 | 2.718 | 3.5420 |
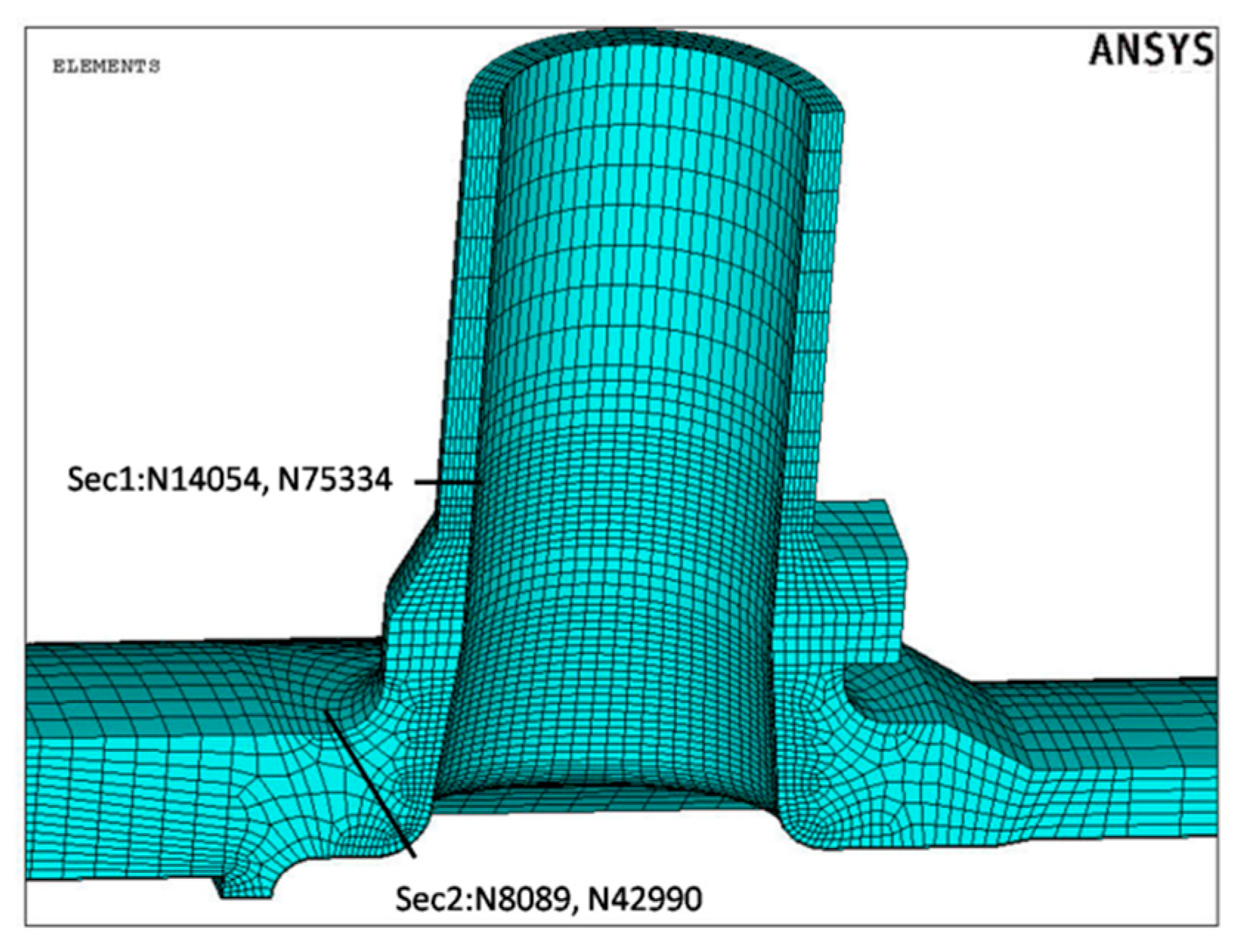
| Node | Pair | TranA | TranB | Ui | Fen-GD-V0 | Fen-GD-V1 | Fen-RPP-V0 | Fen-RPP-V1 |
|---|---|---|---|---|---|---|---|---|
| 14054 (F316) | 1 | 1 | 6 | 0.00056 | 8.13 | 7.13 | 8.05 | 7.05 |
| 2 | 6 | 15 | 0.00025 | 6.81 | 5.97 | 6.68 | 5.86 | |
| 3 | 6 | 6 | 0.00044 | 6.81 | 5.97 | 6.68 | 5.86 | |
| 8089 (SA-508) | 1 | 1 | 3 | 0.15256 | 6.18 | 9.95 | 5.98 | 9.57 |
| 2 | 1 | 5 | 0.02080 | 6.42 | 10.41 | 6.23 | 10.05 | |
| 3 | 5 | 6 | 0.00008 | 5.01 | 7.35 | 5.05 | 7.23 | |
| 4 | 6 | 6 | 0.01322 | 5.69 | 8.14 | 5.81 | 7.99 | |
| 5 | 5 | 6 | 0.00002 | 5.01 | 7.35 | 5.05 | 7.02 | |
| 6 | 13 | 14 | 0.00016 | 2.02 | 2.19 | 2.02 | 2.10 | |
| 7 | 5 | 11 | 0.00024 | 3.81 | 5.59 | 3.73 | 5.44 | |
| 8 | 10 | 11 | 0.00066 | 2.68 | 3.63 | 2.59 | 3.47 | |
| 9 | 10 | 12 | 0.00029 | 5.77 | 8.98 | 5.65 | 8.64 | |
| 10 | 13 | 13 | 0.00150 | 2.02 | 2.22 | 2.02 | 2.14 | |
| 11 | 13 | 14 | 0.00006 | 2.02 | 2.19 | 2.02 | 2.10 | |
| 12 | 10 | 11 | 0.00002 | 2.98 | 4.17 | 2.86 | 3.96 | |
| 13 | 10 | 15 | 0.00001 | 7.04 | 11.46 | 7.05 | 11.47 |
| Node | CUF-air | CUF-water-GD-V0 | CUF-water-GD-V1 | CUF-water-RPP-V0 | CUF-water-RPP-V1 | CUF-water-CONSER |
|---|---|---|---|---|---|---|
| 14,054 | 0.00125 | 0.00931 | 0.00816 | 0.00917 | 0.00804 | 0.01288 |
| 8089 | 0.18962 | 1.15985 | 1.85393 | 1.12715 | 1.78466 | 2.30957 |
| Node | TranA | TranB | Ui | Fen-GD-V0 | Fen-GD-V1 | Fen-RPP-V0 | Fen-RPP-V1 |
|---|---|---|---|---|---|---|---|
| 69587 | 2 | 31 | 0.00146 | 3.16 | 2.60 | 3.39 | 2.80 |
| 2 | 37 | 0.00154 | 3.15 | 2.58 | 3.37 | 2.78 | |
| 2 | 34 | 0.00012 | 3.30 | 2.70 | 3.56 | 2.92 | |
| 2 | 26 | 0.00066 | 3.27 | 2.68 | 3.55 | 2.92 | |
| 2 | 36 | 0.00003 | 3.18 | 2.61 | 3.52 | 2.89 | |
| 21 | 36 | 0.00003 | 2.66 | 2.17 | 2.37 | 1.92 | |
| 21 | 22 | 0.00002 | 2.65 | 2.16 | 2.35 | 1.91 | |
| 14 | 21 | 0.00030 | 2.77 | 2.26 | 2.32 | 1.88 | |
| 3 | 21 | 0.00027 | 2.62 | 2.13 | 2.26 | 1.83 | |
| 1 | 3 | 0.00009 | 3.27 | 2.68 | 3.56 | 2.94 |
| Node | CUF-air | CUF-water-GD-V0 | CUF-water-GD-V1 | CUF-water-GD-RPP-V0 | CUF-water-GD-RPP-V1 |
|---|---|---|---|---|---|
| 69,587 | 0.00452 | 0.01407 | 0.01154 | 0.01474 | 0.01214 |
| 58,140 | 0.00146 | 0.00423 | 0.00346 | 0.00350 | 0.00287 |
| 69,489 | 0.00341 | 0.01054 | 0.00864 | 0.01093 | 0.00901 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, X.; Xie, H.; Zhang, Y.; Xiong, F.; Bai, X.; Jiang, L.; Kan, Q. Investigation on Analysis Method of Environmental Fatigue Correction Factor of Primary Coolant Metal Materials in LWR Water Environment. Metals 2021, 11, 233. https://doi.org/10.3390/met11020233
Shao X, Xie H, Zhang Y, Xiong F, Bai X, Jiang L, Kan Q. Investigation on Analysis Method of Environmental Fatigue Correction Factor of Primary Coolant Metal Materials in LWR Water Environment. Metals. 2021; 11(2):233. https://doi.org/10.3390/met11020233
Chicago/Turabian StyleShao, Xuejiao, Hai Xie, Yixiong Zhang, Furui Xiong, Xiaoming Bai, Lu Jiang, and Qianhua Kan. 2021. "Investigation on Analysis Method of Environmental Fatigue Correction Factor of Primary Coolant Metal Materials in LWR Water Environment" Metals 11, no. 2: 233. https://doi.org/10.3390/met11020233
APA StyleShao, X., Xie, H., Zhang, Y., Xiong, F., Bai, X., Jiang, L., & Kan, Q. (2021). Investigation on Analysis Method of Environmental Fatigue Correction Factor of Primary Coolant Metal Materials in LWR Water Environment. Metals, 11(2), 233. https://doi.org/10.3390/met11020233





