Distortion-Induced Fatigue Reassessment of a Welded Bridge Detail Based on Structural Stress Methods
Abstract
:1. Introduction
2. Structural Stress Methods
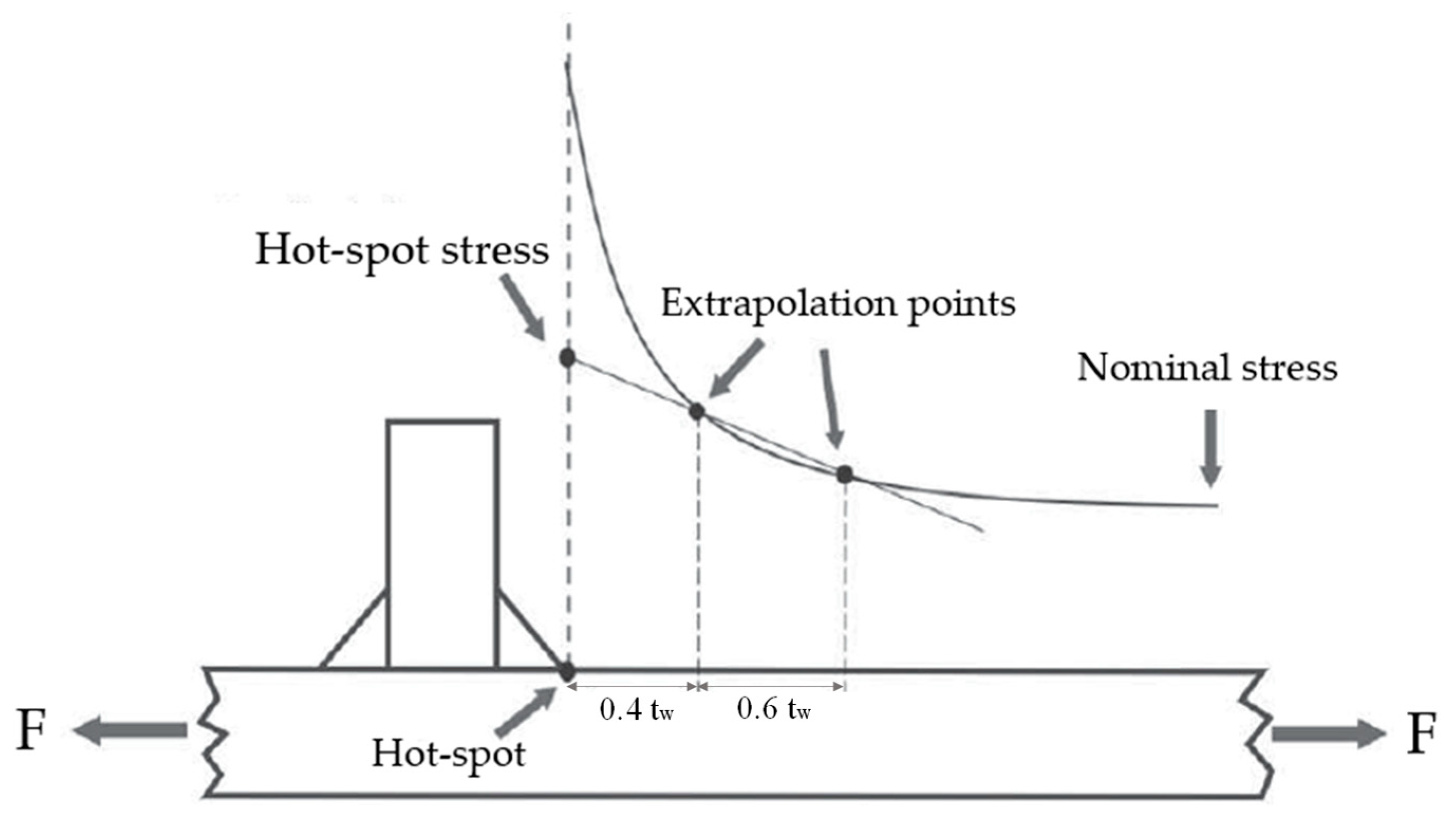
2.1. Hot-Spot Stress Method
2.2. The Master S-N Curve
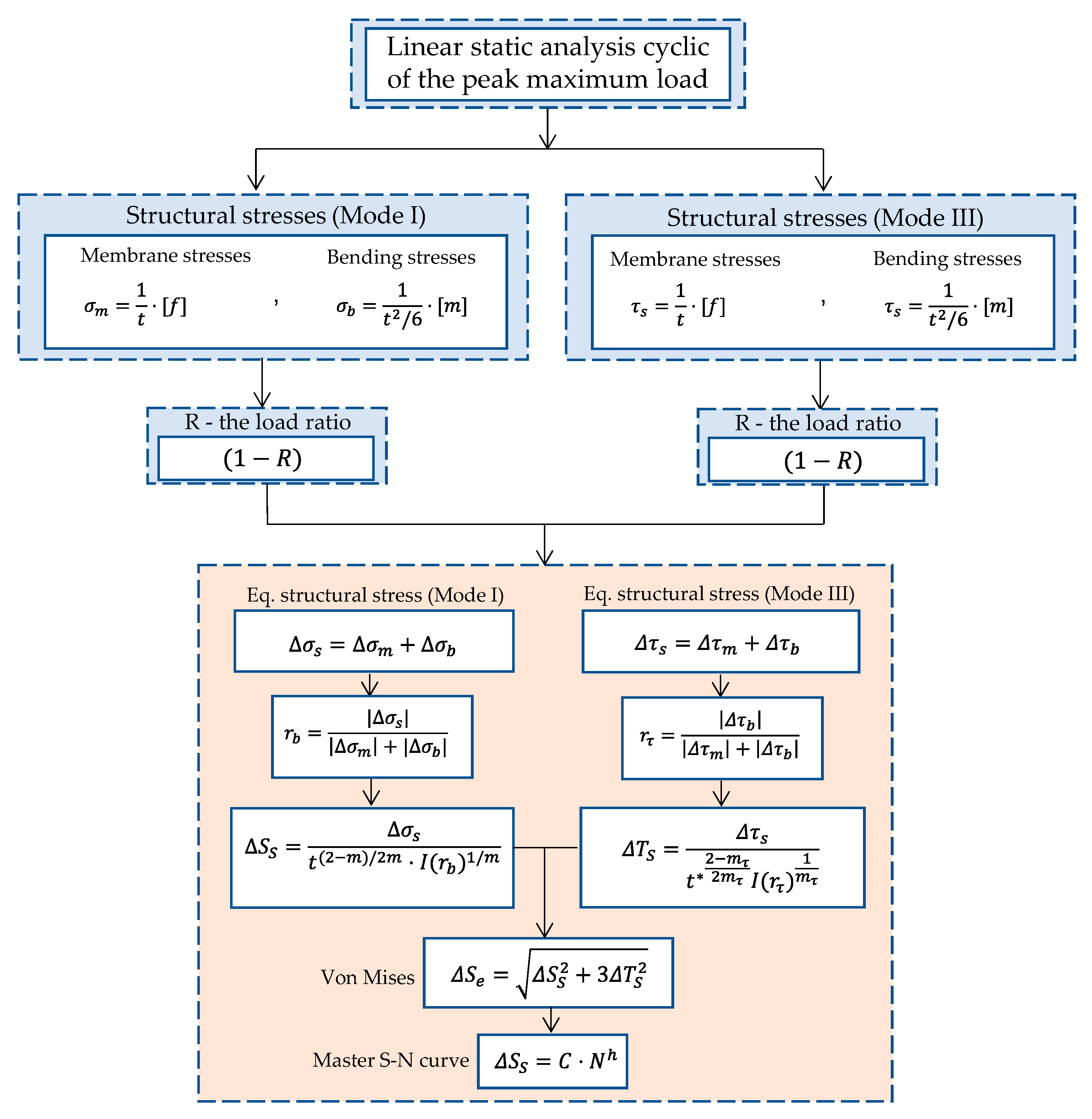
2.2.1. The Master S-N Curve (Mode I)
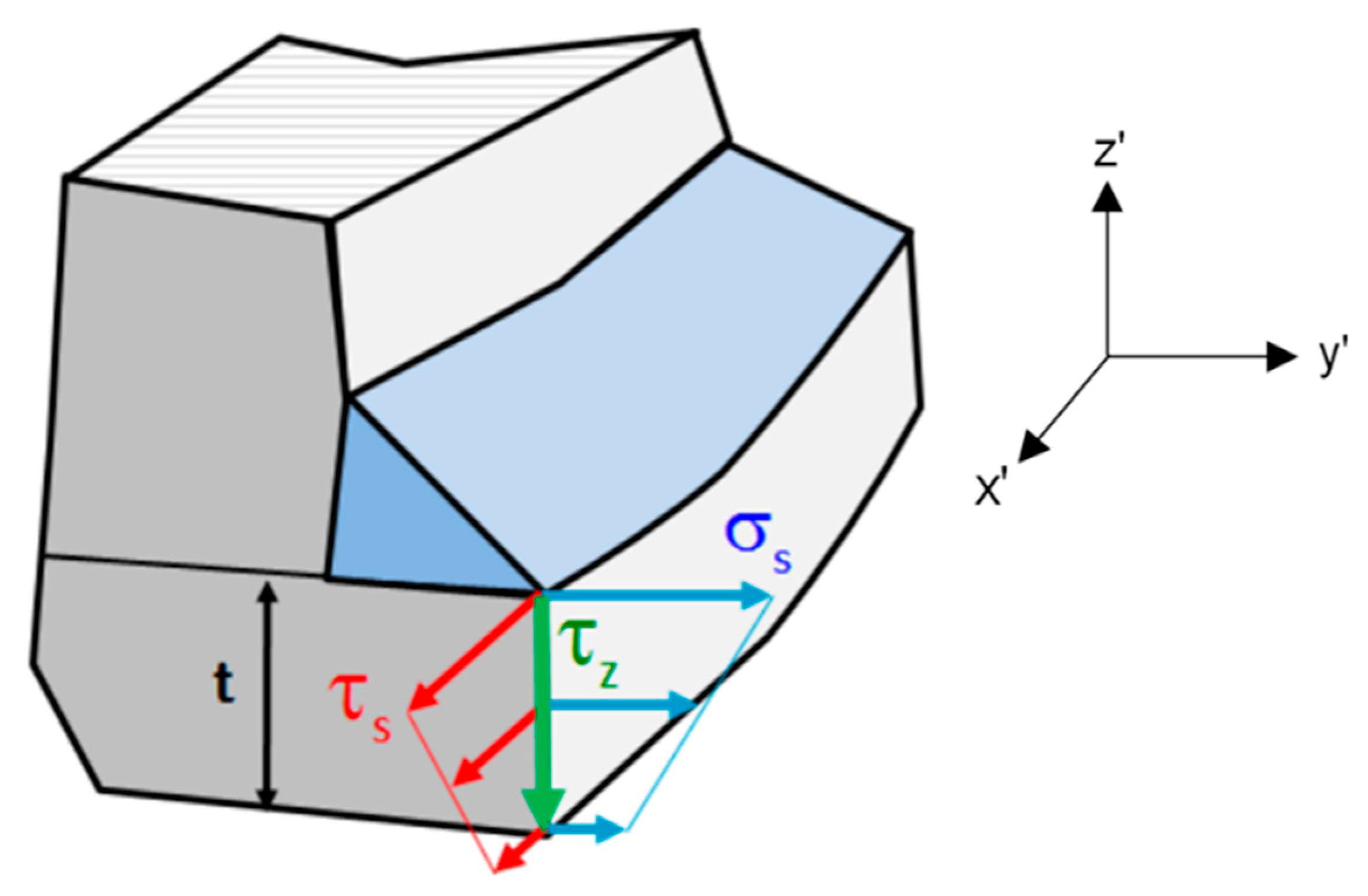
2.2.2. The Master S-N Curve Method for Multiaxial Fatigue Analysis (Mixed-Mode I + III)
3. Description of the Fatigue Test Setup
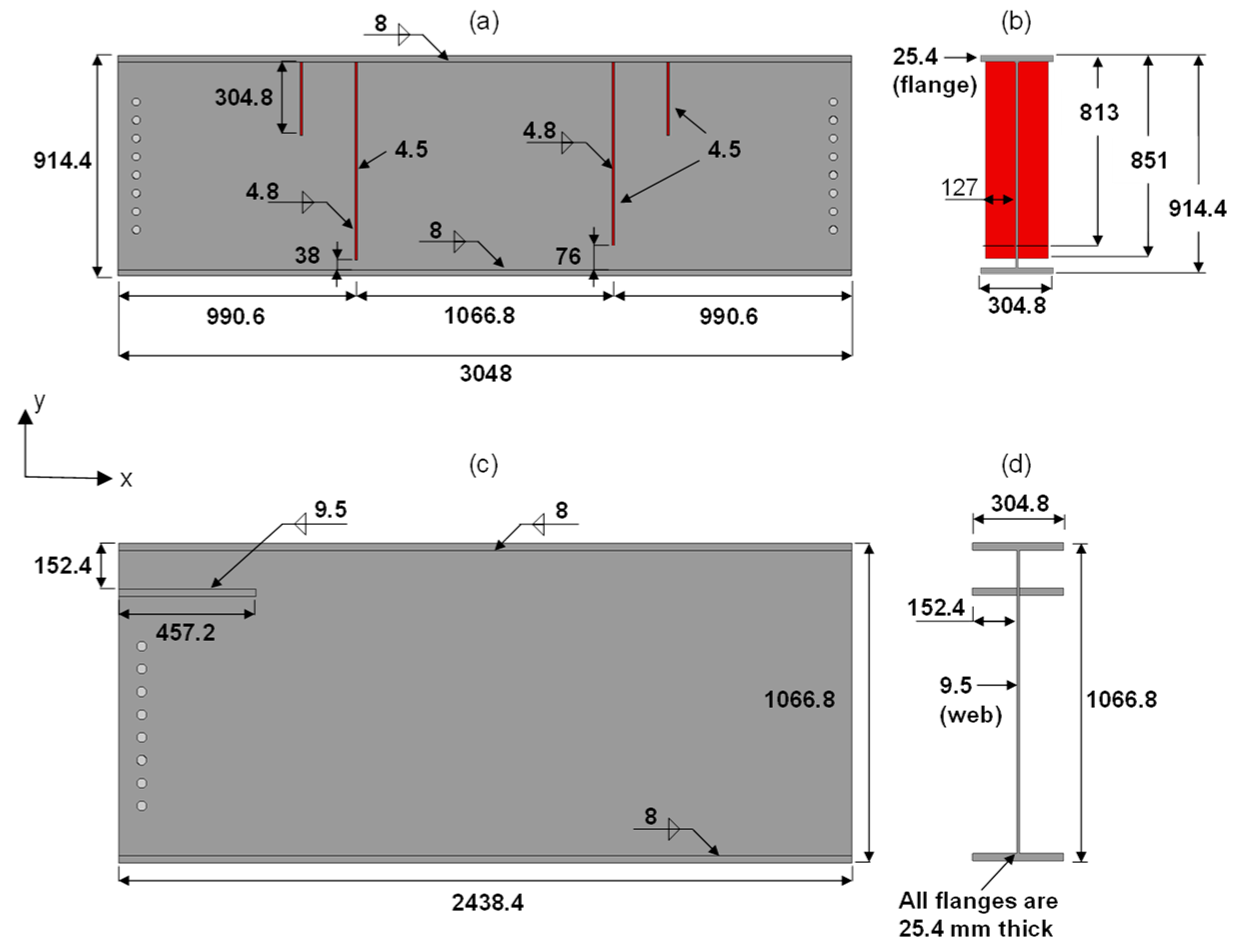
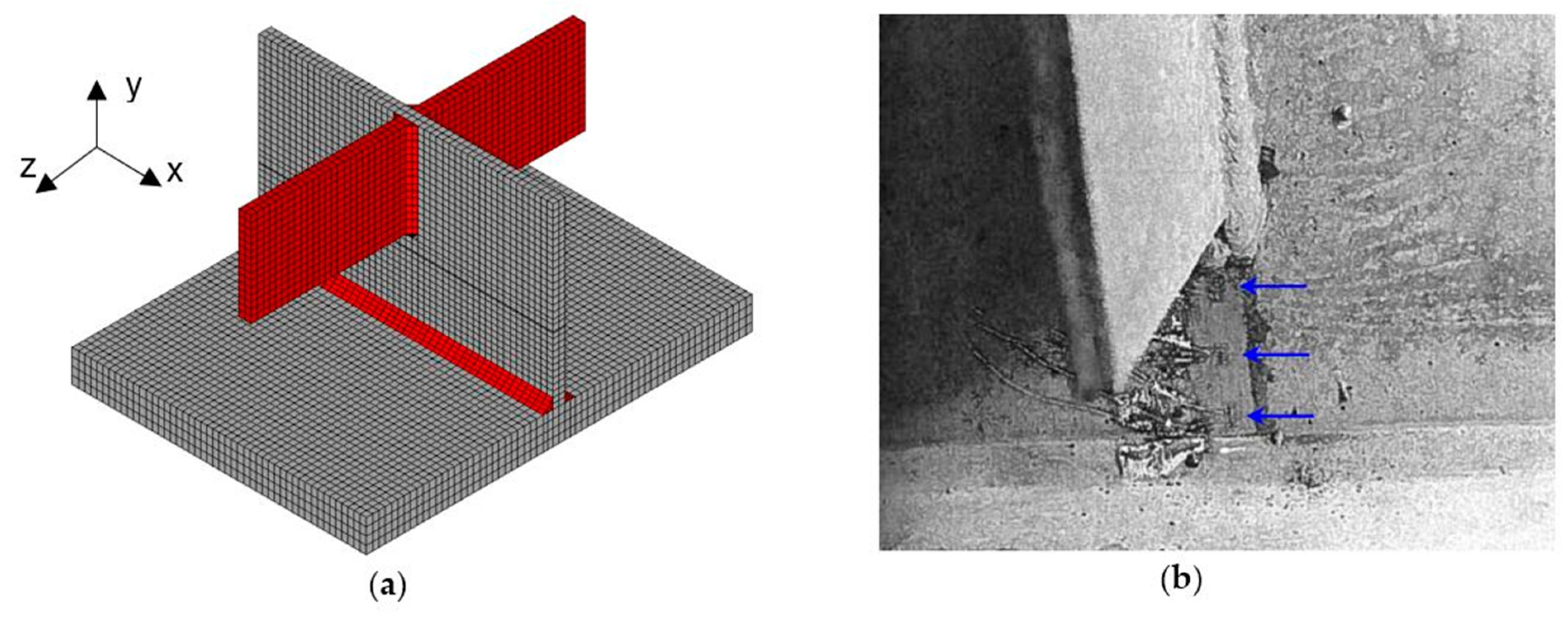
3.1. Description of the Numerical Models
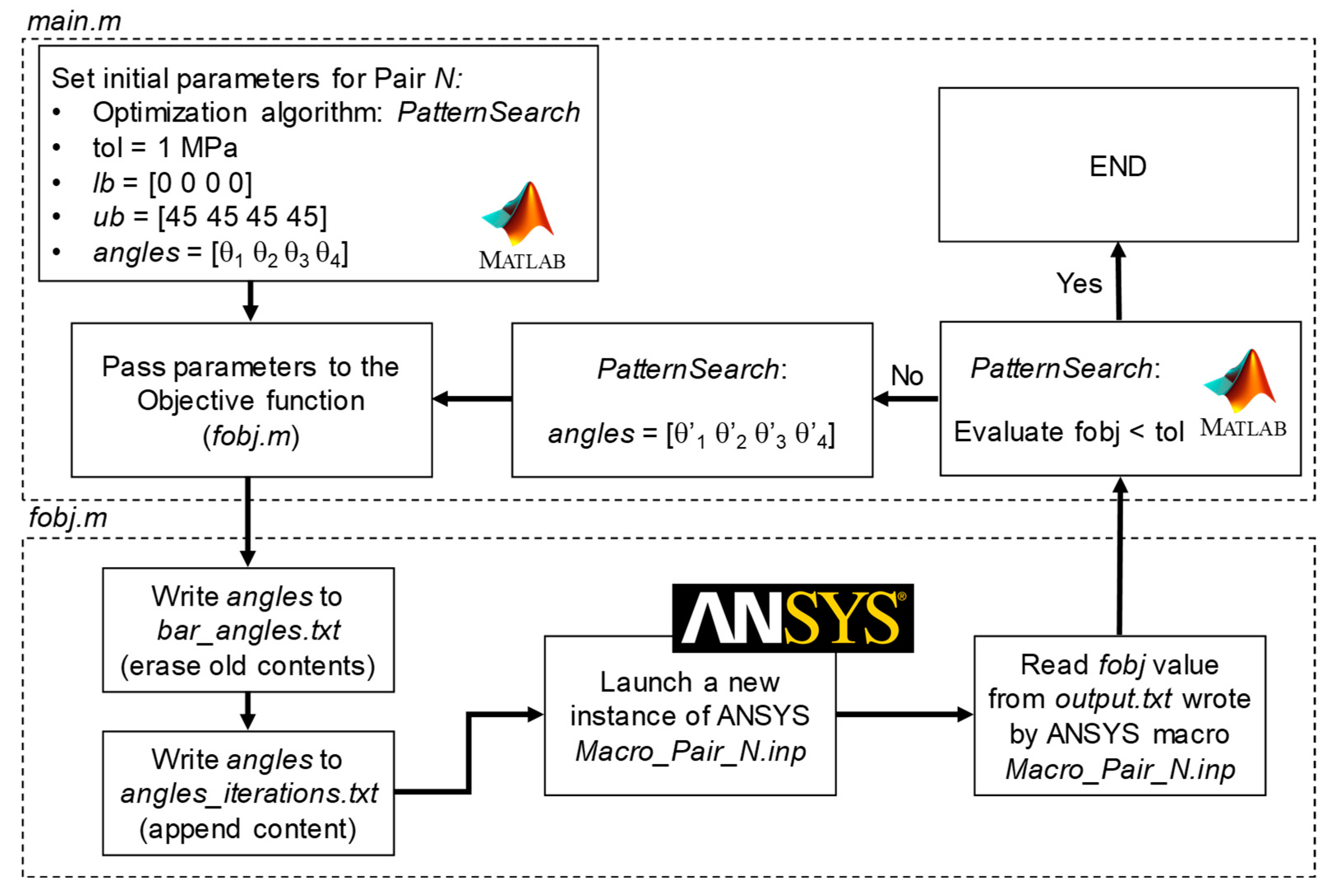
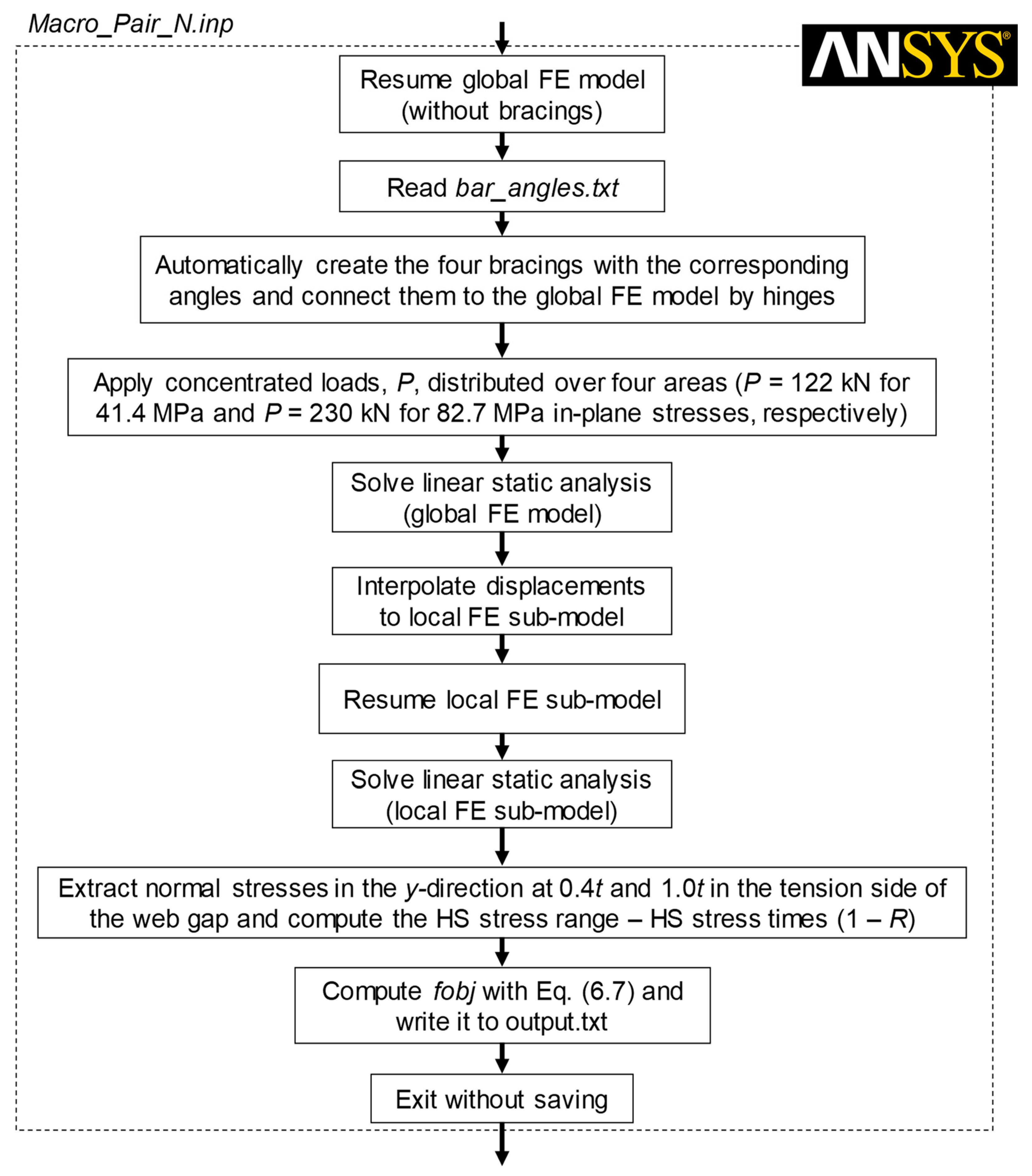
3.2. Numerical Model Calibration Methodology
4. Results and Discussion
4.1. Validation of the S-N Hot-Spot Curve Approach for the Distortion-Induced Fatigue Program
4.2. Validation of the Master S-N Curve Approach for the Distortion-Induced Fatigue Program
5. Conclusions and Future Prospects
- Based on the real system, it was modelled numerically in order to perform the computational analysis, and then a methodology for the calibration was proposed. In this way, it resulted that the local and global stresses were successfully determined, reaching a difference of less than 1%.
- Both methods (hot-spot stress and master S-N curve) were successfully applied. With the hot-spot stress method, the points were distributed above FAT 90 and with respect to the S-N master curve method, the points collapsed within the narrow band (curves interval). Nevertheless, the master curve can be more attractive, taking into account the need for one S-N curve usage, even for structural details.
- This study highlights the advantages of using the master curve and the structural equilibrium equivalent mesh insensitive structural stresses in the fatigue design of welded bridge details, even in cases of complex load transfer mechanisms. Moreover, the availability of a dedicated post-processor made the analysis quite effective.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pang, J.C.; Li, S.X.; Wang, Z.G.; Zhang, Z.F. General relation between tensile strength and fatigue strength of metallic materials. Mater. Sci. Eng. A 2013, 564, 331–341. [Google Scholar] [CrossRef]
- Ye, X.W.; Su, Y.H.; Jin, T.; Chen, B.; Han, J.P. Master S-N Curve-Based Fatigue Life Assessment of Steel Bridges Using Finite Element Model and Field Monitoring Data. Int. J. Struct. Stab. Dyn. 2019, 19, 1940013. [Google Scholar] [CrossRef]
- Liu, N.; Xiao, J.; Cui, X.; Liu, P.; Lua, J. A continuum damage mechanics (Cdm) modeling approach for prediction of fatigue failure of metallic bolted joints. In AIAA Scitech 2019 Forum; Aerospace Research Central: Reston, VA, USA, 2019; pp. 1–11. [Google Scholar] [CrossRef]
- Luo, P.; Yao, W.; Li, P. A notch critical plane approach of multiaxial fatigue life prediction for metallic notched specimens. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 854–870. [Google Scholar] [CrossRef]
- Alencar, G.; de Jesus, A.; da Silva, J.G.S.; Calcada, R. Fatigue cracking of welded railway bridges: A review. Eng. Fail. Anal. 2019, 104, 154–176. [Google Scholar] [CrossRef]
- Alencar, G.; de Jesus, A.; da Silva, J.G.S.; Calçada, R. A finite element post-processor for fatigue assessment of welded structures based on the Master SN curve method. Int. J. Fatigue 2021, 153, 106482. [Google Scholar] [CrossRef]
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components; Springer: Cham, Switzerland, 2016; Volume 47. [Google Scholar]
- Méndez, G.T.; Cuamatzi-Meléndez, R.; Hernández, A.A.; Capula-Colindres, S.I.; Angeles-Herrera, D.; Velázquez, J.C.; Vazquez-Hernández, O. Correlation of stress concentration factors for T-welded connections–finite element simulations and fatigue behavior. Soldag. Inspeção 2017, 22, 194–206. [Google Scholar] [CrossRef] [Green Version]
- Motaleb, M.; Lindquist, W.; Ibrahim, A.; Hindi, R. Repair assessment for distortion-induced fatigue cracks in a seismically retrofitted double-deck bridge complex. Eng. Struct. 2019, 183, 124–134. [Google Scholar] [CrossRef]
- Dellenbaugh, L.; Kong, X.; Al-Salih, H.; Collins, W.; Bennett, C.; Li, J.; Sutley, E.J. Development of a distortion-induced fatigue crack characterization methodology using digital image correlation. J. Bridg. Eng. 2020, 25, 4020063. [Google Scholar] [CrossRef]
- Alencar, G.; Hong, J.K.; de Jesus, A.; da Silva, J.G.S.; Calçada, R. The Master SN curve approach for fatigue assessment of welded bridge structural details. Int. J. Fatigue 2021, 152, 106432. [Google Scholar] [CrossRef]
- Cavaco, J.A. Managing fatigue susceptible details on critical railway bridges at CN. In Proceedings of the Bridge Maintenance, Safety Management, Health Monitoring and Informatics-IABMAS’08, Seoul, Korea, 13–17 July 2008. [Google Scholar]
- Alencar, G.; de Jesus, A.M.P.; Calçada, R.A.B.; da Silva, J.G.S. Fatigue life evaluation of a composite steel-concrete roadway bridge through the hot-spot stress method considering progressive pavement deterioration. Eng. Struct. 2018, 166, 46–61. [Google Scholar] [CrossRef]
- Rikeros, D. Fatigue Assessment of Rail Track Detail on Movable Bridge in Estonia Based on 2D/3D Finite Element Modelling Using Hot-Spot Stresses. Master’s Thesis, Department of Structural Engineering, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Aygül, M.; Al-Emrani, M.; Urushadze, S. Modelling and fatigue life assessment of orthotropic bridge deck details using FEM. Int. J. Fatigue 2012, 40, 129–142. [Google Scholar] [CrossRef]
- Aygül, M. Fatigue Analysis of Welded Structures Using the Finite Element Method; Chalmers Tekniska Hogskola: Gothenburg, Sweden, 2012; ISBN 1392881838. [Google Scholar]
- IIW. Recommendations for Fatigue Design of Welded Joints and Components; Hobbacher, A.F., Ed.; IIW Docume; International Institute of Welding (IIW): Kolkata, India, 2016; ISBN 9781855733152. [Google Scholar]
- Poutiainen, I.; Tanskanen, P.; Marquis, G. Finite element methods for structural hot spot stress determination—A comparison of procedures. Int. J. Fatigue 2004, 26, 1147–1157. [Google Scholar] [CrossRef]
- Iqbal, N.; Fang, H.; Naseem, A.; Kashif, M.; Backer, H. De A numerical evaluation of structural hot-spot stress methods in rib-to-deck joint of orthotropic steel deck. Appl. Sci. 2020, 10, 6924. [Google Scholar] [CrossRef]
- Niemi, E.; Fricke, W.; Maddox, S.J. Structural hot-spot stress approach to fatigue analysis of welded components. IIW Doc 2018, 13, 1800–1819. [Google Scholar]
- Dong, P.; Hong, J.K. The master SN curve approach to fatigue of piping and vessel welds. Weld. World 2004, 48, 28–36. [Google Scholar]
- Dong, P.; Hong, J.K. The master S-N curve approach to fatigue evaluation of offshore and marine structures. In Proceedings of the OMAE04-23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; pp. 1–9. [Google Scholar]
- Alencar, G. Structural Stress-Based Methodologies for Fatigue Assessment of Welded Railway Bridges. Ph.D. Thesis, University of Porto, Porto, Portugal, 2021. [Google Scholar]
- ASME. ASME: API 579-1/ASME FFS-1 Fitness-For-Service, Secion VIII-Division 2: Rules for Construction of Pressure Vessels; American Society of Mechanical Engineers: New York, NY, USA, 2016; p. 96. [Google Scholar]
- Boiler, A. Rules for Construction of Pressure vessels; American Society of Mechanical Engineers: New York, NY, USA, 2013; ISBN 0791834727. [Google Scholar]
- Niu, C.; Xie, S.; Li, X.; Wang, W. Research on stress state level evaluation method of complex steel welded structures. Int. J. Struct. Integr. 2021, 12, 109–122. [Google Scholar] [CrossRef]
- Xie, S.; Li, C.; Wang, J.; Li, W.; Niu, C. Study on welded joints’ stress state grade of aluminum alloy EMU body. Int. J. Struct. Integr. 2021, 12, 123–137. [Google Scholar] [CrossRef]
- Dong, P.; Hong, J.K.; Osage, D.A.; Prager, M. Master S-N Curve Method for Fatigue Evaluation of Welded Components. 2002. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Master+S-N+curve+method+for+fatigue+evaluation+of+welded+components&btnG= (accessed on 25 November 2021).
- Yaghoubshahi, M.; Alinia, M.M.; Milani, A.S. Master S-N curve approach to fatigue prediction of breathing web panels. J. Constr. Steel Res. 2017, 128, 789–799. [Google Scholar] [CrossRef]
- Fisher, J.W.; Barthelemy, B.M.; Mertz, D.R.; Edinger, J.A. Fatigue Behavior of Full-Scale Welded Bridge Attachments; Report No. 227; Transportation Research Board: Bethlehem, PA, USA, 1980. [Google Scholar]
- Viana, C.O. Avaliação Global-Local da vida em Fadiga de uma Junta Soldada do vão de Acesso da Ponte de Alcácer do Sal. Dissertação de Mestrado, Universidade Federal de Minas Gerais, Minas Gerais, Brasi, 2019. [Google Scholar]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Recent developments in local concepts of fatigue assessment of welded joints. Int. J. Fatigue 2009, 31, 2–11. [Google Scholar] [CrossRef]
- Casavola, C.; Pappalettere, C. Discussion on local approaches for the fatigue design of welded joints. Int. J. Fatigue 2009, 31, 41–49. [Google Scholar] [CrossRef]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- Niemi, E.; Fricke, W.; Maddox, S.J. Fatigue Analysis of Welded Components: Designer’s Guide to the Structural Hot-Spot Stress Approach; Woodhead Publishing: Swaston, UK, 2006; ISBN 1845696662. [Google Scholar]
- Marin, T.; Nicoletto, G. Fatigue design of welded joints using the finite element method and the 2007 ASME Div. 2 Master curve. Frat. Integrità Strutt. 2009, 3, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Bijlaard, F.S.K. Eurocode 3: Design of steel structures-part 1-9: Fatigue. In Proceedings of the International Symposium on Fatigue and Fracture of Steel Structures, Singapore, 4 December 2007; Nanyang Technological University: Singapore, 2008; pp. 20–31. [Google Scholar]
- Saini, D.S.; Karmakar, D.; Ray-Chaudhuri, S. A review of stress concentration factors in tubular and non-tubular joints for design of offshore installations. J. Ocean Eng. Sci. 2016, 1, 186–202. [Google Scholar] [CrossRef] [Green Version]
- Doerk, O.; Fricke, W.; Weissenborn, C. Comparison of different calculation methods for structural stresses at welded joints. Int. J. Fatigue 2003, 25, 359–369. [Google Scholar] [CrossRef]
- Silveira, J.A.; Mezzomo, G.P.; Goedel, F. Evaluation of structural stress method and master curve for fatigue life prediction of a welded joint. Rev. Int. Metod. Numer. Para Calc. Y Disen. En Ing. 2017, 33. [Google Scholar] [CrossRef] [Green Version]
- Hobbacher, A. Recommendations for fatigue design of welded joints and components. IIW document XIII-2151-07. XV-1254r1-07, Paris2007. 2007. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Recommendations+for+fatigue+design+of+welded+joints+and+components&btnG= (accessed on 25 November 2021).
- Heshmati, M. Fatigue Life Assessment of Bridge Details Using Finite Element Method; Chalmers University of Technology, Chalmers Tekniska Hogskola: Gothenburg, Sweden, 2012. [Google Scholar]
- ASME VIII Div2 Secion. VIII-Division 2: Rules for Construction of Pressure Vessels. ASME Boiler Pressure and Vessel Code; USA. 2013. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=43.%09ASME+VIII+Div2+Secion.+VIII-Division+2%3A+Rules+for+Construction+of+Pressure+Vessels%3B+ASME+Boiler+Pressure+and+Vessel+Code%3B+USA%2C+2013.&btnG= (accessed on 25 November 2021).
- Hong, J.K.; Forte, T.P. Fatigue evaluation procedures for multiaxial loading in welded structures using Battelle structural stress approach. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. American Society of Mechanical Engineers Digital Collection, 1 October 2014. [Google Scholar]
- Teixeira, G. Vibration Fatigue of Welded Joints-Case Studies Using Verity. In Proceedings of the Dassault Systèmes User Conference, Hanau, Germany, 4–6 December 2018. [Google Scholar]
- Fisher, J.W.; Albrecht, P.; Yen, B.T.; Klingerman, D.J.; McNamee, B.M. Fatigue strength of steel beams with welded stiffeners and attachments. NCHRP Rep. 1974. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Fatigue+strength+of+steel+beams+with+welded+stiffeners+and+attachments&btnG= (accessed on 25 November 2021).
- Fisher, J.W.; Jin, J.; Wagner, D.C.; Yen, B.T. NCHRP Report 336: Distortion-Induced Fatigue Cracking in Steel Bridges; National Research Council of Washington: Washington, DC, USA, 1990.
- Audet, C.; Kokkolaras, M. Blackbox and Derivative-Free Optimization: Theory, Algorithms and Applications; Springer: New York, NY, USA, 2016; ISBN 1389-4420. [Google Scholar]
- Fisher, J.W.; Jin, J.W.; David, C.; Yen, B. Distortion-Induced Fatigue Cracking in Steel Bridges; Transportation Research Board: Washington, DC, USA, 1990; Volume 336, ISBN 0309048591. [Google Scholar]





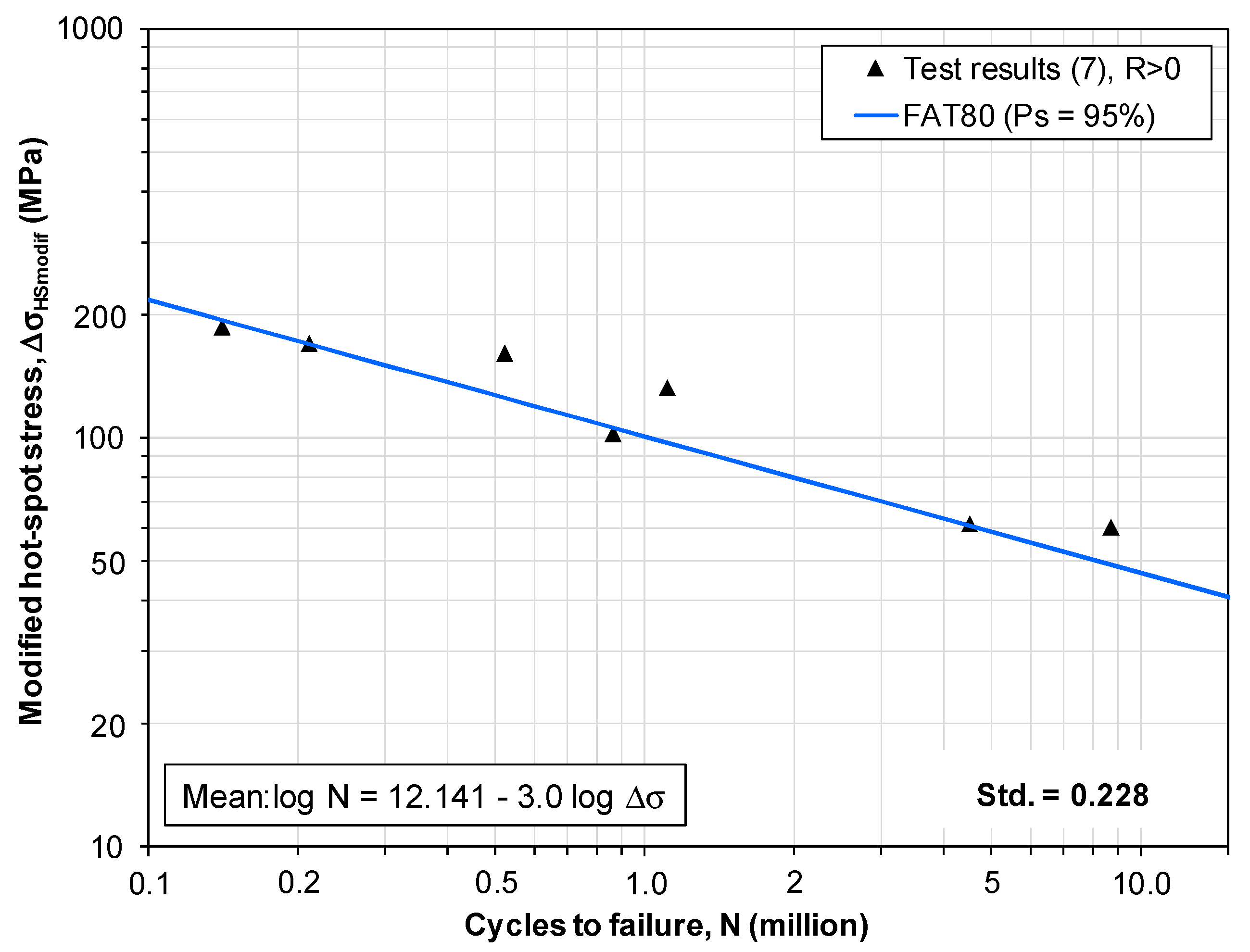

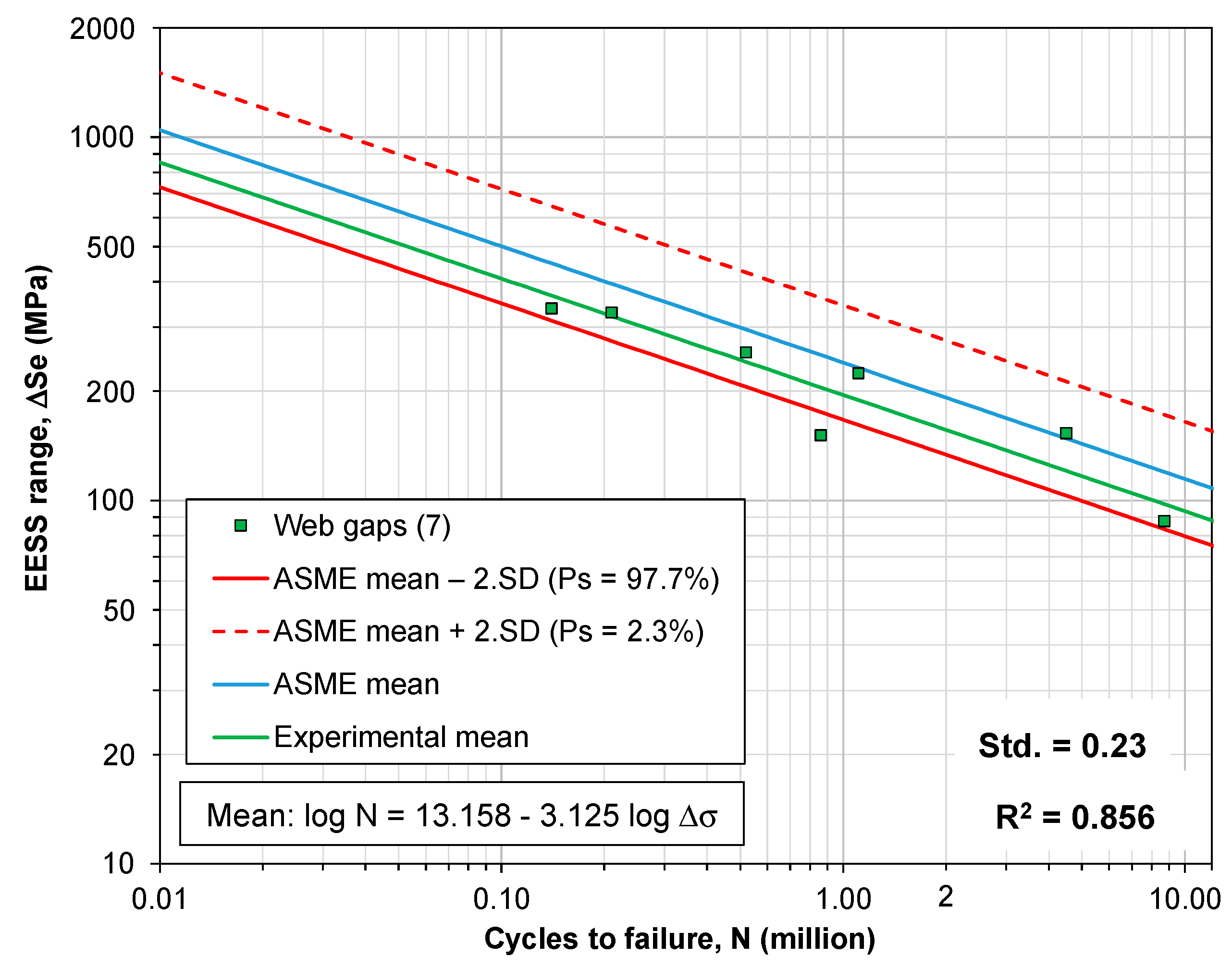
| Statistical Basis | C | h |
|---|---|---|
| Mean | 19,930.2 | −0.3195 |
| +2 SD | 28,626.5 | |
| −2 SD | 13,875.8 | |
| +3 SD | 34,308.1 | |
| −3 SD | 11,577.9 |
| Steel Bracings Slopes (Decimal Degrees °) | No. of Iterations | ||||
|---|---|---|---|---|---|
| Girder | Left Girders | Right Girders | |||
| θ1 | θ2 | θ3 | θ4 | ||
| G2 | 3.21 | 10.97 | 10.65 | 12.83 | 53 |
| G5 | 8.25 | 12.82 | 12.10 | 5.72 | 46 |
| G6 | 4.58 | 12.20 | 7.76 | 13.95 | 51 |
| G8 | 4.43 | 12.40 | 6.88 | 14.51 | 51 |
| G10 | 6.25 | 12.09 | 12.03 | 7.82 | 61 |
| G11 | 4.69 | 11.44 | 4.50 1 | 4.50 1 | 28 |
| G12 | 4.50 1 | 4.50 1 | 0.72 | 6.78 | 39 |
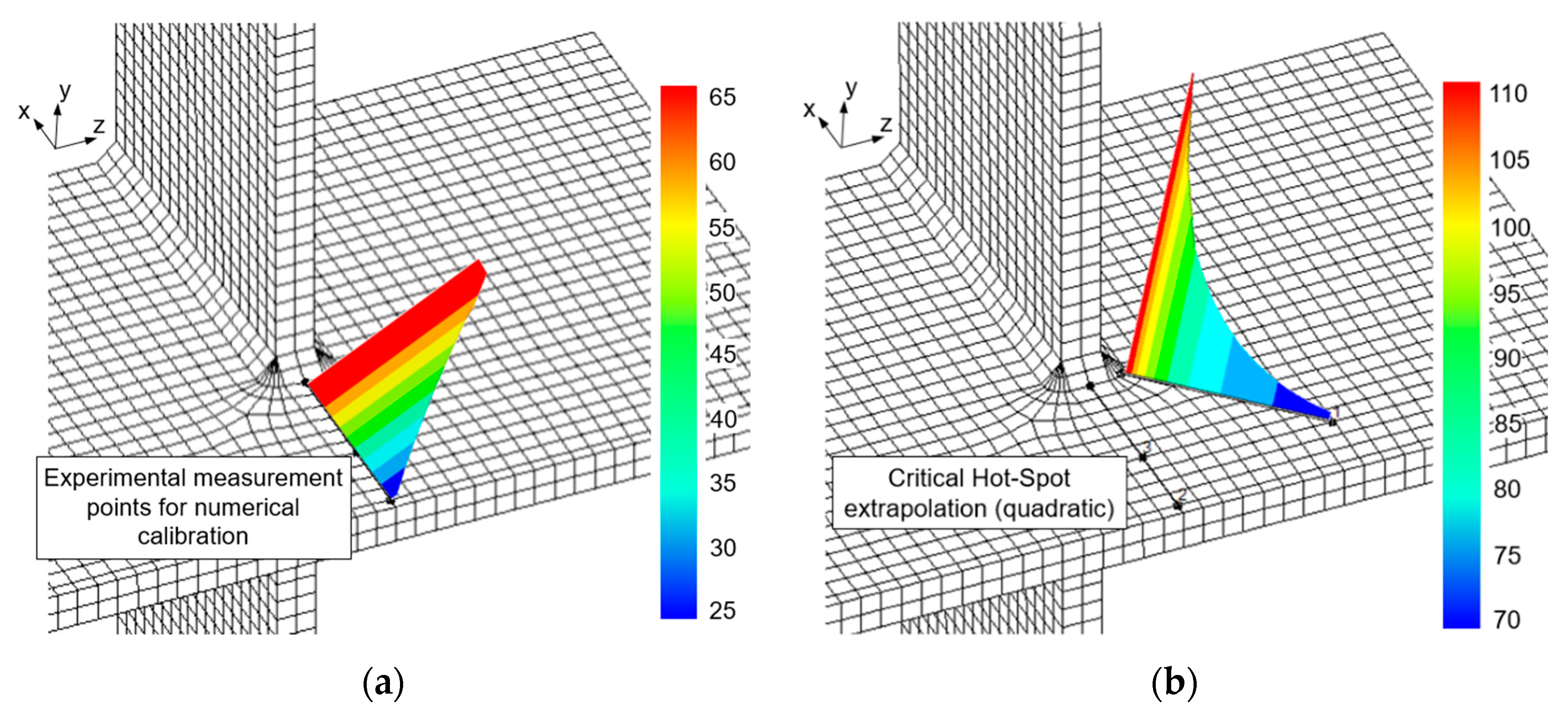
| Girder | Applied FE Loads, Pmax (kN) | Web Gap Length 2 (mm) | In-Plane Stress Range 1, Δσ (MPa) Δσ = σMAX × (1 − R) | Out-of-Plane Hot-Spot Stress Range 2, ΔσHS (MPa) | Hot-Spot (Inclined) (MPa) Computed Quadratic (Figure 12b) | EESS Range, ΔSe (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| ΔσHS = σHSMAX × (1 − R) | Modes I + III | ||||||||
| Linear Rule (0.4 tw, 1.0 tw) (Figure 12a) | ΔSe = SS × (1 − R) | ||||||||
| Measured | Computed | Measured 3 | Computed | Error | Computed | ||||
| G2 | 122.04 | 45.97 | 41.36 | 41.27 | 61.36 | 61.78 | 0.68% | 109.57 | 153.64 |
| G5 | 122.04 | 49.02 | 41.36 | 41.25 | 60.67 | 61.28 | 1.01% | 65.01 | 87.75 |
| G6 | 122.04 | 49.53 | 41.36 | 41.22 | 132.38 | 132.00 | 0.29% | 165.29 | 223.95 |
| G8 | 122.04 | 51.05 | 41.36 | 41.20 | 160.65 | 160.15 | 0.31% | 188.38 | 255.72 |
| G10 | 229.62 | 51.31 | 82.74 | 83.54 | 102.04 | 101.43 | 0.60% | 104.19 | 151.13 |
| G11 | 229.62 | 53.59 | 82.74 | 83.10 | 170.30 | 169.61 | 0.41% | 225.28 | 329.39 |
| G12 | 229.62 | 48.26 | 82.74 | 82.43 | 186.85 | 186.52 | 0.18% | 233.66 | 337.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quissanga, V.; Alencar, G.; de Jesus, A.; Calçada, R.; da Silva, J.G.S. Distortion-Induced Fatigue Reassessment of a Welded Bridge Detail Based on Structural Stress Methods. Metals 2021, 11, 1952. https://doi.org/10.3390/met11121952
Quissanga V, Alencar G, de Jesus A, Calçada R, da Silva JGS. Distortion-Induced Fatigue Reassessment of a Welded Bridge Detail Based on Structural Stress Methods. Metals. 2021; 11(12):1952. https://doi.org/10.3390/met11121952
Chicago/Turabian StyleQuissanga, Vencislau, Guilherme Alencar, Abílio de Jesus, Rui Calçada, and José Guilherme S. da Silva. 2021. "Distortion-Induced Fatigue Reassessment of a Welded Bridge Detail Based on Structural Stress Methods" Metals 11, no. 12: 1952. https://doi.org/10.3390/met11121952
APA StyleQuissanga, V., Alencar, G., de Jesus, A., Calçada, R., & da Silva, J. G. S. (2021). Distortion-Induced Fatigue Reassessment of a Welded Bridge Detail Based on Structural Stress Methods. Metals, 11(12), 1952. https://doi.org/10.3390/met11121952