Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior
Abstract
:1. Introduction
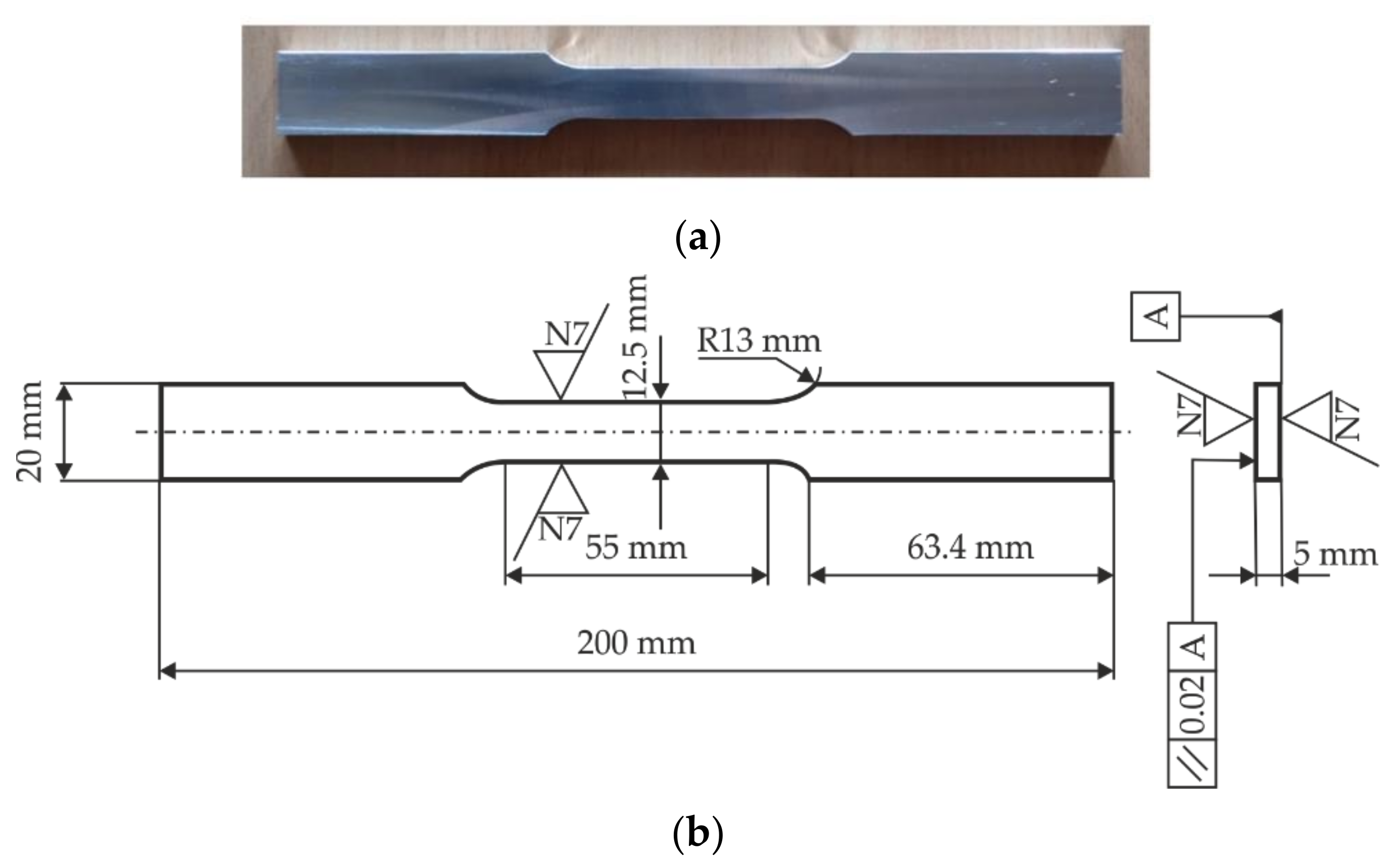
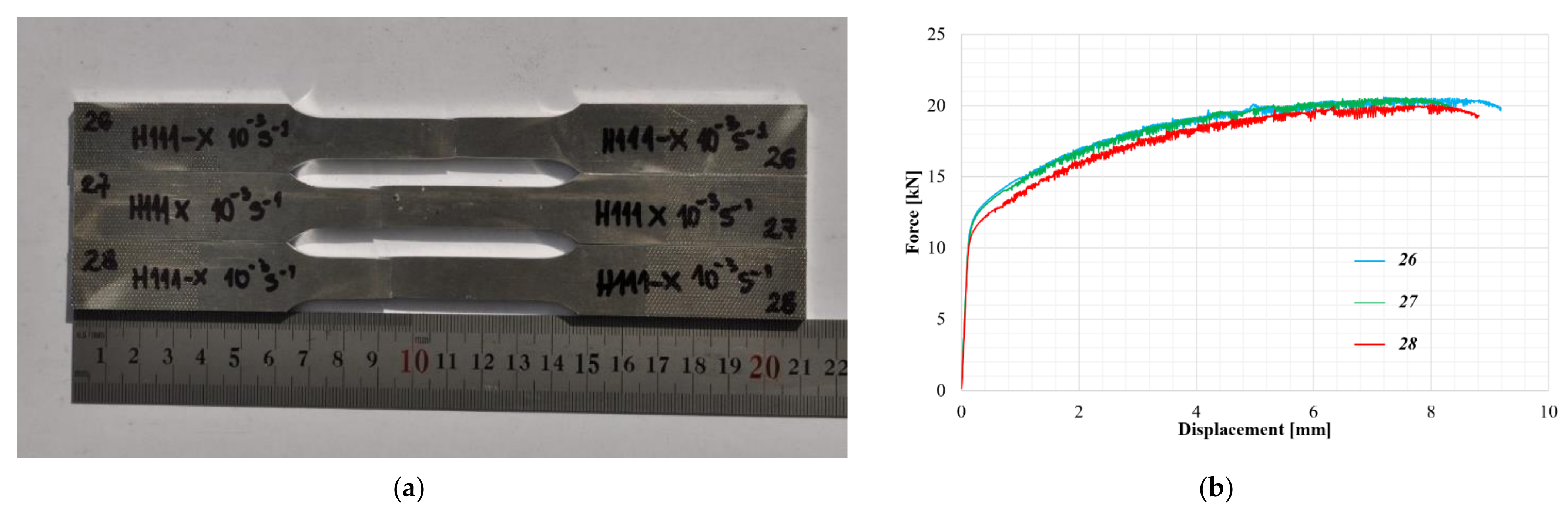
2. Experimental Investigation of AA5083-H111 Specimens
3. Phase-Field Damage Model and von Mises Plasticity for AA5083
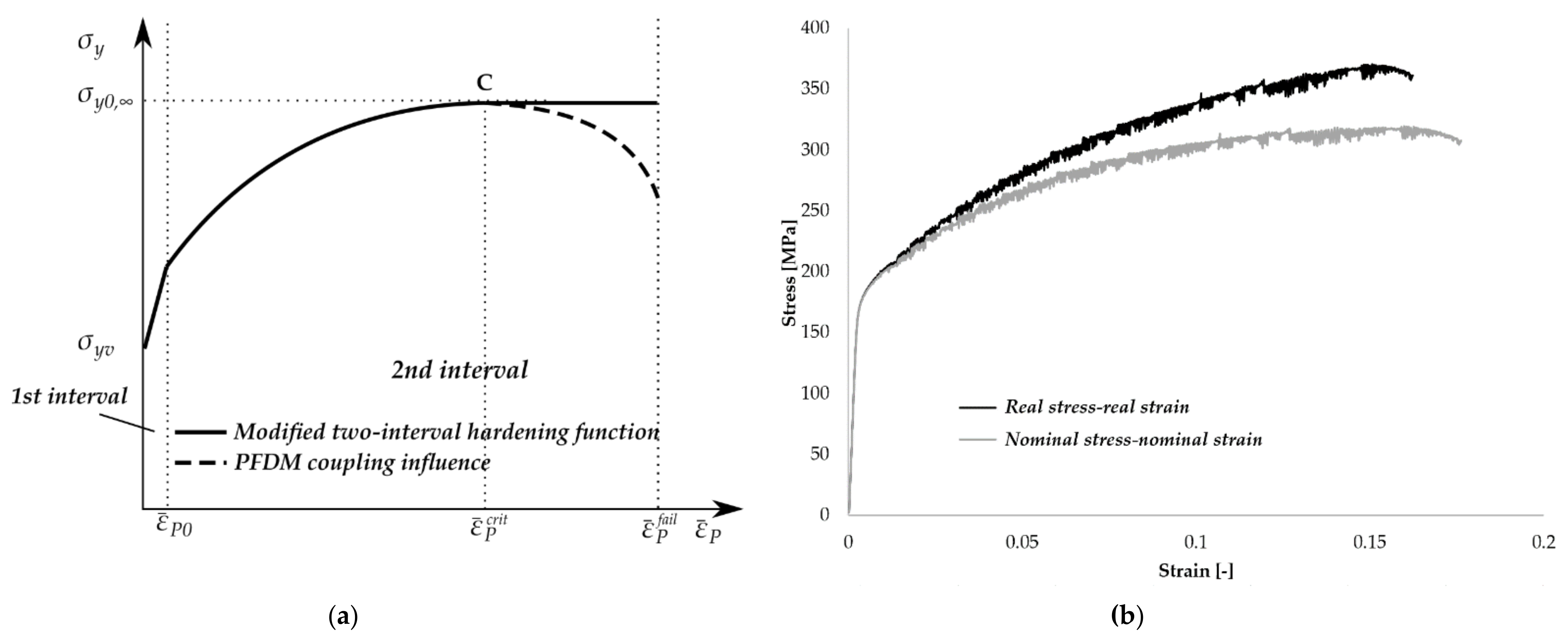
3.1. Short Overview of the von Mises Plasticity and Modifications of Two-Intervals Hardening Function for AA5083 Structures
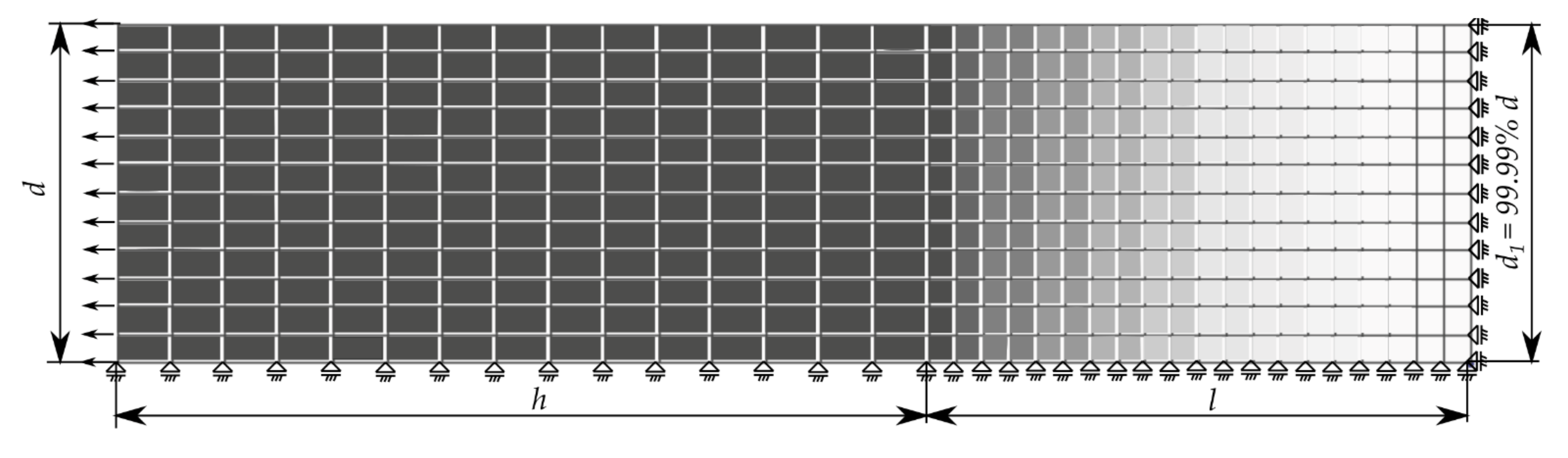
3.2. Verification of the Proposed Two-Intervals Yield Function Modification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| internal potential energy | ||
| damage phase-field variable | ||
| characteristic length-scale parameter | ||
| increment | ||
| volume | ||
| total deformation gradient | ||
| elastic deformation gradient | ||
| elastic deviatoric stress | ||
| elastic strain | ||
| plastic strain | ||
| equivalent plastic strain | ||
| degradation function | ||
| elastic constitutive matrix | ||
| elastic-plastic constitutive matrix | ||
| “damaged” Cauchy stress | ||
| “undamaged” Cauchy stress | ||
| Linear hardening modulus | ||
| critical fracture energy release rate per unit volume | ||
| initial yield stress | ||
| saturation hardening stress | ||
| hardening exponent | ||
| hardening modulus | ||
| body force field per unit volume | ||
| boundary traction per unit area | ||
| unit outer normal to the surface | ||
| equivalent stress | ||
| coupling variable | ||
| critical equivalent plastic strain | ||
| maximal equivalent plastic strain for linear hardening plasticity interval | ||
| failure equivalent plastic strain | ||
| yield stress of current yield surface | ||
| real stress | ||
| nominal stress | ||
| surface | ||
| extensiometer gauge length | ||
| gradient operator | ||
| external potential energy | ||
| internal potential energy density | ||
| elastic energy density of virgin material | ||
| plastic energy density, | ||
| total strain | ||
| plastic deformation gradient | ||
| isochoric elastic deformation gradient | ||
| elastic left Cauchy-Green strain | ||
| Hencky strain | ||
| mean strain | ||
| mean stress | ||
| shear modulus | ||
| bulk modulus | ||
| Young’s modulus | ||
| Poisson’s ratio | ||
| time | ||
| unit tensor | ||
| elastic deviatoric strain | ||
| interpolation matrix for displacements | ||
| interpolation matrix for damage phase-field | ||
| matrix of interpolation functions derivatives for displacements | ||
| matrix of interpolation functions derivatives for damage phase-field | ||
| damage phase-field vector of nodal values | ||
| damage strain | ||
| internal forces vector | ||
| external forces vector | ||
| residue vector for the damage phase-field | ||
| residue vector for the displacement field | ||
| tangent stiffness matrix for damage phase-field | ||
| tangent stiffness matrix for displacement field | ||
| nodal displacements vector | ||
| yield function | ||
| real strain | ||
| nominal strain | ||
| nominal cross-section area | ||
| force | ||
| variation of variable |
Appendix A. Stress Integration Algorithm for von Mises Large Strain Plasticity
- Input values:
- Initial conditions (save at the integration point level):
- Calculate the trial elastic deviatoric strain:
- Trial elastic deviatoric stress:
- If the condition is satisfied, the solution is and , and one can go to 7.
- Find the equivalent plastic strain increment, , of the function (NEW HARDENING FUNCTION, with respect to [1])
- 7.
- Update of the left Cauchy-Green strain tensor:
- 8.
- Mean stress and total stress:
- 9.
- Calculate the elastic deviatoric strain:
- 10.
- The total elastic strain is:
- 11.
- Elastic strain energy density:
- 12.
- Coupling variable:
- 13.
- Calculate the elasto-plastic matrix:
- 14.
- Return: σ0, , CEP,
References
- Živković, J.; Dunić, V.; Milovanović, V.; Pavlović, A.; Živković, M. A Modified Phase-Field Damage Model for Metal Plasticity at Finite Strains: Numerical Development and Experimental Validation. Metals 2021, 11, 47. [Google Scholar] [CrossRef]
- Dunić, V.; Pieczyska, E.A.; Kowalewski, Z.L.; Matsui, R.; Slavković, R. Experimental and Numerical Investigation of Mechanical and Thermal Effects in TiNi SMA during Transformation-Induced Creep Phenomena. Materials 2019, 12, 883. [Google Scholar] [CrossRef] [Green Version]
- Dunić, V.; Pieczyska, E.; Tobushi, H.; Staszczak, M.; Slavković, R. Experimental and numerical thermo-mechanical analysis of shape memory alloy subjected to tension with various stress and strain rates. Smart Mater. Struct. 2014, 23, 055026. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, T.; Hayden, M.; Roe, C. Effects of the stress state on plasticity and ductile failure of an aluminum 5083 alloy. Int. J. Plast. 2009, 25, 2366–2382. [Google Scholar] [CrossRef]
- Zhou, J.; Gao, X.; Hayden, M.; Joyce, J.A. Modeling the ductile fracture behavior of an aluminum alloy 5083-H116 including the residual stress effect. Eng. Fract. Mech. 2012, 85, 103–116. [Google Scholar] [CrossRef]
- Darras, B.M.; Abed, F.H.; Pervaiz, S.; Abdu-Latif, A. Analysis of damage in 5083 aluminum alloy deformed at different strain rates. Mater. Sci. Eng. A 2013, 568, 143–149. [Google Scholar] [CrossRef]
- Lee, H.W.; Basaran, C.A. Review of Damage, Void Evolution, and Fatigue Life Prediction Models. Metals 2021, 11, 609. [Google Scholar] [CrossRef]
- Abuzaid, W.; Hawileh, R.; Abdalla, J. Mechanical Properties of Strengthening 5083-H111 Aluminum Alloy Plates at Elevated Temperatures. Infrastructures 2021, 6, 87. [Google Scholar] [CrossRef]
- Bouhamed, A.; Mars, J.; Jrad, H.; Wali, M.; Dammak, F. Experimental and numerical methodology to characterize 5083-aluminium behavior considering non-associated plasticity model coupled with isotropic ductile damage. Int. J. Solids Struct. 2021, 229, 111139. [Google Scholar] [CrossRef]
- Christopher, C.M.L.; Sasikumar, T.; Santulli, C.; Fragassa, C. Neural network prediction of aluminum–silicon carbide tensile strength from acoustic emission rise angle data. FME Trans. 2018, 46, 253–258. [Google Scholar] [CrossRef]
- Fragassa, C.; Babič, M.; Pavlovic, A.; do Santos, E.D. Machine Learning Approaches to Predict the Hardness of Cast Iron. Tribol. Ind. 2020, 42, 1–9. [Google Scholar] [CrossRef]
- Babic, M.; Calì, M.; Nazarenko, I.; Fragassa, C.; Ekinovic, S.; Mihaliková, M.; Janjić, M.; Belič, I. Surface Roughness Evaluation in Hardened Materials by Pattern Recognition Using Network Theory. Int. J. Interact. Des. Manuf. 2018, 13, 211–219. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G.; Pavlovic, A. Tribological aspects of cast iron investigated via fracture toughness. Tribol. Ind. 2016, 38, 1–10. [Google Scholar]
- Dauber, C.; Vannucchi de Camargo, F.; Alves, A.K.; Pavlovic, A.; Fragassa, C.; Bergmann, C.P. Erosion Resistance of Engineering Ceramics (Al2O3, ZrO2, Si3N4) and Comparative Assessment Through Wiederhorn and Evans Equations. Wear 2019, 432–433, 202938. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Li, J.; Saharan, A.; Koric, S.; Ostoja-Starzewski, M. Elastic-plastic transitions in 3D random materials: Massively parallel simulations, fractal morphogenesis and scaling function. Philos. Mag. 2012, 92, 2733–2758. [Google Scholar] [CrossRef]
- Tian, N.; Wang, G.; Zhou, Y.; Liu, K.; Zhao, G.; Zuo, L. Study of the Portevin-Le Chatelier (PLC) Characteristics of a 5083 Aluminum Alloy Sheet in Two Heat Treatment States. Materials 2018, 11, 1533. [Google Scholar] [CrossRef] [Green Version]
- ASTM International. ASTM E646—00: Standard Test Method for Tensile Strain-Hardening Exponents (n-Values) of Metallic Sheet Materials; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Molnár, G.; Gravouil, A. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Pañeda, E.M.; Golahmar, A.; Niordson, C.F. A phase field formulation for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2018, 342, 742–761. [Google Scholar] [CrossRef] [Green Version]
- Miehe, C.; Schänzel, L.-M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Dunić, V.; Slavković, R. Implicit stress integration procedure for large strains of the reformulated Shape Memory Alloys material model. Contin. Mech. Thermodyn. 2020, 32, 1287–1309. [Google Scholar] [CrossRef]
- Simo, J.C.; Miehe, C. Associative coupled thermoplasticity at finite strains: Formulation, numerical analysis and implementation. Comput. Methods Appl. Mech. Eng. 1992, 98, 41–104. [Google Scholar] [CrossRef]
- Navidtehrani, Y.; Betegón, C.; Pañeda, E.M. A simple and robust Abaqus implementation of the phase field fracture method. Appl. Eng. Sci. 2021, 6, 100050. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; K.J. Bathe: Watertown, MA, USA, 2014. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. Finite Element Method: Solid and Fluid Mechanics Dynamics and Non-Linearity; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Shishvan, S.; Assadpour-asl, S.; Pañeda, E.M. A mechanism-based gradient damage model for metallic fracture. Eng. Fract. Mech. 2021, 255, 107927. [Google Scholar] [CrossRef]

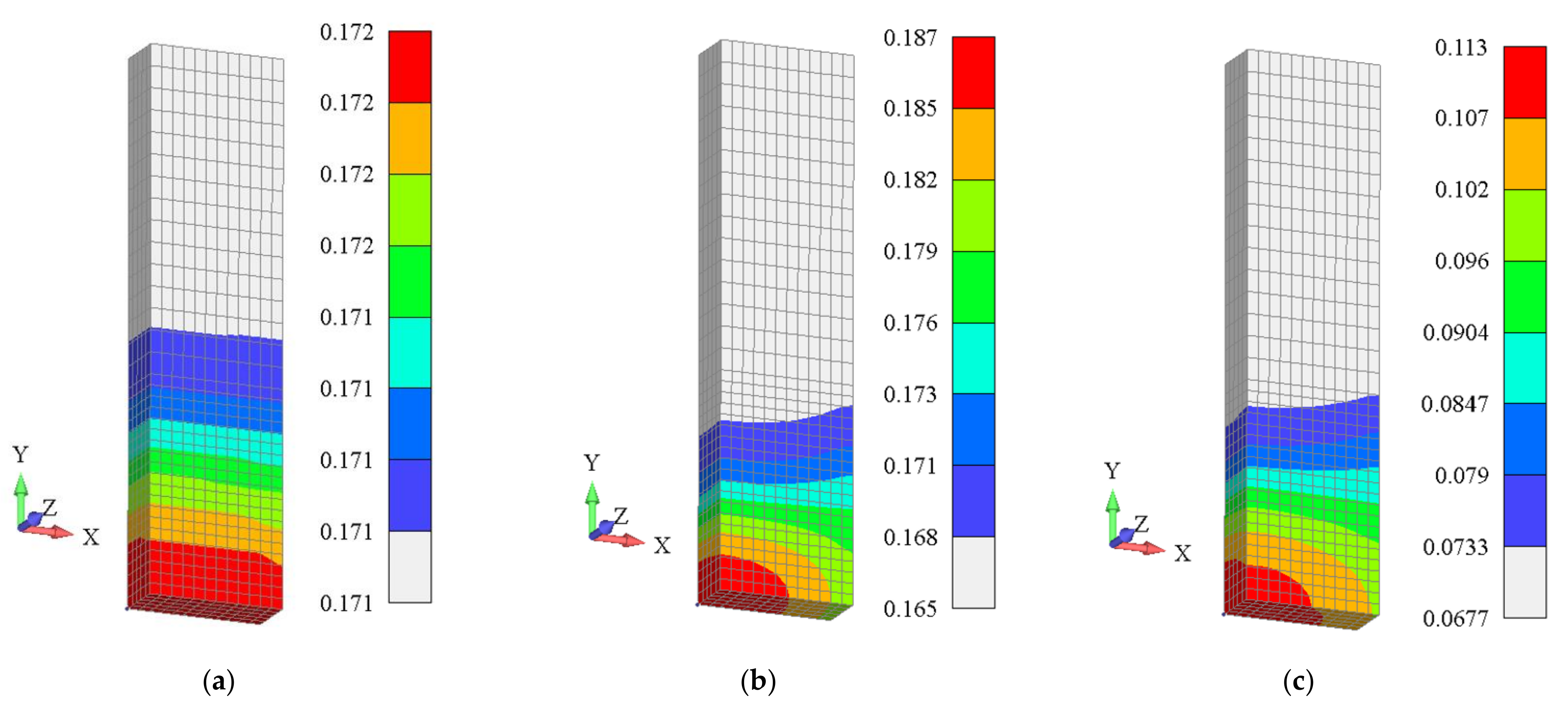
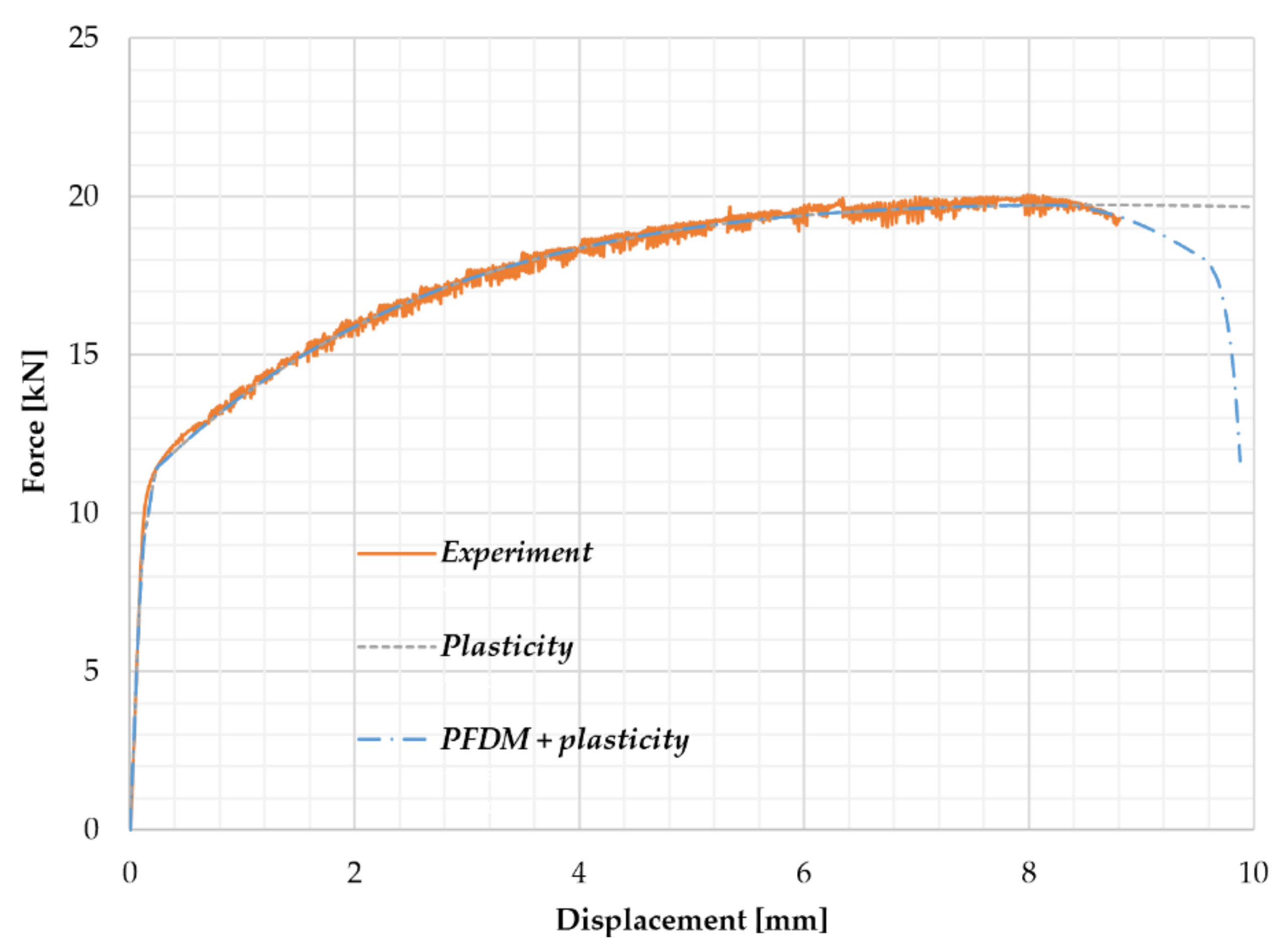
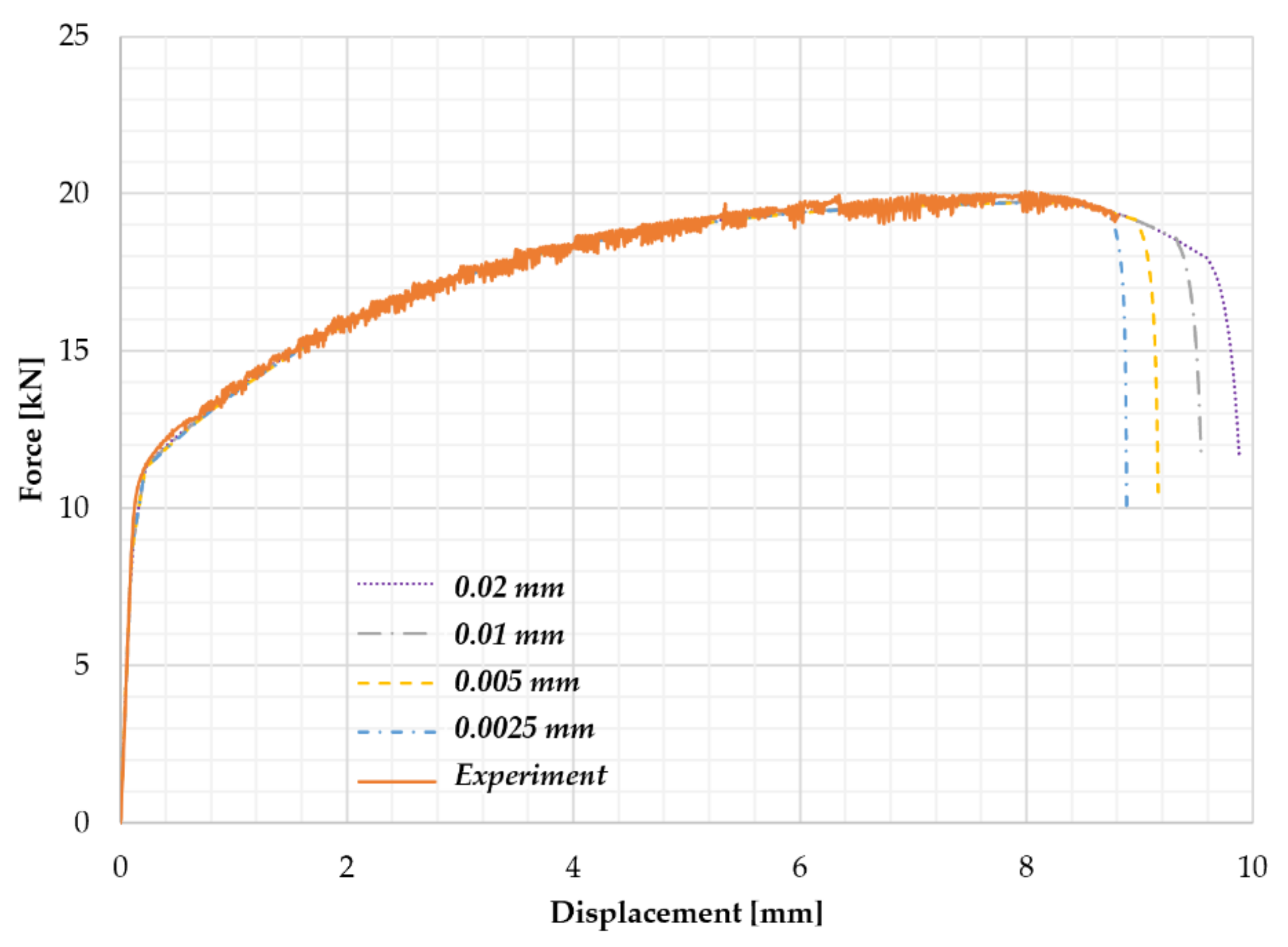

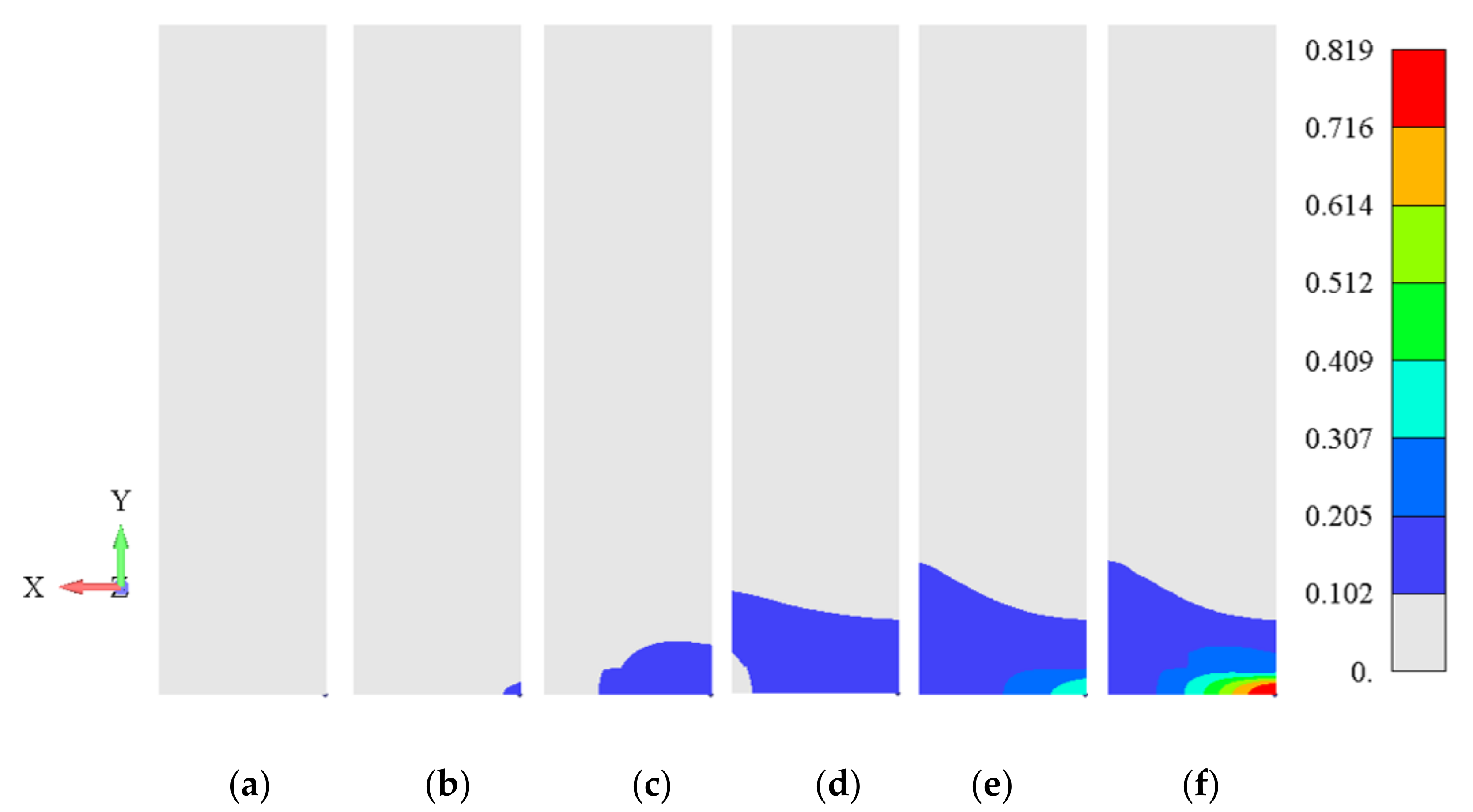
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| 0.172 | 0.360 | 0.036 | 0.639 | 4.651 | 0.074 | 0.094 | 0.021 | balance |
| 69.0 | 0.33 | 137.63 | 370.25 | 103.26 | 15.99 | 5.66 | 0.01 | 0.14 | 0.0017 | 24642.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunić, V.; Živković, J.; Milovanović, V.; Pavlović, A.; Radovanović, A.; Živković, M. Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior. Metals 2021, 11, 1685. https://doi.org/10.3390/met11111685
Dunić V, Živković J, Milovanović V, Pavlović A, Radovanović A, Živković M. Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior. Metals. 2021; 11(11):1685. https://doi.org/10.3390/met11111685
Chicago/Turabian StyleDunić, Vladimir, Jelena Živković, Vladimir Milovanović, Ana Pavlović, Andreja Radovanović, and Miroslav Živković. 2021. "Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior" Metals 11, no. 11: 1685. https://doi.org/10.3390/met11111685
APA StyleDunić, V., Živković, J., Milovanović, V., Pavlović, A., Radovanović, A., & Živković, M. (2021). Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior. Metals, 11(11), 1685. https://doi.org/10.3390/met11111685









