Experimental and Numerical Analysis on TIG Arc Welding of Stainless Steel Using RSM Approach
Abstract
:1. Introduction
2. The Finite Element Modeling Procedure
2.1. Initialization
2.1.1. Element Type
2.1.2. Material Properties
2.1.3. Meshing Technique
2.2. Heat Transfer Analysis
2.2.1. Heat Source Model
2.2.2. Boundary Conditions
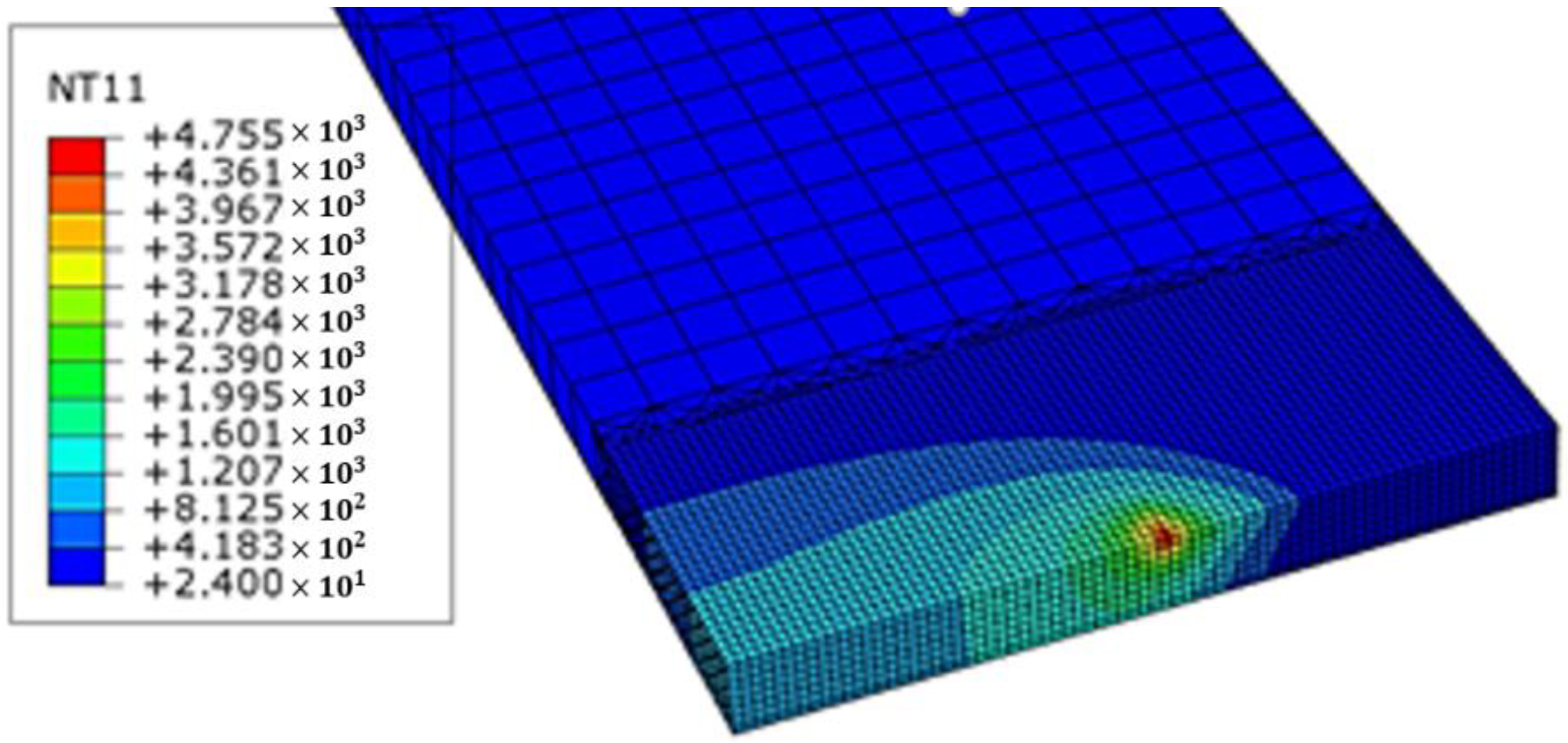
2.2.3. Post-Processing
3. Experimental Procedure
3.1. Welding Process
3.2. Specimen Preparation
3.3. Metallurgical Characterization
4. Statistical Modeling and Validation
4.1. Design of Experiments
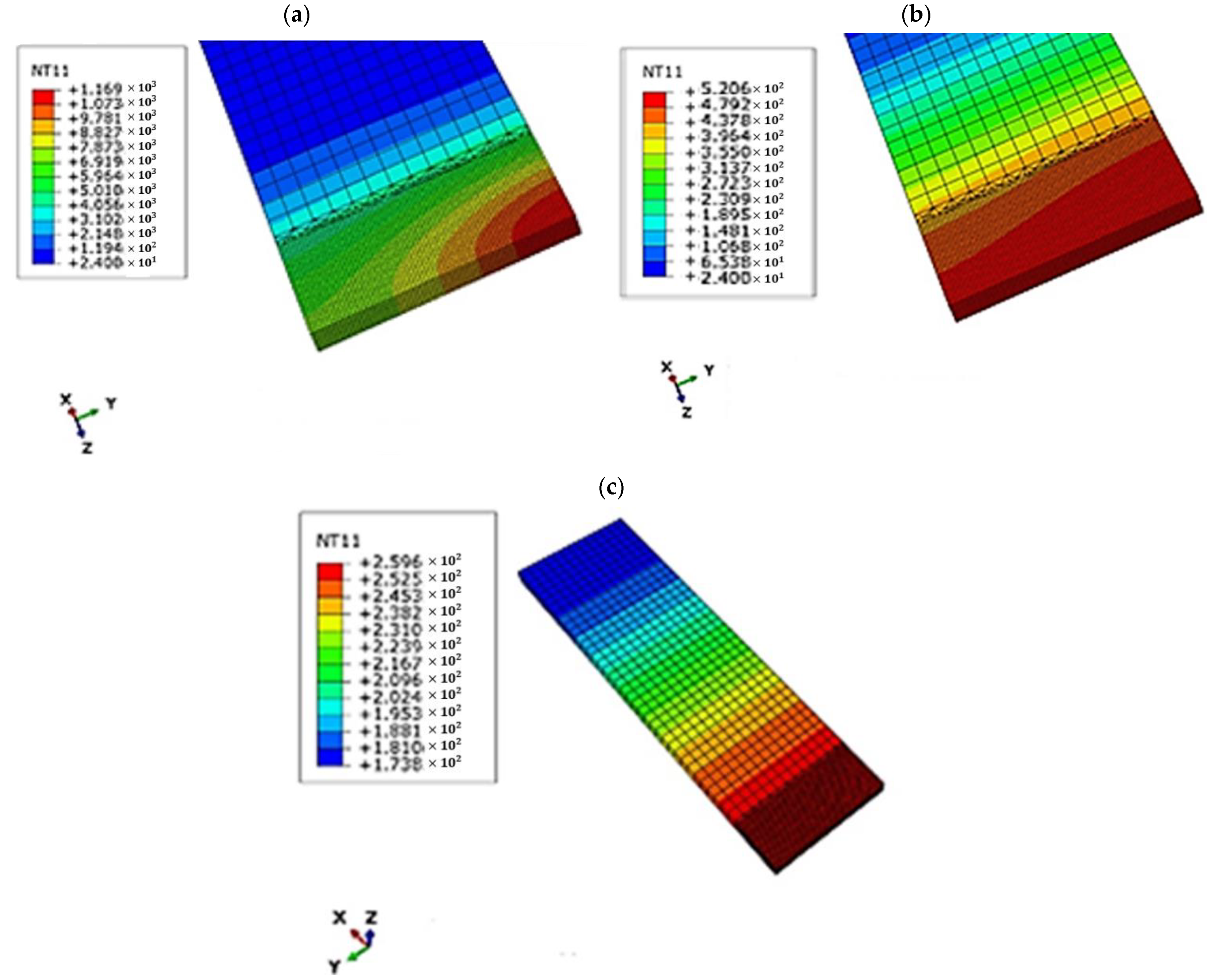
4.2. TIG Welding FEM Simulation Results
4.3. TIG Welding Experimental Results
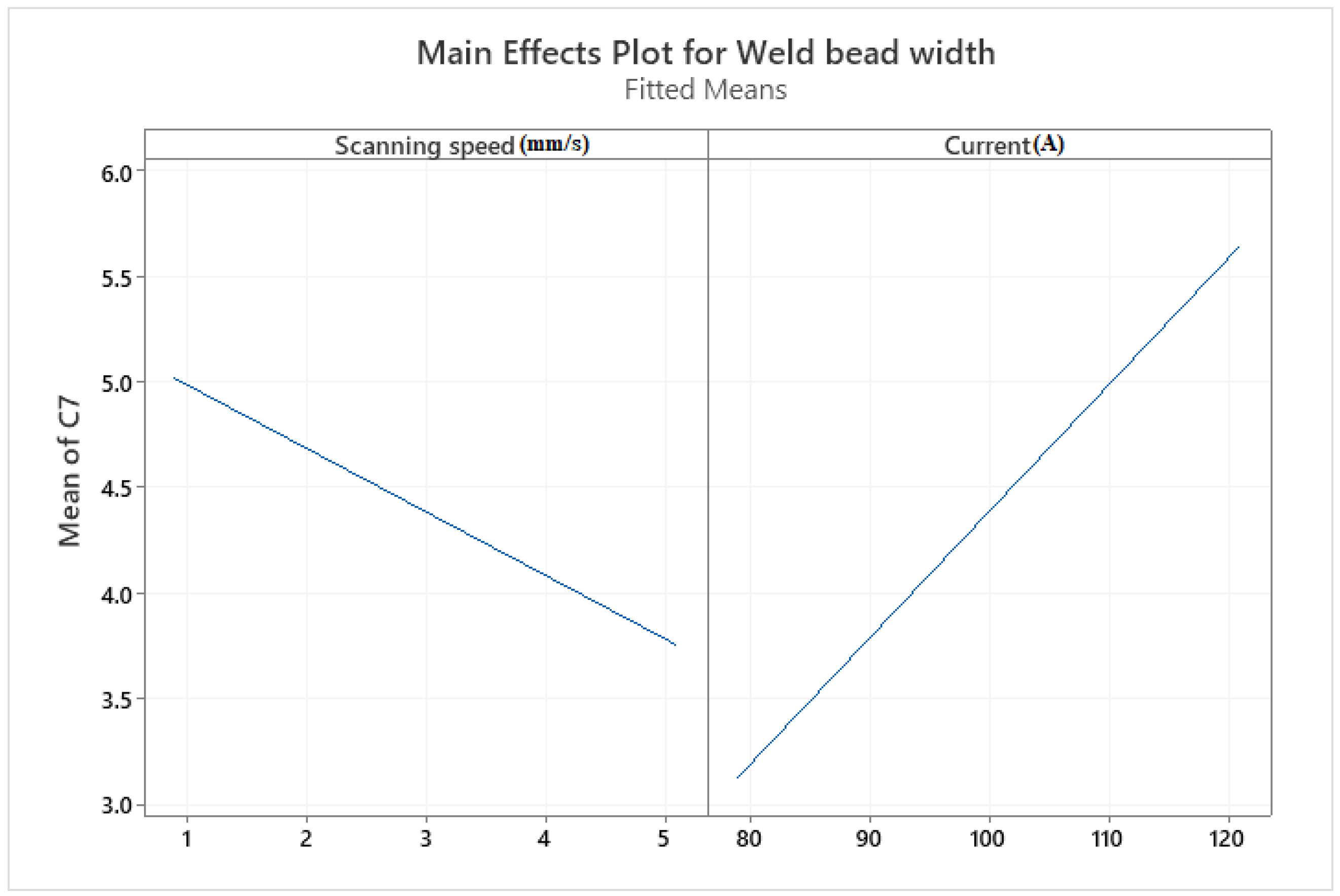
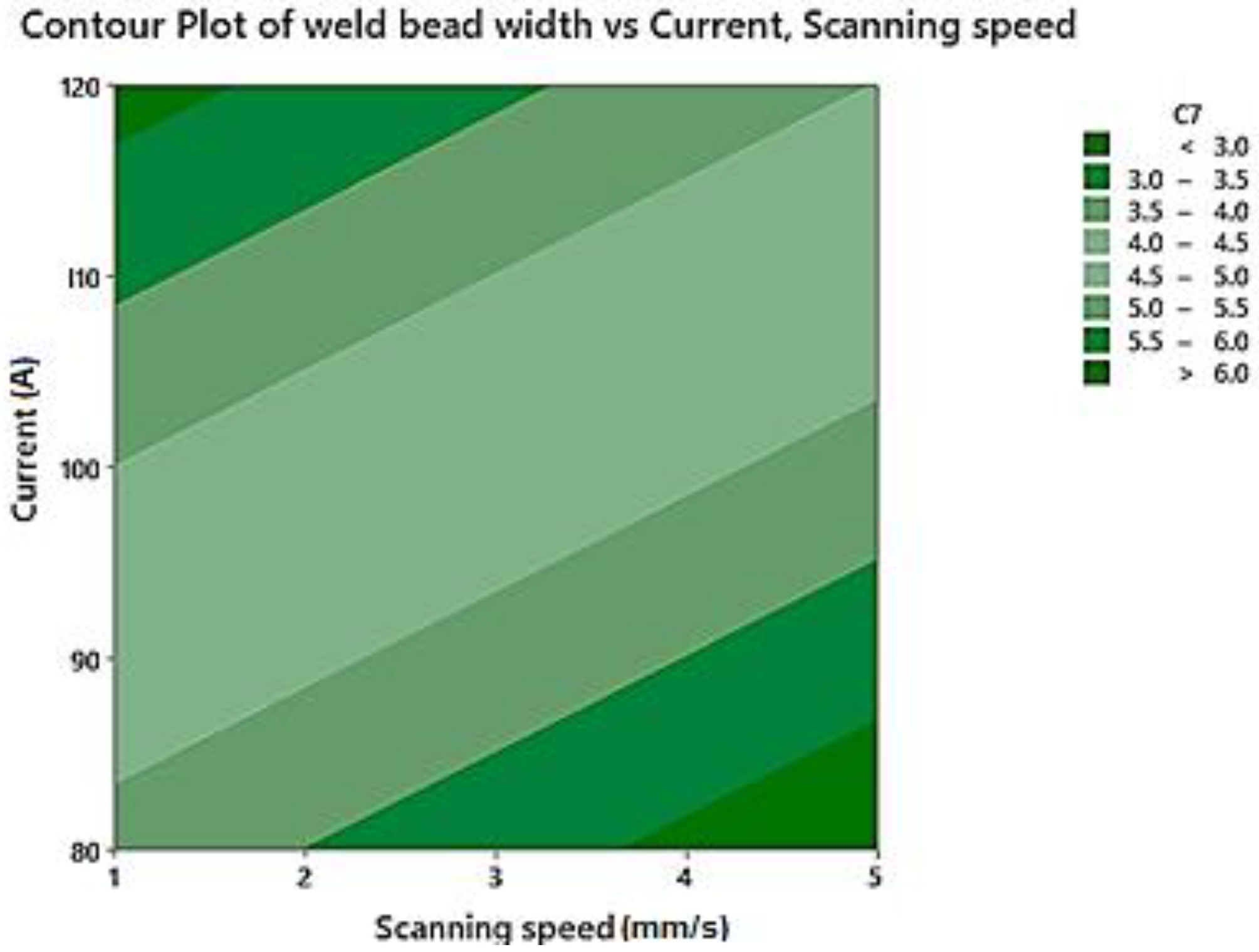
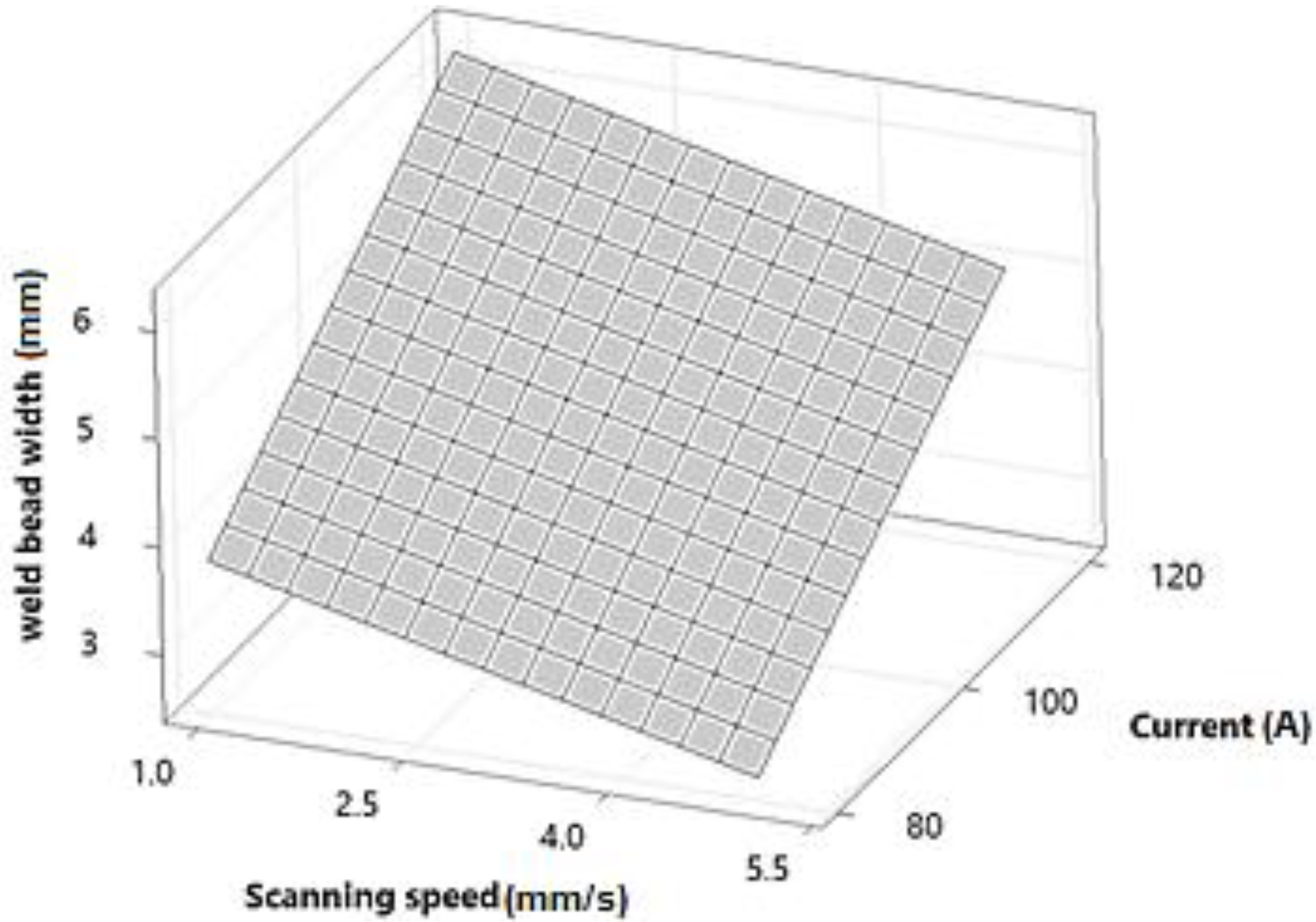
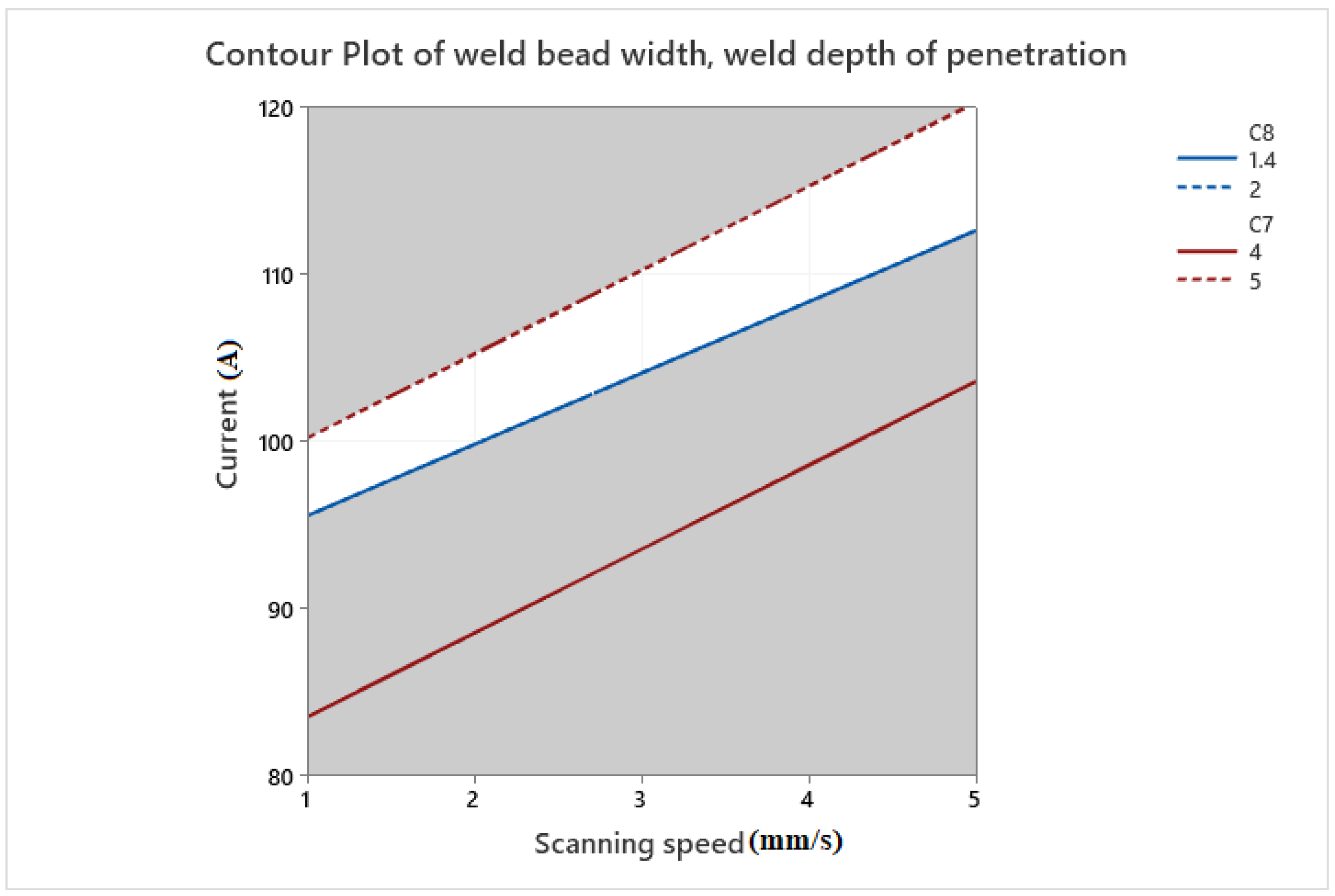
4.3.1. Weld Bead Width
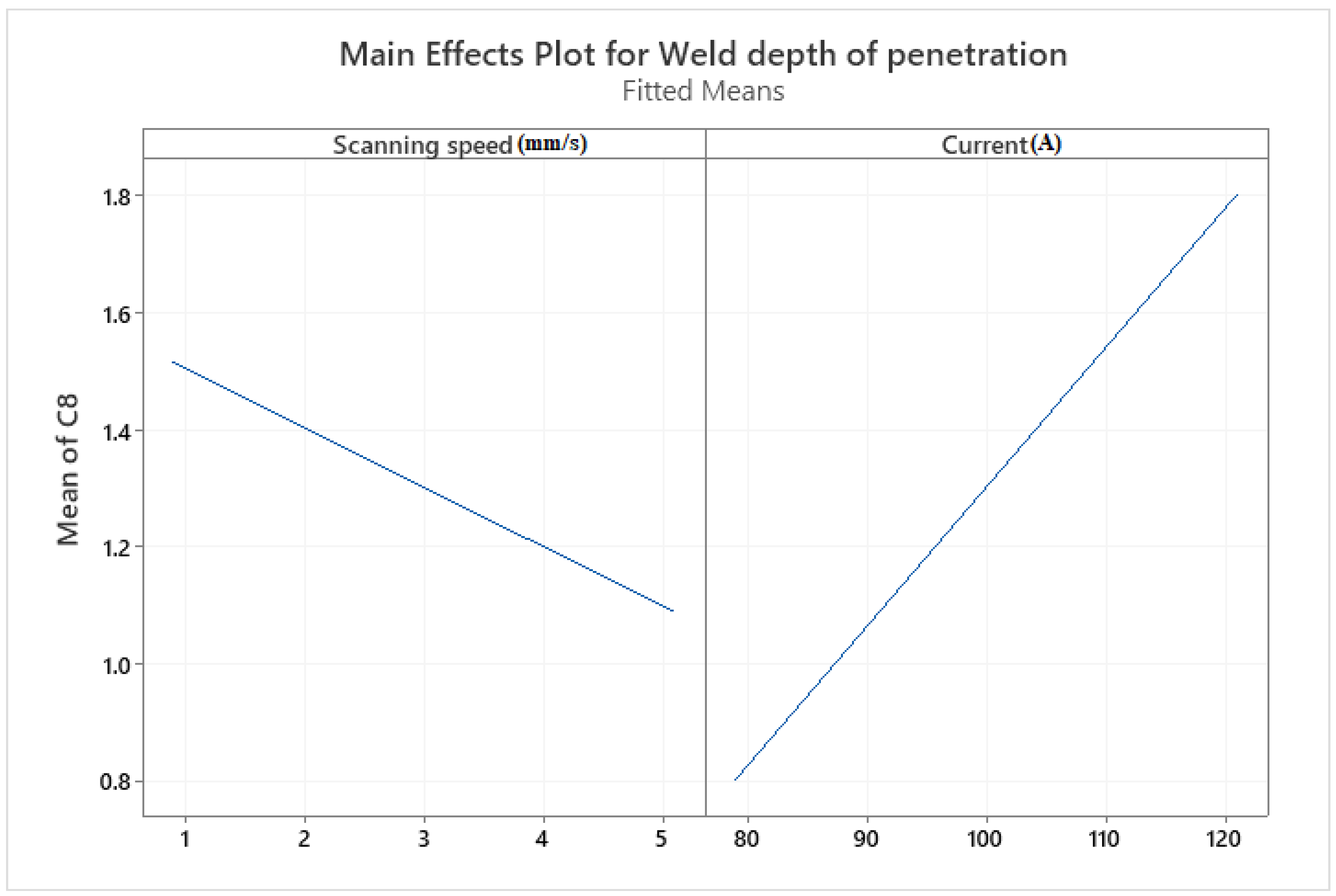
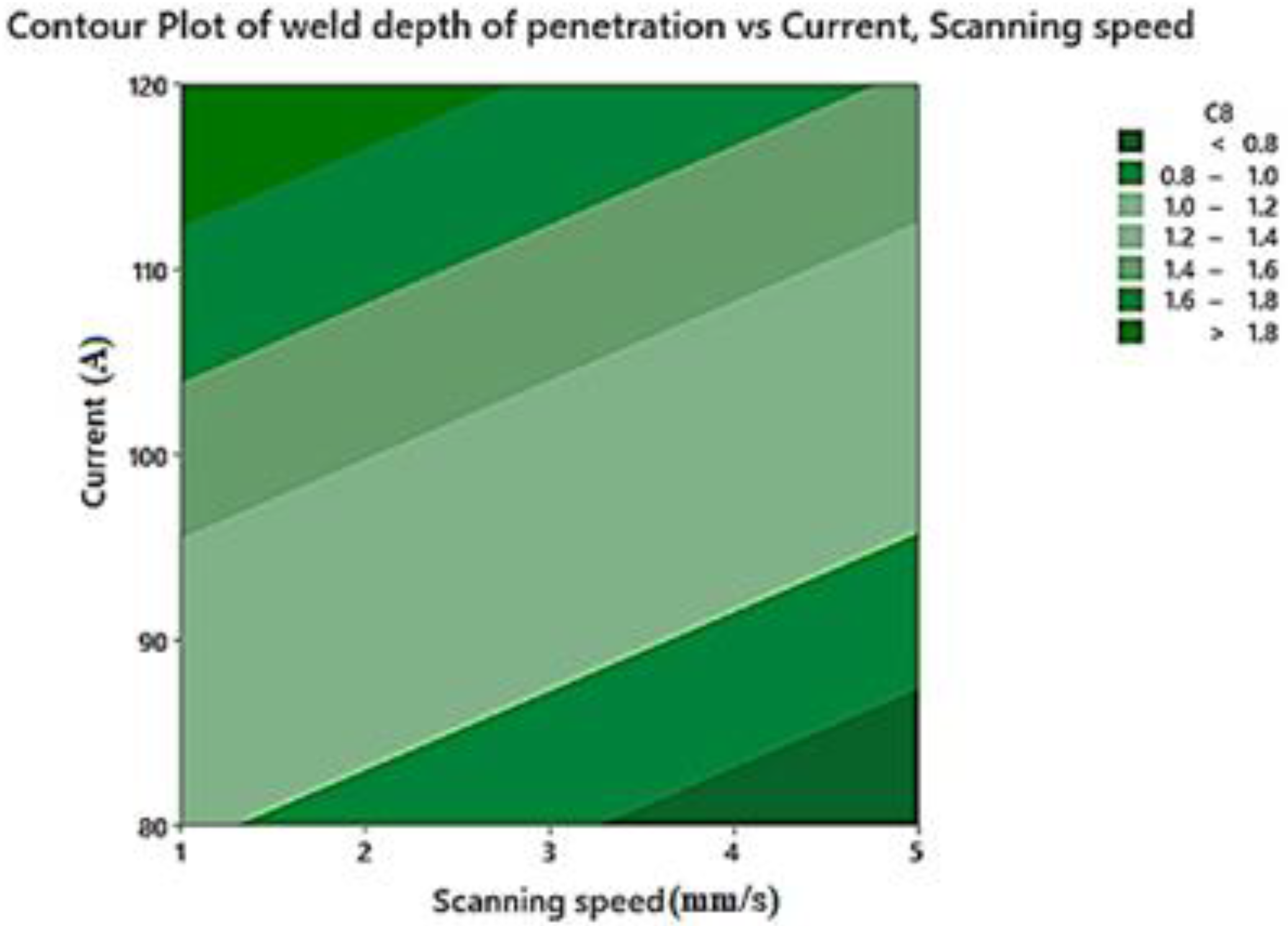
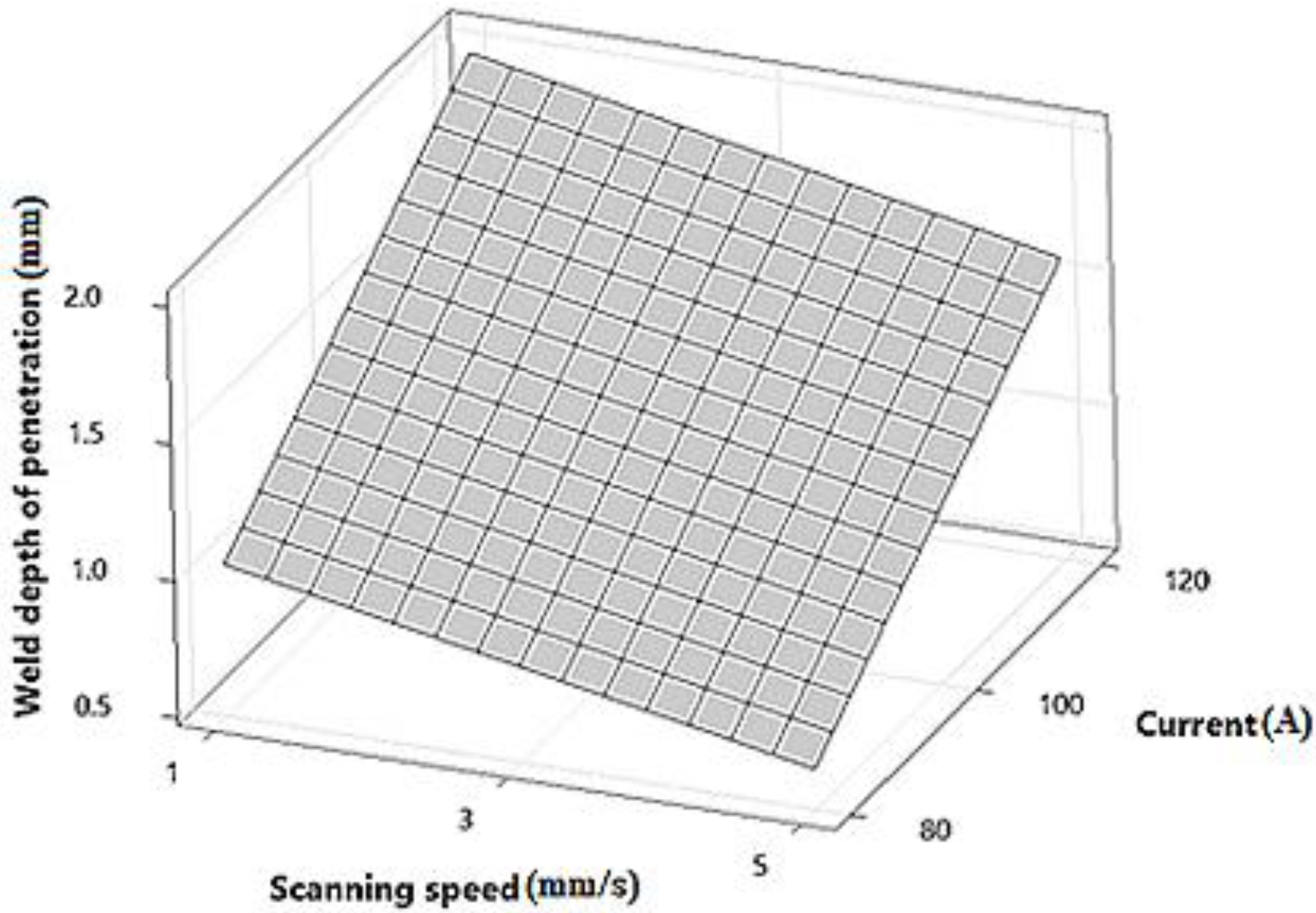
4.3.2. Weld Depth of Penetration
5. Optimization
6. Conclusions
- Among the input variables of 1.4418 stainless steel TIG welding, scanning speed is the most significant factor with a reverse effect on all weld bead dimensions.
- Results revealed that increasing the current and decreasing scanning speed, causes the weld bead width to widen and the depth of penetration extended, due to increased input energy transmitted to the material and it conducts to an increase in the melted volume.
- By applying a multi-objective optimization, through the desirability approach, the optimum settings of the TIG welding process are scanning speed (V) = 2.69 mm/s, Current (C) = 120 A.
- In the highest desired condition, the weld bead width of the welded part diminishes to 5.7 mm, and the depth of penetration increases to 1.8 mm.
- By conducting the thermal FEM analysis tests for 10 different cases and comparing them with experimental approaches, the predicted model has an average 9.7% relative error. As a result, this model shows the robustness of the present FEM model utilized for TIG Arc welding of 1.4418 stainless steel.
- With obtained results in this research, we can choose optimum input factors to reach a convenient weld seam with full penetration weld and wide weld bead. Moreover, with these input factors, optimum samples with high mechanical strength can be reached.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Dixit, P.K. Investigating the effects of filler material and heat treatment on hardness and impact strength of TIG weld. Mater. Today Proc. 2019, 26, 2776–2782. [Google Scholar] [CrossRef]
- Ramakrishnan, A.; Rameshkumar, T.; Rajamurugan, G.; Sundarraju, G.; Selvamuthukumaran, D. Experimental investigation on mechanical properties of TIG welded dissimilar AISI 304 and AISI 316 stainless steel using 308 filler rod. Mater. Today Proc. 2021, 45, 8207–8211. [Google Scholar] [CrossRef]
- Singh, S.R.; Khanna, P. A-TIG (activated flux tungsten inert gas) welding: A review. Mater. Today Proc. 2020, 44, 808–820. [Google Scholar] [CrossRef]
- Kadir, M.H.A.; Asmelash, M.; Azhari, A. Investigation on welding distortion in stainless steel sheet using gas tungsten arc welding process. Mater. Today Proc. 2020, 46, 1674–1679. [Google Scholar] [CrossRef]
- Xia, C.; Pan, Z.; Fei, Z.; Zhang, S.; Li, H. Vision based defects detection for Keyhole TIG welding using deep learning with visual explanation. J. Manuf. Process. 2020, 56, 845–855. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Arif, A.; Veerababu, M. Investigation of numerical modelling of TIG welding of austenitic stainless steel (304L). Mater. Today Proc. 2020, 27, 1636–1640. [Google Scholar] [CrossRef]
- Vinoth, V.; Sudalaimani, R.; Veera Ajay, C.; Suresh Kumar, C.; Sanjeevi Prakash, K. Optimization of mechanical behaviour of TIG welded 316 stainless steel using Taguchi based grey relational analysis method. Mater. Today Proc. 2021, 45, 7986–7993. [Google Scholar] [CrossRef]
- Kumar, M.S.; Begum, S.R. Simulation of hybrid (LASER-TIG) welding of stainless steel plates using design of experiments. Mater. Today Proc. 2020, 37, 3755–3758. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, D.L.; Na, Y.; Zhou, Y.; Han, X.L.; Wang, J. Effects of TIG welding parameters on morphology and mechanical properties of welded joint of Ni-base superalloy. Procedia Eng. 2011, 10, 37–41. [Google Scholar] [CrossRef] [Green Version]
- Natrayan, L.; Anand, R.; Kumar, S.S. Optimization of process parameters in TIG welding of AISI 4140 stainless steel using Taguchi technique. Mater. Today Proc. 2020, 37, 1550–1553. [Google Scholar] [CrossRef]
- Narang, H.; Singh, U.; Mahapatra, M.; Jha, P. Prediction of the weld pool geometry of TIG arc welding by using fuzzy logic controller. Int. J. Eng. Sci. Technol. 2012, 3, 77–85. [Google Scholar] [CrossRef] [Green Version]
- Reda, R.; Magdy, M.; Rady, M. Ti–6Al–4V TIG Weld Analysis Using FEM Simulation and Experimental Characterization. Iran. J. Sci. Technol.-Trans. Mech. Eng. 2020, 44, 765–782. [Google Scholar] [CrossRef]
- Sridhara, S.N.S.; Allada, S.C.S.; Sai, P.V.S.; Banala, S.; Subbiah, R.; Marichamy, S. Tensile strength performance and optimization of Al 7068 using TIG welding process. Mater. Today Proc. 2020, 45, 2017–2021. [Google Scholar] [CrossRef]
- Panji, M.; Baskoro, A.S.; Widyianto, A. Effect of Welding Current and Welding Speed on Weld Geometry and Distortion in TIG Welding of A36 Mild Steel Pipe with V-Groove Joint. IOP Conf. Ser. Mater. Sci. Eng. 2019, 694, 012026. [Google Scholar] [CrossRef]
- Venkata Krishna, D.; Mahesh, E.; Kiran, G.; Suchethan, G.S.; Mouli, G.C. Numerical Analysis on the effect of welding parameters in TIG welding for INCONEL 625 alloy. Int. J. Eng. Tech. 2016, 2, 134–140. [Google Scholar]
- Aghaee Attar, M.; Ghoreishi, M.; Malekshahi Beiranvand, Z. Prediction of weld geometry, temperature contour and strain distribution in disk laser welding of dissimilar joining between copper & 304 stainless steel. Optik (Stuttg). 2020, 219, 165288. [Google Scholar] [CrossRef]
- Moradi, M.; Ghoreishi, M.; Rahmani, A. Numerical and Experimental Study of Geometrical Dimensions on Laser-TIG Hybrid Welding of Stainless Steel 1.4418. J. Mod. Process. Manuf. Prod. 2016, 5, 21–31. [Google Scholar]
- Baruah, M.; Bag, S. Influence of pulsation in thermo-mechanical analysis on laser micro-welding of Ti6Al4V alloy. Opt. Laser Technol. 2017, 90, 40–51. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B. 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Casalino, G.; Michele, D.; Perulli, P. FEM model for TIG hybrid laser butt welding of 6 mm thick austenitic to martensitic stainless steels. Procedia CIRP. 2020, 88, 116–121. [Google Scholar] [CrossRef]
- Moradi, M.; Ghoreishi, M.; Torkamany, M.J. Modelling and optimization of Nd:YAG laser and tungsten inert gas (TIG) hybrid welding of stainless steel. Lasers Eng. 2014, 27, 211–230. [Google Scholar]
- Moradi, M.; Moghadam, M.K.; Shamsborhan, M.; Beiranvand, Z.M.; Rasouli, A.; Vahdati, M.; Bakhtiari, A.; Bodaghi, M. Simulation, statistical modeling, and optimization of CO2 laser cutting process of polycarbonate sheets. Optik (Stuttg). 2021, 225, 164932. [Google Scholar] [CrossRef]
- Moradi, M.; Ghoreishi, M.; Khorram, A. Process and Outcome Comparison Between Laser, Tungsten Inert Gas (TIG) and Laser-TIG Hybrid Welding. Lasers Eng. 2018, 39, 379–391. [Google Scholar]
- Zhang, B.; Shi, Y.; Cui, Y.; Wang, Z.; Hong, X. Prediction of keyhole TIG weld penetration based on high-dynamic range imaging. J. Manuf. Process. 2021, 63, 179–190. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Parvizi, A.; Moradi, M. Multi-objective topology optimization of deep drawing dissimilar tailor laser welded blanks; experimental and finite element investigation. Opt. Laser Technol. 2020, 125, 106029. [Google Scholar] [CrossRef]
- Tahmasbi, V.; Ghoreishi, M.; Zolfaghari, M. Investigation, sensitivity analysis, and multi-objective optimization of effective parameters on temperature and force in robotic drilling cortical bone. Proc. Inst. Mech. Eng. Part. H J. Eng. Med. 2017, 231, 1012–1024. [Google Scholar] [CrossRef]





| Temperature (K) | Specific Heat (W/mK) | Thermal Conductivity (J/Kgm3) |
|---|---|---|
| 293 | 430 | 15 |
| 373 | 460 | 20 |
| 673 | 520 | 25 |
| 1073 | 580 | 35 |
| 1473 | 640 | 45 |
| Variables | Double Ellipsoidal Distribution | Heat Input Fractions | ||||
|---|---|---|---|---|---|---|
| values | b (mm) | c (mm) | ||||
| 5 | 15 | 10 | 2 | 0.5 | 1.5 | |
| Element | Fe | Cr | Ni | Mo | Mn | Cu | Si | W | Al | V | C |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight percentage (%) | Bal | 15.9 | 4.89 | 0.86 | 0.72 | 0.22 | 0.2 | 0.15 | 0.1 | 0.1 | 0.037 |
| Variable | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| Welding Current (C, A) | 80 | 90 | 100 | 110 | 120 |
| Welding scanning speed (V, mm/s) | 1 | 2 | 3 | 4 | 5 |
| Tests | Input Variables (Coded Values) | Input Variables (Actual Values) | Output Responses | |||
|---|---|---|---|---|---|---|
| Sample No. | Scanning Speed (mm/s) | Current (A) | Scanning Speed (mm/s) | Current (A) | Weld Bead Width (mm) | Weld Depth of Penetration (mm) |
| 1 | −1 | −1 | 2 | 90 | 4.35 | 1.17 |
| 2 | +1 | −1 | 4 | 90 | 3.54 | 0.97 |
| 3 | −1 | +1 | 2 | 110 | 4.85 | 1.53 |
| 4 | +1 | +1 | 4 | 110 | 4.51 | 1.41 |
| 5 | −2 | 0 | 1 | 100 | 5.09 | 1.67 |
| 6 | +2 | 0 | 5 | 100 | 3.86 | 1.22 |
| 7 | 0 | −2 | 3 | 80 | 3.12 | 0.81 |
| 8 | 0 | +2 | 3 | 120 | 5.98 | 1.84 |
| 9 | 0 | 0 | 3 | 100 | 4.36 | 1.32 |
| 10 | 0 | 0 | 3 | 100 | 4.19 | 1.08 |
| Tests | Input Variables | Weld Bead Width | Weld Depth of Penetration | |||||
|---|---|---|---|---|---|---|---|---|
| Sample No. | Scanning Speed (mm/s) | Current (A) | Experimental Results (mm) | Simulation Results (mm) | Percent Error % | Experimental Results (mm) | Simulation Results (mm) | Percent Error % |
| 1 | 2 | 90 | 4.35 | 3.7 | 17 | 1.17 | 1.4 | 3.3 |
| 2 | 4 | 90 | 3.86 | 3.9 | 0.2 | 0.97 | 1 | 4 |
| 3 | 2 | 110 | 4.85 | 4.3 | 12.1 | 1.53 | 1.3 | 15.3 |
| 4 | 4 | 110 | 4.51 | 4.3 | 10.5 | 1.41 | 1.3 | 19.8 |
| 5 | 1 | 100 | 5.09 | 4.8 | 7.2 | 1.67 | 1.7 | 1.4 |
| 6 | 5 | 100 | 3.86 | 3.1 | 20 | 1.22 | 1 | 25.2 |
| 7 | 3 | 80 | 3.12 | 3 | 6 | 0.81 | 0.7 | 10.5 |
| 8 | 3 | 120 | 5.98 | 5.4 | 11.2 | 1.84 | 1.6 | 10.7 |
| 9 | 3 | 100 | 4.36 | 4.1 | 8.1 | 1.32 | 1.2 | 11.3 |
| 10 | 3 | 100 | 4.19 | 4.1 | 5.3 | 1.08 | 1.2 | 10.8 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | VIF |
|---|---|---|---|---|---|---|
| Model | 5.39402 | 2 | 2.69701 | 37.12 | 0.000 | |
| Scanning speed (V) | 1.08601 | 1 | 1.08601 | 14.95 | 0.006 | 1.0 |
| Current (C) | 4.30801 | 1 | 4.30801 | 59.29 | 0.000 | 1.0 |
| Lack-of-Fit | 0.49418 | 6 | 0.08236 | 5.70 | 0.310 | |
| Pure Error | 0.01445 | 1 | 0.01445 | |||
| Total | 5.90265 | 9 | ||||
| R-Squared = 91.38% | R-Squared (Adj) = 88.92% | |||||
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | VIF |
|---|---|---|---|---|---|---|
| Model | 0.80567 | 2 | 0.40283 | 25.9 | 0.001 | |
| Scanning speed (V) | 0.12403 | 1 | 0.12403 | 7.97 | 0.026 | 1.0 |
| Current (C) | 0.68163 | 1 | 0.68163 | 43.82 | 0.000 | 1.0 |
| Lack-of-Fit | 0.08009 | 6 | 0.01335 | 0.46 | 0.808 | |
| Pure Error | 0.02880 | 1 | 0.02880 | |||
| Total | 0.91456 | 9 | ||||
| R-Squared = 88.09% | R-Squared (Adj) = 84.69% | |||||
| Parameter/Response | Variable | Goal | Lower | Upper | Importance | Composite Desirability | |
|---|---|---|---|---|---|---|---|
| Parameters | Scanning speed | in range | 1 | 5 | --- | --- | |
| Current | in range | 80 | 120 | --- | --- | ||
| Response | Criteria 1 | Weld bead width (W) | Minimize | 3.12 | 5.98 | 1 | 0.57 |
| Weld depth of penetration (P) | Maximize | 0.81 | 1.84 | 1 | |||
| Criteria 2 | Weld bead width (W) | Minimize | 3.12 | 5.98 | 1 | 0.60 | |
| Weld depth of penetration (P) | Maximize | 0.81 | 1.84 | 5 | |||
| Criteria 3 | Weld bead width (W) | Minimize | 3.12 | 5.98 | 1 | 0.53 | |
| Weld depth of penetration (P) | Maximize | 0.81 | 1.84 | 4 | |||
| Solution | Optimum Input Parameters | Composite Desirability % | Output Responses | ||||
|---|---|---|---|---|---|---|---|
| Scanning Speed | Current | Weld Bead Width | Weld Depth of Penetration | ||||
| 1 | Coded value | −0.2 | +2 | 54% | Predicted | 5.67449 | 1.80947 |
| Actual value | 2.69697 | 120 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sattarpanah Karganroudi, S.; Moradi, M.; Aghaee Attar, M.; Rasouli, S.A.; Ghoreishi, M.; Lawrence, J.; Ibrahim, H. Experimental and Numerical Analysis on TIG Arc Welding of Stainless Steel Using RSM Approach. Metals 2021, 11, 1659. https://doi.org/10.3390/met11101659
Sattarpanah Karganroudi S, Moradi M, Aghaee Attar M, Rasouli SA, Ghoreishi M, Lawrence J, Ibrahim H. Experimental and Numerical Analysis on TIG Arc Welding of Stainless Steel Using RSM Approach. Metals. 2021; 11(10):1659. https://doi.org/10.3390/met11101659
Chicago/Turabian StyleSattarpanah Karganroudi, Sasan, Mahmoud Moradi, Milad Aghaee Attar, Seyed Alireza Rasouli, Majid Ghoreishi, Jonathan Lawrence, and Hussein Ibrahim. 2021. "Experimental and Numerical Analysis on TIG Arc Welding of Stainless Steel Using RSM Approach" Metals 11, no. 10: 1659. https://doi.org/10.3390/met11101659
APA StyleSattarpanah Karganroudi, S., Moradi, M., Aghaee Attar, M., Rasouli, S. A., Ghoreishi, M., Lawrence, J., & Ibrahim, H. (2021). Experimental and Numerical Analysis on TIG Arc Welding of Stainless Steel Using RSM Approach. Metals, 11(10), 1659. https://doi.org/10.3390/met11101659








