Phenomenological Models and Peculiarities of Evaluating Fatigue Life of Aluminum Alloys Subjected to Dynamic Non-Equilibrium Processes
Abstract
:1. Introduction
2. Materials and Methods of Research
2.1. Methods of Mechanical Tests
2.2. Evaluation Methods of Physical-Mechanical Properties of Surface Layers of Aluminum Alloys
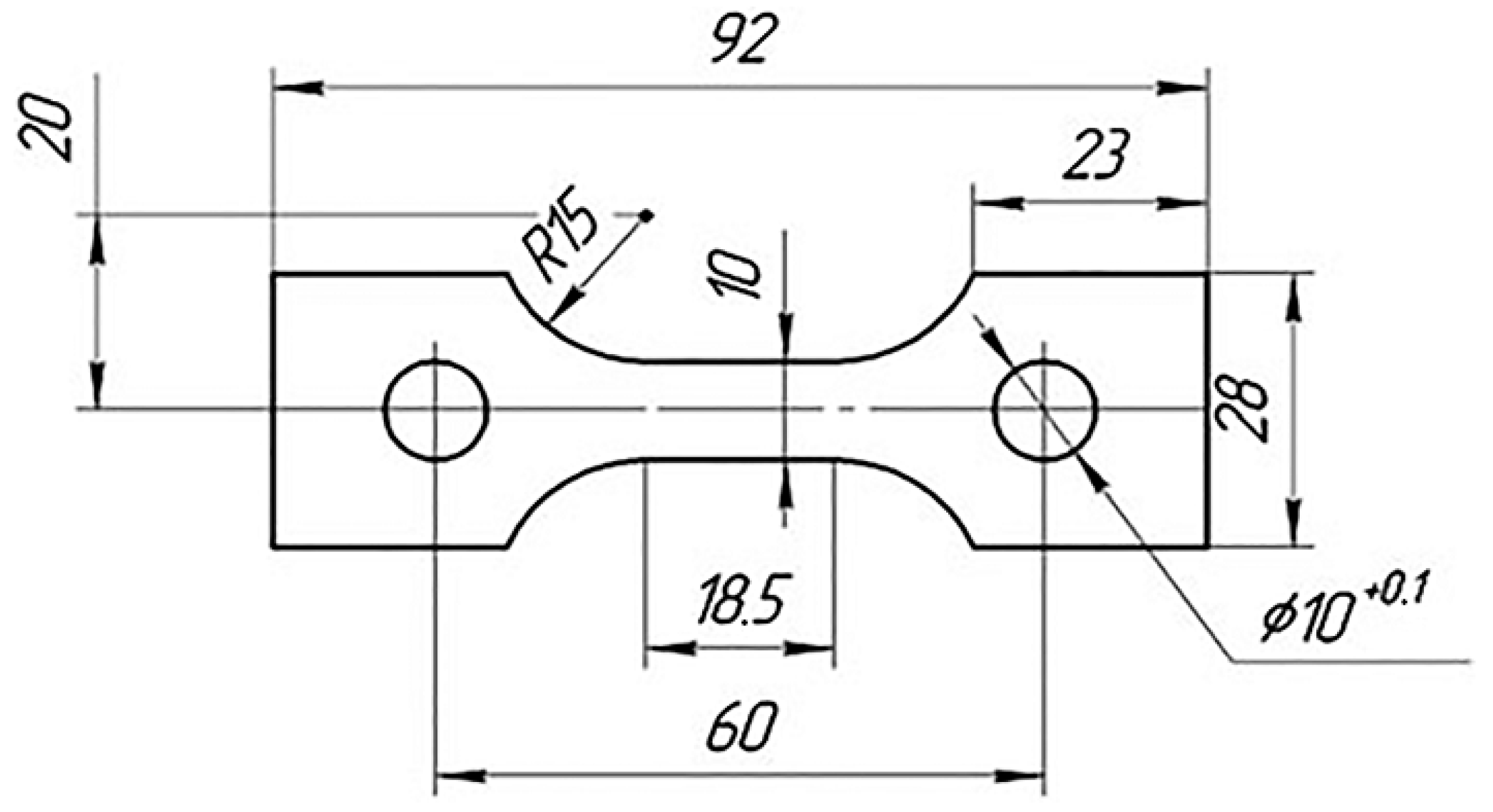
2.3. Materials and Specimen for Test
3. Analysis of Experimental Results of Fatigue Testing in the Initial State
3.1. Physical-Mechanical Models for Predicting the Fatigue Life of Aluminum Alloys in the Initial State
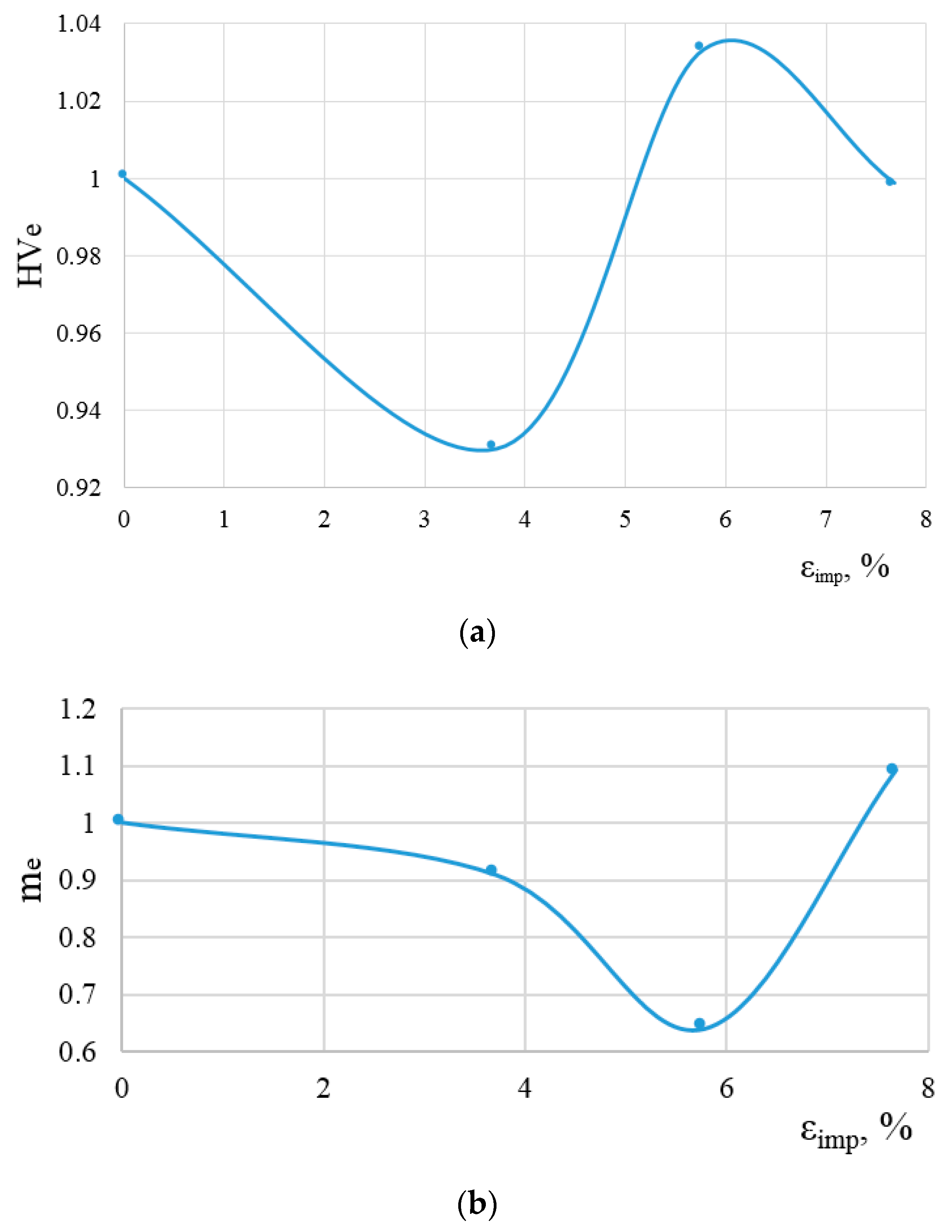
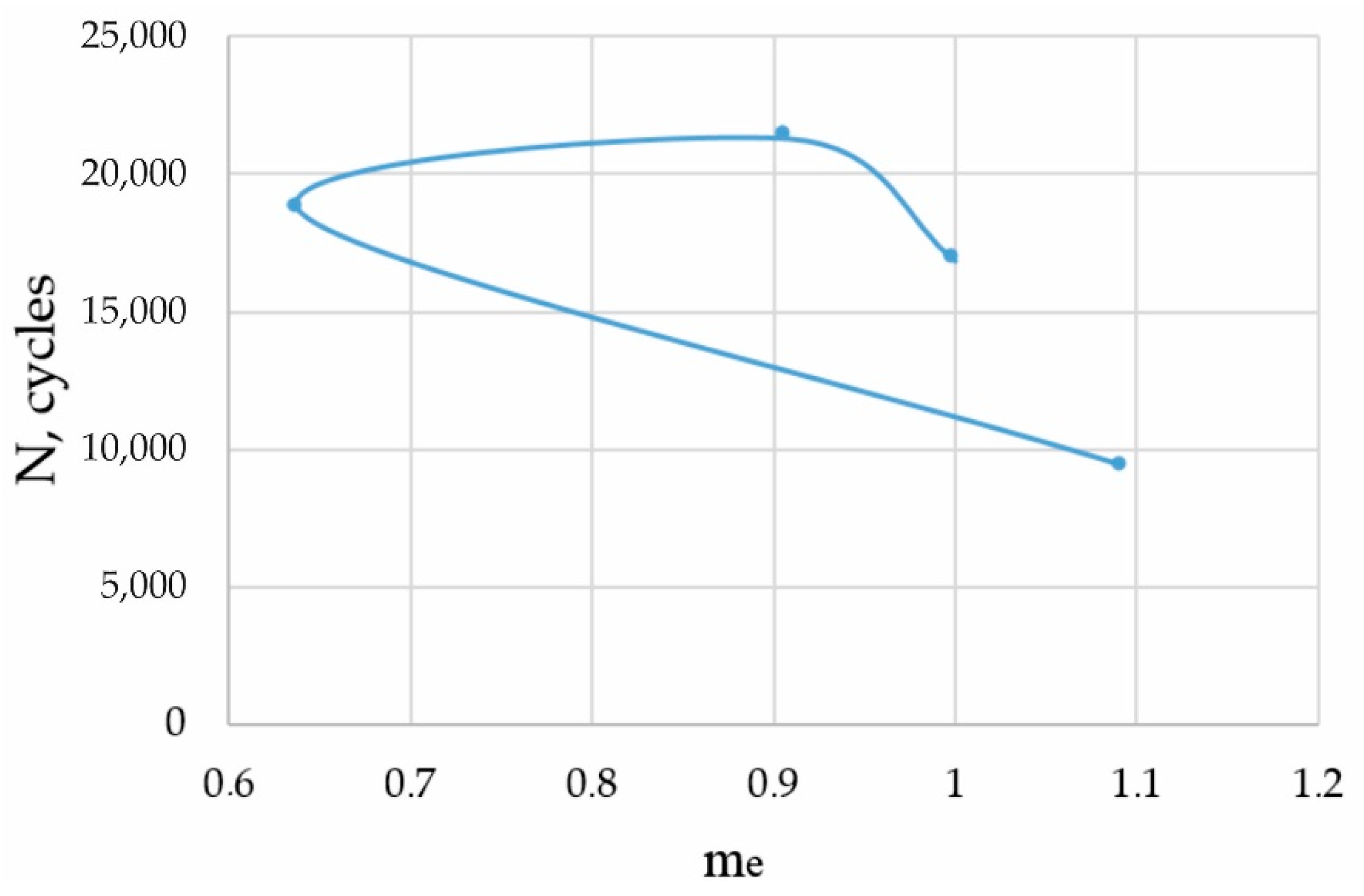
3.2. Physical-Mechanical Model for Predicting Fatigue Life of Aluminum Alloy after Preliminary Introduction of Impulse Energy of Optimal Intensity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sakin, R. Investigation of bending fatigue-life of aluminum sheets based on rolling direction. Alex. Eng. J. 2018, 57, 35–47. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M. Multi-objective probabilistic optimum monitoring planning considering fatigue damage detection, maintenance, reliability, service life and cost. Struct. Multidisc. Optim. 2018, 57, 39–54. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Maskery, I.; Tuck, C.; Ashcroft, I.; Everitt, N.M. Improving the fatigue behaviour of a selectively laser melted aluminium alloy: Influence of heat treatment and surface quality. Mater. Des. 2016, 104, 174–182. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Y.; Gao, X.; Wu, Y.; Hutchinson, C. Training high-strength aluminum alloys to withstand fatigue. Nat. Commun. 2020, 11, 5198. [Google Scholar] [CrossRef] [PubMed]
- Ueno, A.; Miyakawa, S.; Yamada, K.; Sugiyama, T. Fatigue behavior of die casting aluminum alloys in air and vacuum. Procedia Eng. 2010, 2, 1937–1943. [Google Scholar] [CrossRef] [Green Version]
- Khonsari, M.M.; Amiri, M. Introduction to Thermodynamics of Mechanical Fatigue, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012; 166p. [Google Scholar] [CrossRef]
- Brodova, I.G.; Petrova, A.N.; Razorenov, S.V.; Shorokhov, E.V. Interconnection of structural characteristics with dynamic properties of A5083 aluminum alloy. Inorg. Mater. Appl. Res. 2019, 10, 168–173. [Google Scholar] [CrossRef]
- Borodin, E.N.; Bratov, V. Non-equilibrium approach to prediction of microstructure evolution for metals undergoing severe plastic deformation. Mater. Charact. 2018, 141, 267–278. [Google Scholar] [CrossRef]
- Kaibyshev, O.; Valiev, R. Non-equilibrium structure of grain boundaries and properties of metals. J. Phys. Coll. 1985, 46, C4-641–C4-644. [Google Scholar] [CrossRef]
- Nazarov, A.A. On the role of non-equilibrium grain-boundary structure in the yield and flow stress of polycrystals. Philos. Mag. A 1994, 69, 327–340. [Google Scholar] [CrossRef]
- Hutsaylyuk, V. The peculiarity of cyclic elastic-plastic deformation of aluminum alloys D16ChATV under the conditions of the previous combined load. Mech. Adv. Mater. Struct. 2020, 27, 1246–1255. [Google Scholar] [CrossRef]
- Chausov, M.; Brezinová, J.; Pylypenko, A.; Maruschak, P.; Titova, L.; Guzanová, A. Modification of mechanical properties of high-strength titanium alloys VT23 and VT23M due to impact-oscillatory loading. Metals 2019, 9, 80. [Google Scholar] [CrossRef] [Green Version]
- Chausov, M.; Brezinova, J.; Zasimchuk, E.; Maruschak, P.; Khyzhun, O.; Pylypenko, A.; Bazarnik, P.; Brezina, J. Effect of structure self-organization of aluminum alloy D16ChATW under impact-oscillatory loading on its fatigue life. J. Mater. Eng. Perform. 2021, 30, 6235–6242. [Google Scholar] [CrossRef]
- Chausov, M.; Zasimchuk, E.; Maruschak, P.; Khyzhun, O.; Pylypenko, A.; Prentkovskis, O.; Brezinová, J. Influence of impact-oscillatory loading on fatigue life of aluminium alloy 2024-T351. Iran. J. Sci. Technol. Trans. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Shankar, M.R.; Chandrasekar, S.; Compton, W.D.; King, A.H. Characteristics of aluminum 6061-T6 deformed to large plastic strains by machining. Mater. Sci. Eng. 2005, 410–411, 364–368. [Google Scholar] [CrossRef]
- Kwon, K.; Frangopol, D.M. Fatigue life assessment and lifetime management of aluminum ships using life-cycle optimization. J. Ship Res. 2012, 56, 91–105. [Google Scholar] [CrossRef]
- Gao, Y.X.; Yi, J.Z.; Lee, P.D.; Lindley, T.C. A micro-cell model of the effect of microstructure and defects on fatigue resistance in cast aluminum alloys. Acta Mater. 2004, 52, 5435–5449. [Google Scholar] [CrossRef]
- Ignatovich, S.R.; Menou, A.; Karuskevich, M.V.; Maruschak, P.O. Fatigue damage and sensor development for aircraft structural health monitoring. Theor. Appl. Fracture Mech. 2013, 65, 23–27. [Google Scholar] [CrossRef]
- Zhu, D.; Xu, L.; Wang, F.; Liu, T.; Lu, K. Evolution of metal surface topography during fatigue. Metals 2017, 7, 66. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Limodin, N.; El Bartali, A.; Charkaluk, E. Coupling of X-ray computed tomography and surface in situ analysis combined with digital image correlation method to study low cycle fatigue damage micromechanisms in lost foam casting A319 alloy. Fatigue Fracture Eng. Mater. Struct. 2021, 44, 916–932. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, Z.J.; Duan, Q.Q.; Zhang, P.; Zhang, Z.F. Improving the fatigue strength of 7075 alloy through aging. Mater. Sci. Eng. A 2018, 738, 24–30. [Google Scholar] [CrossRef]
- Maruschak, P.; Konovalenko, I.; Karuskevich, M.; Gliha, V.; Vuherer, T. Automated diagnostics of damage to an aluminum alloy under the conditions of high-cycle fatigue. Mater. Tehnol. 2013, 47, 357–361. [Google Scholar]
- Nykyforchyn, H.M.; Ostash, O.P.; Tsyrul’nyk, O.T.; Andreiko, I.M.; Holovatyuk, Y.V. Electrochemical evaluation of the in-service degradation of an aircraft aluminum alloy. Mater. Sci. 2008, 44, 254–259. [Google Scholar] [CrossRef]
- Ignatovich, S.R.; Karuskevich, M.V.; Yutskevich, S.S. Deformation relief of the surface as a characteristic of fatigue damage of clad aluminum alloys. Part 1. Deformation relief evolution under cyclic loading. Strength Mater. 2020, 52, 707–714. [Google Scholar] [CrossRef]
- Panin, V.E.; Surikova, N.S.; Elsukova, T.F.; Egorushkin, V.E.; Pochivalov, Y. Nanostructured phase boundaries in aluminum under severe cyclic plastic deformation. Phys. Mesomech. 2010, 13, 103–112. [Google Scholar] [CrossRef]
- Karuskevich, M.; Ignatovich, S.; Karuskevich, O.; Maslak, T.; Pejkowski, Ł.; Kurdel, P. Fatigue and overstress indicators for ultralight and light aircraft. Fatigue Fracture Eng. Mater. Struct. 2021, 44, 595–598. [Google Scholar] [CrossRef]
- Pantelakis, S.G.; Petroyiannis, P.V.; Bouzakis, K.D.; Mirisidis, I. Surface hardness increase of 2024 aluminum alloy subjected to cyclic loading. Theor. Appl. Fracture Mech. 2007, 48, 68–81. [Google Scholar] [CrossRef]
- Bouzakis, K.-D.; Mirisidis, I.; Pantelakis, S.G.; Chamos, A.N. Fatigue induced alteration of the superficial strength properties of 2024 aluminum alloy. J. Mater. Sci. Technol. 2011, 27, 776–784. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetalic Inclusions, 1st ed.; Academic Press: Cambridge, MA, USA, 2002; p. 384. [Google Scholar]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetalic Inclusions, 2nd ed.; Academic Press: Cambridge, MA, USA, 2019; p. 758. [Google Scholar]
- Schneller, W.; Leitner, M.; Leuders, S.; Sprauel, J.M.; Grun, F.; Pfeifer, T.; Jantschner, O. Fatigue strength estimation methodology of additively manufactured metallic bulk material. Addit. Manuf. 2021, 39, 101688. [Google Scholar] [CrossRef]
- Aigner, R.; Leitner, M.; Stoschka, M. On the mean stress sensitivity of cast aluminium considering imperfections. Mater. Sci. Eng. A 2019, 758, 172–184. [Google Scholar] [CrossRef]
- Solberg, K.; Wan, D.; Berto, F. Fatigue assessment of as-built and heat-treated Inconel 718 specimens produced by additive manufacturing including notch effects. Fatigue Fracture Eng. Mater. Struct. 2020, 43, 2326–2336. [Google Scholar] [CrossRef]
- Lebedev, A.A.; Muzyka, N.R.; Volchek, N.L. Determination of damage accumulated in structural materials by the parameters of scatter of their hardness characteristics. Strength Mater. 2002, 34, 317–321. [Google Scholar] [CrossRef]
- Lebedev, A.; Golubovskiy, Y.; Lokoshchenko, O. Determination of limit levels of damage in materials after operation under conditions of thermomechanical loads. J. Ternopil Natl. Tech. Univ. 2011, 16, 7–14. [Google Scholar]
- Novikov, A.; Bulakh, P.; Byalonovich, A. Determination of the Level of Scattered Damage by LM-Hardness Method. Sci. J. Ternopil National Tech. Univ. 2018, 1, 18. [Google Scholar]
- Chausov, N.G.; Voityuk, D.G.; Pilipenko, A.P.; Kuz’menko, A.M. Setup for testing materials with plotting complete stress–strain diagrams. Strength Mater. 2004, 36, 532–537. [Google Scholar] [CrossRef]
- Chausov, N.G.; Pilipenko, A.P. Influence of dynamic overloading on fracture kinetics of metals at the final stages of deformation. Mechanika 2004, 48, 13–18. [Google Scholar]
- Chausov, M.G.; Berezin, V.B.; Pylypenko, A.P.; Hutsaylyuk, V.B. Strain field evolution on the surface of aluminum sheet alloys exposed to specific impact with oscillation loading. J. Strain. Anal. 2014, 50, 61–62. [Google Scholar] [CrossRef]
- Zasimchuk, E.; Turchak, T.; Chausov, N. Hydrodynamic plastic flow in metal materials. Results Mater. 2020, 6, 100090. [Google Scholar] [CrossRef]
- Chausov, M.; Maruschak, P.; Zasimchuk, E.; Pylypenko, A.; Bishchak, R.; Burda, I. About Physical Aspects of Increasing Durability of Aluminum Alloys Due to Impact-Oscillatory Loading. In Lecture Notes in Intelligent Transportation and Infrastructure; Springer: Berlin, Germany, 2020; pp. 572–580. [Google Scholar] [CrossRef]
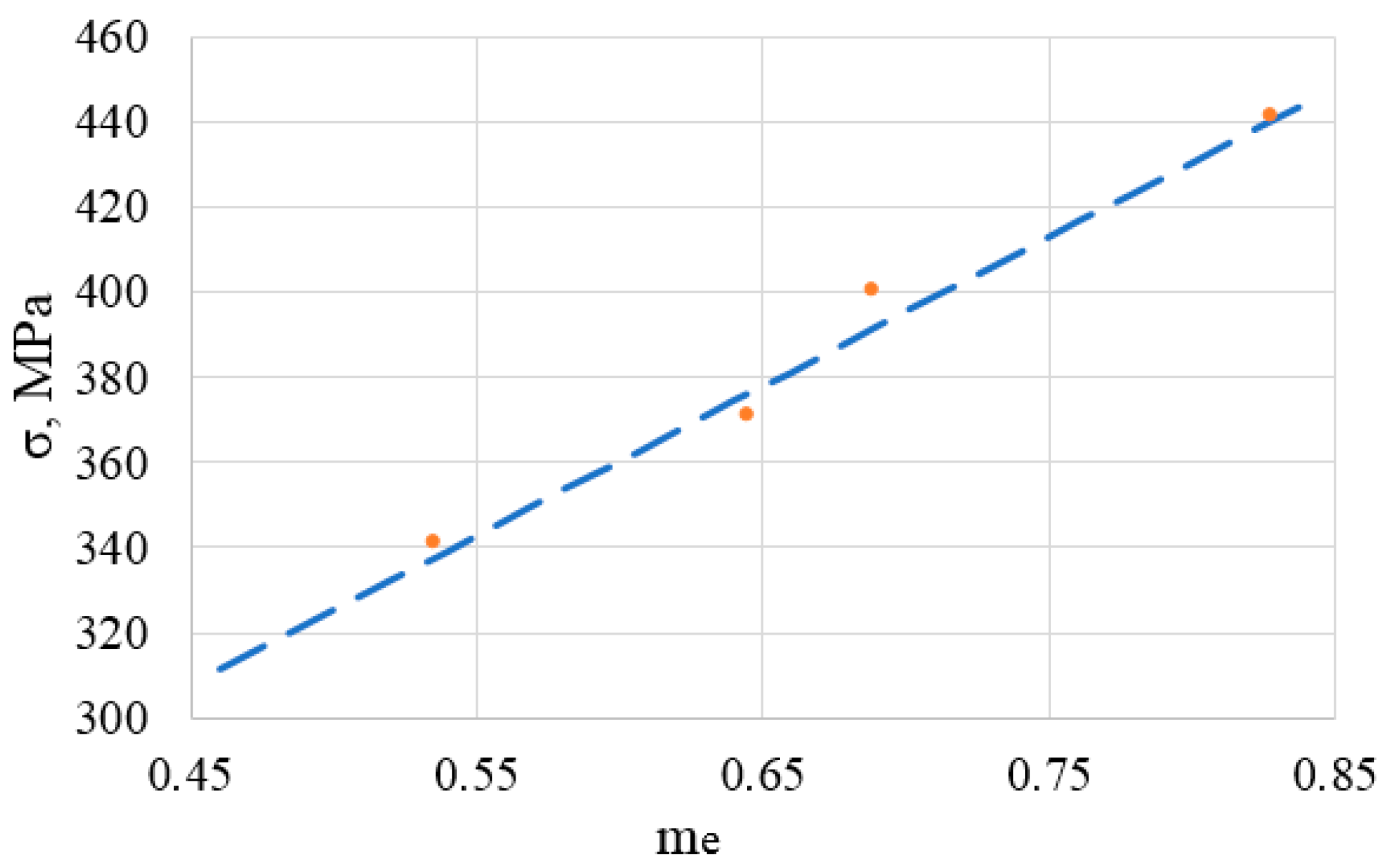
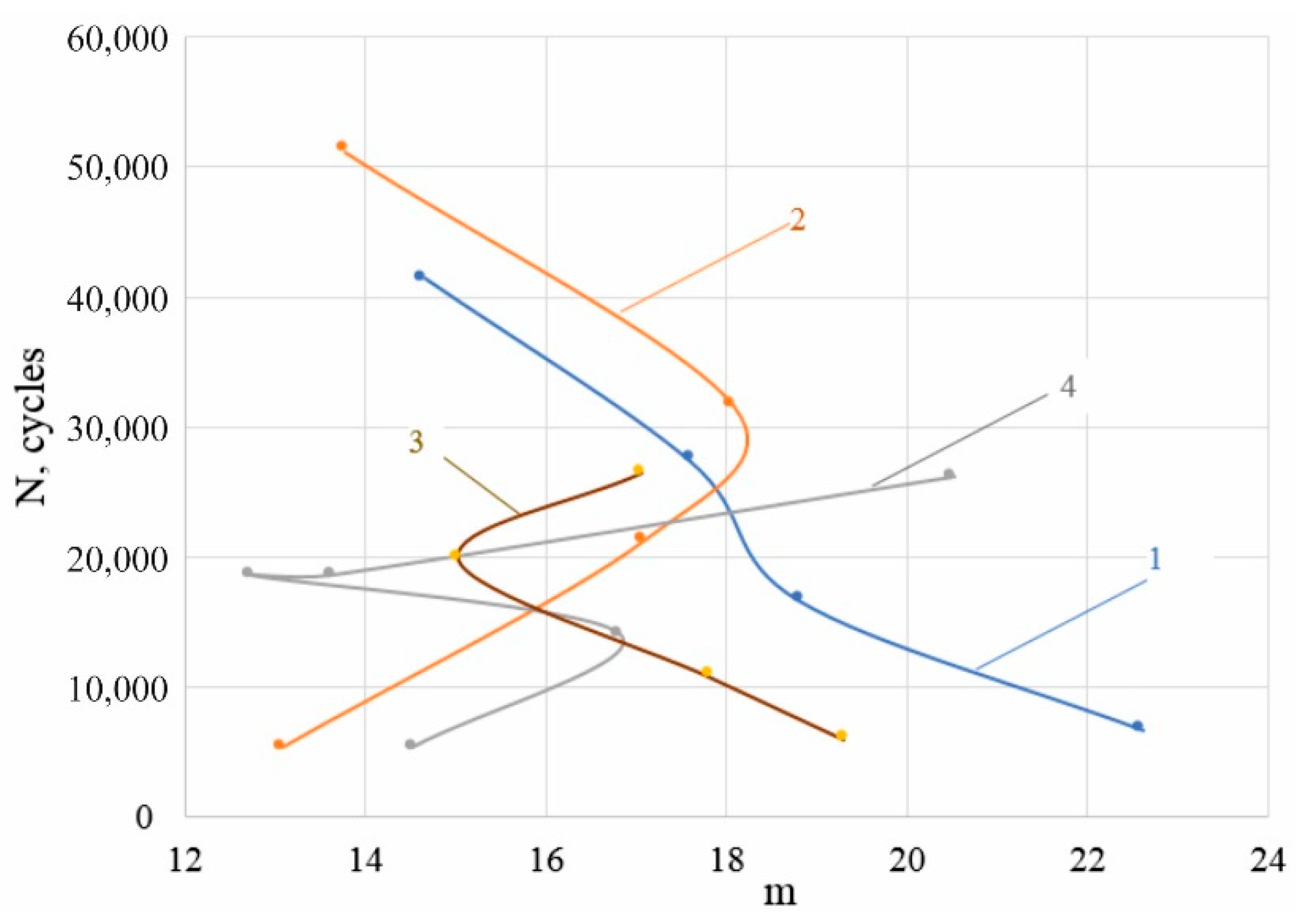
 , cycles to failure (D16ChATW);
, cycles to failure (D16ChATW);  , cycles to failure (2024-Т351). Data from [13,14].
, cycles to failure (2024-Т351). Data from [13,14].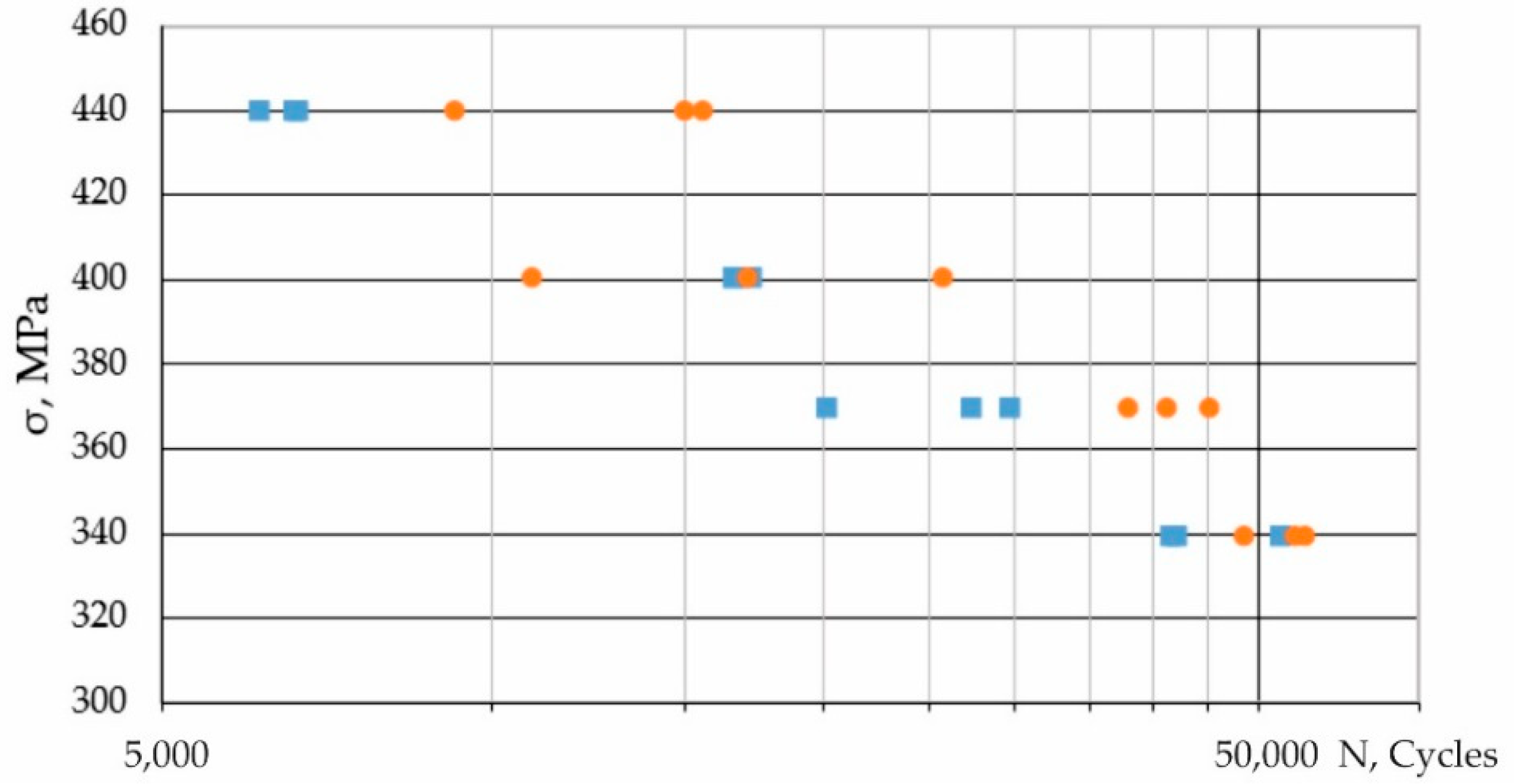
 ) and after DNP: (a) εimp = 3.7% (
) and after DNP: (a) εimp = 3.7% (  ); (b) εimp = 5.4% (
); (b) εimp = 5.4% (  ); (c) εimp = 7.7% (
); (c) εimp = 7.7% (  ).
).
 ) and after DNP: (a) εimp = 3.7% (
) and after DNP: (a) εimp = 3.7% (  ); (b) εimp = 5.4% (
); (b) εimp = 5.4% (  ); (c) εimp = 7.7% (
); (c) εimp = 7.7% (  ).
).
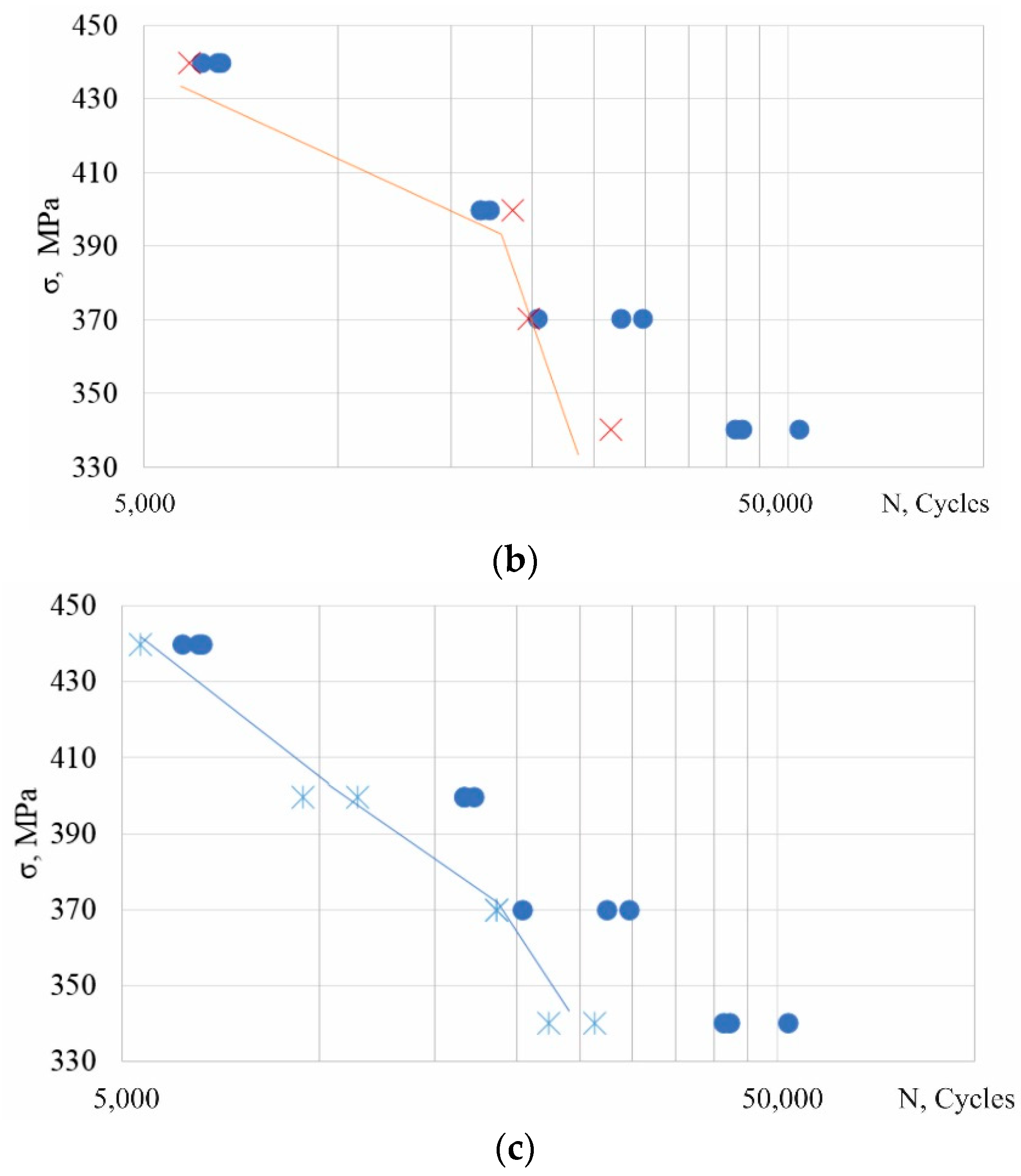
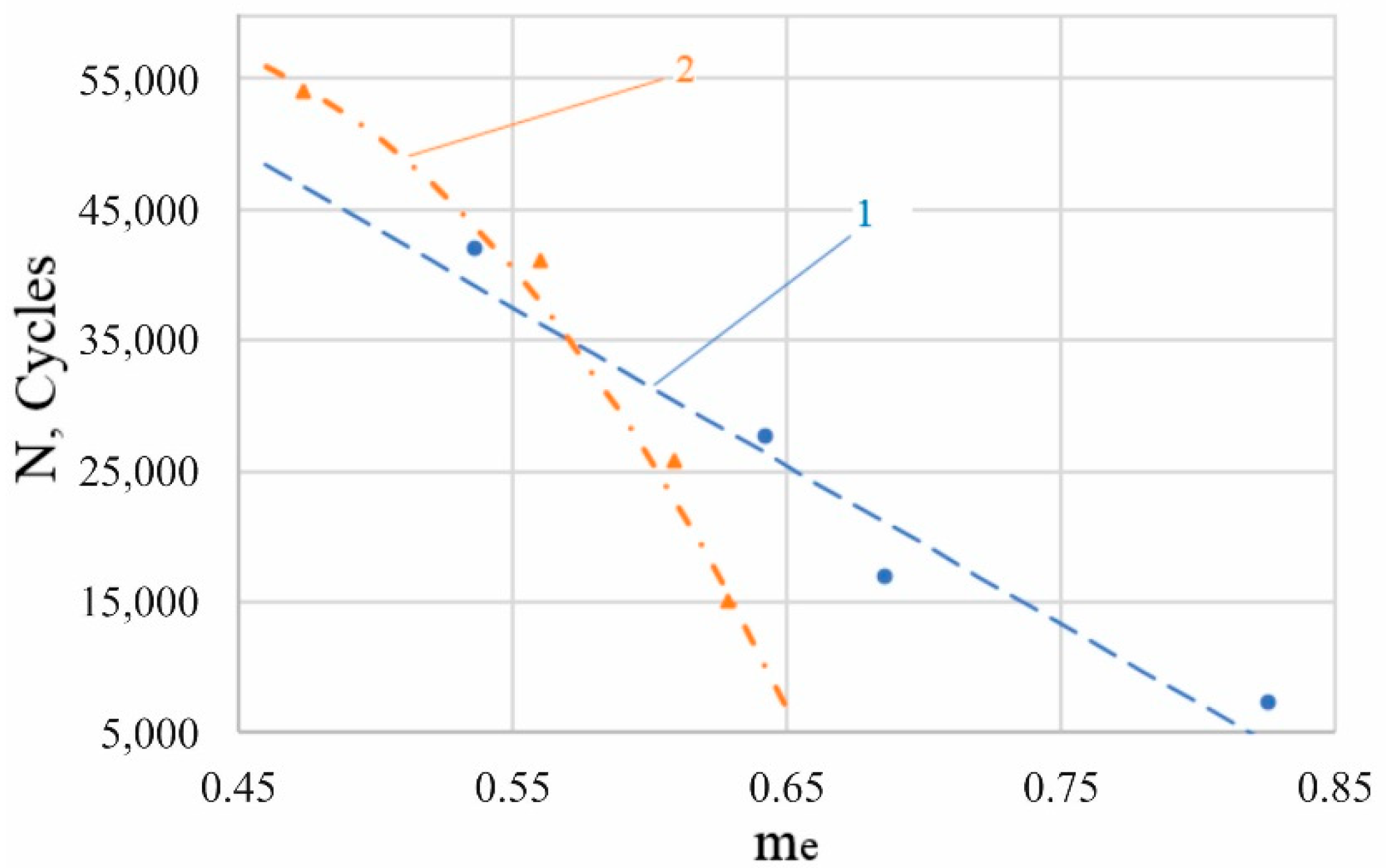
 indicates the alloy condition after the DNP and exposure for 6–7 months;
indicates the alloy condition after the DNP and exposure for 6–7 months;  indicates the initial state of the alloy; blue lines indicate data scatter in the initial state date form [13].
indicates the initial state of the alloy; blue lines indicate data scatter in the initial state date form [13].
 indicates the alloy condition after the DNP and exposure for 6–7 months;
indicates the alloy condition after the DNP and exposure for 6–7 months;  indicates the initial state of the alloy; blue lines indicate data scatter in the initial state date form [13].
indicates the initial state of the alloy; blue lines indicate data scatter in the initial state date form [13].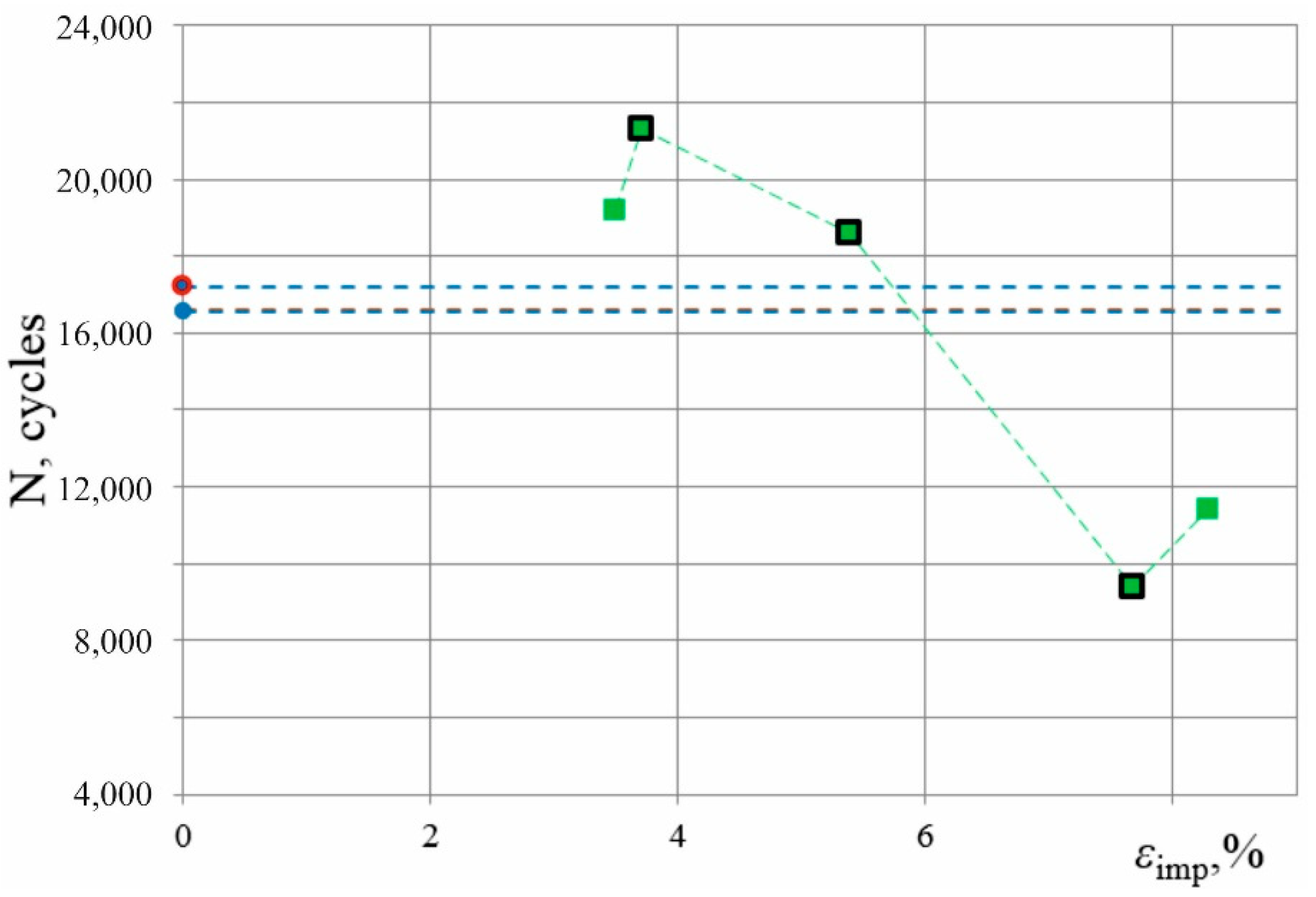

| Alloys | E (MPa) | (MPa) | (MPa) | (%) |
|---|---|---|---|---|
| 2024-T351 | 0.72·105 | 342 | 462 | 20.5 |
| D16 ChATW | 0.71·105 | 322 | 452 | 21.5 |
| Alloy 2024-T351 (%) | |||||||
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti |
| 0.05 | 0.13 | 4.7 | 0.70 | 1.5 | 0.01 | 0.02 | 0.04 |
| Alloy D16ChATW (%) | |||||||
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti |
| 0.11 | 0.18 | 4.4 | 0.63 | 1.4 | 0.01 | 0.01 | 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chausov, M.; Pylypenko, A.; Maruschak, P.; Menou, A. Phenomenological Models and Peculiarities of Evaluating Fatigue Life of Aluminum Alloys Subjected to Dynamic Non-Equilibrium Processes. Metals 2021, 11, 1625. https://doi.org/10.3390/met11101625
Chausov M, Pylypenko A, Maruschak P, Menou A. Phenomenological Models and Peculiarities of Evaluating Fatigue Life of Aluminum Alloys Subjected to Dynamic Non-Equilibrium Processes. Metals. 2021; 11(10):1625. https://doi.org/10.3390/met11101625
Chicago/Turabian StyleChausov, Mykola, Andrii Pylypenko, Pavlo Maruschak, and Abdellah Menou. 2021. "Phenomenological Models and Peculiarities of Evaluating Fatigue Life of Aluminum Alloys Subjected to Dynamic Non-Equilibrium Processes" Metals 11, no. 10: 1625. https://doi.org/10.3390/met11101625
APA StyleChausov, M., Pylypenko, A., Maruschak, P., & Menou, A. (2021). Phenomenological Models and Peculiarities of Evaluating Fatigue Life of Aluminum Alloys Subjected to Dynamic Non-Equilibrium Processes. Metals, 11(10), 1625. https://doi.org/10.3390/met11101625







