Experimental and Molecular Dynamic Study of Grain Refinement and Dislocation Substructure Evolution in HSLA and IF Steels after Severe Plastic Deformation

Abstract

In this study, large-scale molecular dynamic simulations were performed to analyze the dislocation substructure interaction with various types of obstacles present in microalloyed steels during severe plastic deformation. Specifically, fully functional numerical models of the atomic upsetting test were developed, with particular emphasis on the presence of precipitates inside the microstructure grains. The obtained results compared with the microstructural tests, performed using Electron Backscatter Diffraction (EBSD) and Transmission Electron Microscope (TEM) techniques, allowed for a more accurate assessment of the microstructure refinement mechanisms by means of the in-situ recrystallization effect in the deformed samples subjected to the multi-axis compression using the MaxStrain system (Dynamic Systems Inc., New York, NY, USA).

1. Introduction

Although the fundamental challenge of pursuing computer simulation accuracy and efficiency is the same in both manufacturing and materials sciences, computer modelling of physical phenomena in materials has special concerns because of significant diversity in the chemical and structural compositions. The microstructure, thermodynamic, rheological and mechanical properties of materials are strongly dependent on conditions such as chemical composition, lattice structure, stacking fault energy, temperature, and strain rate. Due to these special concerns, the underlying interaction models are diverse, and new simulation methods are often required to obtain statistically meaningful results.

Investigated in the present study, high strength low alloy (HSLA), as a common structural material, gives many new application possibilities, which result from ultrafine-grained microstructures produced with the use of severe plastic deformation (SPD) techniques. The studies conducted so far have shown that low-carbon steels with microalloying elements require a greater accumulation of deformation energy to initiate in-situ recrystallization, but the effects in the form of grain refinement are definitely stronger [1,2,3]. At the same time, due to the fact that microalloyed, advanced high strength steels (AHSS) constantly have a large share in the market, and because the degree of microstructure refinement allows for obtaining new and improved mechanical properties, the authors decided to focus on this topic, including the use of new techniques for modeling microstructure development, i.e., molecular dynamics (MD). The main problem, compared to Face Centered Cubic (FCC), is that the Body Centered Cubic (BCC) structure is characterized by a much more complex nature of the work hardening mechanism. When the solid solution and precipitation strengthening operate in the material, the problem also becomes much more complex. However, this is a really very interesting issue, and computer simulation support gives new possibilities in this field. The presented research concerns an attempt to use the MD technique as a possibility of predicting and controlling microstructural phenomena present in microalloyed steels subjected to SPD processes. As a relatively new simulation method, molecular dynamics are still undergoing rapid development. In the past decades, numerous studies were conducted on technical performance and there have been significant advances in techniques and consolidation models, as well as numerous applications [4,5,6]. Molecular dynamics (MD) simulations are widely used to understand complex systems, including, e.g., liquids, solids or different compositions of these two states [7,8,9]. By providing the positions of particles as a function of time, in particular, MD simulations help rationalize the behavior of complex systems [10,11]. With the development of modern technology and new functional materials, it was discovered that the microscopic properties, strengthening mechanisms and diffusion mechanism of the metals and alloys affect the macroscopic performance of structural materials significantly. As a new emerging powerful numerical tool, the molecular dynamics provide a huge opportunity in the field of modern engineering of materials and processing.

In this study, large-scale MD simulations were performed to analyze the dislocation substructure interaction with various types of obstacles present in microalloyed steels during severe plastic deformation. Specifically, fully functional numerical models of the atomic upsetting test were developed, with particular emphasis on the presence of precipitates inside the microstructure grains. The obtained results compared with the microstructural tests, performed using EBSD and TEM techniques, allowed for a more accurate assessment of the microstructure refinement mechanisms by means of the in-situ recrystallization effect in the deformed samples subjected to the SPD at the MaxStrain system [12]. The test cases were selected in such a way that it was possible to analyze the influence of key defects of the crystal lattice, such as: grain boundaries, precipitation, dislocations, and vacancies on heterogeneity in the stress distributions during deformation. For comparison, calculations were made on analogous samples without precipitates. However, the main novelty of this investigation lies on the possibility of assessing heterogeneity in the stress field occurring in the area of precipitations, as well as in the area of linear and surface defects, which reveal the stress field formed in the vicinity of the formed grains during continuous recrystallization, which accompanies SPD processes of microalloyed BCC systems.

2. Materials and Methods

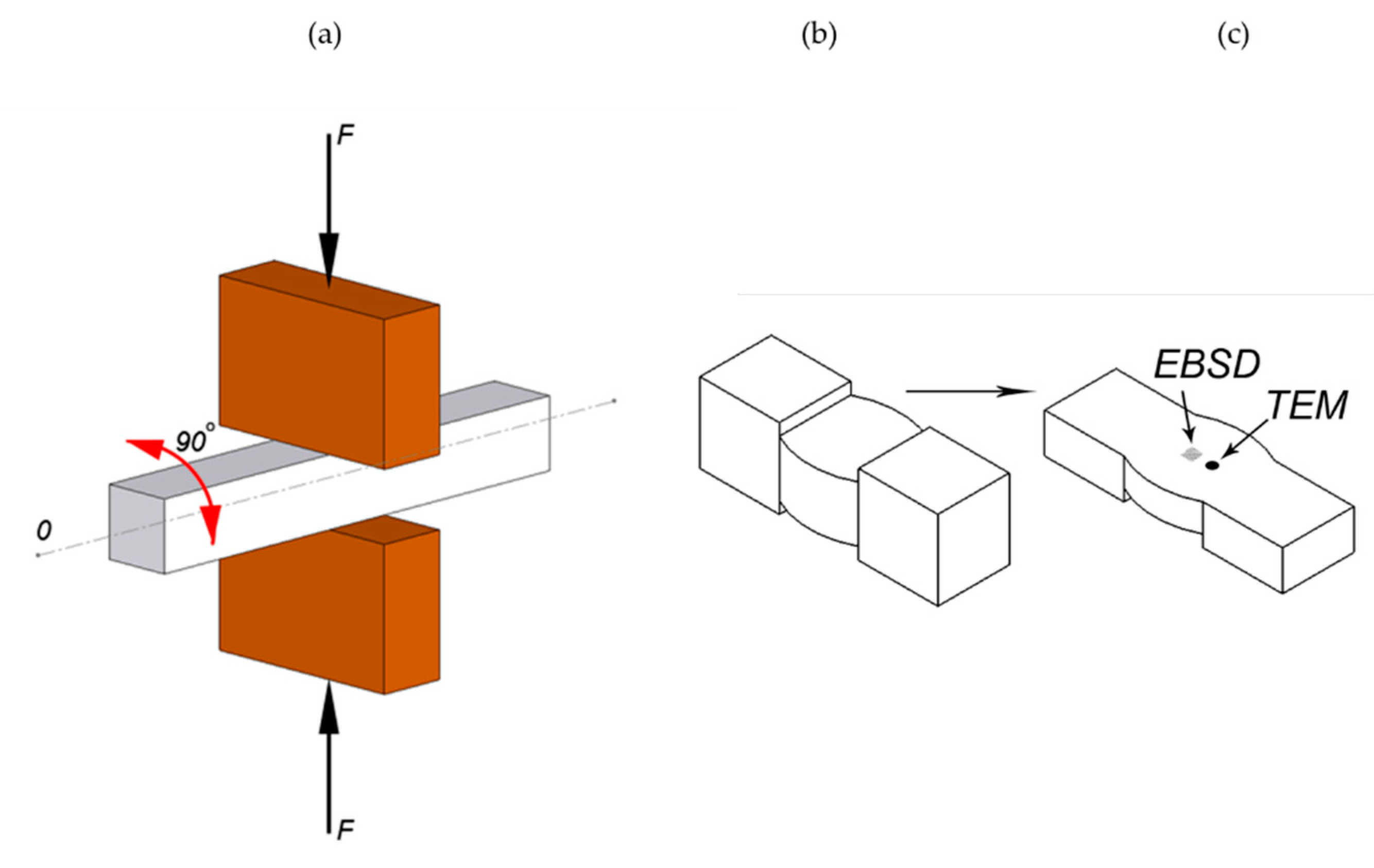
For the purpose of the current study, a series of accumulative compressive deformations using the MaxStrain system was performed. In this system, the longitudinal axis of the specimen is blocked, which allows for high deformation energy accumulation in the specimen (Figure 1a). After the first compression cycle, the sample is rotated by 90 degrees around its longitudinal axis and the second deformation cycle is applied. This procedure can be repeated until the required level of total strain is obtained. For the purpose of this current work, 27 mm long rectangular specimens with 10 × 10 mm cross-section were machined from as-hot rolled plates (parallel to rolling direction). Two steels with chemical compositions summarized in

Table 1. Basic chemical compositions of the studied steels (in wt %).

Steel	C	Mn	Si	Al	Nb	Ti	Fe
HSLA	0.07	1.36	0.27	0.02	0.067	0.031	Bal.
IF	0.0022	0.11	0.009	0.037	-	0.073	Bal.

were used. The hot rolling process included standard thermomechanical plate rolling where roughing stage above the non-recrystallization temperature (Tnr) and finishing stages (below Tnr) were realized. Plates were cooled down with an increased cooling rate in order to ensure a uniform, refined structure. The average grain size of HSLA steel was 15 μm, whereas the average grain size of IF steel was around 80 μm.

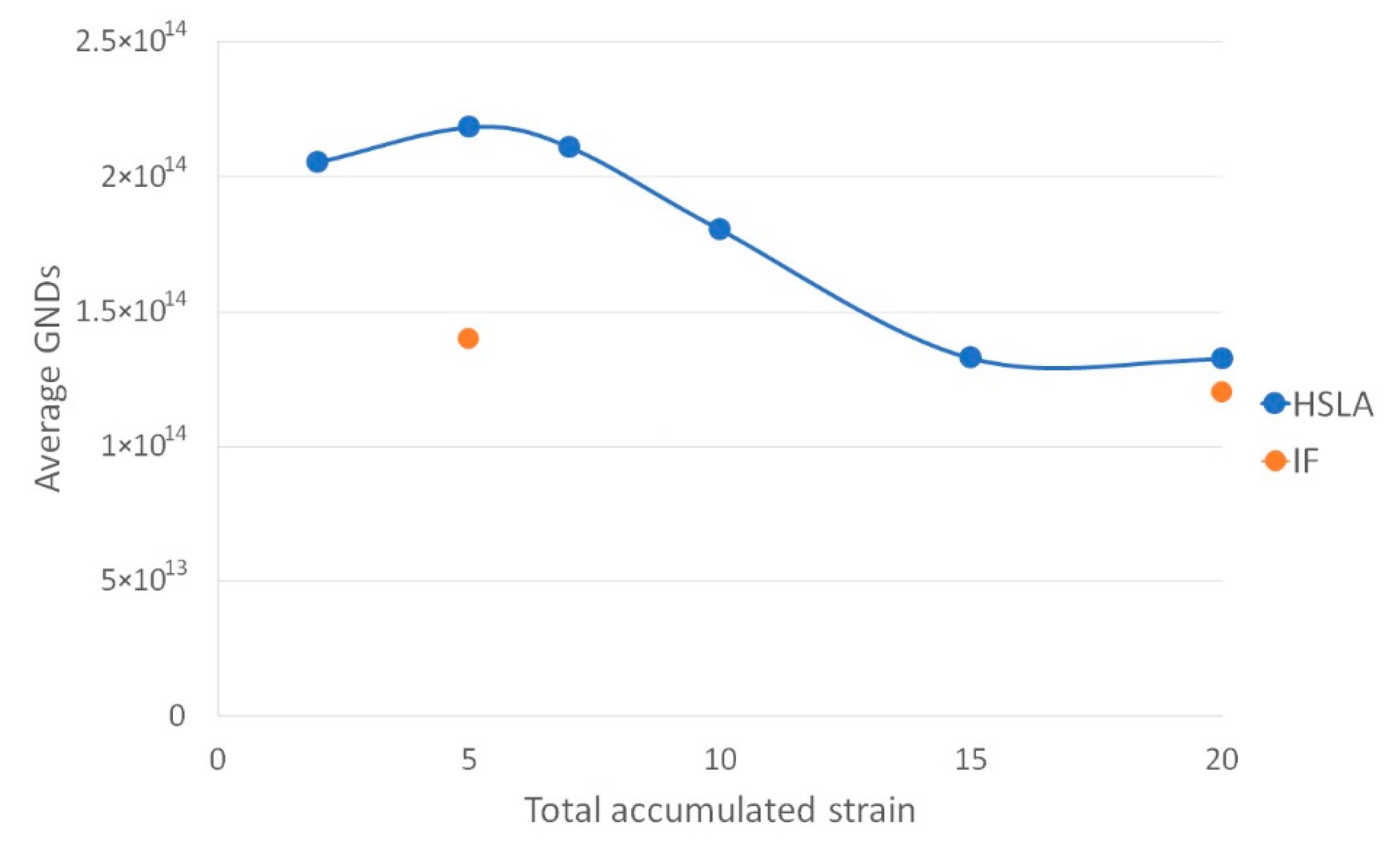
The basic material used in the present work was HSLA steel. This is Nb-microalloyed steel, which can be characterized by high precipitation hardening due to the presence of disperse, strain-induced Nb (C,N). In the case of HSLA steel, total accumulative strains of 2, 5, 7, 10 and 20 were applied at room temperature with 4, 10, 20 and 40 compressive deformations, respectively (an equivalent strain of 0.5 per pass). The second studied material was interstitial free (IF) steel. It is characterized by a pure BCC (ferritic) structure, free of precipitation, and thus it was used as a reference material. In this case, only two deformation schedules with total strains of 5 and 20 were applied. Directly after straining, specimens were heated up to the temperature of T_A = 500 °C and annealed for t_A = 1200 s in order to stabilize highly energetic ultrafine grains. This level of temperature, in the case of steel, accelerates the dislocation substructure rearrangements and process of the continuous recrystallization (in-situ) due to, generally speaking, increased ability of the dislocations to the movement.

In order to study the development of a dislocation structure, JEM-2010ARP transmission electron microscope (Jeol, Tokyo, Japan) operated at a nominal voltage of 200 kV was used. For TEM work, a 0.2 mm thick cross-section was cut from the deformed specimens according to the schematic presented in Figure 1. The specimen was mechanically ground and polished down to 0.05 mm thick foils in the same way as the EBSD samples (please see below). Large electron-transparent areas were obtained in the foil by conventional twin jet electropolishing using Nital.

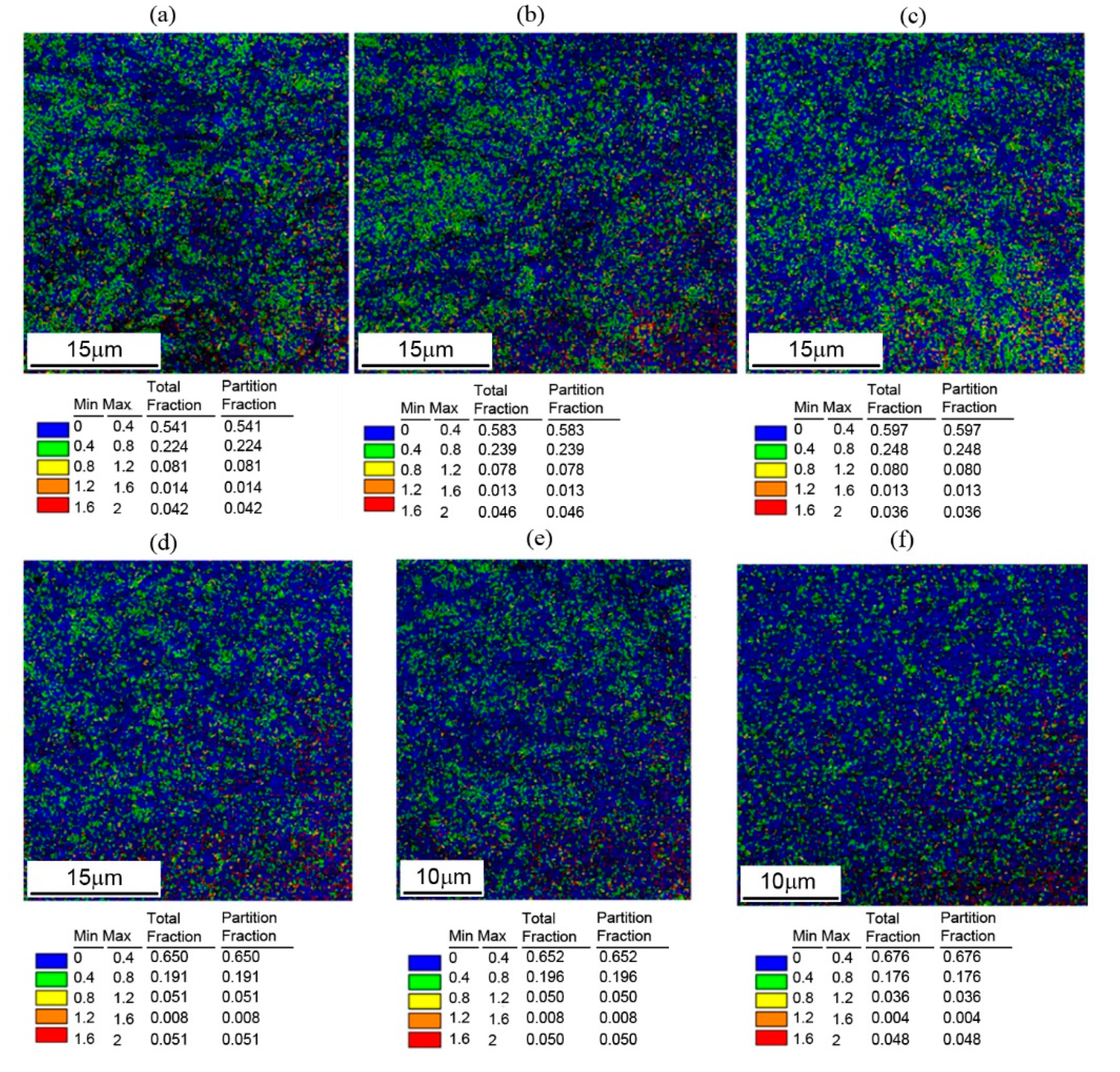
The geometrically necessary dislocations density (GNDs) were assessed using NovaNano 450 (FEI, Hillsboro, OR, USA) Scanning Electron Microscopy (SEM) operated at 20 kV, equipped with TSL Electron Backscatter Diffraction camera (EDAX, Mahwah, NJ, USA). SEM observations were performed according to the schematic presented in Figure 1. Specimens were mounted in conductive bakelite using a hot mounting press, then mechanically grinded using SiC papers for 2 min each (600, 800, 1200, 2400 grits). Then, diamond-based suspensions were used for polishing (particle sizes of 6, 3 and 1 µm) for 5 min using each pad. Finally, colloidal silica oxide polishing suspension (OPS)—with a particle size of 0.04 µm - was used (for 2 min). The EBSD data were used to calculate the geometrically necessary dislocations (GNDs) density. In the literature, several different approaches to calculate GNDs density can be found [13,14]. In the current work, the calculation of GNDs was based on dislocation density tensor, according to Field et al. [15]. The dislocation density tensor can be described based on the relationship with the dislocations that is present in the neighborhood, by the equation:

$$\alpha ={\displaystyle \sum }_{i=1}^K{\rho }^i\left(b^i\otimes z^i\right)$$

(1)

In this approach, dislocations represent a geometrical definition of dislocation i with Burgers vector bⁱ and slip plane normal direction zⁱ, and ρⁱ is the scalar dislocation density of dislocation i. The dislocation density tensor method considers both edge and screw dislocations. Other dislocation structures that are made consist of the dislocation density tensor, e.g., dislocation dipole is treated as statistically stored dislocations. The maximum misorientation between neighboring points should be entered and the threshold value was 5°, larger misorientations were not considered in the GDNs density calculation. The presented method was used as an automated calculation in the TSL OIM Analysis software (version 4.1, EDAX, USA).

3. Results and Discussion

Figure 2 presents the development of microstructure during SPD straining as a function of accumulative equivalent strain. It can be seen, both by means of TEM and SEM/EBSD, that strong grain refinement is visible after the total accumulative strain of 5 up to that strain, with strong rearrangement of low angle grain boundaries (LABs) (in the form of dislocation cells is visible). This process is assisted by the fine, disperse Nb (C,N), which are present in HSLA steel as an effect of the strain-induced precipitation process that occurred during thermomechanical processing of the initial plate. Fine, disperse particles play a crucial role in acting as obstacles for moving dislocations and, therefore, in the subdivision of grains into a stable, dense dislocation substructure. Additionally, these arrangements of dislocation cells and disperse Nb (C,N) provide an additional strain hardening effect that is beneficial from the point of view of increased ductility.

Presented in Figure 3, KAM distributions provide additional information regarding the development of dislocation substructure during accumulative deformation. The KAM parameters represent the value of the local deformation. When the values of the KAM parameters increase, the density of geometrically necessary dislocation increases too. The maximum threshold value of the misorientation angle between neighboring points in the kernel of 2° was used in the KAM parameters of distribution analysis. As can be seen from Figure 3, with the increasing strain, the intensity of KAM increases first—Figure 3a–c—and then decreases with further severe plastic deformation.

Figure 4 presents the distribution of GND values (calculated directly in the TSL OIM software) in IF and HSLA steels after MaxStrain deformations of 5 and 20. As can be seen, in the IF steel (without second-phase particles), after the strain of 5, the level of dislocation density is much lower compared to HSLA steel, where local misorientation gradients in microstructure are high. A lack of disperse obstacles in IF steel form a much more “clear” structure—i.e., free of high concentration of crystallographic defects. They exist only in the vicinity of grain boundaries, whereas in the case of microalloyed steel, the defects are present in the whole area. This can be explained by the mechanism of in-situ recrystallization, which in this material recovers the effects of large deformation. However, after severe plastic deformation (the accumulative total strain of 20), the situation changes, i.e., both materials are characterized by a high level of misorientation gradient, which, nevertheless, is still lower in the case of interstitial-free steel. As a direct effect of the presence of precipitations in HSLA steel, much stronger grain refinement is observed.

Presented in Figure 5, the summary of the measurement of average GNDs (calculated using Equation (1)) provides new insight into the mechanism of grain refinement in microalloyed steel. It can be seen (what was already observed in both TEM and EBSD data) that total strain up to 5 (in SPD) increases the dislocation density providing the dense network of dislocation cells.

Further SPD straining clears up the grains and causes their transition into more stable, high angle grain boundaries. These effects are not as much pronounced in the case of interstitial-free steel where the pure BCC structure, without additional obstacles, is less prone to grain refinement.

Presented within this chapter, data will be utilized for Molecular Dynamic study, which is presented in the next chapter.

4. Modeling

Molecular dynamics (MD) are one of the modeling techniques that allow tracking atoms rearrangement of the studied area of interest [16]. Assuming the initial positions of each atom and using Newton’s second law of motion, one can predict the changes in the arrangements of the atoms in time upon, e.g., external forces:

$$F_i=m_i{a}_{i \hspace{1em}\hspace{1em}\hspace{1em}} \frac{d{x}_i}{dt}=V_i \hspace{1em}\hspace{1em}\hspace{1em}\frac{d{V}_i}{dt}= \frac{F_i}{m}$$

(2)

where: m_i—mass, a_i—accelerations, x_i—displacements, V_i—velocities, F_i—forces, t—time.

In practice, an analytical solution of Equation (2) for bodies consisting of numerous atoms is impossible. Therefore, in this presented work, numerical integration methods based on the expansion of Taylor series have been used:

$$x_i\left(t+\mathsf{\Delta }t\right)= x_i\left(t\right)+ V_i\left(t\right)\mathsf{\Delta }t+ \frac{1}{2} a_i\mathsf{\Delta }{t}^2+ \dots$$

(3)

The force F_i acting on the i-th atom is thus determined using interatomic potential, which is a function of all atoms’ positions and its value denotes potential energy of the whole system. In order to obtain the value of the force, the potential should be differentiated after the position of the given atom. The model defined in this way allows for the description of the motion of atoms, and thus the observation of changes taking place in the tested system, and enables the determination of the macroscopic parameters of the material.

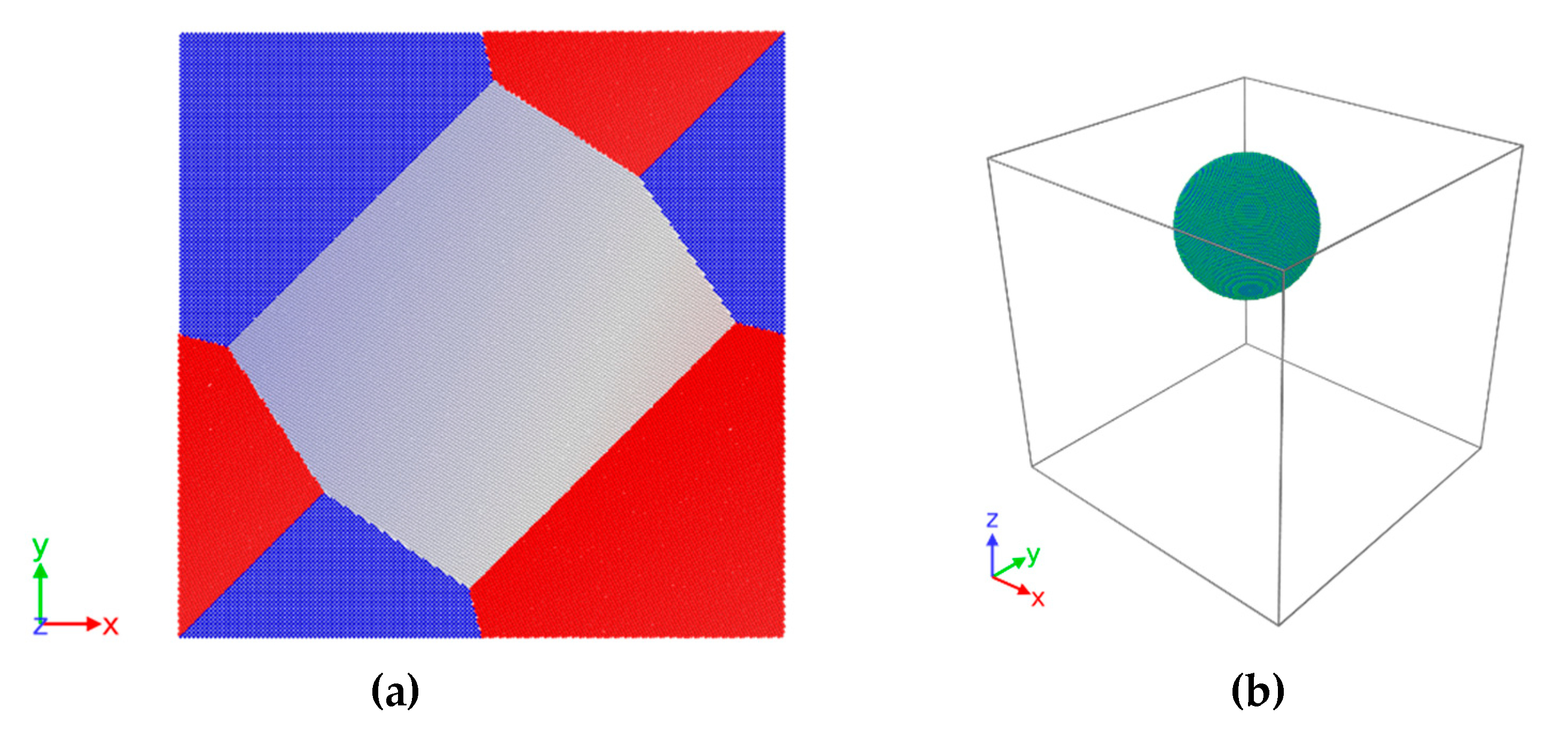
Within the current work, Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) software (Sandia National Labs, Albuquerque, USA and Temple University, Philadelphia, USA) was used to simulate compression of the unit cell presented in Figure 6. The key step at this stage was to determine the modified embedded atom method (MEAM) for Fe-Nb-N system based on the literature data. Then, using Atomsk software (developed by Pierre Hirel, University of Lille, France) [17] and developed by the authors’ bash layer scripts, the atoms arrangement process was automated allowing control of parameters, such as number and orientation of grains as well as control of the percentage of NbN. The unit cell of 400 × 400 × 400 Å, consisting of three ferrite grains, was generated using nuclei placed at three positions (I: 40, 360, 200 Å; II: 200, 200, 200 Å and III: 360, 40, 200 Å) using Voronoi diagrams. Periodic boundary conditions were imposed. More than 5 mln atoms were used with 1% of vacancies and 1% of Fe atoms were substituted by Nb atoms. Simulation of compression along the x axis (Figure 6b) was performed. Ten percent strain was used, and simulation time was 40 ps. In order to study the effect of grain orientation and effect of precipitation, four schemes were used (

Table 2. MD modeling schemes used in the present work.

MD Scheme	Grain 1 (Blue) Orientation	Grain 2 (Gray) Orientation	Grain 3 (Red) Orientation
Low-angle grain boundaries/solid solution (LS)	0°; 0°; 0°	1°; 2°; 1°	−1°; −2°; −1°
Low-angle grain boundaries/with precipitation (LP)
High-angle grain boundaries/solid solution (HS) High-angle grain boundaries/with precipation (HP)	0°; 0°; 0°	15°; 18°; 15°	15°; 18°; 15°

).

In the first two schemes (L), grains were misoriented with low angles of disorientation (low angle grain boundaries), whereas in the two latter schemes (H), misorientation angles were higher to represent high angle grain boundaries. In two cases (LS and HS) no precipitation was present, whereas in the two other cases (LP and HP), spherical niobium nitride precipitation (with 85 Å radius and 1.7% atoms volume) was placed at 147.22, 239.64, 286.96 Å (Figure 6b).

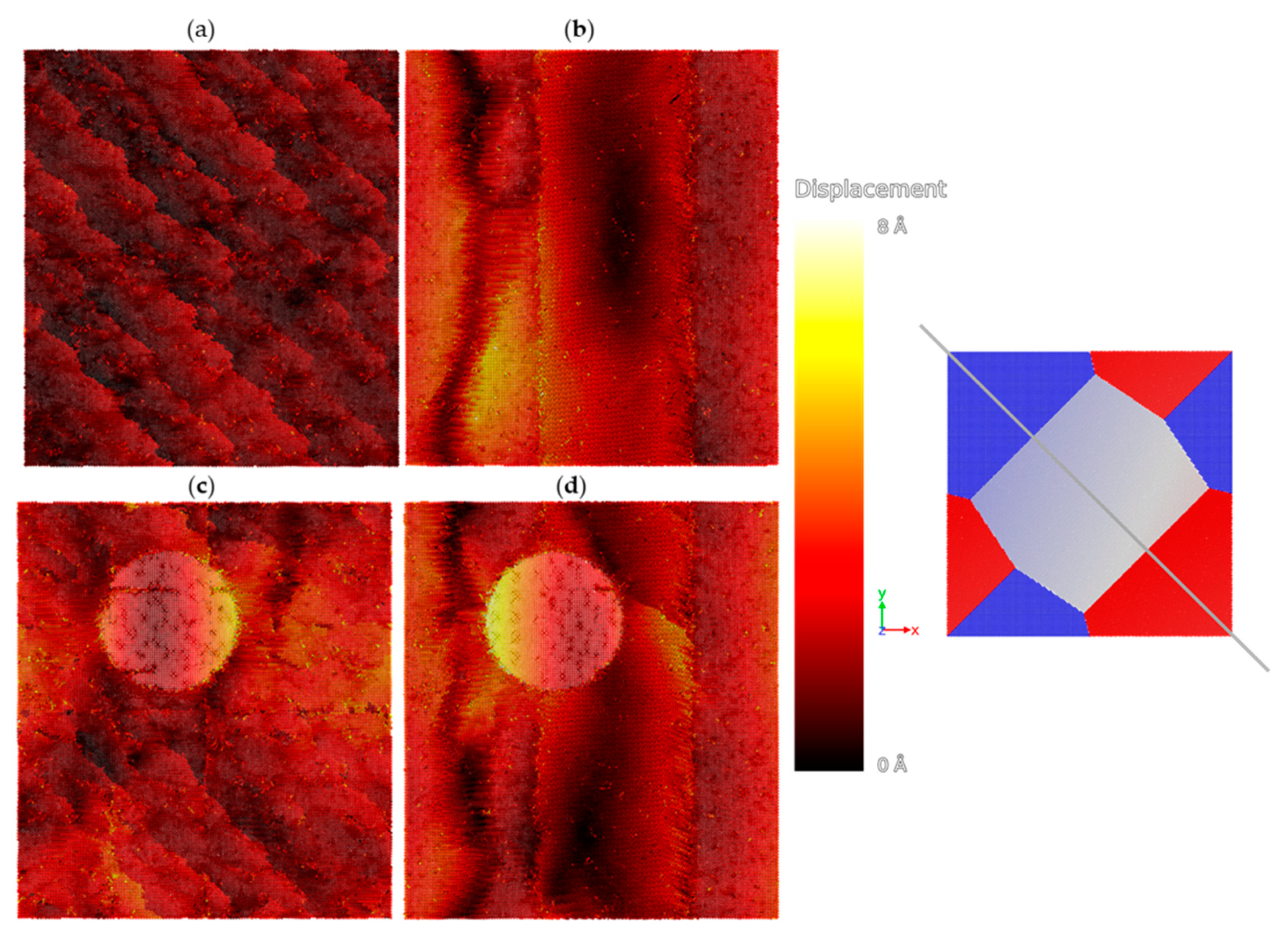
Figure 7 presents the rearrangement of atoms after the initial stage of compression ([1,1,0] section plane of 10 Å thick). In the case of solid solution state (with no second phase particle), different distributions of atoms are visible. In the case of LS specimen, the rearrangement of atoms is more “marble like”, which is in line with observations from the literature [18,19] as well as previously observed by the authors in the TEM work results for IF steel [3]. This can be attributed to the higher driving force for in-situ recrystallization of this solid solution BCC structure compared to precipitation-hardened counterparts. In addition, in the case of higher misorientations between grains, larger atom displacements observed what is caused by the grain boundaries, which cannot be passed across by moving atoms. In the case of HS material, a high concentration of atoms is visible in the vicinity of high-angle grain boundaries (HABs). It leads to a higher dislocation density level that was presented experimentally in Figure 4a. When precipitation is inserted into the structure (Figure 7c,d), both the low- and high-angle grain boundary grains are characterized by larger gradients of atom arrangements. In this case, when the precipitation is at the high angle grain boundary it also undergoes higher atom movements, which is caused by higher shear stresses (Figure 8d) compared to precipitation at the low angle grain boundaries (Figure 8c). In both cases: LABs and HABs, the precipitation effect is clearly visible. 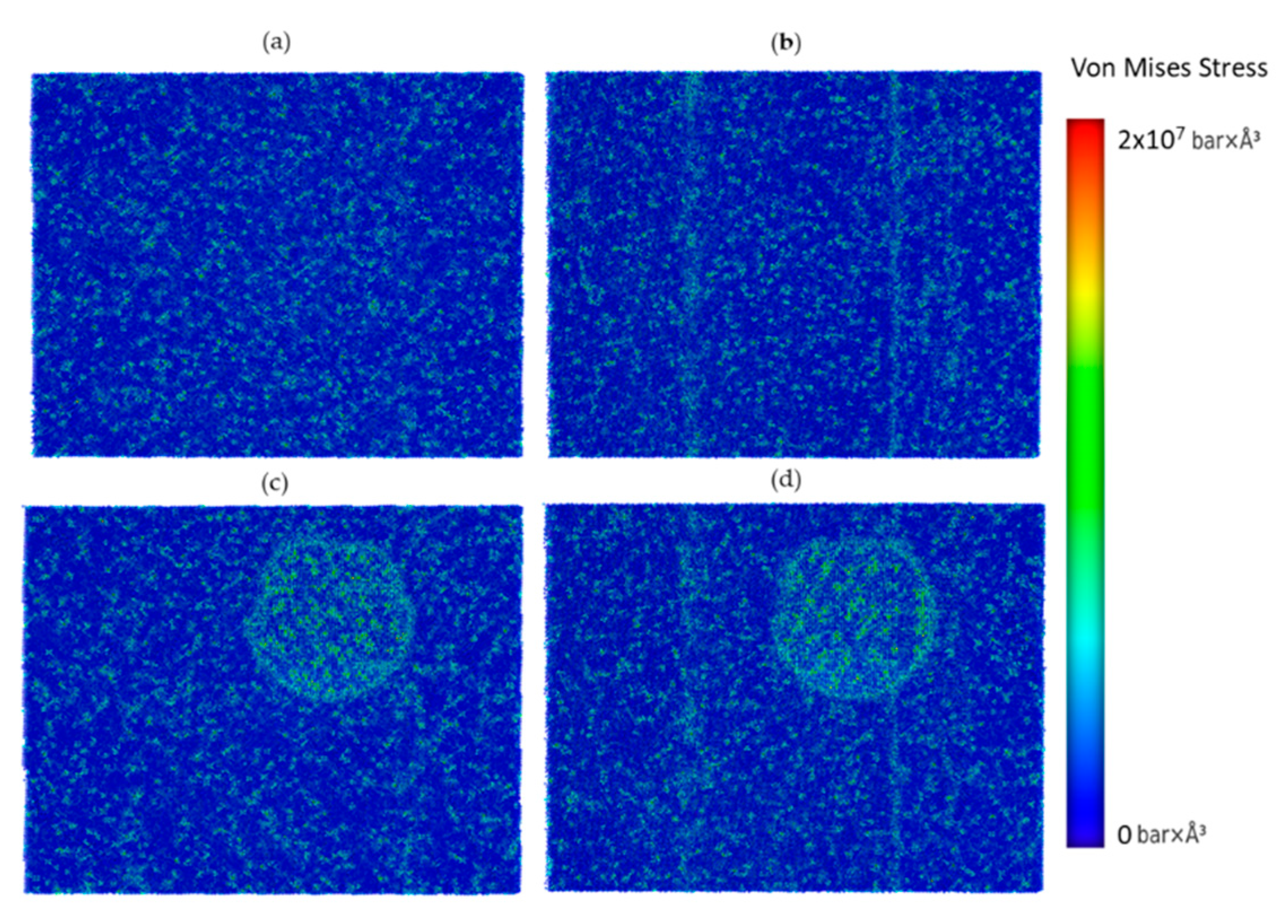Presented in Figure 8, the von Mises stress distributions have higher max values in the case of the precipitation-strengthened structure compared to the solid solution one (Figure 8a,b).

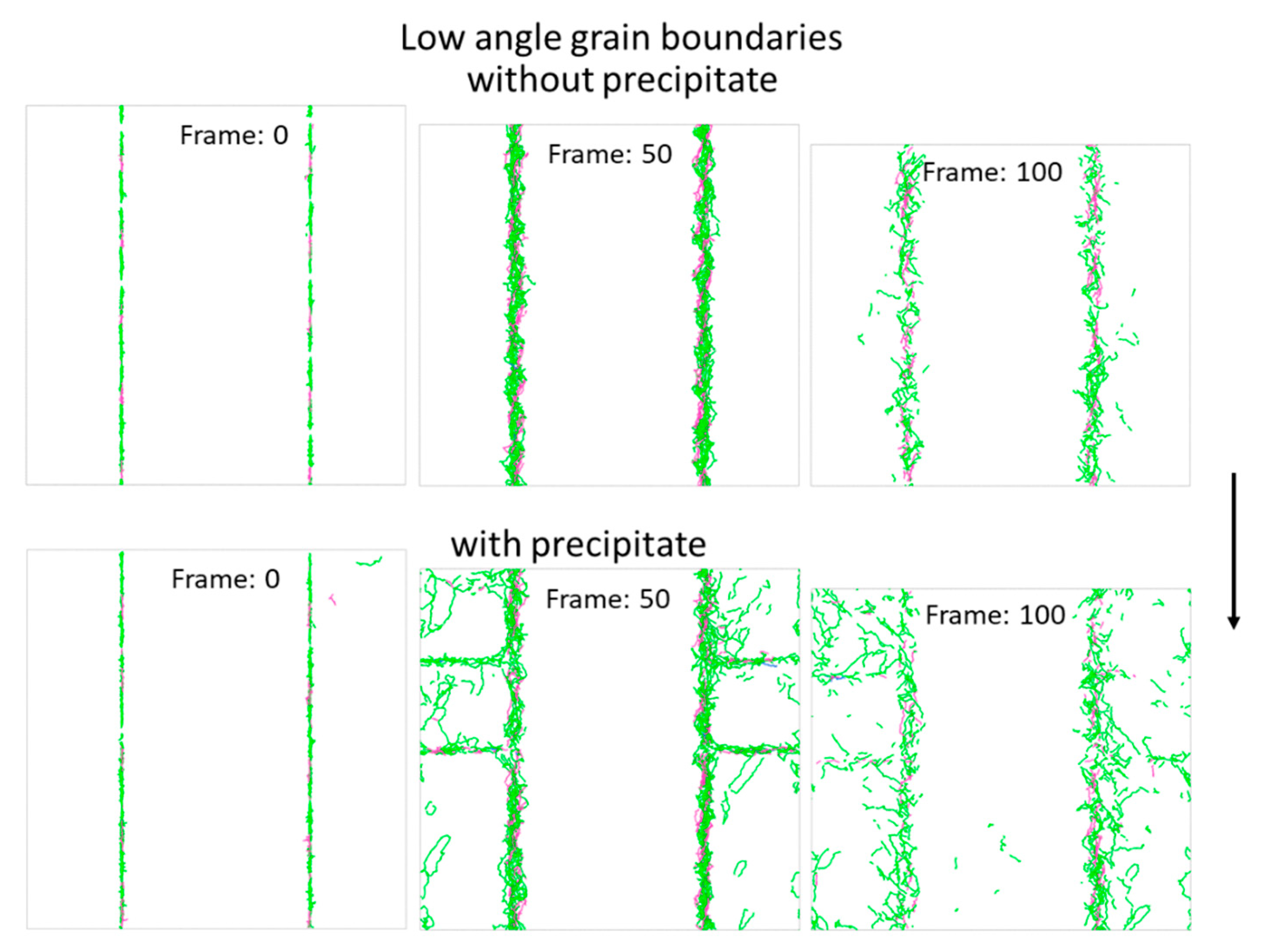
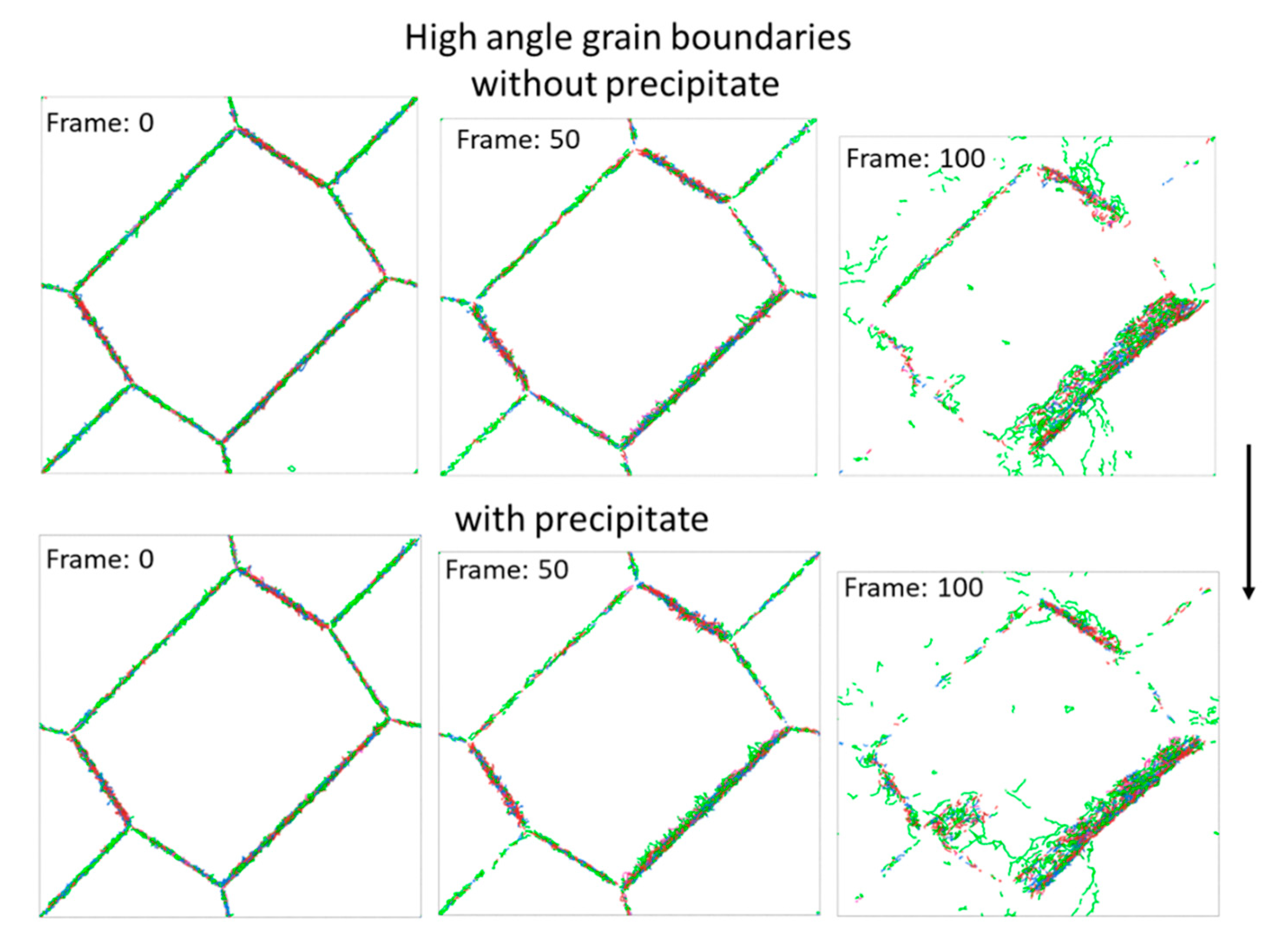
Figure 9 and Figure 10 present the development of dislocations during compression of structure with low and high angle grain boundaries, respectively. It can be seen that in the case of LABs, with the increase in deformation, the number of dislocations at low angle grain boundaries increases. When the precipitation is introduced, the more pronounced cell structure is formed, which is in line with the observations at the early stages of the MaxStrain deformation (see Figure 2).

In the case of high angle grain boundaries (Figure 10) at the beginning of deformation, grain boundaries are sharper compared to those presented in Figure 9 (LS scenario), which results probably from the fact that higher grain boundary misorientations act more as sinks for dislocations. Only at higher strains, grain boundaries become wider and many more dislocations are piled up there. Additionally, when the second phase particle is introduced, more dislocations are formed in the vicinity of the particle (Orowan mechanism).

The presented research is a further step towards linking GNDs with MD, by approximating the relationship between the nanoscale analysis and the microscale effects of the phenomena related to the impact of various types of obstacles in the way of moving dislocations and the substructure built from them. In the present study, stress fields were adopted as the main platform for discussing qualitative relationships, which are generated in the nanoscale analysis and the interaction is observed in the microscale effects. The ability to explain these mechanisms cannot be overestimated from the point of view of the physical fundaments of continuous recrystallization (in-situ) responsible for the process of grain refinement by SPD.

Despite the limitations of the MD modelling (computation time, number and size of atomic structures), the presented results confirm the capability of the proposed approach to capture characteristic features of the dislocation rearrangements and substructure formation during SPD processing. The proposed implementation of the MD method to the analysis of the type of dislocation structure and interaction with fine particles of precipitates under the conditions of solid solution strengthening may be an important element of further research on the multiscale analysis and provides a tool for qualitative representation of the phenomena accompanying the production of Ultrafine-grained (UFG) microalloyed steels using SPD techniques.

5. Conclusions

In this study, numerical simulation with the use of an MD algorithm was applied to investigate the process of developing the dislocation substructures, as well as their interaction through the stress field with various obstacles present in the tested BCC material, i.e., microalloyed steel. The analysis of the process of creating the walls of the cells of the dissociation cells as nuclei of new grains, taking into account the heterogeneity of the dislocation density and the current stress field, allowed for the assessment of the essence of the differences observed during the microstructural studies between the microstructures of microalloyed and IF steels. For this purpose, scanning microscopy and EBSD technique were used and thus the basic mechanisms of dislocation substructure formation in the in-situ recrystallization process have been reflected.

The experimental results presented in this study show that the multi-axis compression in the MaxStrain system, as a method to produce SPD effects, is capable of refining the microstructure in microalloyed steel. It was observed that due to the presence of various obstacles in the dislocation path involved in the development of the dislocation substructure during deformation, the in-situ recrystallization effect was more difficult to achieve than in IF steel. However, for the same reason, more dislocations were generated in the deformed samples, which in the end, after exceeding the accumulated strain value equal to 5, favored the grain refinement process, i.e., increased the number of dislocation cells and the process of transforming the low-angle grain boundaries into high-angle grain boundaries.

The comparison of the results obtained during experiments and MD modelling confirms the capability of the presented approach to capture characteristic features of the dislocation rearrangements and substructure formation during SPD processing. The proposed implementation of the MD method for the analysis of grain size and orientation, as well as interaction with fine particles of precipitates under conditions of solid solution strengthening, may be an important element of further research on the multiscale analysis and provides a tool for qualitative representation of the phenomena accompanying the production of UFG microalloyed steels using SPD techniques.