Prediction of Fatigue Crack Growth in Metallic Specimens under Constant Amplitude Loading Using Virtual Crack Closure and Forman Model
Abstract
1. Introduction
2. Theoretical Background
2.1. Crack Propagation Model
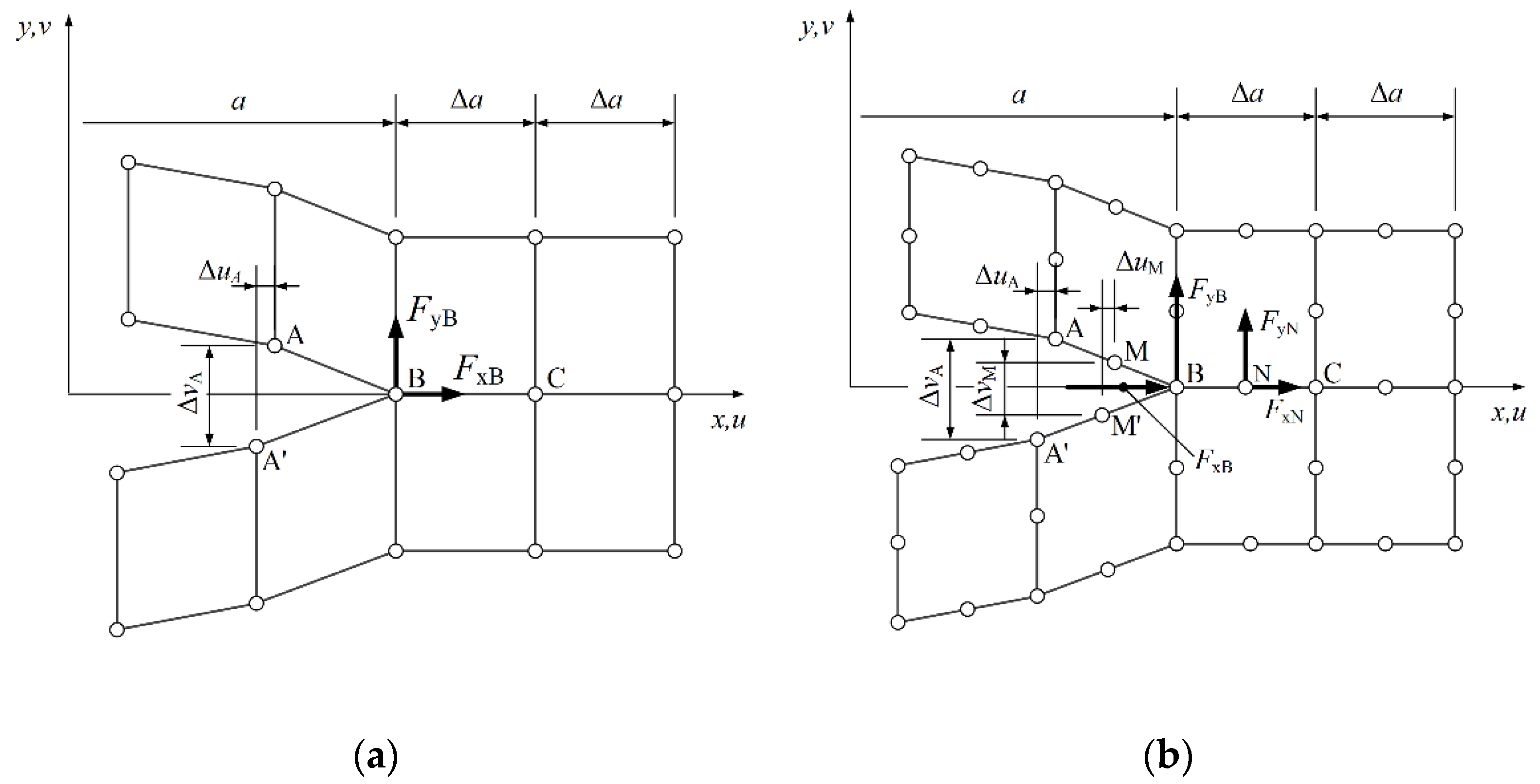
2.2. Virtual Crack Closure Formulation for 4 and 8-Node Two-dimensional (2D) FEA
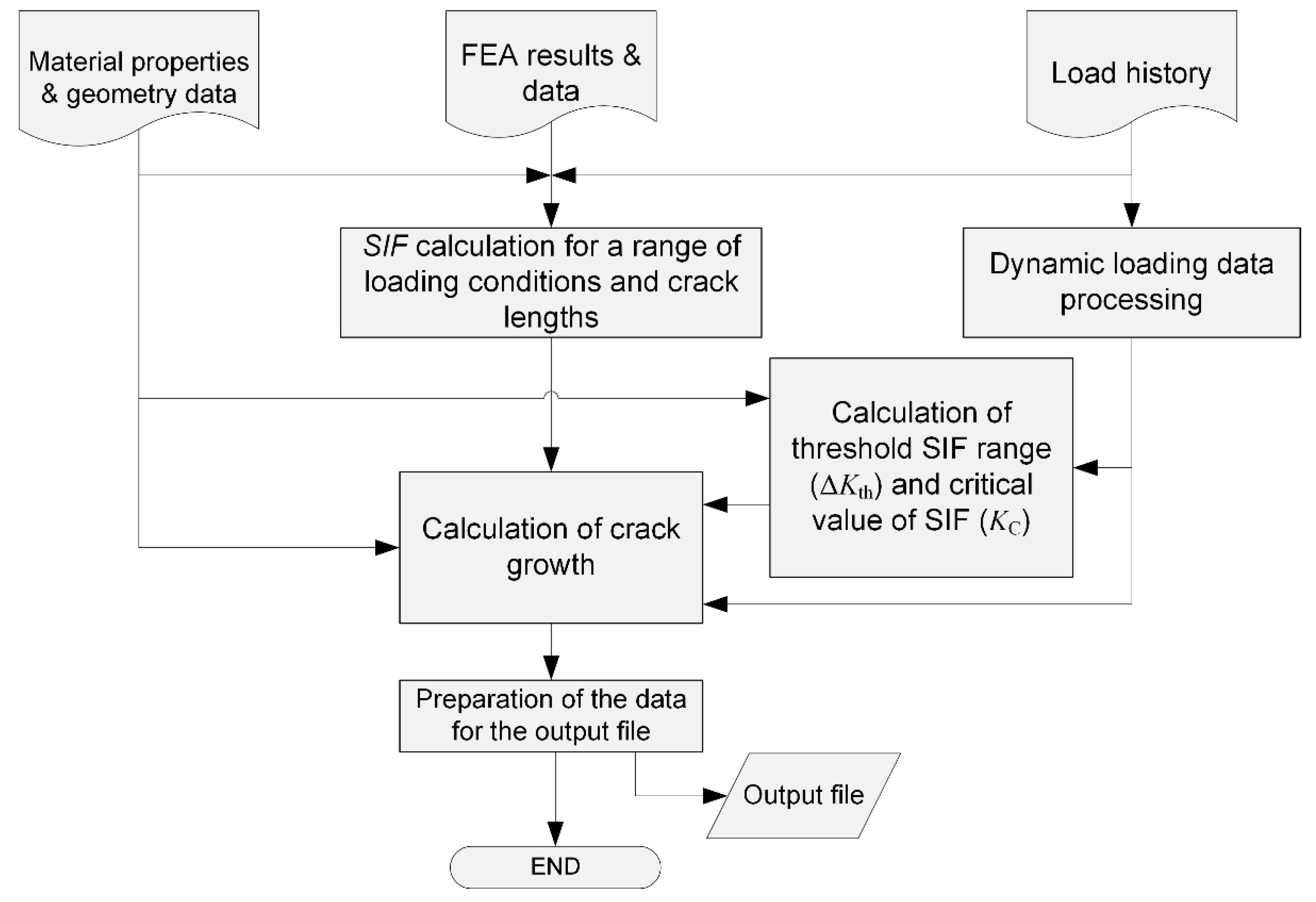
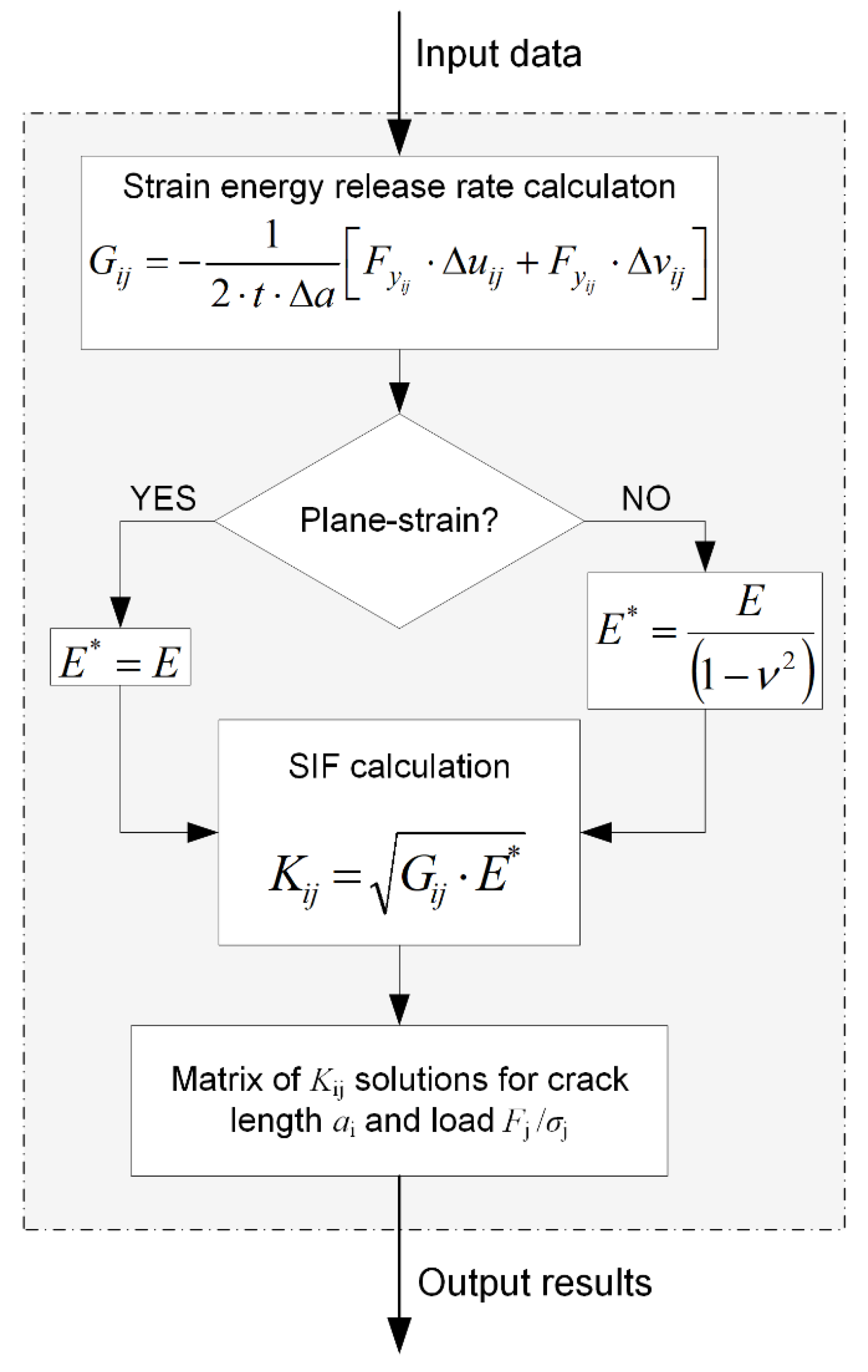
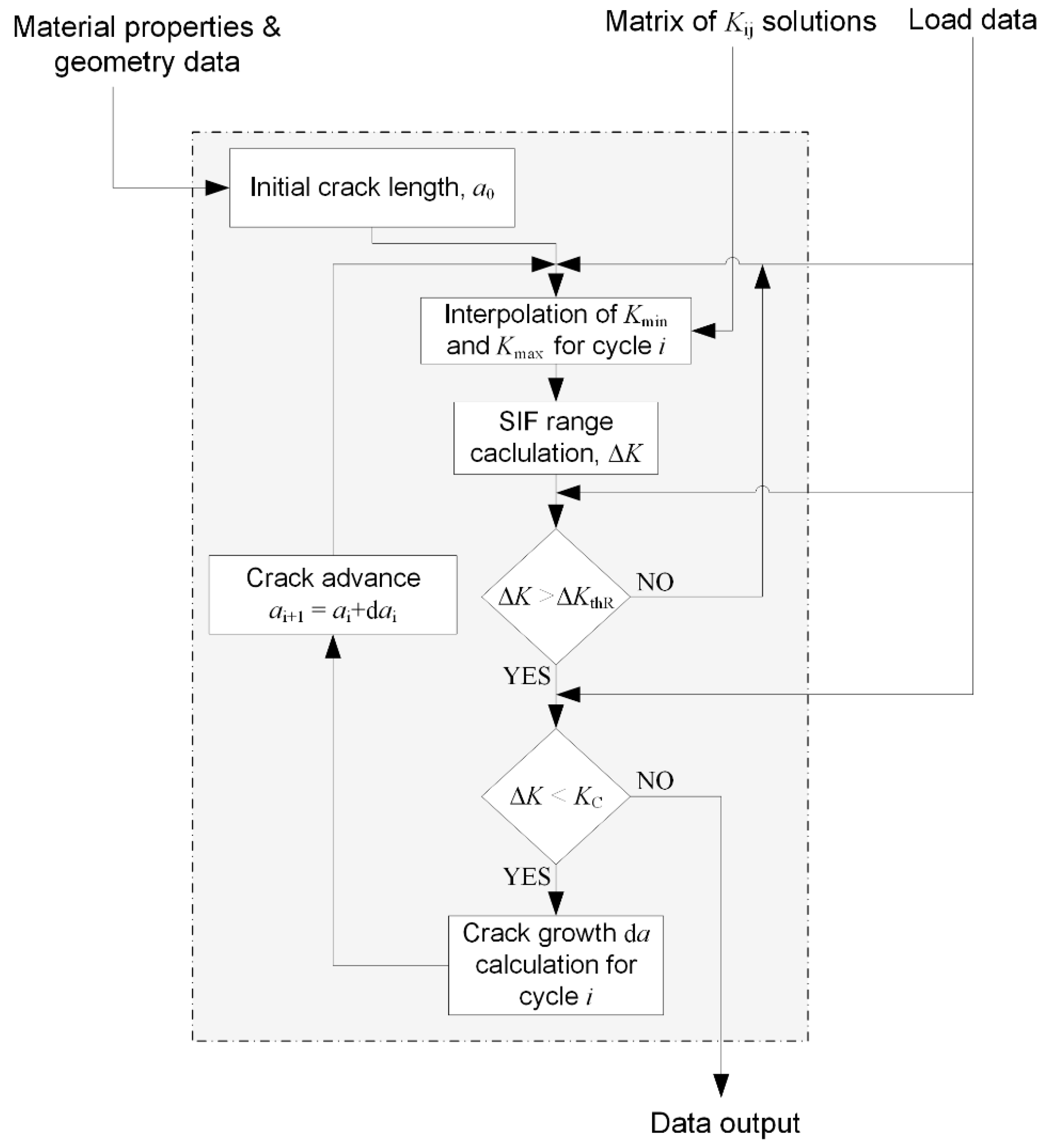
3. Computer Algorithm
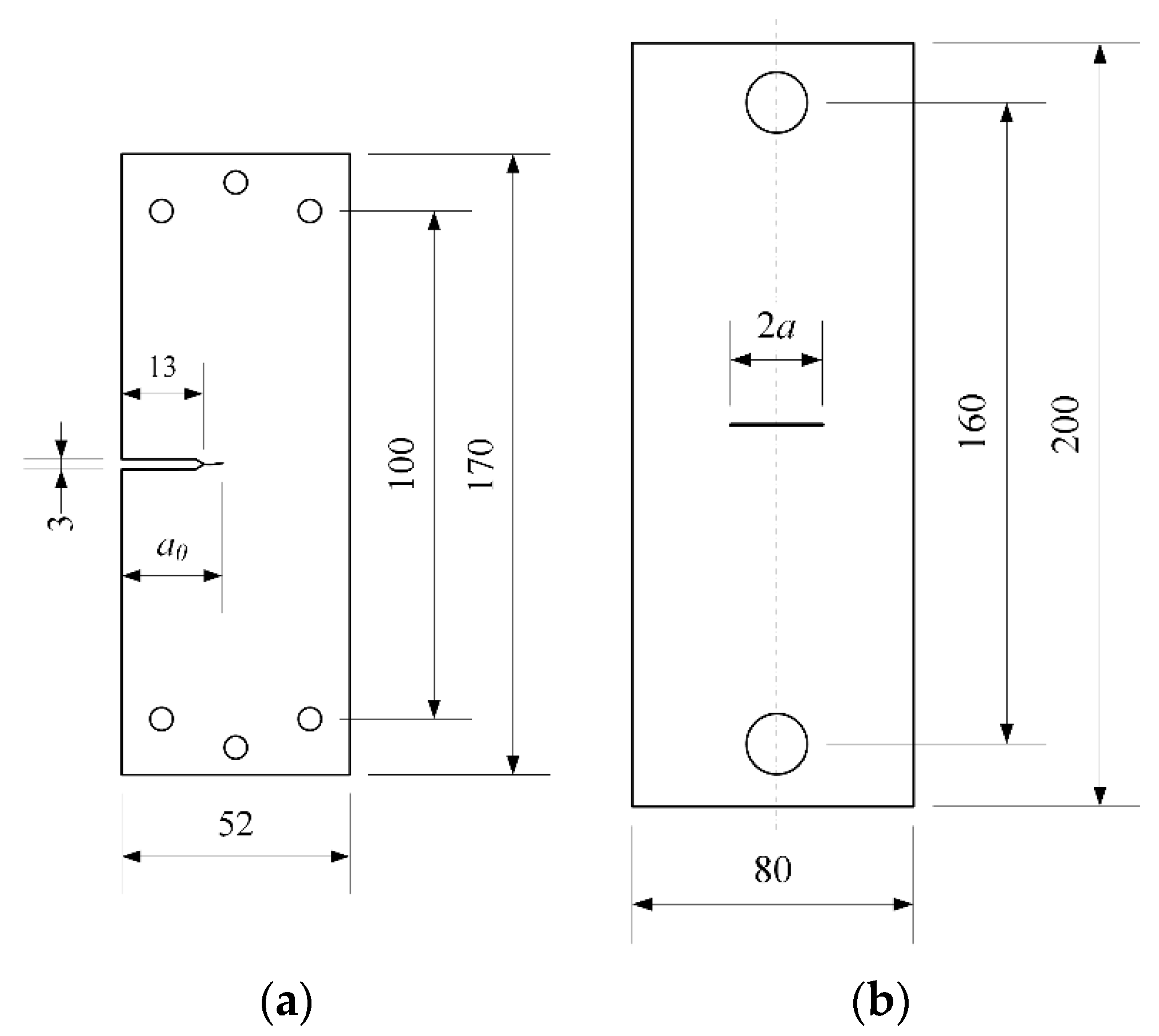
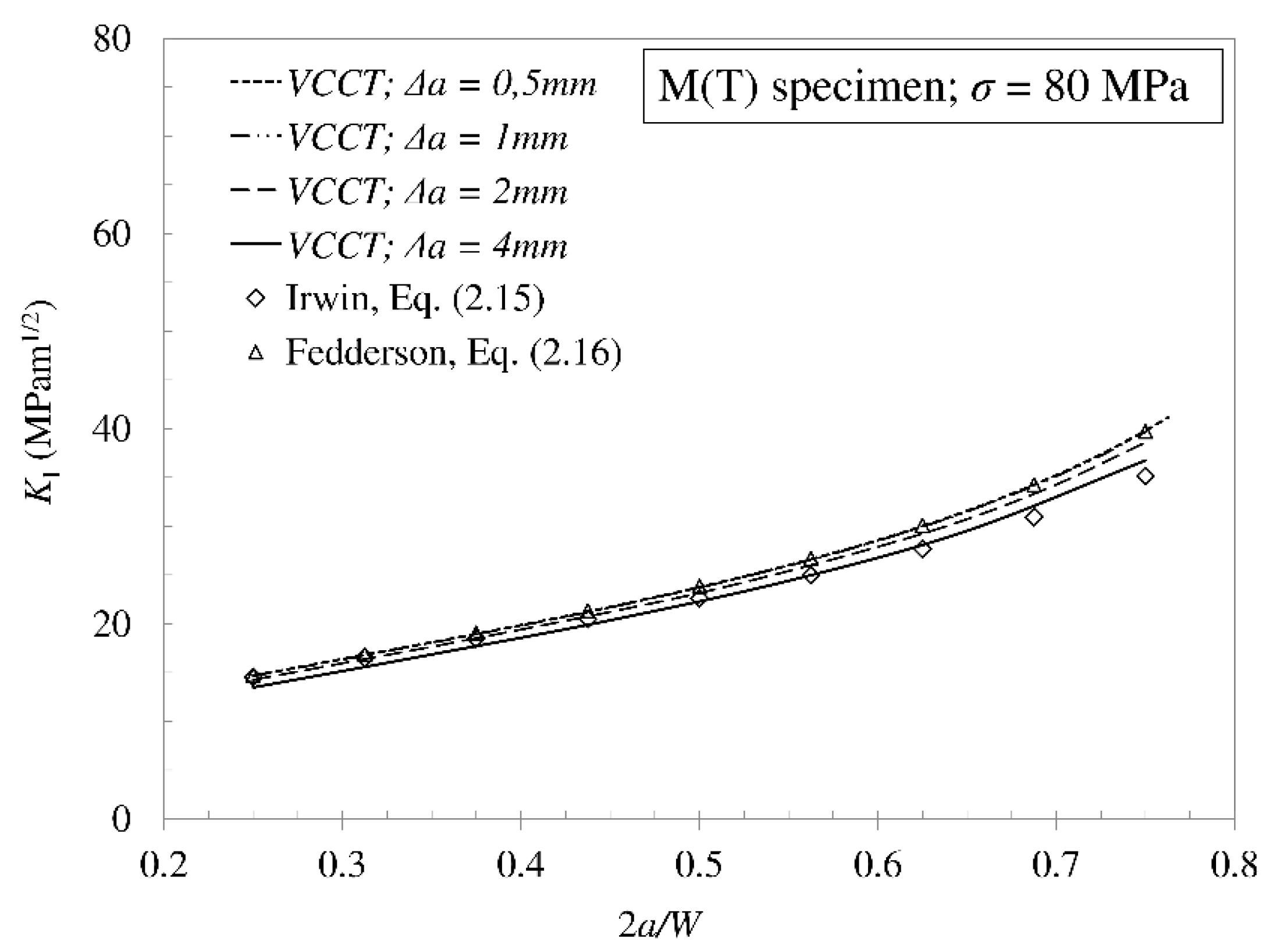
4. Test Cases and FEA Details
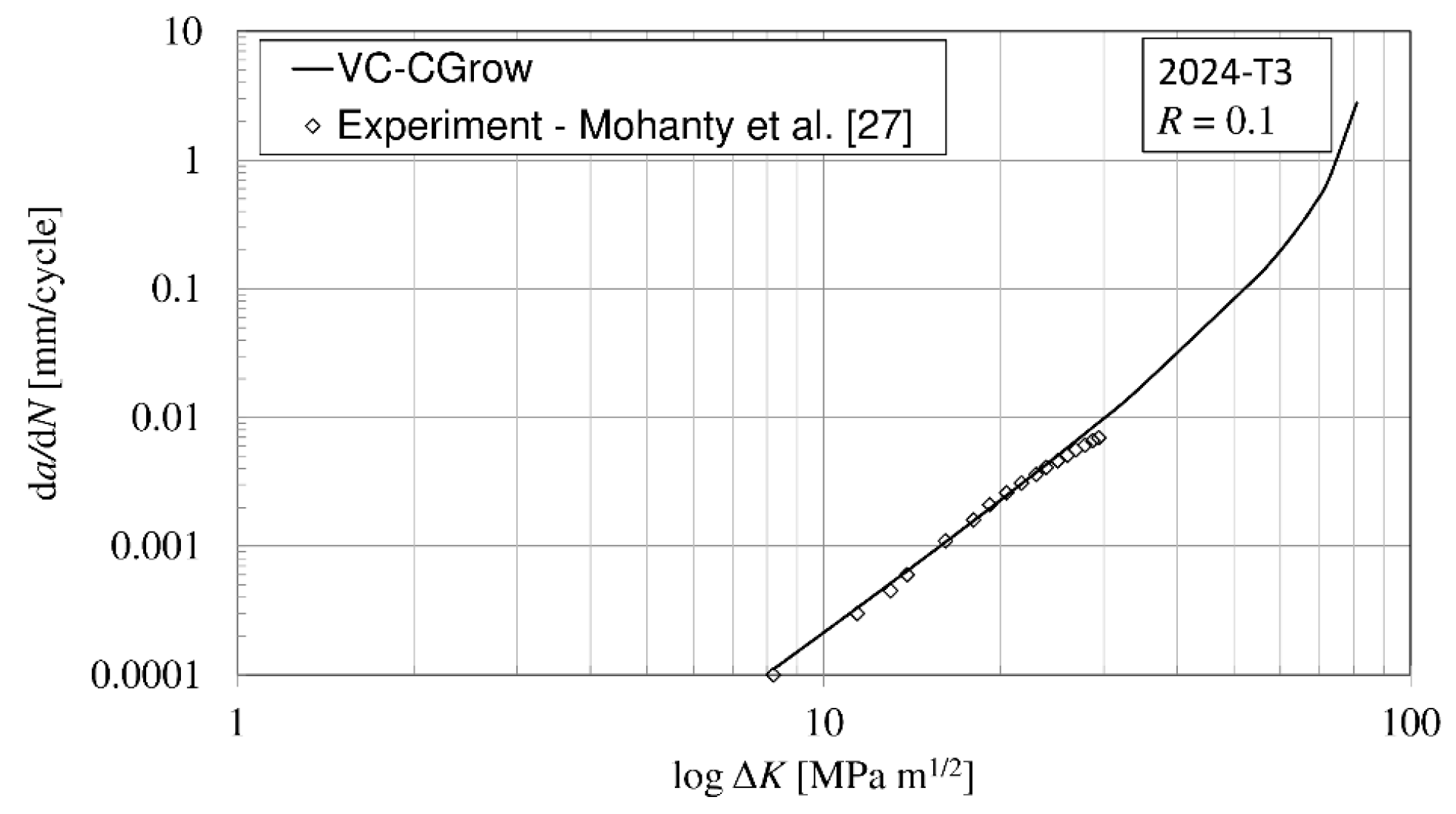
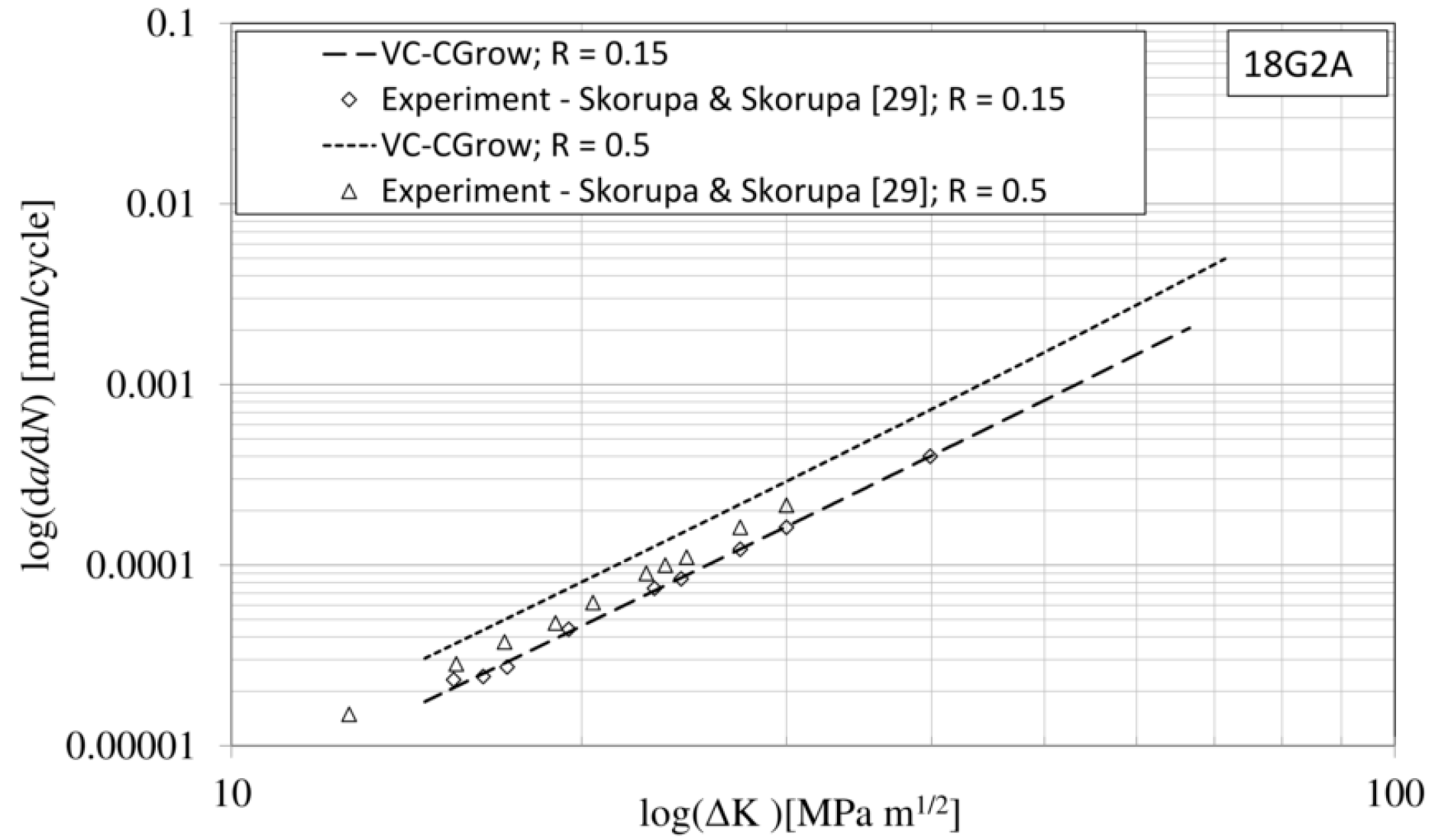
5. Results
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a0 | initial crack size |
| ai | crack size for cycle i |
| a | crack size |
| a/w | relative crack size |
| CF, mF | material constants for Forman model |
| CVN | Charpy impact energy |
| da/dN | crack propagation rate |
| Δa | crack extension, length of the elements at the crack front |
| ΔK | stress intensity factor range for a load cycle |
| ΔKth0 | threshold stress intensity factor range for R = 0 |
| ΔKthR | threshold stress intensity factor range for specific load asymmetry ratio R |
| Δu | shear displacement at crack surface node |
| Δv | opening displacement at crack surface node |
| ΔW | work required to close the crack along one element side |
| E | elasticity modulus |
| F | specimen loading force |
| Fmin | minimum loading force in a cycle |
| Fmax | maximum loading force in a cycle |
| Fx | shear force at the crack tip |
| Fy | opening force at the crack tip |
| G | strain energy release rate |
| GI | strain energy release rate for crack opening mode I |
| GII | strain energy release rate for crack opening mode II |
| K | stress intensity factor |
| KI | stress intensity factor for crack opening mode I |
| KII | stress intensity factor for crack opening mode II |
| Kmin | minimum stress intensity factor in a load cycle |
| Kmax | maximum stress intensity factor in a load cycle |
| KIc | critical stress intensity factor for plane-strain conditions, fracture toughness |
| Kc | critical stress intensity factor |
| Nef | experimental results for cycles to failure |
| Npf | predicted cycles to failure |
| R | load asymmetry ratio |
| σ | normal stress |
| σUTS | ultimate tensile strength |
| σmin | minimum normal stress in a cycle |
| σmax | maximum normal stress in a cycle |
| σy, σ0.2 | yield stress |
| t | specimen and element thickness |
| u | x-coordinate of crack surface node after load |
| v | y-coordinate of crack surface node after load |
| w | specimen width |
| ν | Poisson ratio |
References
- Ina, J.; Vallentyne, M.; Hamandi, F.; Shugart, K.; Boin, M.; Laughlin, R.; Goswami, T. Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper I–Analysis of the Plate. Metals 2018, 8, 180. [Google Scholar] [CrossRef]
- Beden, S.M.; Abdullah, S.; Arrifin, A.K. Review of Fatigue Crack Propagation Models for Metallic Components. Eur. J. Sci. Res. 2009, 28, 364–397. [Google Scholar]
- Schijve, J. Fatigue of Structures and Materials, 2nd ed.; Springer Science + Bussines Media: Dordrecht, The Netherlands, 2009; pp. 14–32. [Google Scholar]
- Brnić, J. Engineering Structures and Material Behavior; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2018; pp. 239–309. [Google Scholar]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 2nd ed.; CRC Press LLC: Boca Raton, FL, USA, 1995; pp. 29–255. [Google Scholar]
- Sudhakar, Y.; Wall, A.W. Mesh refitting approach: A simple method to model mixed-mode crack propagation in nonlinear elastic solids. Adv. Model Simul. Eng. Sci. 2017, 4, 2. [Google Scholar] [CrossRef]
- Vukelic, G.; Brnic, J. Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance. Metals 2016, 6, 40. [Google Scholar] [CrossRef]
- Hamandi, F.; Laughlin, R.; Goswami, T. Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations. Metals 2018, 8, 279. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Funari, F.M.; Greco, F.; Lonetti, P.; Luciano, R. Numerical modeling based on moving mesh method to simulate fast crack propagation. Fra. Int. Strut. 2019, 14, 410–422. [Google Scholar] [CrossRef]
- Murotani, K.; Yagawa, G.; Choi, J.B. Adaptive finite elements using hierarchical mesh and its application to crack propagation analysis. Comput. Method Appl. M 2013, 253, 1–14. [Google Scholar] [CrossRef]
- Funari, M.F.; Lonetti, P.; Spadea, S. A crack growth strategy based on moving mesh method and fracture mechanics. Theor. Appl. Fract. Mec. 2019, 102, 103–115. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Funari, F.M.; Greco, F.; Lonetti, P.; Luciano, R.; Penna, R. Dynamic crack growth based on moving mesh method. Compos. Part B-Eng. 2019, 174, 107053. [Google Scholar] [CrossRef]
- Paris, P.C.; Gomez, M.P.; Anderson, W.E. A rational Analytical Theory of Fatigue. Trend Eng. 1961, 13, 9–14. [Google Scholar]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2001; pp. 166–176. [Google Scholar]
- Farahmand, B. Fracture Mechanics of Metals, Composites, Welds, and Bolted Joints: Aplication of LEFM, EPFM, and FMDM Theory; Kluwer Academic Publishers: Norwell, MA, USA, 2001; pp. 137–155. [Google Scholar]
- Krueger, R. Virtual crack closure technique: History, approach and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A Finite Element Calculation of Stress Intensity Factors by a Modified Crack Closure Integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Hellen, T.K. On the Method of Virtual Crack Extension. Int. J. Numer. Method Eng. 1975, 9, 187–207. [Google Scholar] [CrossRef]
- Parks, D.M. Virtual Crack Extension: A General Finite Element Technique for J-integral Evaluation. In Proceedings of the First International Conference of Numerical Methods in Fracture Mechanics, Swansea, UK, 9–13 January 1978; Pineridge Press: Swansea, UK, 1978; pp. 464–479. [Google Scholar]
- Rybicki, E.F.; Schmueser, D.W.; Fox, J. An Energy Release Rate Approach for Stable Crack Growth in the Free-Edge Delamination Problem. J. Compo. Mater. 1977, 11, 470–487. [Google Scholar] [CrossRef]
- Kuna, M. Finite Elements in Fracture Mechanics: Theory–Numerics–Aplications; Springer Science + Bussines Media: Dordrecht, The Netherlands, 2013; pp. 227–240. [Google Scholar]
- Leski, A. Implementation of the Virtual Crack Closure Technique in Engineering FE Calculations. Finite Elem. Anal. Des. 2007, 43, 261–268. [Google Scholar] [CrossRef]
- Bonhomme, J.; Argüelles, A.; Viña, J.; Viña, I. Numerical and experimental validaton of computational models for mode I composite fracture failure. Comp. Mater. Sci. 2009, 45, 993–998. [Google Scholar] [CrossRef]
- Tavares, S.M.O.; Moreira, P.M.G.P.; Pastrama, S.D.; de Castro, P.M.S.T. Stress Intensity Factors by Numerical Evaluation in Cracked Structures. In Proceedings of the 11th Portuguese Conference on Fracture, Lisbon, Portugal, 13–15 February 2008. [Google Scholar]
- Dowling, L.E. Mechanical Behavior of Materials, 4th ed.; Pearson: Boston, MA, USA, 2013; pp. 542–619. [Google Scholar]
- Raju, I.S. Calculation of strain-energy release rates with higher order and singular order elements. Eng. Fract. Mech. 1987, 28, 251–278. [Google Scholar] [CrossRef]
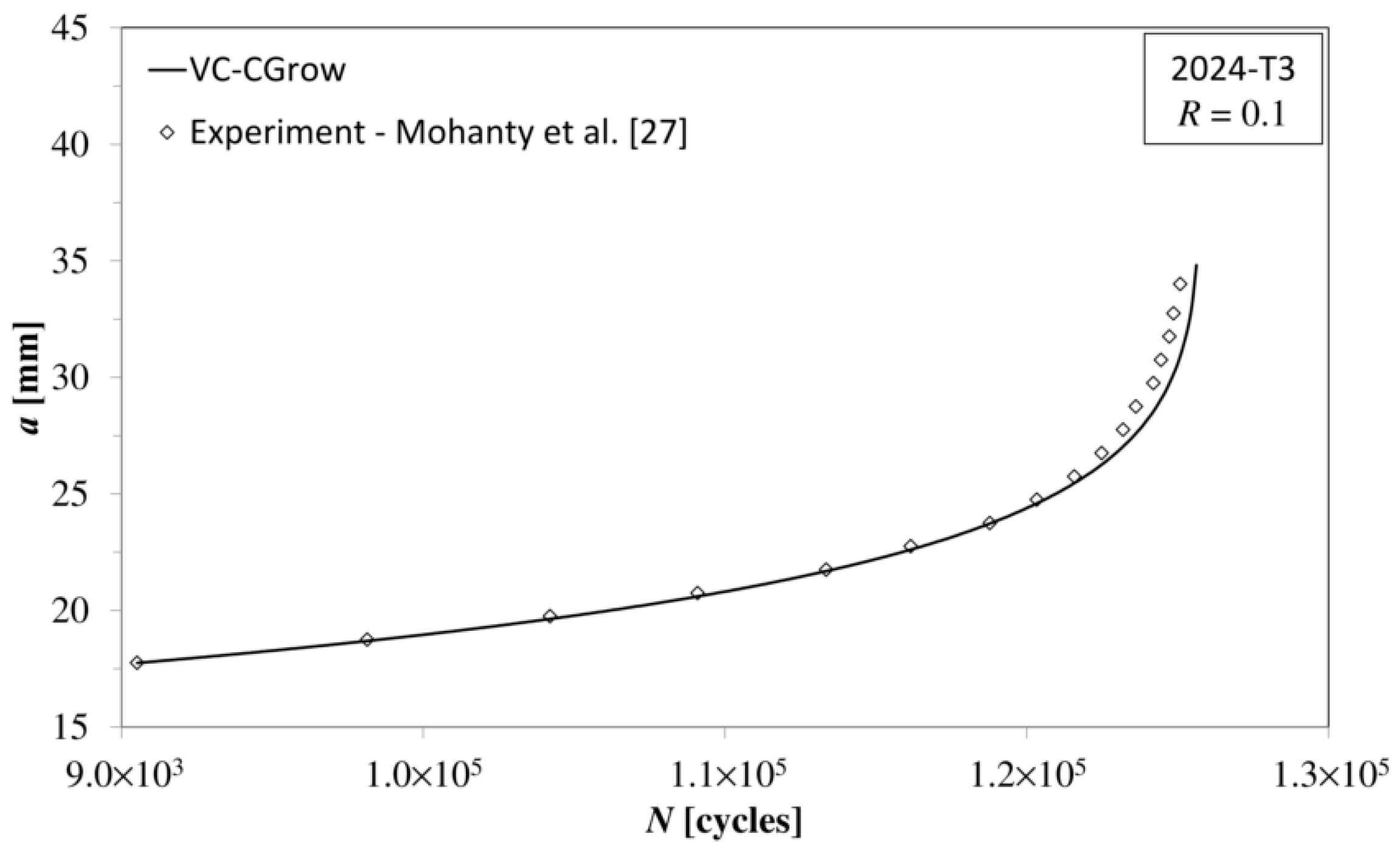
- Mohanty, J.R.; Verma, B.B.; Ray, P.K. Prediction of fatigue crack growth and residual life using an exponential model: Part I (constant amplitude loading). Int. J. Fatigue 2009, 31, 418–424. [Google Scholar] [CrossRef]
- ASTM Standards. Annual Book of ASTM Standards, Metals-Mechanical Testing; Elevated and Low-Temperature Tests; Metallography, Vol. 03.01; ASTM International: Baltimore, MD, USA, 2018. [Google Scholar]
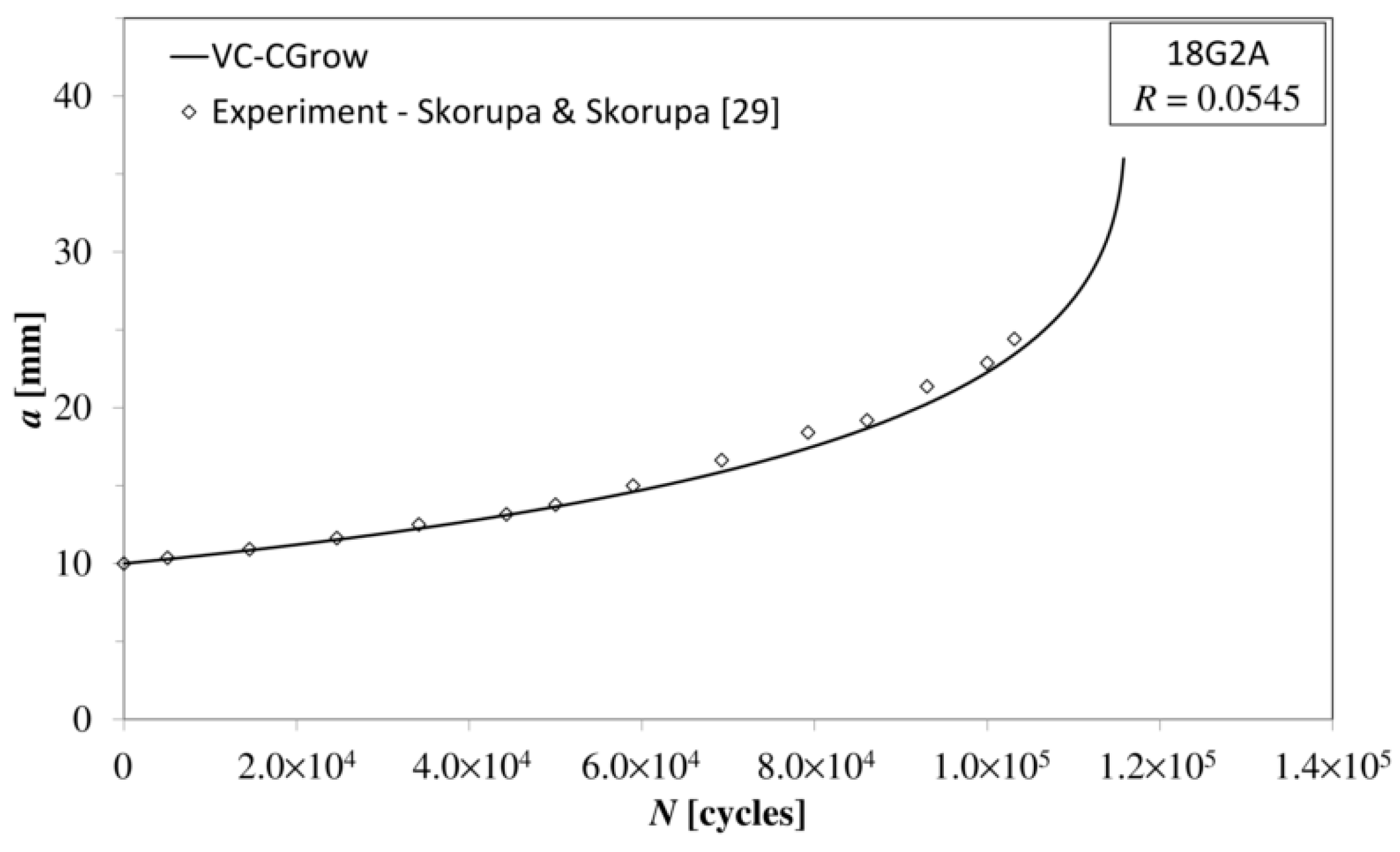
- Skorupa, M.; Skorupa, A. Experimental results and predictions on fatigue crack growth in structural steel. Int. J. Fatigue 2005, 27, 1016–1028. [Google Scholar] [CrossRef]
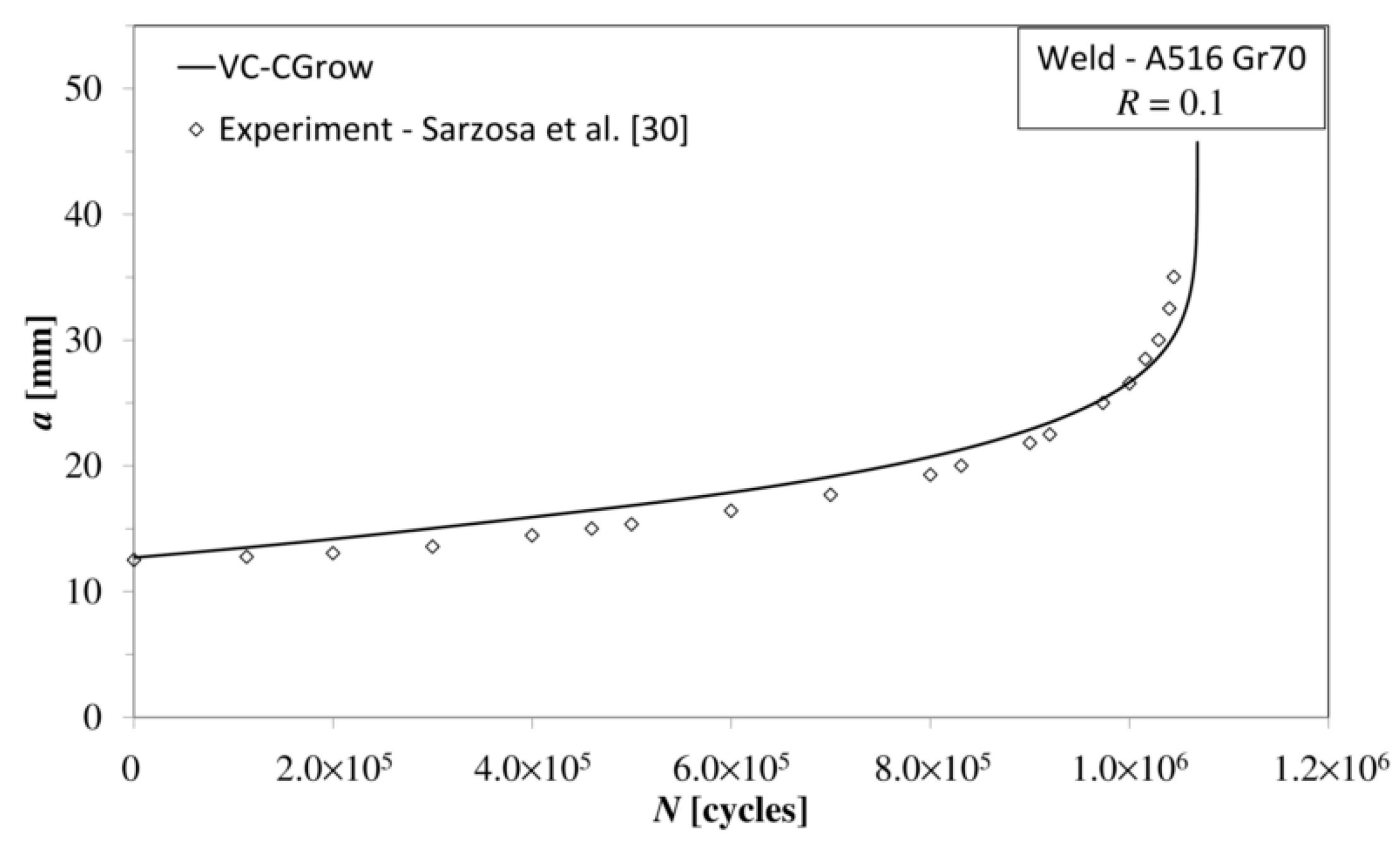
- Sarzosa, D.F.B.; Godefroid, L.B.; Ruggieri, C. Fatigue crack growth assessment in welded components including crack closure effects: Experiments and 3-D numerical modeling. Int. J. Fatigue 2013, 47, 279–291. [Google Scholar] [CrossRef]
- Brnic, J.; Krscanski, S.; Lanc, D.; Brcic, M.; Turkalj, G.; Canadija, M.; Niu, J. Analysis of the mechanical behavior, creep resistance and uniaxial fatigue strength of martensitic steel X46Cr13. Materials 2017, 10, 388. [Google Scholar] [CrossRef]


| TEST CASE | 1 | 2 | 3 | |
|---|---|---|---|---|
| Material | 2024-T3 | 18G2A (1.0562) | A516 Gr70 (1.0473) 45% overmatch weld | |
| Yield Strength σy, MPa | 324 | 398 | 511 | |
| Ultimate Tensile strength σUTS, MPa | 469 | 540 | 580 | |
| Young Modulus E, GPa | 73.1 | 210 | 210 | |
| Poisson ratio ν | 0.33 | 0.3 | 0.3 | |
| Plane-Strain Fracture Toughness KIc, MPa | 37 | 68 * | 91 * | |
| Forman Constants | CF | 1 × 10−5 | 2.23 × 10−6 | 5.31 × 10−7 ** |
| mF | 3.2094 | 3.073 | 3.256 ** | |
| TEST CASE | 1 | 2 | 3 | |
|---|---|---|---|---|
| Specimen Geometry | Single Edge Cracked Plate | M(T) | C(T) | |
| Specimen Thickness t, mm | 6.5 | 4 | 12.5 | |
| Initial Crack Size a0, mm | 17.75 | 10 | 12.7 | |
| Maximum Load | Fmax. kN | 7.2 | - | 7.061 |
| σmax. MPa | 21.3 | 137.5 | - | |
| Minimum Load | Fmin. kN | 0.72 | - | 0.7061 |
| σmin. MPa | 2.13 | 7.5 | - | |
| Load Asymmetry Ratio R | 0.1 | 0.0545 | 0.1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krscanski, S.; Brnic, J. Prediction of Fatigue Crack Growth in Metallic Specimens under Constant Amplitude Loading Using Virtual Crack Closure and Forman Model. Metals 2020, 10, 977. https://doi.org/10.3390/met10070977
Krscanski S, Brnic J. Prediction of Fatigue Crack Growth in Metallic Specimens under Constant Amplitude Loading Using Virtual Crack Closure and Forman Model. Metals. 2020; 10(7):977. https://doi.org/10.3390/met10070977
Chicago/Turabian StyleKrscanski, Sanjin, and Josip Brnic. 2020. "Prediction of Fatigue Crack Growth in Metallic Specimens under Constant Amplitude Loading Using Virtual Crack Closure and Forman Model" Metals 10, no. 7: 977. https://doi.org/10.3390/met10070977
APA StyleKrscanski, S., & Brnic, J. (2020). Prediction of Fatigue Crack Growth in Metallic Specimens under Constant Amplitude Loading Using Virtual Crack Closure and Forman Model. Metals, 10(7), 977. https://doi.org/10.3390/met10070977




.JPG)