Research on Fatigue Crack Propagation of 304 Austenitic Stainless Steel Based on XFEM and CZM
Abstract
1. Introduction
2. Experimental Conditions and Results
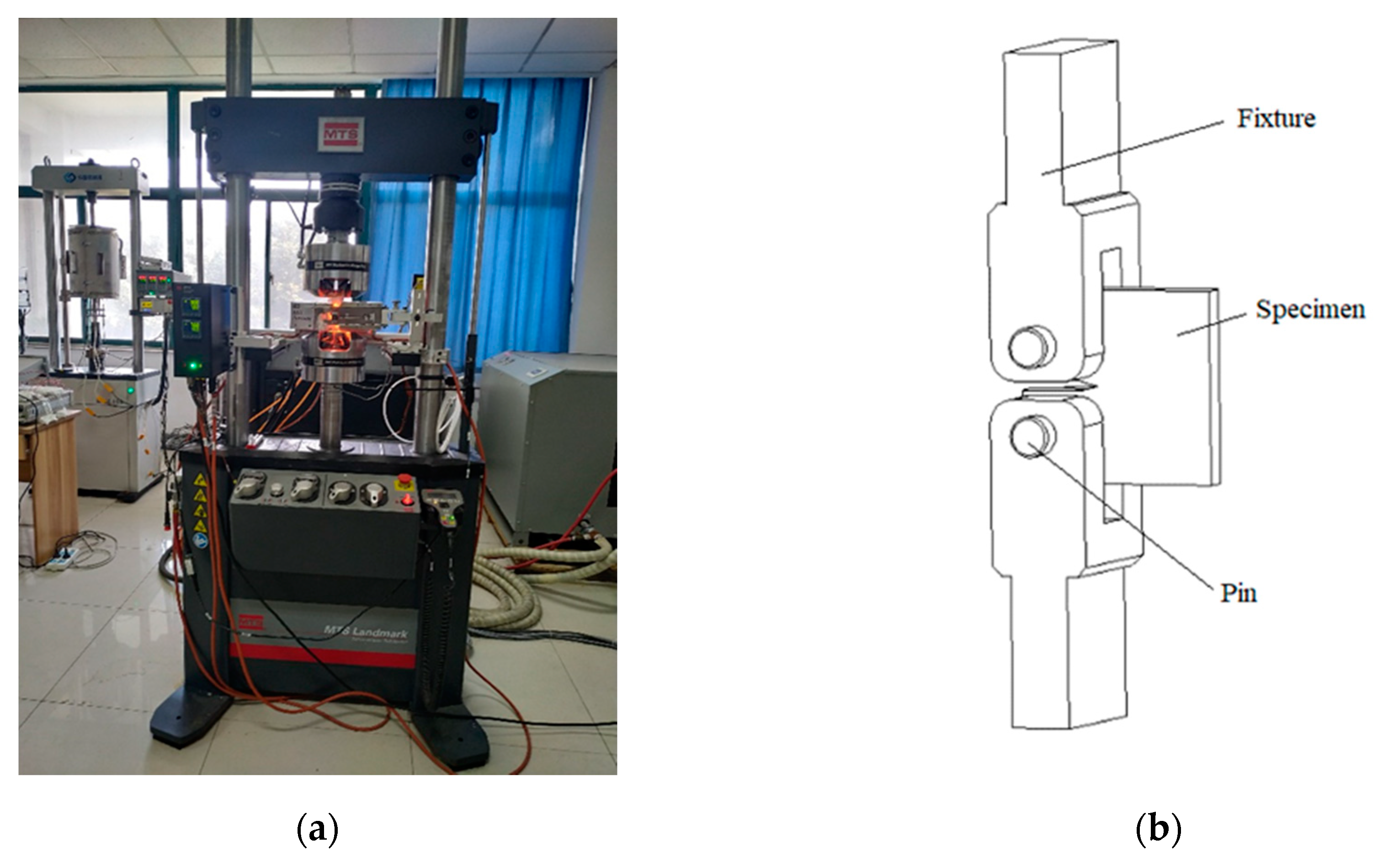
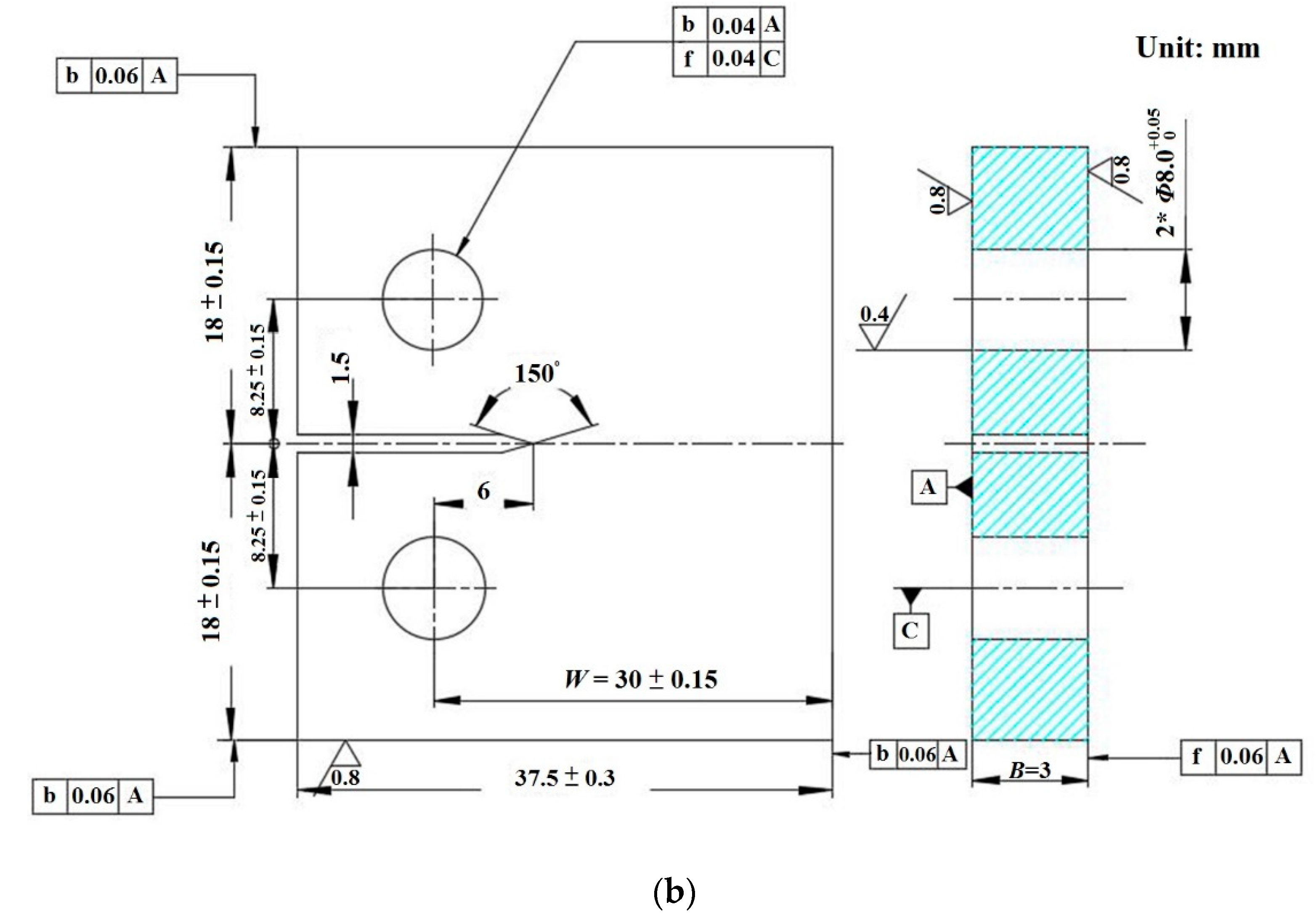
2.1. Preparation for Fatigue Tensile Test
2.2. Experimental Results
3. Simulation of Fatigue Crack Propagation Based on XFEM
3.1. Theory of Extended Finite Element
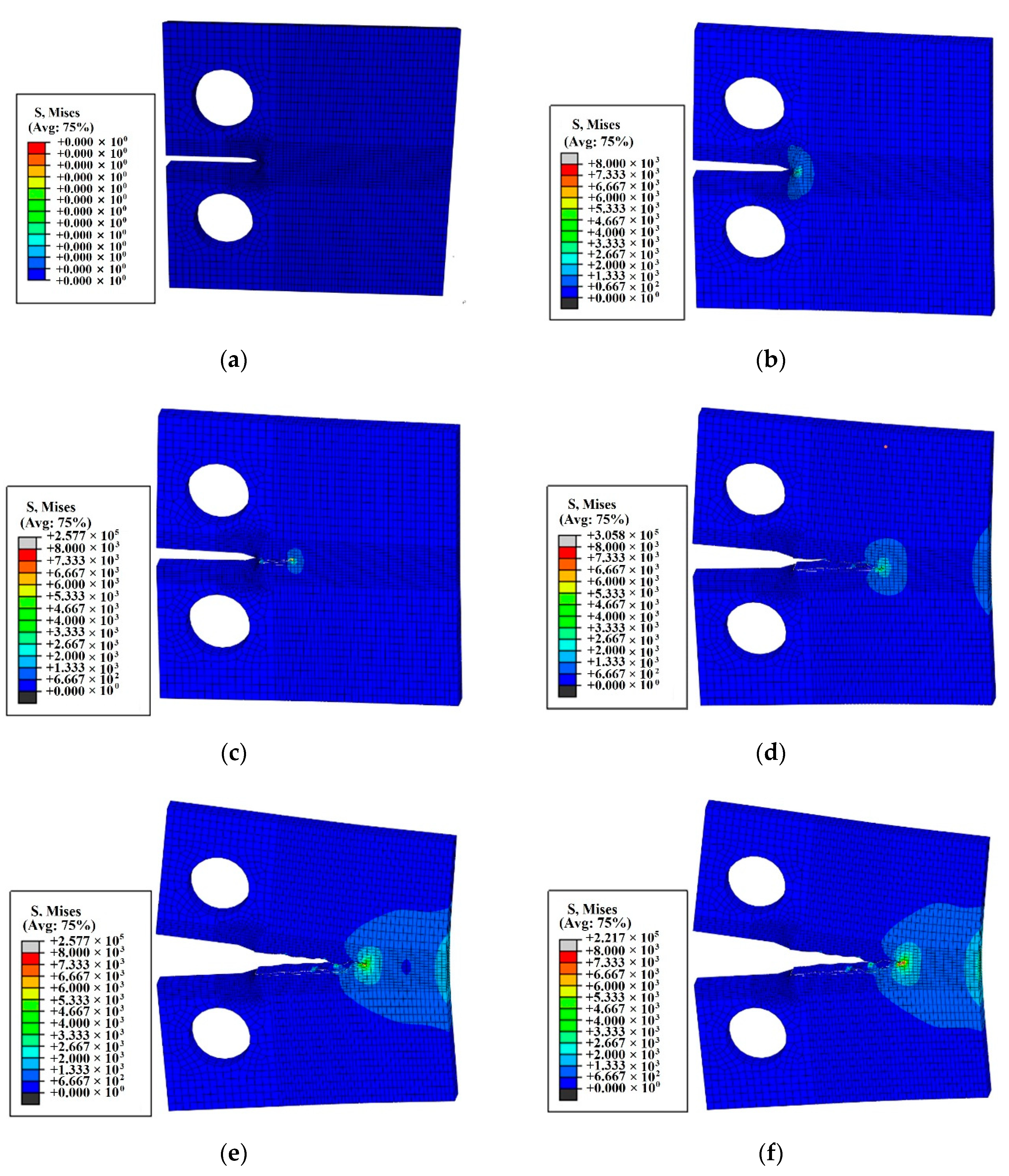
3.2. Simulated Results Based on XFEM
4. Simulation of Fatigue Crack Propagation Based on Bilinear CZM
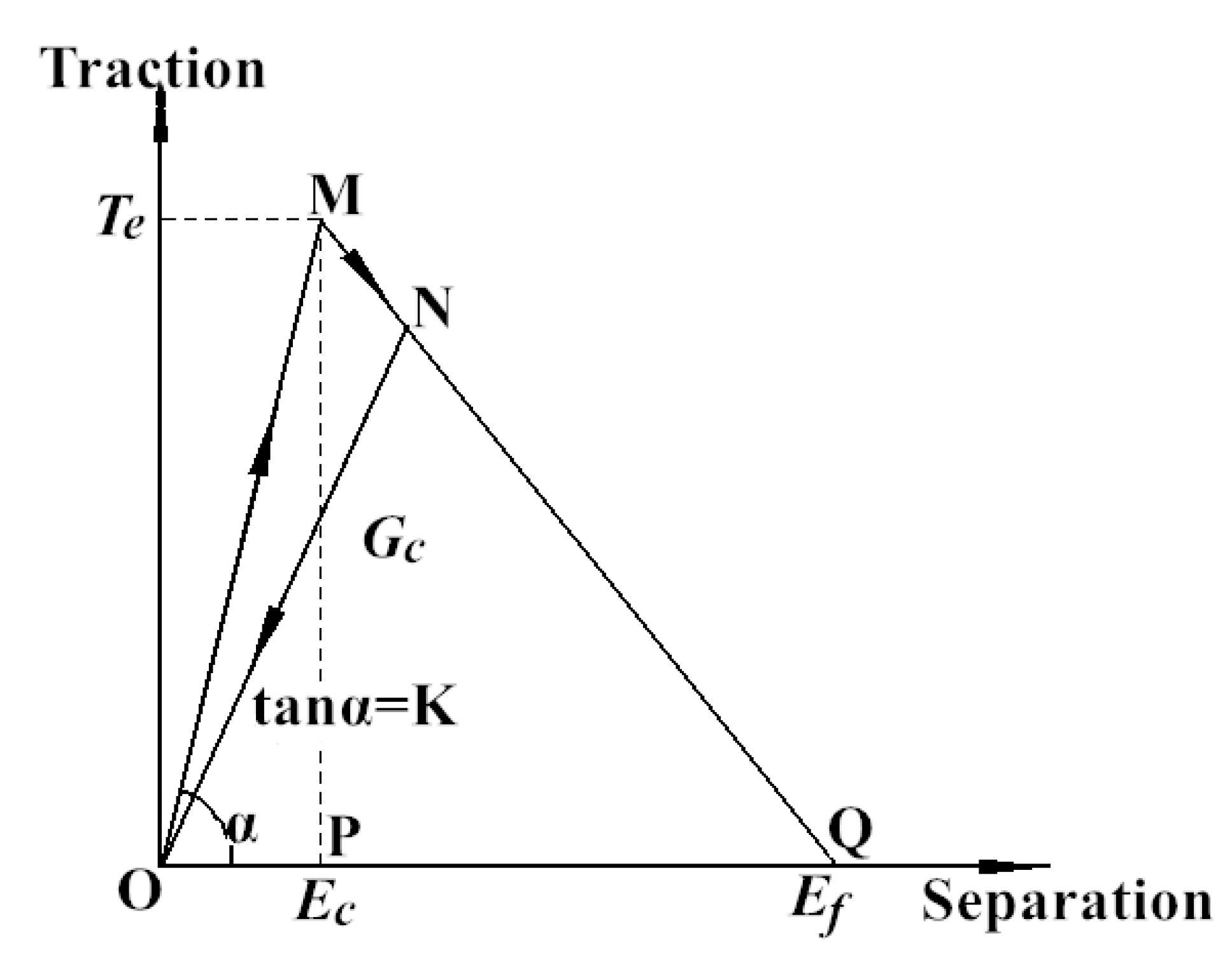
4.1. Bilinear CZM Theoretical Model
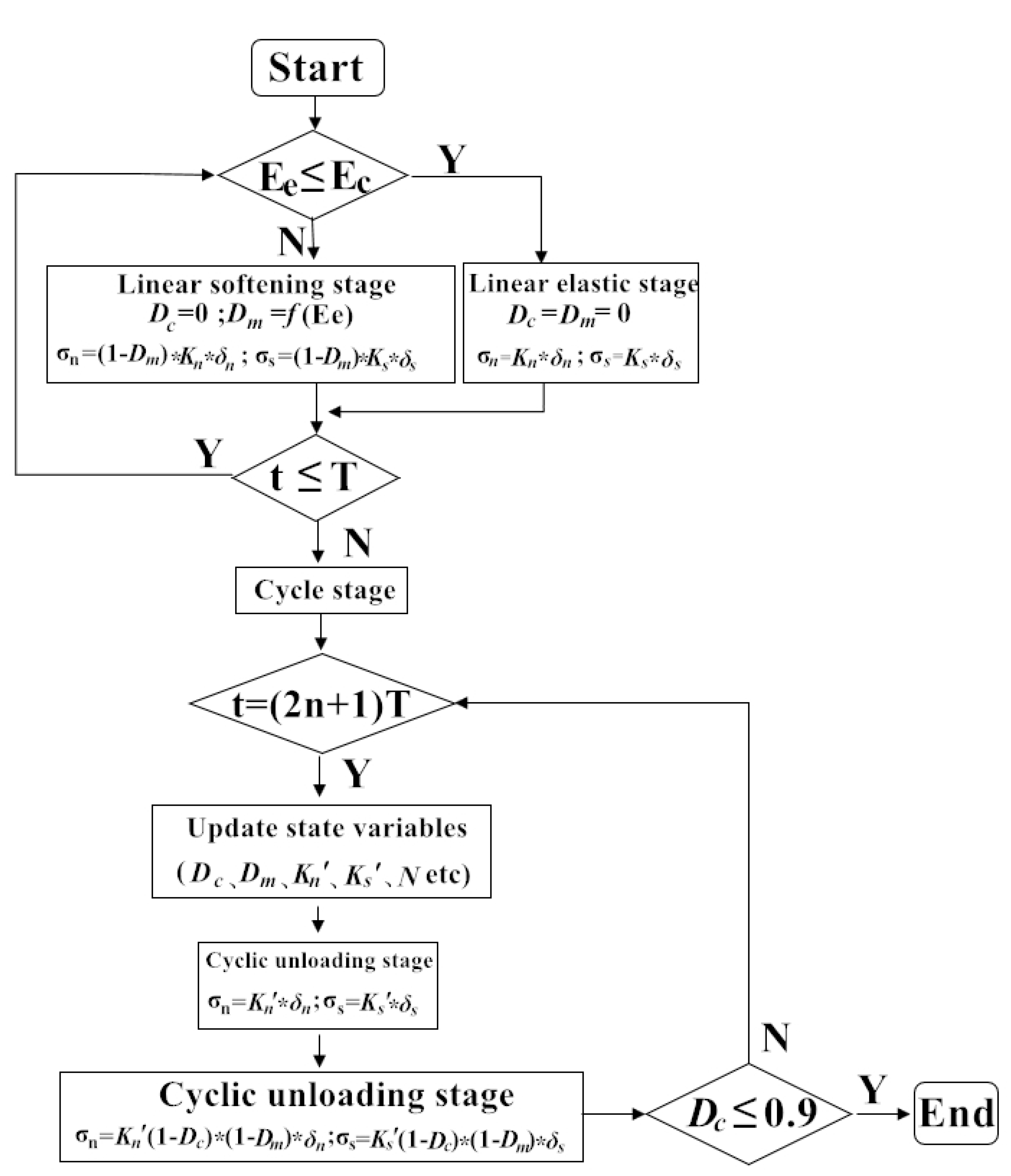
4.2. VUMAT Subroutine Based on Bilinear CZM
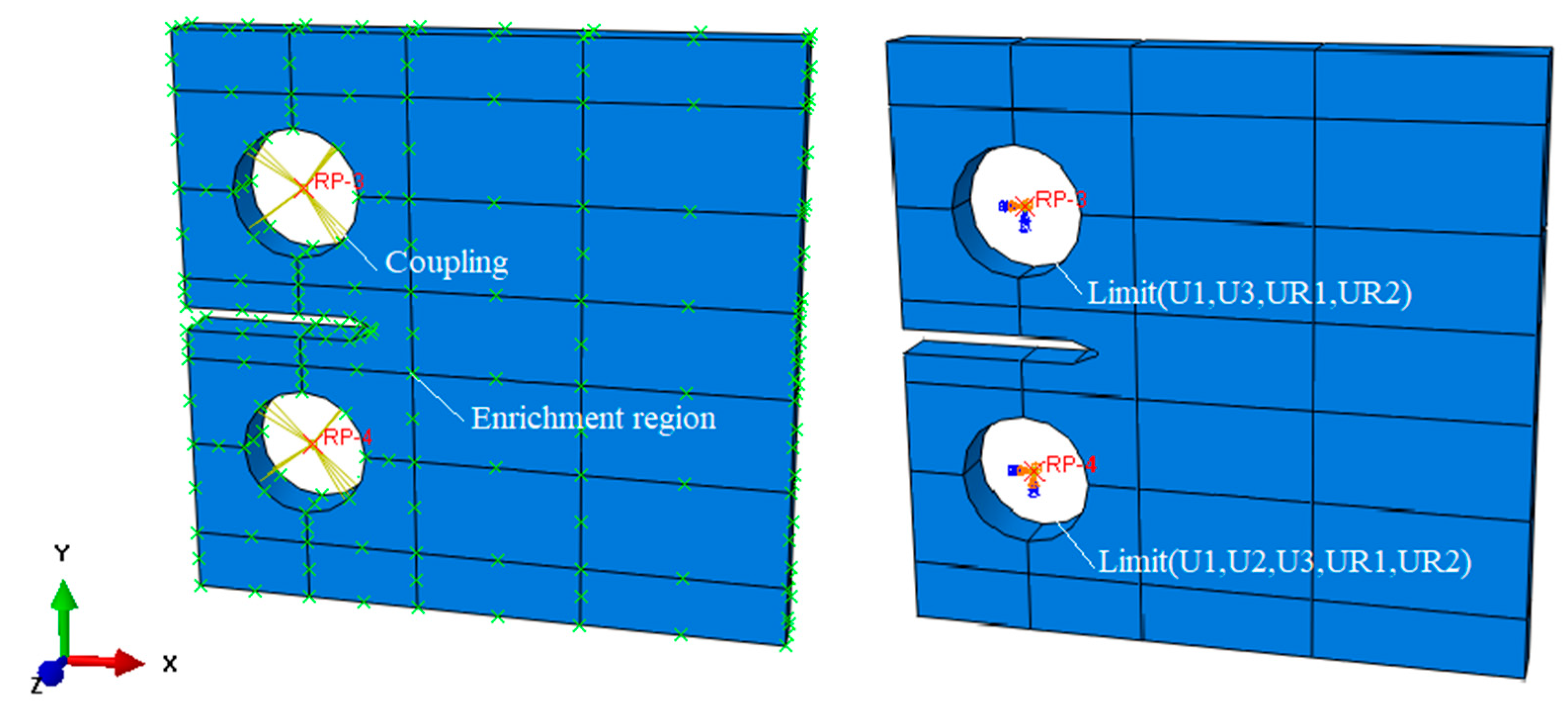
4.3. Finite Element Model
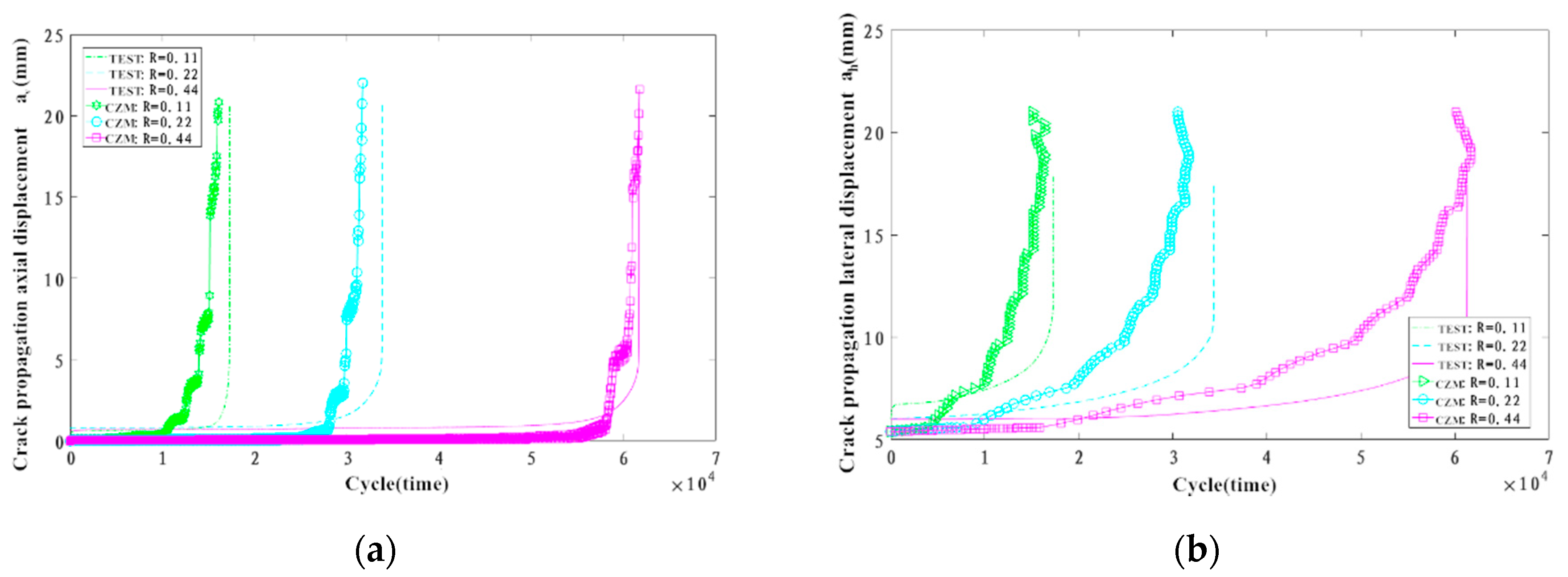
4.4. Simulated Results Based on Bilinear CZM
5. Conclusions
- (1)
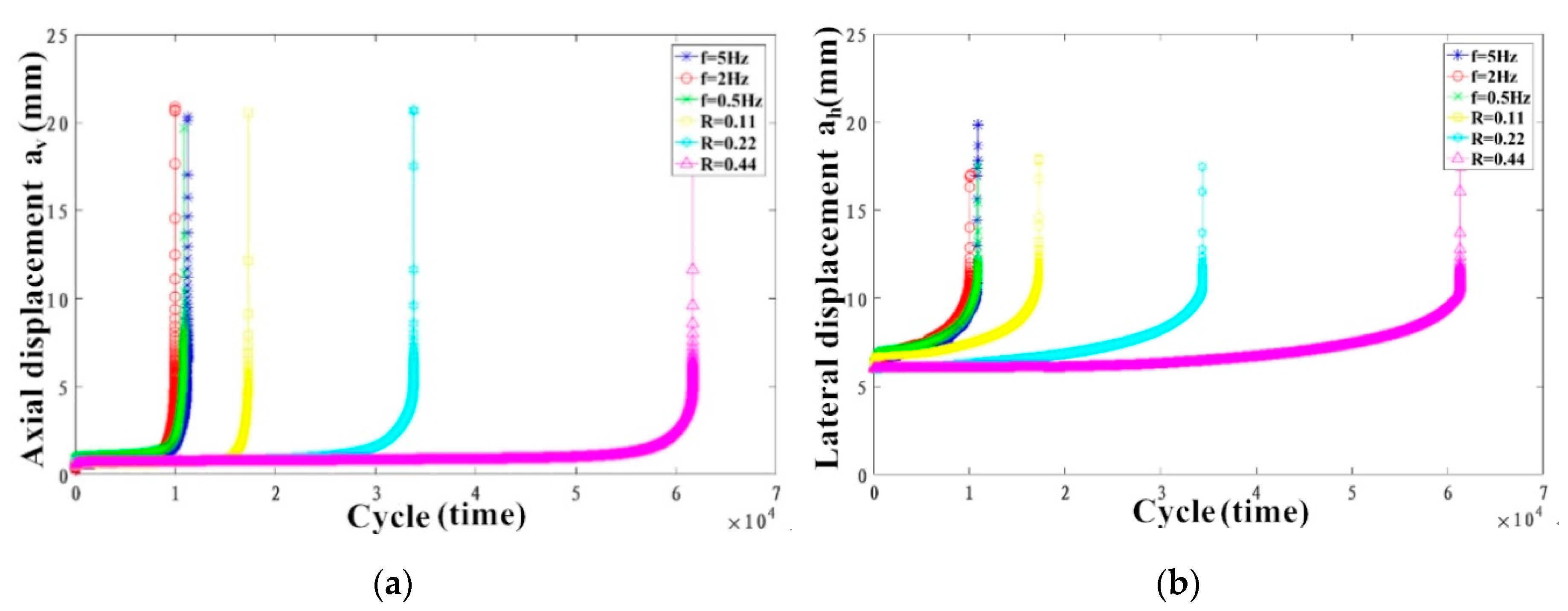
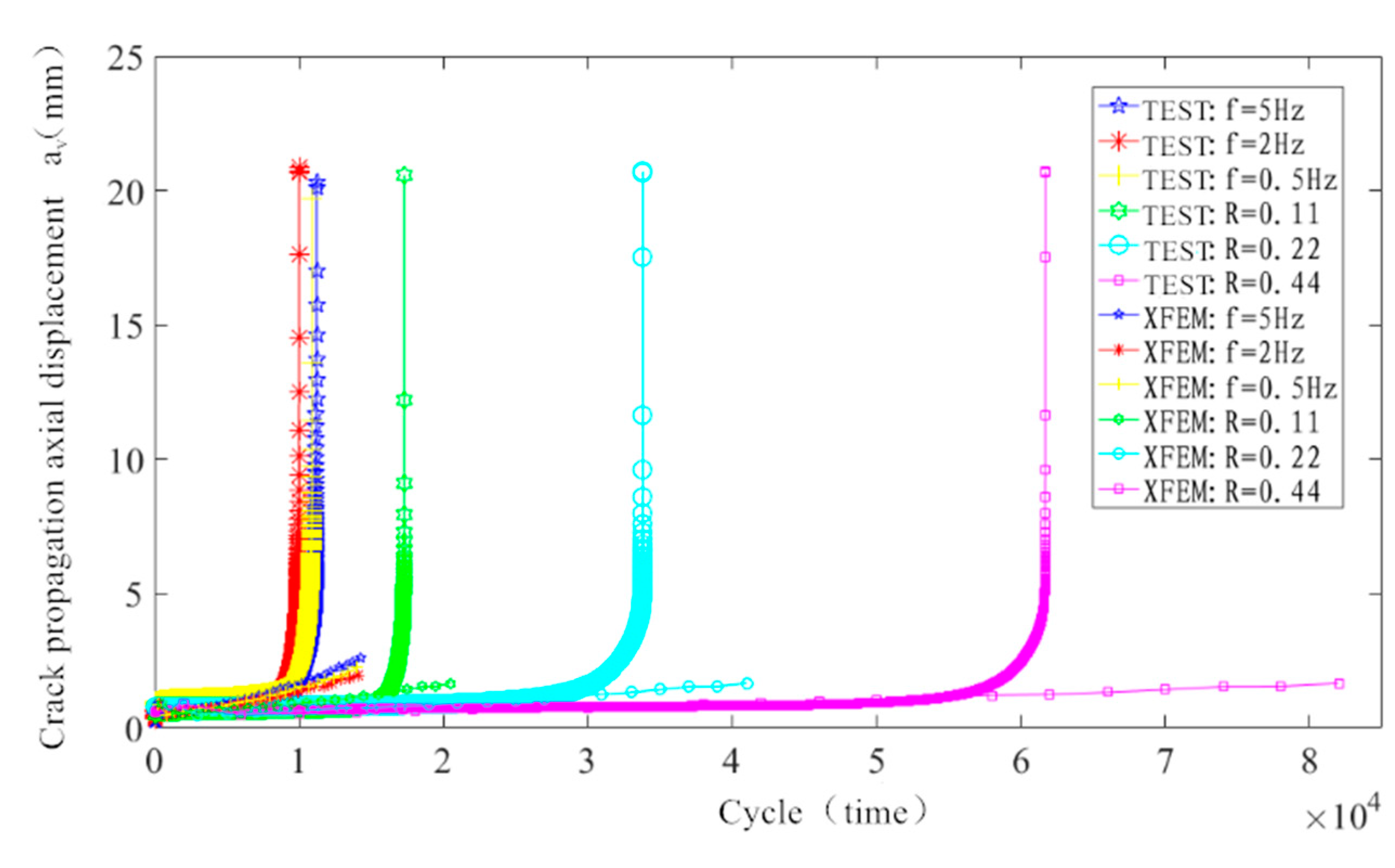
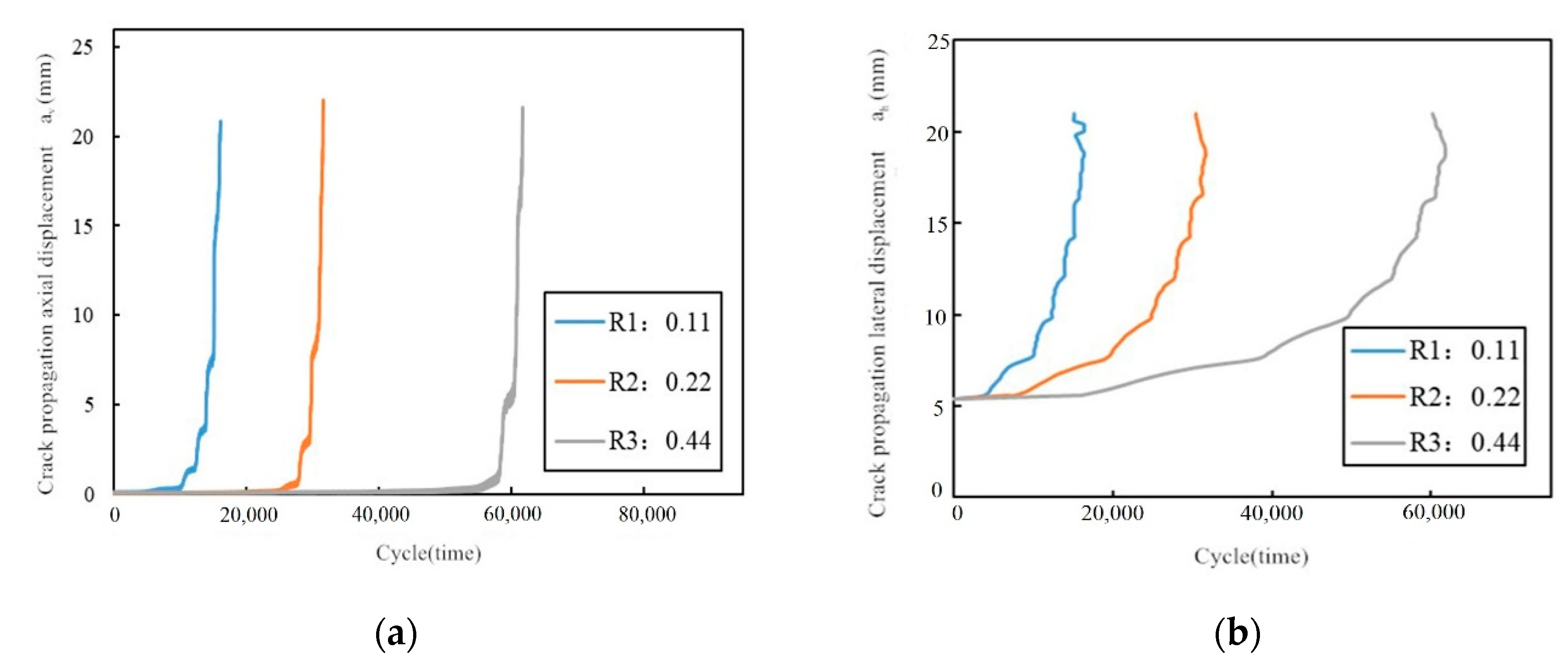
- The difference between the fatigue life of CT specimens measured at different frequencies, f, was small in this experiment, revealing that the f has little effect on the fatigue life. The smaller the stress ratio, R, is, the faster the crack propagates steadily, and the smaller the fatigue life, N, is.
- (2)
- The simulated results with the XFEM are in good agreement with the experimental data in the crack stability extension period. However, there are some deviations in the crack nucleation period. Moreover, the simulated and experimental data in the crack rapid rupture period are quite different. Therefore, the crack propagation path simulated by the XFEM model agrees well with the experimental result, but the predicted fatigue life is not accurate.
- (3)
- The simulated results by the CZM were compared with the experimental results at different stress ratios, R. Results show that the CZM can predict the fatigue crack propagation life very well in this paper, but it has certain limitations because the crack propagation path is preset. However, if all elements’ sides have CZM property, and FE mesh is reasonably fine, predefinition of crack path should not be required to predict a crack path of growing crack.
Author Contributions
Funding
Conflicts of Interest
References
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Daux, C.; Nicolas, M.; Dolbow, J.; Sukumar, N.; Belytschko, T. Arbitrary branched and intersecting cracks with the extended finite element method. Int. J. Numer. Methods Eng. 2000, 48, 1741–1760. [Google Scholar] [CrossRef]
- Sukumar, N.; Prévost, J.-H. Modeling quasi-static crack growth with the extended finite element method Part I: Computer implementation. Int. J. Solids Struct. 2003, 40, 7513–7537. [Google Scholar] [CrossRef]
- Bordas, S.; Nguyen, P.V.; Dunant, C.; Guidoum, A.; Nguyen-Dang, H. An extended finite element library. Int. J. Numer. Methods Eng. 2007, 71, 703–732. [Google Scholar] [CrossRef]
- Wyart, E.; Duflot, M.; Coulon, D.; Martiny, P.; Pardoen, T.; Remacle, J.-F.; Lani, F. Substructuring FE–XFE approaches applied to three-dimensional crack propagation. J. Comput. Appl. Math. 2008, 215, 626–638. [Google Scholar] [CrossRef][Green Version]
- Giner, E.; Sukumar, N.; Tarancón, J.E.; Fuenmayor, F.; Fernández, F.J.F. An Abaqus implementation of the extended finite element method. Eng. Fract. Mech. 2009, 76, 347–368. [Google Scholar] [CrossRef]
- Shi, J.; Chopp, D.; Lua, J.; Sukumar, N.; Belytschko, T. Abaqus implementation of extended finite element method using a level set representation for three-dimensional fatigue crack growth and life predictions. Eng. Fract. Mech. 2010, 77, 2840–2863. [Google Scholar] [CrossRef]
- Cheng, L.; Luo, Z.; Yu, Y.; Zhao, L.; Zhou, C. Study on the interaction mechanism between hydraulic fracture and natural karst cave with the extended finite element method. Eng. Fract. Mech. 2019, 222, 106680. [Google Scholar] [CrossRef]
- Mishra, R.; Burela, R.G. Thermo-electro-mechanical fatigue crack growth simulation in piezoelectric solids using XFEM approach. Theor. Appl. Fract. Mech. 2019, 104, 102388. [Google Scholar] [CrossRef]
- Abdullah, N.A.; Akbar, M.; Wirawan, N.; Curiel-Sosa, J.L. Structural integrity assessment on cracked composites interaction with aeroelastic constraint by means of XFEM. Compos. Struct. 2019, 229, 111414. [Google Scholar] [CrossRef]
- Elruby, A.; Nakhla, S. Strain energy density based damage initiation in heavily cross-linked epoxy using XFEM. Theor. Appl. Fract. Mech. 2019, 103, 102254. [Google Scholar] [CrossRef]
- Leonov, M.Y.; Panasyuk, V.V. The development of the smallest crack in solids. J. Prykl. Mesh. 1959, 5, 391–401. [Google Scholar]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equi-librium Cracks in Brittle Fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Camacho, G.T.; Ortiz, M. Computational modelling of impact damage in brittle materials. Int. J. Solids Struct. 1996, 33, 2899–2938. [Google Scholar] [CrossRef]
- Ghodrati, M.; Ahmadian, M.; Mirzaeifar, R. Three-dimensional study of rolling contact fatigue using crystal plasticity and cohesive zone method. Int. J. Fatigue 2019, 128, 105208. [Google Scholar] [CrossRef]
- Ghovanlou, M.K.; Jahed, H.; Khajepour, A. Cohesive zone modeling of fatigue crack growth in brazed joints. Eng. Fract. Mech. 2014, 120, 43–59. [Google Scholar] [CrossRef]
- Feng, Y.; Mei, D.; Wang, Y. Cohesive zone method based multi particle finite element simulation of compaction densification process of Al and NaCl laminar composite powders. J. Phys. Chem. Solids 2019, 134, 35–42. [Google Scholar] [CrossRef]
- De-Andrés, A.; Pérez, J.; Ortiz, M. Elastoplastic finite element analysis of three-dimensional fatigue crack growth in aluminum shafts subjected to axial loading. Int. J. Solids Struct. 1999, 36, 2231–2258. [Google Scholar] [CrossRef]
- Roe, K.L.; Siegmund, T. An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng. Fract. Mech. 2003, 70, 209–232. [Google Scholar] [CrossRef]
- Enayatpour, S.; Van Oort, E.; Patzek, T. Thermal shale fracturing simulation using the Cohesive Zone Method (CZM). J. Nat. Gas Sci. Eng. 2018, 55, 476–494. [Google Scholar] [CrossRef]
- Chen, D.; Li, G.; Wang, Y.; Xiao, Q. Research on fatigue crack propagation of a T-joint based on XFEM and TSA. Eng. Fract. Mech. 2019, 222, 106707. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Li, Y.; Li, X. A study of the numerical simulation technique for fatigue crack closure. Mech. Sci. Technol. 2006, 25, 1233–1237. [Google Scholar]
- Wang, Z.; Yu, T. A multiscale extended finite element method for modeling three-dimensional crack problems. Rock Soil Mech. 2014, 35, 2702–2708. [Google Scholar]
- He, L.; Liu, Z.; Gu, J.; Wang, J.; Men, K. Fatigue Crack Propagation Path and Life Prediction Based on XFEM. J. Northwest. Polytech. Univ. 2019, 37, 737–743. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2006, 74, 1665–1682. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.; Shioya, T. A rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials. Eng. Fract. Mech. 2004, 72, 1383–1410. [Google Scholar] [CrossRef]





| Variable | Values of Control Group Parameters | ||
|---|---|---|---|
| Frequency | 5 Hz | 2 Hz | 1 Hz |
| Stress ratio | 0.11 | 0.22 | 0.44 |
| Variable | Axial Fatigue Life (N) | Lateral Fatigue Life (N) | Average Life (N) |
|---|---|---|---|
| f = 5 Hz | 11,247 | 10,875 | 11,061 |
| f = 2 Hz | 10,023 | 10,116 | 10,070 |
| f = 0.5 Hz | 10,082 | 10,892 | 10,487 |
| R = 0.11 | 17,269 | 17,294 | 17,282 |
| R = 0.22 | 33,811 | 34,358 | 34,085 |
| R = 0.44 | 61,678 | 61,309 | 61,494 |
| Step | First Analysis Step | Second Analysis Step | ||||
|---|---|---|---|---|---|---|
| Time (s) | 0 | 0.5 | 1 | 0 | 0.5 | 1 |
| Force (N) | 0 | 10,000 | 500 | 500 | 5000 | 500 |
| Mesh Size | 0.5 mm | 0.6 mm | 0.7 mm | 0.8 mm | 0.9 mm | 1.0 mm | 1.1 mm | 1.2 mm |
|---|---|---|---|---|---|---|---|---|
| Fatigue life | 11,780 | 11,730 | 11,620 | 11,690 | 11,670 | 11,580 | 11,750 | 11,700 |
| Percentage of deviation | 11.8% | 11.3% | 10.2% | 10.9% | 10.7% | 9.8% | 11.5% | 11% |
| Cycles (time) | 200 | 500 | 1000 | 4000 | 6000 | 8000 | 10,000 | 12,000 | 15,000 | 17,000 |
| ∆K (Mpa·m1/2) | 34.72 | 38.04 | 40.81 | 44.57 | 46.79 | 49.02 | 54.44 | 63.15 | 69.78 | 84.28 |
| Plastic Strain | Yield Stress (Mpa) |
|---|---|
| 0 | 180 |
| 0.01 | 191.1 |
| 0.02 | 239.5 |
| 0.03 | 277.7 |
| 0.04 | 310.6 |
| 0.05 | 340.3 |
| 0.06 | 367.6 |
| 0.07 | 363.1 |
| 0.08 | 417.2 |
| 0.09 | 440.1 |
| 0.1 | 550 |
| 0.2 | 1000 |
| 0.5 | 3000 |
| 2 | 10,000 |
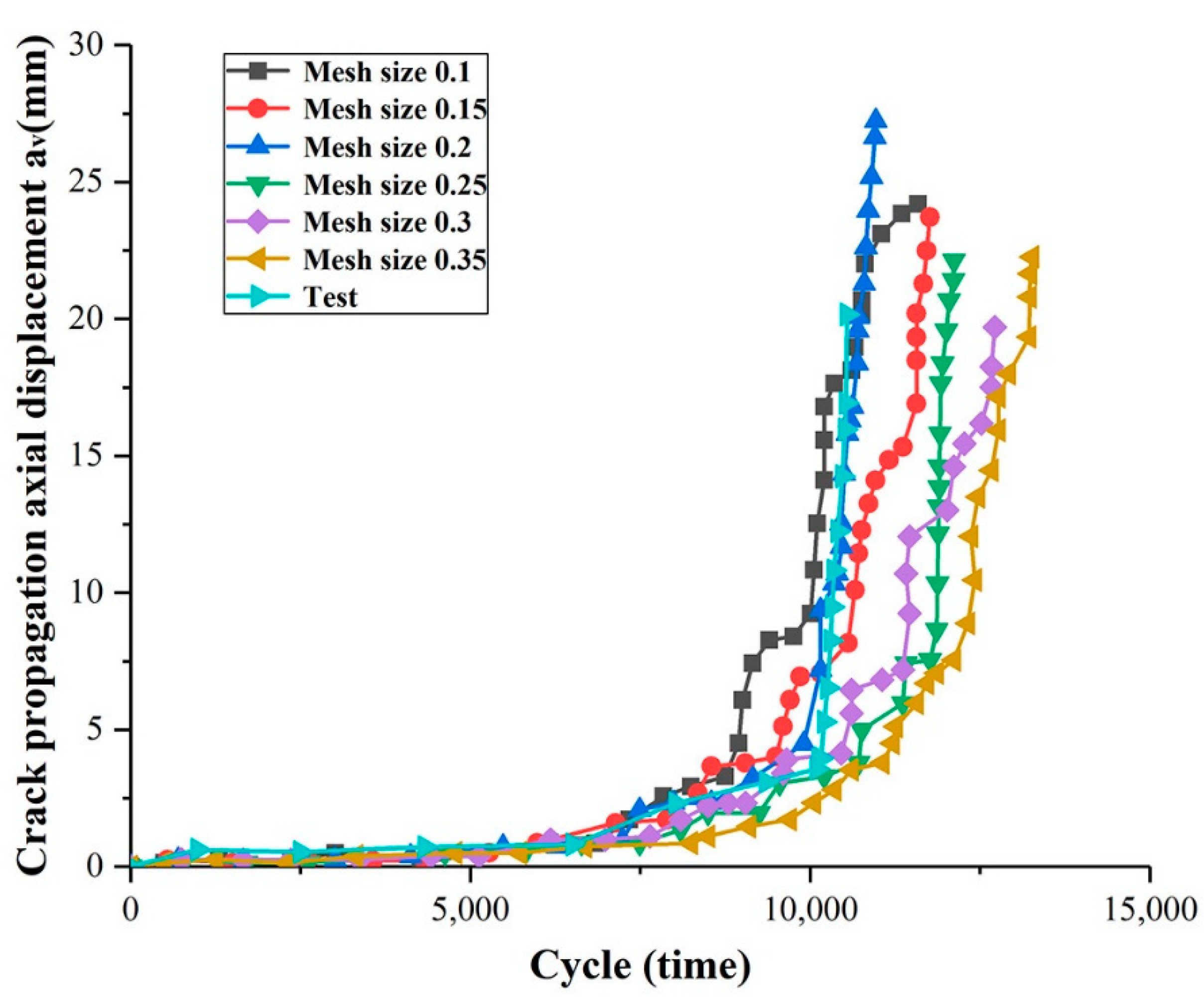
| Mesh Size | 0.1 mm | 0.15 mm | 0.2 mm | 0.25 mm | 0.3 mm | 0.35 mm |
|---|---|---|---|---|---|---|
| Fatigue life | 11,600 | 11,750 | 10,970 | 12,100 | 12,700 | 13,250 |
| Percentage of deviation | 10.1% | 11.5% | 4.1% | 14.8% | 20.5% | 25.7% |
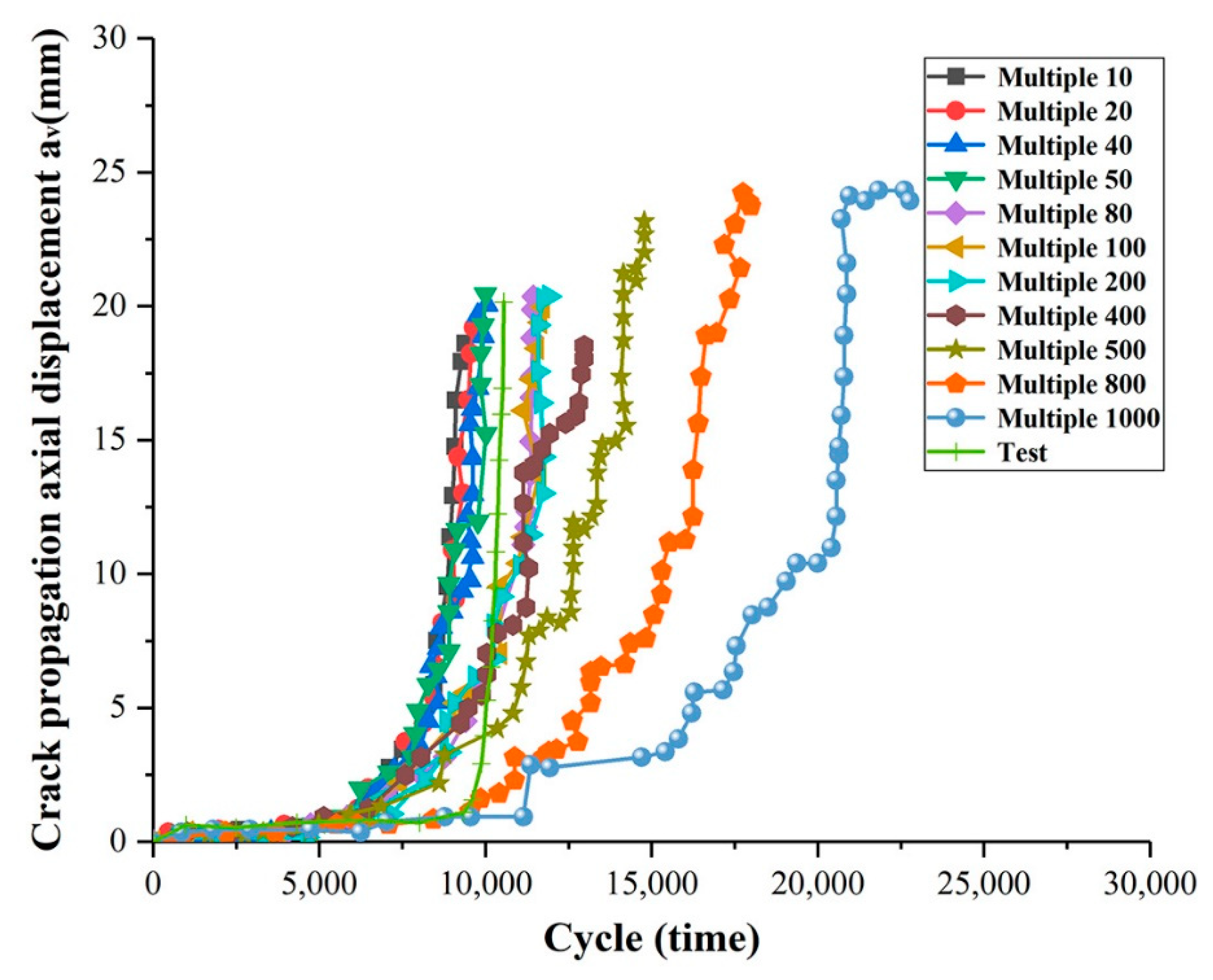
| Multiple | Fatigue Life | Percentage of Deviation |
|---|---|---|
| 10 | 9370 | 11.1% |
| 20 | 9640 | 8.5% |
| 40 | 10,040 | 4.7% |
| 50 | 10,000 | 5.1% |
| 80 | 11,440 | 8.5% |
| 100 | 11,700 | 11.0% |
| 200 | 11,920 | 13.1% |
| 400 | 12,900 | 22.4% |
| 500 | 14,820 | 40.6% |
| 800 | 17,920 | 70.0% |
| 1000 | 22,800 | 116.3% |
| Stress Ratio (R) | Experimental Fatigue Life (N) | CZM Simulation Fatigue Life (N) | Deviation |
|---|---|---|---|
| 0.11 | 17,282 | 16,100 | 6.8% |
| 0.22 | 34,085 | 31,700 | 7.0% |
| 0.44 | 61,494 | 61,700 | 0.3% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Xu, J.; Du, X.; Zhang, Y.; Zhou, F. Research on Fatigue Crack Propagation of 304 Austenitic Stainless Steel Based on XFEM and CZM. Metals 2020, 10, 727. https://doi.org/10.3390/met10060727
Hu X, Xu J, Du X, Zhang Y, Zhou F. Research on Fatigue Crack Propagation of 304 Austenitic Stainless Steel Based on XFEM and CZM. Metals. 2020; 10(6):727. https://doi.org/10.3390/met10060727
Chicago/Turabian StyleHu, Xiaodong, Jie Xu, Xiangmei Du, Yong Zhang, and Fan Zhou. 2020. "Research on Fatigue Crack Propagation of 304 Austenitic Stainless Steel Based on XFEM and CZM" Metals 10, no. 6: 727. https://doi.org/10.3390/met10060727
APA StyleHu, X., Xu, J., Du, X., Zhang, Y., & Zhou, F. (2020). Research on Fatigue Crack Propagation of 304 Austenitic Stainless Steel Based on XFEM and CZM. Metals, 10(6), 727. https://doi.org/10.3390/met10060727




