A Comprehensive Mathematical Model of Electroslag Remelting with Two Series-Connected Electrodes Based on Sequential Coupling Simulation Method
Abstract
1. Introduction
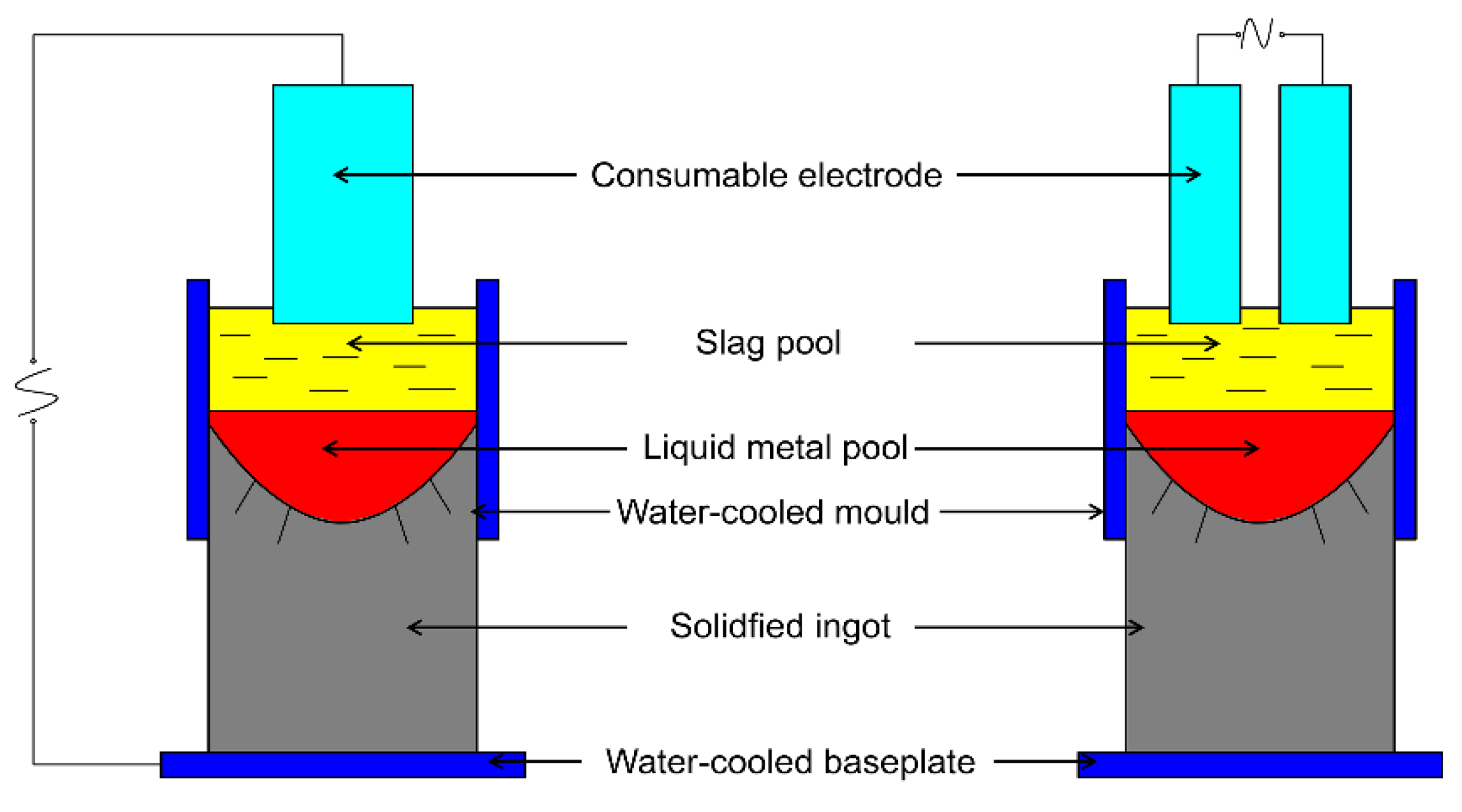
2. Mathematical Modeling
2.1. A. Governing Equations
2.1.1. Electromagnetic Field Control Equation
2.1.2. Fluid Control Equation
2.1.3. Multiphase Flow
2.1.4. Heat Transfer Control Equation
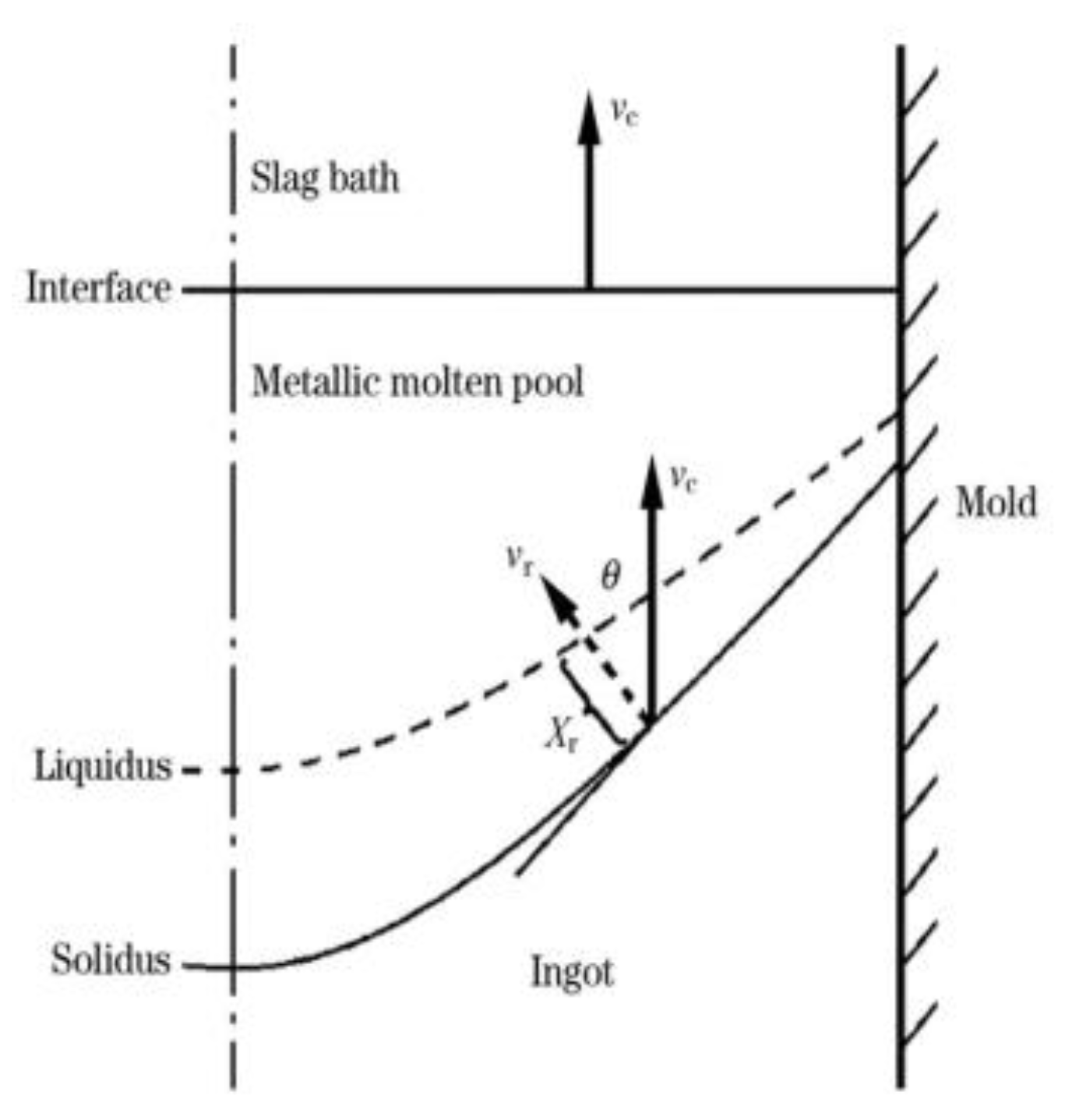
2.1.5. Governing Equation for Droplet
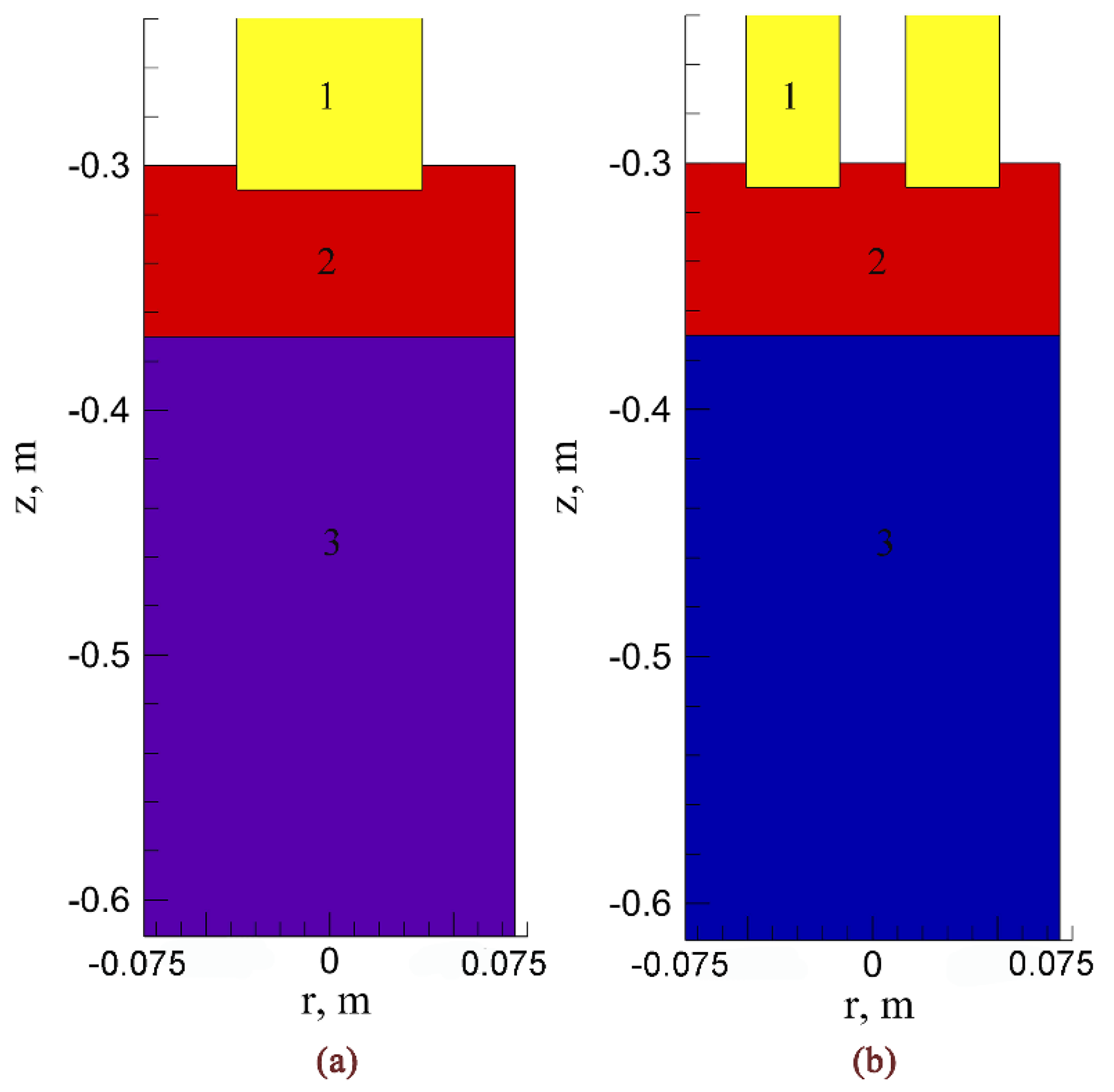
2.2. Multi-Physical Field Steady State Model Conditions
2.2.1. Electromagnetic Boundary Condition
2.2.2. Heat Transfer Boundary Condition
2.2.3. Flow Boundary Condition
2.3. Transient Model of Electrode Melting and Droplet Dropping Conditions
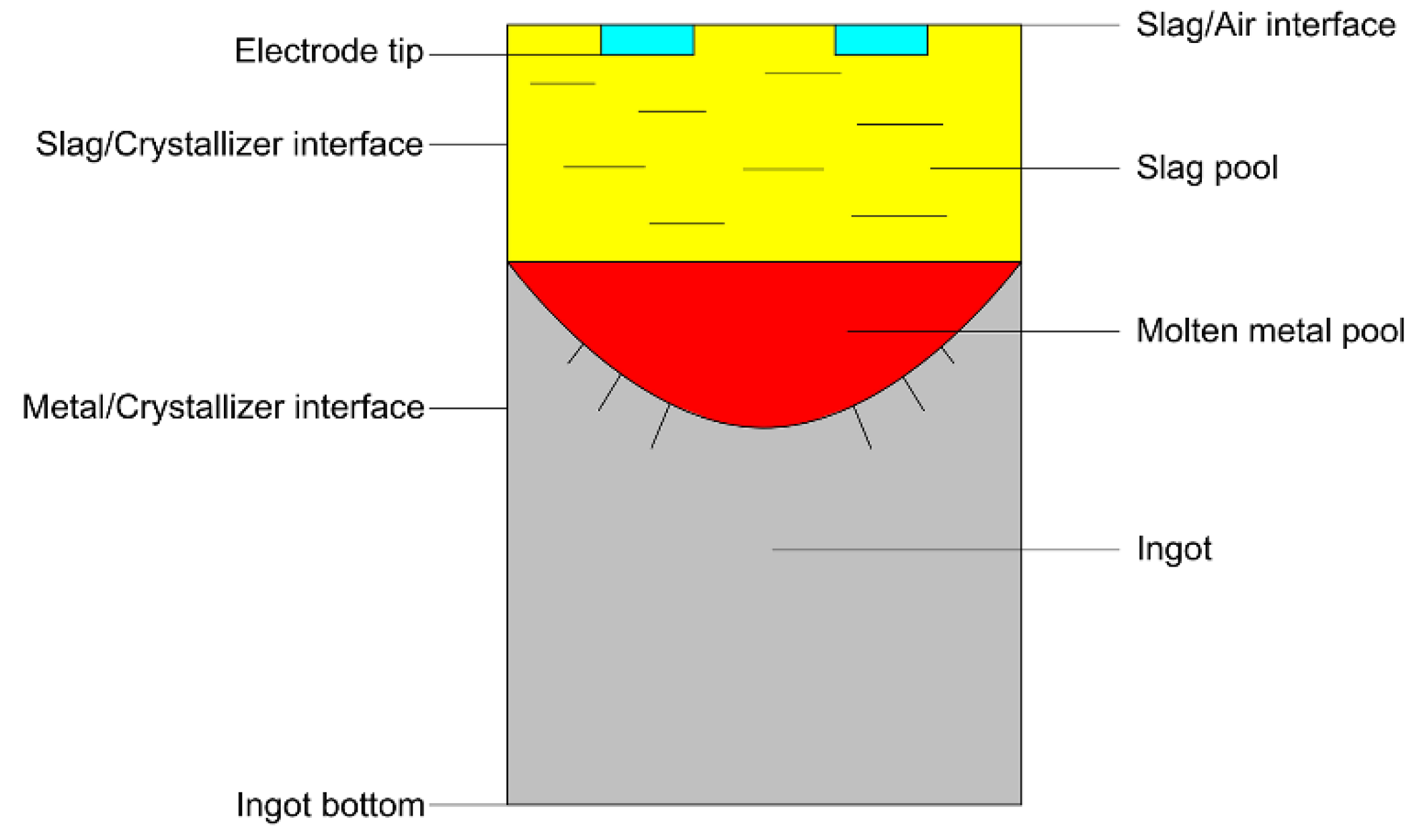
2.4. Multi-Phase Transient Model of Molten Metal Pool Boundary Conditions
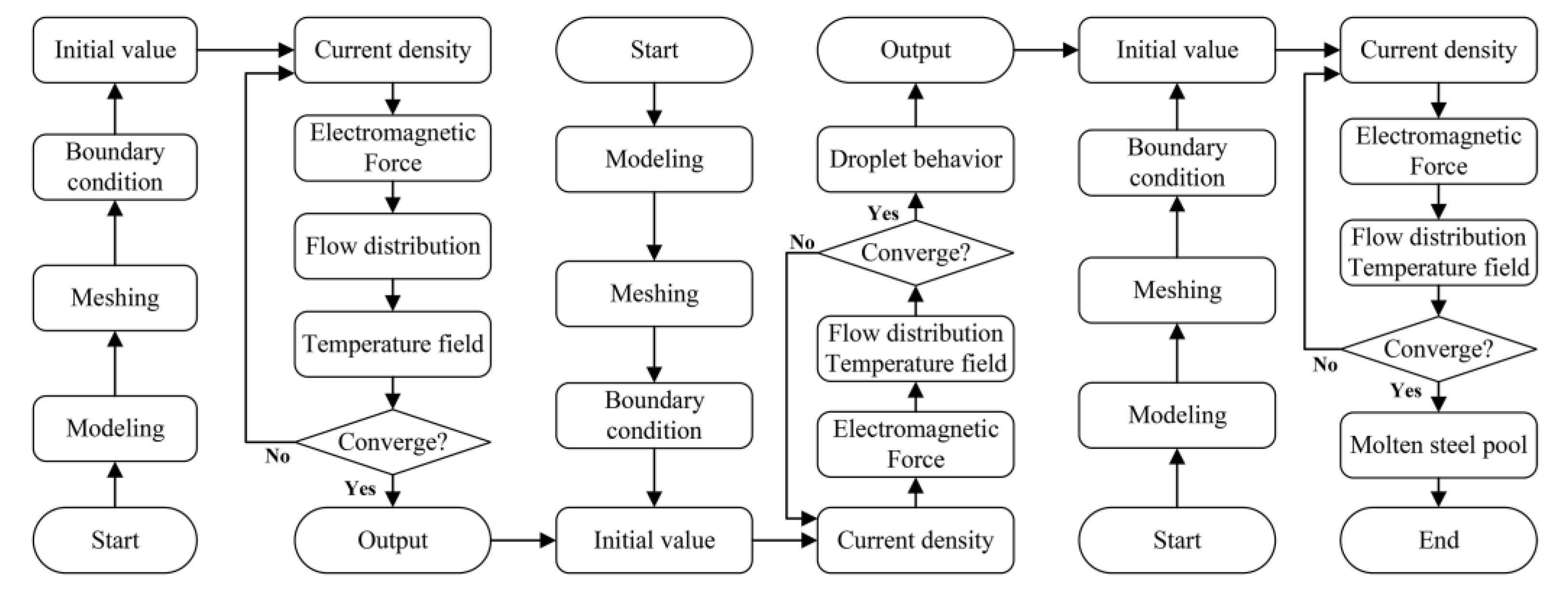
2.5. Calculation Strategy
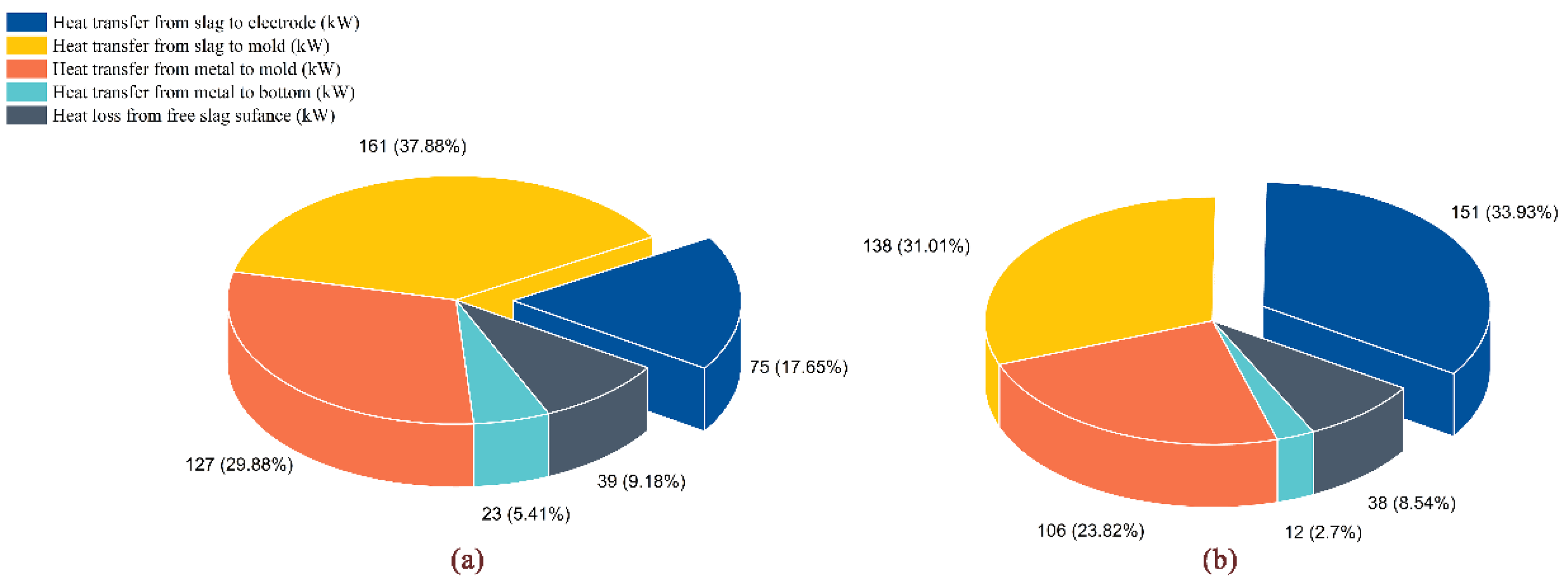
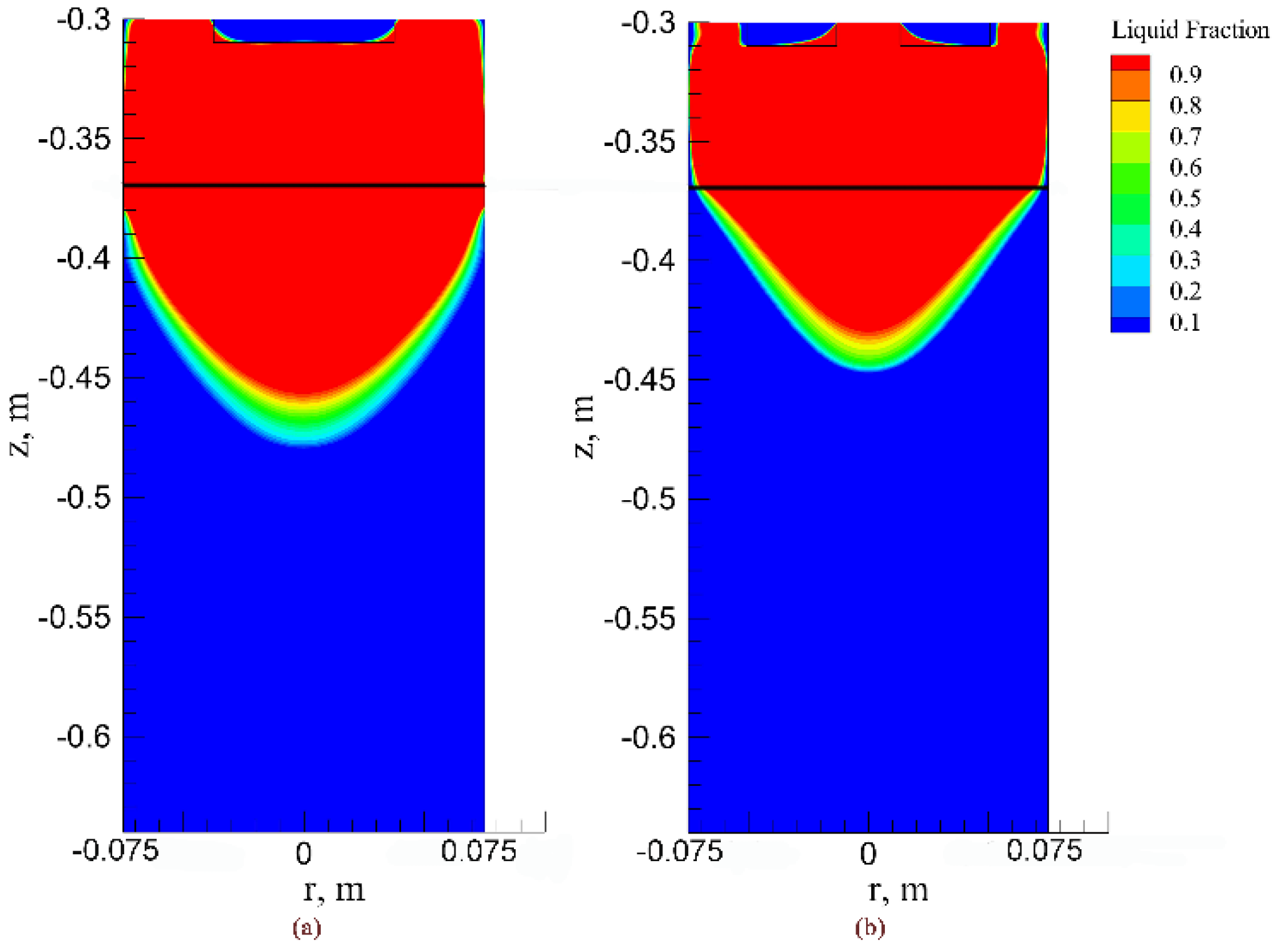
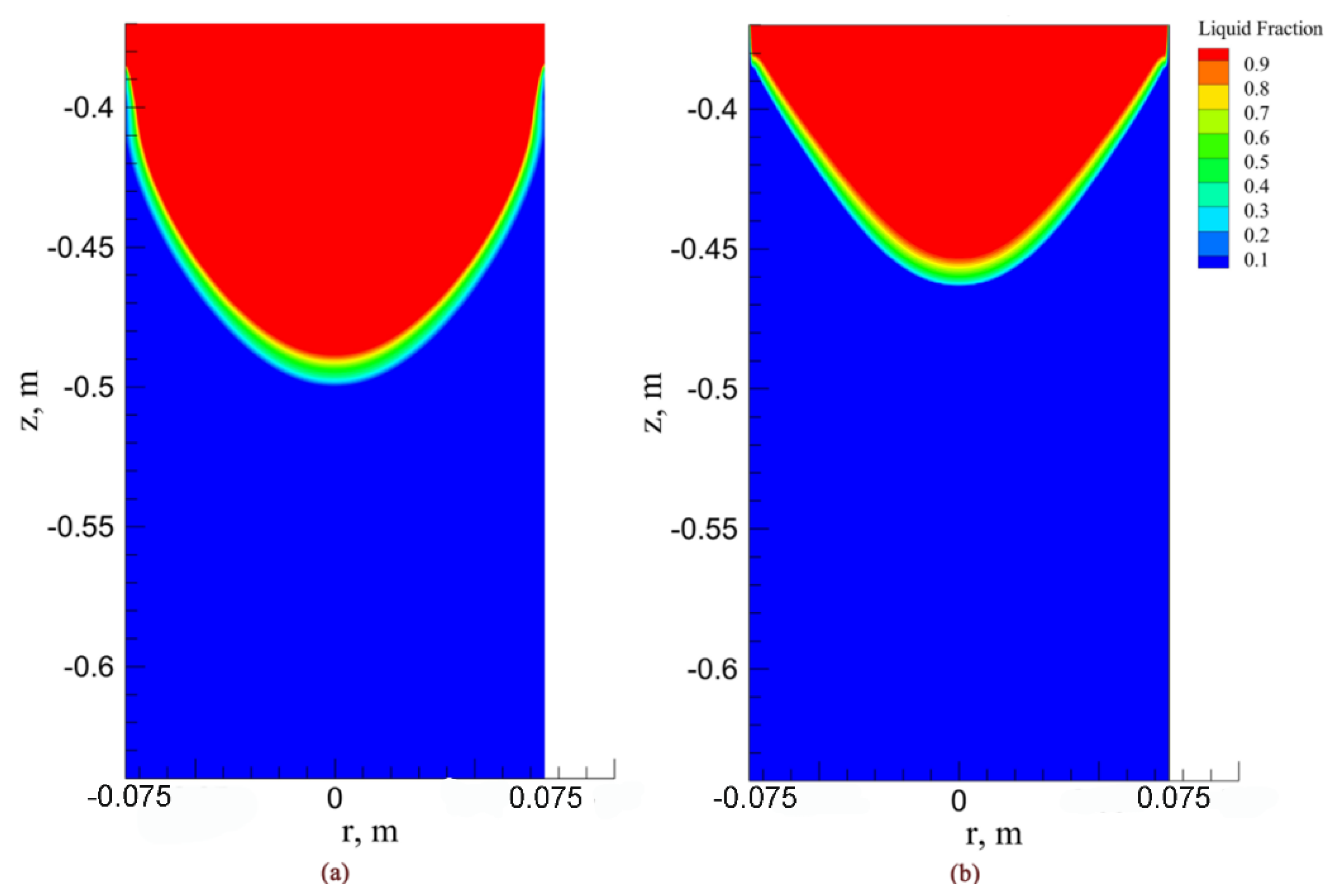
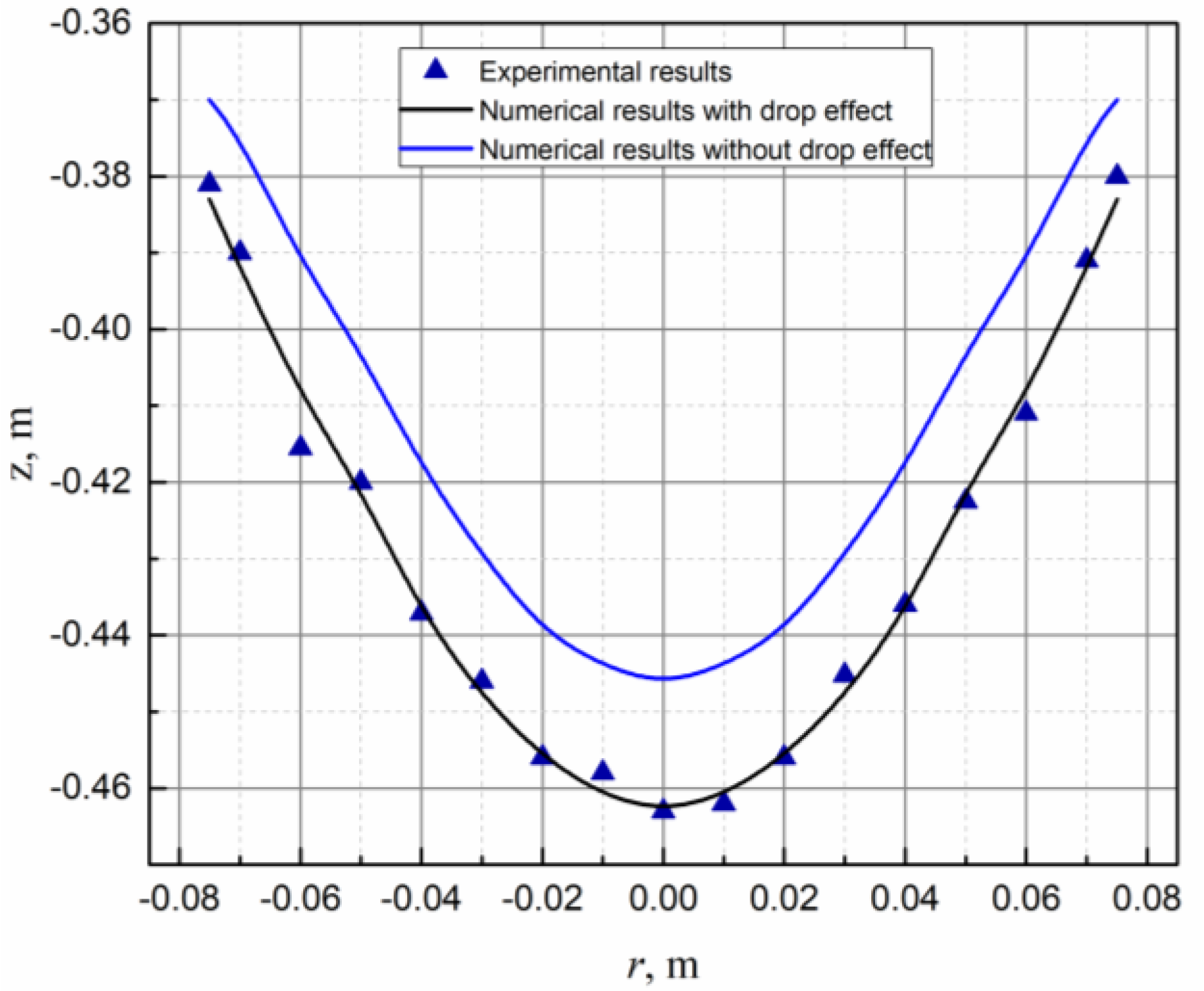
3. Results and Discussion
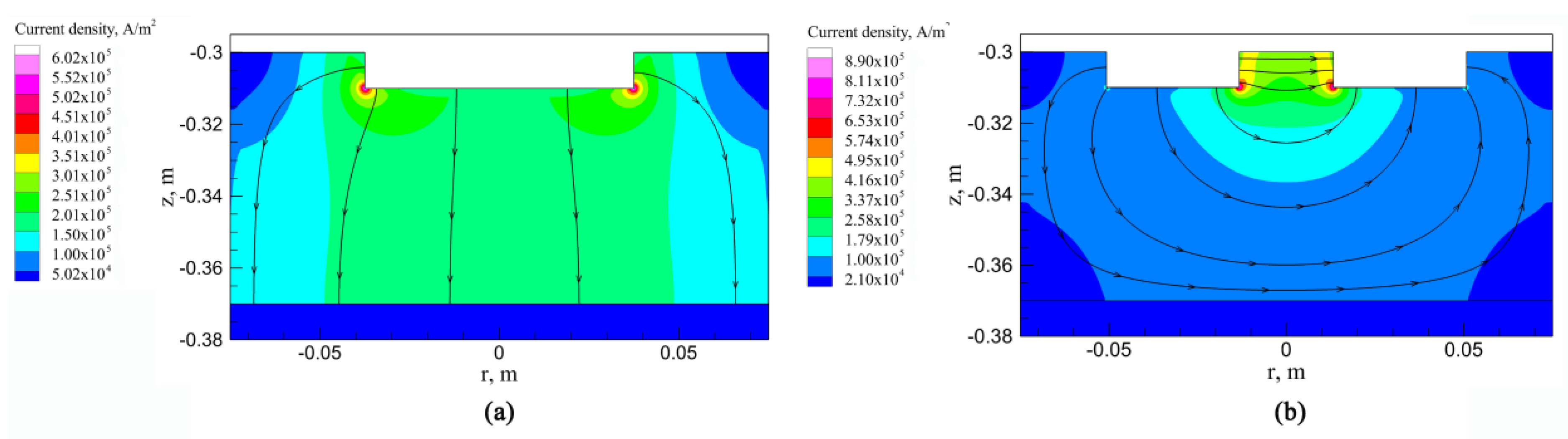
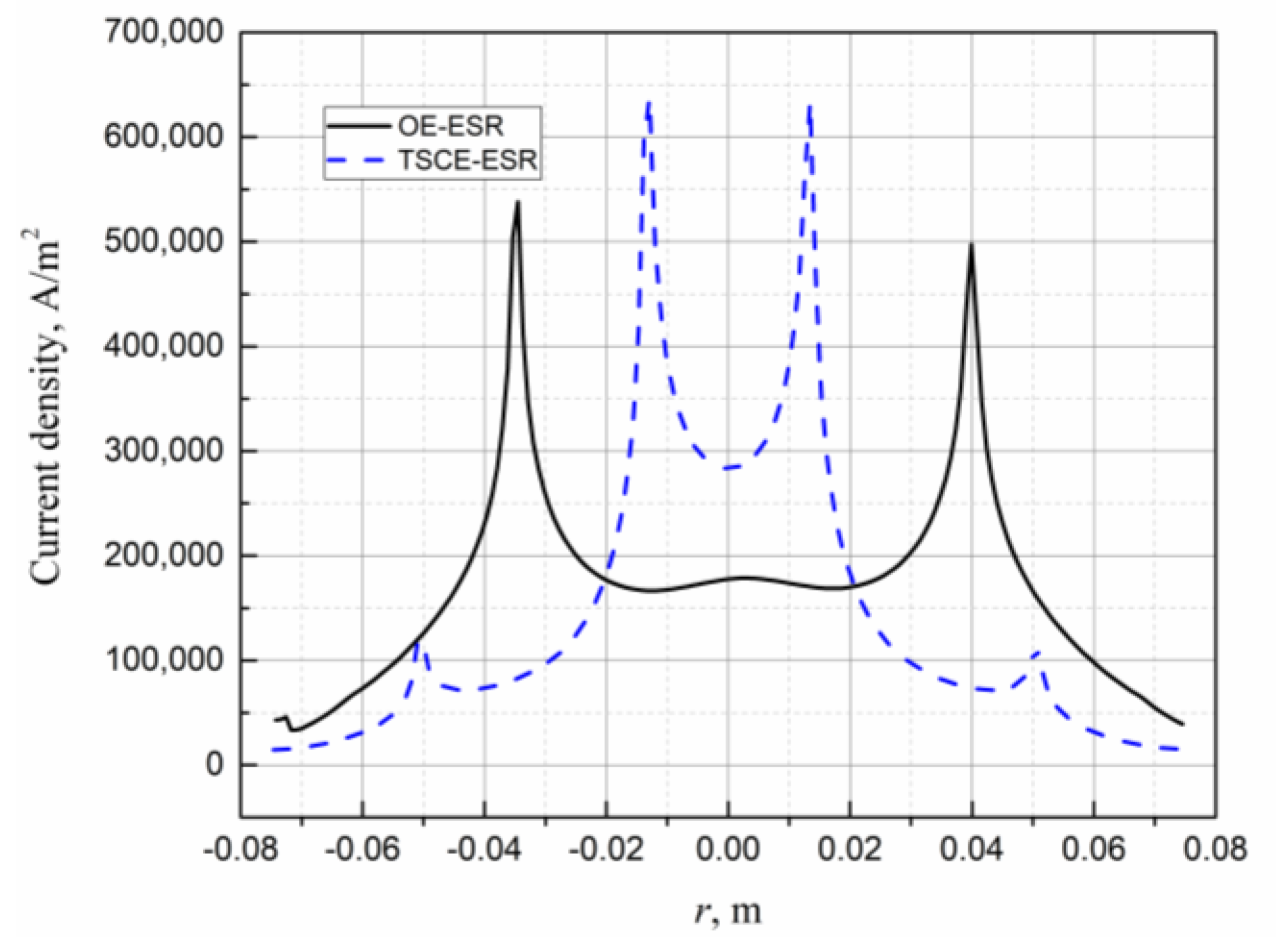
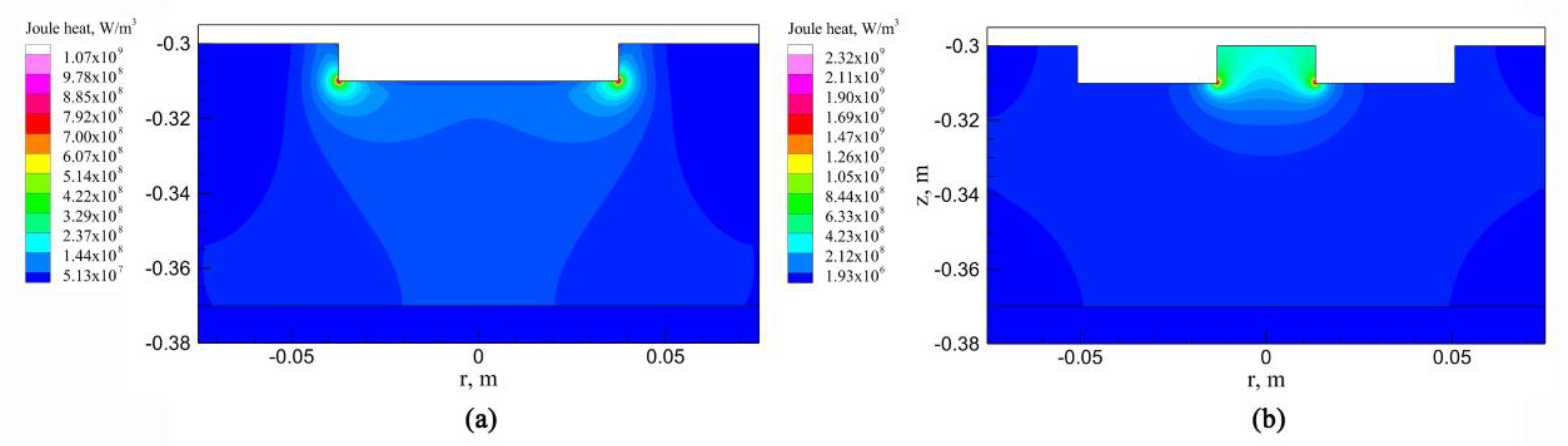
3.1. Electromagnetic Field
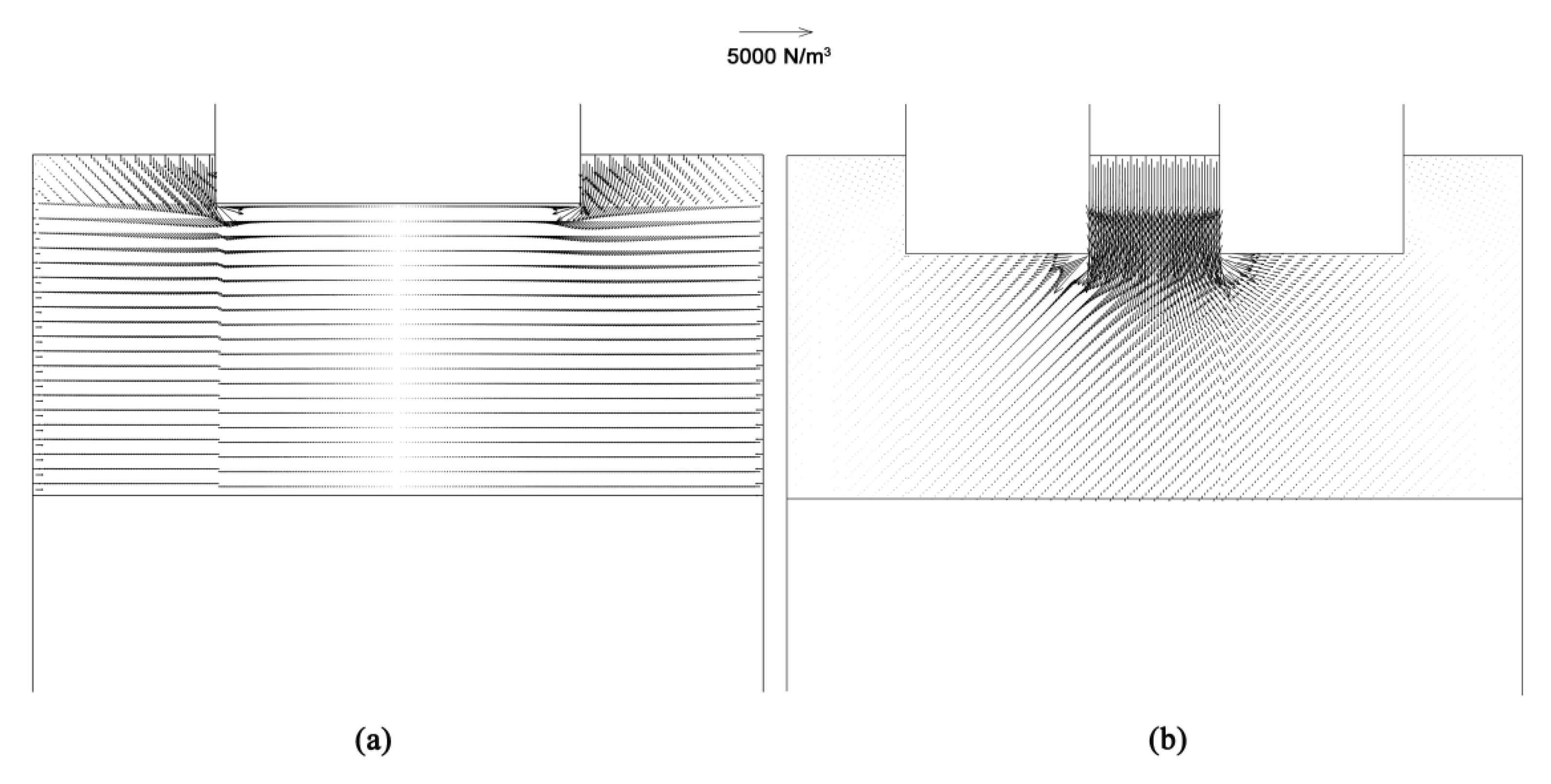
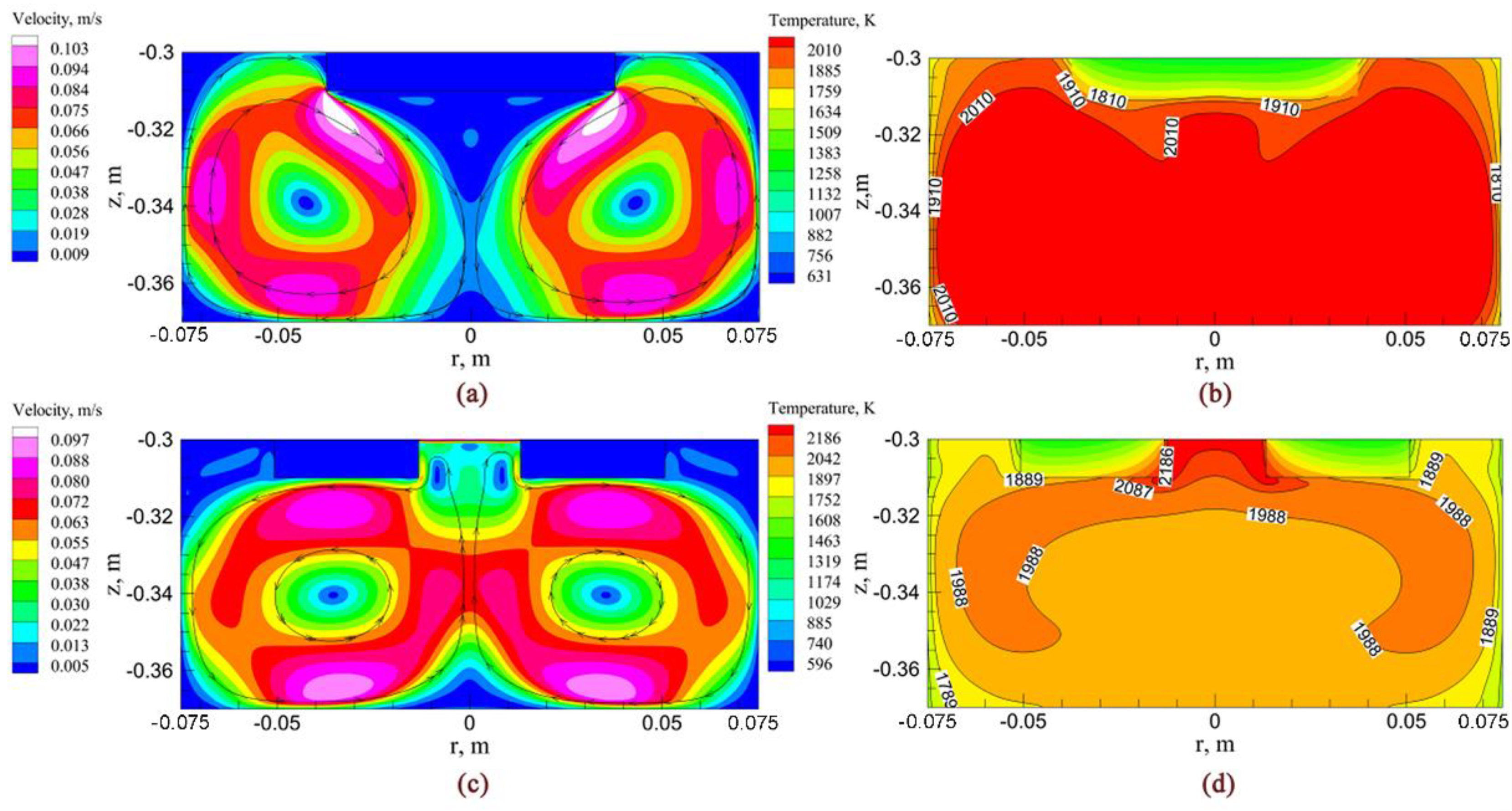
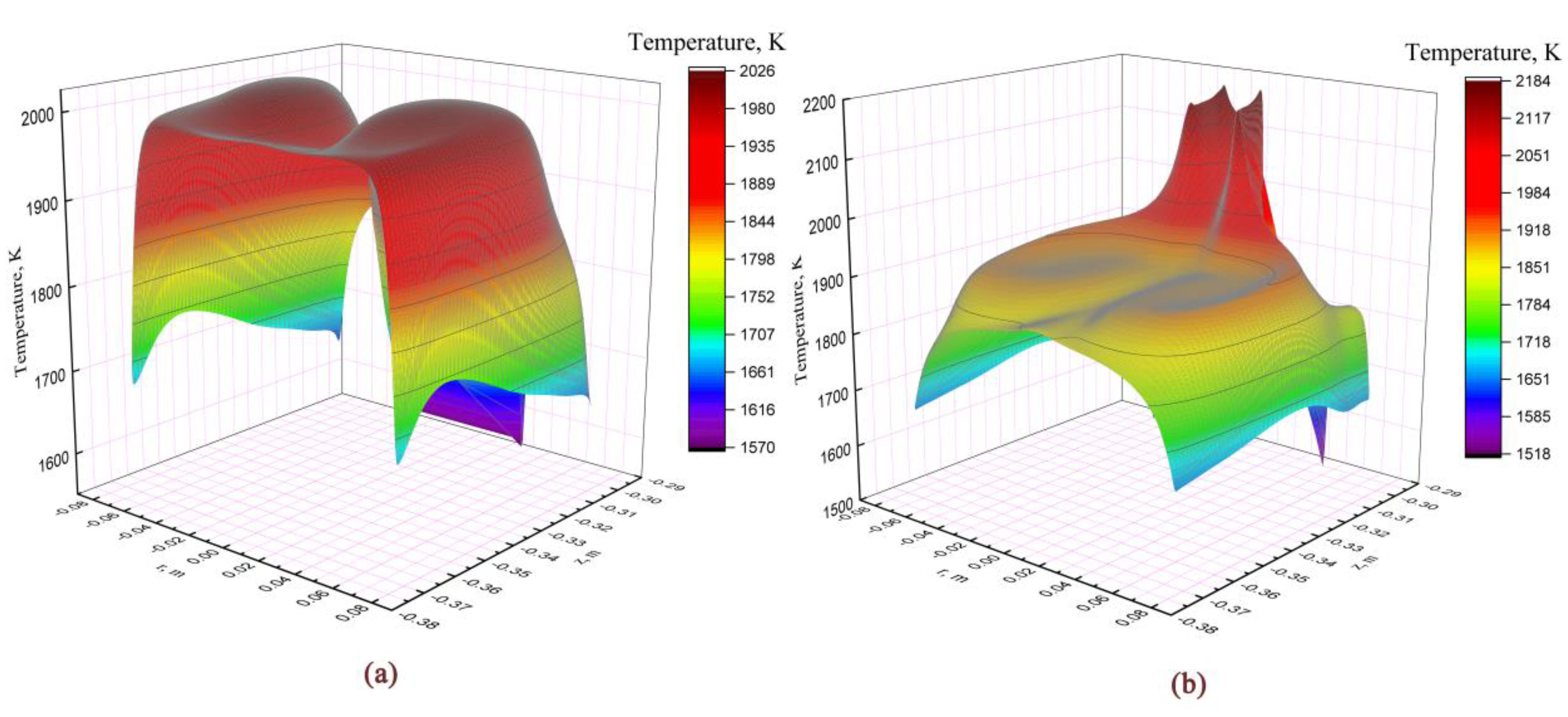
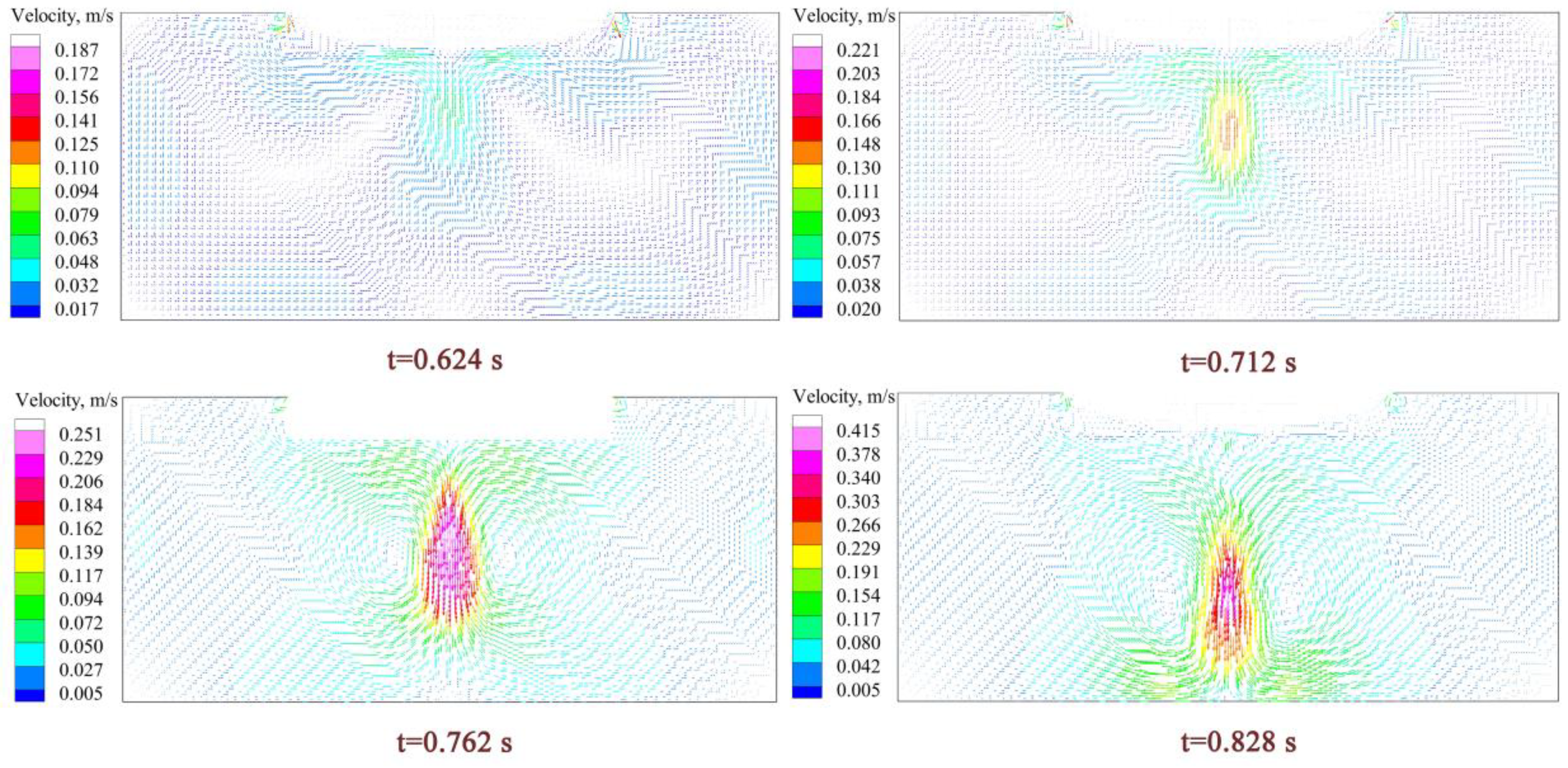
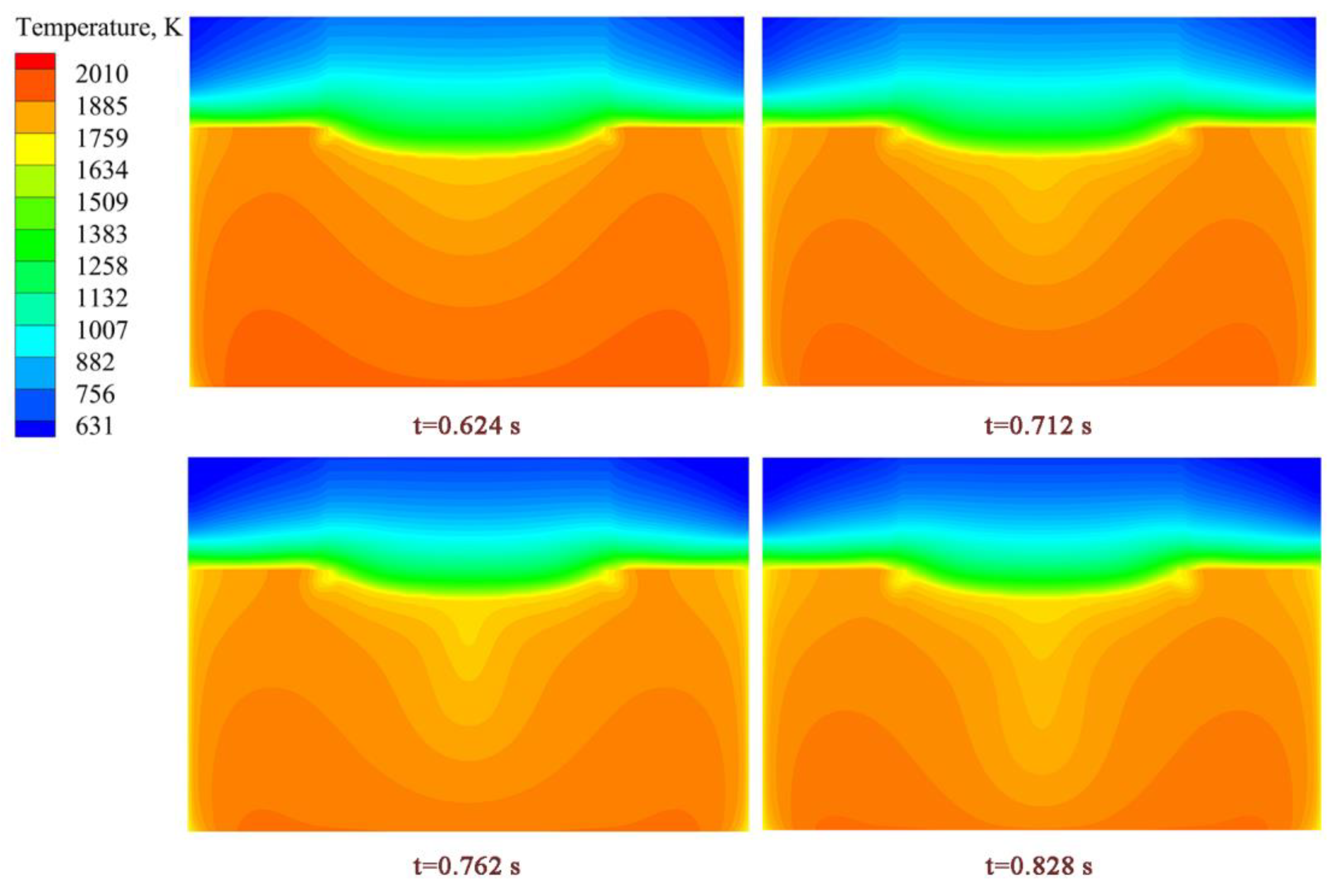
3.2. Velocity Field and Temperature Field
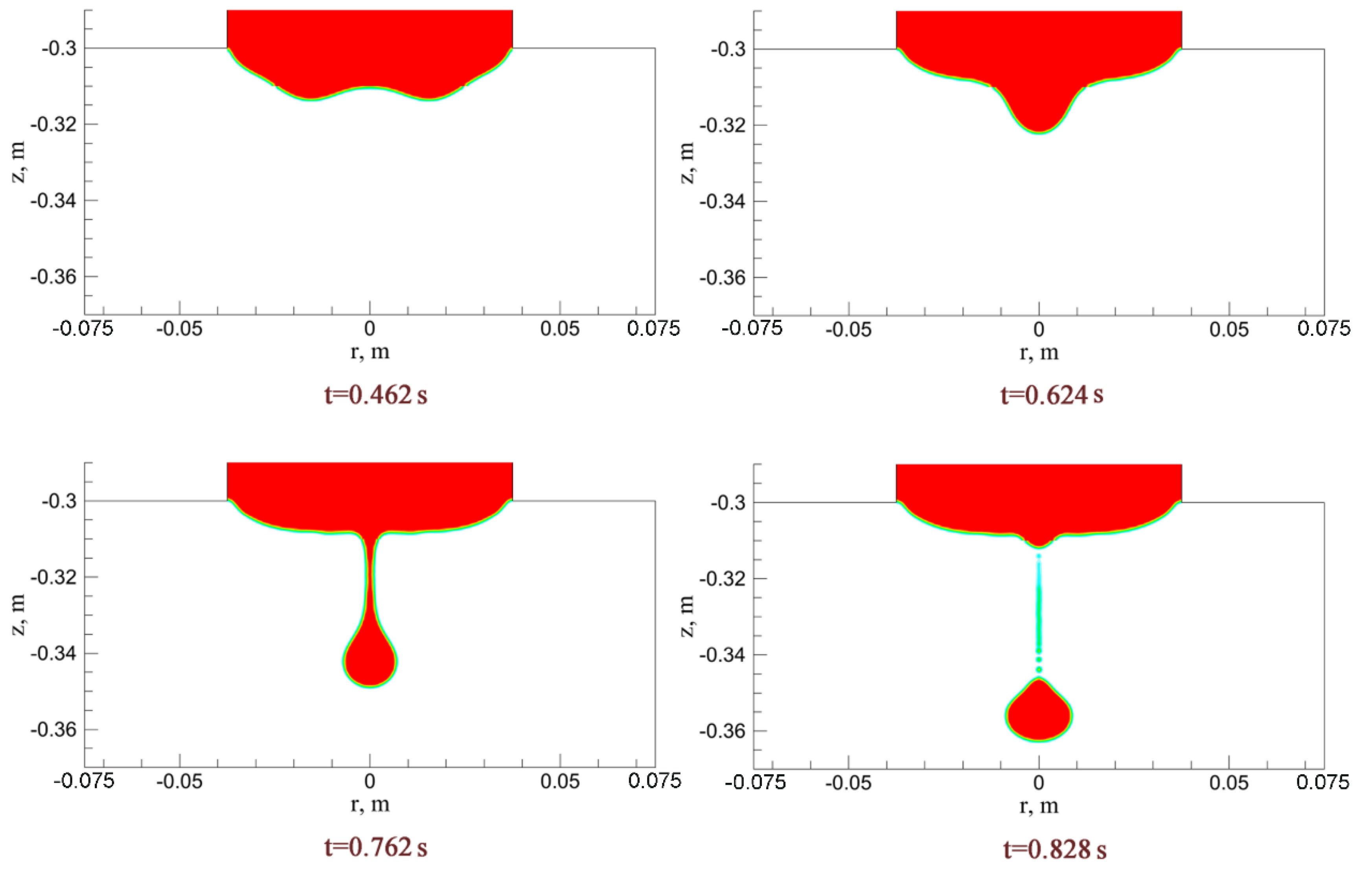
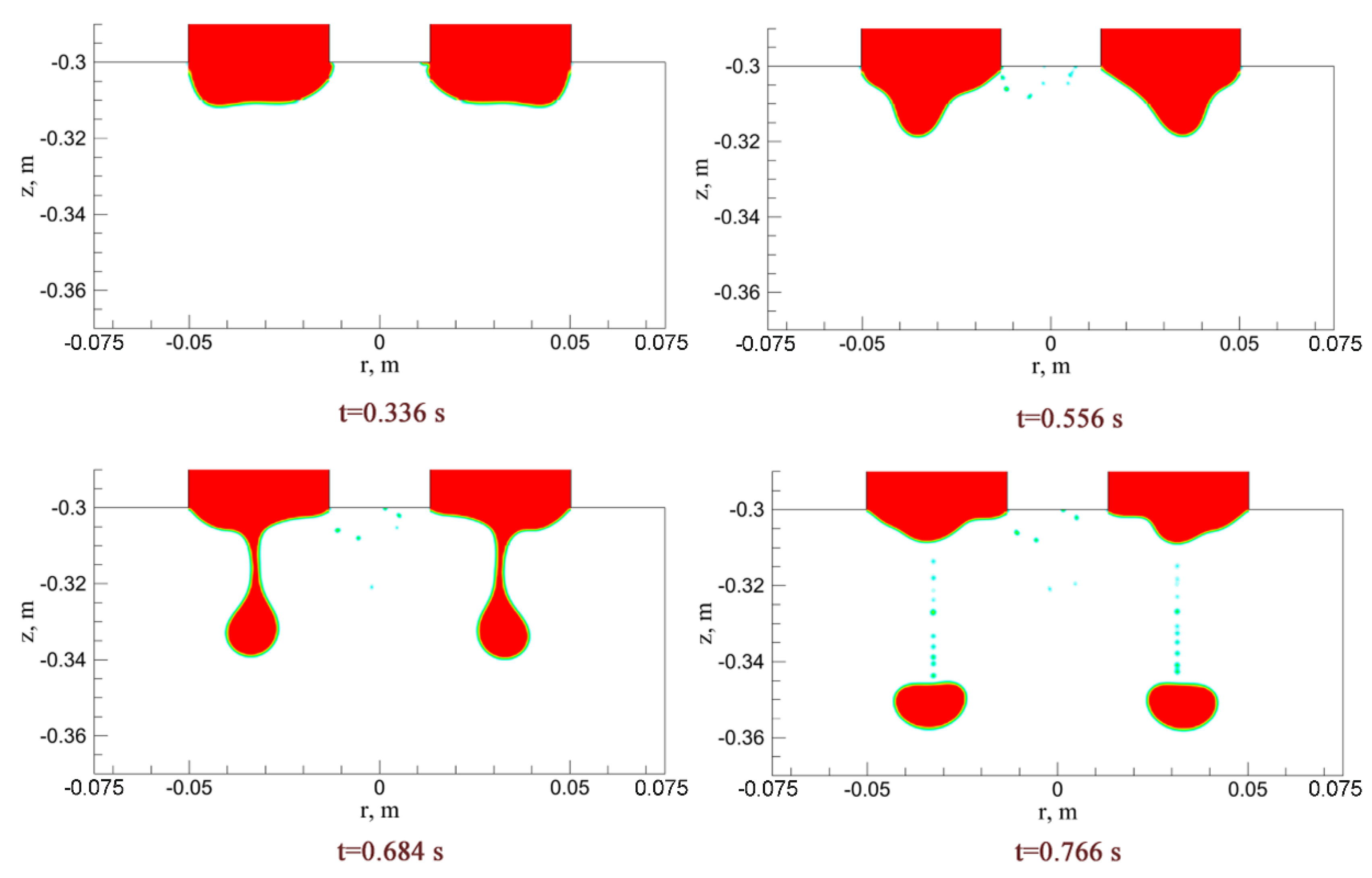
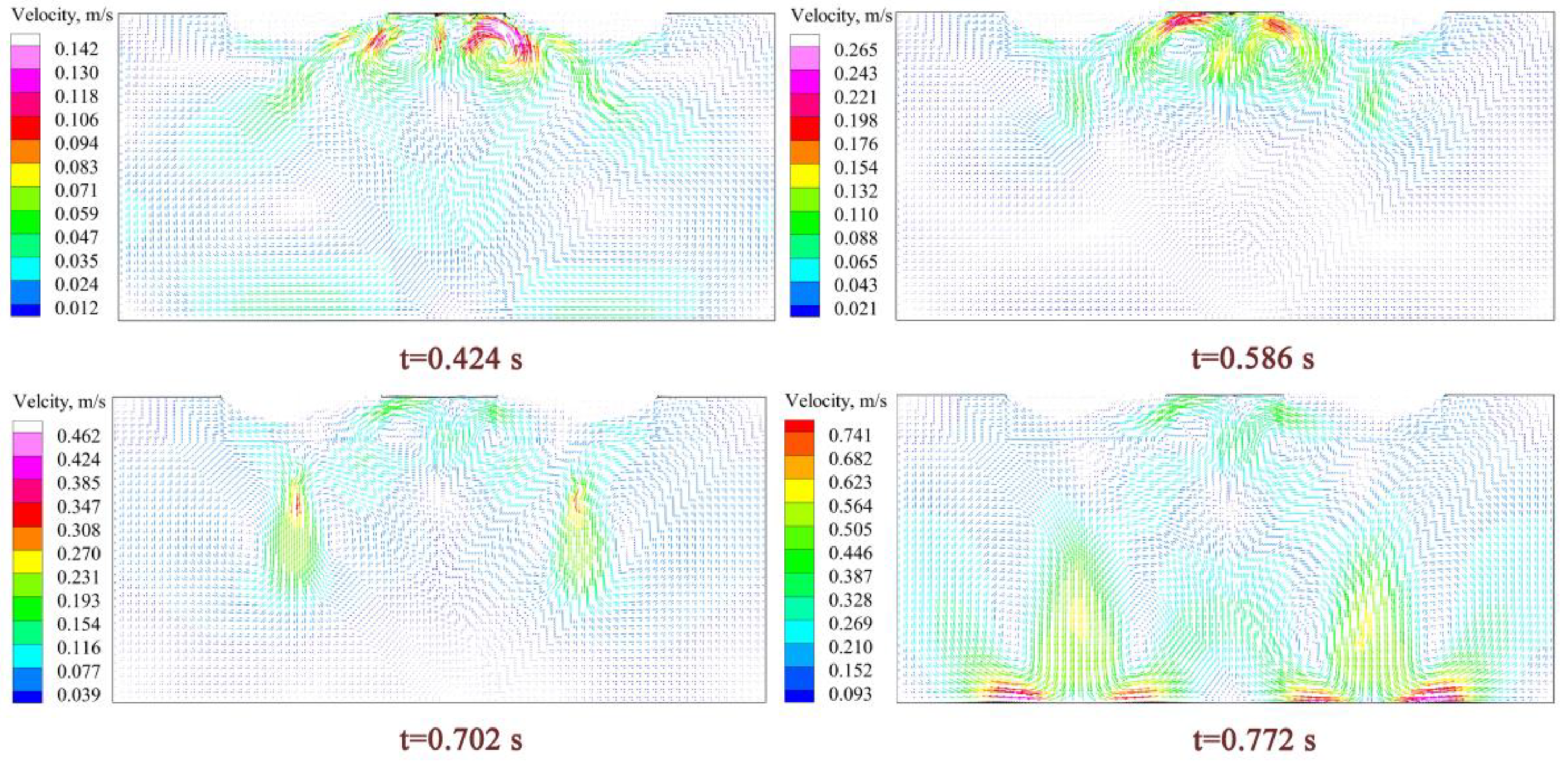
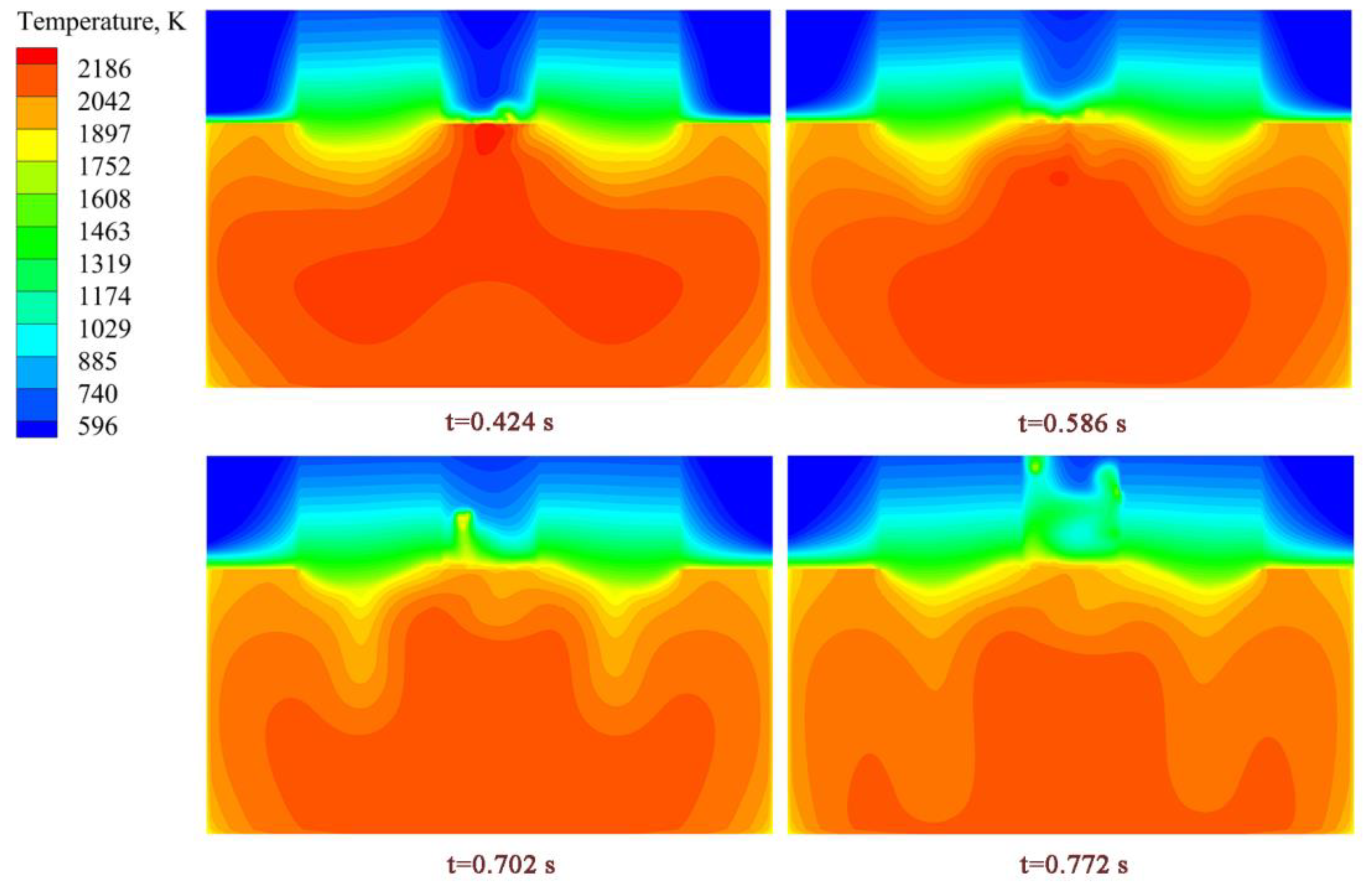
3.3. Simulation Results of Droplet Formation and Dripping Process
3.4. Remelting Rate and Molten Metal Pool
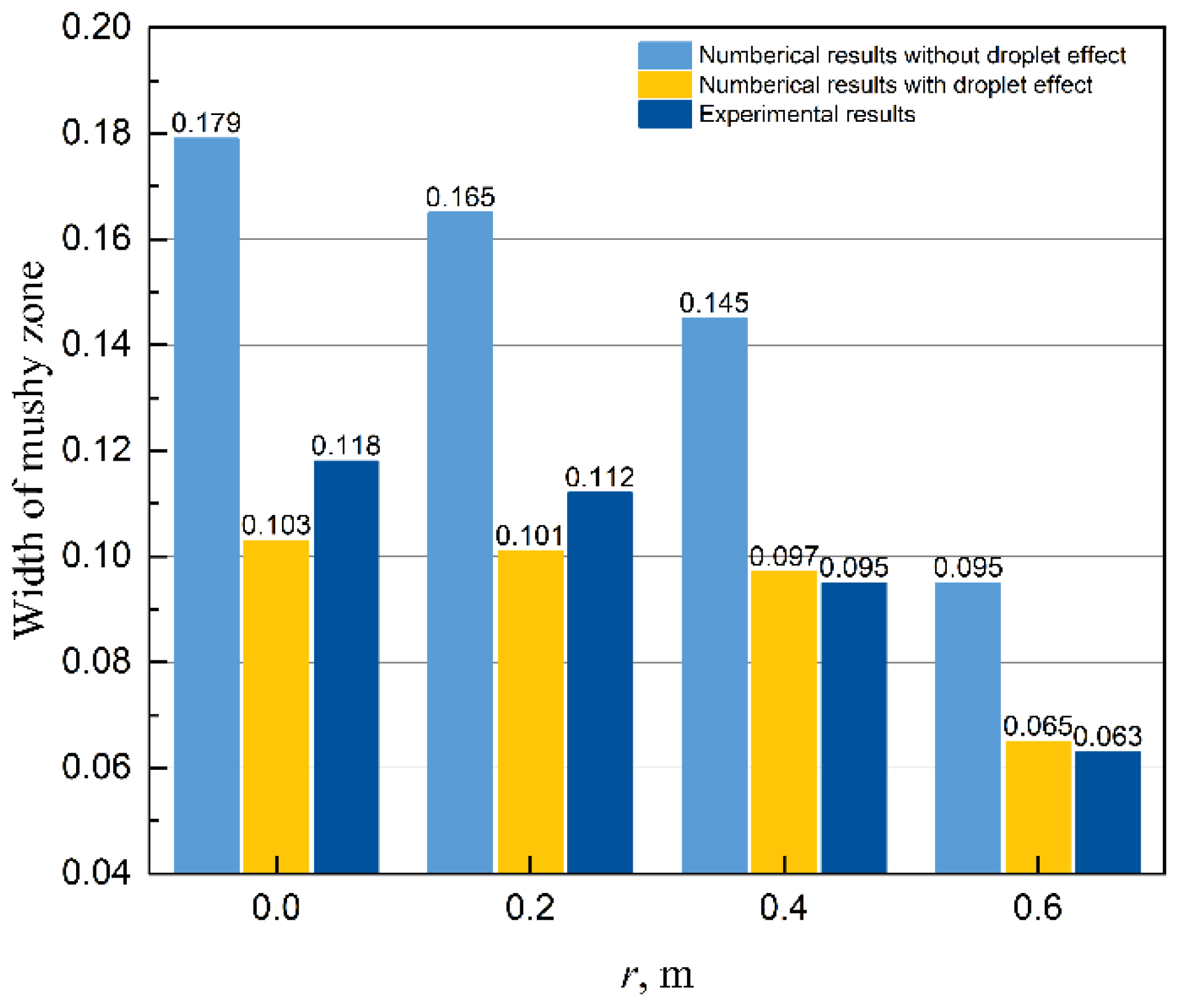
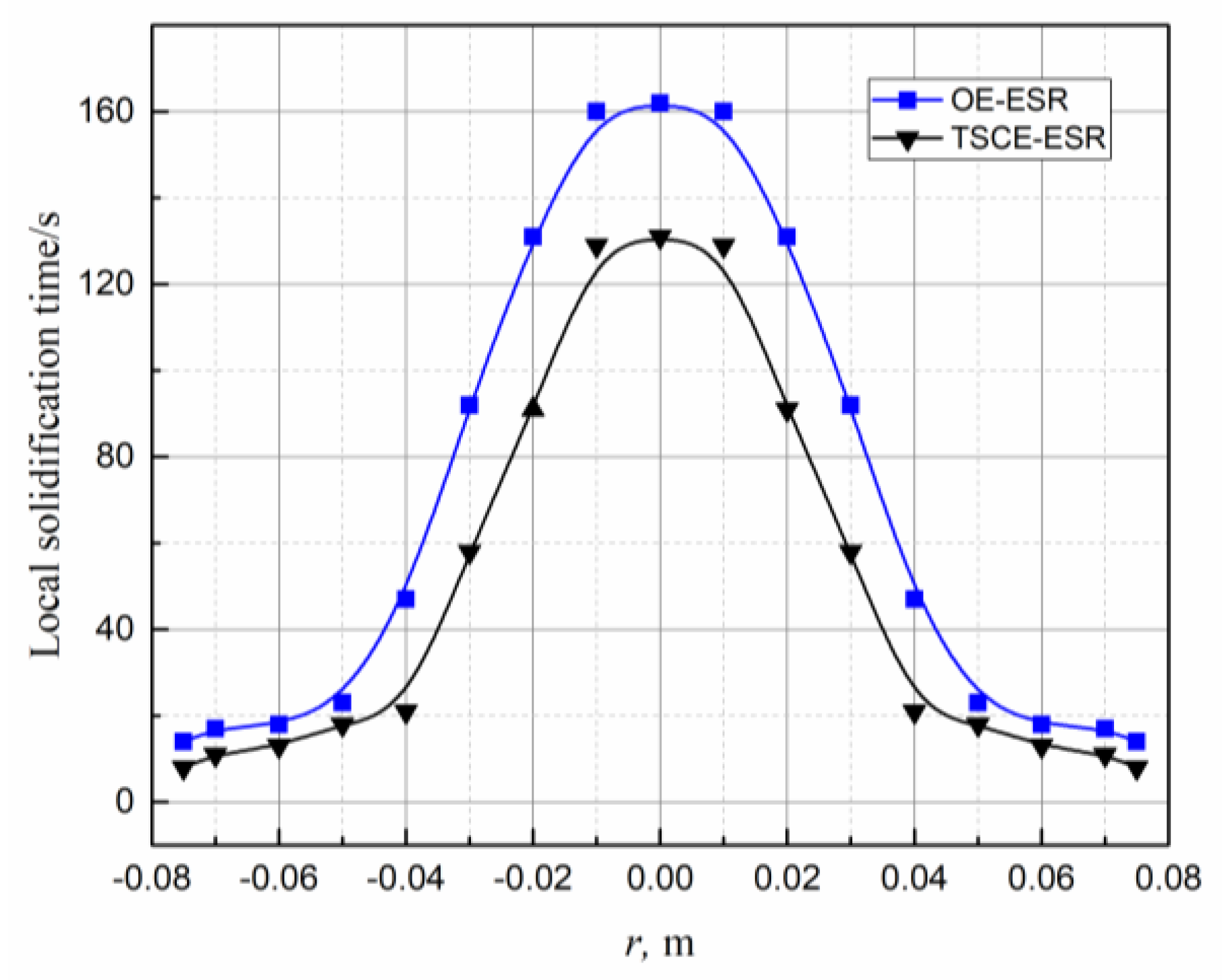
3.5. Validation of Mathematical Model
3.6. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| E | Electric Field (V·m−1) |
| H | Magnetic field intensity (A·m−1) |
| J | Current density (A·m−2) |
| B | Magnetic flux density (T) |
| t | Time (s) |
| ρ | Density of fluid (kg·m−3) |
| v | Velocity (m·s−1) |
| P | Pressure (Pa) |
| μeff | Effective viscosity of the fluid (Pa·s) |
| Floc | Electromagnetic force (N·m−3) |
| μ0 | Vaccum permeabilitbility (H·m−1) |
| Qj | Joule heat per unit volume (W·m−3) |
| σ | Electroconductibility (S·m−1) |
| ut | Turbulent velocity (m·s−1) |
| U | Velocity of droplet (m·s−1) |
| rd | Radius of droplet (m) |
| qd | Density of droplet (kg·m−3) |
| CD | Resistance coefficient |
| λ | Conductivity of liquid (S·m−1) |
| Cp | The thermal capacity of slag (J·kg−1·K−1) |
| Tdp | Temperature of droplet (K) |
| LST | Local solidification time (s) |
| Vr | Local solidification rate (mm·s−1) |
| Rc | Local cooling rate (K·s−1) |
| de | The Diameter of Droplet (m) |
| σd | Surface tension (N·m−1) |
| ρm | Density of metal (kg·m−3) |
| ρs | Density of slag (kg·m−3) |
| HS | Coefficient of position (1) |
| τ | Droplet residence time in the slag pool (s) |
| Vt | Terminal velocity (m·s−1) |
| We | Weber number (ρm·Vt2·d·r·σd−1) |
| Pd | Physical property group |
| Re | Reynolds number (ρm·Vt2·d·μ−1) |
| me | Melt rate (kg·s−1) |
| T0 | Reference temperature (K) |
| R | Radius of the electrode (m) |
| qse | Heat flux from slag to electrode (W·m−2) |
| TL | Liquidus temperature (K) |
| Tme | Melting point of electrode (K) |
| I0 | Current (A) |
| Qc | Heat of convection heat transfer (W·m−2·K−1) |
| A | Heat exchange area (m2) |
| h | Heat transfer coefficient (W·m−2·K−1) |
| CP,d | Heat capacity of the droplet (J·kg−1·K−1) |
| X | Solid-liquid two-phase zone width (mm) |
| G | Liquid temperature gradient (K·mm−1) |
| d | Secondary dendrite spacing (mm) |
References
- Anon, J. High quality billets by electroslag rapid remelting. Steel Times Int. 1997, 21, 20–25. [Google Scholar]
- Wang, F.; Li, B.K. Electromagnetic field and joule heating of an electroslag remelting process with two series-connected electrodes. J. Northeast. Univ. 2011, 32, 533–536. [Google Scholar]
- Li, B.K.; Wang, B.; Tsukihashi, F. Modeling of electromagnetic field and liquid metal pool shape in an electroslag remelting process with two series-connected electrodes. Metall. Mater. Trans. B 2014, 45, 1122–1132. [Google Scholar] [CrossRef]
- Kelkar, K.; Patankar, S.; Mitchell, A. Computational Modeling of the Electroslag Remelting Process Used for the Production of Ingots of High-Performance Alloys. In Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting, Austin, TX, USA, 22–25 September 2013; Springer: Cham, Germany. [Google Scholar]
- Weber, V.; Jardy, A.; Dussoubs, B.; Ablitzer, D. A Comprehensive model of the electroslag remelting process: Description and validation. Metall. Mater. Trans. B 2009, 40, 271–280. [Google Scholar] [CrossRef]
- Li, B.K.; Wang, F.; Tsukihashi, F. Current, magnetic field and joule heating in electroslag remelting processes. ISIJ Int. 2012, 52, 1289–1295. [Google Scholar] [CrossRef]
- Rückert, A.; Pfeifer, H. Mathematical modelling of the flow field, temperature distribution, melting and solidification in the electroslag remelting process. Magnetohydrodynamics 2009, 45, 527–533. [Google Scholar] [CrossRef]
- Li, B.K.; Li, R.; Wang, B. Formation and Drop of Metal Droplets in Slag Bath of Electroslag Remelting Processes, 2nd ed.; Materials Processing Fundamentals: Cham, Germany, 2013; pp. 121–127. [Google Scholar]
- Giesselmann, N.; Rückert, A.; Eickhoff, M. Coupling of multiple numerical models to simulate electroslag remelting process for alloy 718. ISIJ Int. 2015, 55, 1408–1415. [Google Scholar] [CrossRef][Green Version]
- Liu, S.; Zhu, H.E.; Cai, H.U. Numerical simulation of the formation and the dripping of droplet in the electroslag remelting process. Therm. Sci. 2017, 14, 78–82. [Google Scholar] [CrossRef]
- Dong, Y.W.; Jiang, Z.H.; Li, Z.B. Mathematical model for electroslag remelting process. J. Iron Steel Res. Int. 2007, 14, 7–12. [Google Scholar] [CrossRef]
- Dilawari, A.; Szekely, J. A mathematical model of slag and metal flow in the ESR process. Metall. Mater. Trans. B 1977, 8, 227–236. [Google Scholar] [CrossRef]
- Yanke, J.; Fezi, K.; Trice, R. Simulation of slag-skin formation in electroslag remelting using a volume-of-fluid method. Numer. Heat Transf. Part A 2015, 67, 268–292. [Google Scholar] [CrossRef]
- Patel, A.D. Effect of Electrode Pipe and Mold Current on Electromagnetic Fields in ESR. In Proceedings of the International Symposium on Liquid Metal Processing and Casting LMPC, Nancy, France, 2–5 September 2007. [Google Scholar]
- Li, B.K.; Wang, Q. Theory and Technology of Electroslag Remelting Based on Numerical Simulation; Science Press: Beijing, China, 2016; pp. 30–32. [Google Scholar]
- Bahrami, A.; Valentine, D.T.; Helenbrook, B.T. Study of mass transport in autogenous GTA welding of dissimilar metals. Int. J. Heat Mass Transf. 2015, 85, 41–53. [Google Scholar] [CrossRef]
- Yanke, J.; Krane, M. A Parametric Study of Slag Skin Formation in Electroslag Remelting. In Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting, Austin, TX, USA, 22–25 September 2013; Springer: Cham, Germany. [Google Scholar]
- Hernandez-Morales, B.; Mitchell, A. Review of mathematical models of fluid flow, heat transfer, and mass transfer in electroslag remelting process. Ironmak. Steelmak. 1999, 26, 423–438. [Google Scholar] [CrossRef]
- Kharicha, A.; Schützenhöfer, W. Influence of the slag/pool interface on the solidification in an electro-slag remelting process. Mat. Sci. Forum 2010, 12, 229–236. [Google Scholar] [CrossRef]
- Kharicha, A.; Schützenhöfer, W. On the importance of electric currents flowing directly into the mould during an ESR process. Steel Res. Int. 2008, 79, 632–636. [Google Scholar] [CrossRef]
- Nastac, L.; Sundarraj, S. The stochastic modeling of solidification structures in alloy 718 remelt ingots. JOM 1998, 50, 30–35. [Google Scholar] [CrossRef]
- Sheng, Y.Y. Transport phenomena in electric smelting of nickel matte: Part II. Mathematical modeling. Metall. Trans. B 1998, 29, 85–94. [Google Scholar] [CrossRef]
- Campbell, J. Fluid flow and droplet formation in the electroslag remelting process. JOM 1970, 22, 23–35. [Google Scholar] [CrossRef]
- Jiang, Z.H. Electroslag Metallurgy, 1st ed.; Science Press: Beijing, China, 2015; p. 387. [Google Scholar]
- Dilawari, A.H.; Szekely, J. Heat transfer and fluid flow phenomena in electroslag refining. Metall. Mater. Trans. B 1978, 9, 77–87. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y. A comprehensive 3D mathematical model of the electroslag remelting process. Metall. Mater. Trans. B 2015, 46, 1837–1849. [Google Scholar] [CrossRef]
- Hu, S.; Kinter, R. The fall of single liquid drops through water. AIChE J. 1955, 1, 42–48. [Google Scholar] [CrossRef]
- Choudhary, M.; Szekely, J. Modelling of fluid flow and heat transfer in industrial-scale ESR system. Ironmak. Steelmak. 1981, 8, 225–232. [Google Scholar]
- Li, Z.B. Electroslag Metallurgy Theory and Practice, 1st ed.; Metallurgical Industry Press: Beijing, China, 2011; p. 32. [Google Scholar]
- Tong, W.J.; Li, W.M.; Zang, X.M. Droplet formation and dripping behavior during the electroslag remelting process with two series-connected electrodes. Metals 2020, 10, 386. [Google Scholar] [CrossRef]
- Li, W.M.; Jiang, Z.H. Carbide segregation control in electro-slag remelting withdrawal process of large cross-section high-speed steels. J. Cent. South Univ. 2017, 17, 15–21. [Google Scholar]
- Flemings, M. Solidification processing. Metall. Mater. Trans. B 1974, 5, 2121–2134. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Physical Properties of Slag | |
| Density, kg·m−3 | 2850 |
| Specific capacity, J·kg−1·K−1 | 1404 |
| Thermal conductivity, W·m−1·K−1 | 10.45 |
| Viscosity, kg·m−1·s−1 | 0.01 |
| Emissivity | 0.6 |
| Expansion coefficient, K−1 | 0.0001 |
| Physical Properties of Steel | |
| Density, kg·m−3 | 7200 |
| Specific capacity, J·kg−1·K−1 | 502 |
| Thermal conductivity, W·m−1·K−1 | 31.9 |
| Steel solidus temperature, K | 1723 |
| Steel liquidus temperature, K | 1693 |
| Latent heat of solidification, J·kg−1 | 247,000 |
| Process Parameters | |
| Electrode immersion depth, m | 0.02 |
| Mold diameter, m | 0.14 |
| Electrode length, m | 0.31 |
| Slag height, m | 0.07 |
| Current, A | 4000 |
| Process | Average Temperature in Slag Pool (K) | Radial Temperature Gradient at Slag/Electrode Interface (K) |
|---|---|---|
| OE-ESR | 1996.7 | 338.17 |
| TSCE-ESR | 1838.4 | 201.78 |
| OE-ESR | TSCE-ESR | ||||||
|---|---|---|---|---|---|---|---|
| No. | Calculated Diameter | Average | Theoretical Diameter | No. | Calculated Diameter | Average | Theoretical Diameter |
| 1 | 14.92 | 15.06 | 15.1 | 1 | 12.99 | 13.11 | 13.47 |
| 2 | 15.17 | 2 | 13.27 | ||||
| 3 | 15.02 | 3 | 13.16 | ||||
| 4 | 14.88 | 4 | 12.94 | ||||
| 5 | 15.31 | 5 | 13.19 | ||||
| Items | OE-ESR | TSCE-ESR |
|---|---|---|
| Average velocity of slag pool at steady state (m/s) | 0.052 | 0.051 |
| Maximum average velocity of slag pool at transient state (m/s) | 0.062 | 0.093 |
| The rate of growth (%) | 19.2 | 82.3 |
| Items | Average Droplet Diameter (mm) | Remelting Rate (kg·s−1) |
|---|---|---|
| OE-ESR | 15.06 | 0.0151 |
| TSCE-ESR | 13.11 | 0.0321 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, W.; Li, W.; Zang, X.; Li, H.; Jiang, Z.; Li, D. A Comprehensive Mathematical Model of Electroslag Remelting with Two Series-Connected Electrodes Based on Sequential Coupling Simulation Method. Metals 2020, 10, 658. https://doi.org/10.3390/met10050658
Tong W, Li W, Zang X, Li H, Jiang Z, Li D. A Comprehensive Mathematical Model of Electroslag Remelting with Two Series-Connected Electrodes Based on Sequential Coupling Simulation Method. Metals. 2020; 10(5):658. https://doi.org/10.3390/met10050658
Chicago/Turabian StyleTong, Wenjie, Wanming Li, Ximin Zang, Huabing Li, Zhouhua Jiang, and Dejun Li. 2020. "A Comprehensive Mathematical Model of Electroslag Remelting with Two Series-Connected Electrodes Based on Sequential Coupling Simulation Method" Metals 10, no. 5: 658. https://doi.org/10.3390/met10050658
APA StyleTong, W., Li, W., Zang, X., Li, H., Jiang, Z., & Li, D. (2020). A Comprehensive Mathematical Model of Electroslag Remelting with Two Series-Connected Electrodes Based on Sequential Coupling Simulation Method. Metals, 10(5), 658. https://doi.org/10.3390/met10050658




