1. Introduction
Fatigue is an important degradation mechanism for pressure vessels and piping systems, especially in nuclear power plants (NPPs). Consequently, a great deal of scientific work has been undertaken and numerous tests have been performed to understand the principles and find rules to deal with this issue [
1]. Fatigue evaluation plays a significant role in assuring the integrity of aged plant components. The fact that the fatigue life may be reduced in (nuclear) aggressive environments was first discovered in Japan in the 1980’s and in the last four decades, this situation has been widely studied in NPPs [
2].
However, experimental results have indicated that additional parameters should be taken into account to describe the influence of the coolant on the fatigue performance of pressure vessels and piping systems of light water reactors (LWRs) [
1]. Different laboratory works have identified the influence of key parameters on fatigue cracking and have established the effects of these key parameters on the fatigue life of selected steels used in nuclear plants [
3,
4]. These key parameters are the strain rate, the fluid/metal temperature, and the concentration of dissolved oxygen (DO) in the water. Other parameters, such as water flow or thermal treatment, also have some influence, while the sulphur content also has an influence in carbon and low alloy steels.
Nevertheless, it is also known that there are other parameters affecting the fatigue life, such as the surface roughness [
5,
6], mean stress [
5,
6], and existence of hold periods in the strain waveform [
7,
8], which are not directly considered in the fatigue design of NPP components. The effect of these parameters is implicitly considered in safety factors or design curves, but their precise effect is not well-known and great benefits (e.g., better designs and higher safety) could be obtained in the case of developing better knowledge on them, which has been the main aim of the INCEFA-PLUS project [
4].
In any case, environmentally assisted fatigue must be taken into account in two situations: license renewal applications for nuclear power plants [
5] and the design of new reactors [
6].
Two assessment philosophies have traditionally been proposed for incorporating the effects of LWR coolant environments into fatigue evaluations.
The development of environmentally adjusted design fatigue curves is the first of these philosophies. The environmental effect is directly considered through the application of curves, and the fatigue cumulative usage factor is directly obtained through the application of tools, such as the Miner´s rule:
where
ni is the applied number of cycles of a given load pair,
Ni is the allowable number of cycles for this load pair (derived from design fatigue curves obtained for the particular environment and temperature being analysed), and m is the number of load pairs being considered.
The second philosophy is the use of a fatigue life correction factor,
Fen, to adjust fatigue usage values (calculated with a design air curve) for environmental effects. The
Fen factor, which can be understood as an environmental correction factor in terms of cycles, has the following form [
9]:
where
N25 is the number of cycles required for the peak tensile stress to drop 25% from its initial value,
N25A is the fatigue life (in cycles) in air at room temperature,
N25W is the fatigue life (in cycles) in water at the temperature of interest,
P is a constant for a given temperature and dissolved oxygen content, and
is the strain rate during the rising load phase (%·s
−1).
The
Fen factor is applied in the fatigue cumulative usage factor (CUF) derived from the Miner´s rule (or any other similar approach) as follows:
where
ni is the applied number of cycles of a given load pair,
Ni is the allowable number of cycles for this load pair (obtained from curves derived in air conditions),
Fen,i is the corresponding environmental factor, and m is the number of load pairs being considered. The
Fen factor depends, for a particular type of material, on the temperature, dissolved oxygen, sulphur content, and strain rate.
Within this framework, national and international efforts have been dedicated to the development of environmental fatigue assessment (EFA) procedures, and have provided a number of documents based on different assumptions and assessment philosophies. The first aim of this paper is to summarize the current situation regarding the different EFA procedures and how they incorporate environmental effects into the analyses.
On the other hand, fatigue monitoring systems (FMS) constitute an alternative for the fatigue assessment of components and structures. These systems allow this type of assessment to be performed (regardless of the EFA procedure being used) in a real-time, automated way and, for this purpose, require the records of all the parameters affecting the stress state of the component being assessed. This kind of approach is an alternative to the traditional consideration of design loads (i.e., design transients), which is a simpler and more conservative way to derive the stress state in nuclear structural components. The second aim of this work is to visualize the differences derived from the use of real loads (provided by FMS) instead of design loads.
Finally, with the purpose of exemplifying the previous considerations in a real case, the NUREG/CR-6909 [
3] methodology is applied in a case study of a real nuclear structural component, and the corresponding fatigue cumulative usage factor when using design loads and real loads is derived.
Section 2 presents a summary of the main EFA procedures,
Section 3 describes the differences between design loads and monitorized (real) loads, and
Section 4 includes the case study. Finally,
Section 5 presents the corresponding conclusions.
2. Incorporating Environmental Effects into Fatigue Assessments
The development of fatigue models to be applied in NPPs encompasses not only the corresponding fatigue curves, but also the incorporation of environmental effects and mean stress effects into fatigue assessments. There are a number of EFA procedures, many of which are related to national regulations, whose implicit physical assumptions are not always fully equivalent. This section provides an overview of the different EFA procedures used worldwide, their main corresponding characteristics, and how they deal with environmental fatigue.
2.5. RCC-M Approach
Two proposals to modify the RCC-M code (or Requests for Modification (RM)) were submitted in late 2014 and were incorporated into the 2016 version of the RCC-M code [
11], as Rules in Probationary Phase. This so-called RCC-M approach encompassed not only a proposal for a fatigue curve, but also a dedicated method to incorporate environmental effects.
The mean air curve specified in this document is identical to the one in NUREG/CR-6909. This conclusion was reached [
23] based on a statistical comparison of the air data available and the NUREG/CR-6909.
The coefficients on life and strain amplitude were determined as the combination of international research and the results from French experimental campaigns [
24]. Concerning the factor on life, it is calculated as the statistical combination of aggravating parameters linked to the component effect, the loading effect, and data scatter. These three categories recall the ones in NUREG/CR-6909 (surface roughness, loading history, size effect, and data scatter), but each one is intended to cover a much wider range of effects than NUREG/CR-6909. For instance, the component effect covers the surface roughness, the size effect, and the effect of a strain gradient through the thickness. The objective of covering a wider range of effects is to acknowledge interactions between effects [
24], as well as to leave room for other effects that are unaccounted for. The final coefficients are given as ranges, which are combined through statistical methods, as in NUREG/CR-6909. This leads to a final coefficient of 10.
Concerning the factor on strain amplitude, as in NUREG/CR -6909, it is recognised that the combination of the aggravating effect is not applicable and that the greatest aggravating effect is applicable. In this case, the largest value is the one associated with data scatter and calculated through the application of four statistical evaluations [
25]. It is finally fixed as 1.4.
Relative to the mean stress, the method is identical to NUREG/CR-6909 and consists of the Goodman mean stress correction.
Finally, regarding EAF, the proposal is a combination of the NUREG/CR-6909 approach and the introduction of the
Fen-integrated criterion. The
Fen-integrated quantity translates the part of environmental effects, which is considered to already be covered, or “integrated”, in the design fatigue curve. The general idea is to perform EAF assessment and evaluate the
Fen factor using the NUREG/CR-6909 approach, and then compare the
Fen value with the
Fen-integrated criterion. If the
Fen value is greater than the
Fen-integrated value, then the usage factor needs to include EAF; if the
Fen value is smaller than the
Fen-integrated value, the environmental effects are already covered by the design fatigue curve and no additional effort is required. This
Fen-integrated criterion was established thanks to French experimental campaigns [
24] and a statistical calculation similar to NUREG/CR-6909. A summary of the methodology can be found in
Table A1.
It is worth noting that this approach is exclusively applicable to stainless steel grades that conform to the RCC-M specifications.
4. The Case Study
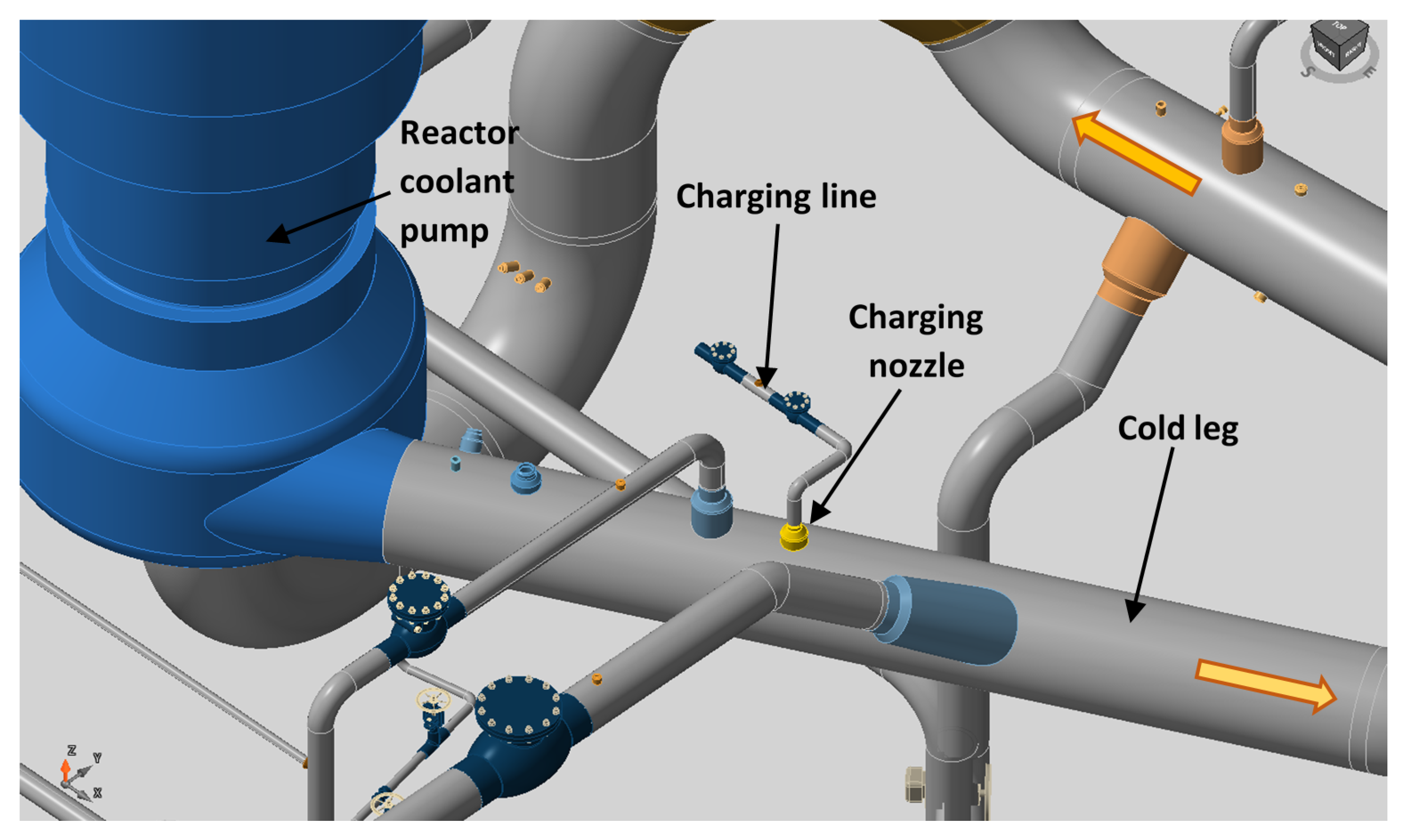
This section describes the environmental fatigue assessment (EFA) in a real nuclear structural component. More precisely, the analysis was performed in the inner radius of the charging nozzle of a PWR NPP.
Figure 3 presents a scheme of the system, with the charging line, the charging nozzle, and the cold leg of the reactor coolant system (RCS), which are some of the components involved.
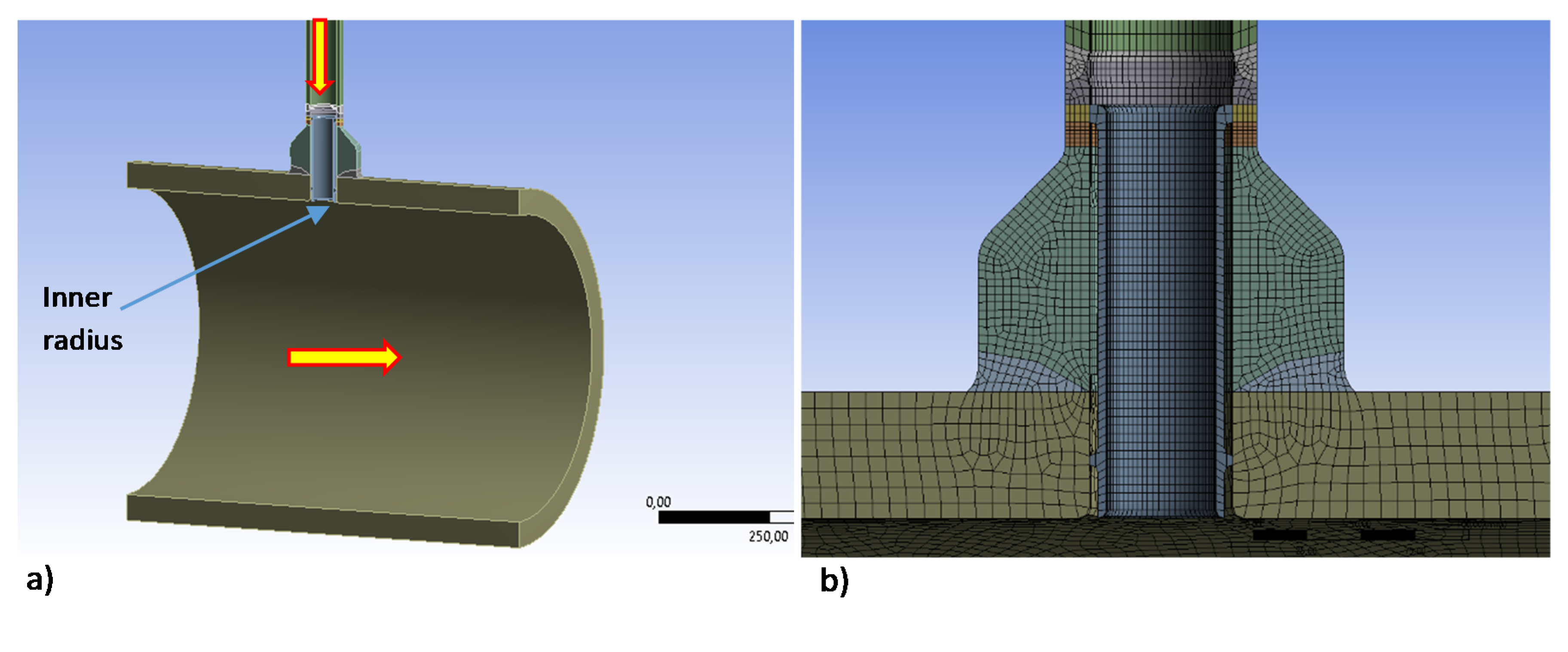
Figure 4 shows a scheme of the charging nozzle and the inner radius location at which the EFA was performed, together with the FEA model used in the stress calculation. The nozzle connects the charging line of the chemical and volume control system (CVCS) with the cold leg of the reactor coolant system (RCS) of the PWR plant. The cold leg had an inner diameter of 698.5 mm (27.5 inch) and an outer diameter of 816.34 mm (22.86 inch), whereas the inner and outer diameters of the nozzle were 66.65 mm (2.624 inch) and 88.9 mm (3.5 inch), respectively. The cold leg was made of stainless steel SA-351 Gr. CF8A and the charging nozzle was made of stainless steel SA-376 TP316, following ASME specifications.
The inner radius is typically the critical location of the charging nozzle when performing EFA. This statement has been widely validated worldwide through numerous assessments in the nuclear fleet, and has been confirmed by the stress analysis performed in this particular case, where higher stress variations appeared in such a location.
The stress report of the corresponding NPP indicates a design CUF in this inner radius location of 0.9 in 40 years.
The resulting T-joint was symmetrical in the longitudinal direction, so the FE analysis was completed by modeling one-half of the geometry. The same mesh was used to solve both thermal and mechanical problems.
Fatigue damage was analysed by using fatONE (Fatigue Management System) [
38], which allows the stresses caused by design transients and real transients at critical locations to be evaluated.
Each component analysed requires the corresponding boundary conditions to be determined at every moment. These conditions are derived from the measurements provided by the instrumentation that has previously been installed in the NPP.
Temperature, pressure, and flow data defined at the design stage of the NPP are used to derive the design stresses at each particular location, whereas real-time stresses are derived from the data provided by the plant instrumentation. In both cases, FEA and the use of transference constants and Green functions are required. Finally, once the stresses are known (design stresses or real stresses), it is possible to complete the fatigue assessment.
When dealing with EFA, fatONE is able to implement different expressions of
Fen. In this case, the NUREG/CR-6909 Rev.0 [
14] formulation provided for stainless steels was used, together with the NUREG/CR-6909 new design fatigue curve for stainless steels in air (Table 9 in [
14]):
with
T is the working temperature,
dε/
dt is the strain rate, and
O is the dissolved oxygen (DO) (0.04 ppm in the cases analysed). Quantification of the differences obtained when using other
Fen expressions provided by alternative procedures may be consulted in [
39]. Such differences are generally very moderate, although significant variations (up to 80%) have been detected for some particular cases. In the case of austenitic stainless steel 304L, a difference of 30% was observed in the worst case [
39].
This case study evaluates two sequences of transients and, additionally, these transients were analysed as design transients and real transients. Therefore, four EFAs have been completed.
The first sequence, which is more simple, consists of a cool-down, followed by a heat-up, process. The second sequence corresponds to a whole cycle of the plant for two refueling operations (18 months).
Table 1 presents the list of transients and the number of design occurrences for this particular NPP.
Table 2 shows the transients of the second sequence (the first sequence is straightforward, with transients A and B).
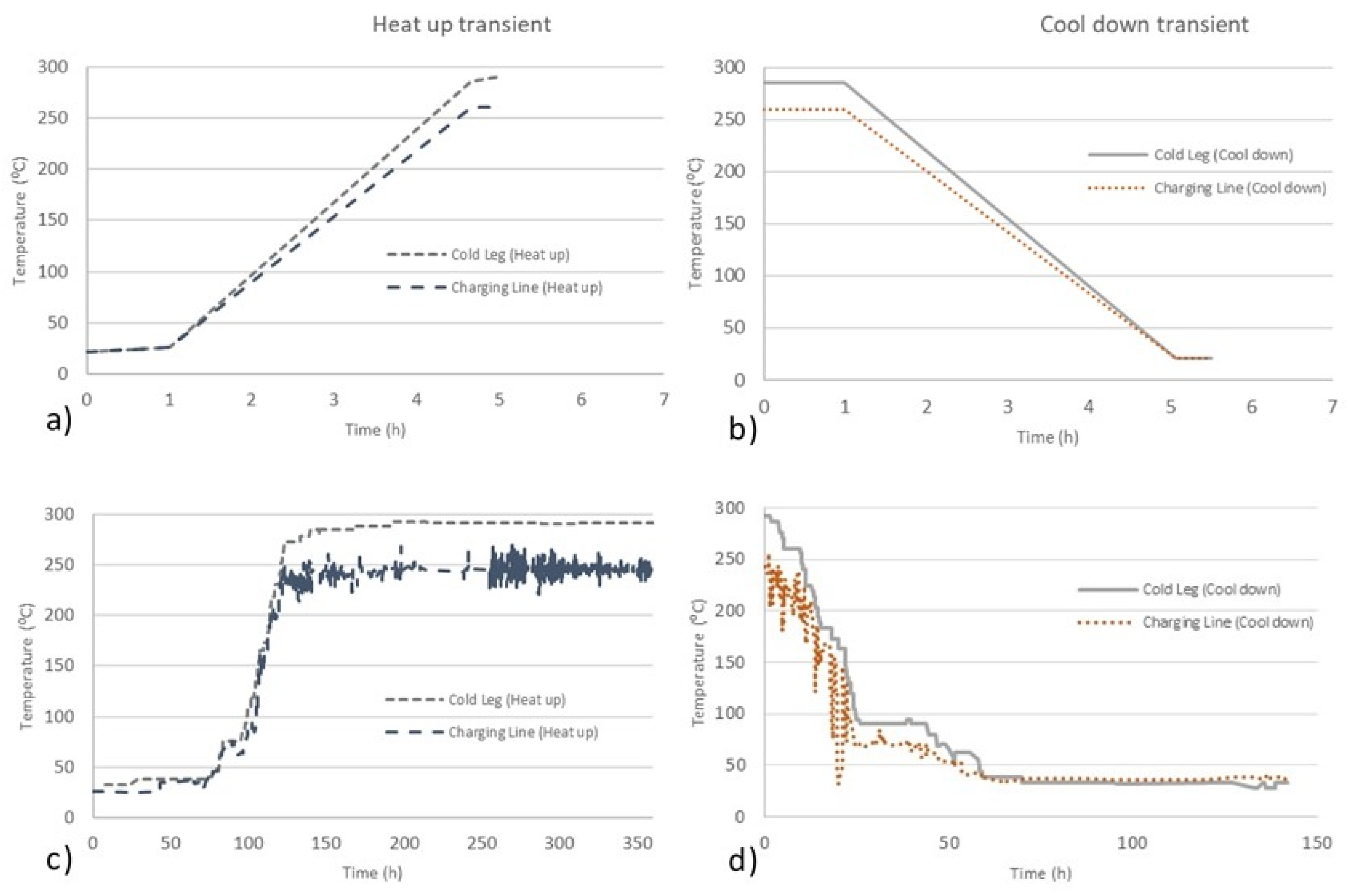
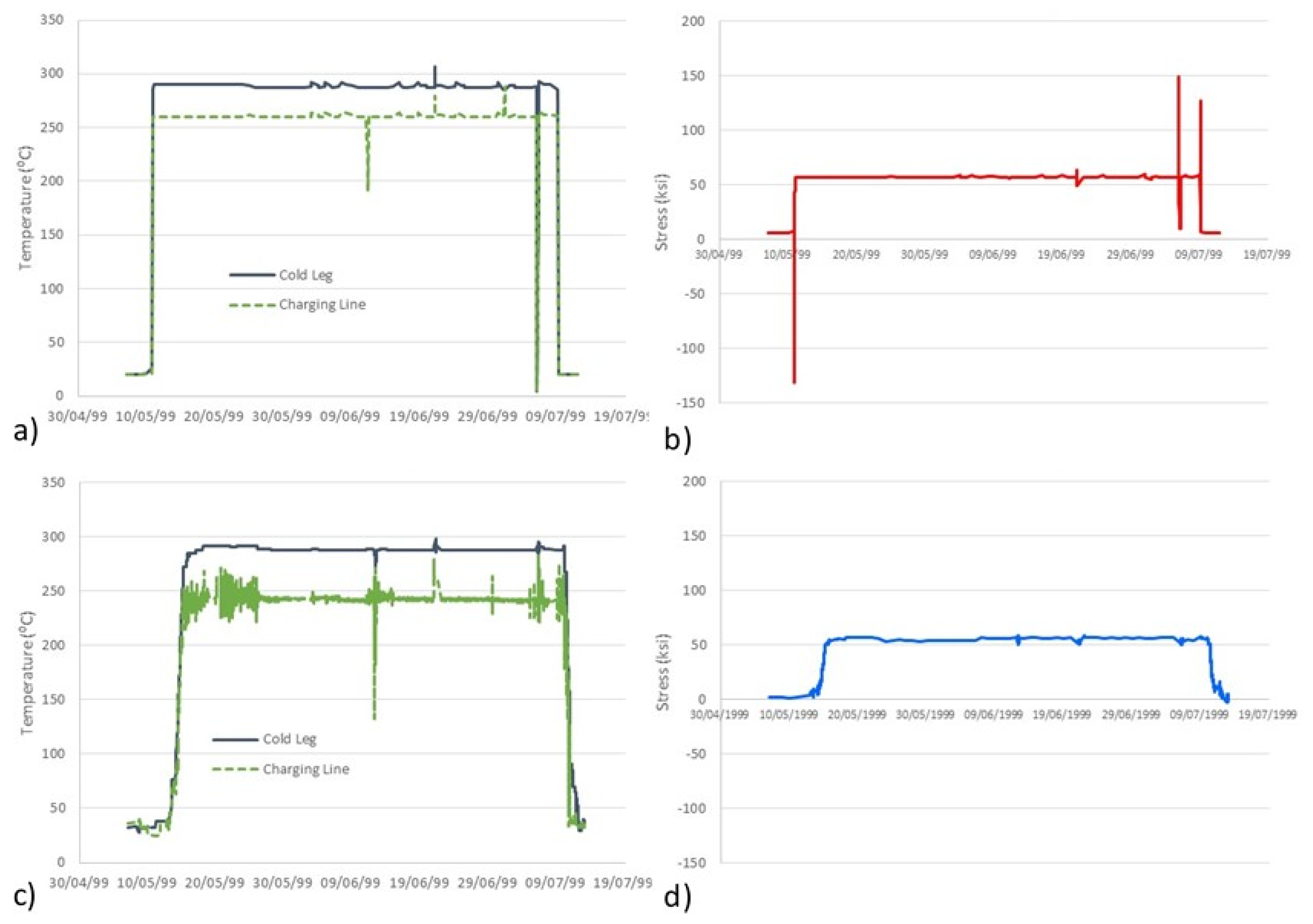
Figure 5 shows a comparison of the design and real (in-plant) transients (heat-up and cool-down). It can be observed that real transients have a longer duration than design transients: design transients usually take 5 h, while real heat-ups may take up to 3 days and cool-downs may take up to 2 days for the NPP concerned here.
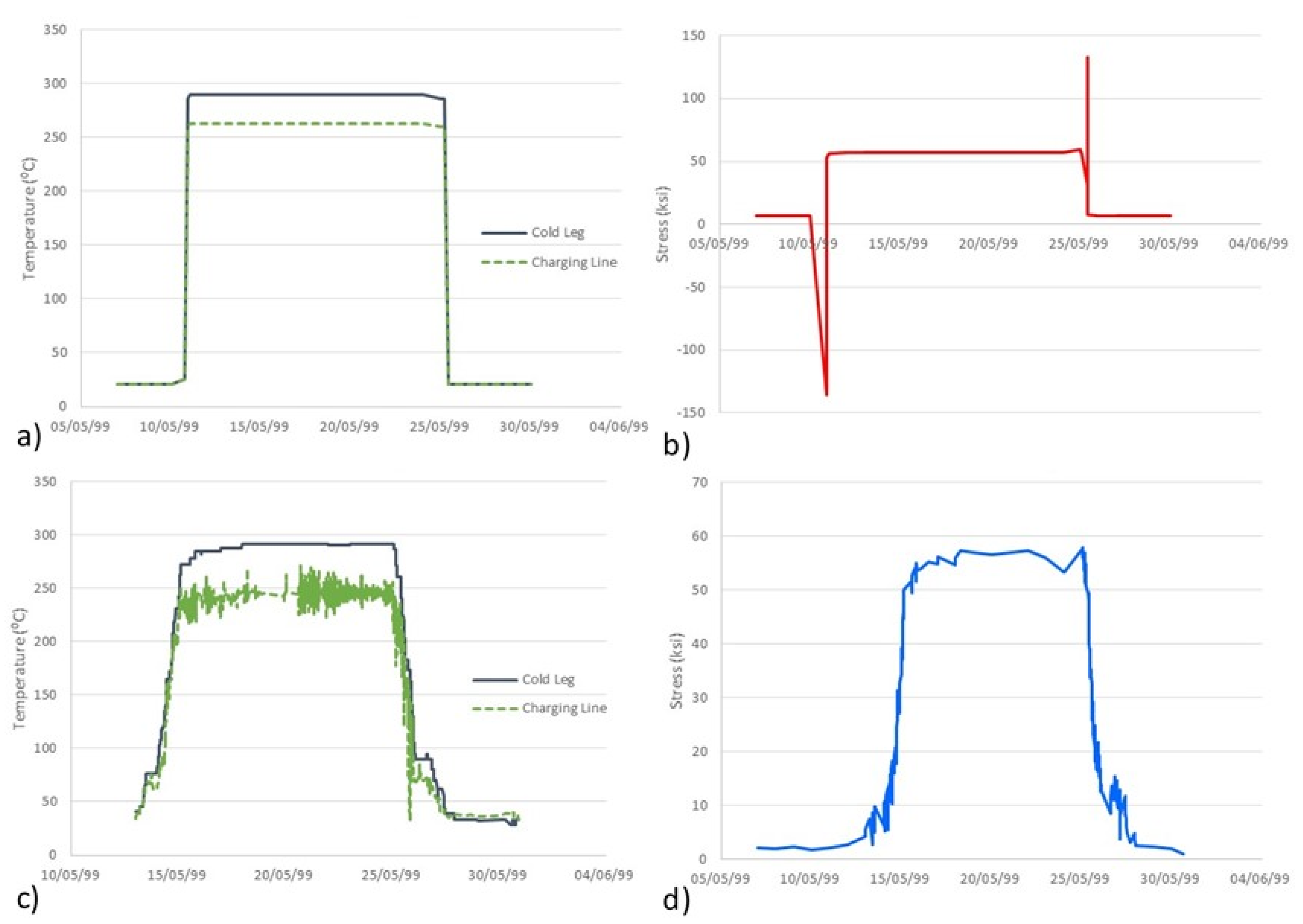
Figure 6 shows the corresponding evolution of the temperature and one of the stress components in the component being analysed during the heat-up cool-down sequence. It is important to notice how the use of Green functions in combination with abrupt transients (e.g., design transients) leads to significant stress peaks that do not appear when the transients take longer times (e.g., actual transients). Likewise,
Figure 7 shows the evolution of temperature and one stress component during the second sequence of transients. Beyond the different durations of the transients (which directly affect the strain rate and, thus, the
Fen factor), the stress values derived in the analyses exhibit peak values (then, stress ranges) which are significantly different when considering design and real (in-plant) transients.
Considering this, the EFA could be completed. As mentioned above, the assessment followed NUREG/CR-6909 [
14].
Table 3 shows the resulting CUFs, with the different intermediate results gathered in
Appendix B. The term CUF refers to the cumulative usage factor without any consideration of environmental effects, and CUF
en refers to the cumulative usage factor considering the environmental effects (CUF
en = CUF·F
en). Cycle counting was performed by employing the Rainflow approach, following the guidelines presented in [
40].
A sharp reduction can be observed in the CUF obtained when using real data from monitoring systems. When the environmental effect is not measured, the consideration of real stresses reduces the CUF by a factor of 620 (first sequence) or 271 (second sequence); when the environmental effect is considered through the Fen factor, the CUFen factor is reduced by a factor of 1785 (first sequence) or 816 (second sequence). Therefore, for the cases analysed here, the consideration of real data (vs. design data) not only reduces the loads (and stress ranges) used in fatigue analysis, but also reduces the environmental effects through a lower Fen factor. All this has evident consequences for the structural integrity assessment of the components and demonstrates the overconservatism associated with the use of design transients.
Author Contributions
Conceptualization, S.C. (Sergio Cicero); methodology, S.C. (Sergio Cicero), S.C. (Sam Cuvillez), T.M., S.A., Y.V., and R.C.; software, Y.V. and R.C.; validation, S.C. (Sergio Cicero) Y.V., and R.C.; formal analysis, S.C. (Sergio Cicero), S.C. (Sam Cuvillez), T.M., S.A., Y.V., and R.C.; investigation, S.C. (Sergio Cicero), S.C. (Sam Cuvillez), T.M., S.A., Y.V., and R.C.; writing—original draft preparation, S.C. (Sergio Cicero) and T.M.; writing—review and editing, S.C. (Sergio Cicero), S.C. (Sam Cuvillez), T.M., S.A., Y.V., and R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EURATOM, grant number 662320.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rothenhöfer, H.; König, G. Managing Environmental Fatigue of the Real Components in a PWR. In Proceedings of the ASME 2010 Pressure Vessels and Pipping Conference, Bellevue, WA, USA, 18–22 July 2010; PVP2010-25979; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 247–254. [Google Scholar]
- Nakamura, T.; Miyama, S. Environmental Fatigue Evaluation in PLM Activities of PWR plant. E-J. Adv. Maint. 2010, 2, 82–100. [Google Scholar]
- Chopra, O.K.; Stevens, G.L. Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials; NUREG/CR-6909 Rev.1, Final Report; U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2018.
- Mottershead, K.; Bruchhausen, M.; Cuvilliez, S.; Cicero, S. INCEFA-PLUS Increasing Safety in Nuclear Power Plants by Covering Gaps in Environmental Fatigue Assessment. In Proceedings of the ASME 2019 Pressure Vessels and Piping Conference, San Antonio, TX, USA, 14–19 July 2019; Volume 1A: Codes and Standards, PVP2019-93276; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Office of Nuclear Reactor Regulation. Standard Review Plan for Review of License Renewal Applications for Nuclear Power Plants; Final Report (NUREG-1800, Revision 2); U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2010.
- Office of Nuclear Reactor Regulation. Regulatory Guide 1.207: Guidelines for Evaluating Fatigue Analyses Incorporating the Life Reduction of Metal Components Due to the Effects of the Light-Water Reactor Environment for New Reactors; U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2007.
- Solin, J.; Reese, S.; Karabaki, H.E.; Mayinger, W. Fatigue of stainless steel in simulated operational conditions: Effects of PWR water, temperature and holds. In Proceedings of the ASME 2014 Pressure Vessels and Pipping Conference, Anaheim, CA, USA, 20–24 July 2014; Volume 1: Codes and Standards, PVP2014-28465; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Solin, J.; Reese, S.H.; Karabaki, H.E.; Mayinger, W. Research on hold time effects in fatigue of stainless steel: Simulation of normal operation between fatigue transients. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 1A: Codes and Standards, PVP2015-45098; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Mehta, H.S.; Gosselin, S.R. Environmental Factor Approach to Account for Water Effects in Pressure Vessel and Piping Fatigue Evaluations. Nucl. Eng. Des. 1998, 181, 175–197. [Google Scholar] [CrossRef]
- Nuclear Boiler and Pressure Vessel Code—Section III, 2007 ed.; American Society of Mechanical Engineers: New York, NY, USA, 2007.
- RCC-M, Règles de Construction et de Conception des Matériel Mécaniques de l´îlot Nucléaires REP, 2007 ed.; AFCEN: Courbevoie, France, 2007.
- Langer, B. Design of Pressure Vessels for Low-Cycle Fatigue. J. Basic Eng. 1962, 84, 389–399. [Google Scholar] [CrossRef]
- Chopra, O.K.; Shack, W.J. Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials; NUREG/CR-6909 Rev.0, ANL-06/08; U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2007.
- Chopra, O.K.; Stevens, G.L. Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials; NUREG/CR-6909 Rev.1 DRAFT ANL-12/60; U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2014.
- Hald, A. Statistical Theory with Engineering Applications; John Wiley and Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- ASME Code Case N-761, Fatigue Design Curves for Light Water Reactor (LWR) Environments, Section III, Division 1; American Society of Mechanical Engineers: New York, NY, USA, 2010.
- ASME Code Case N-792-1, Fatigue Evaluation Including Environmental Effects, Section III, Division 1; American Society of Mechanical Engineers: New York, NY, USA, 2010.
- O’Donnell, W.J.; O’Donnell, W.J.; O’Donnell, T.P. Proposed New Fatigue Design Curves for Austenitic Stainless Steels, Alloy 600 and Alloy 800. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; PVP2005-71409; American Society of Mechanical Engineers: New York, NY, USA, 2005; pp. 109–132. [Google Scholar]
- EN 13445-3 version V1, Unfired Pressure Vessels—Part 3: Design; European Committee for Standardization: Brussels, EU, USA, 2014.
- Wilhelm, P.; Steinmann, P.; Rudolph, J. Fatigue strain-life behavior of austenitic stainless steels in pressurized water reactor environments. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 1A: Codes and Standards, PVP2015-45011; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- AD 2000 Merkblatt S2: 2012, Analysis for Cyclic Loading; German Institute for Standardisation: Berlin, Germany, 2012.
- Haibach, E. Betriebsfestigkeit: Verfahren und Daten zur Bauteilberechnung, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Métais, T.; Courtin, S.; Genette, P.; De Baglion, L.; Gourdin, C.; Le Roux, J.C. Overview of French Proposal of Updated Austenitic SS Fatigue Curves and of a Methodology to Account for EAF. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 1A: Codes and Standards, PVP2015-45158; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Le Duff, J.A.; Lefrançois, A.; Vernot, J.P.; Bossu, D. Effect of loading signal shape and of surface finish on the low cycle fatigue behavior of 304L stainless steel in PWR environment. In Proceedings of the ASME 2010 Pressure Vessels and Pipping Conference, Bellevue, WA, USA, 18–22 July 2010; PVP2010-26027; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 233–241. [Google Scholar]
- Blatman, G.; Métais, T.; Le Roux, J.C.; Cambier, S. Statistical analyses of high cycle fatigue French data for austenitic SS. In Proceedings of the ASME 2014 Pressure Vessels and Pipping Conference, Anaheim, CA, USA, 20–24 July 2014; Volume 3: Design and Analysis, PVP2014-28409; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- JSME. Codes for Nuclear Power Generation Facilities, Rules on Design and Construction for Nuclear Power Plants, the First Part: Light Water Reactor Structural Design Standard, JSME S NC1-2008 ed.; The Japan Society of Mechanical Engineers: Tokyo, Japan, 2008. [Google Scholar]
- Kanasaki, H.; Higuchi, M.; Asada, S.; Yasuda, M.; Sera, T. Proposal of Fatigue Life Equations for Carbon & Low-Alloy Steels and Austenitic Stainless Steels as a Function of Tensile Strength. In Proceedings of the ASME 2013 Pressure Vessels and Piping Conference, Paris, France, 14–18 July 2013; Volume 1A: Codes and Standards, PVP2013-97770; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Asada, S.; Hirano, T.; Sera, T. Study on a New Design Fatigue Evaluation Method. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 1A: Codes and Standards, PVP2015-45089; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Asada, S.; Zhang, S.; Takanashi, M.; Nomura, Y. Study on Incorporation of a New Design Fatigue Curve into the JSME Environmental Fatigue Evaluation Method. In Proceedings of the ASME 2019 Pressure Vessels and Piping Conference, San Antonio, TX, USA, 14–19 July 2019; Volume 3: Design and Analysis, PVP2019-93273; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- ISO 4287:1997, Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters; The International Organization for Standardization: Geneva, Switzerland, 1997.
- JNES-SS-1005, Environmental Fatigue Evaluation Method for Nuclear Power Plants; Japan Nuclear Energy Safety Organization: Tokyo, Japan, 2011.
- KTA 3201.2 (2017-11) Components of the Reactor Coolant Pressure Boundary of Light Water Reactors Part 2: Design and Analysis; KTA-Geschaeftsstelle: Salzgitter, Germany, 2017.
- Schuler, X.; Herter, K.H.; Rudolph, J. Derivation of Design Fatigue Curves for Austenitic Stainless Steel Grades 1.4541 and 1.4550 within the German Nuclear Safety Standard KTA 3201.2. In Proceedings of the ASME 2013 Pressure Vessels and Piping Conference, Paris, France, 14–18 July 2013; Volume 1B: Codes and Standards, PVP2013-97138; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Reese, S.H.; Rudolph, J. Environmentally Assisted Fatigue (EAF) Rules and Screening Options in the Context of Fatigue Design Rules within German Nuclear Safety Standards. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 6A: Materials and Fabrication, PVP2015-45022; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Ware, A.G.; Morton, D.K.; Nitzel, M.E. Application of NUREG/CR-5999 Interim Fatigue Curves to Selected Nuclear Power Plant Components; NUREG/CR-6260 INEL-95/0045; Idaho National Engineering Laboratory: Idaho Falls, ID, USA, 1995.
- Cicero, R. Evaluación del Gasto en Fatiga de Vasijas a Presión de Reactors Nucleares Considerando el Efecto Ambiental Mediante el Empleo de Datos Reales. Ph.D. Thesis, Universidad de Cantabria, Santander, Spain, 2013. [Google Scholar]
- Software Specifications for FatiguePro, 3rd ed.; Structural Integrity Associates Report Nº SIR-99-051, Revision 1, SI File n EPRI.136Q-401; Structural Integrity Associates: San Jose, CA, USA, 2001.
- Software fatONE, Fatigue Management System, version 3.1.9577; Innomerics, S.L.: Madrid, Spain, 2020.
- Hannink, M.H.C.; Blom, F.J.; Quist, P.W.B.; de Jong, A.E.; Besuijen, W. Demonstration of Fatigue for LTO License of NPP Borssele. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; Volume 3: Design and Analysis, PVP2015-45791; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Gray, M.A.; Verlinich, M.M. Guidelines for Addressing Environmental Effects in Fatigue Usage Calculations; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2012. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).