Experimental Model Study of Liquid–Liquid and Liquid–Gas Interfaces during Blast Furnace Hearth Drainage
Abstract
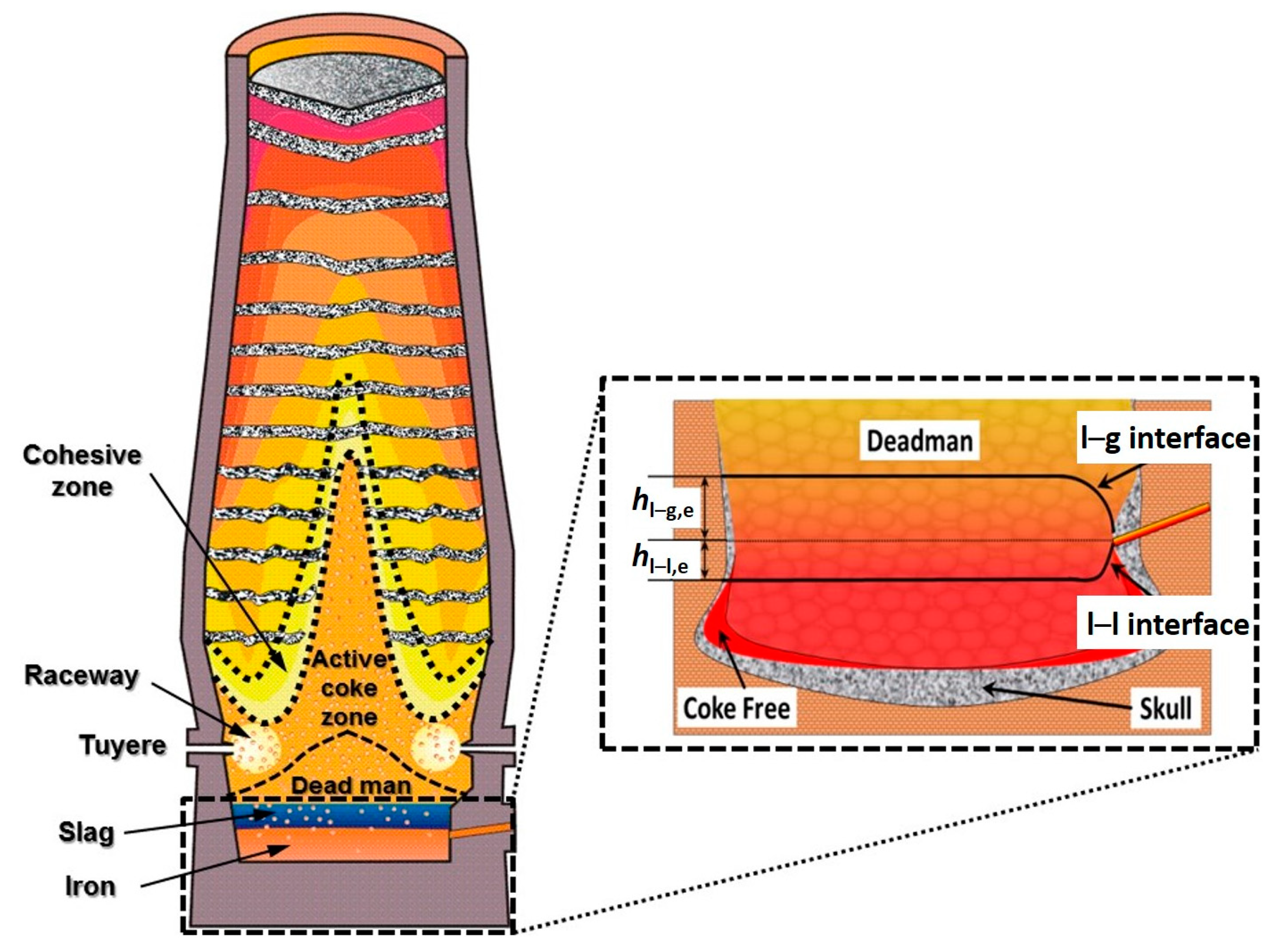
1. Introduction
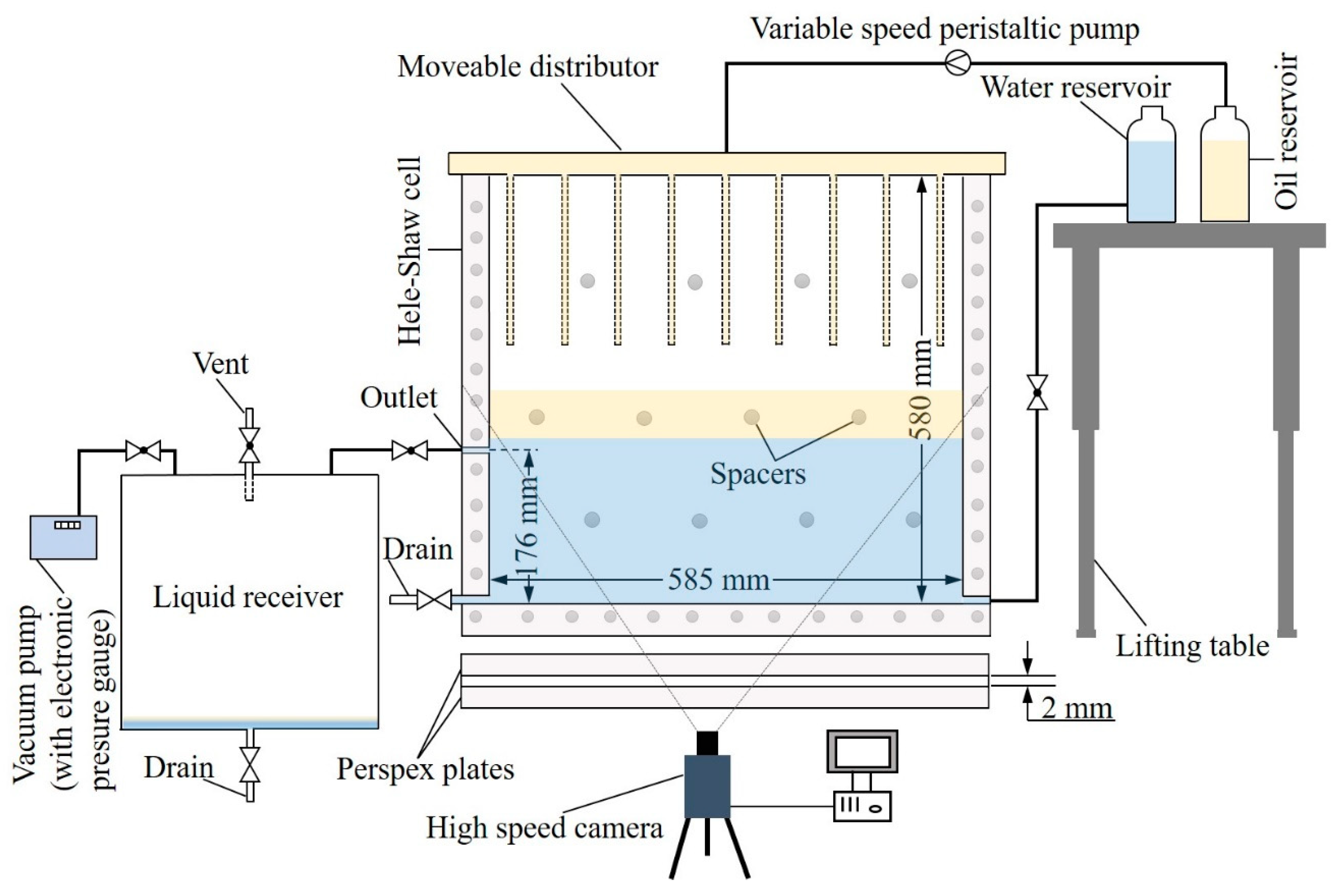
2. Experimental Setup
2.1. Apparatus Arrangement and Procedure
- (1)
- The lifting table was elevated to a certain level, followed by opening the ball valve to charge water into the model until the predetermined level was reached.
- (2)
- The moveable oil distributor was fixed on top of the model and the peristaltic pump was started at low pumping speed to feed oil into the model slowly to create an oil layer with uniform and desired thickness.
- (3)
- A settling time of a few minutes was allowed for both l–g and l–l interfaces to become absolutely stable. After this, the oil distributor was removed from the top of the model.
- (4)
- The vacuum pump was switched on until the desired under-pressure was obtained in the receiver.
- (5)
- The high-speed camera was turned on to record the drainage process.
- (6)
- The outlet was opened fully. When air started blowing out through the outlet, the outlet was closed and the camera was switched off.
- (7)
- The vent was opened to recover the receiver pressure, and the drain of the receiver was opened to empty the receiver.
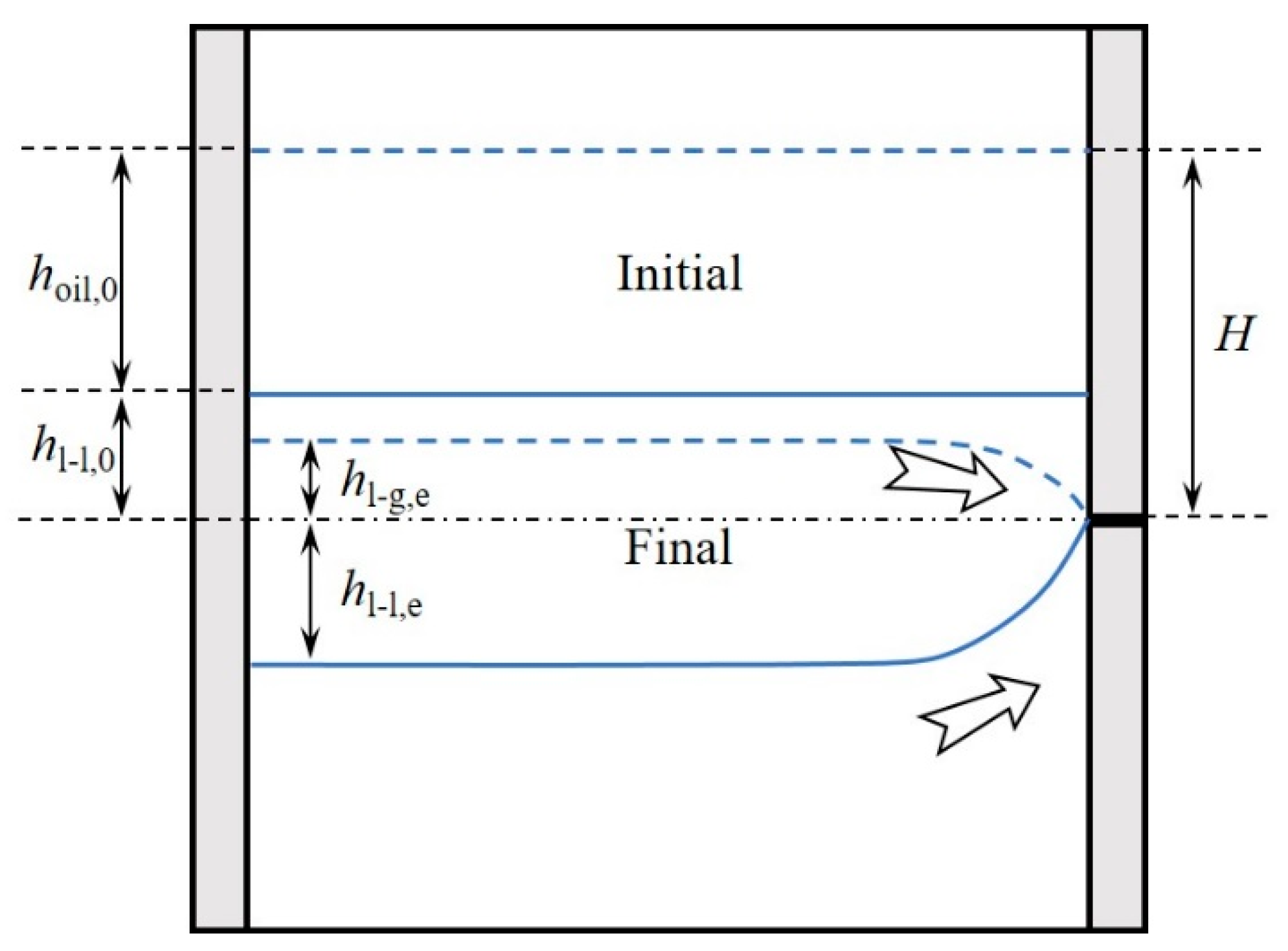
2.2. Experimental Conditions and Analytical Methods
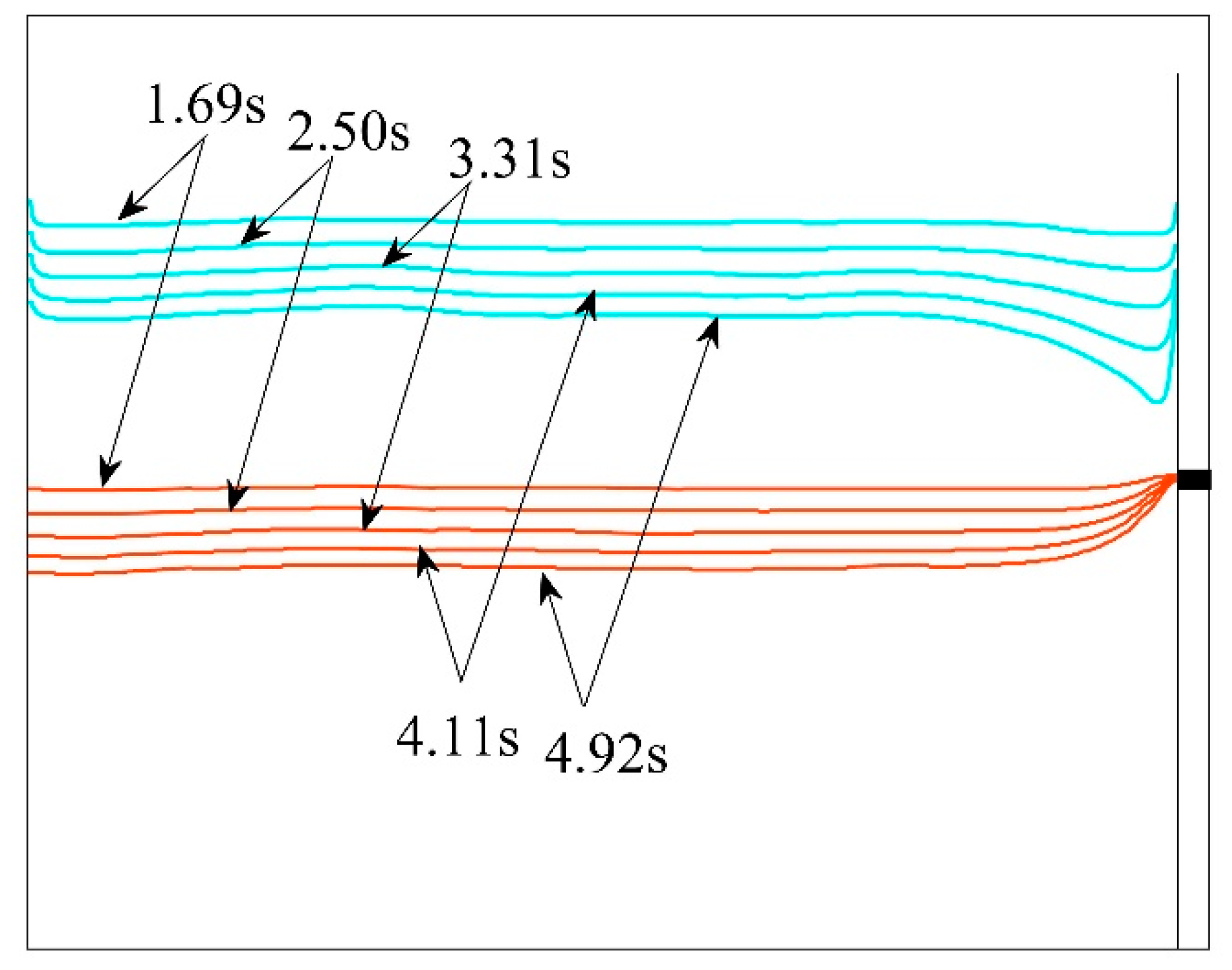
3. Results and Discussion
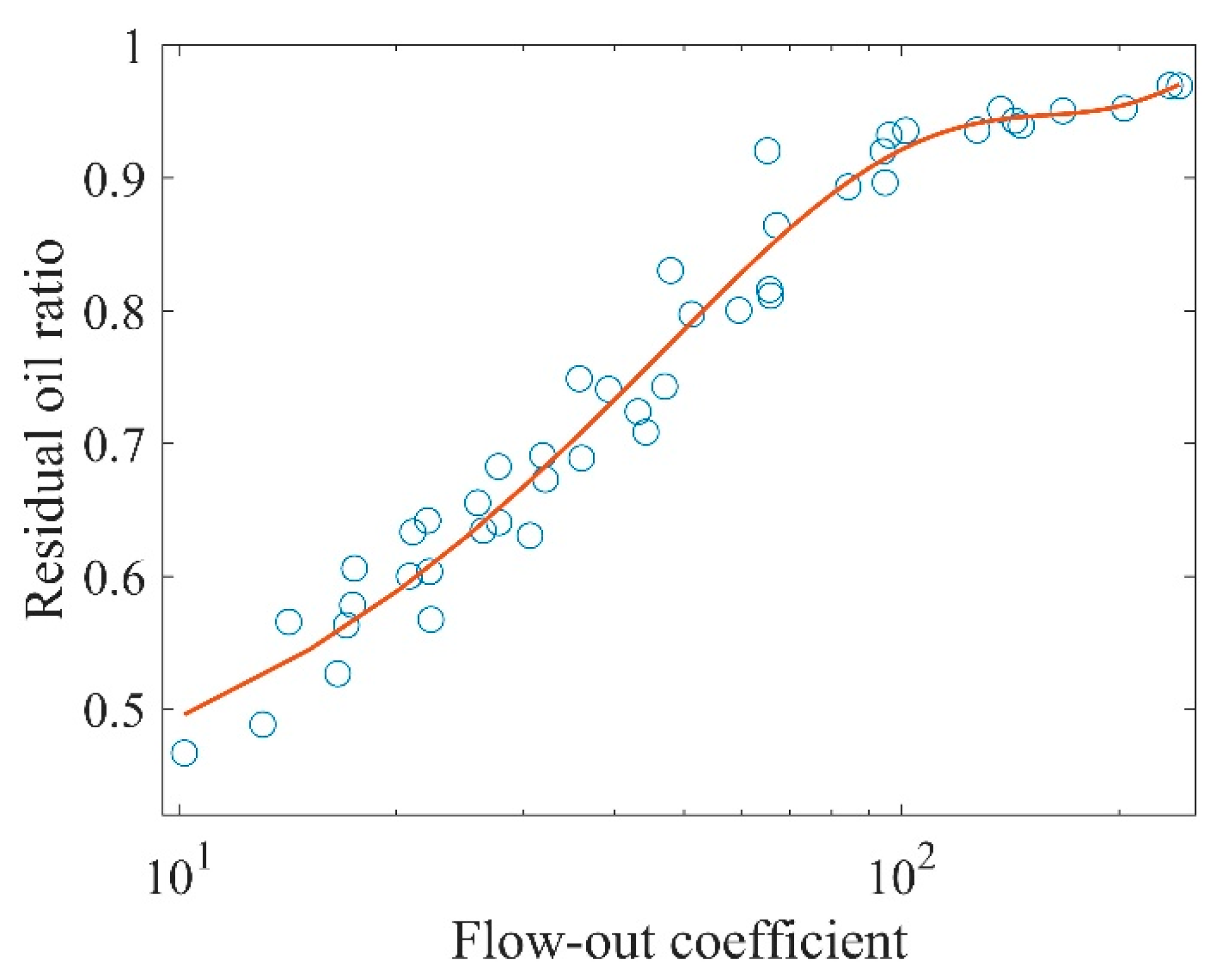
3.1. Influence on Residual Ratio, Tapping Time
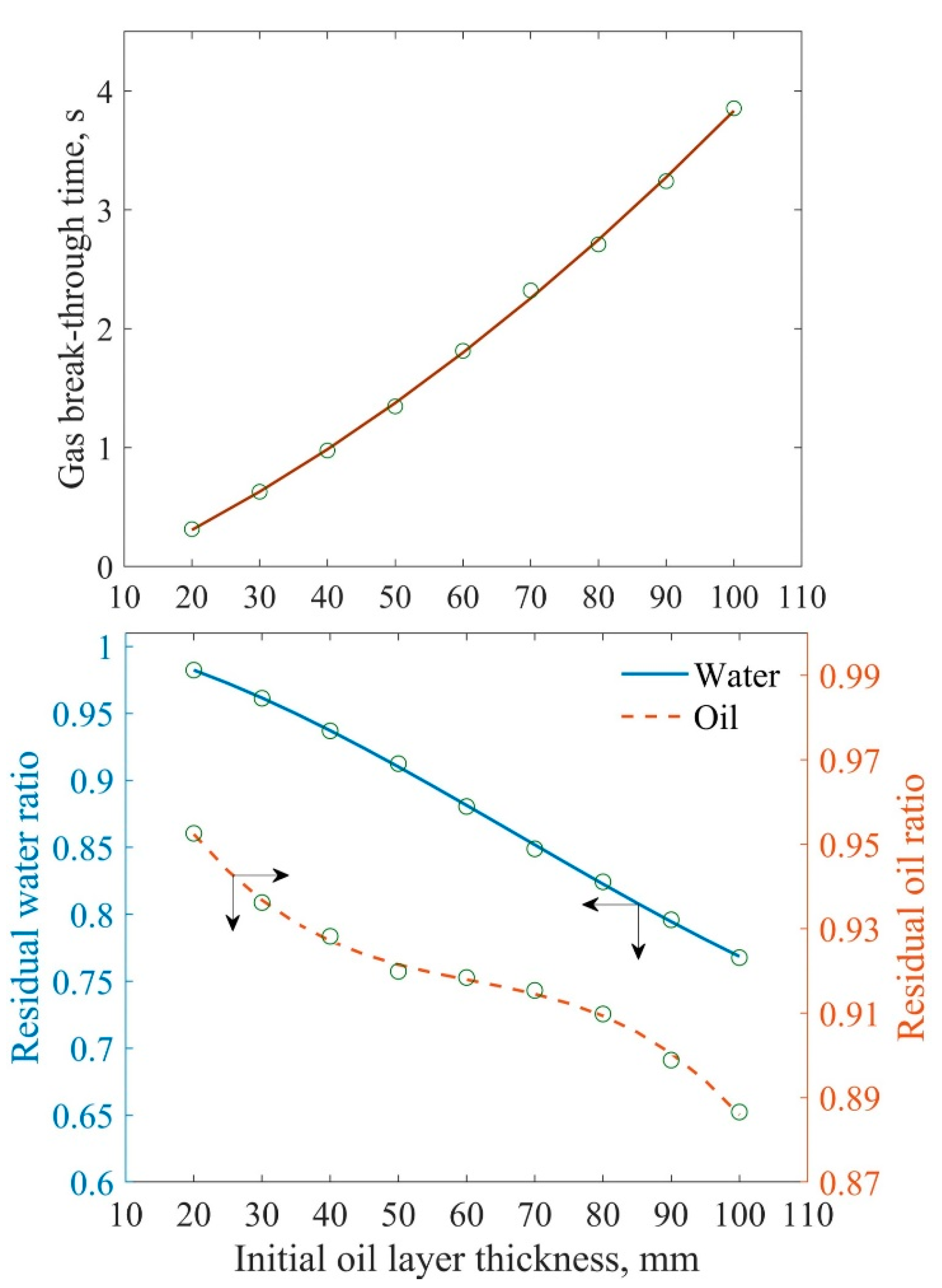
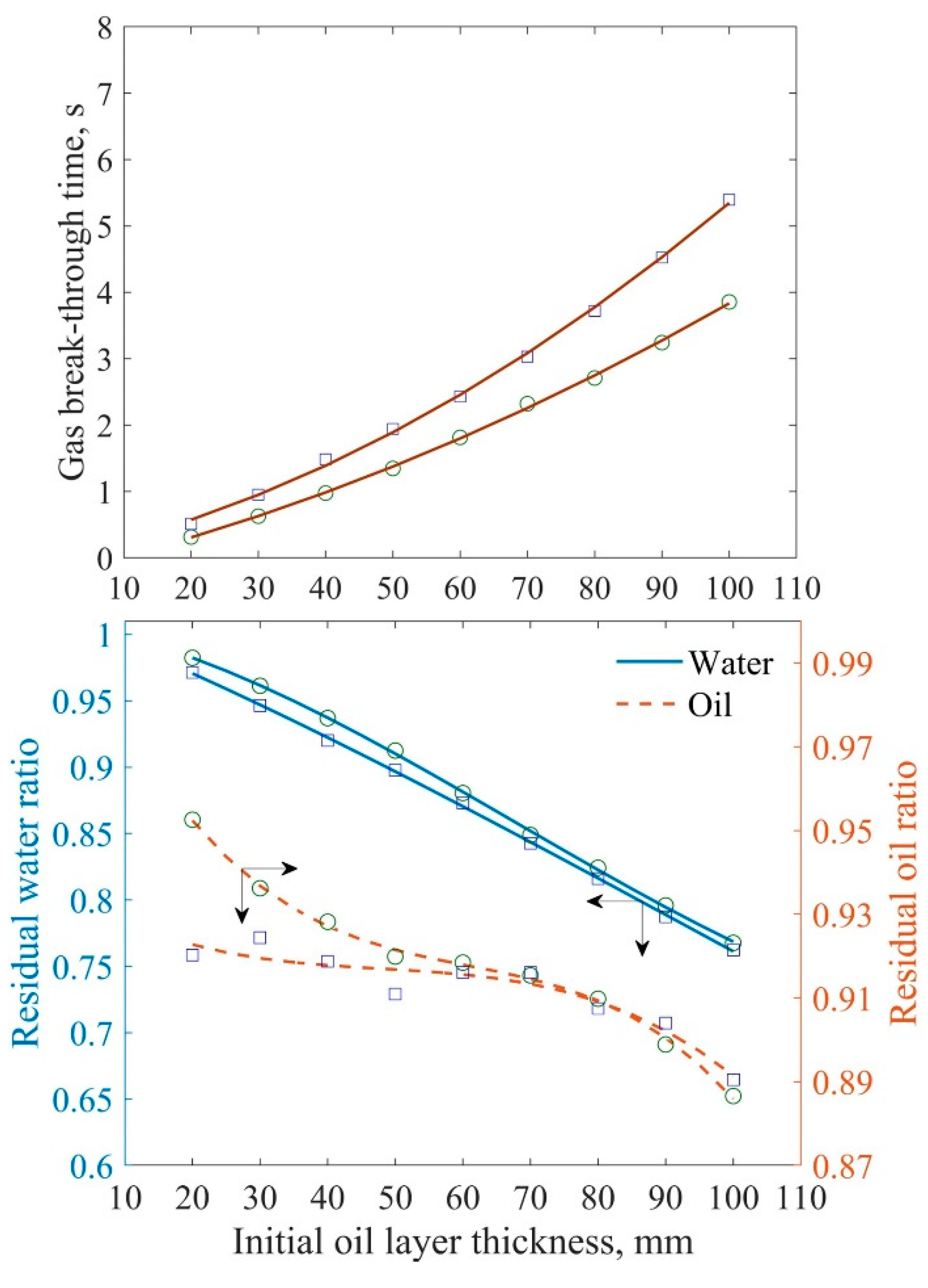
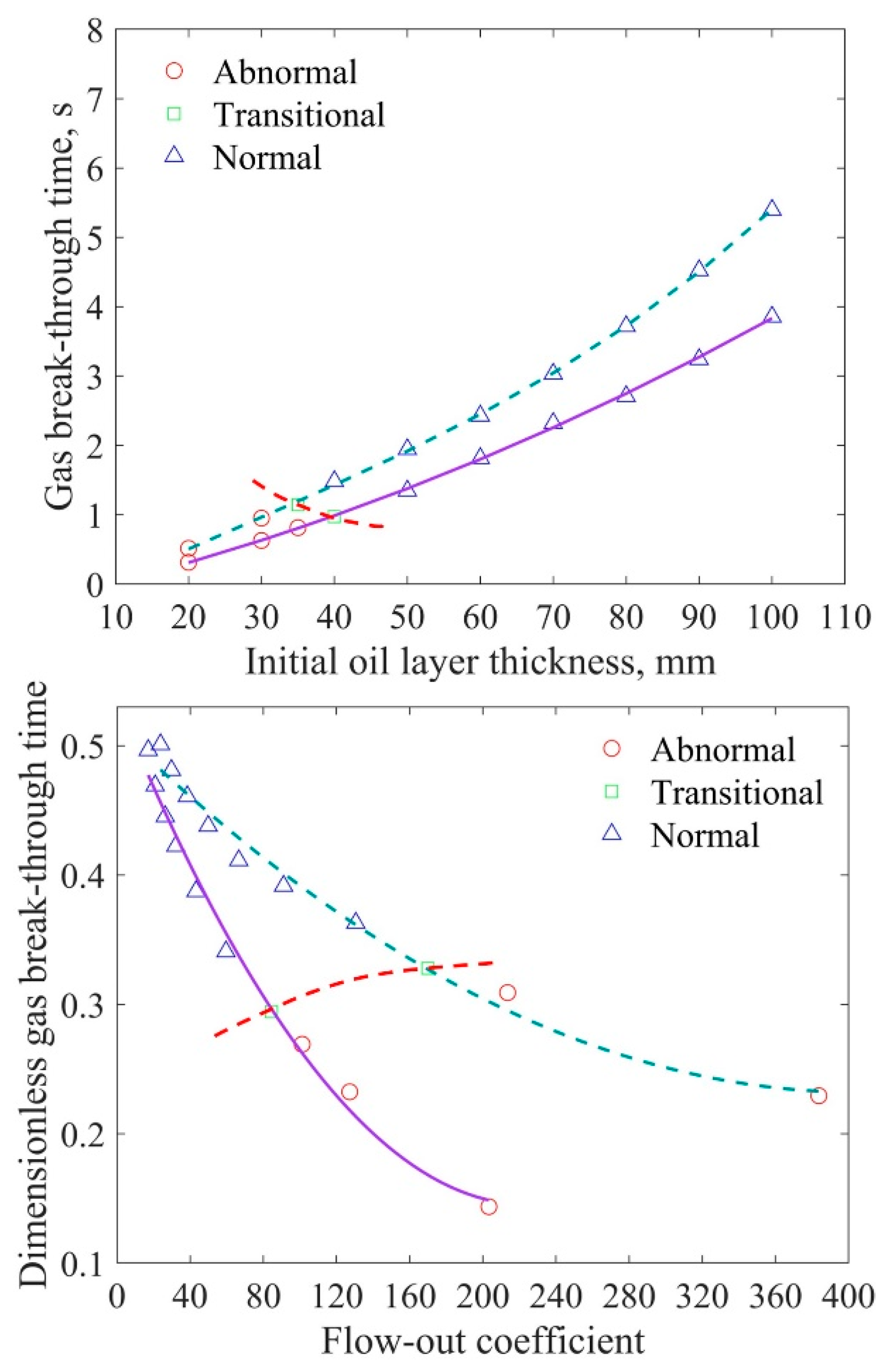
3.1.1. Influence of Initial Oil Layer Thickness
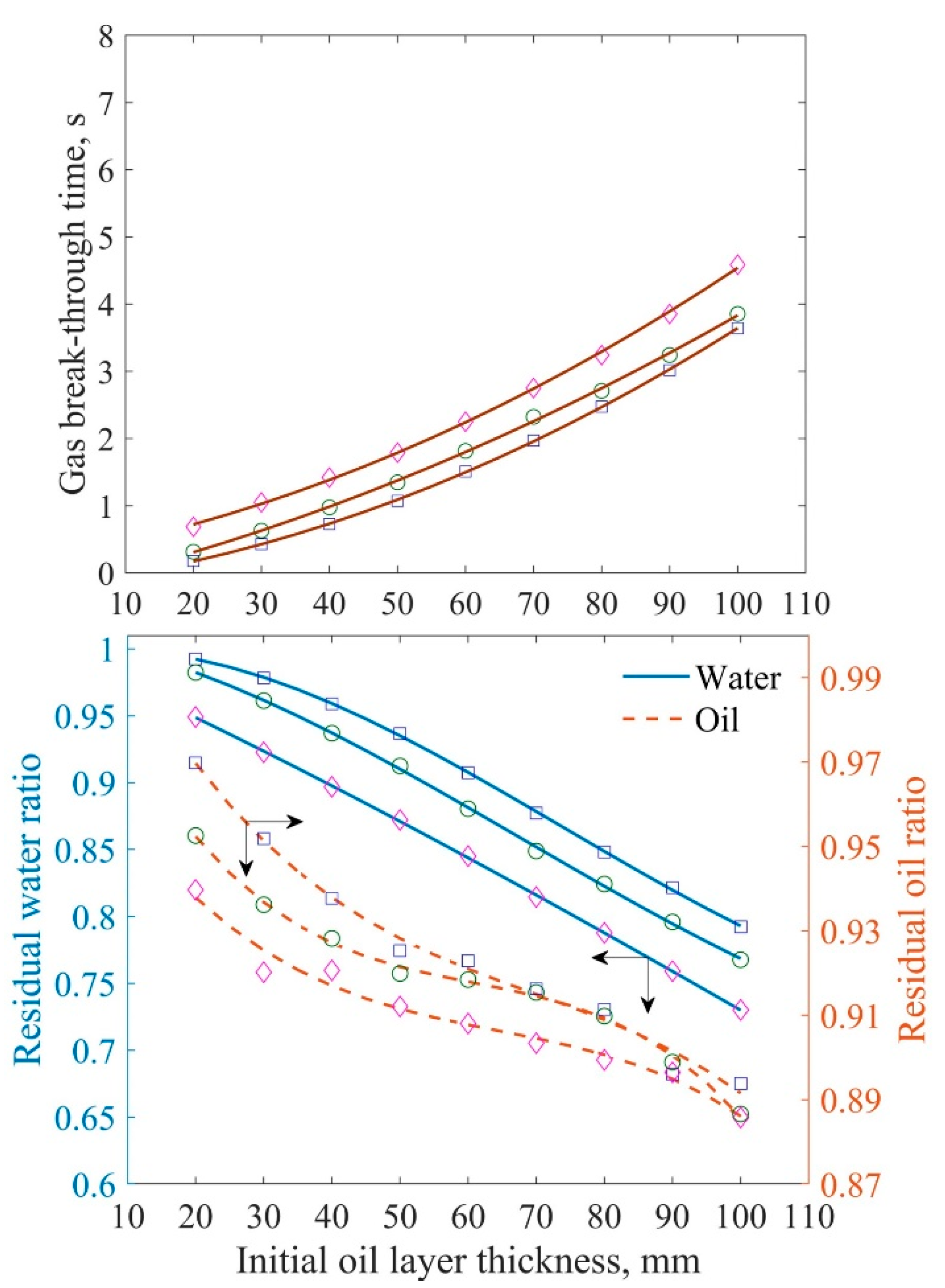
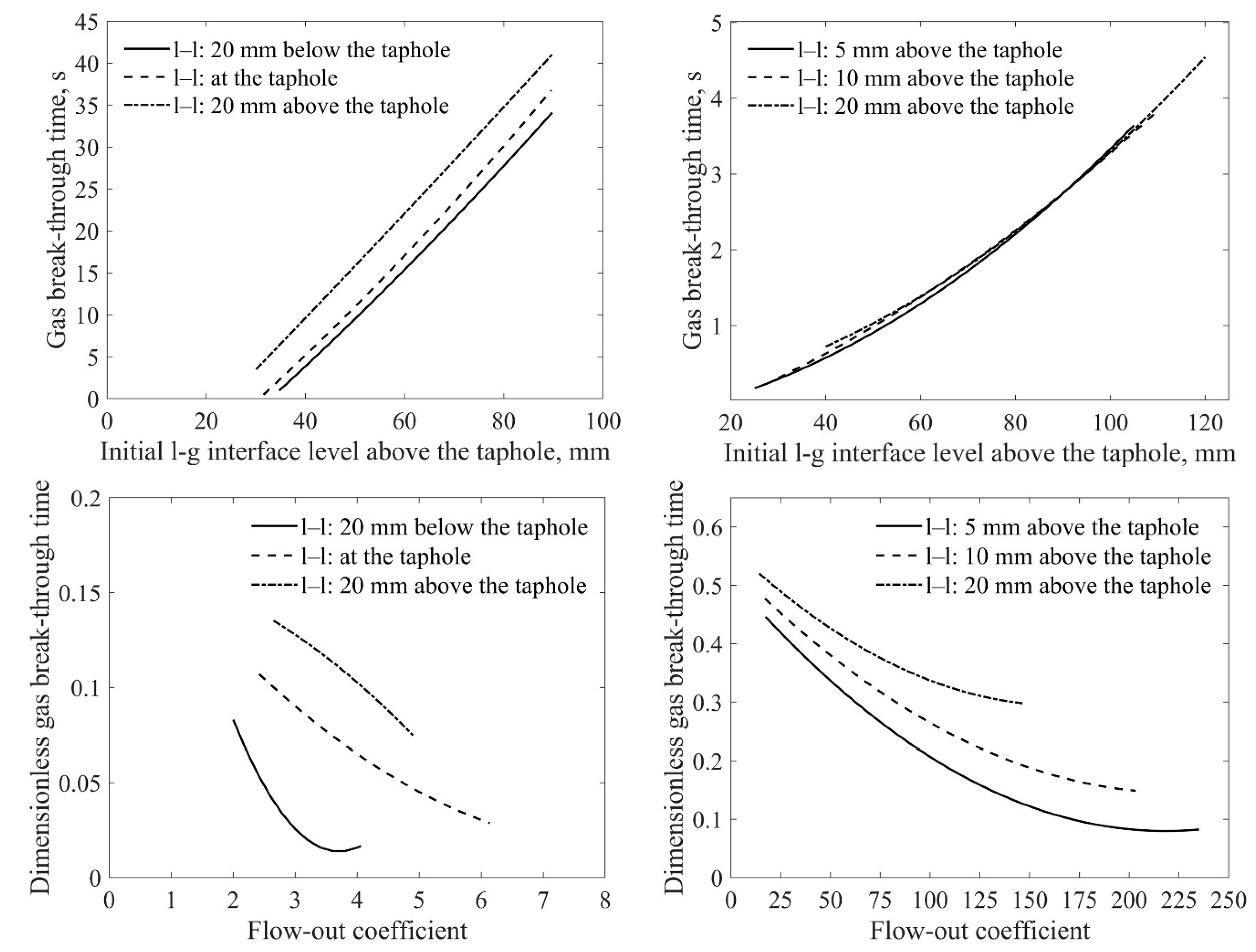
3.1.2. Influence of the Initial l–l Interface Level
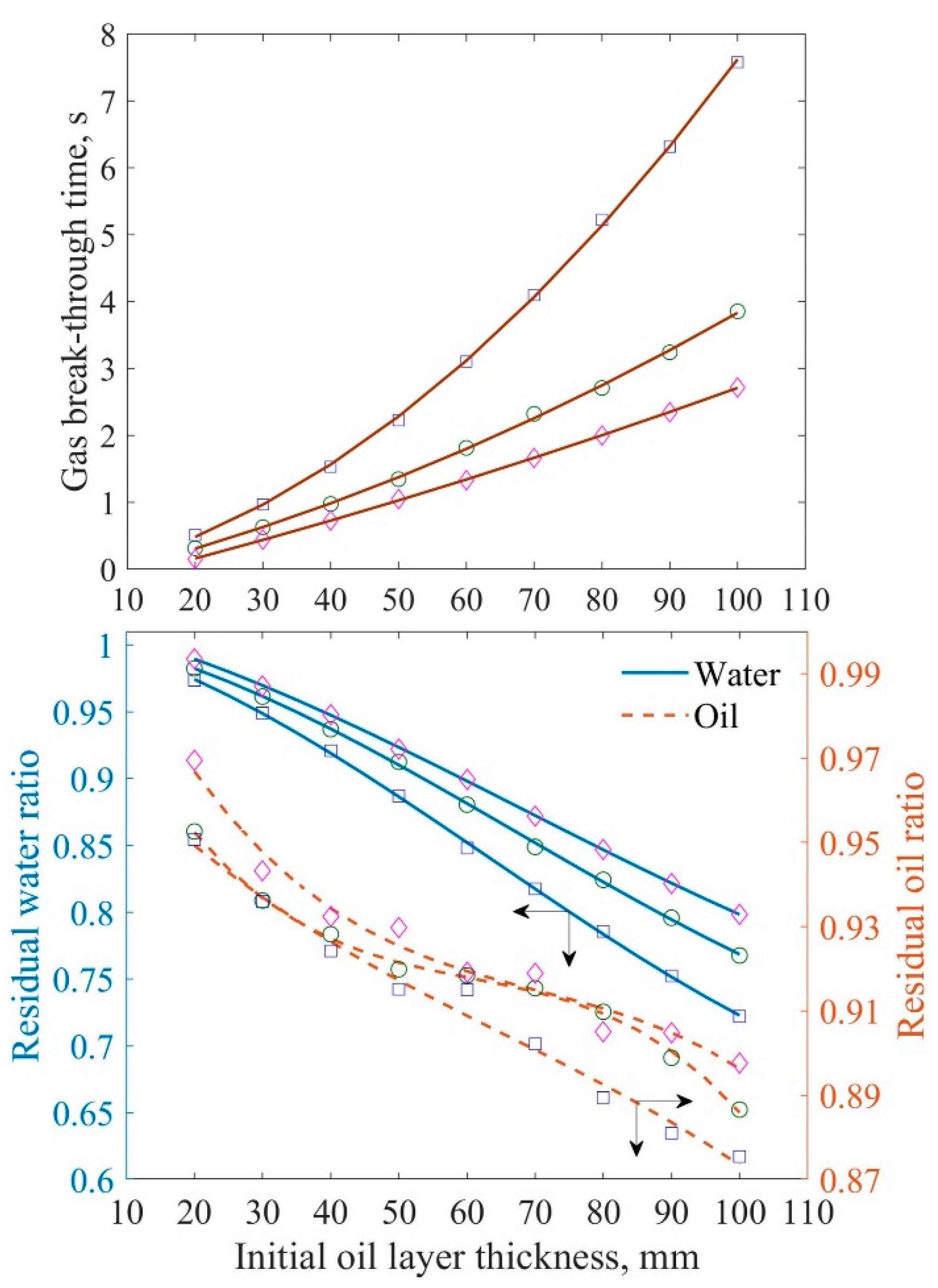
3.1.3. Influence of Pressure Difference
3.1.4. Influence of Oil Viscosity
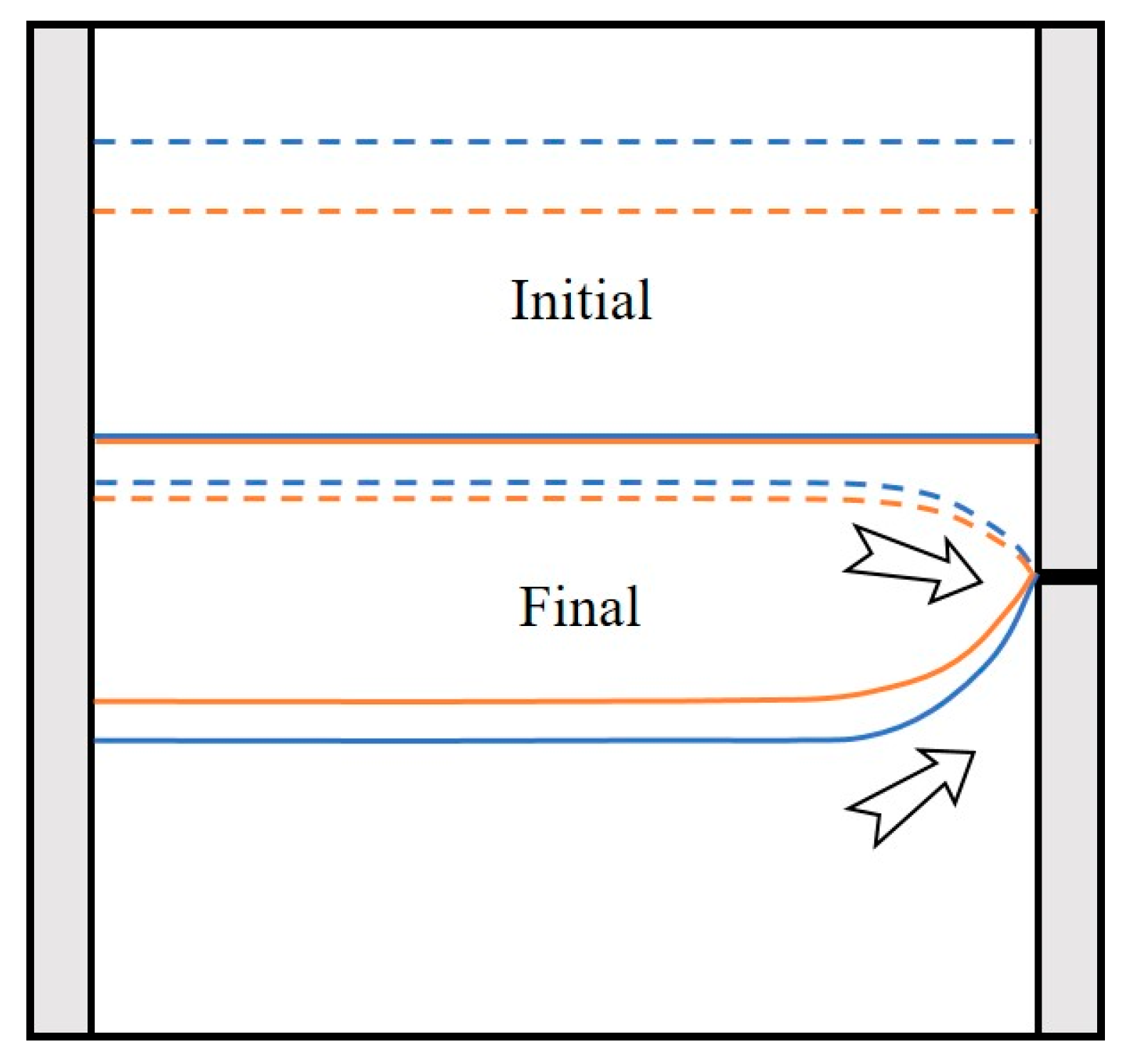
3.2. Effect of the Factors on the End State
3.2.1. Effect of the Initial l–l Interface Level
3.2.2. Effect of the Pressure Difference
3.2.3. Effect of Oil Viscosity
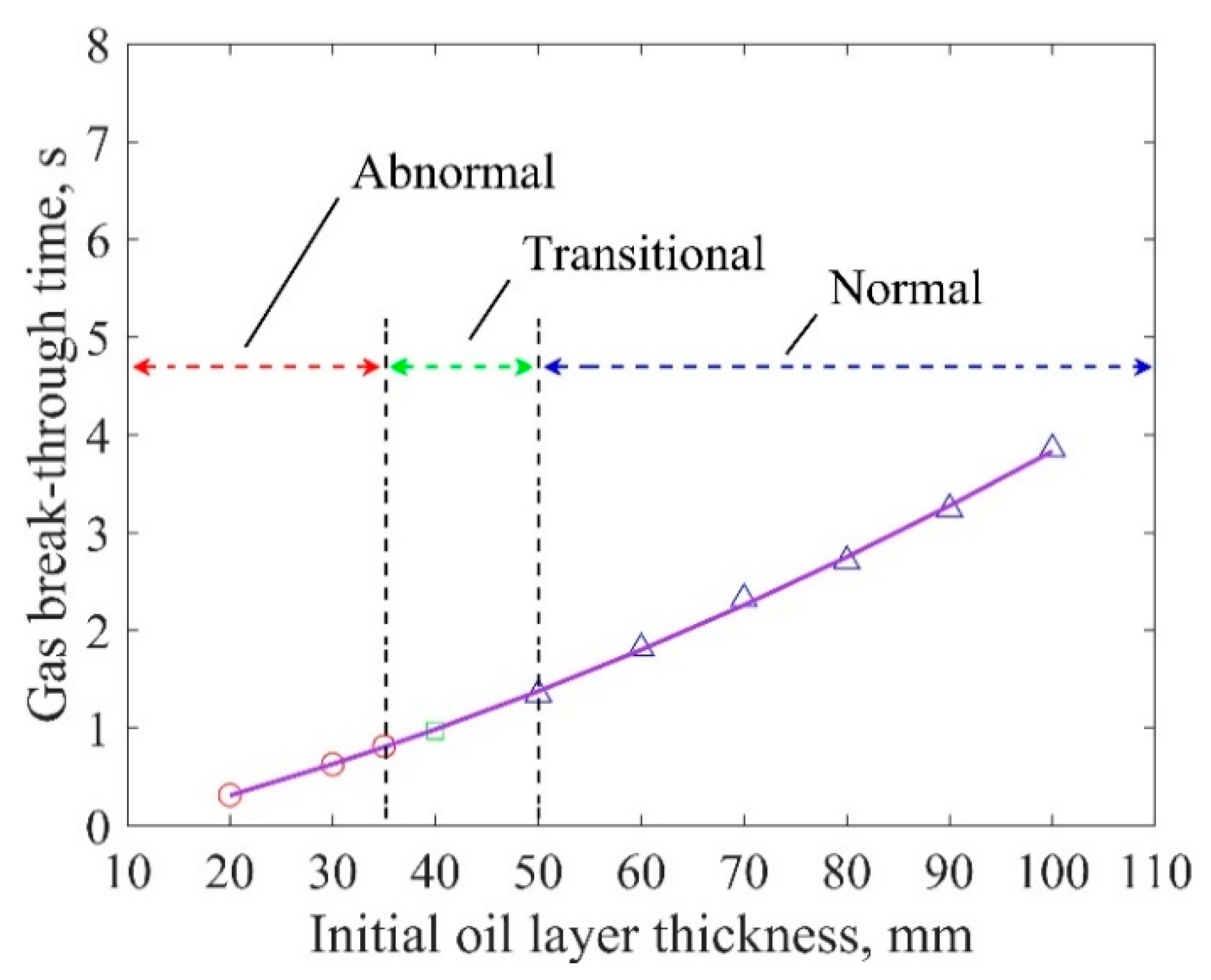
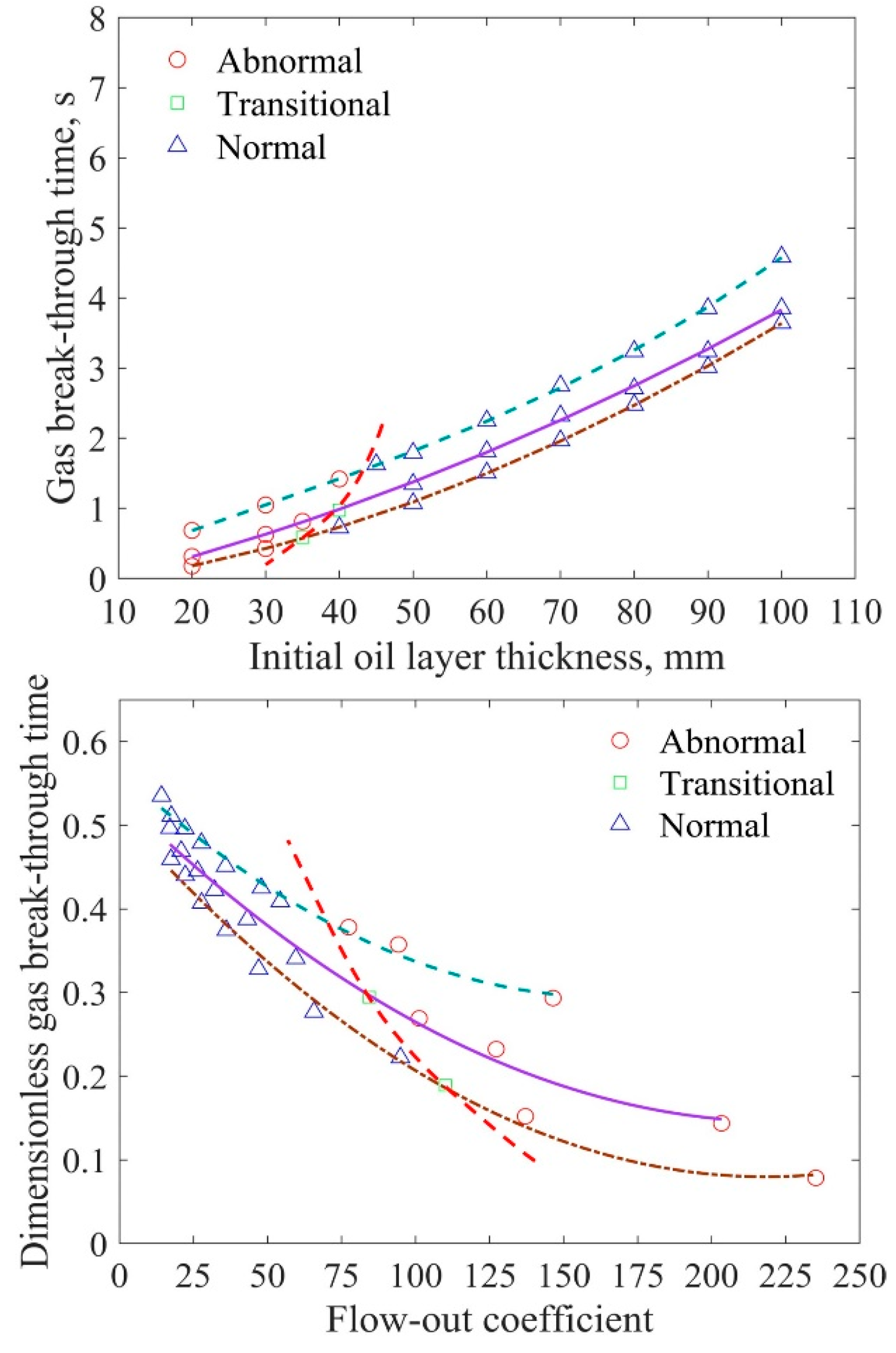
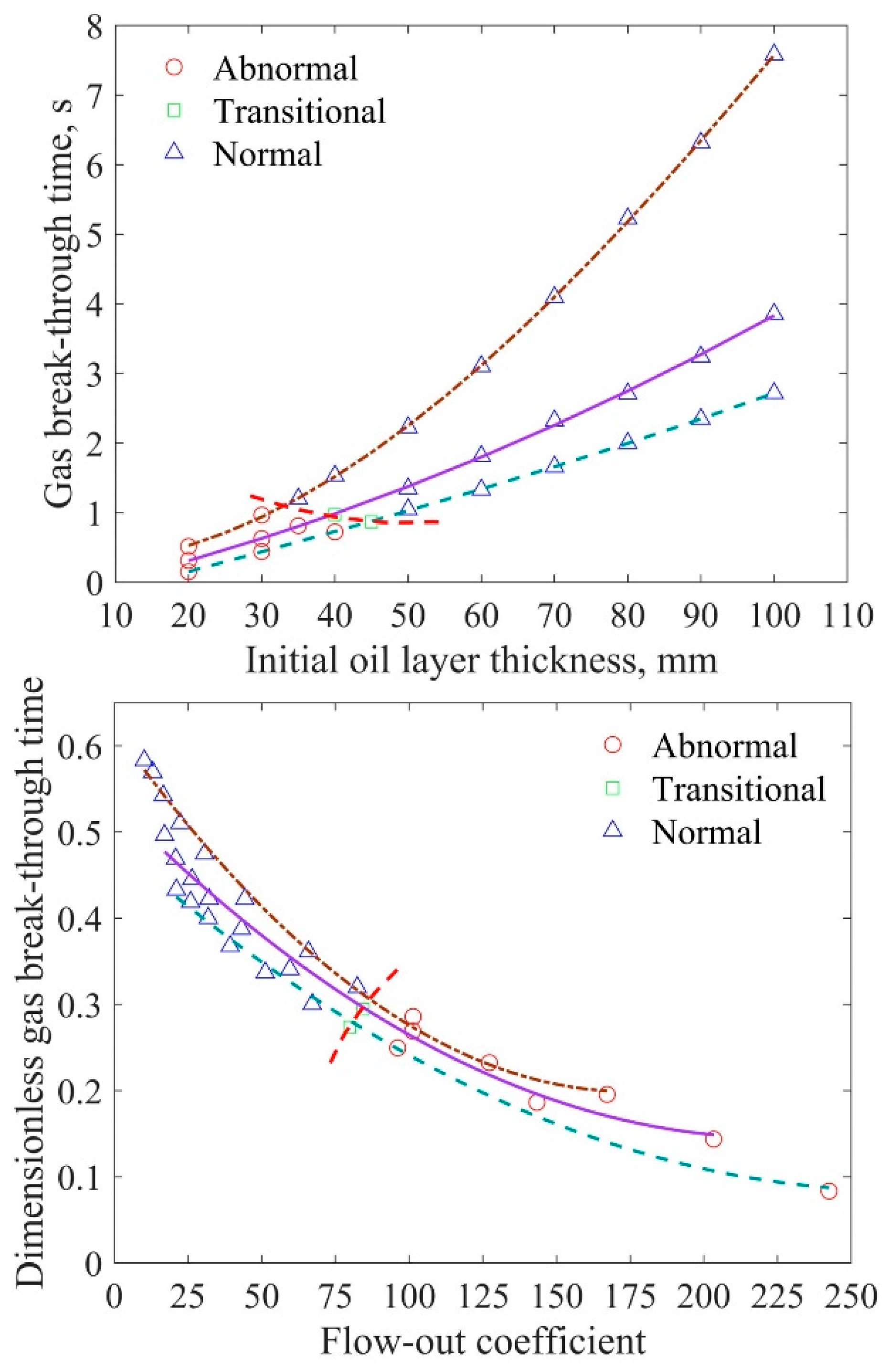
3.3. Comparison with Earlier Findings
4. Conclusions
- (1)
- An increase in the initial oil layer thickness (i.e., more accumulated slag in the hearth) extends the draining time and decreases the residual ratios of both liquids. In addition, the likelihood of abnormal drainage also decreases.
- (2)
- With a higher initial l–l interface level, the draining time increases and the residual liquid ratios decrease. The likelihood of abnormal drainage increases.
- (3)
- With an increased pressure difference (“driving force”) in the system, the residual liquids ratios and the likelihood of abnormal drainage increase, while the gas breakthrough time decreases.
- (4)
- An increase of oil viscosity increases the tapping time and reduces the likelihood of abnormal drainage and residual ratios of both liquids.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geerdes, M.; Toxopeus, H.; vd Vliet, C. Modern Blast Furnace Ironmaking: An Introduction, 2nd ed.; IOS Press BV: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Brännbacka, J. Model Analysis of Dead-Man Floating State and Liquid Levels in the Blast Furnace Hearth. Ph.D. Thesis, Åbo Akademi University, Turku, Finland, 2004. [Google Scholar]
- Pinczewski, W.V.; Tanzil, W.B.U.; Hoschke, M.I.; Burgess, J.M. Simulation of the drainage of two liquids from a blast furnace hearth. Tetsu-to-Hagane 1982, 68, S111. [Google Scholar]
- Tanzil, W.B.U.; Zulli, P.; Burgess, J.M.; Pinczewski, W.V. Experimental model study of the physical mechanisms governing blast furnace hearth drainage. Trans. Iron Steel Inst. Jpn. 1984, 24, 197–205. [Google Scholar] [CrossRef]
- Tanzil, W.B.U. Blast Furnace Hearth Drainage. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 1985. [Google Scholar]
- Zulli, P. Blast Furnace Hearth Drainage with and without a Coke-Free Layer. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 1991. [Google Scholar]
- Shao, L.; Saxén, H. Simulation study of blast furnace drainage using a two-fluid model. Ind. Eng. Chem. Res. 2013, 52, 5479–5488. [Google Scholar] [CrossRef]
- He, Q.; Zulli, P.; Evans, G.M.; Tanzil, F. Free surface instability and gas entrainment during blast furnace drainage. Dev. Chem. Eng. Miner. Process. 2006, 14, 249–258. [Google Scholar] [CrossRef]
- He, Q.; Evans, G.; Zulli, P.; Tanzil, F. Cold model study of blast gas discharge from the taphole during the blast furnace hearth drainage. ISIJ Int. 2012, 52, 774–778. [Google Scholar] [CrossRef]
- Iida, M.; Ogura, K.; Hakone, T. Analysis of drainage rate variation of molten iron and slag from blast furnace during tapping. ISIJ Int. 2008, 48, 412–419. [Google Scholar] [CrossRef]
- Nouchi, T.; Yasui, M.; Takeda, K. Effects of particle free space on hearth drainage efficiency. ISIJ Int. 2003, 43, 175–180. [Google Scholar] [CrossRef]
- Roche, M.; Helle, M.; van der Stel, J.; Louwerse, G.; Shao, L.; Saxén, H. Off-line model of blast furnace liquid levels. ISIJ Int. 2018, 58, 2236–2245. [Google Scholar] [CrossRef]
- Fukutake, T.; Okabe, K. Influences of slag tapping conditions on the amount of residual slag in the blast furnace hearth. Trans. Iron Steel Inst. Jpn. 1976, 16, 317–323. [Google Scholar] [CrossRef]
- Brännbacka, J.; Torrkulla, J.; Saxén, H. Simple simulation model of blast furnace hearth. Ironmak. Steelmak. 2005, 32, 479–486. [Google Scholar] [CrossRef]
- Brännbacka, J.; Saxén, H. Modeling the liquid levels in the blast furnace hearth. ISIJ Int. 2001, 41, 1131–1138. [Google Scholar] [CrossRef]
- Roche, M.; Helle, M.; van der Stel, J.; Louwerse, G.; Shao, L.; Saxén, H. On-line estimation of liquid levels in the blast furnace hearth. Steel Res. Int. 2019, 90, 1800420. [Google Scholar] [CrossRef]
- Nishioka, K.; Maeda, T.; Shimizu, M. Effect of various in-furnace conditions on blast furnace hearth drainage. ISIJ Int. 2005, 45, 1496–1505. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, H.; Yu, A.; Zulli, P. Numerical investigation of the transient multiphase flow in an ironmaking blast furnace. ISIJ Int. 2010, 50, 515–523. [Google Scholar] [CrossRef]
- Vångö, M.; Pirker, S.; Lightenegger, T. Unresolved CFD–DEM modeling of multiphase flow in densely packed particle beds. Appl. Math. Model. 2018, 56, 501–516. [Google Scholar] [CrossRef]
- Bambauer, F.; Wirtz, S.; Sherer, V.; Bartusch, H. Transient DEM-CFD simulation of solid and fluid flow in a three dimensional blast furnace model. Powder Technol. 2018, 334, 53–64. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media, 1st ed.; American Elsevier Company: New York, NY, USA, 1972; p. 133. [Google Scholar]
- Liu, W.; Mondal, D.N.; Shao, L.; Saxén, H. An image analysis-based method for automatic data extraction from pilot draining experiments. Ironmak. Steelmak 2020. submitted manuscript. [Google Scholar]
- Tsuchiya, N.; Fukutake, T.; Yamauchi, Y.; Matsumoto, T. In-furnace conditions as prerequisites for proper use and design of Mud to control blast furnace taphole length. ISIJ Int. 1998, 38, 116–125. [Google Scholar] [CrossRef]

| Properties | System | |
|---|---|---|
| BF: Slag–Iron | Model: Oil–Water | |
| Density of phase 1, (kg/m3) | 6800 | 998 |
| Dynamic viscosity of phase 1, (Pa·s) | 0.0068 | 0.001 |
| Density of phase 2, (kg/m3) | 2800 | 855 |
| Dynamic viscosity of phase 2, (Pa·s) | 0.43 | 0.131, 0.254 |
| Experimental Group Number | Δp bar | Initial l–l Interface Level mm | Oil Viscosity Pa·s | Initial Oil Layer Thickness mm |
|---|---|---|---|---|
| 1 | 0.3 | 10 | 0.131 | 20–100 |
| 2 | 0.2 | 10 | 0.131 | - |
| 3 | 0.4 | 10 | 0.131 | - |
| 4 | 0.3 | 5 | 0.131 | - |
| 5 | 0.3 | 20 | 0.131 | - |
| 6 | 0.3 | 10 | 0.254 | - |
| Initial Oil Layer Thickness mm | Experimental Group | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||||
| hl-g,e mm | hl-l,e mm | hl-g,e mm | hl-l,e mm | hl-g,e mm | hl-l,e mm | hl-g,e mm | hl-l,e mm | hl-g,e mm | hl-l,e mm | hl-g,e mm | hl-l,e mm | |
| 20 | 28.2 | +8.0 | 26.7 | +6.6 | 30.9 | +10.4 | 25.8 | +5.2 | 31.2 | +12.0 | 25.8 | +6.2 |
| 30 | 33.1 | +3.4 | 30.9 | +1.3 | 35.7 | +5.7 | 32.8 | +2.8 | 35.6 | +6.4 | 30.6 | +1.4 |
| 35 | 35.6 | +1.3 | 32.8 | 1.5 | — | — | 35.6 | +0.2 | — | — | 33.1 | 1.0 |
| 40 | 37.9 | 1.0 | 34.3 | 4.8 | 40.5 | +1.7 | 37.9 | 1.7 | 39.8 | +1.1 | 35.0 | 3.4 |
| 45 | — | — | — | — | 43.4 | 0.6 | — | — | 42.1 | 2.1 | — | — |
| 50 | 42.5 | 6.0 | 37.6 | 11.1 | 45.6 | 3.3 | 43.5 | 5.7 | 44.1 | 4.3 | 39.9 | 8.2 |
| 60 | 46.6 | 12.2 | 40.4 | 18.7 | 50.5 | 7.7 | 48.1 | 11.7 | 48.0 | 10.2 | 44.7 | 13.3 |
| 70 | 50.8 | 18.1 | 42.6 | 25.7 | 55.5 | 13.4 | 51.6 | 17.2 | 51.8 | 16.9 | 49.0 | 18.8 |
| 80 | 54.2 | 23.5 | 45.1 | 31.9 | 59.3 | 18.6 | 55.7 | 23.7 | 55.6 | 22.5 | 52.8 | 24.5 |
| 90 | 58.4 | 29.1 | 47.5 | 39.1 | 63.6 | 24.5 | 58.8 | 28.8 | 59.7 | 28.8 | 56.9 | 30.2 |
| 100 | 60.9 | 35.0 | 50.9 | 45.7 | 68.7 | 29.2 | 63.3 | 35.0 | 62.0 | 35.5 | 60.2 | 35.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Shao, L.; Saxén, H. Experimental Model Study of Liquid–Liquid and Liquid–Gas Interfaces during Blast Furnace Hearth Drainage. Metals 2020, 10, 496. https://doi.org/10.3390/met10040496
Liu W, Shao L, Saxén H. Experimental Model Study of Liquid–Liquid and Liquid–Gas Interfaces during Blast Furnace Hearth Drainage. Metals. 2020; 10(4):496. https://doi.org/10.3390/met10040496
Chicago/Turabian StyleLiu, Weiqiang, Lei Shao, and Henrik Saxén. 2020. "Experimental Model Study of Liquid–Liquid and Liquid–Gas Interfaces during Blast Furnace Hearth Drainage" Metals 10, no. 4: 496. https://doi.org/10.3390/met10040496
APA StyleLiu, W., Shao, L., & Saxén, H. (2020). Experimental Model Study of Liquid–Liquid and Liquid–Gas Interfaces during Blast Furnace Hearth Drainage. Metals, 10(4), 496. https://doi.org/10.3390/met10040496






