Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Fabrication by Additive Manufacturing
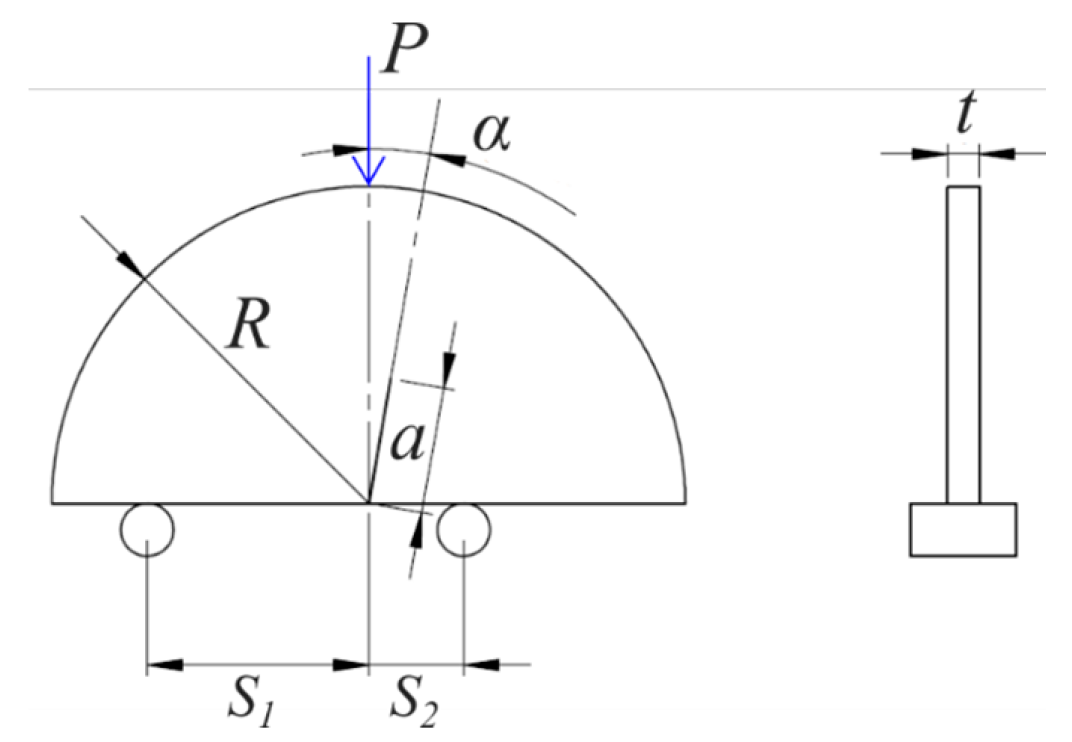
2.2. IASB Specimens
- (1)
- S1/R and S2/R (the ratio between the support spans and the specimen radius);
- (2)
- a/R (the ratio between the crack length and the specimen radius);
- (3)
- α (the angle between the crack line and the load direction).
2.3. Experimental Setup
3. Results
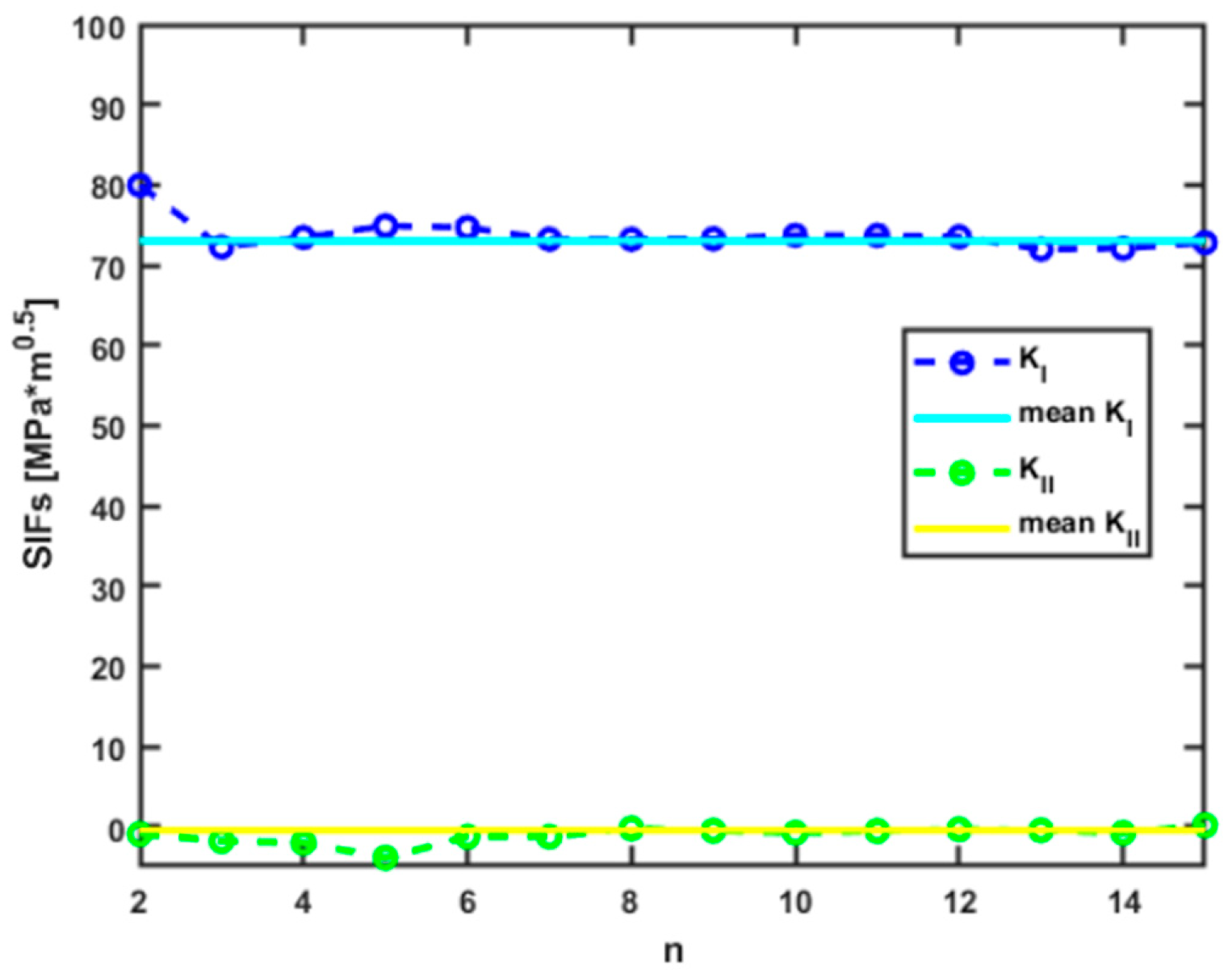
3.1. Evaluation of Stress Intensity Factors by the Critical Fracture Load Method
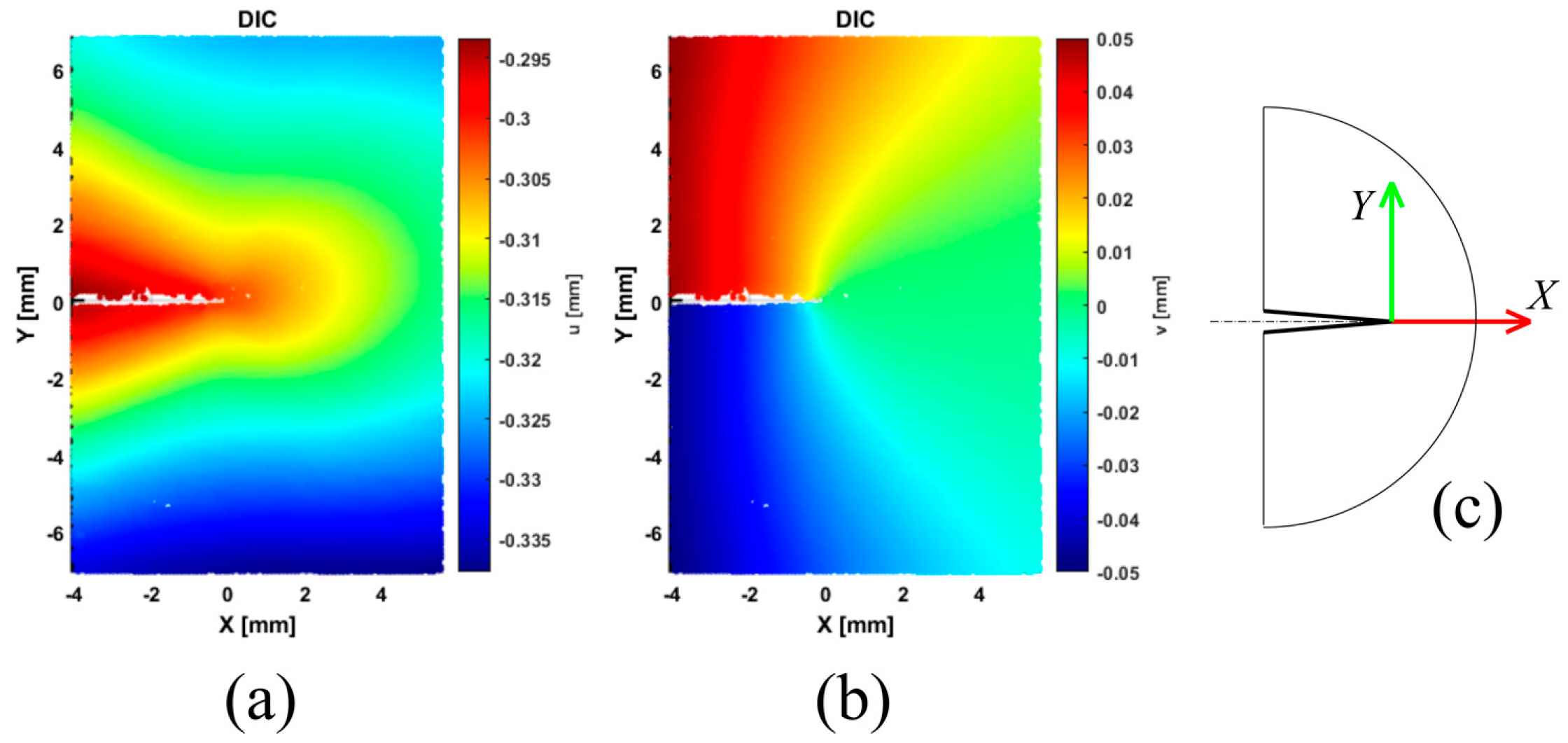
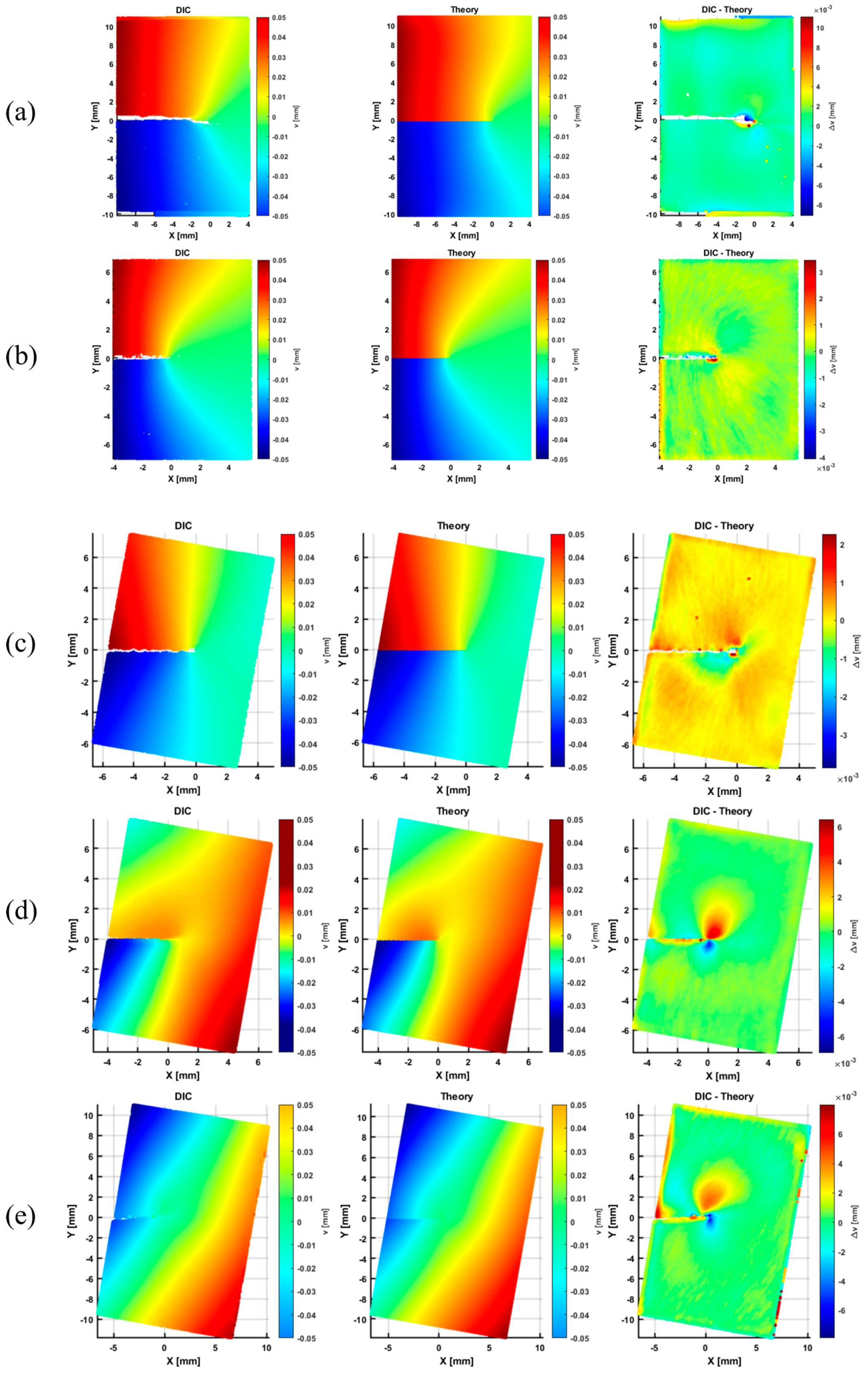
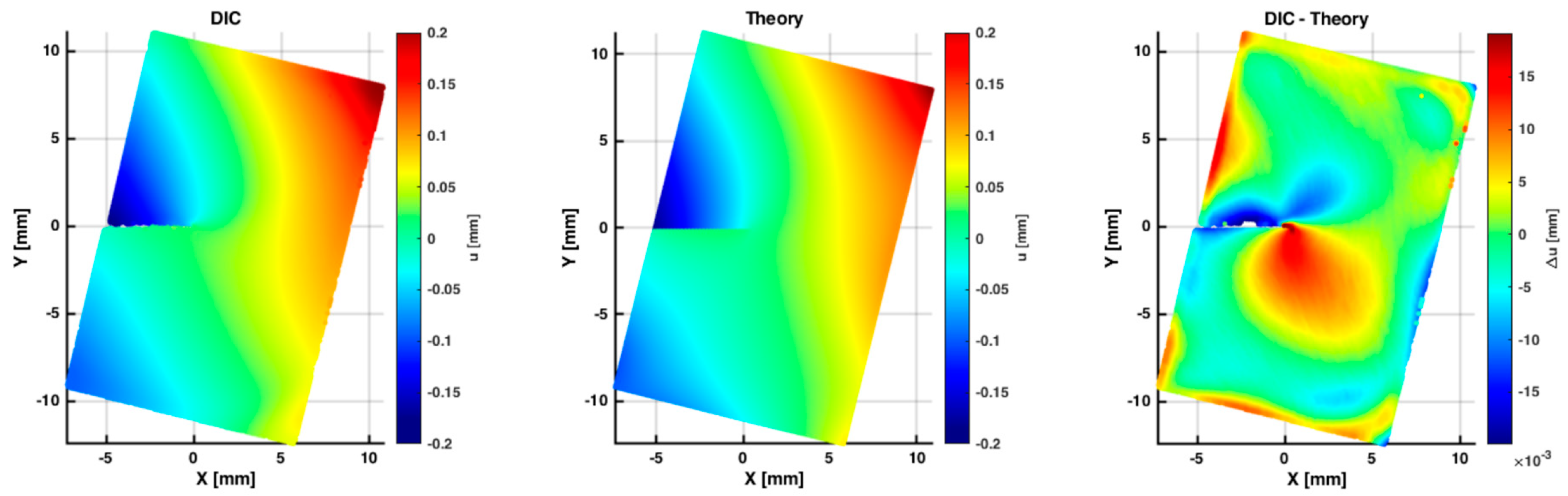
3.2. Evaluation of Stress Intensity Factors by the DIC Full Displacement Field
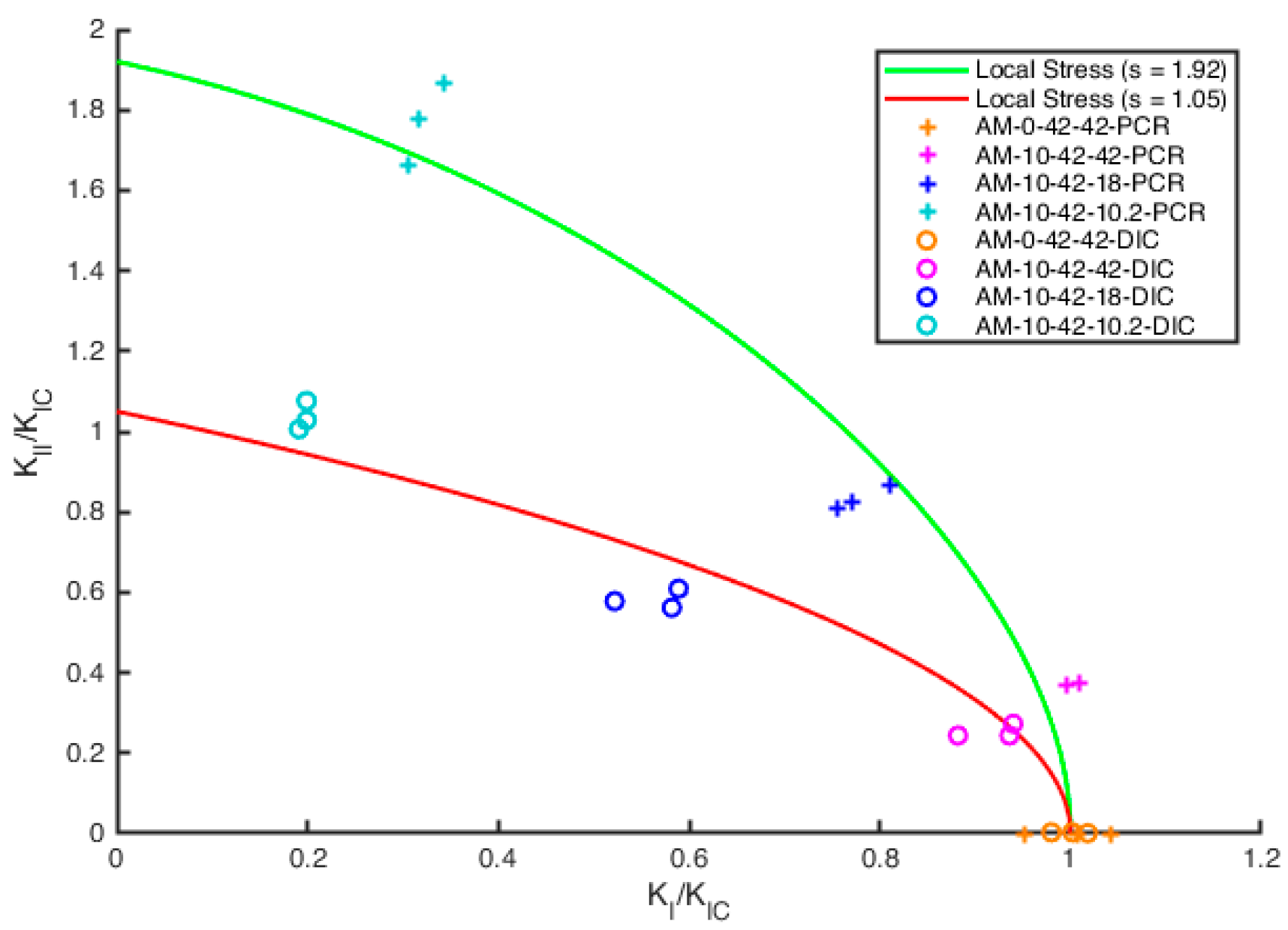
3.3. Generalized Mixed-Mode Local Stress Criterium
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kruth, J.; Mercelis, P.; van Vaerenbergh, J.; Froyen, L.; Rombouts, M. Binding mechanisms in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2005, 11, 26–36. [Google Scholar] [CrossRef]
- Zhang, W.; Melcher, R.; Travitzky, N.; Bordia, R.K.; Greil, P. Three-dimensional printing of complex-shaped alumina/glass composites. Adv. Eng. Mater. 2009, 11, 1039–1043. [Google Scholar] [CrossRef]
- Brugo, T.; Palazzetti, R.; Ciric-Kostic, S.; Yan, X.T.; Minak, G.; Zucchelli, A. Fracture Mechanics of laser sintered cracked polyamide for a new method to induce cracks by additive manufacturing. Polym. Test. 2016, 50, 301–308. [Google Scholar] [CrossRef]
- Williams, J.G.; Ewing, P.D. Fracture under complex stress—The angled crack problem. Int. J. Fract. Mech. 1972, 8, 441–446. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Poniridis, P.I. Crack initiation under biaxial loading with higher-order approximation. Eng. Fract. Mech. 1989, 32, 351–360. [Google Scholar] [CrossRef]
- Silva, A.L.L.; de Jesus, A.M.P.; Xavier, J.; Correia, J.A.F.O.; Fernandes, A.A. Combined analytical-numerical methodologies for the evaluation of mixed-mode (I + II) fatigue crack growth rates in structural steels. Eng. Fract. Mech. 2017, 185, 124–138. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Ayatollahi, M.R. Brittle fracture evaluation of a fine grain cement mortar in combined tensile-shear deformation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 987–994. [Google Scholar] [CrossRef]
- Lim, I.L.; Johnston, I.W.; Choi, S.K.; Boland, J.N. Fracture testing of a soft rock with semi-circular specimens under three-point bending. Part 2—Mixed-mode. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 199–212. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M.; Saghafi, H. An improved semi-circular bend specimen for investigating mixed mode brittle fracture. Eng. Fract. Mech. 2011, 78, 110–123. [Google Scholar] [CrossRef]
- Darban, H.; Haghpanahi, M.; Assadi, A. Determination of crack tip parameters for ascb specimen under mixed mode loading using finite element method. Comput. Mater. Sci. 2011, 50, 1667–1674. [Google Scholar] [CrossRef]
- Saghafi, H.; Monemian, S.A. New fracture toughness test covering mixed-mode conditions and positive and negative t-stresses. Int. J. Fract. 2010, 165, 135–138. [Google Scholar] [CrossRef]
- Saghafi, H.; Zucchelli, A.; Minak, G. Evaluating fracture behavior of brittle polymeric materials using an IASCB specimen. Polym. Test. 2013, 32, 133–140. [Google Scholar] [CrossRef]
- Moore, A.J.; Tyrer, J.R. The evaluation of fracture mechanics parameters from electronic speckle pattern interferometric fringe patterns. Opt. Lasers Eng. 1993, 19, 325–336. [Google Scholar] [CrossRef]
- Peters, H.W.; Ranson, F.W. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar]
- McNeill, S.R.; Peters, W.H.; Sutton, M.A. Estimation of stress intensity factor by digital image correlation. Eng. Fract. Mech. 1987, 28, 101–112. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity, 4th ed.; Springer: Berlin, Germany, 1977. [Google Scholar]
- Nurse, A.D.; Patterson, E.A. Determination of predominantly mode II stress intensity factors from isochromatic data. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 1339–1354. [Google Scholar] [CrossRef]
- Lopez-Crespo, P.; Shterenlikht, A.; Patterson, E.A.; Yates, J.R.; Withers, P.J. The stress intensity of mixed mode cracks determined by digital image correlation. J. Strain Anal. Eng. Des. 2008, 43, 769–780. [Google Scholar] [CrossRef]
- Yoneyama, S.; Ogawa, T.; Kobayashi, Y. Evaluating mixed-mode stress intensity factors from full-field displacement fields obtained by optical methods. Eng. Fract. Mech. 2007, 74, 1399–1412. [Google Scholar] [CrossRef]
- Yates, J.R.; Zanganeh, M.; Asquith, D.; Tai, Y.H. Quantifying Crack Tip Displacement Fields: T-Stress and CTOA. In Proceedings of the Crack Paths, Vicenza, Italy, 23–25 September 2009. [Google Scholar]
- Beretta, S.; Patriarca, L.; Rabbolini, S. Stress intensity factor calculation from displacement fields. Frat. ED Integrità Strutt. 2017, 11, 269–276. [Google Scholar] [CrossRef]
- Bonniot, T.; Doquet, V.; Mai, S.H. Determination of effective stress intensity factors under mixed-mode from digital image correlation fields in presence of contact stresses and plasticity. Strain 2020, 56, e12332. [Google Scholar] [CrossRef]
- Croccolo, D.; de Agostinis, M.; Fini, S.; Olmi, G.; Vranic, A.; Ciric-Kostic, S. Influence of the build orientation on the fatigue strength of eos maraging steel produced by additive metal machine: How the build direction affects the fatigue strength of additive manufacturing processed parts. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 637–647. [Google Scholar] [CrossRef]
- Palanca, M.; Brugo, T.M.; Cristofolini, L. Use of digital image correlation to investigate the biomechanics of the vertebra. J. Mech. Med. Biol. 2015, 15, 1540004. [Google Scholar] [CrossRef]
- Williams, M.L. On the stress distribution at the base of a stationary crack. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Tan, C.; Zhou, K.; Ma, W.; Zhang, P.; Liu, M.; Kuang, T. Microstructural evolution, nanoprecipitation behavior and mechanical properties of selective laser melted high-performance grade 300 maraging steel. Mater. Des. 2017, 134, 23–34. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Threshold stress intensity factor and crack growth rate prediction under mixed-mode loading. Eng. Fract. Mech. 2007, 74, 332–345. [Google Scholar] [CrossRef]
- Smith, D.J.; Ayatollahi, M.R.; Pavier, M.J. The role of t-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 137–150. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 3rd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2005. [Google Scholar]
- Abd-Elhady, A.A. Mixed mode I/II stress intensity factors through the thickness of disc type specimens. Eng. Solid Mech. 2013, 1, 119–128. [Google Scholar] [CrossRef]


| Property | Value |
|---|---|
| Sintered Density | 8.0–8.1 g/cm³ |
| Elastic Modulus | 180 ± 20 GPa |
| Yield Strength | min. 1862 MPa |
| Tensile Strength | min. 1930 MPa |
| Hardness | typ. 50–56 HRC |
| Ductility (Notched Charpy Impact Test) | 11 ± 4 J |
| Type | α (deg) | S2 (mm) | S1 (mm) | n | Mode | Me |
|---|---|---|---|---|---|---|
| SM | 0 | 42 | 42 | 3 | Mode I | 1 |
| AM | 0 | 42 | 42 | 3 | Mode I | 1 |
| AM | 10 | 42 | 42 | 3 | Mixed I-II | 0.77 |
| AM | 10 | 42 | 18 | 3 | Mixed I-II | 0.48 |
| AM | 10 | 42 | 10.2 | 3 | Mode II | 0.12 |
| Specimen Configuration | By Critical Fracture Load (PCR) | By Crack Tip Displacement Field (DIC) | DIC vs. PCR | |||
|---|---|---|---|---|---|---|
| KI (MPa | KII (MPa | Δ KI (%) | Δ KII (%) | |||
| SM-0-42-42-1 | 32.1 | 0.0 | 58.3 | 1.2 | 81 | - |
| SM-0-42-42-2 | 30.4 | 0.0 | 56.1 | 2.9 | 85 | - |
| SM-0-42-42-3 | 33.7 | 0.0 | 60.5 | 2.3 | 80 | - |
| AM-0-42-42-1 | 42.5 | 0.0 | 73.5 | 0.2 | 73 | - |
| AM-0-42-42-2 | 44.9 | 0.0 | 76.4 | 0.1 | 70 | - |
| AM-0-42-42-3 | 46.6 | 0.0 | 75.2 | 0.2 | 61 | - |
| AM-10-42-42-1 | 44.4 | 16.5 | 70.5 | 20.5 | 59 | 25 |
| AM-10-42-42-2 | 44.6 | 16.5 | 66.2 | 18.3 | 49 | 11 |
| AM-10-42-42-3 | 45.1 | 16.7 | 70.2 | 18.3 | 56 | 10 |
| AM-10-42-18-1 | 33.7 | 36.1 | 43.7 | 42.2 | 30 | 17 |
| AM-10-42-18-2 | 36.3 | 38.8 | 39.2 | 43.4 | 8 | 12 |
| AM-10-42-18-3 | 34.4 | 36.9 | 44.2 | 45.7 | 28 | 24 |
| AM-10-42-10.2-1 | 15.3 | 83.5 | 14.9 | 77.1 | -2 | -8 |
| AM-10-42-10.2-2 | 13.6 | 74.2 | 14.4 | 75.5 | 5 | 2 |
| AM-10-42-10.2-3 | 14.2 | 79.4 | 14.9 | 80.8 | 5 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campione, I.; Brugo, T.M.; Minak, G.; Tomić, J.J.; Bogojević, N.; Kostić, S.Ć. Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch. Metals 2020, 10, 400. https://doi.org/10.3390/met10030400
Campione I, Brugo TM, Minak G, Tomić JJ, Bogojević N, Kostić SĆ. Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch. Metals. 2020; 10(3):400. https://doi.org/10.3390/met10030400
Chicago/Turabian StyleCampione, Ivo, Tommaso Maria Brugo, Giangiacomo Minak, Jelena Janković Tomić, Nebojša Bogojević, and Snežana Ćirić Kostić. 2020. "Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch" Metals 10, no. 3: 400. https://doi.org/10.3390/met10030400
APA StyleCampione, I., Brugo, T. M., Minak, G., Tomić, J. J., Bogojević, N., & Kostić, S. Ć. (2020). Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch. Metals, 10(3), 400. https://doi.org/10.3390/met10030400






