Transient Simulation of Bath Temperature inside Aluminum Reduction Cells
Abstract
:1. Introduction
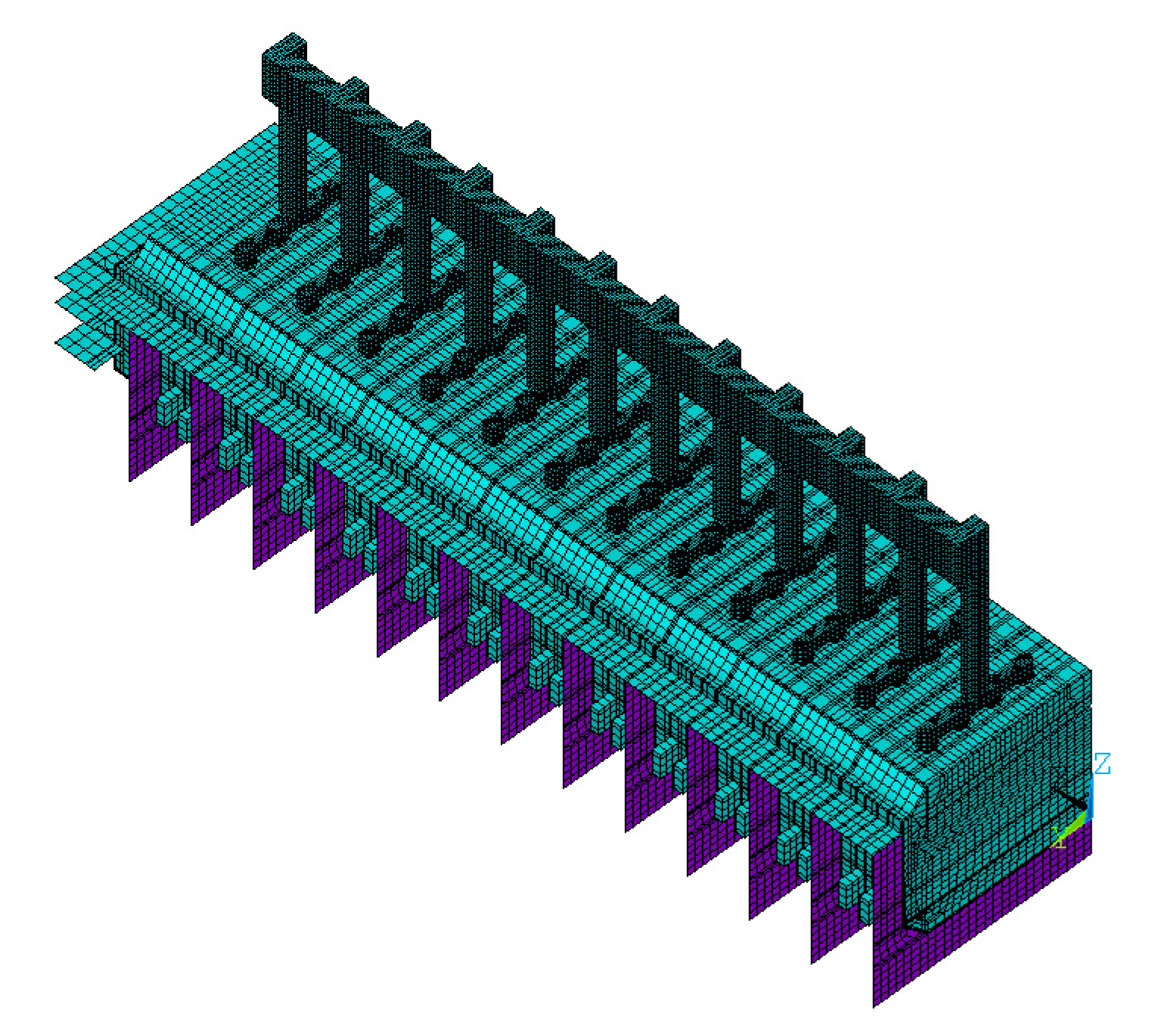
2. Finite Element Simulation Model
2.1. Model Simplification and Assumptions
- (1).
- There is no crust or sludge in the molten aluminum.
- (2).
- Both the superheat and flow rate are sufficient such that alumina can be completely dissolved without sediments.
- (3).
- No influences of other operations are considered. Parameters of the aluminum reduction cell for modeling are listed in Table 1.
2.2. Control Equation
- J is the current density, A·m−2;
- E is the electrical field, V·m−1;
- U is the electrical potential, V;
- is the electrical conductivity, Ω−1·m−1, changing along with temperature;
- p is the change density;
- is the permittivity.
- T—Temperature, K;
- t—time, s;
- kx, ky, kz—thermal conductivity, W·m−1K−1;
- qS—strength of heat source or sink, J/m3, including Joule self-heating power and the other heat generation rate defined in the model.
- ρ—material density, kg/m3;
- c—thermal capacity, W·kg−1K−1.
2.3. Material Properties and Boundary Conditions
- (1).
- Heat convection and radiation boundary conditions are applied on the pot’s external surface. The heat convection coefficient of the pot’s side is 5 w·m−1K−1; that of the anode cover’s surface is 10 w·m−1K−1; and that of the anode butt/rod’s surface is 15 w·m−1K−1.
- (2).
- Current input conditions are applied on the anode rod’s top.
- (3).
- Zero potential conditions are applied on the steel bar’s end.
2.4. Simulation Conditions
2.4.1. Numerical Scheme
2.4.2. Mesh Resolution
2.4.3. Convergence and Tolerance
3. Results
3.1. Comparison with Measurement Data
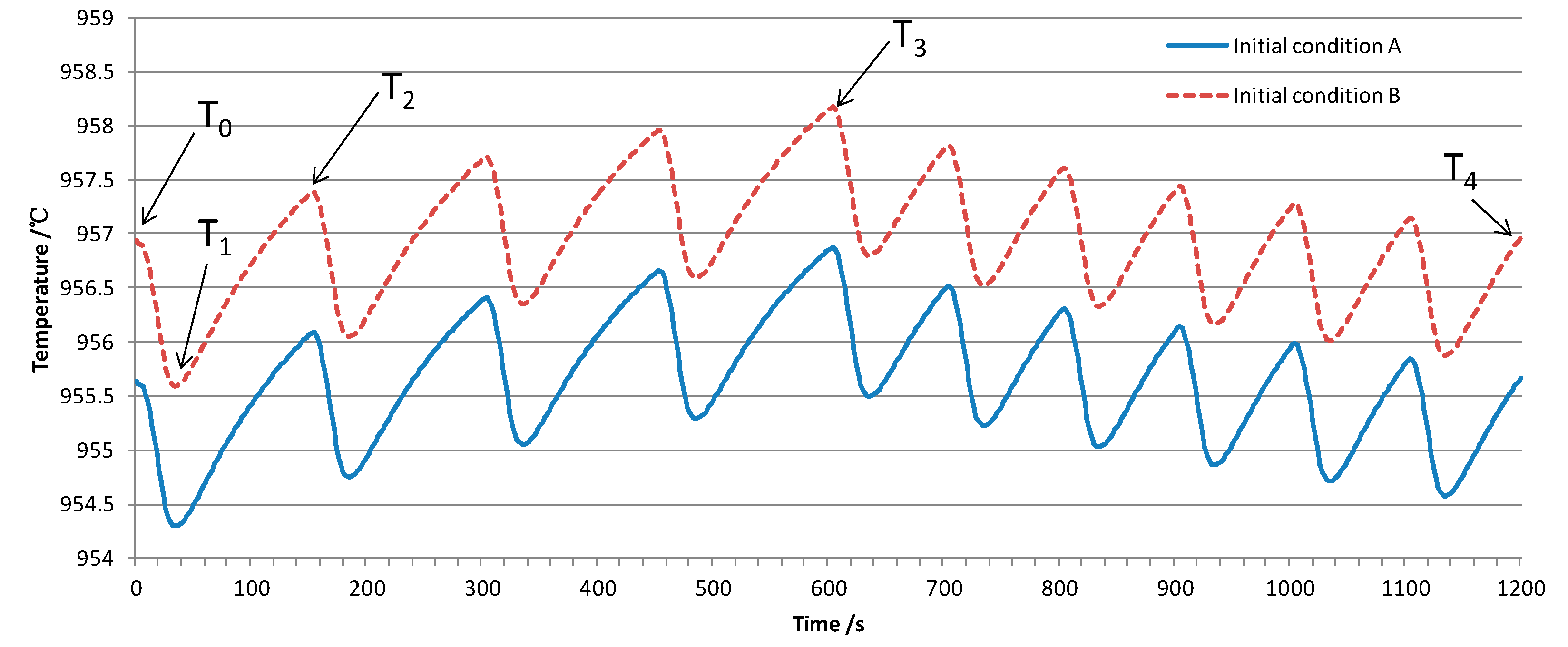
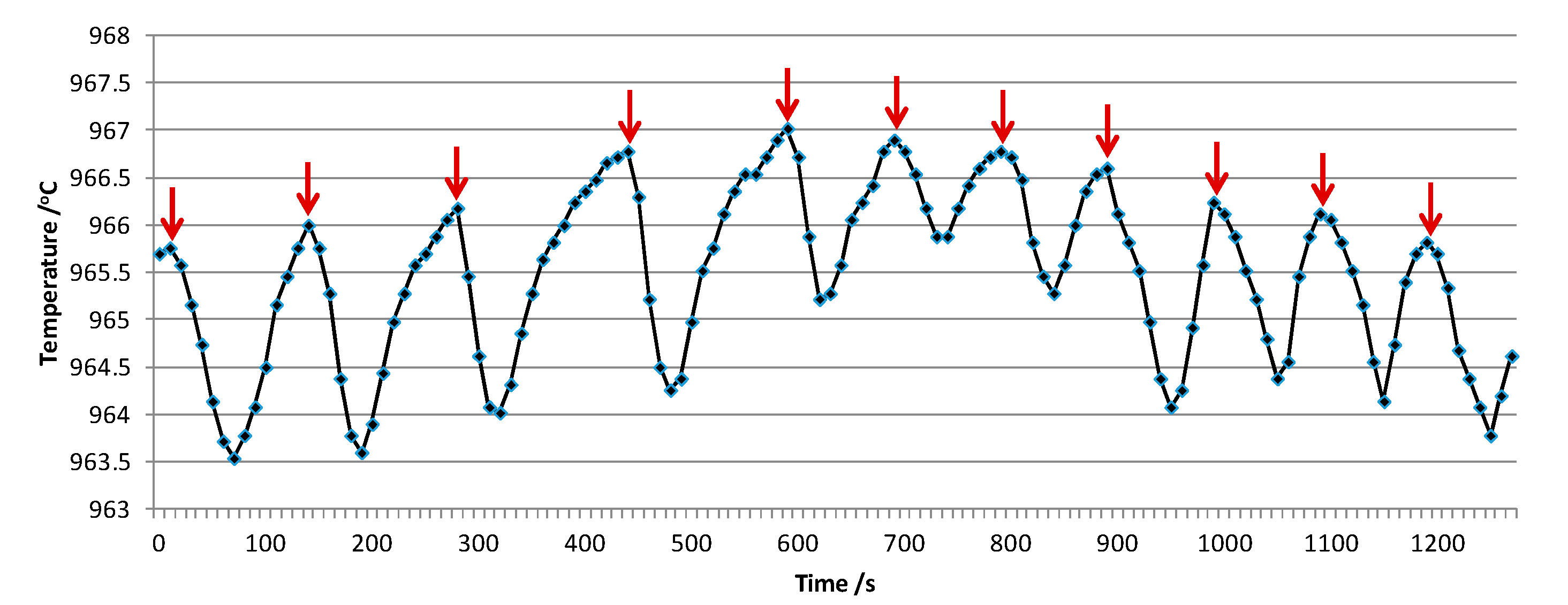
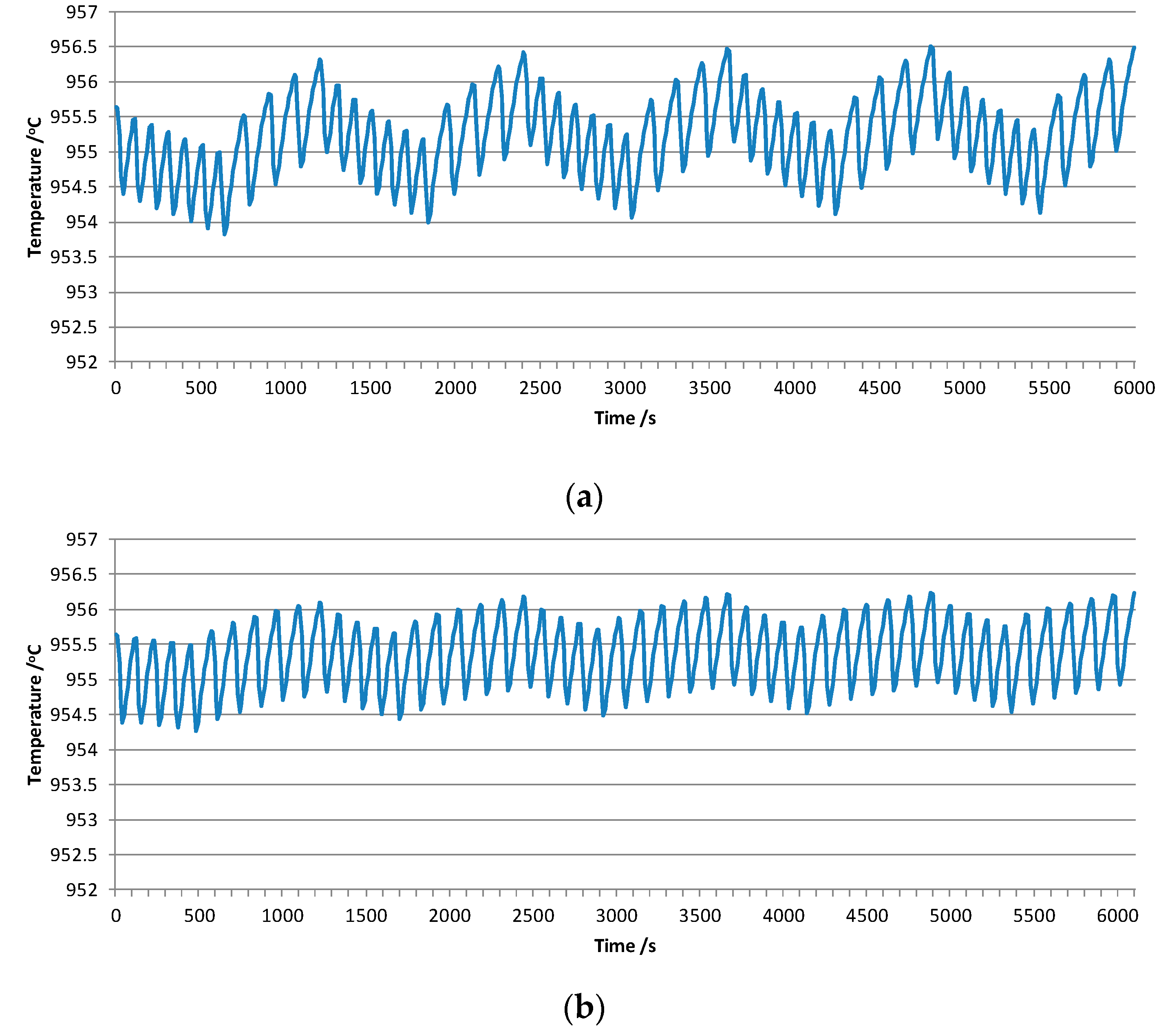
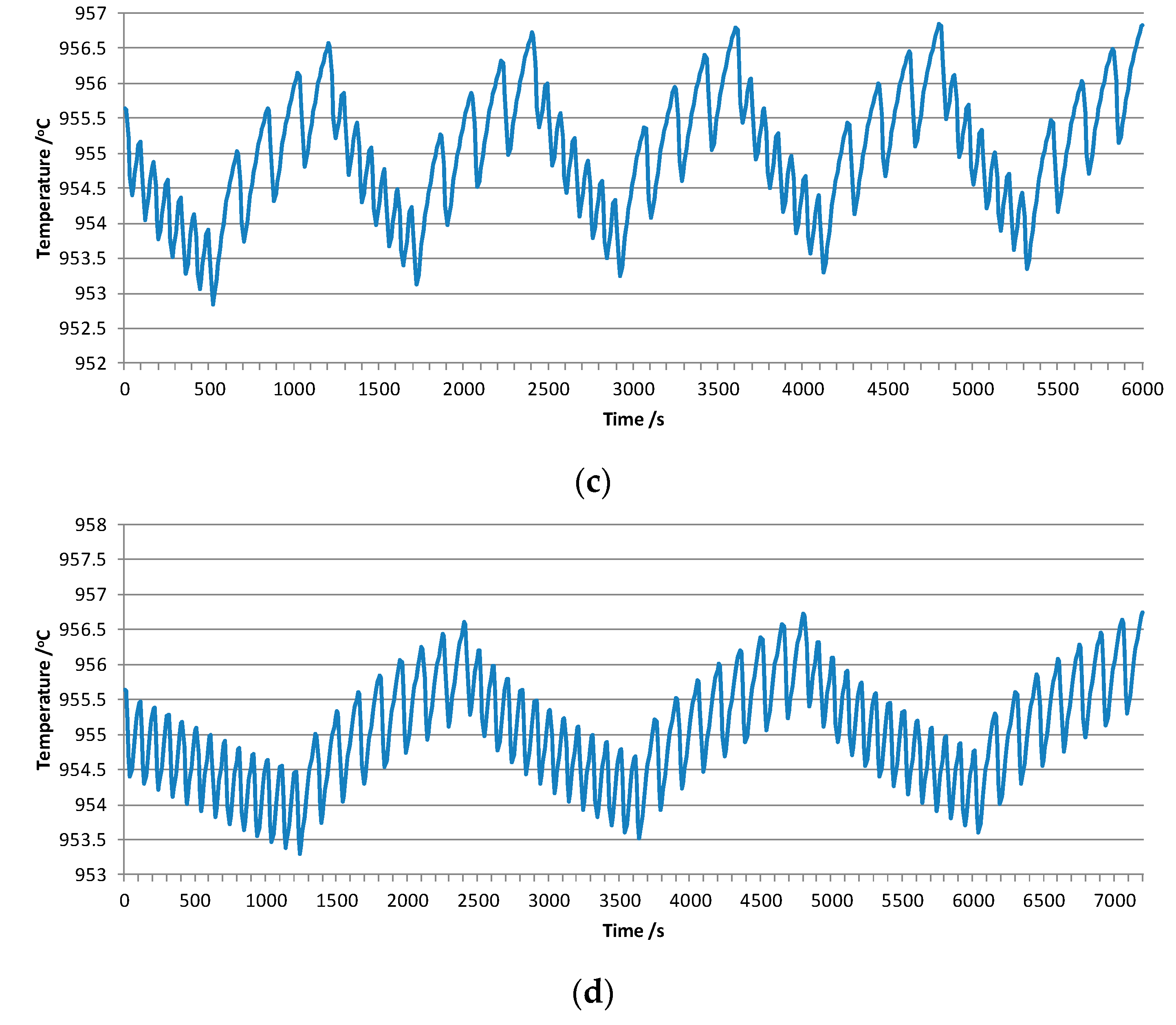
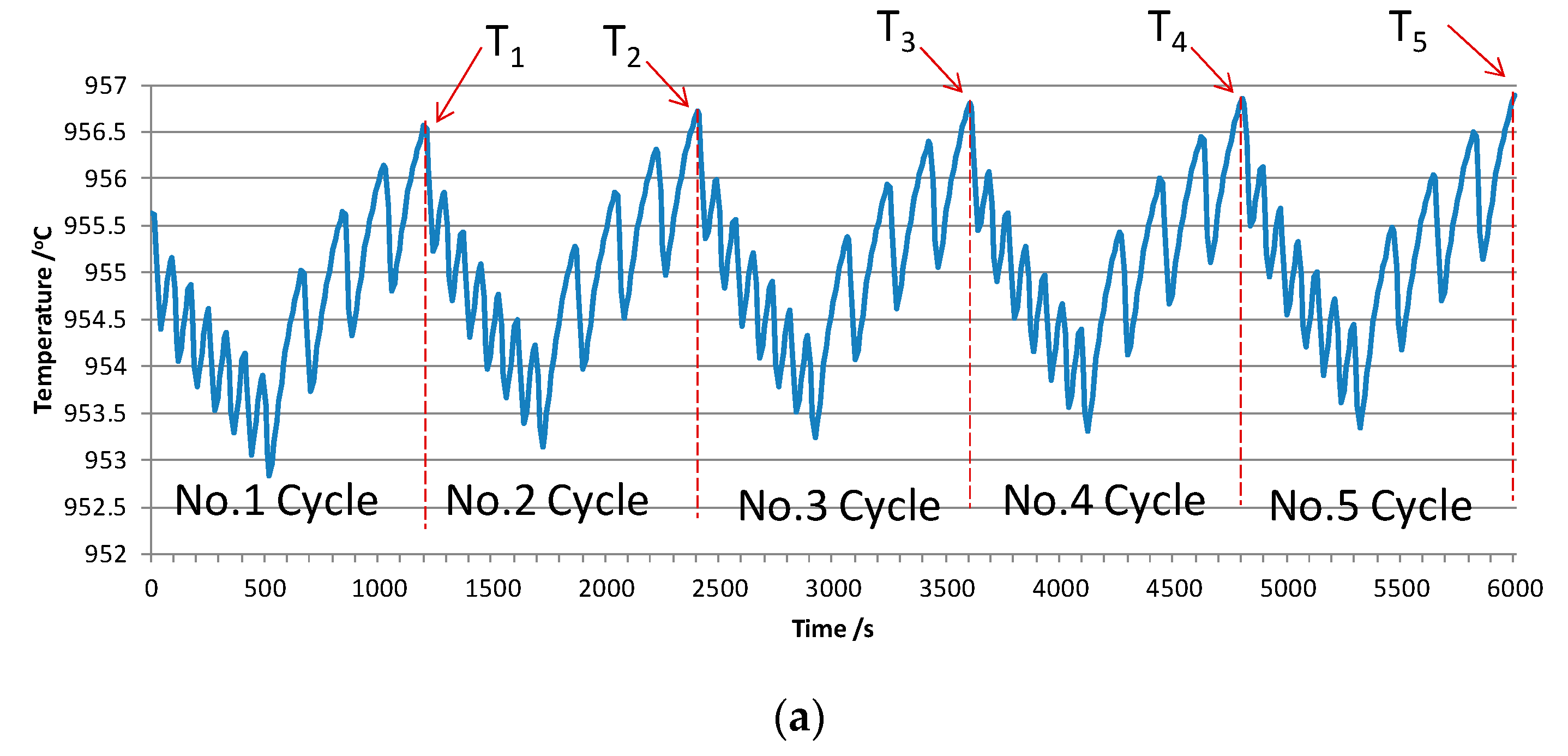
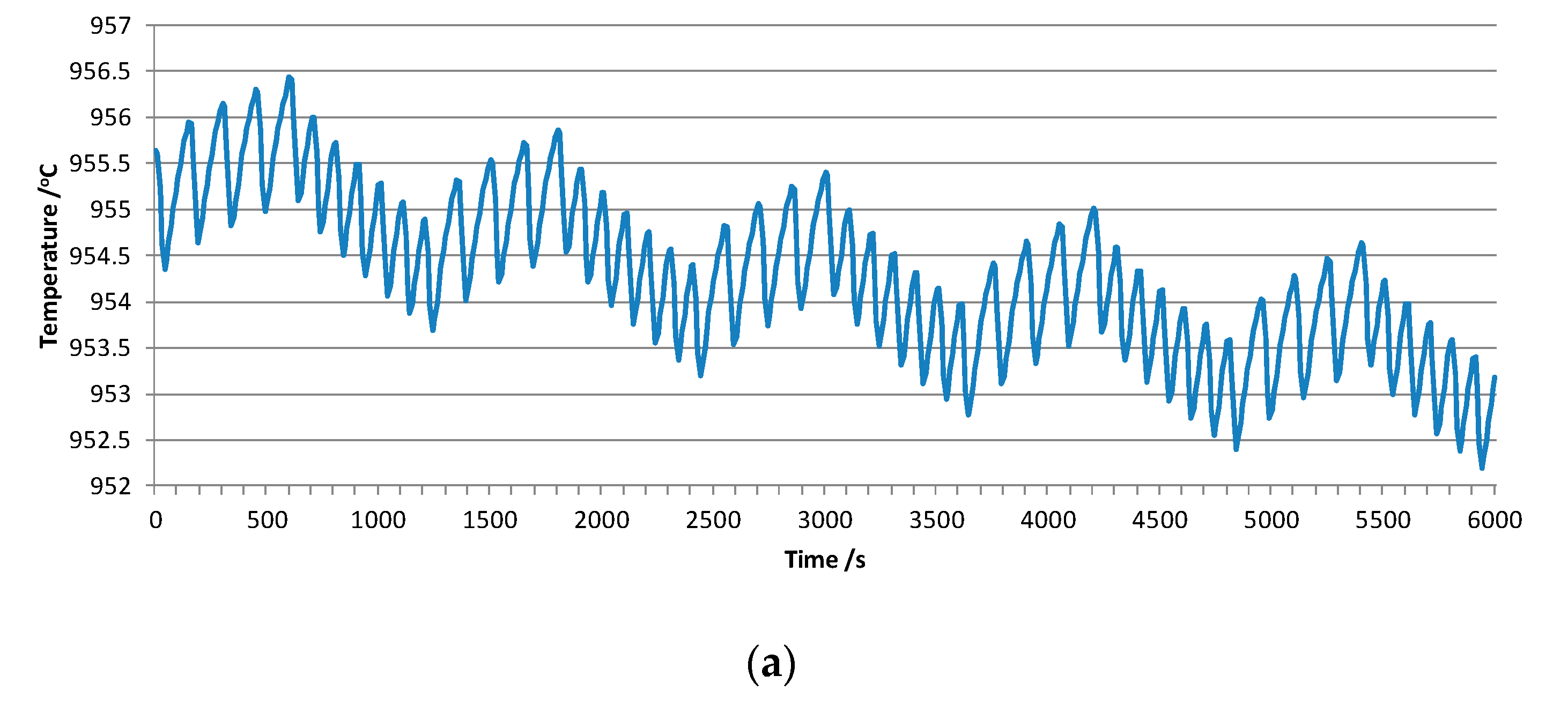
3.1.1. Typical Simulated Curve
3.1.2. Sensitivity of the Simulated Curve
3.1.3. Measurement Data
- Cell amperage: 500 kA.
- Cell conditions: cell voltage was 3.96 v; metal level was 30 cm; bath level was 18 cm.
- Dose weight of six feeders: 1.79–1.82 kg; average 1.8 kg.
- Thermocouple type: K type; precision is 0.1 °C.
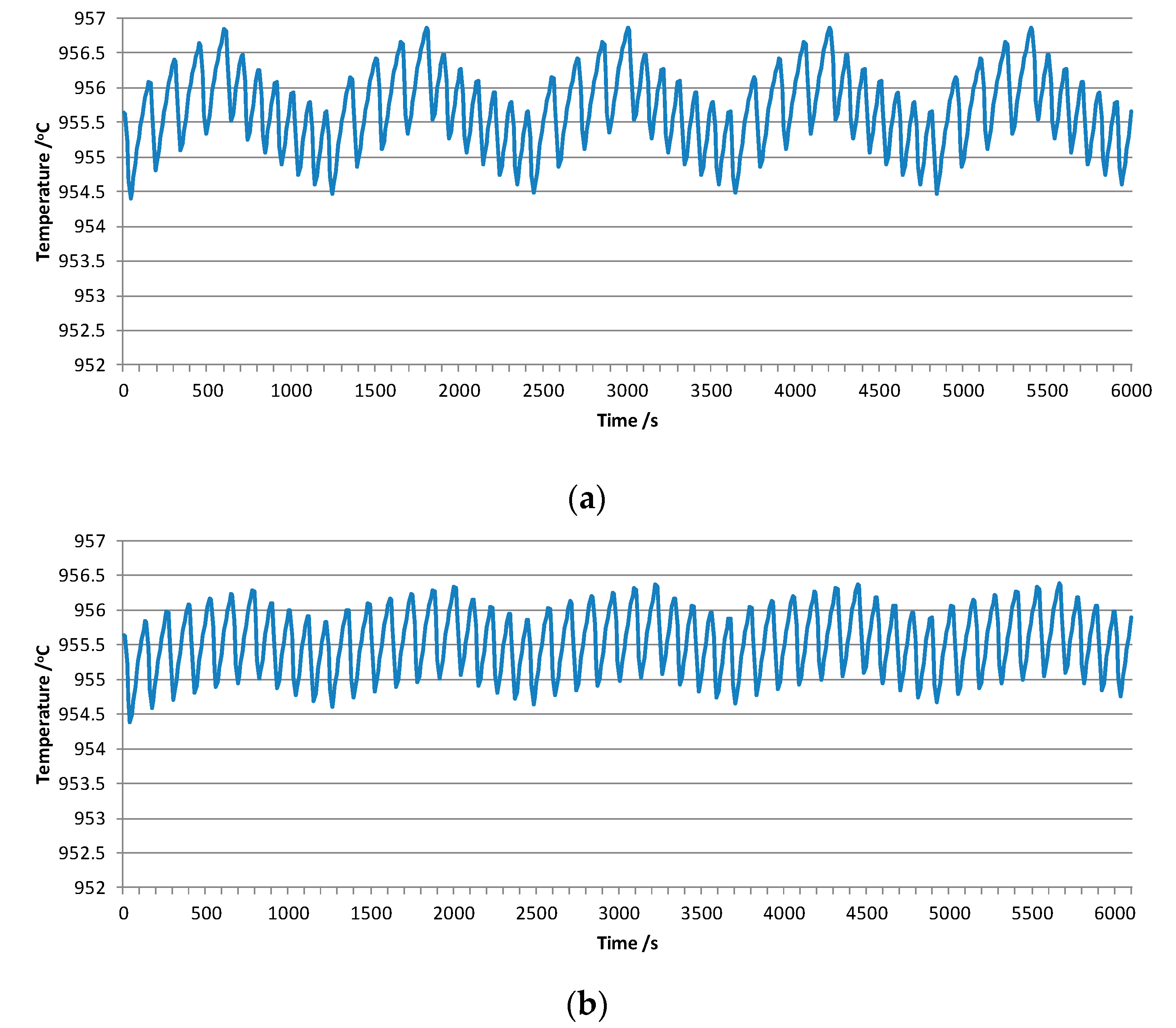
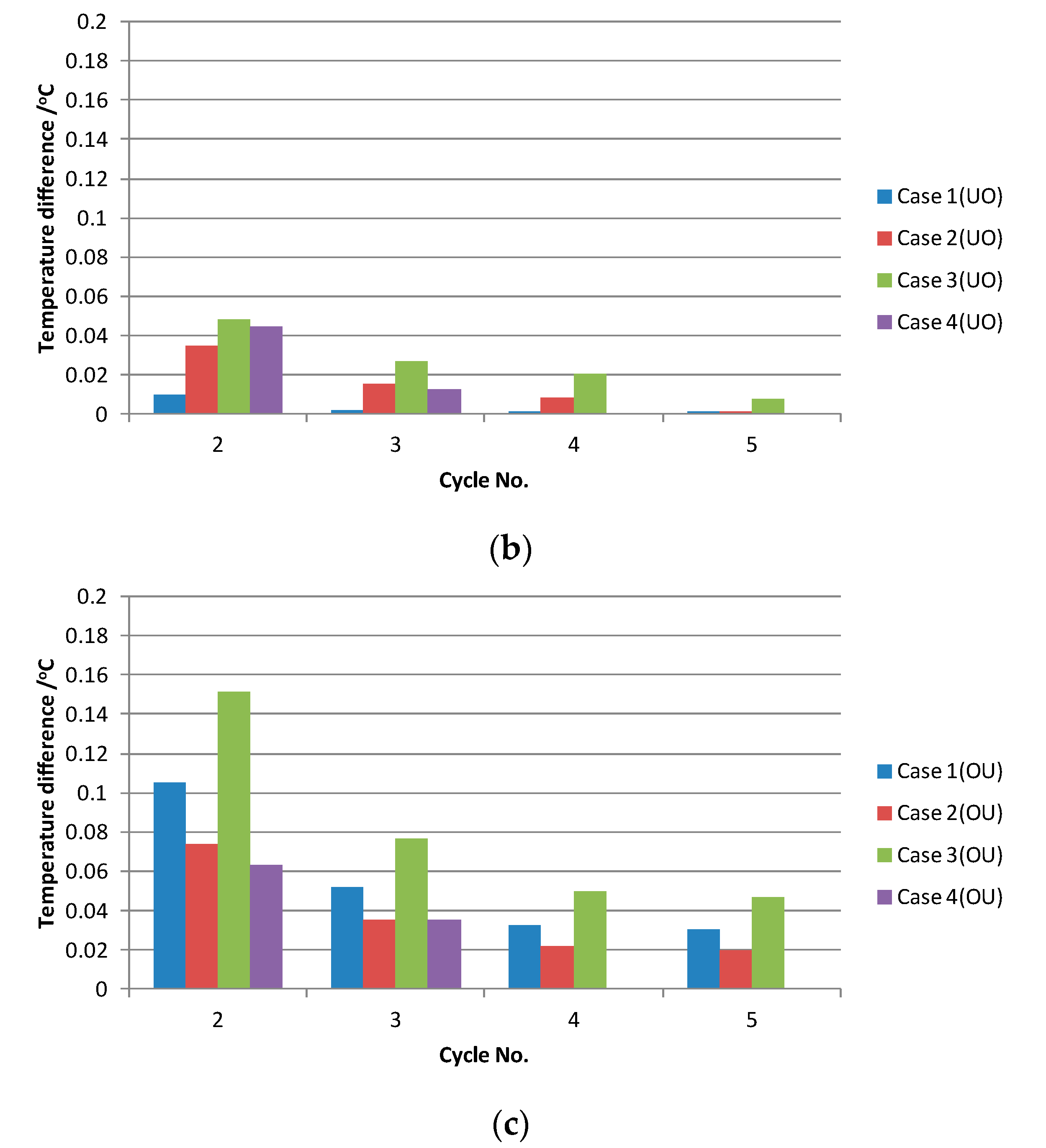
3.2. Influences of Different Feeding Interval Systems
3.3. Influence of the Ratio between Pheat and Pfeeding on Temperature Fluctuation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bielder, P.; Banta, L. Analysis and Correction of Heat Balance Issues in Aluminum Reduction Cells. In Proceedings of the TMS Light Metals, San Diego, CA, USA, 2–6 March 2003; pp. 441–448. [Google Scholar]
- Taylor, M.P.; Welch, B.J.; Keniry, J.T. Effect of Electrochemical Changes on the Heat Balance in Aluminum Smelting Cells. J. Electroanal. Chem. Interfacial Electrochem. 1984, 168, 179–192. [Google Scholar] [CrossRef]
- Liu, J.; Taylor, M.P.; Dorreen, M. Observations of freeze layer formation during heat balance shifts in cryolite-based smelting bath. Int. J. Mater. Res. 2017, 108, 507–514. [Google Scholar] [CrossRef]
- Valles, A.; Lenis, V.; Rao, M. Prediction of Ledge Profile in Hall-Heroult Cells. In Proceedings of the TMS Light Metals, Las Vegas, NV, USA, 12–16 February 1995; pp. 309–313. [Google Scholar]
- Ahmed, H. Prediction of the Thermal Aspects of Egyptalum Prototype High-amperage Pre-baked Aluminum Reduction Cells. In Proceedings of the TMS Light Metals, San Francisco, CA, USA, 27 February–3 March 1994; pp. 333–338. [Google Scholar]
- Taylor, M.P.; Liu, X.; Fraser, K.J. The Dynamics and Performance of Reduction Cell Electrolytes. In Proceedings of the TMS Light Metals, Anaheim, CA, USA, 18–22 February 1990; pp. 259–266. [Google Scholar]
- Pei-lin, D.; Heng, W.; Jun, H. Effect of feeding in aluminum reduction cell on electrolyte temperature. Chin. J. Nonferrous Met. 2016, 26, 430–438. [Google Scholar]
- Thonstad, J.; Solherim, A.; Rolseth, S. The dissolution of alumina in cryolite melts. In Essential Readings in Light Metals; Bearne, G., Ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Thomas, H. Numerical Simulation and Optimization of the Alumina Distribution in an Aluminium Electrolysis pot. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2011. [Google Scholar]
- Li, M.; Gao, Y.; Bai, X.; Li, Y.; Hou, W.; Wang, Y. Simulation of alumina particle dissolution in 300 kA aluminum electrolytic cell. Chin. J. Nonferrous Metals 2017, 27, 1738–1747. [Google Scholar]
- You-Cai, L. Kinetics Study of Alumina Crust Formation and Dissolution in Aluminum Electrolysis. Ph.D. Thesis, North East University, Shenyang, China, 2018. [Google Scholar]
- Kobbeltvedt, O.; Moxnes, B.P. On the Bath Flow, Alumina Distribution and Anode Gas Release in Aluminium Cells. In Proceedings of the TMS Light Metals, Orlando, FA, USA, 9–13 February 1997; pp. 257–264. [Google Scholar]
- Lavoie, P.; Taylor, M.P.; Metson, J.B. A review of alumina feeding and dissolution factors in aluminum reduction cells. Metall. Mater. Trans. B 2016, 47, 2690–2696. [Google Scholar] [CrossRef]
- McFadden, F.J.; Welch, B.J.; Whitfield, D. Control of Temperature in Aluminium Reduction Cells—Challenges in Measurements and Variability. In Proceedings of the TMS Light Metals, New Orleans, LA, USA, 11–15 February 2001; pp. 1171–1178. [Google Scholar]
- Soares, F.; Oliveira, R.; Castro, M. Bath Temperature Inference through Soft Sensors Using Neural Networks. In Proceedings of the TMS Light Metals, Washington, DC, USA, 14–18 February 2010; pp. 467–472. [Google Scholar]
- Bruggeman, J.N.; Danka, D.J. Two-dimensional Thermal Modeling of the Hall- Héroult Cell. In Proceedings of the TMS Light Metals, Anaheim, CA, USA, 18–22 February 1990; pp. 203–209. [Google Scholar]
- Berge, B.; Grjotheim, K.; Krohn, C.; Næumann, R.; Tørklep, K. Recent studies of convection in commercial aluminum reduction cells. Metall. Trans. 1973, 4, 1945–1952. [Google Scholar] [CrossRef]
- Grjotheim, K.; Krohn, C.; Naeumann, R.; Tørklep, K. On convection in aluminum reduction cells. Metall. Trans. 1970, 1, 3133–3141. [Google Scholar]
- Fuqiang, W.; Qinsong, Z.; Wei, L.; Youjian, Y.; Zhaowen, W. Impact of local cathode electrical cut-off on bath-metal two-phase flow in an aluminum reduction cell. Metals 2020, 10, 110. [Google Scholar]
- Zhibin, Z.; Yuqing, F.; Philip, S.M.; Peter, J.W.; Zhaowen, W.; Mark, C. Numerical modeling of flow dynamics in the aluminum smelting process: Comparison between air–water and co2–cryolite systems. Metall. Mater. Trans. B 2017, 48, 1200–1216. [Google Scholar]
- Liu, Y.; Jie, L. Modern Aluminum Electrolysis; Metallurgy industry Press: Beijing, China, 2008. [Google Scholar]
- Kuschel, G.I.; Welch, B.J. Further Studies of Alumina Dissolution under Conditions Similar to Cell Operation. In Proceedings of the TMS Light Metals, New Orleans, LA, USA, 17–21 February 1991; pp. 112–118. [Google Scholar]
- Peter, K. Theory; ANSYS, Inc.: Canonsburg, PA, USA, 2005. [Google Scholar]
- Fletcher, C.A.J. Galerkin Finite-Element Methods. In Computational Galerkin Methods; Springer Series in Computational Physics; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Ansys, Handbook Ansys 9; Ansys, Inc.: Canonsburg, PA, USA, 2005.




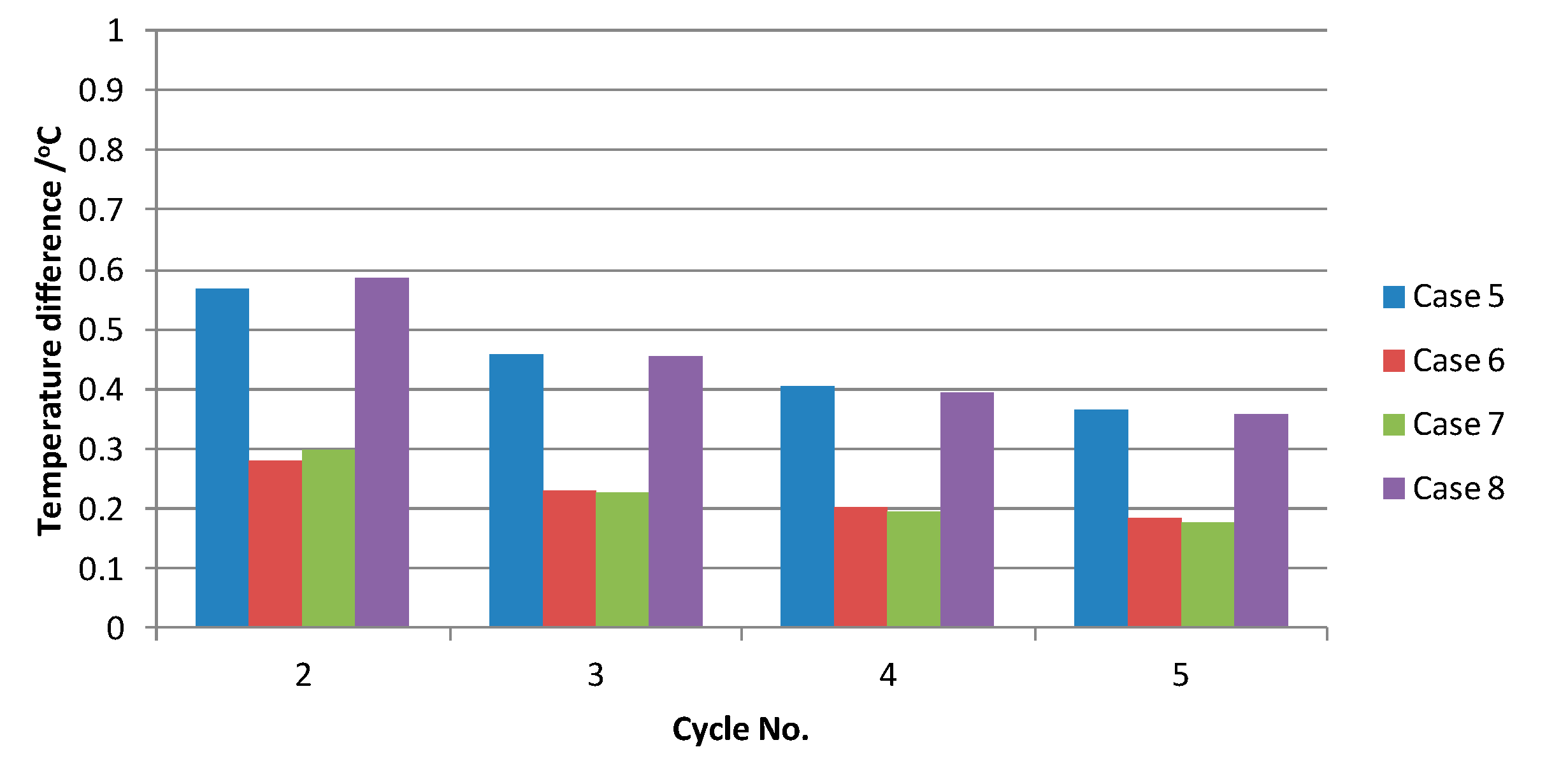
| Current/kA | Bath Level/mm | Metal Level/mm | ACD/mm | Numbers of Anode | Anode Size/mm | Anode Raphe/mm | Cathode Size/mm |
|---|---|---|---|---|---|---|---|
| 500 | 180 | 300 | 45 | 48 | 1850 × 700 × 620 | 200 | 3790 × 720 × 530 |
| Feeding Type | Item | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|---|
| Under feeding | Last time (s) | 600 | 780 | 720 | 1200 |
| Feeding intervals (s) | 150 | 130 | 180 | 150 | |
| Feeding rate (kg/s) | 0.072 | 0.083 | 0.06 | 0.072 | |
| Feeding count | 4 | 6 | 4 | 8 | |
| Over feeding | Last time (s) | 600 | 440 | 480 | 1200 |
| Feeding intervals (s) | 100 | 110 | 80 | 100 | |
| Feeding rate (kg/s) | 0.108 | 0.098 | 0.135 | 0.108 | |
| Feeding count | 6 | 4 | 6 | 12 | |
| Total feeding count | 10 | 10 | 10 | 20 | |
| Pfeeding (kW) | 240.66 | 237.71 | 240.66 | 240.66 | |
| Pheat /Pfeeding | 1 | 1 | 1 | 1 | |
| Total time for one cycle (s) | 1200 | 1220 | 1200 | 2400 | |
| Feeding Type | Item | Case 5 | Case 6 | Case 7 | Case 8 |
|---|---|---|---|---|---|
| Under feeding | Last time (s) | 600 | 600 | 600 | 600 |
| Feeding intervals (s) | 150 | 130 | 180 | 150 | |
| Feeding rate (kg/s) | 0.072 | 0.072 | 0.072 | 0.072 | |
| Feeding count | 4 | 4 | 4 | 4 | |
| Over feeding | Last time (s) | 600 | 600 | 600 | 600 |
| Feeding intervals (s) | 100 | 100 | 100 | 100 | |
| Feeding rate (kg/s) | 0.108 | 0.108 | 0.108 | 0.108 | |
| Feeding count | 6 | 6 | 6 | 6 | |
| Total feeding count | 10 | 10 | 10 | 10 | |
| Pfeeding (kW) | 240.66 | 240.66 | 240.66 | 240.66 | |
| Pheat/Pfeeding | 0.9 | 0.95 | 1.05 | 1.1 | |
| Total time for one cycle(s) | 1200 | 1200 | 1200 | 1200 | |
| Characteristic temperature | Element Size ≤ 0.06 m | Initial Condition | Psuck | Thermal Diffusivity of Bath & Metal | Feeding Interval | Differece between Pheat and Pfeeding |
|---|---|---|---|---|---|---|
| T0 | NO | Yes | NO | NO | NO | NO |
| ΔT1 | NO | NO | Yes | Yes | NO | NO |
| ΔT2 | NO | NO | Yes | Yes | Yes | Yes |
| ΔT3 | NO | NO | Yes | Yes | Yes | Yes |
| ΔT4 | NO | NO | NO | NO | Little | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Li, J. Transient Simulation of Bath Temperature inside Aluminum Reduction Cells. Metals 2020, 10, 379. https://doi.org/10.3390/met10030379
Zhu J, Li J. Transient Simulation of Bath Temperature inside Aluminum Reduction Cells. Metals. 2020; 10(3):379. https://doi.org/10.3390/met10030379
Chicago/Turabian StyleZhu, Jiaming, and Jie Li. 2020. "Transient Simulation of Bath Temperature inside Aluminum Reduction Cells" Metals 10, no. 3: 379. https://doi.org/10.3390/met10030379
APA StyleZhu, J., & Li, J. (2020). Transient Simulation of Bath Temperature inside Aluminum Reduction Cells. Metals, 10(3), 379. https://doi.org/10.3390/met10030379




