Low-Temperature Crystal Structure and Mean-Field Modeling of ErxDy1−xAl2 Intermetallics
Abstract
1. Introduction
2. Experimental
3. Modeling
4. Results
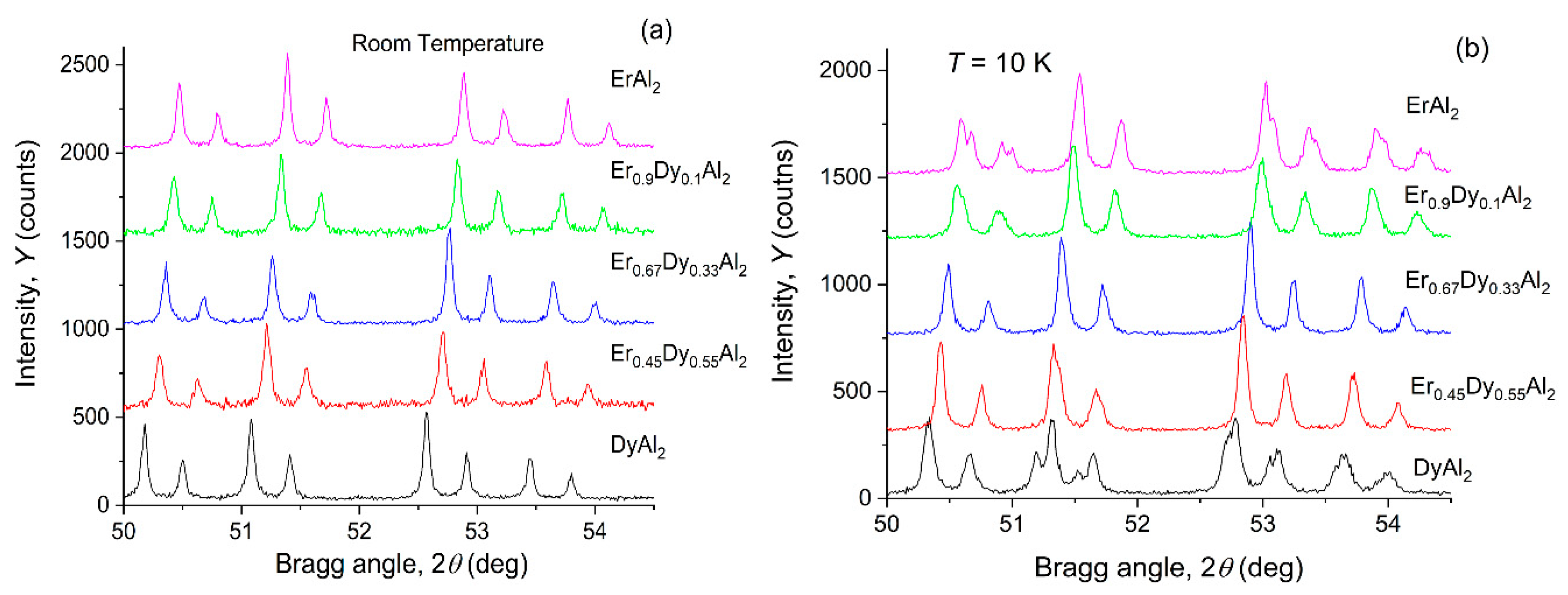
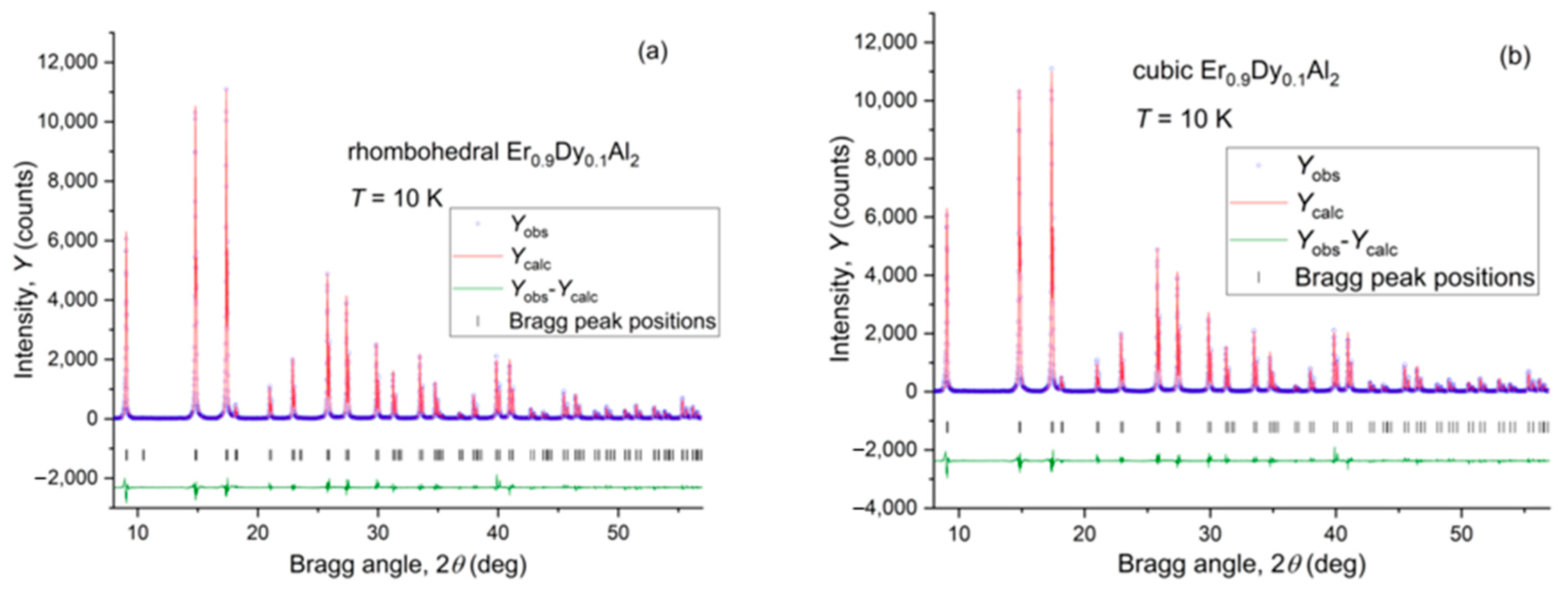
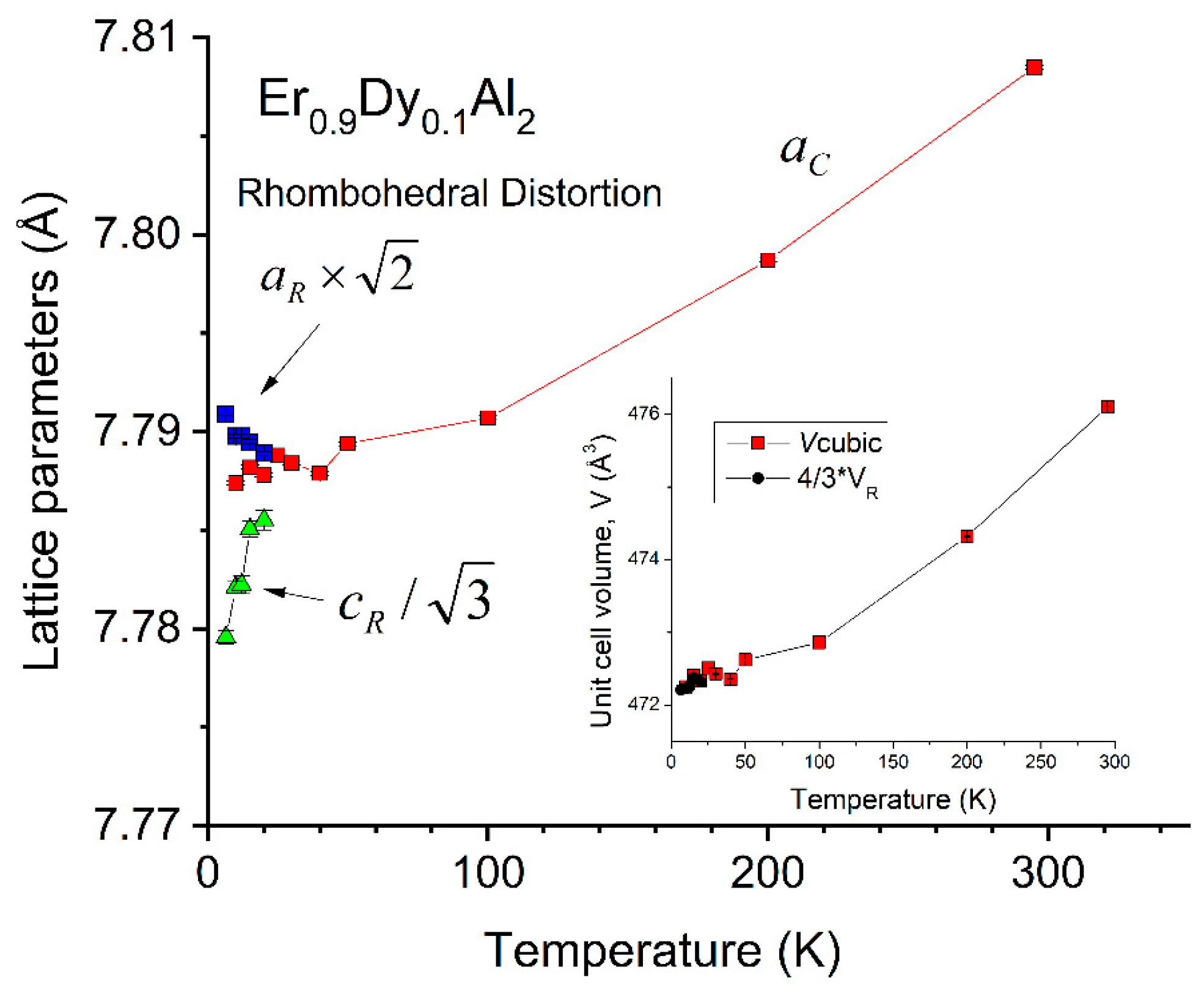
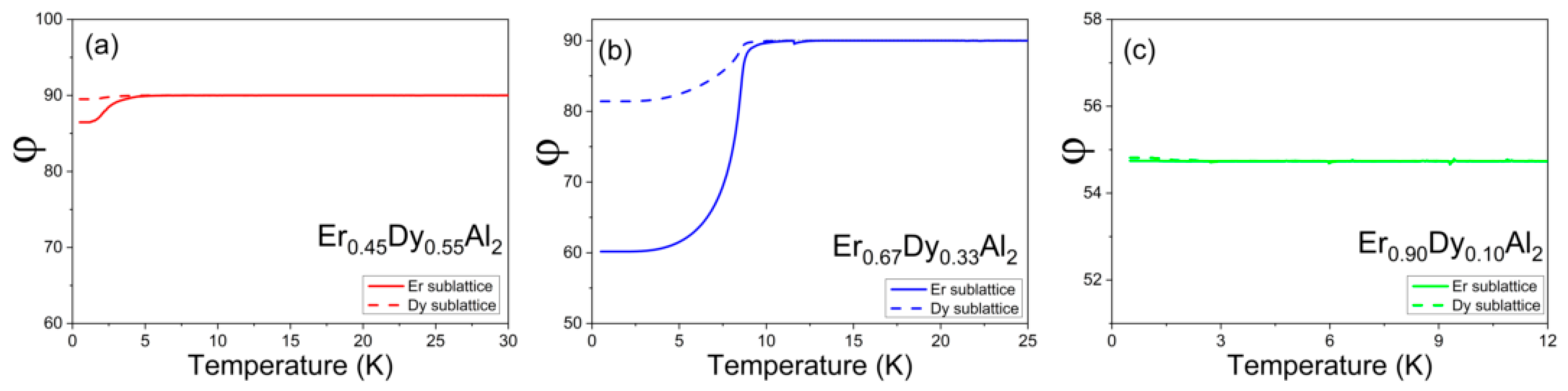
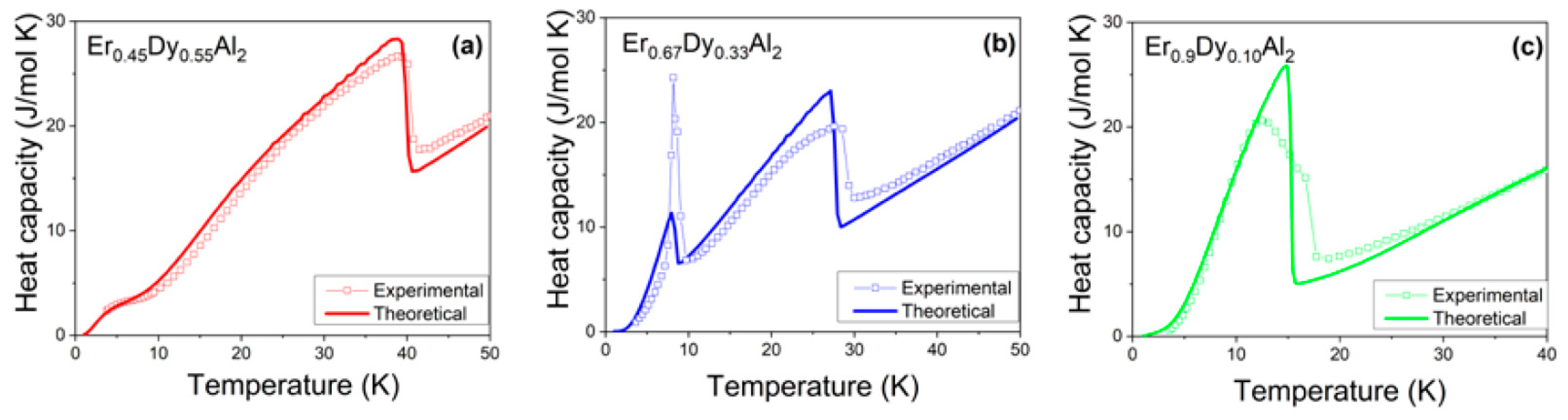
4.1. Er0.9Dy0.1Al2
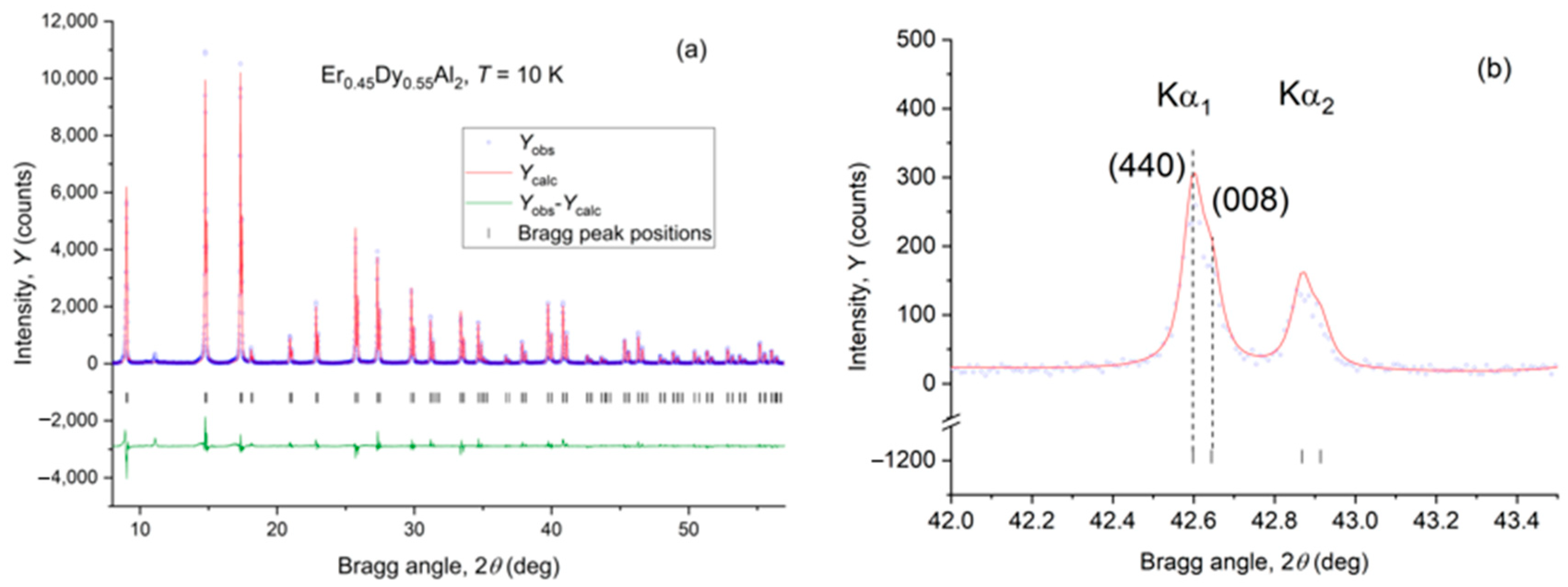
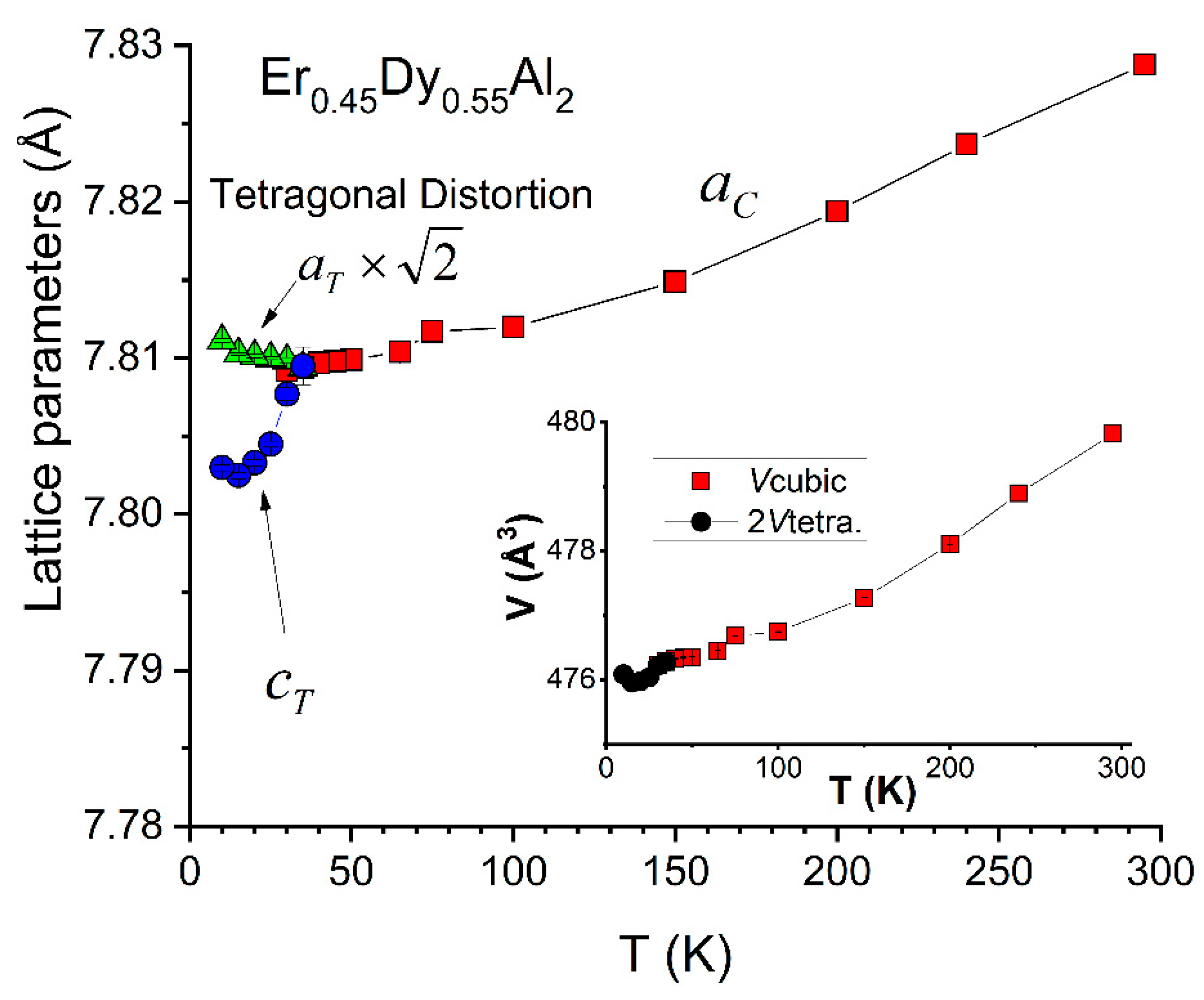
4.2. Er0.45Dy0.55Al2
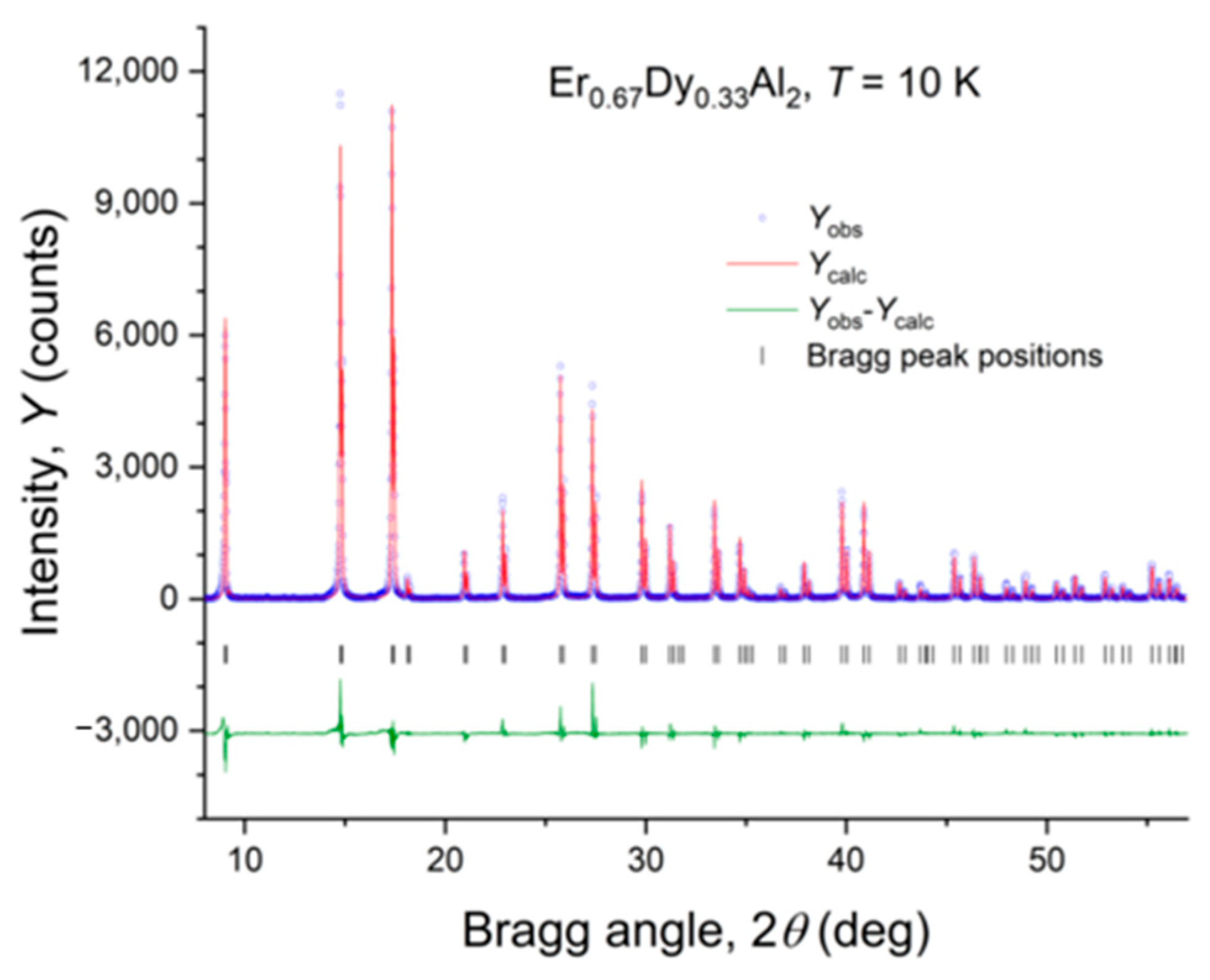
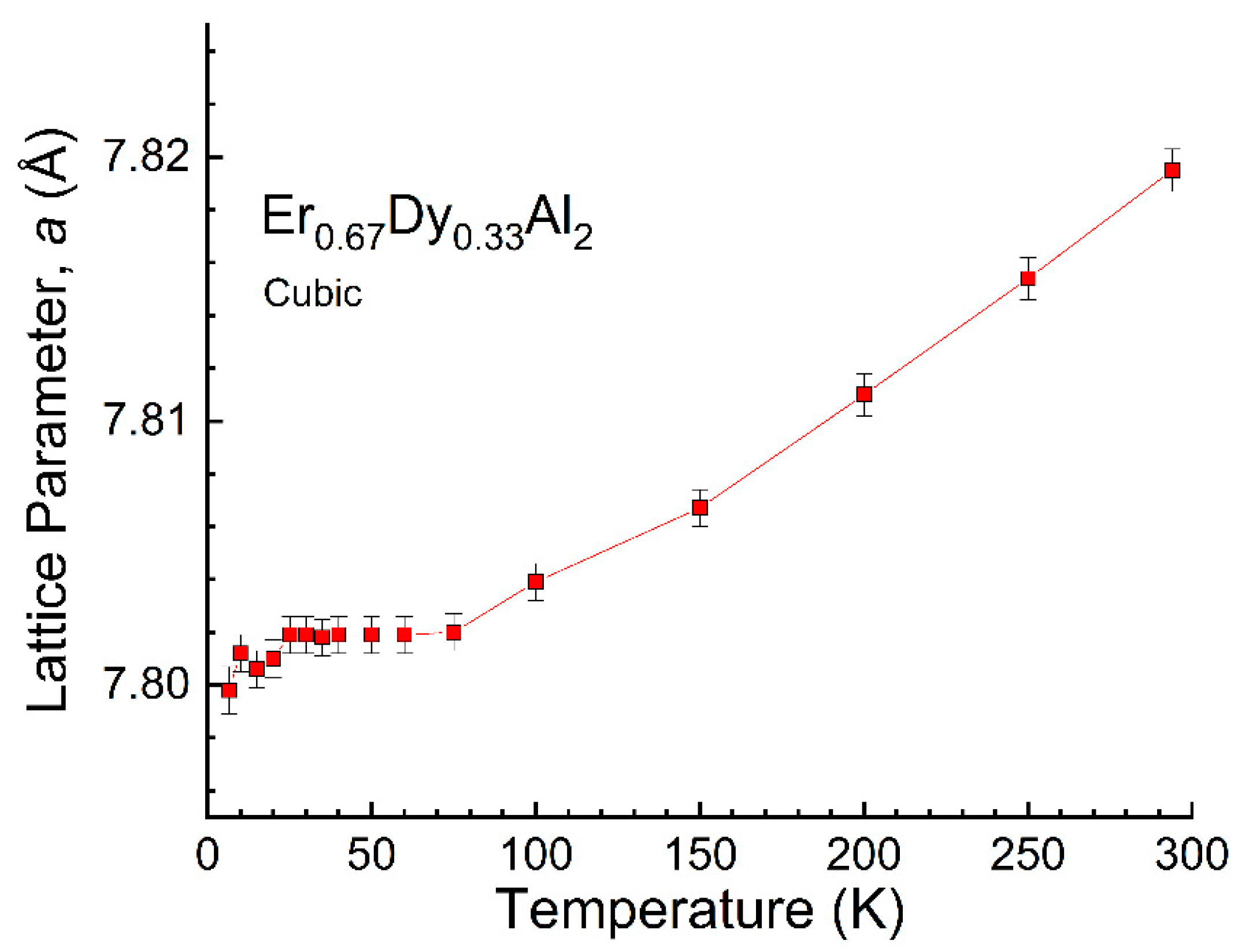
4.3. Er0.67Dy0.33Al2
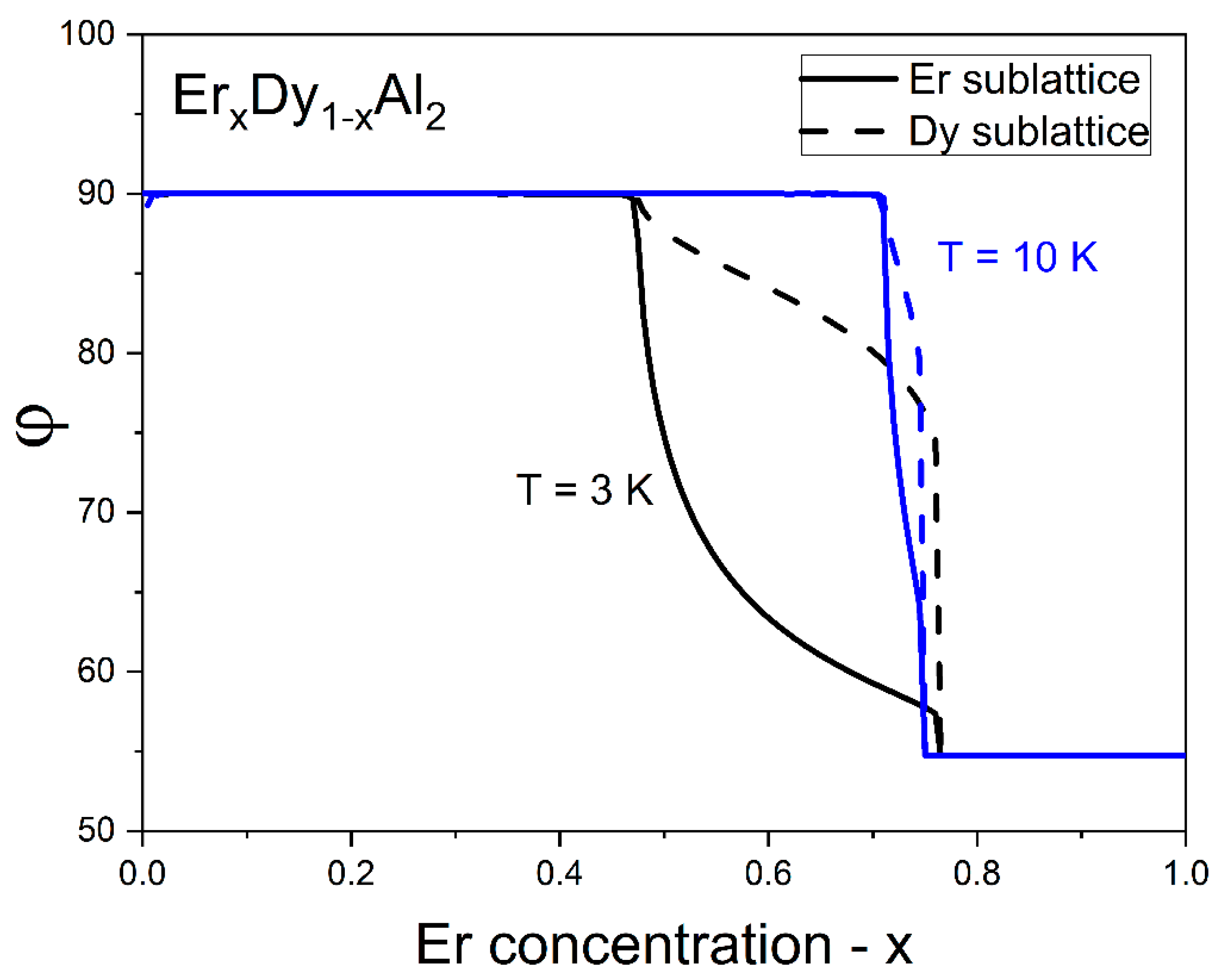
4.4. Easy Magnetization Axis as a Function of Composition
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gschneidner, K.A., Jr. Systematics of the intra rare-earth binary alloy systems. J. Less Common Met. 1985, 114, 29–42. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr. Pressure dependence of the intra rare-earth generalized binary phase-diagram. J. Less Common Met. 1985, 110, 1–10. [Google Scholar] [CrossRef]
- Pathak, A.K.; Paudyal, D.; Mudryk, Y.; Pecharsky, V.K. Role of 4f electrons in crystallographic and magnetic complexity. Phys. Rev. B 2017, 96, 064412. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Takeya, H.; Moorman, J.O.; Pecharsky, V.K. (Dy0.5Er0.5)Al2-a large magnetocaloric effect material for low-temperature magnetic refrigeration. Appl. Phys. Lett. 1994, 64, 253–255. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetocaloric materials. Ann. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
- Korte, B.J.; Pecharsky, V.K.; Gschneidner, K.A., Jr. The correlation of the magnetic properties and the magnetocaloric effect in (Gd1-xErx)NiAl alloys. J. Appl. Phys. 1998, 84, 5677–5685. [Google Scholar] [CrossRef]
- De Gennes, P.G. Interactions indirectes entre couches 4f dans les métaux de terres rares. J. Phys. Radium 1962, 23, 510–521. (In French) [Google Scholar] [CrossRef]
- Kittel, C. Indirect Exchange Interaction in Metals—A Status Report. J. Appl. Phys. 1968, 39, 637–641. [Google Scholar] [CrossRef]
- Levy, P.M. Indirect Exchange in the Rare-Earth Intermetallics. J. Appl. Phys. 1970, 41, 902–904. [Google Scholar] [CrossRef]
- Purwins, H.G.; Leson, A. Magnetic properties of (Rare Earth)Al2 intermetallic compounds. Adv. Phys. 1990, 39, 309–403. [Google Scholar] [CrossRef]
- Hughes, I.D.; Dane, M.; Ernst, A.; Hergert, W.; Luders, M.; Poulter, J.; Staunton, J.B.; Svane, A.; Szotek, Z.; Temmerman, W.M. Lanthanide contraction and magnetism in the heavy rare earth elements. Nature 2007, 446, 650–653. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Helical structures of the heavy rare earth metals. Solid State Commun. 1963, 1, 62–66. [Google Scholar] [CrossRef]
- Andrianov, A.V. Unambiguous dependence of the period of the helicoidal magnetic structure in heavy magnetic rare-earth materials on the ratio c/a of the crystal lattice-possible association with an electron topological transition. JETP Lett. 1992, 55, 666–669. [Google Scholar]
- Von Ranke, P.J.; Alvarenga, T.S.T.; Alho, B.P.; Nobrega, E.P.; Ribeiro, P.O.; Carvalho, A.M.G.; de Sousa, V.S.R.; Caldas, A.; de Oliveira, N.A. Spin reorientation and the magnetocaloric effect in HoyEr(1-y)N. J. Appl. Phys. 2012, 111, 113916. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Phase relationships and crystallography in the pseudobinary system Gd5Si4-Gd5Ge4. J. Alloy. Compd. 1997, 260, 98–106. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Gd5(SixGe1-x)4: An extremum material. Adv. Mater. 2001, 13, 683–686. [Google Scholar] [CrossRef]
- Petit, L.; Paudyal, D.; Mudryk, Y.; Gschneidner, K.A.; Pecharsky, V.K.; Luders, M.; Szotek, Z.; Banerjee, R.; Staunton, J.B. Complex magnetism of lanthanide intermetallics and the role of their valence electrons: Ab initio theory and experiment. Phys. Rev. Lett. 2015, 115, 207201. [Google Scholar] [CrossRef]
- Verhoeven, J.D.; Gibson, E.D.; McMasters, O.D.; Baker, H.H. The growth of single crystal Terfenol-D crystals. Metall. Mater. Trans. A 1987, 18, 223–231. [Google Scholar] [CrossRef]
- Jiles, D.C. The development of highly magnetostrictive rare earth-iron alloys. J. Phys. D Appl. Phys. 1994, 27, 1–11. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. The giant magnetocaloric effect in Gd5(SixGe1-x)4 materials for magnetic refrigeration. Adv. Cryog. Eng. 1998, 43, 1729–1736. [Google Scholar]
- Schelp, W.; Drewes, W.; Leson, A.; Purwins, H.G. Low-temperature heat-capacity of some heavy compounds TbAl2, DyAl2, ErAl2, and TmAl2 in a magnetic-field. J. Phys. Chem. Solids 1986, 47, 855–861. [Google Scholar] [CrossRef]
- Khan, M.; Pathak, A.K.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Anisotropy induced anomalies in Dy1-xTbxAl2. J. Mater. Chem. C 2017, 5, 896–901. [Google Scholar] [CrossRef]
- Pathak, A.K.; Paudyal, D.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Tunable magnetism and structural transformations in mixed light-and heavy-lanthanide dialuminides. Phys. Rev. B 2016, 94, 224406. [Google Scholar] [CrossRef]
- Paudyal, D.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Electronic structure, magnetic properties, and magnetostructural transformations in rare earth dialuminides. J. Appl. Phys. 2014, 115, 17E127. [Google Scholar] [CrossRef]
- Gratz, E.; Markosyan, A.S. Physical properties of RCo2 Laves phases. J. Phys. C Condens. Matter 2001, 13, R385–R413. [Google Scholar] [CrossRef]
- Duc, N.H.; Hien, T.D.; Givord, D.; Franse, J.J.M.; DeBoer, F.R. Exchange interactions in rare-earth transition-metal compounds. J. Magn. Magn. Mater. 1993, 124, 305–311. [Google Scholar] [CrossRef]
- Khmelevskyi, S.; Mohn, P. The order of the magnetic phase transitions in RCo2 (R = rare earth) intermetallic compounds. J. Phys. C Condens. Matter 2000, 12, 9453–9464. [Google Scholar] [CrossRef]
- Mudryk, Y.; Paudyal, D.; Pathak, A.K.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Balancing structural distortions via competing 4f and itinerant interactions: A case of polymorphism in magnetocaloric HoCo2. J. Mater. Chem. C 2016, 4, 4521–4531. [Google Scholar] [CrossRef]
- Nirmala, R.; Mudryk, Y.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Unusual magnetism of Er0.75Dy0.25Al2. Phys. Rev. B 2007, 76, 014407. [Google Scholar] [CrossRef]
- Lima, A.L.; Oliveira, I.S.; Gomes, A.M.; von Ranke, P.J. Origin of anomalous magnetocaloric effect in (Dy1-zErz)Al2 alloys. Phys. Rev. B 2002, 65, 172411. [Google Scholar] [CrossRef]
- Lima, A.L.; Gschneidner, K.A., Jr.; Pecharsky, V.K.; Pecharsky, A.O. Disappearance and reappearance of magnetic ordering upon lanthanide substitution in (Er1-xDyx)Al2. Phys. Rev. B 2003, 68, 134409. [Google Scholar] [CrossRef]
- De Oliveira, N.A.; von Ranke, P.J. Magnetocaloric effect in the Laves phase pseudobinaries (Dy1-cRc)Al2 (R = Er and Ho). J Magn. Magn. Mater. 2008, 320, 386–392. [Google Scholar] [CrossRef]
- Ribeiro, P.O.; Alho, B.P.; Alvarenga, T.S.T.; Nobrega, E.P.; de Sousa, V.S.R.; Carvalho, A.M.G.; Caldas, A.; de Oliveira, N.A.; von Ranke, P.J. Theoretical investigations on magnetocaloric effect in Er1-yTbyAl2 series. J. Magn. Magn. Mater. 2015, 379, 112–116. [Google Scholar] [CrossRef]
- Holm, A.P.; Pecharsky, V.K.; Gschneidner, K.A., Jr.; Rink, R.; Jirmanus, M.N. X-ray powder diffractometer for in situ structural studies in magnetic fields from 0 to 35 kOe between 2.2 and 315 K. Rev. Sci. Instrum. 2004, 75, 1081–1088. [Google Scholar] [CrossRef]
- Hunter, B. Rietica—A visual Rietveld program. International Union of Crystallography Commission on Powder Diffraction Newsletter. 1998. No. 20. Available online: http://rietica.org (accessed on 8 December 2020).
- Rodriguez-Carvajal, J. Recent advances in magnetic-structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Roisnel, T.; Rodriguez-Carvajal, J. WinPLOTR: A Windows tool for powder diffraction pattern analysis. In Epdic 7: European Powder Diffraction, Pts 1 and 2; Delhez, R., Mittemeijer, E.J., Eds.; Trans Tech Publications Ltd.: Zurich-Uetikon, Switzerland, 2001; pp. 118–123. [Google Scholar]
- De Sousa, V.S.R.; Carvalho, A.M.G.; Plaza, E.J.R.; Alho, B.P.; Tedesco, J.C.G.; Coelho, A.A.; de Oliveira, N.A.; von Ranke, P.J. Investigation on the magnetocaloric effect in (Gd,Pr)Al2 solid solutions. J. Magn. Magn. Mater. 2011, 323, 794–798. [Google Scholar] [CrossRef]
- Alho, B.P.; Ribeiro, P.O.; Alvarenga, T.S.T.; Carvalho, A.M.G.; von Ranke, P.J. Magnetocaloric effect in Gd(1-y)DyyAl2. Int. J. Refriger. 2014, 37, 297–302. [Google Scholar] [CrossRef]
- Lea, K.R.; Leask, M.J.M.; Wolf, W.P. Raising of angular momentum degeneracy of f-electron terms by cubic crystal fields. J. Phys. Chem. Solids 1962, 23, 1381. [Google Scholar] [CrossRef]
- Hutchings, M.T. Point-charge calculations of energy levels of magnetic ions in crystalline electric fields. Solid State Phys. Adv. Res. Appl. 1964, 16, 227–273. [Google Scholar]
- Von Ranke, P.J.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Influence of the crystalline electrical field on the magnetocaloric effect of DyAl2, ErAl2, and DyNi2. Phys. Rev. B 1998, 58, 12110–12116. [Google Scholar] [CrossRef]
- Hill, T.W.; Wallace, W.E.; Craig, R.S.; Inoue, T. Low-temperature heat-capacities and related thermal properties of TbAl2 and HoAl2. J. Solid State Chem. 1973, 8, 364–367. [Google Scholar] [CrossRef]
- Finger, L.W.; Cox, D.E.; Jephcoat, A.P. A correction for powder diffraction peak asymmetry due to axial divergence. J. Appl. Crystallogr. 1994, 27, 892–900. [Google Scholar] [CrossRef]
- Howard, C.J. The approximation of asymmetric neutron powder diffraction peaks by sums of gaussians. J. Appl. Crystallogr. 1982, 15, 615–620. [Google Scholar] [CrossRef]
- Dowell, L.G.; Rinfret, A.P. Low-temperature forms of ice as studied by X-ray diffraction. Nature 1960, 188, 1144–1148. [Google Scholar] [CrossRef]
| x (Er) | TC, K | T *, K | T = 295 K | T = 10 K | |||||
|---|---|---|---|---|---|---|---|---|---|
| Space Group | a (Å) | V (Å3) | Space Group | a (Å) | c (Å) | V (Å3) | |||
| 0.45 | 40 | 7 | 7.8263(1) | 479.37(1) | I41/amd | 5.5231(1) | 7.8026(2) | 238.095(6) | |
| 0.67 | 28 | 8 | 7.8196(1) | 478.14(1) | 7.8016(1) | 7.8016(1) | 474.85(1) | ||
| 0.90 | 17 | 12 | 7.8092(1) | 476.24(1) | 5.5082(1) | 13.4795(4) | 354.19(1) | ||
| Space Group | I41/amd | |||
|---|---|---|---|---|
| Atom | ||||
| R(Er+Dy) | 1/8, 1/8, 1/8 | 0, 1/4, 3/8 | 0, 0, 0.1262 | |
| Al1 | 1/2, 1/2, 1/2 | 0, 0, 0 | 0, 0, 1/2 | |
| Al2 | N/A | N/A | ½, 0, 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mudryk, Y.; Alho, B.P.; Ribeiro, P.O.; Pecharsky, V.K. Low-Temperature Crystal Structure and Mean-Field Modeling of ErxDy1−xAl2 Intermetallics. Metals 2020, 10, 1662. https://doi.org/10.3390/met10121662
Mudryk Y, Alho BP, Ribeiro PO, Pecharsky VK. Low-Temperature Crystal Structure and Mean-Field Modeling of ErxDy1−xAl2 Intermetallics. Metals. 2020; 10(12):1662. https://doi.org/10.3390/met10121662
Chicago/Turabian StyleMudryk, Yaroslav, Bruno P. Alho, Paula O. Ribeiro, and Vitalij K. Pecharsky. 2020. "Low-Temperature Crystal Structure and Mean-Field Modeling of ErxDy1−xAl2 Intermetallics" Metals 10, no. 12: 1662. https://doi.org/10.3390/met10121662
APA StyleMudryk, Y., Alho, B. P., Ribeiro, P. O., & Pecharsky, V. K. (2020). Low-Temperature Crystal Structure and Mean-Field Modeling of ErxDy1−xAl2 Intermetallics. Metals, 10(12), 1662. https://doi.org/10.3390/met10121662







