Evaluation of Stationary Creep Rate in Heat-Affected Zone of Martensitic 9–12% Cr Steels
Abstract
1. Introduction
2. Materials and Methods
Modeling
3. Results
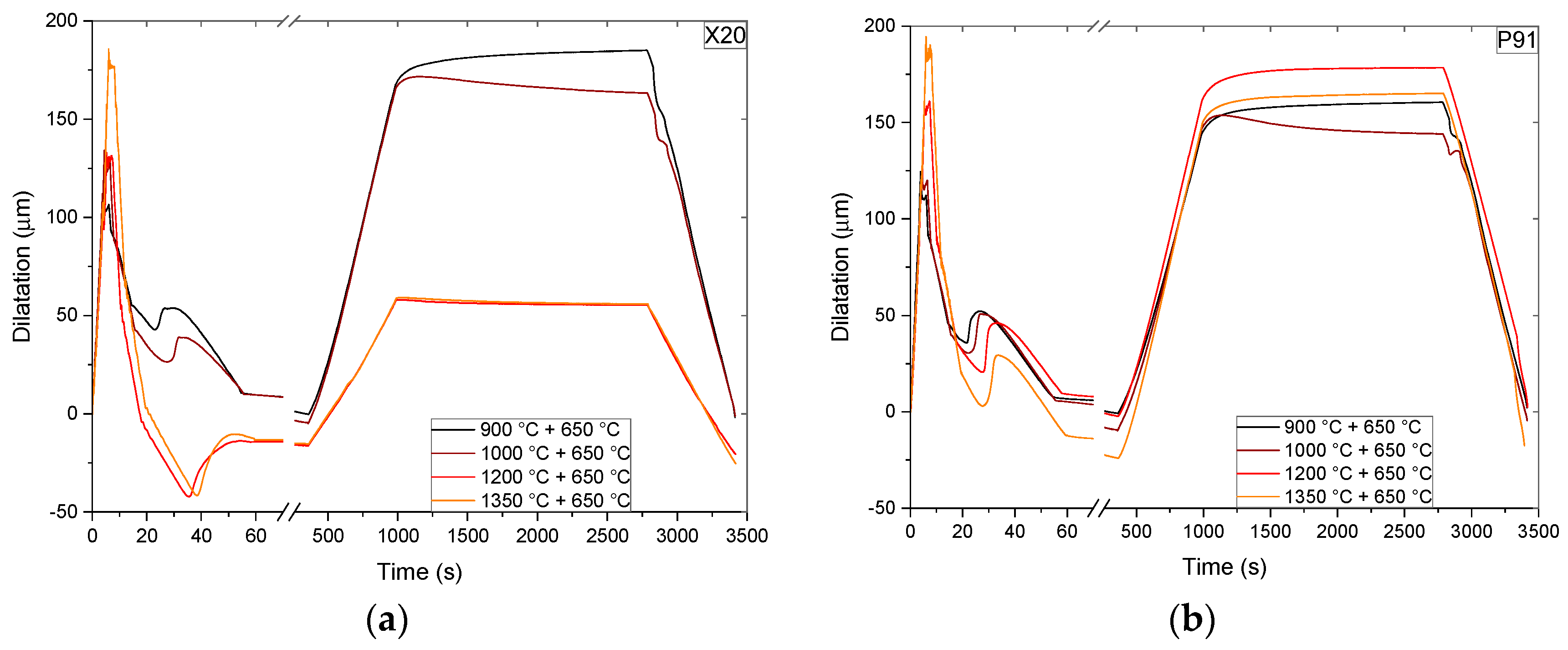
3.1. HAZ Simulations
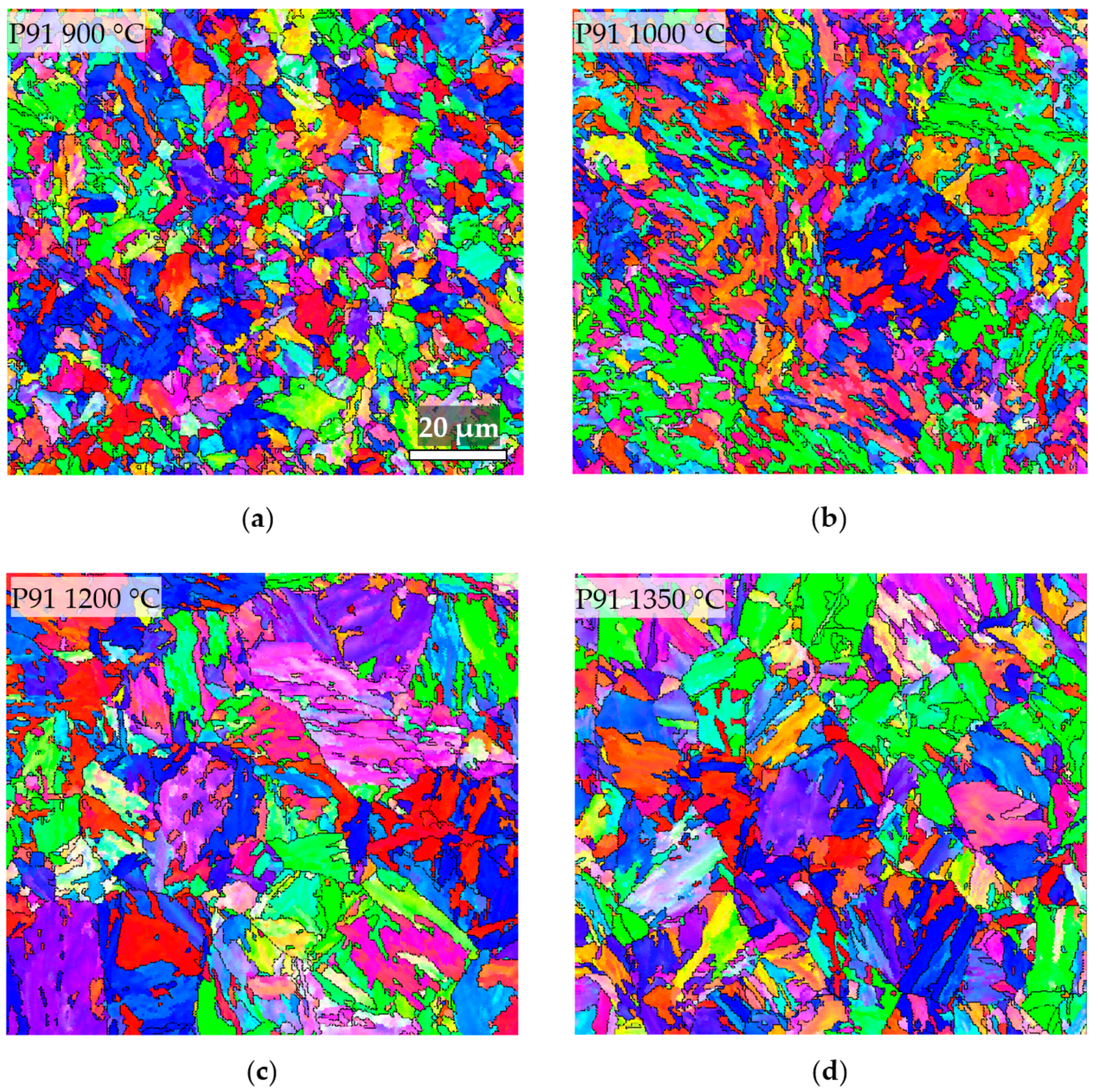
3.2. Prior Austenite Grains (PAG)
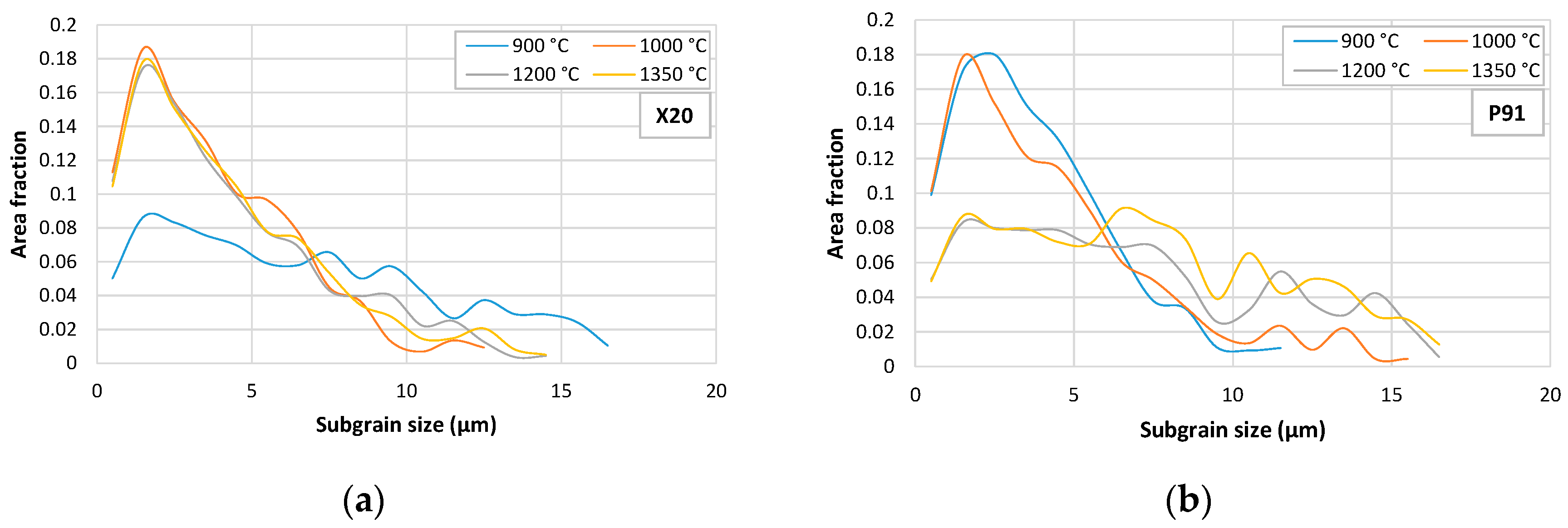
3.3. Martensite Subgrains
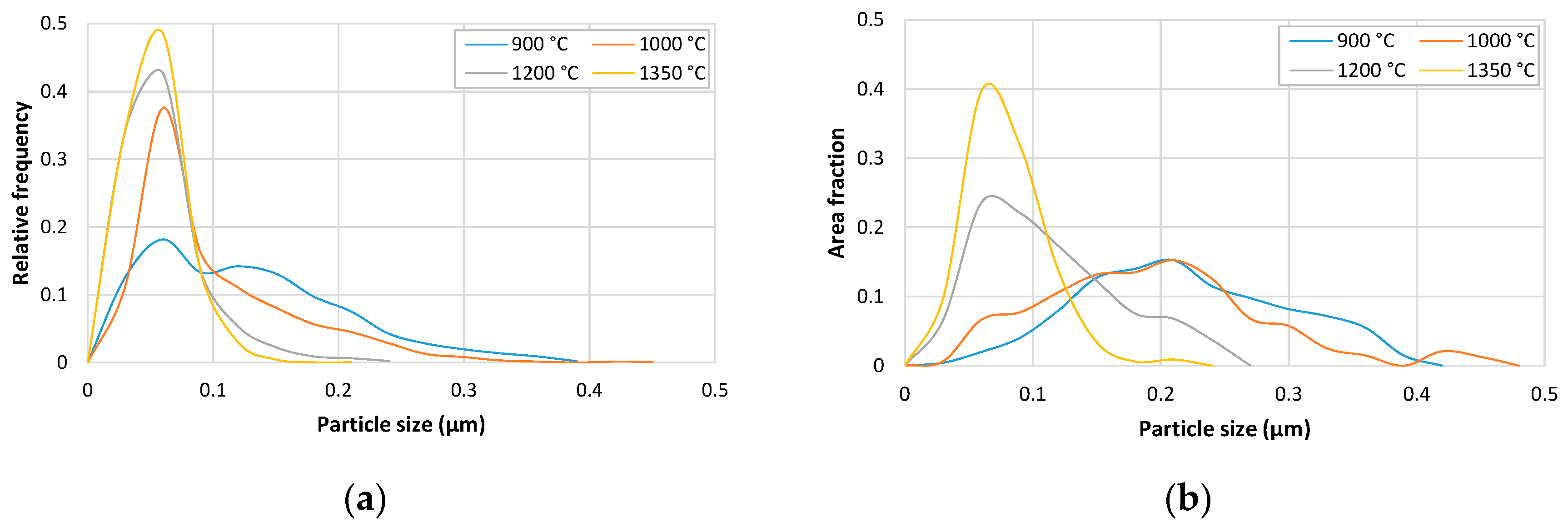
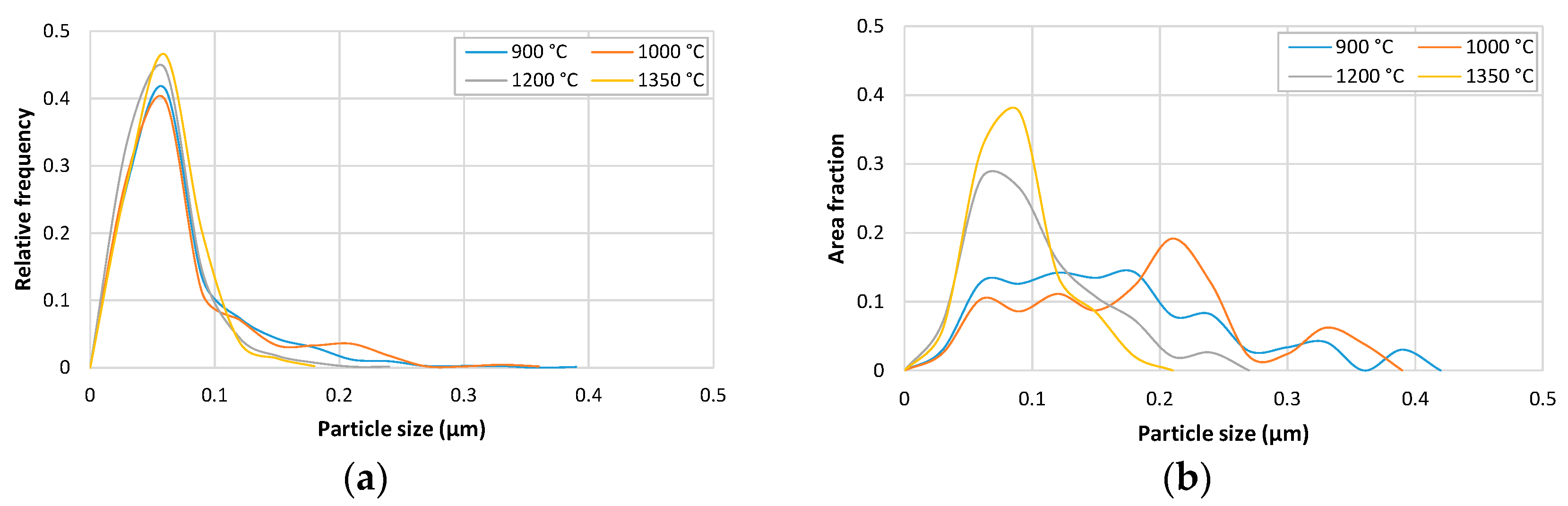
3.4. Precipitates
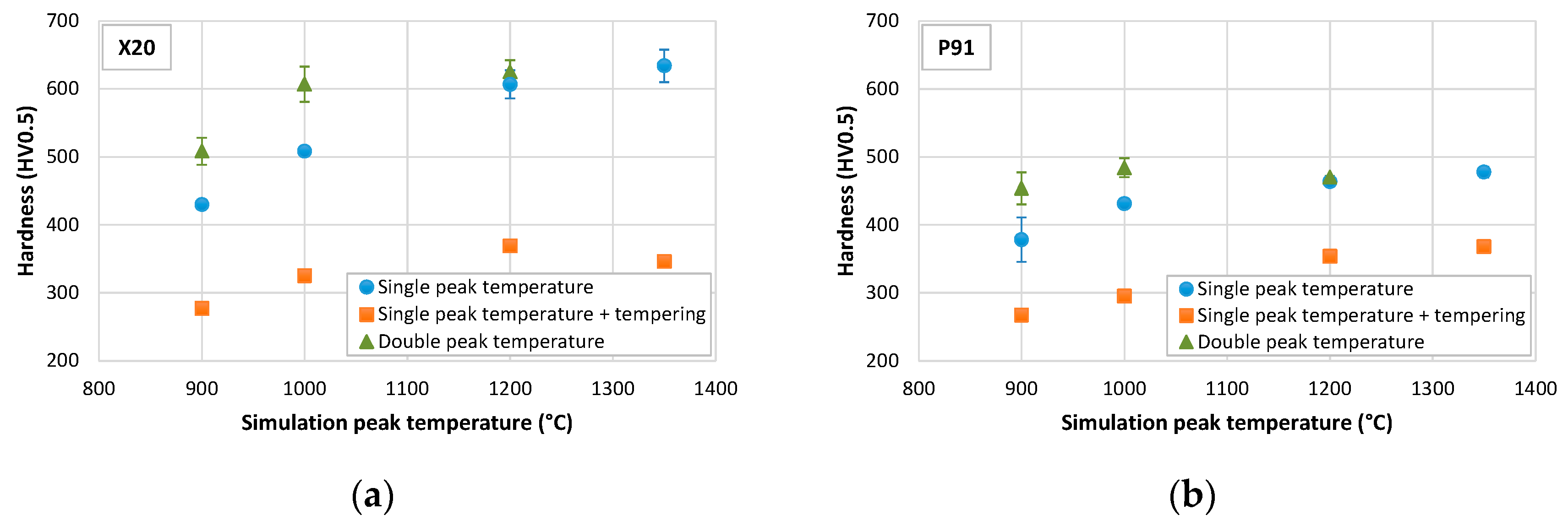
3.5. Hardness and Tensile Properties
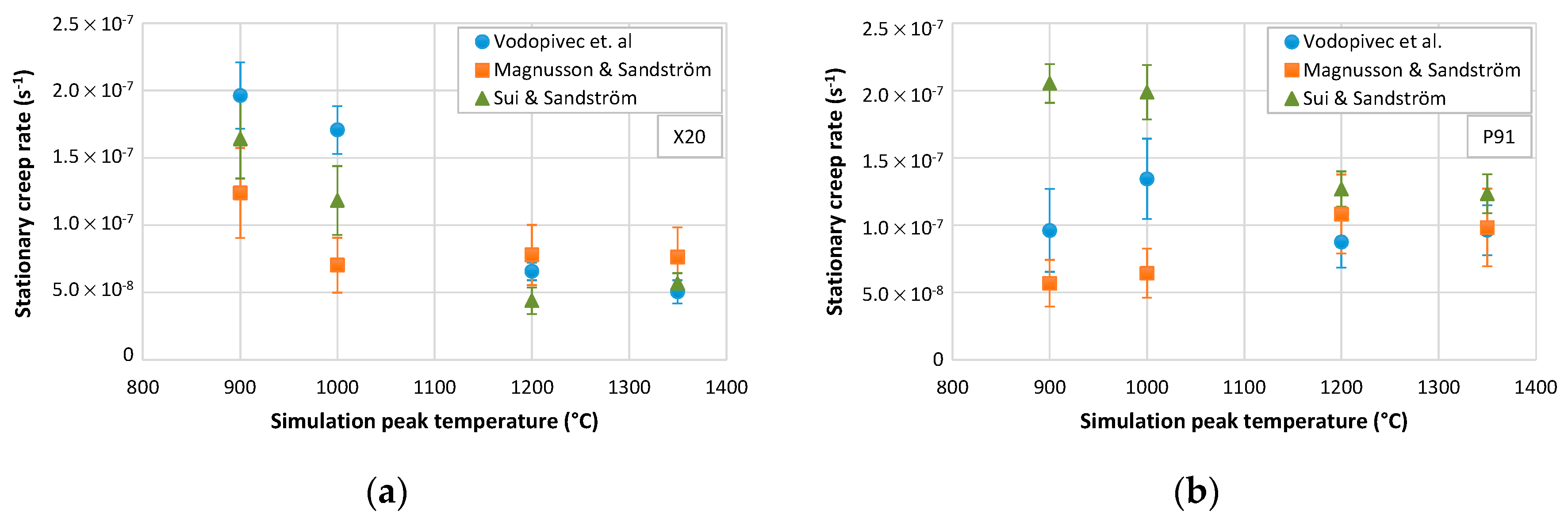
3.6. Modeling Results: Stationary Creep Rate ()
4. Discussion
5. Conclusions
- -
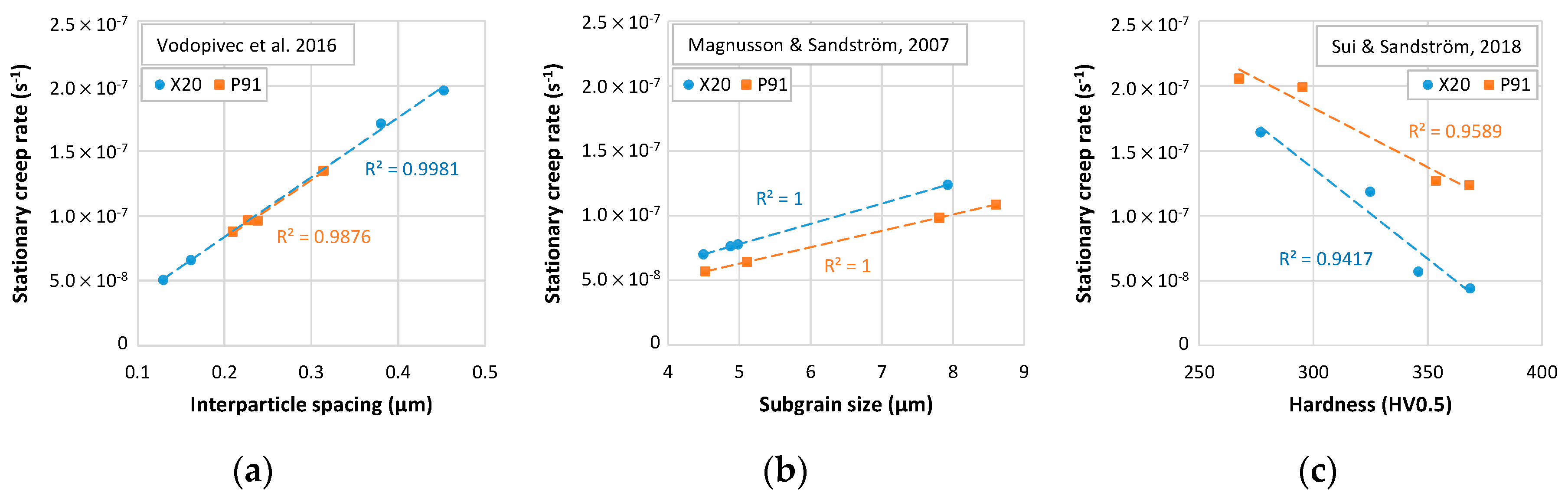
- Evaluation of the stationary creep rate () for the creep test conditions of 170 MPa and 580 °C by the chosen models that use measured and predefined microstructure parameters resulted in the range 4.3 × 10−8–2.5 × 10−7 s−1, being in good agreement with the experimental data with a similar thermal history (2.81 × 10−8 and 2.83 × 10−7 s−1 for the P91 and X20 steels, respectively).
- -
- The model by Vodopivec et al., which relates the to the interparticle spacing, provided a greater difference in the values between the lowest and the highest peak temperatures for the X20 than for the P91 steel.
- -
- The difference in the stationary creep rate () for all peak temperatures and both steels was the smallest when using the Magnusson and Sandström model, which relates the to the subgrain size.
- -
- The model that relates the stationary creep rate to the hardness by Sui and Sandström was the most consistent one in predicting the values, being always lower for higher peak temperatures.
- -
- Depending on the model utilized, a good linear correlation of the evaluated stationary creep rate to the interparticle spacing, subgrain size, or measured hardness was obtained. The latter is the most crucial from the practical standpoint, as hardness is the easiest property to measure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Unit | Parameter | Value | Ref. |
|---|---|---|---|---|
| R | J mol K−1 | Universal gas constant | 8.31 | − |
| kB | J K−1 | Boltzmann constant | 1.38 × 10−23 | − |
| σ | N m−2 | Applied stress | 1.7 × 108 | − |
| T | K | Absolute temperature | 853.15 | − |
| ρmob,X20 | m−2 | Density of mobile dislocations for the X20 1 | 9.01 × 1013 | − |
| ρmob,P91 | m−2 | Density of mobile dislocations for the P91 1 | 7.51 × 1013 | − |
| ν | − | Poisson’s ratio | 0.3 | − |
| n | − | The creep exponent | 2 | [28] |
| ns | − | Number of slip systems | 5 | [26] |
| N | − | Norton exponent | 5 | [23] |
| m | − | Taylor factor | 3.06 | [29] |
| αT | − | Dislocation interaction constant | 0.3 | [40] |
| b | m | Burger’s vector for α-Iron | 2.87 × 10−10 | [23] |
| D0 | m2 s−1 | Self-diffusion pre-exponential factor for α-Iron | 2.76 × 10−4 | [52] |
| QC | J mol−1 | Activation energy for self-diffusion in α-Iron | 2.93 × 105 | [37] |
| ρim | m−2 | Density of immobile dislocations | 1.0 × 1011 | [29] |
| GX20 | N m−2 | Shear modulus of the X20 2 | 7.49 × 1010 | [53] |
| GP91 | N m−2 | Shear modulus of the P91 2 | 6.73 × 1010 | [54] |
| Rm, X20 | N m−2 | Room-temperature tensile strength of the X20 | 7.53 × 108 | [55] |
| Rm, P91 | N m−2 | Room-temperature tensile strength of the P91 | 7.12 × 108 | [55] |
| σy, X20 | N m−2 | Room-temperature yield stress of the X20 | 5.27 × 108 | [55] |
| σy, P91 | N m−2 | Room-temperature yield stress of the P91 | 5.46 × 108 | [55] |
| X20 | s−1 | Stationary creep rate of the X20 | 1.22 × 10−6 | [20] |
| P91 | s−1 | Stationary creep rate of the P91 | 4.97 × 10−7 | [20] |
References
- Abe, F. (Ed.) Creep-Resistant Steels; Woodhead Publishing in Materials; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-1-84569-401-2. [Google Scholar]
- Shen, Y.; Chen, B.; Wang, C. In Situ Observation of Phase Transformations in the Coarse-Grained Heat-Affected Zone of P91 Heat-Resistant Steel During Simulated Welding Process. Metall. Mater. Trans. A 2020, 51, 3371–3376. [Google Scholar] [CrossRef]
- Mariappan, K.; Shankar, V.; Bhaduri, A.K. Comparative evaluation of tensile properties of simulated heat affected zones of P91 steel weld joint. Mater. High Temp. 2020, 37, 114–128. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, Y.; Zhao, J. Elastoplastic Fracture Analysis of the P91 Steel Welded Joint under Repair Welding Thermal Shock Based on XFEM. Metals 2020, 10, 1285. [Google Scholar] [CrossRef]
- Lojen, G.; Vuherer, T. Optimization of PWHT of Simulated HAZ Subzones in P91 Steel with Respect to Hardness and Impact Toughness. Metals 2020, 10, 1215. [Google Scholar] [CrossRef]
- Smith, A.; Asadikiya, M.; Yang, M.; Chen, J.; Zhong, Y. An Investigation of Creep Resistance in Grade 91 Steel through Computational Thermodynamics. Engineering 2020, 6, 644–652. [Google Scholar] [CrossRef]
- Peng, Y.-Q.; Chen, T.-C.; Chung, T.-J.; Jeng, S.-L.; Huang, R.-T.; Tsay, L.-W. Creep Rupture of the Simulated HAZ of T92 Steel Compared to that of a T91 Steel. Materials 2017, 10, 139. [Google Scholar] [CrossRef]
- di Gianfrancesco, A. (Ed.) Materials for Ultra-Supercritical and Advanced Ultra-Supercritical Power Plants; Woodhead Publishing Series in Energy; Woodhead Publishing/Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-08-100558-3. [Google Scholar]
- Morsdorf, L.; Jeannin, O.; Barbier, D.; Mitsuhara, M.; Raabe, D.; Tasan, C.C. Multiple mechanisms of lath martensite plasticity. Acta Mater. 2016, 121, 202–214. [Google Scholar] [CrossRef]
- Shibata, A.; Nagoshi, T.; Sone, M.; Morito, S.; Higo, Y. Evaluation of the block boundary and sub-block boundary strengths of ferrous lath martensite using a micro-bending test. Mater. Sci. Eng. A 2010, 527, 7538–7544. [Google Scholar] [CrossRef]
- Morito, S.; Adachi, Y.; Ohba, T. Morphology and Crystallography of Sub-Blocks in Ultra-Low Carbon Lath Martensite Steel. Mater. Trans. 2009, 50, 1919–1923. [Google Scholar] [CrossRef]
- Liu, X.; Fan, P.; Zhu, L. Characterization of dislocation evolution during creep of 9Cr 1Mo steel using internal friction measurement. Mater. Charact. 2019, 150, 98–106. [Google Scholar] [CrossRef]
- Yadav, S.D.; El-Tahawy, M.; Kalácska, S.; Dománková, M.; Yubero, D.C.; Poletti, C. Characterizing dislocation configurations and their evolution during creep of a new 12% Cr steel. Mater. Charact. 2017, 134, 387–397. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Almer, J.D. Dislocation evolution during tensile deformation in ferritic–martensitic steels revealed by high-energy X-rays. Acta Mater. 2014, 76, 381–393. [Google Scholar] [CrossRef]
- Panait, C.G.; Zielińska-Lipiec, A.; Koziel, T.; Czyrska-Filemonowicz, A.; Gourgues-Lorenzon, A.-F.; Bendick, W. Evolution of dislocation density, size of subgrains and MX-type precipitates in a P91 steel during creep and during thermal ageing at 600C for more than 100,000 h. Mater. Sci. Eng. A 2010, 527, 4062–4069. [Google Scholar] [CrossRef]
- Han, H.; Shen, J.; Xie, J. Effects of Precipitates Evolution on Low Stress Creep Properties in P92 Heat-resistant Steel. Sci. Rep. 2018, 8, 15411. [Google Scholar] [CrossRef]
- Godec, M.; Skobir Balantič, D.A. Coarsening behaviour of M23C6 carbides in creep-resistant steel exposed to high temperatures. Sci. Rep. 2016, 6, 29734. [Google Scholar] [CrossRef]
- Hurtado-Noreña, C.; Danón, C.A.; Luppo, M.I.; Bruzzoni, P. Evolution of Minor Phases in a P91 Steel Normalized and Tempered at Different Temperatures. Procedia Mater. Sci. 2015, 8, 1089–1098. [Google Scholar] [CrossRef]
- Isik, M.I.; Kostka, A.; Yardley, V.A.; Pradeep, K.G.; Duarte, M.J.; Choi, P.P.; Raabe, D.; Eggeler, G. The nucleation of Mo-rich Laves phase particles adjacent to M23C6 micrograin boundary carbides in 12% Cr tempered martensite ferritic steels. Acta Mater. 2015, 90, 94–104. [Google Scholar] [CrossRef]
- Kafexhiu, F.; Podgornik, B.; Vodopivec, F. Ageing effect on the creep performance of simulated weld HAZ for the steels X20 and P91. MATEC Web Conf. 2018, 188, 03004. [Google Scholar] [CrossRef][Green Version]
- Velkavrh, I.; Kafexhiu, F.; Klien, S.; Diem, A.; Podgornik, B. Tempering-Induced Microstructural Changes in the Weld Heat-Affected Zone of 9 to 12 Pct Cr Steels and Their Influence on Sliding Wear. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2017, 48, 109–125. [Google Scholar] [CrossRef]
- Vodopivec, F.; Kafexhiu, F.; Žužek, B.; Podgornik, B. Glide Stress by Stationary Creep of Tempered Martensite with Polyhedral Particles. Steel Res. Int. 2017, 88. [Google Scholar] [CrossRef]
- Yadav, S.D.; Scherer, T.; Prasad Reddy, G.V.; Laha, K.; Sasikala, G.; Albert, S.K.; Poletti, C. Creep modelling of P91 steel employing a microstructural based hybrid concept. Eng. Fract. Mech. 2018, 200, 104–114. [Google Scholar] [CrossRef]
- Murchú, C.Ó.; Leen, S.B.; O’Donoghue, P.E.; Barrett, R.A. A physically-based creep damage model for effects of different precipitate types. Mater. Sci. Eng. A 2017, 682, 714–722. [Google Scholar] [CrossRef]
- Yadav, S.D.; Sonderegger, B.; Stracey, M.; Poletti, C. Modelling the creep behaviour of tempered martensitic steel based on a hybrid approach. Mater. Sci. Eng. A 2016, 662, 330–341. [Google Scholar] [CrossRef]
- Barrett, R.A.; O’Donoghue, P.E.; Leen, S.B. A dislocation-based model for high temperature cyclic viscoplasticity of 9–12Cr steels. Comput. Mater. Sci. 2014, 92, 286–297. [Google Scholar] [CrossRef]
- Oruganti, R.; Karadge, M.; Swaminathan, S. A Comprehensive Creep Model for Advanced 9–10% Cr Ferritic Steels. Procedia Eng. 2013, 55, 727–734. [Google Scholar] [CrossRef][Green Version]
- Vodopivec, F.; Kafexhiu, F.; Žužek, B. Effect of Ferrite Lattice Vacancies on Creep Rate of the Steel X20CrMoV121 in the Range 763–913 K. Steel Res. Int. 2017, 88. [Google Scholar] [CrossRef]
- Magnusson, H.; Sandström, R. Creep Strain Modeling of 9 to 12 Pct Cr Steels Based on Microstructure Evolution. Metall. Mat. Trans. A 2007, 38, 2033–2039. [Google Scholar] [CrossRef]
- Sui, F.; Sandström, R. Creep strength contribution due to precipitation hardening in copper–cobalt alloys. J. Mater. Sci. 2019, 54, 1819–1830. [Google Scholar] [CrossRef]
- Celin, R.; Burja, J.; Kosec, G. A comparison of as-welded and simulated heat affected zone (HAZ) microstructures. Mater. Tehnol. 2016, 50, 455–460. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
- Beausir, J.-J.F.B. Analysis Tools for Electron and X-ray Diffraction, ATEX—Software; Université de Lorraine: Metz, France, 2017. [Google Scholar]
- Vodopivec, F.; Žužek, B.; Jenko, M.; Skobir-Balantič, D.A.; Godec, M. Calculation of stationary creep rate of tempered martensite. Mater. Sci. Technol. 2013, 29, 451–455. [Google Scholar] [CrossRef]
- Magnusson, H.; Sandström, R. The Role of Dislocation Climb across Particles at Creep Conditions in 9 to 12 Pct Cr Steels. Metall. Mat. Trans. A 2007, 38, 2428–2434. [Google Scholar] [CrossRef]
- Magnusson, H.; Sandström, R. Modeling Creep Strength of Welded 9 to 12 Pct Cr Steels. Metall. Mat. Trans. A 2010, 41, 3340–3347. [Google Scholar] [CrossRef]
- Eliasson, J.; Gustafson, Å.; Sandström, R. Kinetic Modelling of the Influence of Particles on Creep Strength. KEM 1999, 171–174, 277–284. [Google Scholar] [CrossRef]
- Nes, E. Modelling of work hardening and stress saturation in FCC metals. Prog. Mater. Sci. 1997, 41, 129–193. [Google Scholar] [CrossRef]
- Spigarelli, S.; Sandström, R. Basic creep modelling of aluminium. Mater. Sci. Eng. A 2018, 711, 343–349. [Google Scholar] [CrossRef]
- Sandström, R.; Hallgren, J. The role of creep in stress strain curves for copper. J. Nucl. Mater. 2012, 422, 51–57. [Google Scholar] [CrossRef]
- Hart, E.W. Theory of dispersion hardening in metals. Acta Metall. 1972, 20, 275–289. [Google Scholar] [CrossRef]
- Martin, J.W. Precipitation Hardening: Theory and Applications; Elsevier Science: Saint Louis, MO, USA, 2014; ISBN 978-0-08-098489-6. [Google Scholar]
- Tamura, M. Verification of Equation for Evaluating Dislocation Density during Steady-state Creep of Metals. J. Mater. Sci. Res. 2017, 6, 20. [Google Scholar] [CrossRef][Green Version]
- Tamura, M. Relation between Sub-grain Size and Dislocation Density During Steady-State Dislocation Creep of Polycrystalline Cubic Metals. J. Mater. Sci. Res. 2018, 7, 26. [Google Scholar] [CrossRef]
- Altendorf, H.; Faessel, M.; Jeulin, D.; Latourte, F. Direct estimation of austenitic grain dimensions in heat affected zones of a martensitic steel from EBSD images: Grain size measures from covariance. J. Microsc. 2015, 258, 87–104. [Google Scholar] [CrossRef] [PubMed]
- Simm, T.; Sun, L.; McAdam, S.; Hill, P.; Rawson, M.; Perkins, K. The Influence of Lath, Block and Prior Austenite Grain (PAG) Size on the Tensile, Creep and Fatigue Properties of Novel Maraging Steel. Materials 2017, 10, 730. [Google Scholar] [CrossRef] [PubMed]
- Abson, D.J.; Jonas, J.J. The Hall–Petch Relation and High-Temperature Subgrains. Metal Sci. J. 1970, 4, 24–28. [Google Scholar] [CrossRef]
- Toth, L.S.; Biswas, S.; Gu, C.; Beausir, B. Notes on representing grain size distributions obtained by electron backscatter diffraction. Mater. Charact. 2013, 84, 67–71. [Google Scholar] [CrossRef]
- Esposito, L. Type IV creep cracking of welded joints: Numerical study of the grain size effect in HAZ. Procedia Struct. Integr. 2016, 2, 919–926. [Google Scholar] [CrossRef][Green Version]
- Perrin, I.J.; Hayhurst, D.R. Continuum damage mechanics analyses of type IV creep failure in ferritic steel crossweld specimens. Int. J. Press. Vessel. Pip. 1999, 76, 599–617. [Google Scholar] [CrossRef]
- Iijima, Y.; Kimura, K.; Hirano, K. Self-diffusion and isotope effect in α-iron. Acta Metall. 1988, 36, 2811–2820. [Google Scholar] [CrossRef]
- EPRI X20 CrMoV12-1 Steel Handbook; EPRI: Palo Alto, CA, USA, 2006; p. 70.
- Murillo-Marrodán, A.; Puchi-Cabrera, E.; García, E.; Dubar, M.; Cortés, F.; Dubar, L. An Incremental Physically-Based Model of P91 Steel Flow Behaviour for the Numerical Analysis of Hot-Working Processes. Metals 2018, 8, 269. [Google Scholar] [CrossRef]
- Kafexhiu, F.; Vodopivec, F.; Turna, J.V. Effect of tempering on the room-temperature mechanical properties of X20CrMoV121 and P91 steels. Materiali Tehnologije 2012, 46, 459–464. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kafexhiu, F.; Burja, J. Evaluation of Stationary Creep Rate in Heat-Affected Zone of Martensitic 9–12% Cr Steels. Metals 2020, 10, 1612. https://doi.org/10.3390/met10121612
Kafexhiu F, Burja J. Evaluation of Stationary Creep Rate in Heat-Affected Zone of Martensitic 9–12% Cr Steels. Metals. 2020; 10(12):1612. https://doi.org/10.3390/met10121612
Chicago/Turabian StyleKafexhiu, Fevzi, and Jaka Burja. 2020. "Evaluation of Stationary Creep Rate in Heat-Affected Zone of Martensitic 9–12% Cr Steels" Metals 10, no. 12: 1612. https://doi.org/10.3390/met10121612
APA StyleKafexhiu, F., & Burja, J. (2020). Evaluation of Stationary Creep Rate in Heat-Affected Zone of Martensitic 9–12% Cr Steels. Metals, 10(12), 1612. https://doi.org/10.3390/met10121612