Design Optimization of a Single-Strand Tundish Based on CFD-Taguchi-Grey Relational Analysis Combined Method
Abstract
1. Introduction
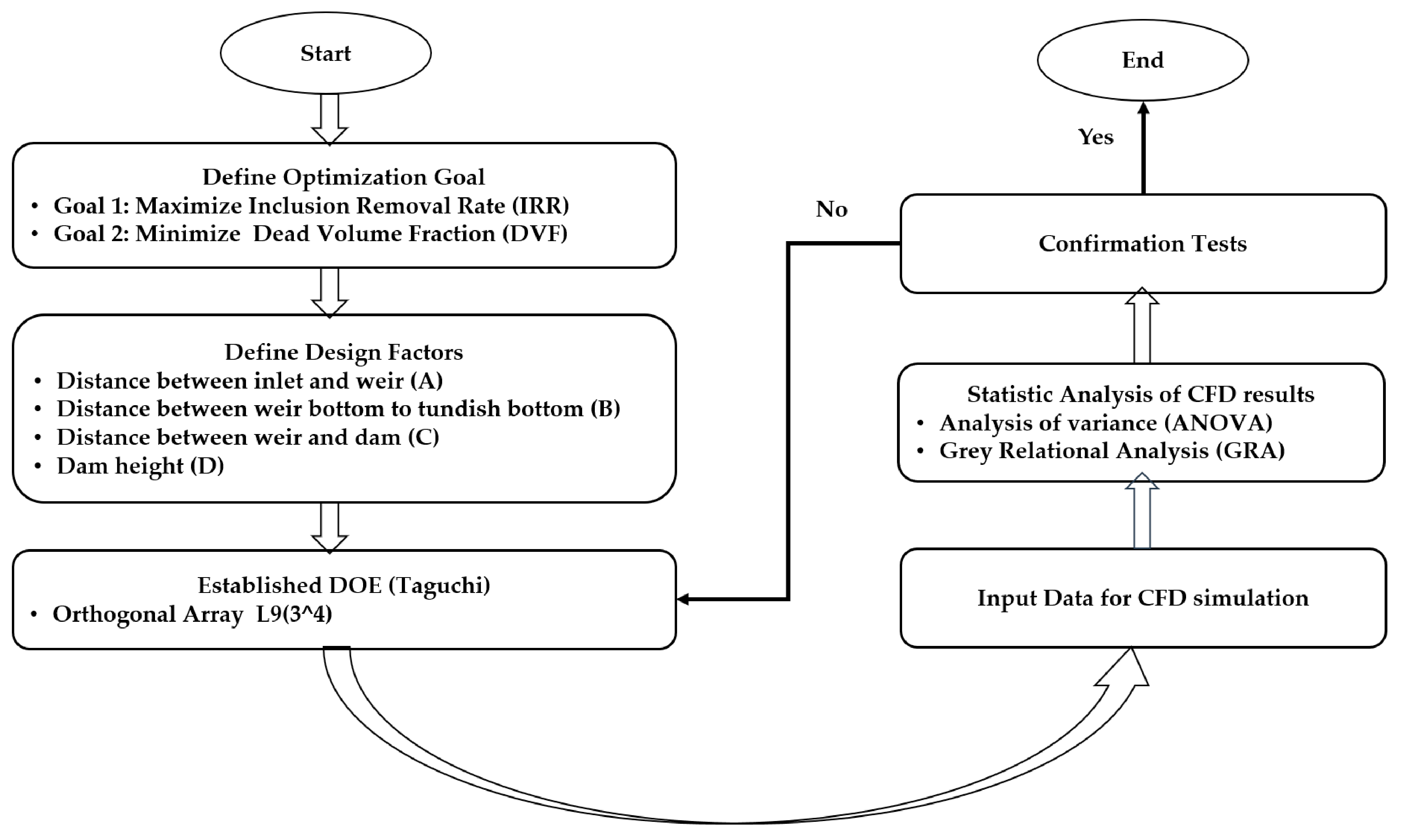
2. Methodology
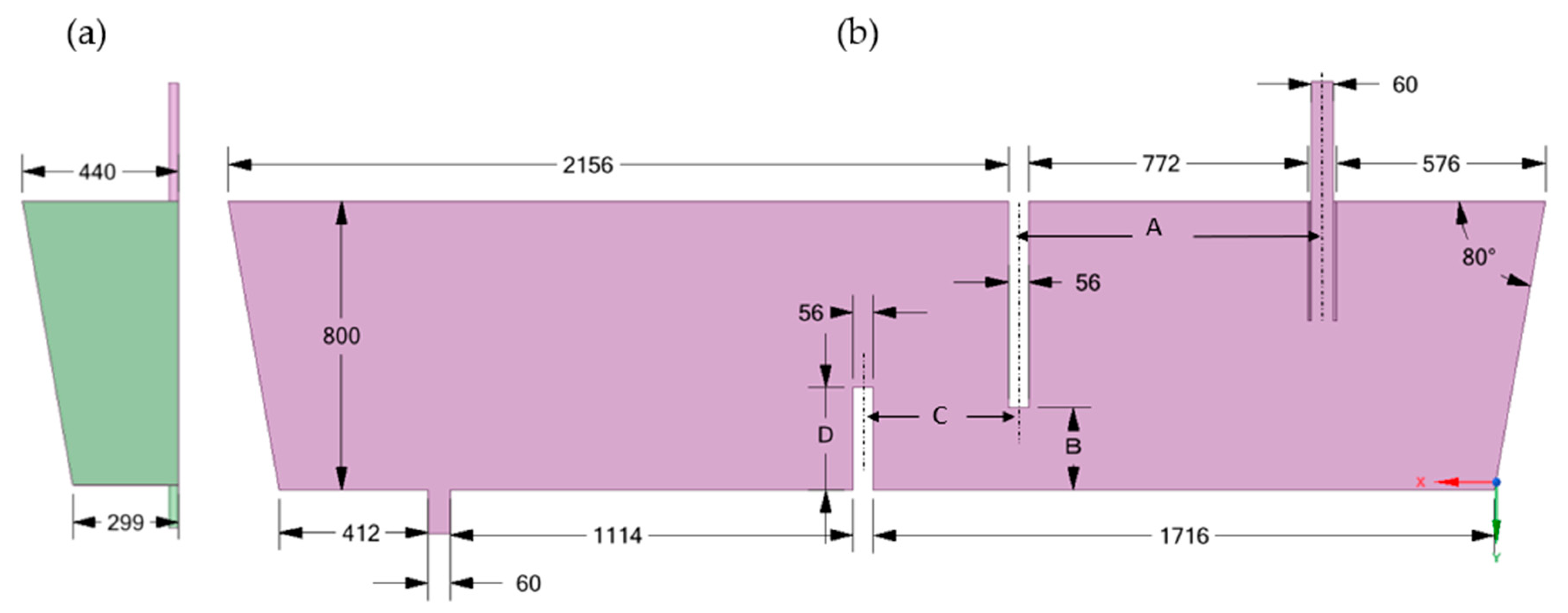
2.1. Design Objectives and Solution Strategy
- (i)
- inclusion remove rate (IRR), which is defined as (1 − inclusions reaching outlet/inclusions injected at inlet);
- (ii)
- dead volume fraction (DVF), which is defined as (1 − calculated mean residence time/theoretical mean residence time).
- (iii)
- The design optimization should be able to meet the conflicting requirements, which are maximizing IRR and minimizing DVF. The design objective was to obtain the optimized values of four design factors (shown in Figure 1):
- (iv)
- A (distance between inlet and weir),
- (v)
- B (distance of tundish bottom to weir),
- (vi)
- C (distance between weir and dam), and
- (vii)
- D (dam height).
2.2. Design of Experiment
2.2.1. Taguchi Design
2.2.2. Analysis of Variance
2.2.3. Grey Relational Analysis
- (i)
- The absolute difference of the compared series and the referential series should be obtained by Equation (8). The maximum and the minimum differences are obtained.
- (ii)
- Calculation of the relational coefficient and relational grade by Equation (9). The distinguishing coefficient p is between 0 and 1. Typically, the distinguishing p value is set to be 0.5.
- (iii)
- The grey relational grade is defined in Equation (10):where is the Grey relational coefficient, w(k) is the weight factor; w(k) is set as 0.5 in this study.
2.3. CFD Model
2.3.1. Model Description
- The model is based on a 3D standard set of the Navier–Stokes equations.
- Isothermal and steady-state liquid flow is considered.
- The motion of inclusions is simulated by solving the force balance equations.
- The realizable k-ε model is used to describe the turbulence.
- The free surface is flat and is kept at a fixed level. The tundish slag layer is not included.
- The surface tension and wettability at slag/steel/inclusion interphase boundaries are not included.
2.3.2. Governing Equations
2.3.3. Numerical Modelling Details
3. Results
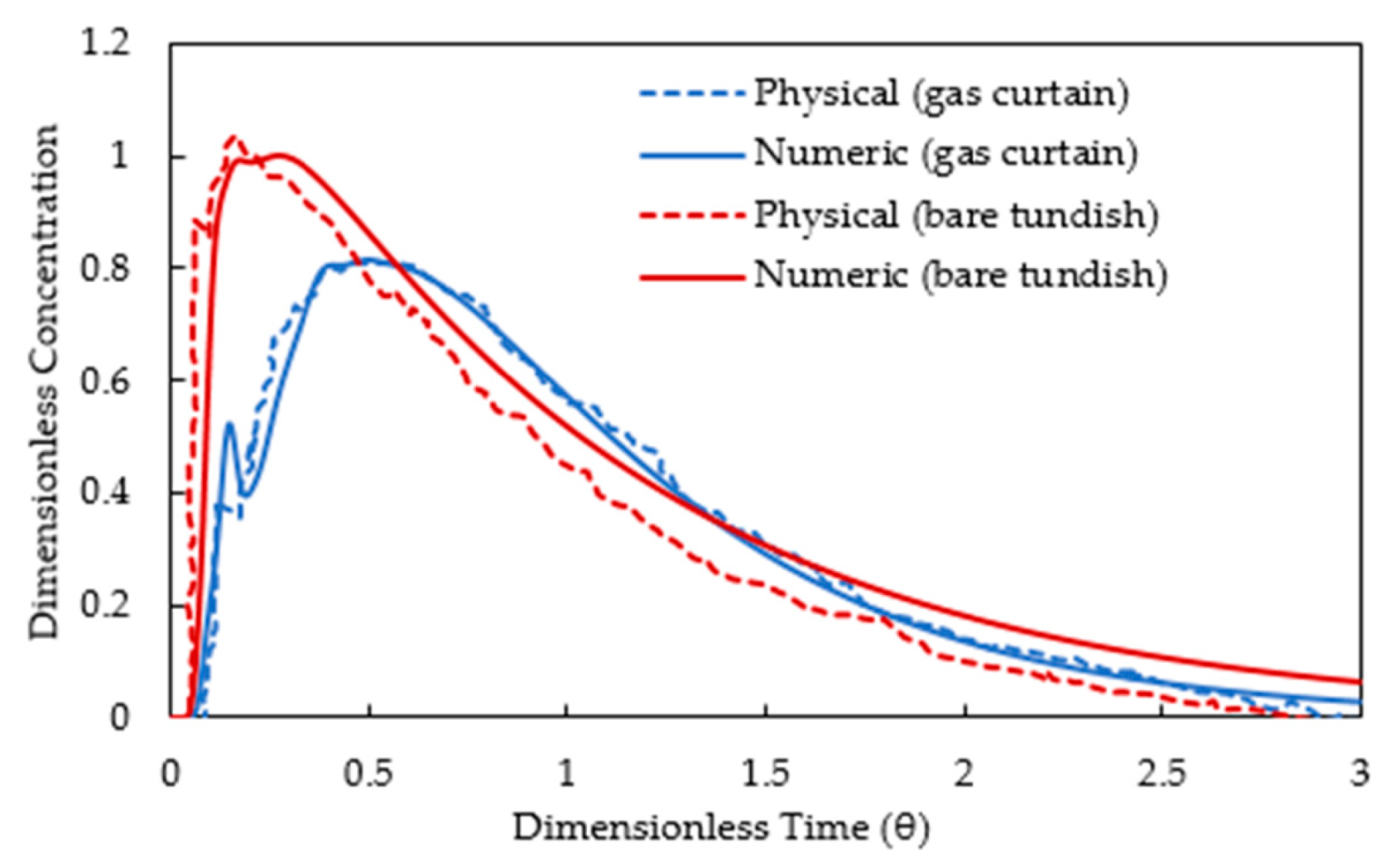
3.1. Validation of CFD Model
3.2. CFD Simulation Results
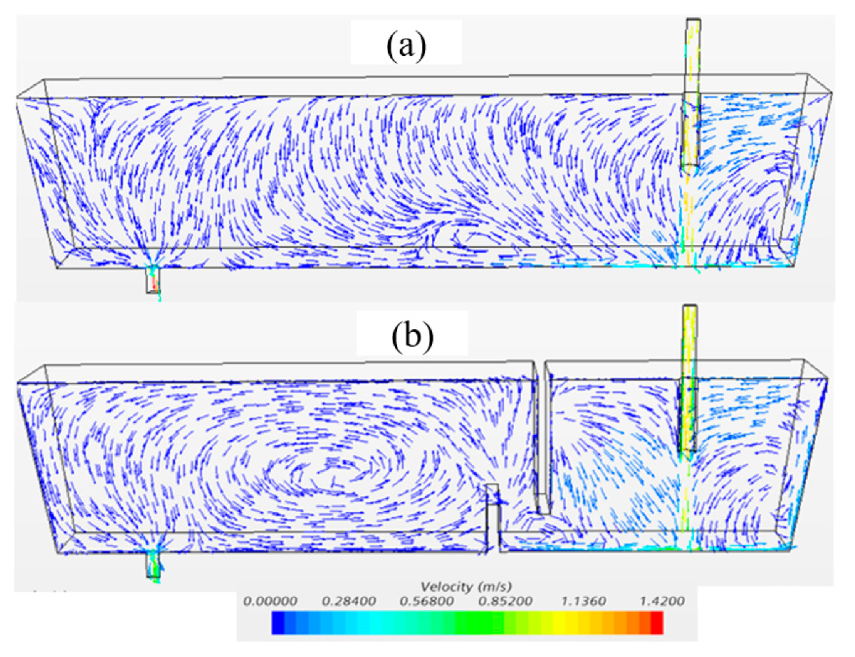
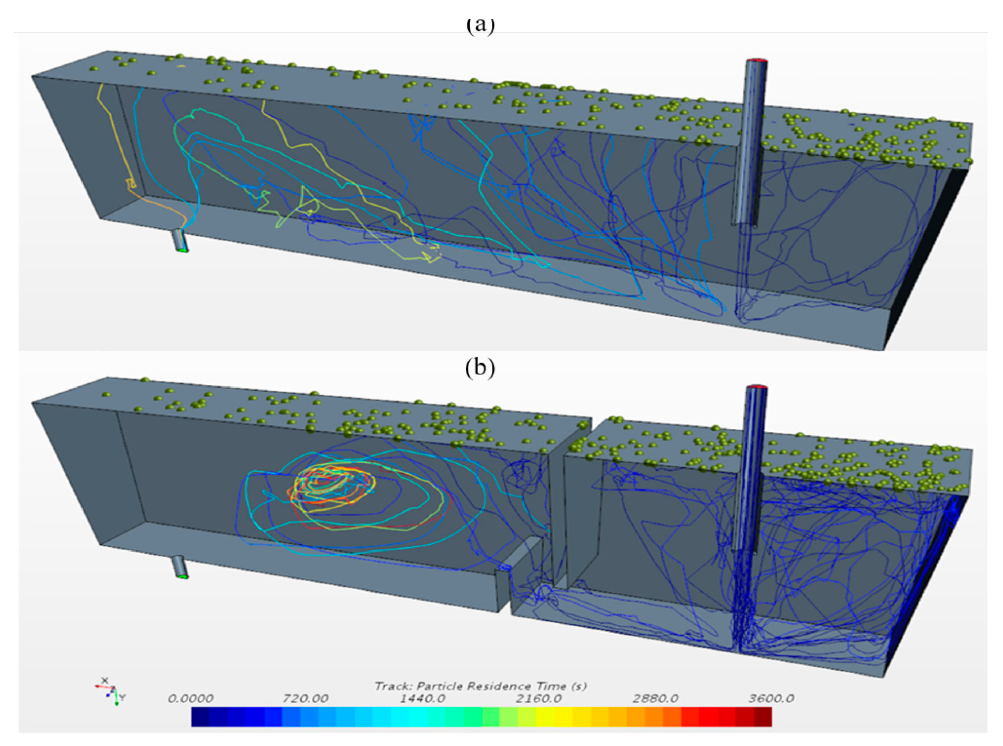
3.2.1. Fluid Flow
3.2.2. Inclusion Tracking
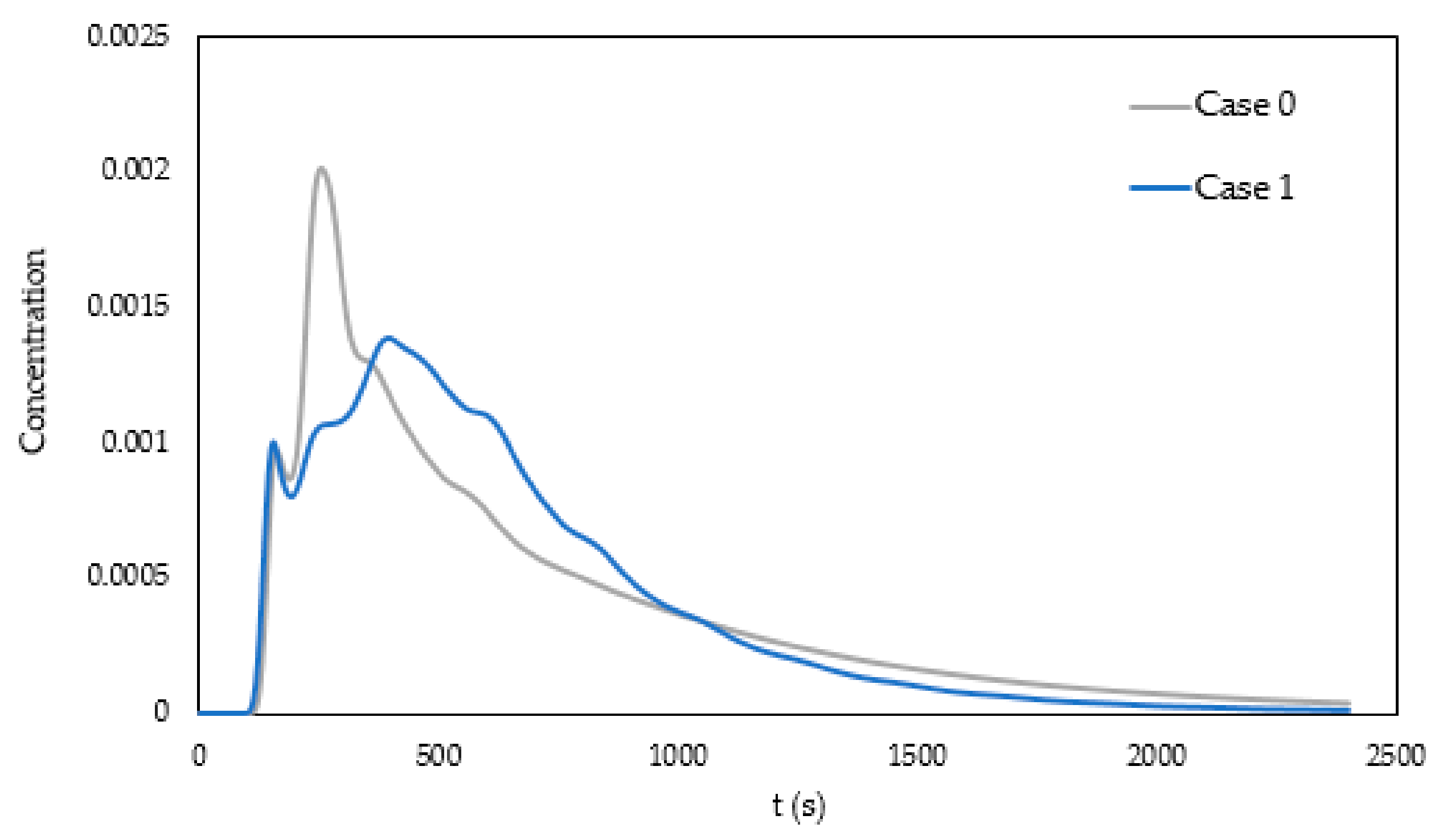
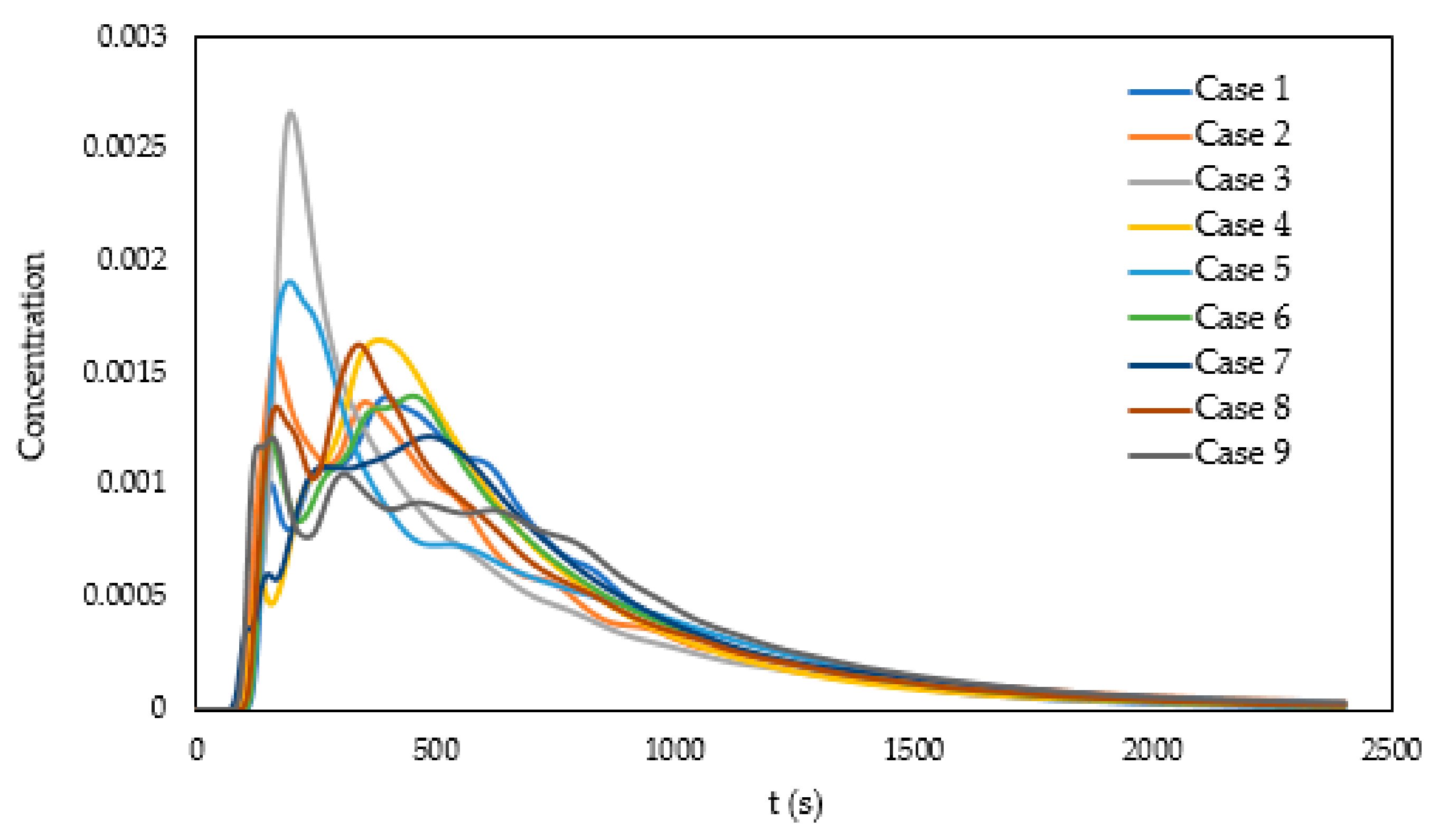
3.2.3. Residence-Time Distribution
3.3. Optimization Analysis
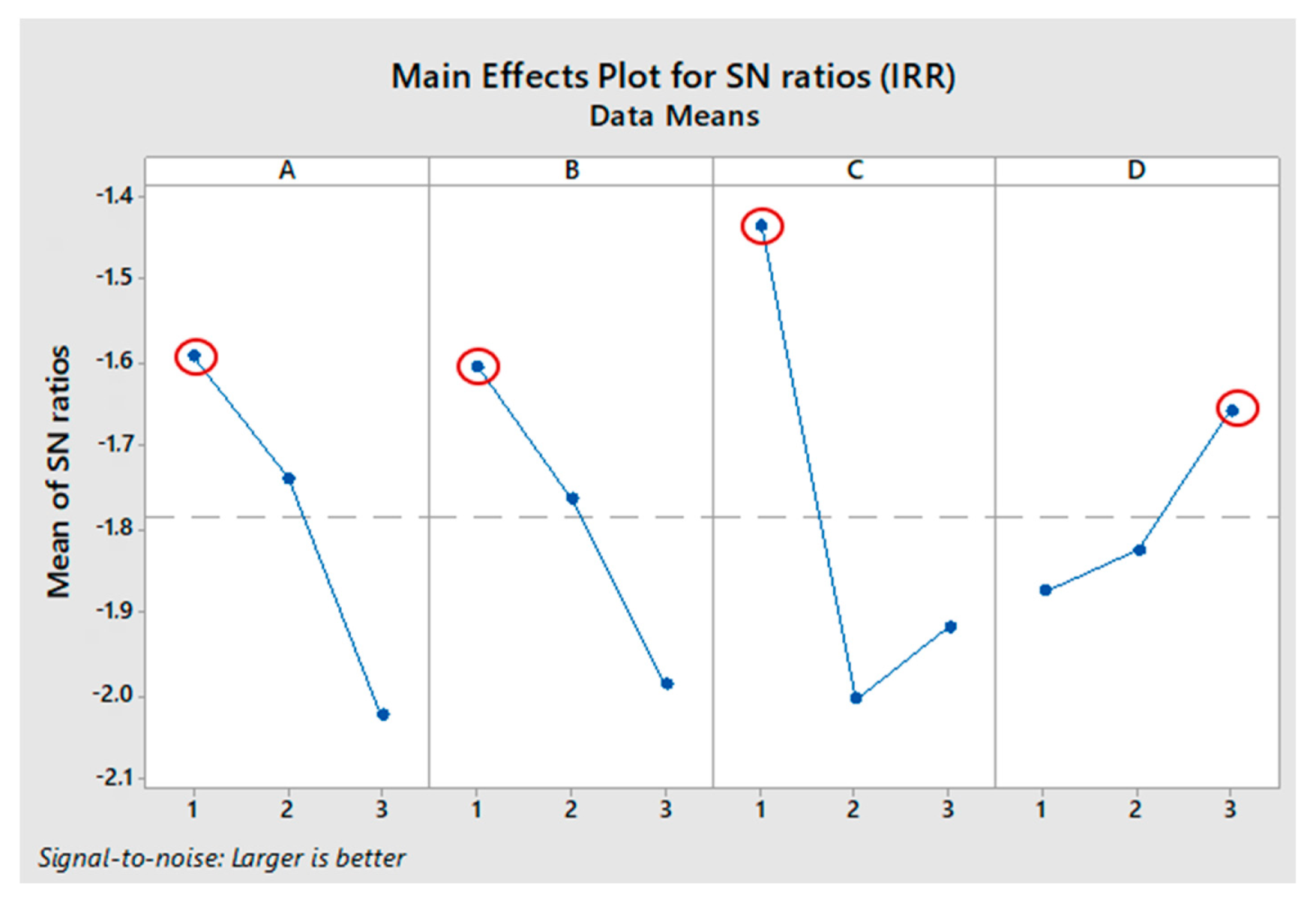
3.3.1. Single Response Optimization-Inclusion Remove Rate
3.3.2. Single Response Optimization-Dead Volume Fraction
3.3.3. Multiple Response Optimization Using the Grey Relational Grade
3.4. Confirmation Tests
4. Summary and Conclusions
- (1)
- The fluid pattern and the residence-time distribution were improved in the tundish furnished with the weir and dam, in comparison with that in the bare tundish. The weir confined high turbulent flow in the entry zone and increased the inclusion removal possibility by the top surface. In addition, the dam drove the flow vertically towards the top surface and enhanced the inclusion removal.
- (2)
- With regard to the design optimization for the single response of IRR, the importance order of the design factors was concluded as C > A > B > D. The optimum levels of the control factors for IRR were determined as the combination of A1, B1, C1, and D3. The reliability of the Taguchi analysis results was verified by ANOVA.
- (3)
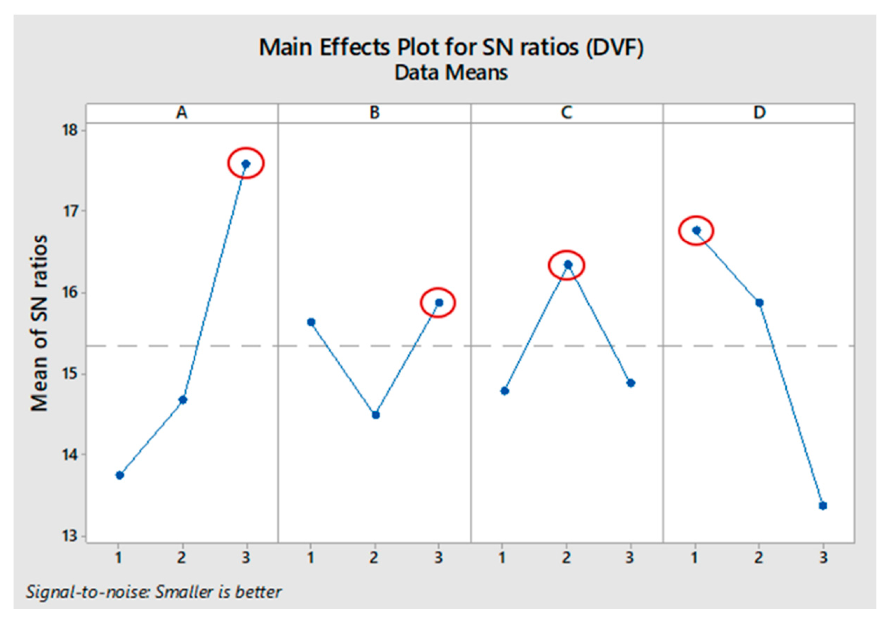
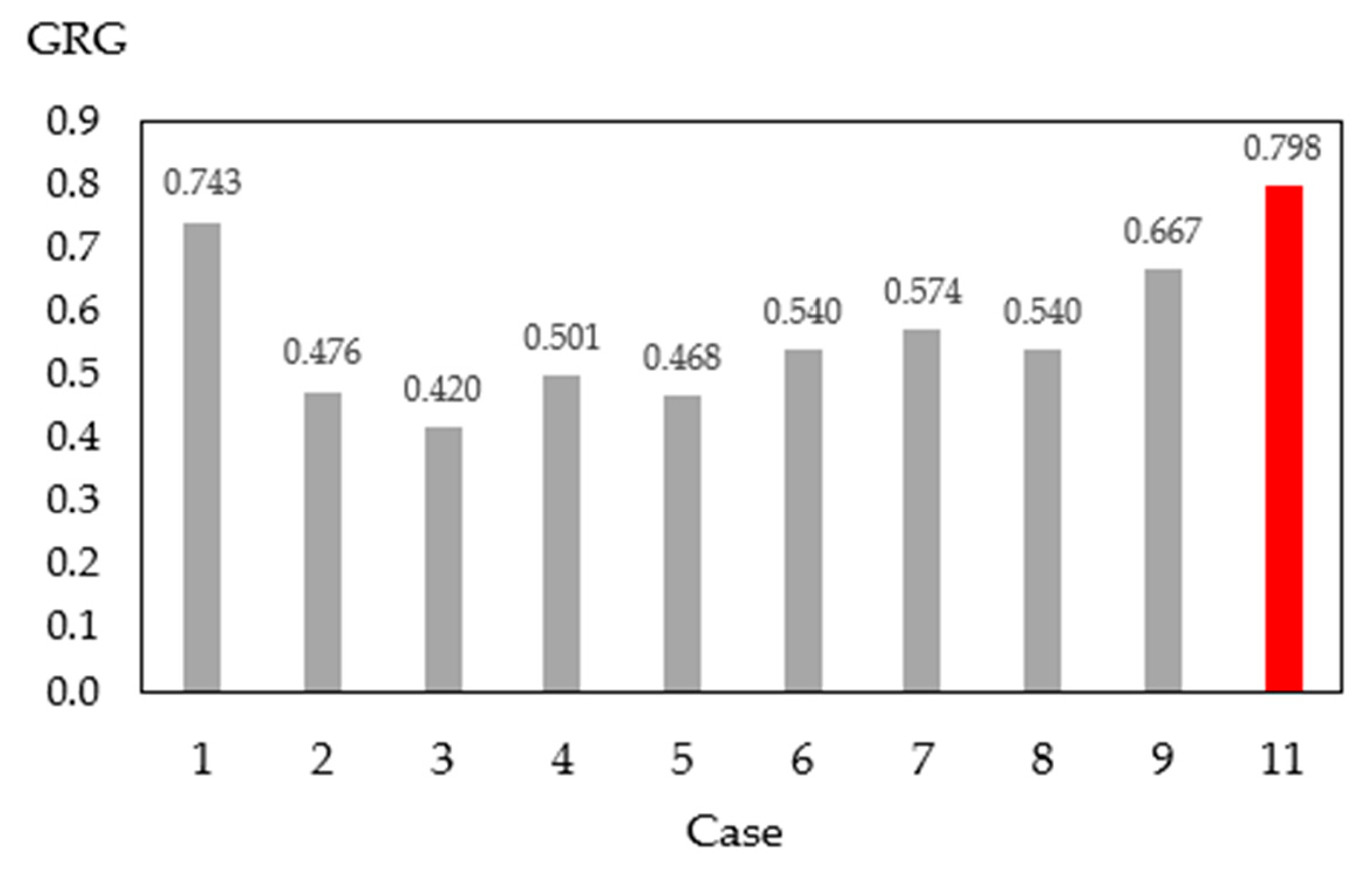
- In terms of single response of DVF, the importance order of the design factors was considered as A > D > C > B. The optimum levels of the control factors for DVF were predicted as the combination of A3, B3, C2, and D1. It was found that the optimum case of DVF had the best performance in minimizing dead volume, but the worst performance in removing inclusion particles. The conflicting responses suggests the necessity of developing a compromised optimization process of multiple objectives. The evaluation of the multiple responses was based on the grey relational grade. The importance order of the design factors for GRG is termed as D > C > B > A. The dam height was the most important factor affecting the GRG. The optimum levels of the control factors were termed as the mixture of A3, B1, C1, and D1.
- (4)
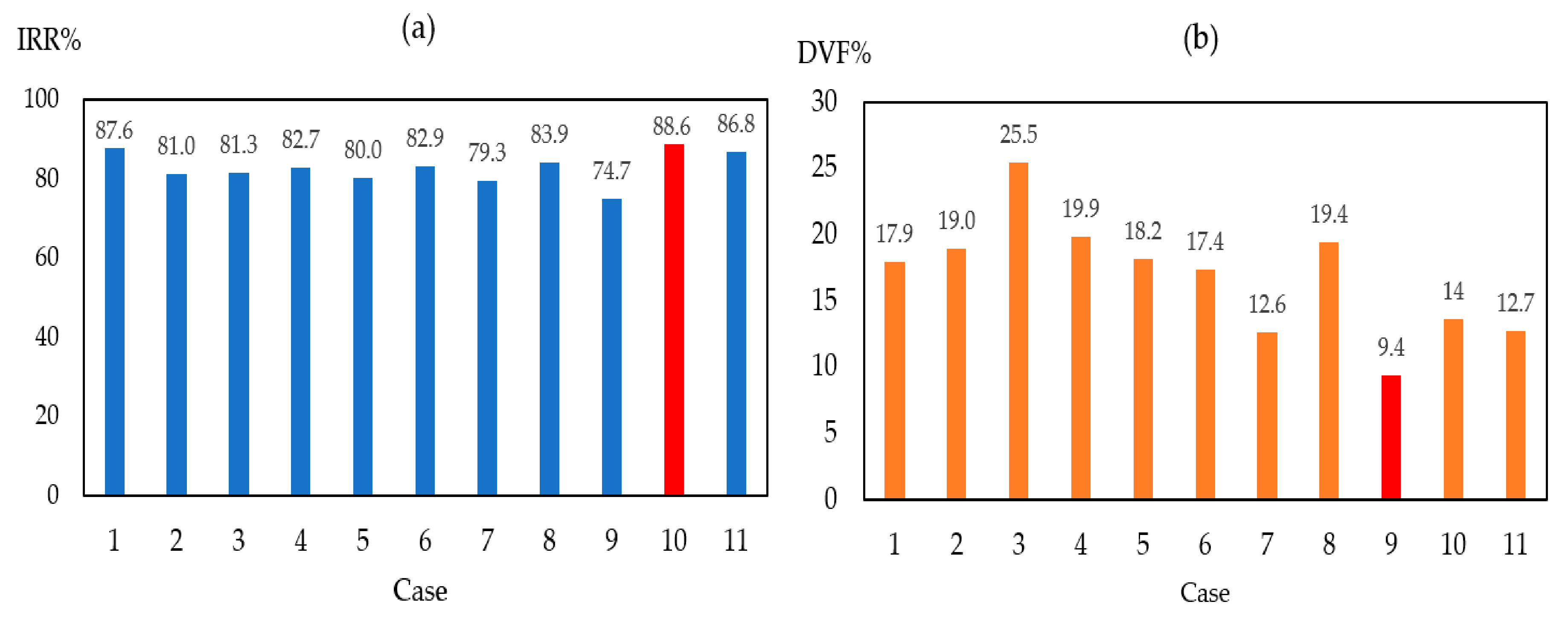
- The confirmation tests with regards to the different responses (IRR, DVF, and GRG) were performed. The optimum results from CFD simulations revealed the increased performance of the responses. An excellent agreement was observed between the CFD simulations and the DOE predictions.
- (5)
- The present study demonstrated that the application of CFD combined with the Taguchi-GRA method was effective in finding the optimal design that improved the tundish performance. The developed method may provide both time and cost savings not only for researchers but also for the steel industry. As shown in this study, a full design space (four design factors and three levels) requires a total of 81 (3 × 3 × 3 × 3) computer runs. By applying the Taguchi orthogonal arrays method, the computer runs can be significantly reduced to 9. Furthermore, the conclusions drawn from small-scale experiments are valid over the entire experimental region spanned by the design factors and their levels. Future work should test the applicability of the developed design methodology in a wider range of experiment conditions.
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Adj SS | Adjusted sums of squares |
| Adj MS | Adjusted mean squares |
| Deff | Effective diffusivity |
| Fd | Drag force |
| Fp | Pressure gradient force |
| Fvm | Virtual mass forces |
| Fg | Gravitational force |
| Fl | Lift force |
| Ftd | Turbulent dispersion |
| g | Gravity |
| Gk | Turbulent kinetic energy |
| k | Turbulent kinetic energy |
| mi | Mass |
| n | observation repeat number |
| SF | Source term |
| s2 | the variance |
| Seq SS | Sequential sums of squares |
| u | Velocity of the flow field |
| vl | The velocity of liquid |
| vp | The velocity of particle |
| Vp | Velocity of particle i |
| υ | Kinematic viscosity |
| xi(k) | sequence for the ith experiment |
| x0(k) | reference sequence |
| y | performance characteristic value |
| Grey relational coefficient | |
| µ | Molecular viscosity |
| µt | Turbulent viscosity |
| ρ | Density |
| w(k) | weight factor of the number k influence |
| Δ | deviation |
Abbreviations
| ANOVA | Analysis of Variance |
| CC | Continuous Casting |
| CAD | Computational Aided Design |
| CFD | Computational Fluid Dynamics |
| DOE | Design of Experiment |
| DVF | Dead Volume Fraction |
| FCD | Flow Control Device |
| GRA | Grey Relational Analysis |
| GRC | Grey Relational Coefficient |
| GRG | Grey Relational Grade |
| IRR | Inclusion Removal Rate |
| OA | Orthogonal Array |
| RTD | Residence-time distribution |
| S/N | Signal-to-noise ratio |
| MST | mean square for treatments |
| MSE | mean square for error |
References
- Szekely, J.; Ilegbusi, O.J. The Physical and Mathematical Modeling of Tundish Operations; Springer Science and Business Media LLC: New York, NY, USA, 1989. [Google Scholar]
- Mazumdar, D.; Guthrie, R.I.L. The Physical and Mathematical Modelling of Continuous Casting Tundish System. ISIJ Int. 1999, 39, 524–547. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Isac, M.; Guthrie, R.I.L. Physical and Mathematical Modelling of Steelmaking Tundish Operations: A Review of the Last Decade (1999–2009). ISIJ Int. 2010, 50, 331–348. [Google Scholar] [CrossRef]
- Mazumdar, D. Review, Analysis, and Modeling of Continuous Casting Tundish Systems. Steel Res. Int. 2019, 90, 1800279. [Google Scholar] [CrossRef]
- Sheng, D.-Y.; Yue, Q. Modeling of Fluid Flow and Residence-Time Distribution in a Five-strand Tundish. Metals 2020, 10, 1084. [Google Scholar] [CrossRef]
- Sheng, D.-Y. Mathematical Modelling of Multiphase Flow and Inclusion Behavior in a Single-Strand Tundish. Metals 2020, 10, 1213. [Google Scholar] [CrossRef]
- Taguchi, G.; Chowdhury, S.; Wu, Y. Taguchi’s Quality Engineering Handbook; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Taguchi, G. Off-line and On-line Quality Control Systems. In Proceedings of the International Conference on Quality Control, Tokyo, Japan, 17–20 October 1978. [Google Scholar]
- Joo, S.; Han, J.W.; Guthrie, R.I.L. Inclusion behavior and heat-transfer phenomena in steelmaking tundish operations: Part III. applications—Computational approach to tundish design. Met. Mater. Trans. A 1993, 24, 779–788. [Google Scholar] [CrossRef]
- Craig, K.J.; De Kock, D.J.; Makgata, K.W.; De Wet, G.J. Mathematical Modeling of Iron and Steel Making Processes. Design Optimization of a Single-strand Continuous Caster Tundish Using Residence Time Distribution Data. ISIJ Int. 2001, 41, 1194–1200. [Google Scholar] [CrossRef]
- Jha, P.K.; Dash, S.K. Employment of different turbulence models to the design of optimum steel flows in a tundish. Int. J. Numer. Methods Heat Fluid Flow 2004, 14, 953–979. [Google Scholar] [CrossRef]
- Hülstrung, J.; Zeimes, M.; Au, A.; Oppermann, W.; Radusch, G. Optimization of the Tundish Design to Increase the Product Quality by means of Numerical Fluid Dynamics. Steel Res. Int. 2005, 76, 59–63. [Google Scholar] [CrossRef]
- Wei, Z.; Bao, Y.; Liu, J.; Gong, W.; Wang, B. Orthogonal analysis of water model study on the optimization of flow control devices in a six-strand tundish. J. Univ. Sci. Technol. Beijing Miner. Met. Mater. 2007, 14, 118–124. [Google Scholar] [CrossRef]
- Kumar, A.; Mazumdar, D.; Koria, S.C. Modeling of Fluid Flow and Residence Time Distribution in a Four-strand Tundish for Enhancing Inclusion Removal. ISIJ Int. 2008, 48, 38–47. [Google Scholar] [CrossRef]
- Singh, V.; Pal, A.R.; Panigrahi, P. Numerical Simulation of Flow-induced Wall Shear Stress to Study a Curved Shape Billet Caster Tundish Design. ISIJ Int. 2008, 48, 430–437. [Google Scholar] [CrossRef][Green Version]
- Yang, S.; Zhang, L.; Li, J.; Peaslee, K. Structure Optimization of Horizontal Continuous Casting Tundishes Using Mathematical Modeling and Water Modeling. ISIJ Int. 2009, 49, 1551–1560. [Google Scholar] [CrossRef][Green Version]
- Cwudziñski, A. Numerical Simulation of Liquid Steel Flow in Wedge-type One-strand Slab Tundish with a Subflux Turbulence Controller and an Argon Injection System. Steel Res. Int. 2010, 81, 123–131. [Google Scholar] [CrossRef]
- Tripathi, A. Numerical Investigation of Electro-magnetic Flow Control Phenomenon in a Tundish. ISIJ Int. 2012, 52, 447–456. [Google Scholar] [CrossRef]
- Shukla, R.; Anapagaddi, R.; Mangal, S.; Singh, A.K. Exploring the Design Space of a Continuous Casting Tundish for Improved Inclusion Removal and Reduced Dead Volume. In Proceedings of the Science and Technology of Ironmaking and Steelmaking, Jamshedpur, India, 16–18 December 2013. [Google Scholar]
- Anapagaddi, R.; Shukla, R.; Goyal, S.; Singh, A. Exploration of the Design Space in Continuous Casting Tundish. In Proceedings of the ASME 2014 International Design Engineering Technical Conference, New York, NY, USA, 17–20 August 2014. [Google Scholar]
- Cloete, J.; Akdogan, G.; Bradshaw, S.; Chibwe, D. Physical and numerical modelling of a four-strand steelmaking tundish using flow analysis of different configurations. J. S. Afr. Inst. Min. Met. 2015, 115, 355–362. [Google Scholar] [CrossRef]
- He, F.; Zhang, L.-Y.; Xu, Q.-Y. Optimization of flow control devices for a T-type five-strand billet caster tundish: Water modeling and numerical simulation. China Foundry 2016, 13, 166–175. [Google Scholar] [CrossRef]
- Buľko, B.; Priesol, I.; Demeter, P.; Gašparovič, P.; Baricová, D.; Hrubovčáková, M. Geometric Modification of the Tundish Impact Point. Metals 2018, 8, 944. [Google Scholar] [CrossRef]
- Rocha, J.R.D.S.; De Souza, E.E.B.; Marcondes, F.; De Castro, J.A. Modeling and computational simulation of fluid flow, heat transfer and inclusions trajectories in a tundish of a steel continuous casting machine. J. Mater. Res. Technol. 2019, 8, 4209–4220. [Google Scholar] [CrossRef]
- Anthony, J. Design of Experiments for Engineers and Scientists; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Minitab 18 Statistical Software; Minitab, Inc.: State College, PA, USA, 2017. Available online: www.minitab.com (accessed on 7 June 2017).
- Fisher, R.A. Statistical Methods for Research Workers; Oliver & Boyd: Edinburgh, UK, 1925. [Google Scholar]
- Deng, J.-L. Control Problems of Grey Systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Grey_relational_analysis (accessed on 27 June 2020).
- Yin, M.-S. Fifteen years of grey system theory research: A historical review and bibliometric analysis. Expert Syst. Appl. 2013, 40, 2767–2775. [Google Scholar] [CrossRef]
- Siemens. STAR-CCM + Version 13.04 User Guide; Siemens PLM Software: Munich, Germany, 2019. [Google Scholar]
- Ghirelli, F.; Hermansson, S.; Thunman, H.; Leckner, B. Reactor residence time analysis with CFD. Prog. Comput. Fluid Dyn. Int. J. 2006, 6, 241. [Google Scholar] [CrossRef]
- Spalding, D. A note on mean residence-times in steady flows of arbitrary complexity. Chem. Eng. Sci. 1958, 9, 74–77. [Google Scholar] [CrossRef]
- Chen, D.; Xie, X.; Long, M.; Zhang, M.; Zhang, L.; Liao, Q. Hydraulics and Mathematics Simulation on the Weir and Gas Curtain in Tundish of Ultrathick Slab Continuous Casting. Met. Mater. Trans. A 2013, 45, 392–398. [Google Scholar] [CrossRef]

| Reference | Code | Study 1 | Strand 1 | Turb. 2 | Tundish Design | ||||
|---|---|---|---|---|---|---|---|---|---|
| Case | Method 3 | FCD 4 | Design Factors 5 | Perform. Feature 6 | |||||
| Joo (1993) [9] | METFLO | n | 2 | k − ε | 13 | - | D, W | SFR, WAI, CFCD, WL, DL, | FP, IRR |
| Craig (2001) [10] | FLUENT | n | 1 | k − ε | 20 | RSM | TI, B, D, W, S | WL, DL BL, BHA, FT | FP, RTD |
| Jha(2004) [11] | - | N | 6 | (vari.) | 6 | - | TI | TM, OL, TIH, ID | RTD |
| Hülstrung (2005) [12] | - | N | 2 | k − ε | 10 | - | S, TI | SFR, ID, IFR, CFCD | V, IRR, RTD |
| Wei (2007) [13] | - | P | 6 | - | 25 | Taguchi | B | BD, HL | RTD |
| Kumar (2008) [14] | FLUENT | N/P | 2–6 | k − ε | 3 | - | D, TI | CFCD | V, RTD |
| Singh (2008) [15] | FLUENT | N/P | 6 | k − ε | 6 | - | TI | WAC, WAIA, TW | V, WSS, RTD |
| Yang (2009) [16] | FLUENT | N/P/I | 2 | k − ε | 5 | - | TI, IL, B, D | DH, ILT | FP, RTD, V, WSS, T, IRR, TO, TN |
| Cwudziński (2010) [17] | FLUENT | N/I | 1 | k − ε | 12 | - | S, TI, D, GPB | CFCD, GPBL, GFR | FP, RTD |
| Tripathi (2012) [18] | FLUENT | N | 1 | k − ε | 9 | - | ED | EDL, MS | V, RTD |
| Shukla (2013) [19] | CFX | N/P | 1 | k − ε | - | Taguchi | D, W | DH, DT, DL, WD, WT, WL, SFR | RTD, IRR |
| Anapagaddi (2014) [20] | CFX | N | 1 | k − ε | 7 | RSM | D, W | IT, SFR, WL, WD, WT, DL, DH, DT | RTD, IRR |
| Cloete (2015) [21] | FLUENT | N/P | 4 | k − ε | 4 | - | TI, D | CFCD, TIS, DH | V, KE, RTD |
| He (2016) [22] | FLUENT | N/P | 5 | k − ε | 3 | - | TI, B | CFCD | FS, V, T |
| Buľko (2018) [23] | FLUENT | N/P | 2 | k − ε | 6 | - | TI | TIS, SFR | RTD, V |
| Sousa Rocha (2019) [24] | CFX | N/P | 2 | k − ε/SST | 3 | - | D, W | CFCD, ID | RTD, IRR, FP, T |
| Factor | Unit | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|
| A | mm | 640 | 840 | 1040 |
| B | mm | 180 | 230 | 280 |
| C | mm | 230 | 430 | 630 |
| D | mm | 220 | 280 | 340 |
| Case | A | B | C | D |
|---|---|---|---|---|
| Case 0 | - | - | - | - |
| Case 1 | 1 | 1 | 1 | 1 |
| Case 2 | 1 | 2 | 2 | 2 |
| Case 3 | 1 | 3 | 3 | 3 |
| Case 4 | 2 | 1 | 2 | 3 |
| Case 5 | 2 | 2 | 3 | 1 |
| Case 6 | 2 | 3 | 1 | 2 |
| Case 7 | 3 | 1 | 3 | 2 |
| Case 8 | 3 | 2 | 1 | 3 |
| Case 9 | 3 | 3 | 2 | 1 |
| Parameter | Value |
|---|---|
| Inlet velocity | 1 m/s |
| Steel density | 7020 kg/m3 |
| Steel viscosity | 0.006 Pa s |
| Reference pressure | 101325 Pa |
| Inclusion velocity | 1 m/s |
| Inclusion size | 50 μm |
| Inclusion density | 5000 kg/m3 |
| Outlet (outflow ratio) | 1 |
| Wall | No slip |
| Top surface | Free slip |
| Tracer inlet (E-curve) | 1 (t ≤ 0–2 s), 0 (t > 2 s) |
| Case | A | B | C | D | IRR | S/N |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.876 | −1.15 |
| 2 | 1 | 2 | 2 | 2 | 0.81 | −1.83 |
| 3 | 1 | 3 | 3 | 3 | 0.813 | −1.8 |
| 4 | 2 | 1 | 2 | 3 | 0.827 | −1.65 |
| 5 | 2 | 2 | 3 | 1 | 0.8 | −1.94 |
| 6 | 2 | 3 | 1 | 2 | 0.829 | −1.63 |
| 7 | 3 | 1 | 3 | 2 | 0.793 | −2.01 |
| 8 | 3 | 2 | 1 | 3 | 0.839 | −1.52 |
| 9 | 3 | 3 | 2 | 1 | 0.747 | −2.53 |
| Level | A | B | C | D |
|---|---|---|---|---|
| 1 | −1.593 | −1.605 | −1.435 | −1.874 |
| 2 | −1.739 | −1.764 | −2005 | −1.825 |
| 3 | −2.024 | −1.987 | −1.917 | −1.658 |
| Delta | 0.431 | 0.382 | 0.570 | 0.216 |
| Rank | 2 | 3 | 1 | 4 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value |
|---|---|---|---|---|---|---|
| A | 2 | 0.002464 | 24.64% | 0.002464 | 0.001232 | 4.09 |
| B | 2 | 0.001918 | 19.18% | 0.001918 | 0.000959 | 3.18 |
| C | 2 | 0.005014 | 50.15% | 0.005014 | 0.002507 | 8.32 |
| Error | 2 | 0.000603 | 6.03% | 0.000603 | 0.000301 | - |
| Total | 8 | 0.009999 | 100.00% | - | - | - |
| Case | ttheo (s) | tmin (s) | tmax (s) | tmean (s) | Vd/V % | Vp/V % | Vm/V % |
|---|---|---|---|---|---|---|---|
| Case 0 | 742 | 100 | 251 | 629 | 15 | 24 | 61 |
| Case 1 | 729 | 365 | 396 | 599 | 18 | 52 | 30 |
| Case 2 | 729 | 92 | 165 | 591 | 19 | 18 | 63 |
| Case 3 | 729 | 99 | 197 | 543 | 26 | 20 | 54 |
| Case 4 | 729 | 95 | 382 | 584 | 20 | 33 | 47 |
| Case 5 | 729 | 103 | 195 | 597 | 18 | 20 | 61 |
| Case 6 | 729 | 224 | 452 | 603 | 17 | 46 | 36 |
| Case 7 | 729 | 76 | 485 | 637 | 13 | 38 | 49 |
| Case 8 | 729 | 134 | 338 | 588 | 19 | 32 | 48 |
| Case 9 | 729 | 83 | 157 | 661 | 9 | 16 | 74 |
| Case | A | B | C | D | DVF | S/N |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.179 | 14.933 |
| 2 | 1 | 2 | 2 | 2 | 0.190 | 14.447 |
| 3 | 1 | 3 | 3 | 3 | 0.255 | 11.869 |
| 4 | 2 | 1 | 2 | 3 | 0.199 | 14.033 |
| 5 | 2 | 2 | 3 | 1 | 0.182 | 14.796 |
| 6 | 2 | 3 | 1 | 2 | 0.174 | 15.195 |
| 7 | 3 | 1 | 3 | 2 | 0.126 | 17.966 |
| 8 | 3 | 2 | 1 | 3 | 0.194 | 14.230 |
| 9 | 3 | 3 | 2 | 1 | 0.094 | 20.579 |
| Level | A | B | C | D |
|---|---|---|---|---|
| 1 | 13.75 | 15.64 | 14.79 | 16.77 |
| 2 | 14.67 | 14.49 | 16.35 | 15.87 |
| 3 | 17.59 | 15.88 | 14.88 | 13.38 |
| Delta | 3.84 | 1.39 | 1.57 | 3.39 |
| Rank | 1 | 4 | 3 | 2 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value |
|---|---|---|---|---|---|---|
| A | 2 | 0.007597 | 45.82% | 0.007597 | 0.003798 | 11.39 |
| C | 2 | 0.001247 | 7.52% | 0.001247 | 0.000623 | 1.87 |
| D | 2 | 0.007070 | 42.64% | 0.007070 | 0.003535 | 10.60 |
| Error | 2 | 0.000667 | 4.02% | 0.000667 | 0.000333 | - |
| Total | 8 | 0.016580 | 100.00% | - | - | - |
| Case | A | B | C | D | IRR | DVF | Normalization | Deviation Sequence | Gray Relational Coefficient | GRG | Rank | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IRR | DVF | IRR | DVF | IRR | DVF | |||||||||
| 1 | 1 | 1 | 1 | 1 | 87.6 | 18 | 1.000 | 0.469 | 0.000 | 0.531 | 1.000 | 0.485 | 0.743 | 1 |
| 2 | 1 | 2 | 2 | 2 | 81.0 | 19 | 0.488 | 0.406 | 0.512 | 0.594 | 0.494 | 0.457 | 0.476 | 7 |
| 3 | 1 | 3 | 3 | 3 | 81.3 | 26 | 0.512 | 0.000 | 0.488 | 1.000 | 0.506 | 0.333 | 0.420 | 9 |
| 4 | 2 | 1 | 2 | 3 | 82.7 | 20 | 0.620 | 0.348 | 0.380 | 0.652 | 0.568 | 0.434 | 0.501 | 6 |
| 5 | 2 | 2 | 3 | 1 | 80.0 | 18 | 0.411 | 0.452 | 0.589 | 0.548 | 0.459 | 0.477 | 0.468 | 8 |
| 6 | 2 | 3 | 1 | 2 | 82.9 | 17 | 0.636 | 0.502 | 0.364 | 0.498 | 0.578 | 0.501 | 0.540 | 5 |
| 7 | 3 | 1 | 3 | 2 | 79.3 | 13 | 0.357 | 0.797 | 0.643 | 0.203 | 0.437 | 0.711 | 0.574 | 3 |
| 8 | 3 | 2 | 1 | 3 | 83.9 | 19 | 0.713 | 0.376 | 0.287 | 0.624 | 0.635 | 0.445 | 0.540 | 4 |
| 9 | 3 | 3 | 2 | 1 | 74.7 | 9 | 0.000 | 1.000 | 1.000 | 0.000 | 0.333 | 1.000 | 0.667 | 2 |
| Case | A | B | C | D | GRG | S/N |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.743 | −2.585 |
| 2 | 1 | 2 | 2 | 2 | 0.476 | −6.456 |
| 3 | 1 | 3 | 3 | 3 | 0.420 | −7.543 |
| 4 | 2 | 1 | 2 | 3 | 0.501 | −5.999 |
| 5 | 2 | 2 | 3 | 1 | 0.468 | −6.594 |
| 6 | 2 | 3 | 1 | 2 | 0.540 | −5.355 |
| 7 | 3 | 1 | 3 | 2 | 0.574 | −4.821 |
| 8 | 3 | 2 | 1 | 3 | 0.540 | −5.350 |
| 9 | 3 | 3 | 2 | 1 | 0.667 | −3.522 |
| Level | A | B | C | D |
|---|---|---|---|---|
| 1 | −5.528 | −4.468 | −4.430 | −4.234 |
| 2 | −5.983 | −6.133 | −5.326 | −5.544 |
| 3 | −4.564 | −5.473 | −6.319 | −6.297 |
| Delta | 1.419 | 1.665 | 1.890 | 2.064 |
| Rank | 4 | 3 | 2 | 1 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value |
|---|---|---|---|---|---|---|
| C | 2 | 0.02171 | 26.13% | 0.02171 | 0.010853 | 1.76 |
| D | 2 | 0.03030 | 36.48% | 0.03030 | 0.015150 | 2.46 |
| B | 2 | 0.01874 | 22.56% | 0.01874 | 0.009372 | 1.52 |
| Error | 2 | 0.01232 | 14.83% | 0.01232 | 0.006160 | - |
| Total | 8 | 0.08307 | 100.00% | - | - | - |
| Response | Design | Case | CFD | Prediction |
|---|---|---|---|---|
| IRR | A1B1C1D3 | 10 | 88.6% | 89.4% |
| DVF | A3B3C2D1 | 9 | 9.4% | 9.35% |
| GRG | A3B1C1D1 | 11 | 0.798 | 0.790 |
| Case 11- IRR: 86.8%; and DVF: 12.7% (CFD calculated) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, D.-Y. Design Optimization of a Single-Strand Tundish Based on CFD-Taguchi-Grey Relational Analysis Combined Method. Metals 2020, 10, 1539. https://doi.org/10.3390/met10111539
Sheng D-Y. Design Optimization of a Single-Strand Tundish Based on CFD-Taguchi-Grey Relational Analysis Combined Method. Metals. 2020; 10(11):1539. https://doi.org/10.3390/met10111539
Chicago/Turabian StyleSheng, Dong-Yuan. 2020. "Design Optimization of a Single-Strand Tundish Based on CFD-Taguchi-Grey Relational Analysis Combined Method" Metals 10, no. 11: 1539. https://doi.org/10.3390/met10111539
APA StyleSheng, D.-Y. (2020). Design Optimization of a Single-Strand Tundish Based on CFD-Taguchi-Grey Relational Analysis Combined Method. Metals, 10(11), 1539. https://doi.org/10.3390/met10111539





