Reply to Comment on the Paper Entitled “A New Cumulative Fatigue Damage Rule Based on Dynamic Residual S-N Curve and Material Memory Concept” by Peng Z., Huang H., Zhou J. and Li Y. Published in Metals (2018; 8(6): 456)

Zhaochun Peng; Hong-Zhong Huang; Jie Zhou; Yan-Feng Li

doi:10.3390/met10010008

,

and

¹

School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

²

Center for System Reliability and Safety, University of Electronic Science and Technology of China, Chengdu 611731, China

^*

Author to whom correspondence should be addressed.

Metals2020, 10(1), 8;https://doi.org/10.3390/met10010008

Version Notes

Order Reprints

Dear Editors,

For the published paper entitled “A new cumulative fatigue damage rule based on dynamic residual S-N curve and material memory concept” (Metals (2018; 8(6): 456)), Kris Hectors and Prof. Wim De Waele give a comment about the incorrect use of the formula of fatigue life prediction. Thanks for the suggestion. The following is our reply for the comment.

According to the comment “Equation (34) implicitly assumes that the number of cycles of each load block can be scaled with the same scalar up to failure, corresponding to

\sum D_{i} = 1

and

\sum n_{i} = N_{pre}

. This is however only true if the damage accumulation is described as a linear function of cycle ratios.”

This description is not true in some special cases. Considering a repeated two-level load block (with two blocks to failure), as shown in Figure 1.

It can also be viewed as a four-level fatigue loading, the specimen is fatigued by σ₁ for n₁ cycles, σ₂ for n₂ cycles, σ₃ for n₃ cycles, and σ₄ for n₄ cycles to failure, where

σ_{1} = σ_{1}^{'}

,

σ_{2} = σ_{2}^{'}

,

σ_{3} = σ_{1}^{'}

,

σ_{4} = σ_{2}^{'}

,

n_{1} = n_{1}^{'}

,

n_{2} = n_{2}^{'}

,

n_{3} = n_{1}^{'}

,

n_{4} = n_{2}^{'}

.

As is known, for a linear damage accumulation model, the damage variable D_i should be a linear function of cycle ratio

n_{i} / N_{f i}

, that is:

D_{i} \propto \frac{n_{i}}{N_{f i}}

(1)

In Equation (1), for Miner rule,

D_{i} = n_{i} / N_{fi}

. For a nonlinear damage model, D_i is defined as a nonlinear function of the cycle ratio, such as Marco-Starkey’s model (

D_{i} = {(n_{i} / N_{fi})}^{a_{i}}

), Chaboche’s continuum damage mechanics model (the formula can be found in Ref [47]).

(1)

Kwofie’s model

For Kwofie’s model, D_i is described as:

D_{i} = \frac{n_{i}}{N_{f i}} \times \frac{\ln (N_{f i})}{\ln (N_{f 1})}

(2)

where

\ln (N_{fi}) / \ln (N_{f 1})

is a constant without

n_{i} / N_{fi}

. D_i is a linear function of cycle ratio

n_{i} / N_{fi}

and that it is a linear damage model.

Fatigue damage is accumulated by taking a summation of the segmental damage caused by each loading stress level.

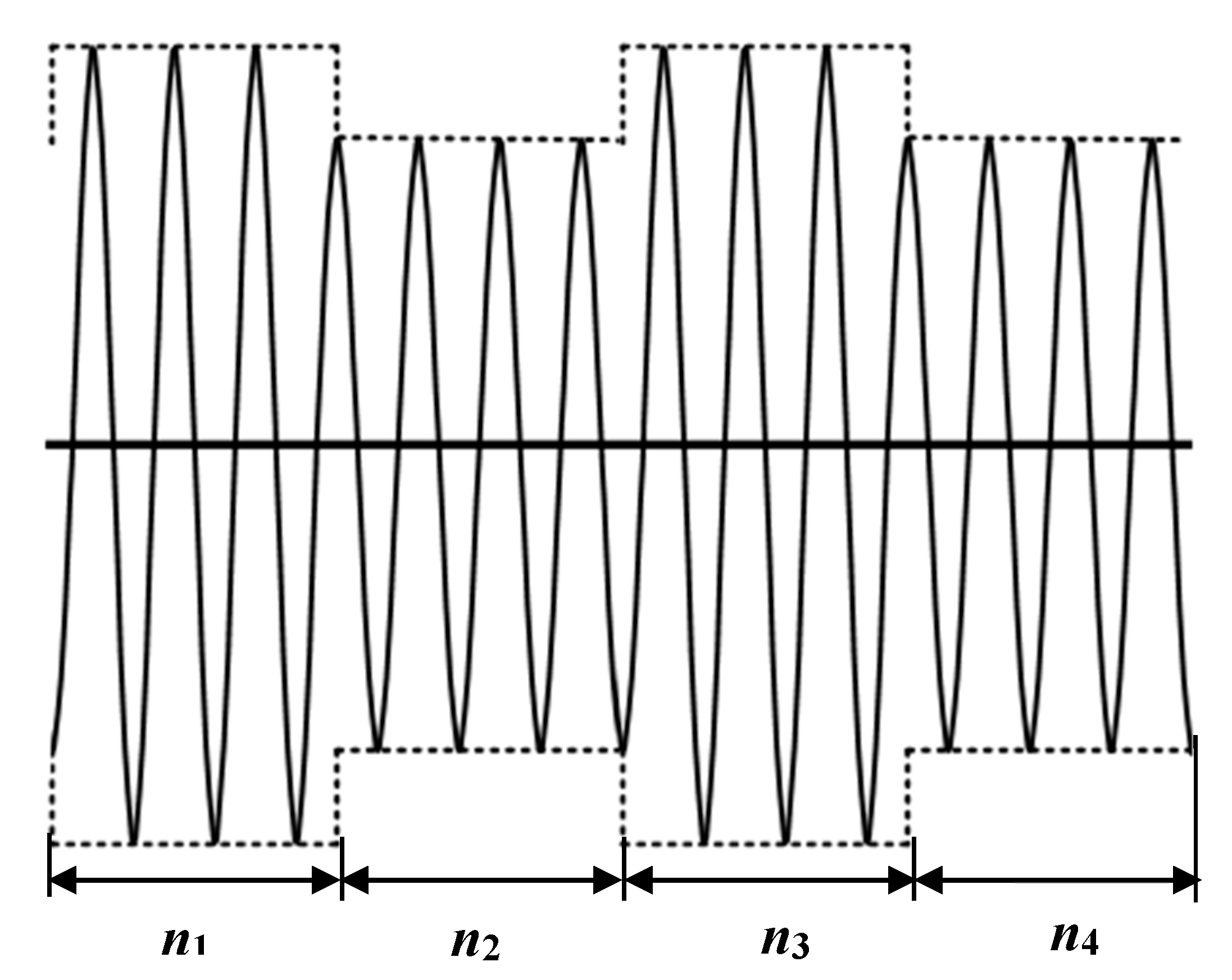
(a): The first-level loading

$D_{1} = \frac{n_{1}}{N_{f 1}} = \frac{n_{1}^{'}}{N_{f 1}}$

(3)
(b): The second-level loading

$D_{2} = \frac{n_{2}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} = \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(4)
(c): The third-level loading

$D_{3} = \frac{n_{3}}{N_{f 3}} \times \frac{\ln (N_{f 3})}{\ln (N_{f 1})} = \frac{n_{1}^{'}}{N_{f 1}} \times \frac{\ln (N_{f 1})}{\ln (N_{f 1})} = \frac{n_{1}^{'}}{N_{f 1}}$

(5)
(d): The fourth-level loading

$D_{4} = \frac{n_{4}}{N_{f 4}} \times \frac{\ln (N_{f 4})}{\ln (N_{f 1})} = \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(6)

The cumulative damage $\sum D_{i}$ is expressed as:

$\sum D_{i} = D_{1} + D_{2} + D_{3} + D_{4} = \frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} + \frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} = 2 \times \frac{n_{1}^{'}}{N_{f 1}} + 2 \times \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(7)

Using the Equation (34), the predicted fatigue life is

$N_{pre} = \frac{\sum n_{i}}{\sum D_{i}} = \frac{n_{1} + n_{2} + n_{3} + n_{4}}{\sum D_{i}} = \frac{2 \times n_{1}^{'} + 2 \times n_{2}^{'}}{2 \times \frac{n_{1}^{'}}{N_{f 1}} + 2 \times \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}} = \frac{n_{1}^{'} + n_{2}^{'}}{\frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}}$

(8)

Equation (8) can be scaled with a scalar C (C = 2).

(2)

A modified Kwofie’s model

Similar to Equation (2), we change the damage variable as:

D_{i} = \frac{n_{i}}{N_{f i}} \times \frac{\ln (N_{f i})}{\ln (N_{f (i - 1)})}

(9)

Compared to Equation (2),

\ln (N_{f 1})

becomes

\ln (N_{f (i - 1)})

, and

\ln (N_{fi}) / \ln (N_{f (i - 1)})

is a constant without of

n_{i} / N_{fi}

. D_i is still a linear function of cycle ratio

n_{i} / N_{f i}

.

(a): The first-level loading

$D_{1} = \frac{n_{1}}{N_{f 1}} = \frac{n_{1}^{'}}{N_{f 1}}$

(10)
(b): The second-level loading

$D_{2} = \frac{n_{2}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} = \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(11)
(c): The third-level loading

$D_{3} = \frac{n_{3}}{N_{f 3}} \times \frac{\ln (N_{f 3})}{\ln (N_{f 2})} = \frac{n_{1}^{'}}{N_{f 1}} \times \frac{\ln (N_{f 1})}{\ln (N_{f 2})}$

(12)
(d): The fourth-level loading

$D_{4} = \frac{n_{4}}{N_{f 4}} \times \frac{\ln (N_{f 4})}{\ln (N_{f 3})} = \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(13)

The cumulative damage $\sum D_{i}$ is expressed as:

$\sum D_{i} = D_{1} + D_{2} + D_{3} + D_{4} = \frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} + \frac{n_{1}^{'}}{N_{f 1}} \times \frac{\ln (N_{f 1})}{\ln (N_{f 2})} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})} = \frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{1}^{'}}{N_{f 1}} \times \frac{\ln (N_{f 1})}{\ln (N_{f 2})} + 2 \times \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}$

(14)

Using the Equation (34), the predicted fatigue life is:

$N_{pre} = \frac{\sum n_{i}}{\sum D_{i}} = \frac{n_{1} + n_{2} + n_{3} + n_{4}}{\sum D_{i}} = \frac{2 \times n_{1}^{'} + 2 \times n_{2}^{'}}{\frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{1}^{'}}{N_{f 1}} \times \frac{\ln (N_{f 1})}{\ln (N_{f 2})} + 2 \times \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}} \neq \frac{2 \times n_{1}^{'} + 2 \times n_{2}^{'}}{2 \times \frac{n_{1}^{'}}{N_{f 1}} + 2 \times \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}} = \frac{n_{1}^{'} + n_{2}^{'}}{\frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times \frac{\ln (N_{f 2})}{\ln (N_{f 1})}}$

(15)

Equation (15) cannot be scaled with a scalar because $\ln (N_{f 1}) / \ln (N_{f 2}) \neq 1$ . As a result, for the linear damage model, it is uncertain whether the number of cycles of each load block can be scaled. This is attributed to $\ln (N_{f (i - 1)})$ in Equation (9). Although $\ln (N_{f (i - 1)})$ is a constant irrelevant with cycle ratio, it is changed with previous fatigue life.

(3)

Proposed model

For the proposed model, D_i is described as:

D_{i} = \frac{n_{i}}{N_{f i}} \times \prod_{j = 1}^{i - 1} {(\frac{N_{f j}}{N_{f (j + 1)}})}^{(\prod_{k = 1}^{j} α_{k}) - 1}

(16)

where

α_{k} = (e^{- n_{k} / N_{fk}} - e^{- 1}) / (1 - e^{- 1})

.

In Equation (16), the loading effect coefficient

\prod_{j = 1}^{i - 1} {(\frac{N_{fj}}{N_{f (j + 1)}})}^{(\prod_{k = 1}^{j} α_{k}) - 1}

(using the symbol

λ_{i}

instead) is associated with fatigue lives

N_{f 1}

,

N_{f 2}

, …,

N_{fi}

and previous cycle ratios

n_{1} / N_{f 1}

,

n_{2} / N_{f 2}

, …,

n_{i - 1} / N_{f (i - 1)}

but without

n_{i} / N_{f i}

. If these previous cycle ratios are determined, then

λ_{i}

becomes a determined value as a constant. The damage variable D_i will be a linear function of cycle ratio

n_{i} / N_{f i}

, in reality it is a linear damage model.

(a): The first-level loading

$D_{1} = \frac{n_{1}}{N_{f 1}} = \frac{n_{1}^{'}}{N_{f 1}}$

(17)
(b): The second-level loading

$D_{2} = \frac{n_{2}}{N_{f 2}} \times λ_{2} = \frac{n_{2}^{'}}{N_{f 2}} \times λ_{2}$

(18)
(c): The third-level loading

$D_{3} = \frac{n_{3}}{N_{f 3}} \times λ_{3} = \frac{n_{1}^{'}}{N_{f 1}} \times λ_{3}$

(19)
(d): The fourth-level loading

$D_{4} = \frac{n_{4}}{N_{f 4}} \times λ_{4} = \frac{n_{2}^{'}}{N_{f 2}} \times λ_{4}$

(20)

The cumulative damage $\sum D_{i}$ is expressed as:

$\sum D_{i} = D_{1} + D_{2} + D_{3} + D_{4} = \frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times λ_{2} + \frac{n_{1}^{'}}{N_{f 1}} \times λ_{3} + \frac{n_{2}^{'}}{N_{f 2}} \times λ_{4}$

(21)

Using the Equation (34), the predicted fatigue life is

$N_{pre} = \frac{\sum n_{i}}{\sum D_{i}} = \frac{n_{1} + n_{2} + n_{3} + n_{4}}{\sum D_{i}} = \frac{2 \times n_{1}^{'} + 2 \times n_{2}^{'}}{\frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}} \times λ_{2} + \frac{n_{1}^{'}}{N_{f 1}} \times λ_{3} + \frac{n_{2}^{'}}{N_{f 2}} \times λ_{4}} = \frac{2 \times n_{1}^{'} + 2 \times n_{2}^{'}}{(1 + λ_{3}) \times \frac{n_{1}^{'}}{N_{f 1}} + (λ_{2} + λ_{4}) \times \frac{n_{2}^{'}}{N_{f 2}}} \neq \frac{n_{1}^{'} + n_{2}^{'}}{\frac{n_{1}^{'}}{N_{f 1}} + \frac{n_{2}^{'}}{N_{f 2}}}$

(22)

Equation (22) cannot be scaled with a scalar because $1 + λ_{3} \neq 2$ and $λ_{2} + λ_{4} \neq 2$ . This is attributed to $λ_{i}$ in Equation (16). $λ_{i}$ is a constant without of the current cycle radio $n_{i} / N_{f i}$ , it is changed and determined by previous cycle ratios from $n_{1} / N_{f 1}$ to $n_{i - 1} / N_{f (i - 1)}$ . It should be pointed out that the loading effect coefficient $λ_{i}$ reveals a significant correlation with previous fatigue loading histories. This finding is an essential distinction with the Miner rule ( $λ_{i} = 1$ ).

(4)

The reason for using Equation (34) to predict fatigue life

In the paper, the prediction of fatigue life contain two steps:

(a): The first step:
The cumulative fatigue damage $\sum_{i = 1}^{k} D_{i}$ is first calculated using different fatigue damage models. It should be emphasized that $\sum_{i = 1}^{k} D_{i}$ denotes the predicted cumulative damage and its calculated value may not be equal to unity for different models. For the experimental value of cumulative damage, it is always defined as unity without using damage models, i.e., $\sum_{i = 1}^{k} D_{i} = 1$ .
(b): The second step:
According to the calculated values of cumulative damage obtained by different models, the fatigue life is thus calculated by Equation (34).

For the experimental result, the cumulative fatigue damage is unity. For different models, if the predicted cumulative damage is unity (i.e.,

\sum D_{i} \to 1

), then the predicted fatigue life should be close to the experimental result (i.e., N_pre→N_exp) and the corresponding damage model becomes more effective.

For the comment in Table 1,

\sum D_{i}

denotes the predicted cumulative damage by different models but not the real value of experimental result (

\sum D_{i} = 1

). In theory, the predicted results cannot be equal to the experimental ones. In row (a), the specimen is fatigued by σ₁ for 13,749 cycles and σ₂ for 51,304 cycles to failure. This is correct because it denotes the real experimental results. However, in row (b) and row (c), the number of loading cycles of n₁ and n₂ are defined as the hypothetical values. The specimen is supposed first fatigued by σ₁ for 18,454 (or 17,497) cycles and then σ₂ for 68,860 (or 65,290) cycles. This situation is not correct (the specimen may be failure when n₂ = 50,000 or other value, and n₂ can only be determined by the experiments). In addition, if n₁ and n₂ are changed, the predicted damage (D₁ and D₂) should also be changed by the cumulative damage models as well as the corresponding predicted fatigue lives. It is meaningless for supposing a particular value of the loading cycles.

Moreover, for Corten’s model as stated by Equation (29), the prediction formula of fatigue life can be found in the paper entitled “A Practical Method for Determining the Corten-Dolan Exponent and Its Application to Fatigue Life Prediction” by Shun-Peng Zhu, Hong-Zhong Huang, Yu Liu, Li-Ping He and Qiang Liao published in Int. J. Turbo Jet-Engines (2012;29: 79–87), on page 81, in Equation (5), that is:

\frac{\sum n_{r}}{N_{g}} = \sum_{i = 1}^{k} \frac{n_{i}}{N_{1}} {(\frac{σ_{i}}{σ_{1}})}^{d}

(23)

where

\sum n_{r} = n_{1} + n_{2} + \dots + n_{k} = \sum_{i = 1}^{k} n_{i}

,

N_{g}

is the predicted fatigue life.

The predicted fatigue life can be written as:

N_{p r e} = N_{g} = \frac{\sum n_{r}}{\sum_{i = 1}^{k} \frac{n_{i}}{N_{1}} {(\frac{σ_{i}}{σ_{1}})}^{d}} = \frac{\sum_{i = 1}^{k} n_{i}}{\sum_{i = 1}^{k} D_{i}}

(24)

This formula is the same as the Equation (34) in our paper.

As stated previously, the use of the Equation (34) for fatigue life prediction should be reasonable.

Author Contributions

Formal analysis, J.Z.; Funding acquisition, Y.-F.L.; Methodology, Z.P.; Supervision, H.-Z.H.; Validation, Y.-F.L.; Writing-original draft, Z.P.; Writing-review & editing, H.-Z.H. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This study was sponsored by the National Natural Science Foundation of China under Grant No. 51775090.

Conflicts of Interest

The authors declare no conflict of interest.

Figure 1. Repeated two-level load block (two blocks).

Table 1. Predicted lifetime calculated by Peng et al. for their non-linear damage model and two block loading sequences (a), with the corresponding damage (b) and the corrected lifetime prediction (c).

High–low loading sequence $σ_{1} = 485 M P a - σ_{2} = 400 M P a$
	$n_{1} / n_{2}$	$n_{1}$	$n_{2}$	$\sum n_{i}$	$α_{1}$	$\sum D_{i}$	$N_{p r e}$
(a) $N_{p r e}$ Peng et al.	0.268	13,749	51,304	65,053	0.6501	0.7450	87,314
(b) Corresponding damage	0.268	18,454	68,860	87,314	0.5491	1.0687
(c) Correct $N_{p r e}$	0.268	17,497	65,290	82,787	0.5689	1.0000	82,786
Low–high loading sequence $σ_{1} = 400 M P a - σ_{2} = 485 M P a$
(a) $N_{p r e}$ Peng et al.	2.341	109,310	46,693	156,003	0.1653	1.1264	138,502
(b) Corresponding damage	2.341	97,047	41,455	138,502	0.2309	1.0221
(c) Correct $N_{p r e}$	2.341	94,482	40,359	134,841	0.2453	1.0000	134,847

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Reply to Comment on the Paper Entitled “A New Cumulative Fatigue Damage Rule Based on Dynamic Residual S-N Curve and Material Memory Concept” by Peng Z., Huang H., Zhou J. and Li Y. Published in Metals (2018; 8(6): 456)

Author Contributions

Acknowledgments

Conflicts of Interest

Article Metrics

Citations

Article Access Statistics