Texture and Lattice Strain Evolution during Tensile Loading of Mg–Zn Alloys Measured by Synchrotron Diffraction
Abstract
1. Introduction
2. Experimental and Simulation Procedure
2.1. Materials
2.2. In Situ Synchrotron Diffraction during Tensile Testing
2.3. Modeling Procedure
3. Results
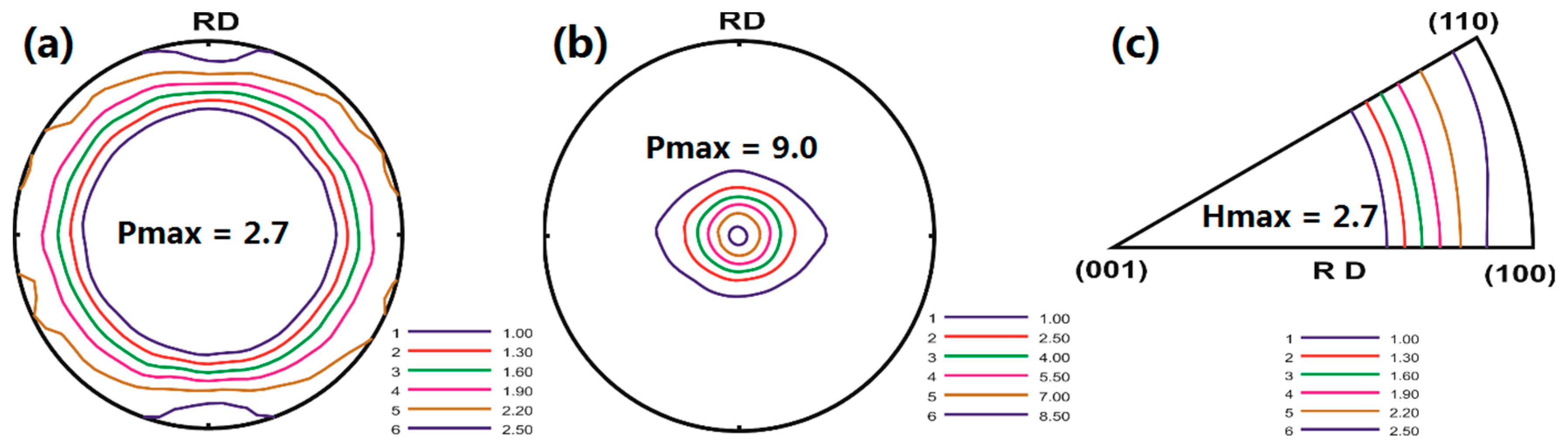
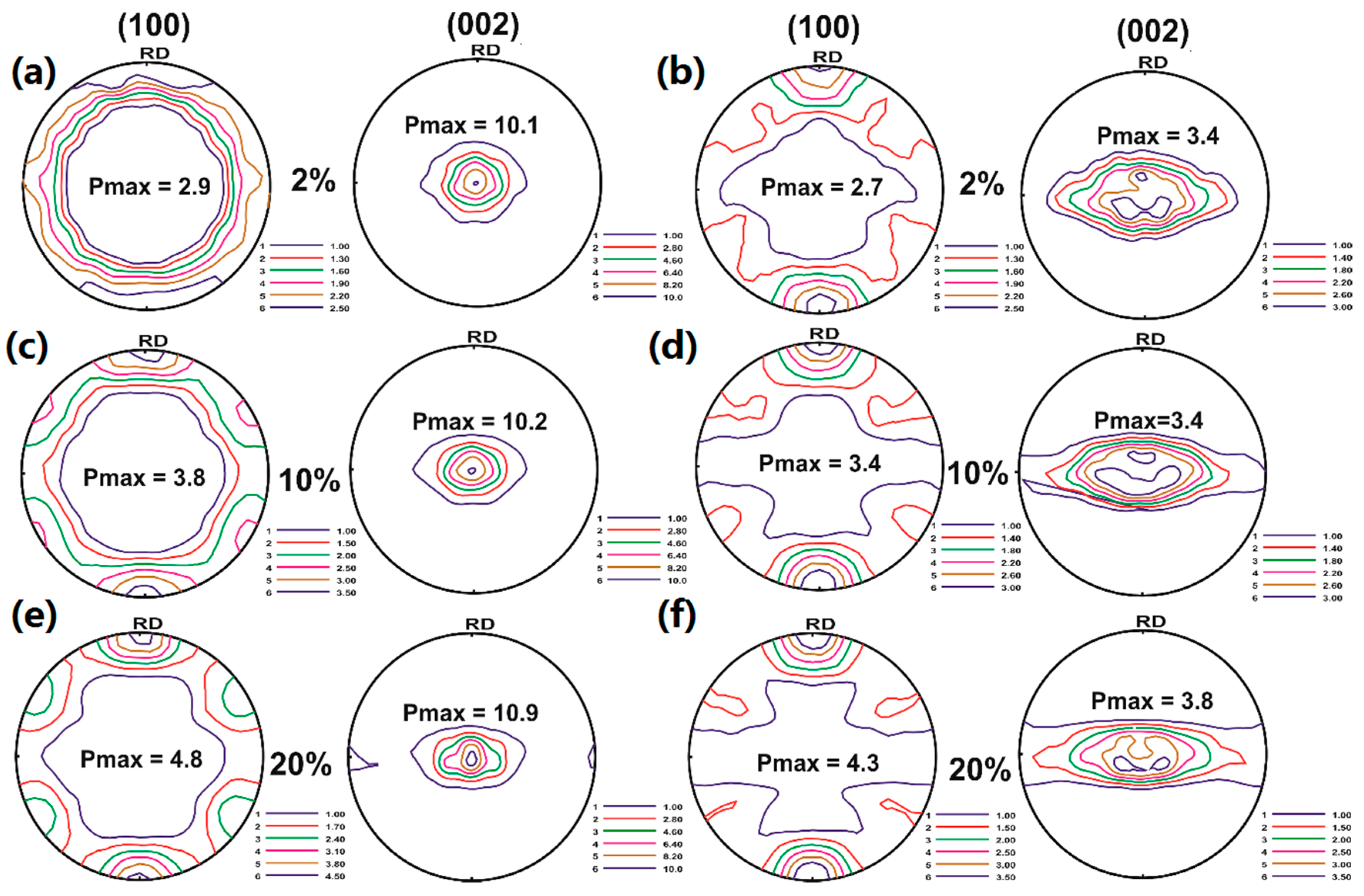
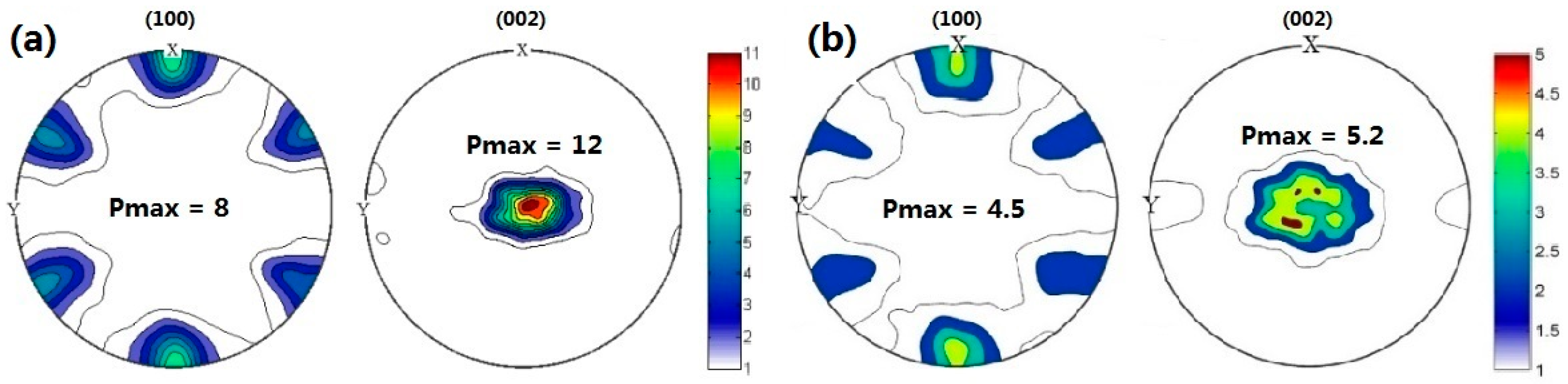
3.1. Microstructure and Texture at the Rolled State
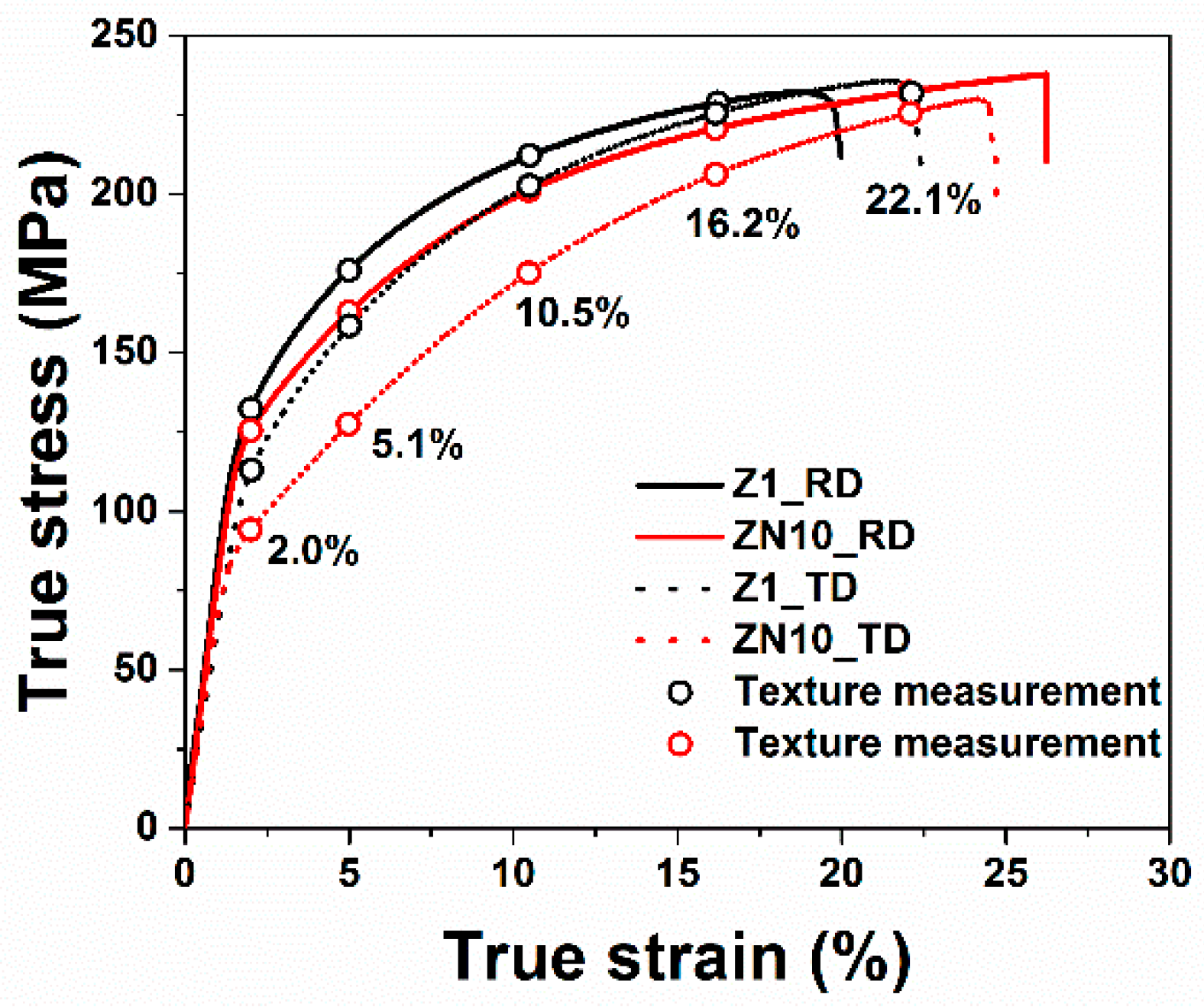
3.2. Mechanical Properties
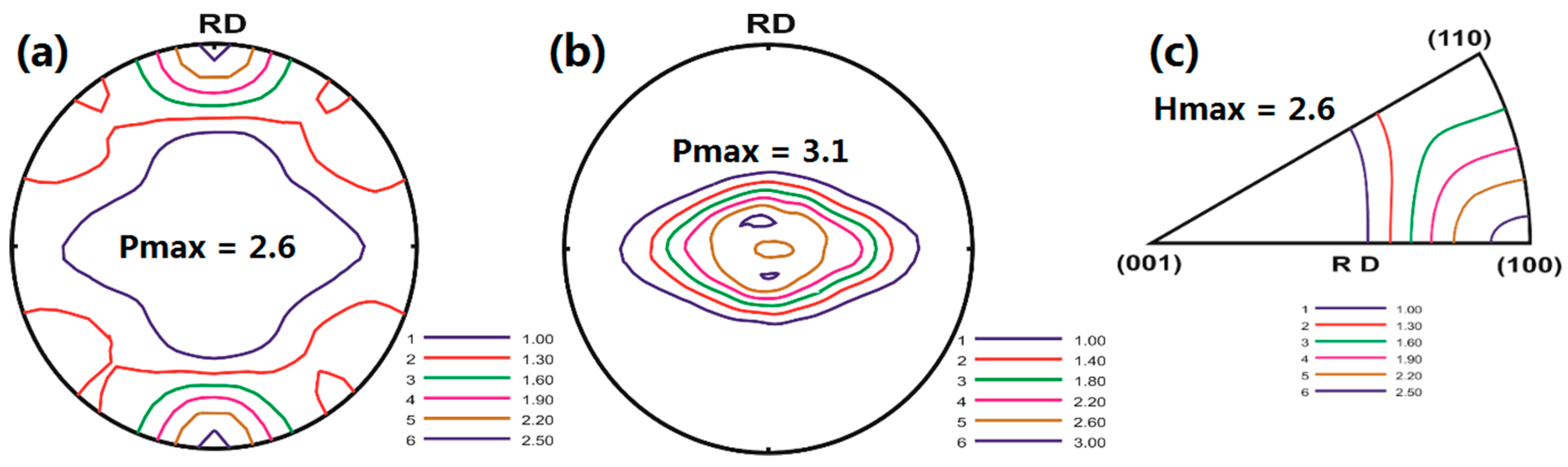
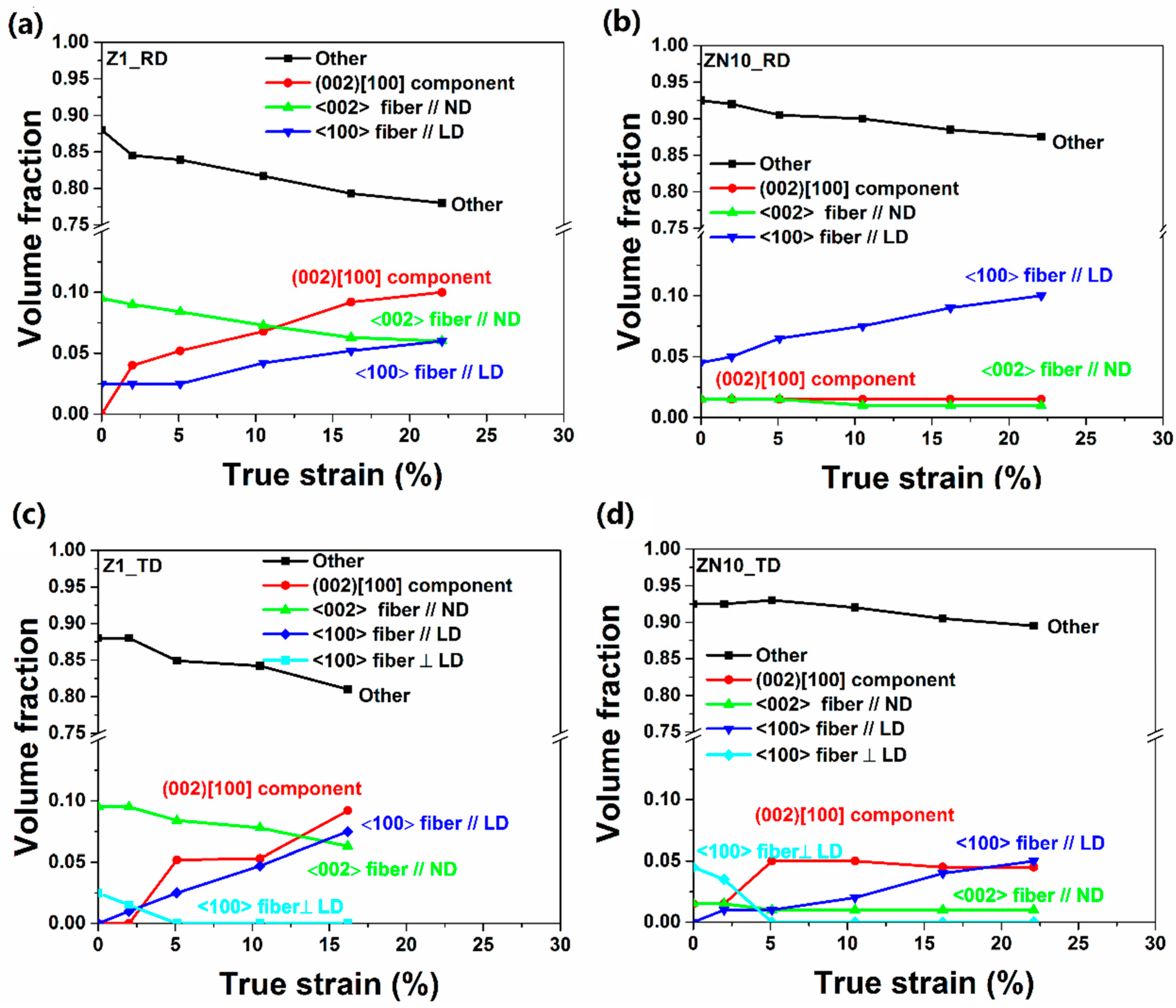
3.3. Texture Evolution during in situ Tensile Test
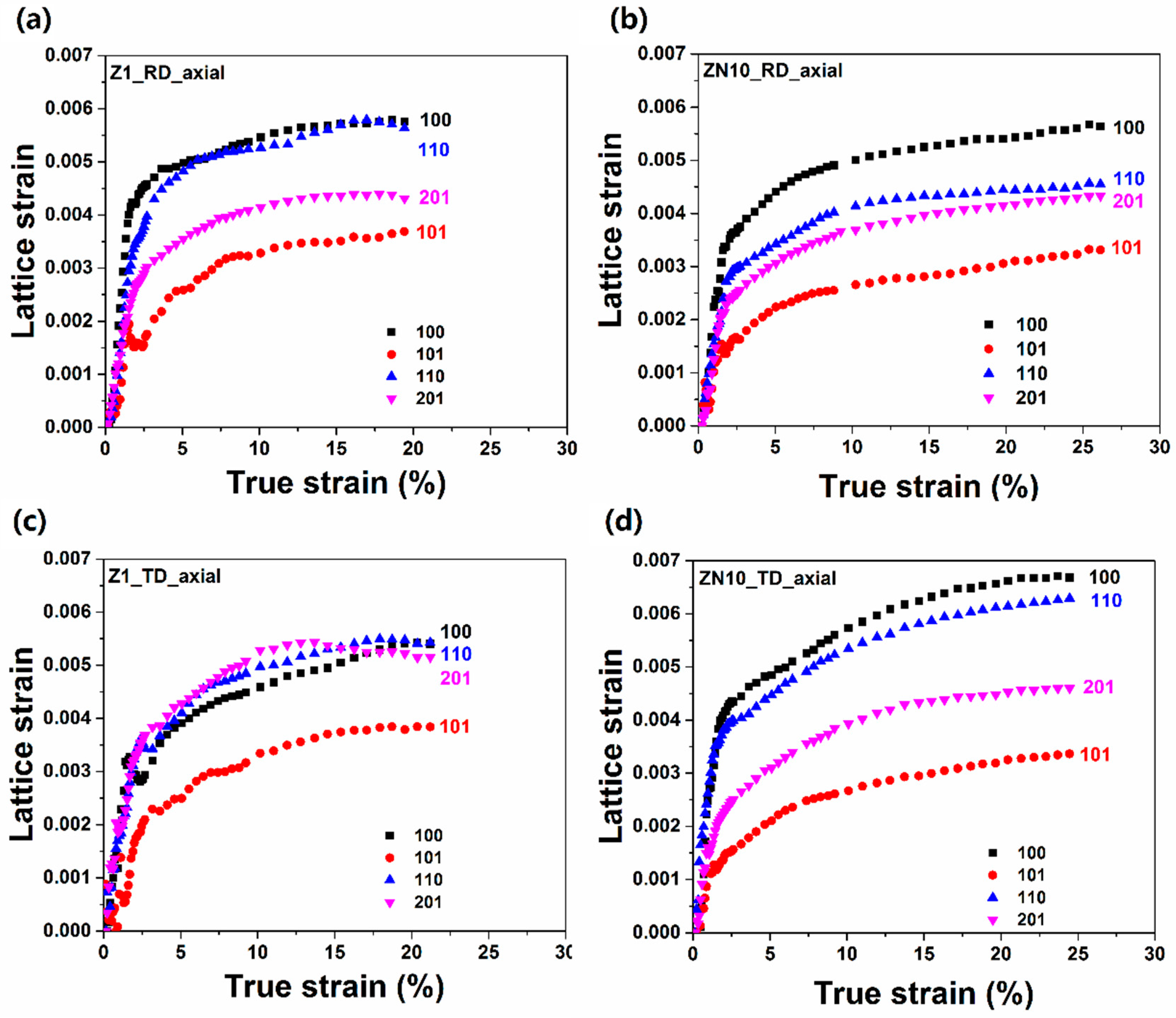
3.4. Lattice Strain Evolution during in Situ Measurements
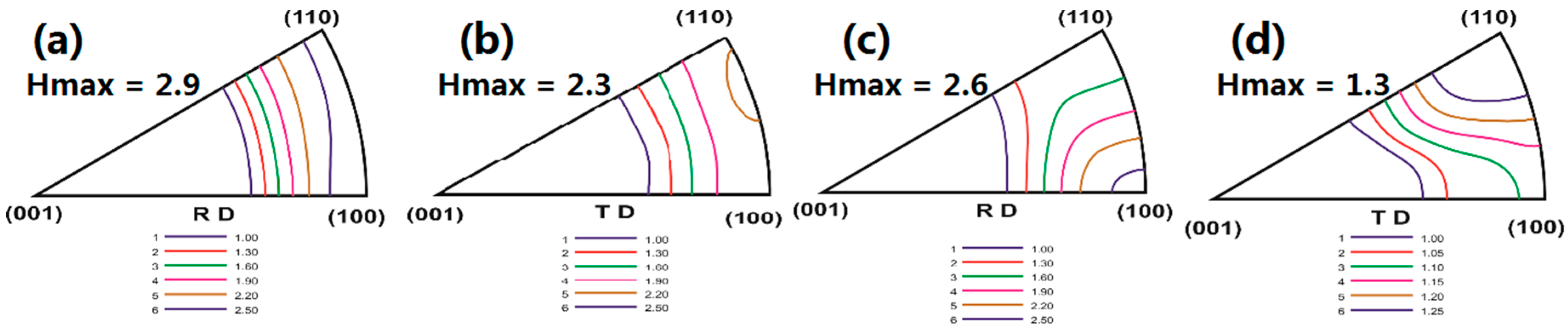
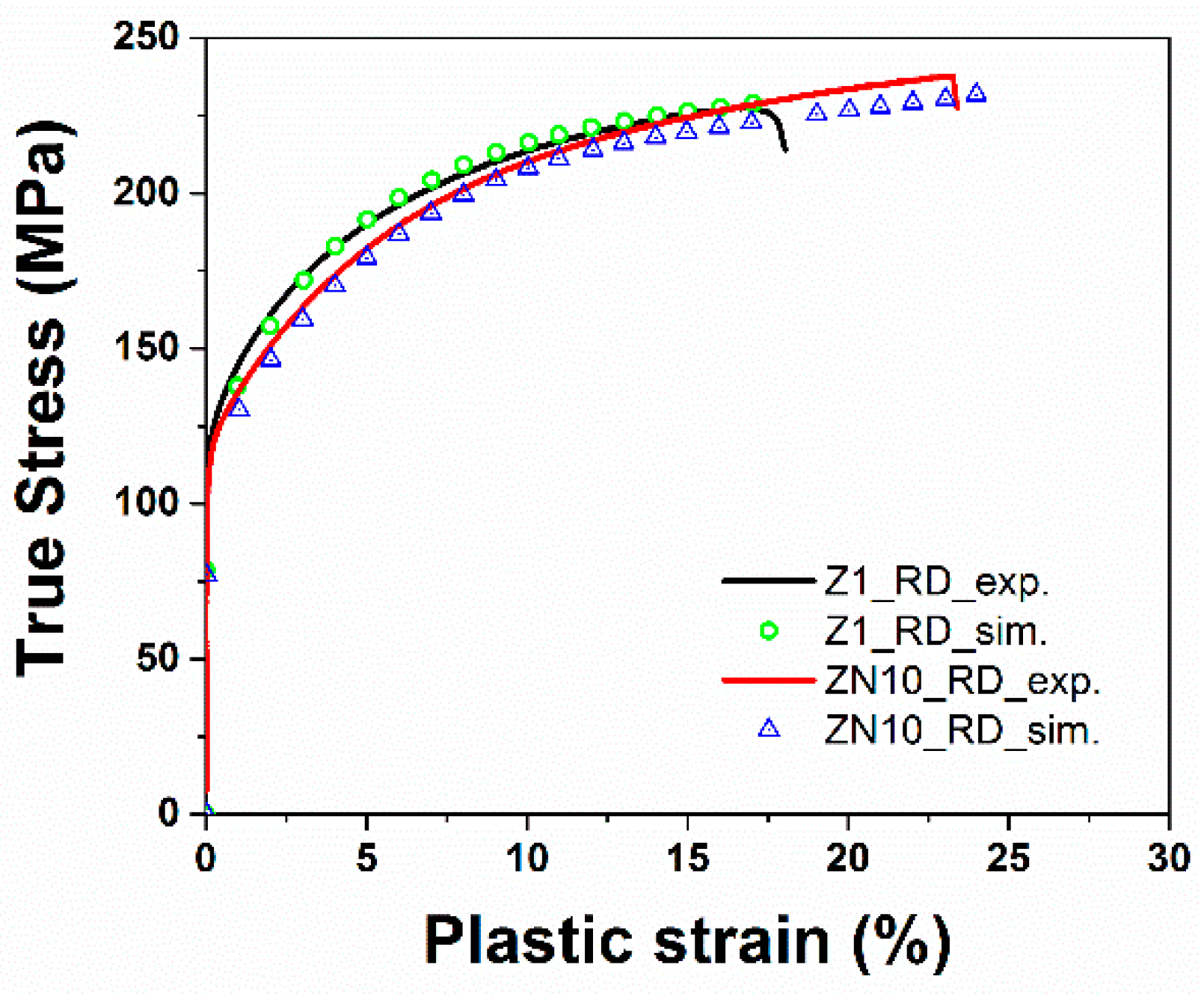
3.5. Modeling Results
4. Discussion
4.1. Initial Texture and Texture Evolution
4.2. Lattice Strain Evolution
4.3. Deformation Mode Activity by EVPSC
- The intensities of simulated pole figures are slightly higher than the experimental pole figures. This higher intensity could be caused by the influence of neighboring crystals on grain rotation rate. In simulation, grain-to-grain interactions on average were taken into account without neighboring effects. However, from experimental results, grain rotation is more difficult since in reality a grain is always surrounded by other grains with different orientations.
- Inhomogeneity of deformations occurs in measurements but not in simulations. In the simulation procedure the strain is homogenously accommodated by the active slip system and twinning [10].
- In simulation, the size of grains with particular orientations are homogenous. The grain size and the volume fraction of grain with certain sizes varies in the materials. Twinning is much easier formed for large grains than the small ones [46].
5. Conclusions
- (a)
- The addition of Nd weakens the texture of Mg–Zn alloy, results in the formation of the {00.2}<10.0> component after hot rolling, which does not exist in the Z1 alloy. The volume fraction of this component remains stable in Nd-containing alloys, but it gradually increases with the increasing strain for Nd-free alloys.
- (b)
- Basal slip in Nd-containing alloys are easier to active during the tensile loading compared to Nd-free alloys, it is in good agreement with the lower yield point of Nd-containing alloy.
- (c)
- The addition of Nd increases the CRSS value of prismatic slip and decreases the CRSS value of pyramidal slip compared to Nd-free alloy.
Author Contributions
Funding
Conflicts of Interest
References
- Friedrich, H.; Schumann, S. Forschungsstrategien für ein zweites “magnesium–zeitalter“ im fahrzeugbau. Mater. Werkst. 2001, 32, 6–12. [Google Scholar] [CrossRef]
- Kelley, E.; Hosford, W. Plane-strain compression of magnesium and magnesium alloy crystals. Trans. Met. Soc. AIME 1968, 242, 5–13. [Google Scholar]
- Lou, X.; Li, M.; Boger, R.; Agnew, S.; Wagoner, R. Hardening evolution of az31b mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Dillamore, I.; Hazel, R.; Watson, T.; Hadden, P. An experimental study of the mechanical anisotropy of some common metals. Int. J. Mech. Sci. 1971, 13, 1049–1061. [Google Scholar] [CrossRef]
- Barnett, M.; Keshavarz, Z.; Beer, A.; Atwell, D. Influence of grain size on the compressive deformation of wrought mg–3al–1zn. Acta Mater. 2004, 52, 5093–5103. [Google Scholar] [CrossRef]
- Yoo, M. Slip, twinning, and fracture in hexagonal close-packed metals. Metall. Trans. A 1981, 12, 409–418. [Google Scholar] [CrossRef]
- Kelley, E. The deformation characteristics of textured magnesium. Trans. Met. Soc. AIME 1968, 242, 654–660. [Google Scholar]
- Bohlen, J.; Nürnberg, M.R.; Senn, J.W.; Letzig, D.; Agnew, S.R. The texture and anisotropy of magnesium–zinc–rare earth alloy sheets. Acta Mater. 2007, 55, 2101–2112. [Google Scholar] [CrossRef]
- Al-Samman, T.; Li, X. Sheet texture modification in magnesium-based alloys by selective rare earth alloying. Mater. Sci. Eng. A 2011, 528, 3809–3822. [Google Scholar] [CrossRef]
- Barnett, M.; Nave, M.; Bettles, C. Deformation microstructures and textures of some cold rolled mg alloys. Mater. Sci. Eng. A 2004, 386, 205–211. [Google Scholar] [CrossRef]
- Del Valle, J.; Carreño, F.; Ruano, O.A. Influence of texture and grain size on work hardening and ductility in magnesium-based alloys processed by ecap and rolling. Acta Mater. 2006, 54, 4247–4259. [Google Scholar] [CrossRef]
- Gall, S.; Coelho, R.; Müller, S.; Reimers, W. Mechanical properties and forming behavior of extruded az31 and me21 magnesium alloy sheets. Mater. Sci. Eng. A 2013, 579, 180–187. [Google Scholar] [CrossRef]
- Dobroň, P.; Chmelík, F.; Yi, S.; Parfenenko, K.; Letzig, D.; Bohlen, J. Grain size effects on deformation twinning in an extruded magnesium alloy tested in compression. Scr. Mater. 2011, 65, 424–427. [Google Scholar] [CrossRef]
- Barnett, M. A rationale for the strong dependence of mechanical twinning on grain size. Scr. Mater. 2008, 59, 696–698. [Google Scholar] [CrossRef]
- Agnew, S.; Mulay, R.; Polesak Iii, F.; Calhoun, C.; Bhattacharyya, J.; Clausen, B. In situ neutron diffraction and polycrystal plasticity modeling of a mg–y–nd–zr alloy: Effects of precipitation on individual deformation mechanisms. Acta Mater. 2013, 61, 3769–3780. [Google Scholar] [CrossRef]
- Stanford, N.; Geng, J.; Chun, Y.; Davies, C.; Nie, J.; Barnett, M. Effect of plate-shaped particle distributions on the deformation behaviour of magnesium alloy az91 in tension and compression. Acta Mater. 2012, 60, 218–228. [Google Scholar] [CrossRef]
- Robson, J.; Stanford, N.; Barnett, M. Effect of precipitate shape on slip and twinning in magnesium alloys. Acta Mater. 2011, 59, 1945–1956. [Google Scholar] [CrossRef]
- Lentz, M.; Klaus, M.; Wagner, M.; Fahrenson, C.; Beyerlein, I.J.; Zecevic, M.; Reimers, W.; Knezevic, M. Effect of age hardening on the deformation behavior of an mg–y–nd alloy: In-situ x-ray diffraction and crystal plasticity modeling. Mater. Sci. Eng. A 2015, 628, 396–409. [Google Scholar] [CrossRef]
- Agnew, S.; Yoo, M.; Tome, C. Application of texture simulation to understanding mechanical behavior of mg and solid solution alloys containing li or y. Acta Mater. 2001, 49, 4277–4289. [Google Scholar] [CrossRef]
- Stanford, N.; Cottam, R.; Davis, B.; Robson, J. Evaluating the effect of yttrium as a solute strengthener in magnesium using in situ neutron diffraction. Acta Mater. 2014, 78, 1–13. [Google Scholar] [CrossRef]
- Sandlöbes, S.; Friák, M.; Zaefferer, S.; Dick, A.; Yi, S.; Letzig, D.; Pei, Z.; Zhu, L.-F.; Neugebauer, J.; Raabe, D. The relation between ductility and stacking fault energies in mg and mg–y alloys. Acta Mater. 2012, 60, 3011–3021. [Google Scholar] [CrossRef]
- Herrera-Solaz, V.; Hidalgo-Manrique, P.; Pérez-Prado, M.T.; Letzig, D.; Llorca, J.; Segurado, J. Effect of rare earth additions on the critical resolved shear stresses of magnesium alloys. Mater. Lett. 2014, 128, 199–203. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, T.-W.; Fu, L.; Tang, B.-Y.; Peng, L.-M.; Ding, W.-J. Ab-initio study of the effect of rare-earth elements on the stacking faults of mg solid solutions. Intermetallics 2012, 29, 21–26. [Google Scholar] [CrossRef]
- Ha, C.; Bohlen, J.; Yi, S.; Zhou, X.; Brokmeier, H.-G.; Schell, N.; Letzig, D.; Kainer, K.U. Influence of nd or ca addition on the dislocation activity and texture changes of mg–zn alloy sheets under uniaxial tensile loading. Mater. Sci. Eng. A 2019, 761, 138053. [Google Scholar] [CrossRef]
- Peng, Q.; Li, X.; Ma, N.; Liu, R.; Zhang, H. Effects of backward extrusion on mechanical and degradation properties of mg–zn biomaterial. J. Mech. Behav. Biomed. Mater. 2012, 10, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Ha, C.; Yi, S.; Bohlen, J.; Zhou, X.; Brokmeier, H.-G.; Schell, N.; Letzig, D.; Kainer, K.U. Deformation and recrystallization mechanisms and their influence on the microstructure development of rare earth containing magnesium sheets. In Proceedings of the TMS Annual Meeting & Exhibition, Phoenix, AZ, USA, 11–15 March 2018; Springer: Berlin, Germany; pp. 209–216. [Google Scholar]
- Kree, V.; Bohlen, J.; Letzig, D.; Kainer, K.U. Metallographische gefügeuntersuchungen von magnesium-legierungen. Prakt. Metallogr. 2004, 41, 233–246. [Google Scholar]
- Brokmeier, H.G. Hot rectangular extrusion textures of six mg-alloys via neutron diffraction. Adv. Eng. Mater. 2018, 20, 1700234. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with Mtex–Free and Open Source Software Toolbox; Klein, H., Schwarzer, R.A., Eds.; Trans Tech Publications: Baech, Switzerland, 2010; pp. 63–68. [Google Scholar]
- Molinari, A.; Canova, G.; Ahzi, S. A self consistent approach of the large deformation polycrystal viscoplasticity. Acta Metall. 1987, 35, 2983–2994. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.; Tomé, C.; Huang, Y. A finite strain elastic–viscoplastic self-consistent model for polycrystalline materials. J. Mech. Phys. Solids 2010, 58, 594–612. [Google Scholar] [CrossRef]
- Chi, Y.; Zhou, X.; Xu, C.; Sun, D.; Qiao, X.; Brokmeier, H.; Zheng, M. The origin of discontinuous yielding in mg alloys under slip-dominated condition studied by in-situ synchrotron diffraction and elastic-viscoplastic self-consistent modeling. Mater. Sci. Eng. A 2019, 754, 562–568. [Google Scholar] [CrossRef]
- Tomé, C.; Lebensohn, R.A.; Kocks, U. A model for texture development dominated by deformation twinning: Application to zirconium alloys. Acta Metall. Mater. 1991, 39, 2667–2680. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Turner, P.; Tomé, C. A study of residual stresses in zircaloy-2 with rod texture. Acta Metall. Mater. 1994, 42, 4143–4153. [Google Scholar] [CrossRef]
- Tomé, C.N. Self-consistent polycrystal models: A directional compliance criterion to describe grain interactions. Model. Simul. Mater. Sci. Eng. 1999, 7, 723. [Google Scholar] [CrossRef]
- Agnew, S.; Mehrotra, P.; Lillo, T.; Stoica, G.; Liaw, P. Texture evolution of five wrought magnesium alloys during route a equal channel angular extrusion: Experiments and simulations. Acta Mater. 2005, 53, 3135–3146. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, Ö. Plastic anisotropy and the role of non-basal slip in magnesium alloy az31b. Int. J. Plast. 2005, 21, 1161–1193. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.; Wang, J.; Tomé, C. A crystal plasticity model for hexagonal close packed (hcp) crystals including twinning and de-twinning mechanisms. Int. J. Plast. 2013, 49, 36–52. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Overview no. 42 texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Schmid, E. Yield Point of Crystals, Critical Shear Stress Law. In Proceedings of the First International Congress for Applied Mechanics, Delft, The Netherland, 22–26 April 1924. [Google Scholar]
- Kamaya, M. A procedure for estimating young’s modulus of textured polycrystalline materials. Int. J. Solids Struct. 2009, 46, 2642–2649. [Google Scholar] [CrossRef]
- Agnew, S. Plastic anisotropy of magnesium alloy az31b sheet. In Essential Readings in Magnesium Technology; Springer: Berlin, Germany, 2016; pp. 351–356. [Google Scholar]
- Steiner, M.; Bhattacharyya, J.; Agnew, S. The origin and enhancement of {0001}< 112¯ 0> texture during heat treatment of rolled az31b magnesium alloys. Acta Materialia 2015, 95, 443–455. [Google Scholar]
- Styczynski, A.; Hartig, C.; Bohlen, J.; Letzig, D. Cold rolling textures in az31 wrought magnesium alloy. Scr. Mater. 2004, 50, 943–947. [Google Scholar] [CrossRef]
- Yi, S.-B.; Davies, C.; Brokmeier, H.-G.; Bolmaro, R.; Kainer, K.; Homeyer, J. Deformation and texture evolution in az31 magnesium alloy during uniaxial loading. Acta Mater. 2006, 54, 549–562. [Google Scholar] [CrossRef]
- Clausen, B.; Lorentzen, T.; Leffers, T. Self-consistent modelling of the plastic deformation of fcc polycrystals and its implications for diffraction measurements of internal stresses. Acta Mater. 1998, 46, 3087–3098. [Google Scholar] [CrossRef]


| Alloys | Sample Direction | YS | UTS | ||
|---|---|---|---|---|---|
| Z1 | RD | 123 | 195 | 16 | 22 |
| TD | 105 | 192 | 18 | 25 | |
| ZN10 | RD | 115 | 188 | 17 | >30 |
| TD | 84 | 181 | 27 | 28 |
| Alloy (Z1) | τ0 | τ1 | θ0 | θ1 |
|---|---|---|---|---|
| <a>—basal | 0.02 | 0.008 | 0.2 | 0 |
| <a>—prismatic | 0.05 | 0.045 | 0.5 | 0 |
| <c + a>—pyramidal 2nd order | 0.09 | 0.08 | 0.8 | 0 |
| Tensile twinning | 0.01 | 0 | 0.2 | 0 |
| Alloy (ZN10) | - | - | - | - |
| <a>—basal | 0.02 | 0.008 | 0.2 | 0 |
| <a>—prismatic | 0.06 | 0.04 | 0.45 | 0 |
| <c + a>—pyramidal 2nd order | 0.07 | 0.08 | 0.8 | 0 |
| Tensile twinning | 0.04 | 0 | 0.2 | 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Ha, C.; Yi, S.; Bohlen, J.; Schell, N.; Chi, Y.; Zheng, M.; Brokmeier, H.-G. Texture and Lattice Strain Evolution during Tensile Loading of Mg–Zn Alloys Measured by Synchrotron Diffraction. Metals 2020, 10, 124. https://doi.org/10.3390/met10010124
Zhou X, Ha C, Yi S, Bohlen J, Schell N, Chi Y, Zheng M, Brokmeier H-G. Texture and Lattice Strain Evolution during Tensile Loading of Mg–Zn Alloys Measured by Synchrotron Diffraction. Metals. 2020; 10(1):124. https://doi.org/10.3390/met10010124
Chicago/Turabian StyleZhou, Xiaohua, Changwan Ha, Sangbong Yi, Jan Bohlen, Norbert Schell, Yuanqing Chi, Mingyi Zheng, and Heinz-Günter Brokmeier. 2020. "Texture and Lattice Strain Evolution during Tensile Loading of Mg–Zn Alloys Measured by Synchrotron Diffraction" Metals 10, no. 1: 124. https://doi.org/10.3390/met10010124
APA StyleZhou, X., Ha, C., Yi, S., Bohlen, J., Schell, N., Chi, Y., Zheng, M., & Brokmeier, H.-G. (2020). Texture and Lattice Strain Evolution during Tensile Loading of Mg–Zn Alloys Measured by Synchrotron Diffraction. Metals, 10(1), 124. https://doi.org/10.3390/met10010124






