The Application of Critical Power, the Work Capacity above Critical Power (W′), and Its Reconstitution: A Narrative Review of Current Evidence and Implications for Cycling Training Prescription
Abstract
1. Introduction
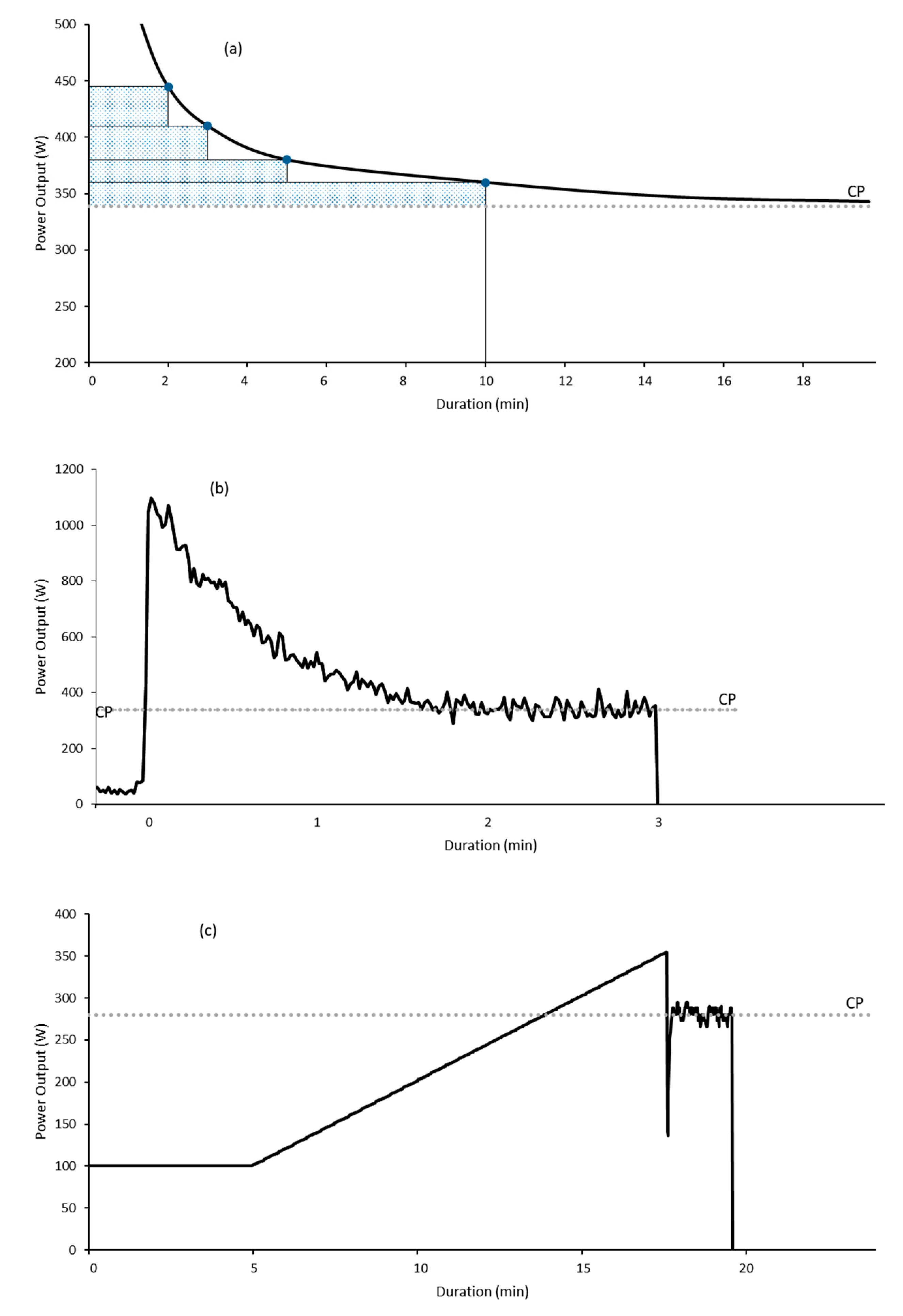
2. Assumptions of the Critical Power Model
- The aerobic supply of energy is unlimited for any duration.
- Cycling efficiency remains constant.
- Power output is limited solely by duration and tends towards infinity as time duration approaches 0 s.
- All power output demands up to CP are immediately and constantly fulfilled by aerobic mechanisms up to that limit.
- At exhaustion W′ is fully depleted, i.e., W′ equals 0 J.
3. Methods for Determining Critical Power and W′
3.1. Constant Work Rate Tests
3.2. Three-Minute All-Out Test
3.3. Ramp All-Out Test
4. W′ Reconstitution
5. The Application of Critical Power and W′ for Training Prescription
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hill, A.V. The physiological basis of athletic records. Nature 1925, 116, 544–548. [Google Scholar] [CrossRef]
- Monod, H.; Scherrer, J. The work capacity of a synergic muscular group. Ergonomics 1965, 8, 329–338. [Google Scholar] [CrossRef]
- Moritani, T.; Nagata, A.; Devries, H.A.; Muro, M. Critical power as a measure of physical work capacity and anaerobic threshold. Ergonomics 1981, 24, 339–350. [Google Scholar] [CrossRef] [PubMed]
- Poole, D.C.; Ward, S.A.; Gardner, G.W.; Whipp, B.J. Metabolic and respiratory profile of the upper limit for prolonged exercise in man. Ergonomics 1988, 31, 1265–1279. [Google Scholar] [CrossRef]
- Davis, H.A.; Bassett, J.; Hughes, P.; Gass, G.C. Anaerobic threshold and lactate turnpoint. Eur. J. Appl. Physiol. Occup. Physiol. 1983, 50, 383–392. [Google Scholar] [CrossRef]
- Cheng, B.; Kuipers, H.; Snyder, A.C.; Keizer, H.A.; Jeukendrup, A.; Hesselink, M. A new approach for the determination of ventilatory and lactate thresholds. Int. J. Sports Med. 1992, 13, 518–522. [Google Scholar] [CrossRef]
- Tanaka, K.; Matsuura, Y.; Kumagai, S.; Matsuzaka, A.; Hirakoba, K.; Asano, K. Relationships of anaerobic threshold and onset of blood lactate accumulation with endurance performance. Eur. J. Appl. Physiol. Occup. Physiol. 1983, 52, 51–56. [Google Scholar] [CrossRef]
- Beneke, R.; von Duvillard, S.P. Determination of maximal lactate steady state response in selected sports events. Med. Sci. Sports Exerc. 1996, 28, 241–246. [Google Scholar] [CrossRef]
- Beaver, W.L.; Wasserman, K.; Whipp, B.J. A new method for detecting anaerobic threshold by gas-exchange. J. Appl. Physiol. 1986, 60, 2020–2027. [Google Scholar] [CrossRef]
- Simon, J.; Young, J.L.; Gutin, B.; Blood, D.K.; Case, R.B. Lactate accumulation relative to the anaerobic and respiratory compensation thresholds. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 1983, 54, 13–17. [Google Scholar] [CrossRef]
- Hill, D.W. The critical power concept—A review. Sports Med. 1993, 16, 237–254. [Google Scholar] [CrossRef] [PubMed]
- Burnley, M.; Doust, J.H.; Vanhatalo, A. A 3-min all-out test to determine peak oxygen uptake and the maximal steady state. Med. Sci. Sports Exerc. 2006, 38, 1995–2003. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.M.; Burnley, M.; Black, M.I.; Poole, D.C.; Vanhatalo, A. The maximal metabolic steady state: Redefining the “gold standard”. Physiol. Rep. 2019, 7, e14098. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, E.A.; Martin, N.R.W.; Bailey, S.J.; Ferguson, R.A. Critical power is positively related to skeletal muscle capillarity and type i muscle fibers in endurance-trained individuals. J. Appl. Physiol. 2018, 125, 737–745. [Google Scholar] [CrossRef]
- Hill, D.W.; Smith, J.C. A comparison of methods of estimating anaerobic work capacity. Ergonomics 1993, 36, 1495–1500. [Google Scholar] [CrossRef]
- Miura, A.; Sato, H.; Sato, H.; Whipp, B.J.; Fukuba, Y. The effect of glycogen depletion on the curvature constant parameter of the power-duration curve for cycle ergometry. Ergonomics 2000, 43, 133–141. [Google Scholar] [CrossRef]
- Valli, G.; Cogo, A.; Passino, C.; Bonardi, D.; Morici, G.; Fasano, V.; Agnesi, M.; Bernardi, L.; Ferrazza, A.M.; Ward, S.A.; et al. Exercise intolerance at high altitude (5050 m): Critical power and w′. Respir. Physiol. Neurobiol. 2011, 177, 333–341. [Google Scholar] [CrossRef]
- Simpson, L.P.; Jones, A.M.; Skiba, P.F.; Vanhatalo, A.; Wilkerson, D. Influence of hypoxia on the power-duration relationship during high-intensity exercise. Int. J. Sports Med. 2015, 36, 113–119. [Google Scholar] [CrossRef]
- Burnley, M.; Jones, A.M. Oxygen uptake kinetics as a determinant of sports performance. Eur. J. Sport Sci. 2007, 7, 63–79. [Google Scholar] [CrossRef]
- Jones, A.M.; Wilkerson, D.P.; DiMenna, F.; Fulford, J.; Poole, D.C. Muscle metabolic responses to exercise above and below the “critical power” assessed using 31p-mrs. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R585–R593. [Google Scholar] [CrossRef]
- Fukuba, Y.; Miura, A.; Endo, M.; Kan, A.; Yanagawa, K.; Whipp, B.J. The curvature constant parameter of the power-duration curve for varied-power exercise. Med. Sci. Sports Exerc. 2003, 35, 1413–1418. [Google Scholar] [CrossRef] [PubMed]
- Poole, D.C.; Burnley, M.; Vanhatalo, A.; Rossiter, H.B.; Jones, A.M. Critical power: An important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 2016, 48, 2320–2334. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.A.; Mills, D.E.; Brown, P.I.; Sharpe, G.R. Prior upper body exercise reduces cycling work capacity but not critical power. Med. Sci. Sports Exerc. 2014, 46, 802–808. [Google Scholar] [CrossRef] [PubMed]
- Morton, R.H. The critical power and related whole-body bioenergetic models. Eur. J. Appl. Physiol. 2006, 96, 339–354. [Google Scholar] [CrossRef] [PubMed]
- Pringle, J.S.M.; Jones, A.M. Maximal lactate steady state, critical power and emg during cycling. Eur. J. Appl. Physiol. 2002, 88, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Brickley, G.; Doust, J.; Williams, C.A. Physiological responses during exercise to exhaustion at critical power. Eur. J. Appl. Physiol. 2002, 88, 146–151. [Google Scholar] [CrossRef]
- Hill, D.W.; Smith, J.C. Determination of critical power by pulmonary gas exchange. Can. J. Appl. Physiol. 1999, 24, 74–86. [Google Scholar] [CrossRef]
- Clark, I.E.; Vanhatalo, A.; Thompson, C.; Joseph, C.; Black, M.I.; Blackwell, J.R.; Wylie, L.J.; Tan, R.; Bailey, S.J.; Wilkins, B.W.; et al. Dynamics of the power-duration relationship during prolonged endurance exercise and influence of carbohydrate ingestion. J. Appl. Physiol. 2019, 127, 726–736. [Google Scholar] [CrossRef]
- Jeukendrup, A.E.; Wallis, G.A. Measurement of substrate oxidation during exercise by means of gas exchange measurements. Int. J. Sports Med. 2005, 26, S28–S37. [Google Scholar] [CrossRef]
- Morton, R.H. Modelling human power and endurance. J. Math. Biol. 1990, 28, 49–64. [Google Scholar] [CrossRef]
- Morton, R.H. A 3-parameter critical power model. Ergonomics 1996, 39, 611–619. [Google Scholar] [CrossRef]
- Gaesser, G.A.; Carnevale, T.J.; Garfinkel, A.; Walter, D.O.; Womack, C.J. Estimation of critical power with nonlinear and linear-models. Med. Sci. Sports Exerc. 1995, 27, 1430–1438. [Google Scholar] [CrossRef]
- Bergstrom, H.C.; Housh, T.J.; Zuniga, J.M.; Traylor, D.A.; Lewis, R.W., Jr.; Camic, C.L.; Schmidt, R.J.; Johnson, G.O. Differences among estimates of critical power and anaerobic work capacity derived from five mathematical models and the three-minute all-out test. J. Strength Cond. Res. 2014, 28, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Di Prampero, P.E. The concept of critical velocity: A brief analysis. Eur. J. Appl. Physiol. Occup. Physiol. 1999, 80, 162–164. [Google Scholar] [CrossRef] [PubMed]
- Burnley, M.; Davison, G.; Baker, J.R. Effects of priming exercise on vo2 kinetics and the power-duration relationship. Med. Sci. Sports Exerc. 2011, 43, 2171–2179. [Google Scholar] [CrossRef] [PubMed]
- Bartram, J.C.; Thewlis, D.; Martin, D.T.; Norton, K.I. Predicting critical power in elite cyclists: Questioning the validity of the 3-minute all-out test. Int. J. Sports Physiol. Perform. 2017, 12, 783–787. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jones, A.M.; Vanhatalo, A.; Burnley, M.; Morton, R.H.; Poole, D.C. Critical power: Implications for determination of vo2max and exercise tolerance. Med. Sci. Sports Exerc. 2010, 42, 1876–1890. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Jones, A.M.; Burnley, M. Application of critical power in sport. Int. J. Sports Physiol. Perform. 2011, 6, 128–136. [Google Scholar] [CrossRef]
- Muniz-Pumares, D.; Pedlar, C.; Godfrey, R.; Glaister, M. A comparison of methods to estimate anaerobic capacity: Accumulated oxygen deficit and w′ during constant and all-out work-rate profiles. J. Sports Sci. 2017, 35, 2357–2364. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Jones, A.M. Influence of prior sprint exercise on the parameters of the “all-out critical power test” in men. Exp. Physiol. 2009, 94, 255–263. [Google Scholar] [CrossRef]
- Marcora, S.M.; Staiano, W. The limit to exercise tolerance in humans: Mind over muscle? Eur. J. Appl. Physiol. 2010, 109, 763–770. [Google Scholar] [CrossRef]
- Salam, H.; Marcora, S.M.; Hopker, J.G. The effect of mental fatigue on critical power during cycling exercise. Eur. J. Appl. Physiol. 2018, 118, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Staiano, W.; Bosio, A.; Morree, H.M.; Rampinini, E.; Marcora, S. The cardinal exercise stopper: Muscle fatigue, muscle pain or perception of effort? Prog. Brain Res. 2018, 240, 175–200. [Google Scholar] [CrossRef] [PubMed]
- Gaesser, G.A.; Wilson, L.A. Effects of continuous and interval training on the parameters of the power-endurance time relationship for high-intensity exercise. Int. J. Sports Med. 1988, 9, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Chorley, A.; Bott, R.P.; Marwood, S.; Lamb, K.L. Slowing the reconstitution of w′ in recovery with repeated bouts of maximal exercise. Int. J. Sports Physiol. Perform. 2019, 14, 149–155. [Google Scholar] [CrossRef]
- Chidnok, W.; Dimenna, F.J.; Bailey, S.J.; Wilkerson, D.P.; Vanhatalo, A.; Jones, A.M. Effects of pacing strategy on work done above critical power during high-intensity exercise. Med. Sci. Sports Exerc. 2013, 45, 1377–1385. [Google Scholar] [CrossRef]
- Murgatroyd, S.R.; Ferguson, C.; Ward, S.A.; Whipp, B.J.; Rossiter, H.B. Pulmonary o-2 uptake kinetics as a determinant of high-intensity exercise tolerance in humans. J. Appl. Physiol. 2011, 110, 1598–1606. [Google Scholar] [CrossRef]
- Murgatroyd, S.R.; Wylde, L.A.; Cannon, D.T.; Ward, S.A.; Rossiter, H.B. A “ramp-sprint” protocol to characterise indices of aerobic function and exercise intensity domains in a single laboratory test. Eur. J. Appl. Physiol. 2014, 114, 1863–1874. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Doust, J.H.; Burnley, M. Determination of critical power using a 3-min all-out cycling test. Med. Sci. Sports Exerc. 2007, 39, 548–555. [Google Scholar] [CrossRef]
- Felippe, L.C.; Melo, T.G.; Silva-Cavalcante, M.D.; Ferreira, G.A.; Boari, D.; Bertuzzi, R.; Lima-Silva, A.E. Relationship between recovery of neuromuscular function and subsequent capacity to work above critical power. Eur. J. Appl. Physiol. 2020, 120, 1237–1249. [Google Scholar] [CrossRef]
- Yong, S.E.; Swisher, A.R.; Ferguson, C.; Cannon, D.T. Maximal sustained isokinetic power at exercise intolerance is not critical power. Int. J. Sports Med. 2019, 40, 631–638. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, E.A.; Martin, N.R.W.; Turner, M.C.; Taylor, C.W.; Ferguson, R.A. The combined effect of sprint interval training and postexercise blood flow restriction on critical power, capillary growth, and mitochondrial proteins in trained cyclists. J. Appl. Physiol. 2019, 126, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Muniz-Pumares, D.; Karsten, B.; Triska, C.; Glaister, M. Methodological approaches and related challenges associated with the determination of critical power and curvature constant. J. Strength Cond. Res. 2019, 33, 584–596. [Google Scholar] [CrossRef] [PubMed]
- Black, M.I.; Jones, A.M.; Bailey, S.J.; Vanhatalo, A. Self-pacing increases critical power and improves performance during severe-intensity exercise. Appl. Physiol. Nutr. Metab. 2015, 40, 662–670. [Google Scholar] [CrossRef]
- Black, M.I.; Jones, A.M.; Blackwell, J.R.; Bailey, S.J.; Wylie, L.J.; McDonagh, S.T.; Thompson, C.; Kelly, J.; Sumners, P.; Mileva, K.N.; et al. Muscle metabolic and neuromuscular determinants of fatigue during cycling in different exercise intensity domains. J. Appl. Physiol. 2017, 122, 446–459. [Google Scholar] [CrossRef]
- Townsend, N.E.; Nichols, D.S.; Skiba, P.F.; Racinais, S.; Periard, J.D. Prediction of critical power and w′ in hypoxia: Application to work-balance modelling. Front. Physiol. 2017, 8, 180. [Google Scholar] [CrossRef]
- Jeukendrup, A.; Saris, W.H.; Brouns, F.; Kester, A.D. A new validated endurance performance test. Med. Sci. Sports Exerc. 1996, 28, 266–270. [Google Scholar] [CrossRef]
- Currell, K.; Jeukendrup, A.E. Validity, reliability and sensitivity of measures of sporting performance. Sports Med. 2008, 38, 297–316. [Google Scholar] [CrossRef]
- Bishop, D.; Jenkins, D.G.; Howard, A. The critical power function is dependent on the duration of the predictive exercise tests chosen. Int. J. Sports Med. 1998, 19, 125–129. [Google Scholar] [CrossRef]
- Morton, R.H. Critical power test for ramp exercise. Eur. J. Appl. Physiol. Occup. Physiol. 1994, 69, 435–438. [Google Scholar] [CrossRef]
- Morton, R.H.; Green, S.; Bishop, D.; Jenkins, D.G. Ramp and constant power trials produce equivalent critical power estimates. Med. Sci. Sports Exerc. 1997, 29, 833–836. [Google Scholar] [CrossRef] [PubMed]
- Thomas, K.; Goodall, S.; Stone, M.; Howatson, G.; St Clair Gibson, A.; Ansley, L. Central and peripheral fatigue in male cyclists after 4-, 20-, and 40-km time trials. Med. Sci. Sports Exerc. 2015, 47, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Karsten, B.; Jobson, S.A.; Hopker, J.; Jimenez, A.; Beedie, C. High agreement between laboratory and field estimates of critical power in cycling. Int. J. Sports Med. 2014, 35, 298–303. [Google Scholar] [CrossRef] [PubMed]
- Brickley, G.; Green, S.; Jenkins, D.G.; McEinery, M.; Wishart, C.; Doust, J.D.; Williams, C.A. Muscle metabolism during constant- and alternating-intensity exercise around critical power. Int. J. Sports Med. 2007, 28, 300–305. [Google Scholar] [CrossRef]
- Karsten, B.; Hopker, J.; Jobson, S.A.; Baker, J.; Petrigna, L.; Klose, A.; Beedie, C. Comparison of inter-trial recovery times for the determination of critical power and w′ in cycling. J. Sports Sci. 2017, 35, 1420–1425. [Google Scholar] [CrossRef]
- Karsten, B.; Jobson, S.A.; Hopker, J.; Stevens, L.; Beedie, C. Validity and reliability of critical power field testing. Eur. J. Appl. Physiol. 2015, 115, 197–204. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Doust, J.H.; Burnley, M. A 3-min all-out cycling test is sensitive to a change in critical power. Med. Sci. Sports Exerc. 2008, 40, 1693–1699. [Google Scholar] [CrossRef]
- Wright, J.; Bruce-Low, S.; Jobson, S.A. The reliability and validity of the 3-min all-out cycling critical power test. Int. J. Sports Med. 2017, 38, 462–467. [Google Scholar] [CrossRef]
- Karsten, B.; Jobson, S.A.; Hopker, J.; Passfield, L.; Beedie, C. The 3-min test does not provide a valid measure of critical power using the srm isokinetic mode. Int. J. Sports Med. 2014, 35, 304–309. [Google Scholar] [CrossRef][Green Version]
- Clark, I.E.; Murray, S.R.; Pettitt, R.W. Alternative procedures for the three-minute all-out exercise test. J. Strength Cond. Res. 2013, 27, 2104–2112. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Doust, J.H.; Burnley, M. Robustness of a 3 min all-out cycling test to manipulations of power profile and cadence in humans. Exp. Physiol. 2008, 93, 383–390. [Google Scholar] [CrossRef]
- Black, M.I.; Durant, J.; Jones, A.M.; Vanhatalo, A. Critical power derived from a 3-min all-out test predicts 16.1-km road time-trial performance. Eur. J. Sport Sci. 2014, 14, 217–223. [Google Scholar] [CrossRef]
- Constantini, K.; Sabapathy, S.; Cross, T.J. A single-session testing protocol to determine critical power and w′. Eur. J. Appl. Physiol. 2014, 114, 1153–1161. [Google Scholar] [CrossRef]
- Bergstrom, H.C.; Housh, T.J.; Zuniga, J.M.; Camic, C.L.; Traylor, D.A.; Schmidt, R.J.; Johnson, G.O. A new single work bout test to estimate critical power and anaerobic work capacity. J. Strength Cond. Res. 2012, 26, 656–663. [Google Scholar] [CrossRef]
- Johnson, T.M.; Sexton, P.J.; Placek, A.M.; Murray, S.R.; Pettitt, R.W. Reliability analysis of the 3-min all-out exercise test for cycle ergometry. Med. Sci. Sports Exerc. 2011, 43, 2375–2380. [Google Scholar] [CrossRef] [PubMed]
- Dicks, N.D.; Jamnick, N.A.; Murray, S.R.; Pettitt, R.W. Load determination for the 3-minute all-out exercise test for cycle ergometry. Int. J. Sports Physiol. Perform. 2016, 11, 197–203. [Google Scholar] [CrossRef]
- Boone, J.; Bourgois, J. The oxygen uptake response to incremental ramp exercise methodogical and physiological issues. Sports Med. 2012, 42, 511–526. [Google Scholar] [CrossRef]
- Whipp, B.J.; Davis, J.A.; Torres, F.; Wasserman, K. A test to determine parameters of aerobic function during exercise. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 1981, 50, 217–221. [Google Scholar] [CrossRef]
- Black, M.I.; Jones, A.M.; Kelly, J.A.; Bailey, S.J.; Vanhatalo, A. The constant work rate critical power protocol overestimates ramp incremental exercise performance. Eur. J. Appl. Physiol. 2016, 116, 2415–2422. [Google Scholar] [CrossRef]
- Chidnok, W.; Fulford, J.; Bailey, S.J.; Dimenna, F.J.; Skiba, P.F.; Vanhatalo, A.; Jones, A.M. Muscle metabolic determinants of exercise tolerance following exhaustion: Relationship to the “critical power”. J. Appl. Physiol. 2013, 115, 243–250. [Google Scholar] [CrossRef]
- Coats, E.M.; Rossiter, H.B.; Day, J.R.; Miura, A.; Fukuba, Y.; Whipp, B.J. Intensity-dependent tolerance to exercise after attaining vo2 max in humans. J. Appl. Physiol. 2003, 95, 483–490. [Google Scholar] [CrossRef] [PubMed]
- Van der Vaart, H.; Murgatroyd, S.R.; Rossiter, H.B.; Chen, C.; Casaburi, R.; Porszasz, J. Selecting constant work rates for endurance testing in copd: The role of the power-duration relationship. COPD J. Chronic Obstr. Pulm. Dis. 2014, 11, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Walker, T.; Burnet, S.; Jobson, S.A. The reliability and validity of the powertap p1 power pedals before and after 100 hours of use. Int. J. Sports Physiol. Perform. 2019, 14, 855–858. [Google Scholar] [CrossRef]
- Nimmerichter, A.; Schnitzer, L.; Prinz, B.; Simon, D.; Wirth, K. Validity and reliability of the garmin vector power meter in laboratory and field cycling. Int. J. Sports Med. 2017, 38, 439–446. [Google Scholar] [CrossRef]
- Hopker, J.; Myers, S.; Jobson, S.A.; Bruce, W.; Passfield, L. Validity and reliability of the wattbike cycle ergometer. Int. J. Sports Med. 2010, 31, 731–736. [Google Scholar] [CrossRef]
- Whittle, C.; Smith, N.; Jobson, S.A. Validity of powertap p1 pedals during laboratory-based cycling time trial performance. Sports 2018, 6, 92. [Google Scholar] [CrossRef]
- Jeukendrup, A.E.; Craig, N.P.; Hawley, J.A. The bioenergetics of world class cycling. J. Sci. Med. Sport 2000, 3, 414–433. [Google Scholar] [CrossRef]
- Abbiss, C.R.; Laursen, P.B. Describing and understanding pacing strategies during athletic competition. Sports Med. 2008, 38, 239–252. [Google Scholar] [CrossRef]
- Abbiss, C.R.; Menaspa, P.; Villerius, V.; Martin, D.T. Distribution of power output when establishing a breakaway in cycling. Int. J. Sports Physiol. Perform. 2013, 8, 452–455. [Google Scholar] [CrossRef]
- De Souza, K.M.; Dekerle, J.; Salvador, P.C.D.; de Lucas, R.D.; Guglielmo, L.G.A.; Greco, C.C.; Denadai, B.S. Rate of utilization of a given fraction of w′ (the curvature constant of the power-duration relationship) does not affect fatigue during severe-intensity exercise. Exp. Physiol. 2016, 101, 540–548. [Google Scholar] [CrossRef]
- Burnley, M.; Vanhatalo, A.; Jones, A.M. Distinct profiles of neuromuscular fatigue during muscle contractions below and above the critical torque in humans. J. Appl. Physiol. 2012, 113, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Morton, R.H.; Billat, L.V. The critical power model for intermittent exercise. Eur. J. Appl. Physiol. 2004, 91, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Chidnok, W.; Dimenna, F.J.; Bailey, S.J.; Vanhatalo, A.; Morton, R.H.; Wilkerson, D.P.; Jones, A.M. Exercise tolerance in intermittent cycling: Application of the critical power concept. Med. Sci. Sports Exerc. 2012, 44, 966–976. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, C.; Rossiter, H.B.; Whipp, B.J.; Cathcart, A.J.; Murgatroyd, S.R.; Ward, S.A. Effect of recovery duration from prior exhaustive exercise on the parameters of the power-duration relationship. J. Appl. Physiol. 2010, 108, 866–874. [Google Scholar] [CrossRef] [PubMed]
- Rossiter, H.B.; Ward, S.A.; Kowalchuk, J.M.; Howe, F.A.; Griffiths, J.R.; Whipp, B.J. Dynamic asymmetry of phosphocreatine concentration and o-2 uptake between the on- and off-transients of moderate- and high-intensity exercise in humans. J. Physiol. Lond. 2002, 541, 991–1002. [Google Scholar] [CrossRef] [PubMed]
- Chidnok, W.; DiMenna, F.J.; Fulford, J.; Bailey, S.J.; Skiba, P.F.; Vanhatalo, A.; Jones, A.M. Muscle metabolic responses during high-intensity intermittent exercise measured by (31)p-mrs: Relationship to the critical power concept. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2013, 305, R1085–R1092. [Google Scholar] [CrossRef]
- Kordi, M.; Menzies, C.; Parker Simpson, L. Relationship between power–duration parameters and mechanical and anthropometric properties of the thigh in elite cyclists. Eur. J. Appl. Physiol. 2018, 118, 637–645. [Google Scholar] [CrossRef]
- Miura, A.; Endo, M.; Sato, H.; Sato, H.; Barstow, T.J.; Fukuba, Y. Relationship between the curvature constant parameter of the power-duration curve and muscle cross-sectional area of the thigh for cycle ergometry in humans. Eur. J. Appl. Physiol. 2002, 87, 238–244. [Google Scholar] [CrossRef]
- Chorley, A.; Bott, R.P.; Marwood, S.; Lamb, K.L. Physiological and anthropometric determinants of critical power, w′ and the reconstitution of w′ in trained and untrained male cyclists. Eur. J. Appl. Physiol. 2020. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Poole, D.C.; DiMenna, F.J.; Bailey, S.J.; Jones, A.M. Muscle fiber recruitment and the slow component of o2 uptake: Constant work rate vs. All-out sprint exercise. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2011, 300, R700–R707. [Google Scholar] [CrossRef]
- Skiba, P.F.; Chidnok, W.; Vanhatalo, A.; Jones, A.M. Modeling the expenditure and reconstitution of work capacity above critical power. Med. Sci. Sports Exerc. 2012, 44, 1526–1532. [Google Scholar] [CrossRef]
- Skiba, P.F.; Jackman, S.; Clarke, D.; Vanhatalo, A.; Jones, A.M. Effect of work and recovery durations on w′ reconstitution during intermittent exercise. Med. Sci. Sports Exerc. 2014, 46, 1433–1440. [Google Scholar] [CrossRef]
- Skiba, P.F.; Clarke, D.; Vanhatalo, A.; Jones, A.M. Validation of a novel intermittent w′ model for cycling using field data. Int. J. Sports Physiol. Perform. 2014, 9, 900–904. [Google Scholar] [CrossRef] [PubMed]
- Sreedhara, V.S.M.; Ashtiani, F.; Mocko, G.M.; Vahidi, A.; Hutchison, R.E. Modeling the recovery of w′ in the moderate to heavy exercise intensity domain. Med. Sci. Sports Exerc. 2020. [Google Scholar] [CrossRef] [PubMed]
- Skiba, P.F.; Fulford, J.; Clarke, D.C.; Vanhatalo, A.; Jones, A.M. Intramuscular determinants of the ability to recover work capacity above critical power. Eur. J. Appl. Physiol. 2015, 115, 703–713. [Google Scholar] [CrossRef] [PubMed]
- Broxterman, R.M.; Skiba, P.F.; Craig, J.C.; Wilcox, S.L.; Ade, C.J.; Barstow, T.J. w′ expenditure and reconstitution during severe intensity constant power exercise: Mechanistic insight into the determinants of w′. Respir. Physiol. Neurobiol. 2016, 4. [Google Scholar] [CrossRef] [PubMed]
- Shearman, S.; Dwyer, D.; Skiba, P.; Townsend, N. Modeling intermittent cycling performance in hypoxia using the critical power concept. Med. Sci. Sports Exerc. 2016, 48, 527–535. [Google Scholar] [CrossRef][Green Version]
- Bartram, J.C.; Thewlis, D.; Martin, D.T.; Norton, K.I. Accuracy of w′ recovery kinetics in high performance cyclists—Modelling intermittent work capacity. Int. J. Sports Physiol. Perform. 2017, 13, 724–728. [Google Scholar] [CrossRef]
- Tomlin, D.L.; Wenger, H.A. The relationship between aerobic fitness and recovery from high intensity intermittent exercise. Sports Med. 2001, 31, 1–11. [Google Scholar] [CrossRef]
- Caen, K.; Bourgois, J.G.; Bourgois, G.; van Der Stede, T.; Vermeire, K.; Boone, J. The reconstitution of w′ depends on both work and recovery characteristics. Med. Sci. Sports Exerc. 2019, 51, 1745–1751. [Google Scholar] [CrossRef]
- Vinetti, G.; Fagoni, N.; Taboni, A.; Camelio, S.; di Prampero, P.E.; Ferretti, G. Effects of recovery interval duration on the parameters of the critical power model for incremental exercise. Eur. J. Appl. Physiol. 2017, 117, 1859–1867. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, S.R.; McKenzie, D.C. The laboratory assessment of endurance performance in cyclists. Can. J. Appl. Physiol. 1994, 19, 266–274. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Robson, S.J.; King, M.J.; Davie, A.J. Correlations between short-course triathlon performance and physiological variables determined in laboratory cycle and treadmill tests. J. Sports Med. Phys. Fit. 1997, 37, 122–130. [Google Scholar]
- Bishop, D.; Jenkins, D.G.; Mackinnon, L.T. The relationship between plasma lactate parameters, wpeak and 1-h cycling performance in women. Med. Sci. Sports Exerc. 1998, 30, 1270–1275. [Google Scholar] [CrossRef]
- Adami, A.; Sivieri, A.; Moia, C.; Perini, R.; Ferretti, G. Effects of step duration in incremental ramp protocols on peak power and maximal oxygen consumption. Eur. J. Appl. Physiol. 2013, 113, 2647–2653. [Google Scholar] [CrossRef]
- Bentley, D.J.; Newell, J.; Bishop, D. Incremental exercise test design and analysis—Implications for performance diagnostics in endurance athletes. Sports Med. 2007, 37, 575–586. [Google Scholar] [CrossRef]
- Paton, C.D.; Hopkins, W.G. Variation in performance of elite cyclists from race to race. Eur. J. Sport Sci. 2006, 6, 25–31. [Google Scholar] [CrossRef]
- Nimmerichter, A.; Eston, R.G.; Bachl, N.; Williams, C. Longitudinal monitoring of power output and heart rate profiles in elite cyclists. J. Sports Sci. 2011, 29, 831–840. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Hawley, J.A.; Burke, L.M. Design and analysis of research on sport performance enhancement. Med. Sci. Sports Exerc. 1999, 31, 472–485. [Google Scholar] [CrossRef]
- Allen, H.; Coggan, A. Training and Racing with a Power Meter; VeloPress: Boulder, CO, USA, 2010. [Google Scholar]
- Van Erp, T.; Sanders, D. Demands of professional cycling races: Influence of race category and result. Eur. J. Sport Sci. 2020, 1–12. [Google Scholar] [CrossRef]
- Borszcz, F.K.; Tramontin, A.F.; Bossi, A.H.; Carminatti, L.J.; Costa, V.P. Functional threshold power in cyclists: Validity of the concept and physiological responses. Int. J. Sports Med. 2018, 39, 737–742. [Google Scholar] [CrossRef] [PubMed]
- Klitzke Borszcz, F.; Ferreira Tramontin, A.; Pereira Costa, V. Is the functional threshold power interchangeable with the maximal lactate steady state in trained cyclists? Int. J. Sports Physiol. Perform. 2019, 14, 1029–1035. [Google Scholar] [CrossRef] [PubMed]
- Inglis, E.C.; Iannetta, D.; Passfield, L.; Murias, J.M. Maximal lactate steady state versus the 20-minute functional threshold power test in well-trained individuals: “Watts” the big deal? Int. J. Sports Physiol. Perform. 2019, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, O.; Simmons, R.; Patterson, S.D.; Waldron, M. Functional threshold power is not equivalent to lactate parameters in trained cyclists. J. Strength Cond. Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Valenzuela, P.L.; Morales, J.S.; Foster, C.; Lucia, A.; de la Villa, P. Is the functional threshold power a valid surrogate of the lactate threshold? Int. J. Sports Physiol. Perform. 2018, 1–6. [Google Scholar] [CrossRef] [PubMed]
- MacInnis, M.J.; Thomas, A.C.Q.; Phillips, S.M. The reliability of 4-minute and 20-minute time trials and their relationships to functional threshold power in trained cyclists. Int. J. Sports Physiol. Perform. 2019, 14, 38–45. [Google Scholar] [CrossRef]
- McGrath, E.; Mahony, N.; Fleming, N.; Donne, B. Is the ftp test a reliable, reproducible and functional assessment tool in highly-trained athletes? Int. J. Exerc. Sci. 2019, 12, 1334–1345. [Google Scholar]
- Gavin, T.P.; Van Meter, J.B.; Brophy, P.M.; Dubis, G.S.; Potts, K.N.; Hickner, R.C. Comparison of a field-based test to estimate functional threshold power and power output at lactate threshold. J. Strength Cond. Res. 2012, 26, 416–421. [Google Scholar] [CrossRef]
- Sanders, D.; Taylor, R.J.; Myers, T.; Akubat, I. A field-based cycling test to assess predictors of endurance performance and establishing training zones. J. Strength Cond. Res. 2017. [Google Scholar] [CrossRef]
- Morgan, P.T.; Black, M.I.; Bailey, S.J.; Jones, A.M.; Vanhatalo, A. Road cycle tt performance: Relationship to the power-duration model and association with ftp. J. Sports Sci. 2019, 37, 902–910. [Google Scholar] [CrossRef]
- Barranco-Gil, D.; Gil-Cabrera, J.; Valenzuela, P.L.; Alejo, L.B.; Montalvo-Perez, A.; Talavera, E.; Moral-Gonzalez, S.; Lucia, A. Functional threshold power: Relationship with respiratory compensation point and effects of various warm-up protocols. Int. J. Sports Physiol. Perform. 2020, 1–5. [Google Scholar] [CrossRef]
- Lillo-Bevia, J.R.; Courel-Ibanez, J.; Cerezuela-Espejo, V.; Moran-Navarro, R.; Martinez-Cava, A.; Pallares, J.G. Is the functional threshold power a valid metric to estimate the maximal lactate steady state in cyclists? J. Strength Cond. Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Klitzke Borszcz, F.; Tramontin, A.F.; Costa, V.P. Reliability of the functional threshold power in competitive cyclists. Int. J. Sports Med. 2020, 41, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Mann, T.; Lamberts, R.P.; Lambert, M.I. Methods of prescribing relative exercise intensity: Physiological and practical considerations. Sports Med. 2013, 43, 613–625. [Google Scholar] [CrossRef] [PubMed]
- Keir, D.A.; Fontana, F.Y.; Robertson, T.C.; Murias, J.M.; Paterson, D.H.; Kowalchuk, J.M.; Pogliaghi, S. Exercise intensity thresholds: Identifying the boundaries of sustainable performance. Med. Sci. Sports Exerc. 2015, 47, 1932–1940. [Google Scholar] [CrossRef]
- Froyd, C.; Millet, G.Y.; Noakes, T.D. The development of peripheral fatigue and short-term recovery during self-paced high-intensity exercise. J. Physiol. Lond. 2013, 591, 1339–1346. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Jones, A.M. Influence of creatine supplementation on the parameters of the “all-out critical power test”. J. Exerc. Sci. Fit. 2009, 7, 9–17. [Google Scholar] [CrossRef][Green Version]
- Ronnestad, B.R.; Hansen, J.; Ellefsen, S. Block periodization of high-intensity aerobic intervals provides superior training effects in trained cyclists. Scand. J. Med. Sci. Sports 2014, 24, 34–42. [Google Scholar] [CrossRef]
- Milanovic, Z.; Sporis, G.; Weston, M. Effectiveness of high-intensity interval training (hit) and continuous endurance training for vo2max improvements: A systematic review and meta-analysis of controlled trials. Sports Med. 2015, 45, 1469–1481. [Google Scholar] [CrossRef]
- Laursen, P.B.; Jenkins, D.G. The scientific basis for high-intensity interval training: Optimising training programmes and maximising performance in highly trained endurance athletes. Sports Med. 2002, 32, 53–73. [Google Scholar] [CrossRef]
| Study | Participants | Protocol Description * | Model † | Principal Findings in Relation to W′ Reconstitution |
|---|---|---|---|---|
| Bartram, et al. [108] | 4 male; elite cyclists | Intermittent: 30 s work/60 s recovery + open ended severe to finish | Skiba2 | Skiba2 underestimated W′ reconstitution. New W′Tau formula proposed for elite cyclists |
| Broxterman, et al. [106] | 6 male | Handgrip repetitions. Tension/relaxation of 50% and 20% duty cycles | Skiba1 | Validated the Skiba1 model over a duty cycle which authors suggested as a proxy for the contraction and relaxation during a pedal revolution. |
| Caen, et al. [110] | 11 male; physical exercise (PE) students | 12 trials: 4 and 8 min exhaustive bouts, with 2,4,6 min recoveries | Skiba1 | Skiba1 underestimated W′ reconstitution more so at 2-min recovery, less so at 6 min. Large individual variations in W′Tau. W′ reconstitution affected by preceding depletion rate, slower depletion = less reconstitution |
| Chidnok, et al. [93] | 7 male; recreationally active | Intermittent: 60 s work/30 s recovery in differing domains | n/a | No recovery in severe domain. Recovery rate of W′ slower than expenditure in relation to critical power (CP). |
| Chidnok, et al. [96] | 9 male; recreationally active | Single leg knee extensions. intermittent 60 s work/18, 30, 48 s recovery | n/a | W′ reconstitution increases with recovery duration. Phosphocreatine and pH levels were always the same at exhaustion. Phosphocreatine recovery correlated to W′ reconstitution but was faster. Phosphocreatine recovery slowed as exercise session progressed. |
| Chorley, et al. [45] | 20 (19 male, 1 female; 9 trained, 11 untrained) | Repeated ramps to exhaustion with 2 min recoveries | Skiba1 | Skiba1 did not fit the protocol, overestimate W′ at exhaustion and underestimating reconstitution during recoveries. W′ reconstitution slowed with repeated bouts of exhaustive exercise. |
| Chorley, et al. [99] | 20 male; (9 trained, 11 untrained) | Repeated ramps to exhaustion with 2 min recoveries | Skiba1 | Assessment of anthropometric and physiological relationships with W′ reconstitution and its slowing following repeated bouts. |
| Felippe, et al. [50] | 10 male; recreationally active | 2 × 6 min constant work rate (CWR) exhaustive bouts separated by 3, 6, 15 min recoveries | n/a | W′ reconstitution compared with neuromuscular recovery. Recovery of voluntary activation faster than W′, no difference between time constants of W′ and maximal voluntary contraction. |
| Ferguson, et al. [94] | 6 male; recreationally active | 6 min CWR exhaustive bout then 3, 6, 15 min recoveries | n/a | W′ reconstitution found to be curvilinear. Half-time of W′ reconstitution was faster than that of blood lactate but slower than that of oxygen uptake (a proxy for phosphocreatine reconstitution) |
| Morton and Billat [92] | 6 male; well trained | Running: intermittent 60, 180, 30 s work, 60, 180 s recovery | n/a | Produced original model of linear W′ reconstitution at same rate as expenditure in relation to CP. Established W′ reconstitution occurred during recovery due to extended distances covered. |
| Shearman, et al. [107] | 11 male; well trained | Intermittent: 60 s work/30 s recovery | Skiba1 | Validated skiba1 in hypoxia with proviso that CP and W′ were also measured at same level of hypoxia |
| Skiba, et al. [101] | 7 male; recreationally active | Intermittent: 60 s work/30 s recovery | Skiba1 | Creation of Skiba1 W′bal model based on intermittent exercise to exhaustion, together with generic Tau equation based on CP. Validated against single rider in a race with W′bal of 1.5 kJ at retirement from race. |
| Skiba, et al. [103] | 8 (6 male, 2 female) 8 well trained triathletes | Assessment of training and race data | Skiba1 | Validation of Skiba1 on training and race data to detect the point of exhaustion. When exhaustion is set at W′bal = 1.5 kJ prediction of exhaustion was 80% appropriately classified as exhausted and 88% appropriately classified as non-exhausted. Recommendation to use 1.5 kJ as practical level of exhaustion. |
| Skiba, et al. [105] | 10 (6 male, 4 female); recreationally active | Intermittent: 60, 40, 20 s work/30, 20, 10, 5 s recovery | Skiba1 | Skiba1 underestimated W′ reconstitution, more so with reduced work and/or recovery durations. Large individual variations in reconstitution rate hence recommendations to individualize Tau. |
| Skiba, et al. [102] | 11 (5 male, 6 female); recreationally active | Cycle and single leg knee extensions. 3 min CWR exhaustive bout then 1, 2, 5, 7 min recoveries | Skiba2 | Skiba2 differential model produced allowing real time W′bal prediction. Large inter and intra individual variations in reconstitution rate observed. |
| Sreedhara, et al. [104] | 7 male; trained | 120 s bout to deplete 50% of W′, followed by 2, 6, 15 min recoveries, followed by 3-min all-out | Skiba2 | Skiba2 overestimated W′ reconstitution, based on the estimated 50% of W′ expended during initial bout. W′ reconstitution did not increase from 6 min to 15 min recovery hence W′ reconstitution was not exponential. |
| Townsend, et al. [56] | 9 male; trained | Intermittent: 40–60 s work/30–60 s recovery | Skiba1 and Skiba2 | Produced a modification equation for CP based on altitude for use in Skiba models to allow W′ reconstitution to be predicted at increasing altitude. |
| Vanhatalo and Jones [40] | 7 male; recreationally active | 30 s sprint, followed by 2- or 15- min recovery then 3-min all-out test | n/a | Prior severe sprint exercise (extent of W′ expenditure unknown) depletes W′ but not CP. W′ reconstruction of 79% after 2 min and fully recovered by 15 min |
| Vinetti, et al. [111] | 7 male; recreationally active | Incremental ramp with steps 30–300 s duration with recovery between each step of 0–180 s. | n/a | Extensive mathematical representation of discontinuous ramp exercise. |
| Study | Participants | Functional Threshold Power Test Method | Validated Against * | Mean Functional Threshold Power (W) | Comparison Mean Power Output (W) | Significantly Different | Correlation Coefficient (r) | Comments |
|---|---|---|---|---|---|---|---|---|
| Barranco-Gil, et al. [132] | 15 male, well trained | 20-min test | RCP | 284 to 286 | 344 ± 32 | Yes | 0.86 to 0.93 | Range of FTP and correlation coefficients due to 3 warm up techniques providing Functional Threshold Power (FTP) values of 286 ± 26 W; 284 ± 26 W; 286 ± 32 W |
| Borszcz, et al. [122] | 23 male, trained | 20-min test | IAT | 236 ± 38 | 344 ± 32 | No | 0.61 | Graded test with large 40 W increments used to determine IAT |
| 60-min test | IAT | 231 ± 33 | 237 ± 29 | No | 0.76 | |||
| Gavin, et al. [129] | 7 male, trained and well trained | 8-min test | OBLA | 301 ± 13 | 293 ± 9 | No (see notes) | 0.70 | OBLA selected from three other Lactate measurements as most appropriate comparison for FTP |
| Inglis, et al. [124] | 18 (12 male 6 female), trained and well trained | 20-min test | MLSS | 261 ± 45 | 243 ± 48 | Yes | 0.96 | |
| Jeffries, et al. [125] | 20 male, well trained | 20-min test | LT (Dmax) | 266 ± 42 | 221 ± 25 | Yes | 0.80 | |
| LT (modified Dmax) | 266 ± 42 | 238 ± 32 | Yes | 0.75 | ||||
| OBLA | 266 ± 42 | 268 ± 30 | No | 0.88 | authors noted that despite no significant difference between FTP and OBLA, large random error made in individual data meant that FTP was not equivalent to OBLA | |||
| IAT | 266 ± 42 | 244 ± 33 | Yes | 0.85 | ||||
| Klitzke Borszcz, et al. [123] | 15 male, trained and well trained | 20-min test | MLSS | 252 ± 23 | 248 ± 25 | No | 0.91 | Nine out of 12 participants had difference between MLSS and FTP of 5% or more |
| Lillo-Bevia, et al. [133] | 11 male, trained | 20-min test | MLSS | 262 ± 19 | 250 ± 16 | Yes | 0.95 | |
| MacInnis, et al. [127] | 8 male, well trained | 60-min test | CP | 309 ± 26 | 325 ± 29 | Yes | 0.91 | Critical power derived from a 4-min and 20-min test, the latter of which is longer than generally accepted for CP testing. |
| McGrath, et al. [128] | 19 (12 male 7 female) well trained | 20-min test | LT (Dmax) | 259 ± 40 | 246 ± 38 | Not reported | 0.94 | authors noted large limits of agreement meaning that FTP was not equivalent to Lactate threshold |
| Morgan, et al. [131] | 12 male, trained | 20-min test | LT (Dmax) | 278 ± 42 | 275 ± 40 | No | 0.92 | authors noted that despite no significant difference between FTP and CP, large limits of agreement meant that FTP was not equivalent to CP |
| Sanders, et al. [130] | 19 male, well trained | 8-min test | LT (DMax) | 341 ± 33 | 279 ± 20 | Very largely different | Not reported | |
| LT (modified Dmax) | 341 ± 33 | 319 ± 29 | Moderately different | Not reported | ||||
| OBLA | 341 ± 33 | 319 ± 25 | Moderately different | Not reported | ||||
| Valenzuela, et al. [126] | 20 male, cyclists | 20-min test | LT (modified Dmax) | 240 ± 35 | 246 ± 24 | No | 0.90 | |
| Subset: 11 recreational cyclists | ≈217 | ≈232 | Yes | 0.88 | subgroup power outputs are derived from mean body mass × w/kg for each subgroup as FTP and LT subgroup means are not quoted in the study. | |||
| Subset: 9 well trained cyclists | ≈269 W | ≈265 | No | 095 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chorley, A.; Lamb, K.L. The Application of Critical Power, the Work Capacity above Critical Power (W′), and Its Reconstitution: A Narrative Review of Current Evidence and Implications for Cycling Training Prescription. Sports 2020, 8, 123. https://doi.org/10.3390/sports8090123
Chorley A, Lamb KL. The Application of Critical Power, the Work Capacity above Critical Power (W′), and Its Reconstitution: A Narrative Review of Current Evidence and Implications for Cycling Training Prescription. Sports. 2020; 8(9):123. https://doi.org/10.3390/sports8090123
Chicago/Turabian StyleChorley, Alan, and Kevin L. Lamb. 2020. "The Application of Critical Power, the Work Capacity above Critical Power (W′), and Its Reconstitution: A Narrative Review of Current Evidence and Implications for Cycling Training Prescription" Sports 8, no. 9: 123. https://doi.org/10.3390/sports8090123
APA StyleChorley, A., & Lamb, K. L. (2020). The Application of Critical Power, the Work Capacity above Critical Power (W′), and Its Reconstitution: A Narrative Review of Current Evidence and Implications for Cycling Training Prescription. Sports, 8(9), 123. https://doi.org/10.3390/sports8090123






