Effects of Submaximal Performances on Critical Speed and Power: Uses of an Arbitrary-Unit Method with Different Protocols
Abstract
1. Introduction
1.1. Empirical Model of Running and Cycling Performances
1.2. Variability of the Performances of Exhausting Exercises.
1.3. Purpose of the Present Study
- the range of tlim can be different for each athlete in protocols 1 and 3;
- the range of speeds and distances (or power-output and work in cycling) can be different for each athlete in protocol 2;
- the same endurance indices can correspond to different maximal aerobic speed (MAS) or maximal aerobic power (MAP in cycling).
2. Methods
2.1. Arbitrary Units
2.1.1. Arbitrary Units in Protocols 1 and 2
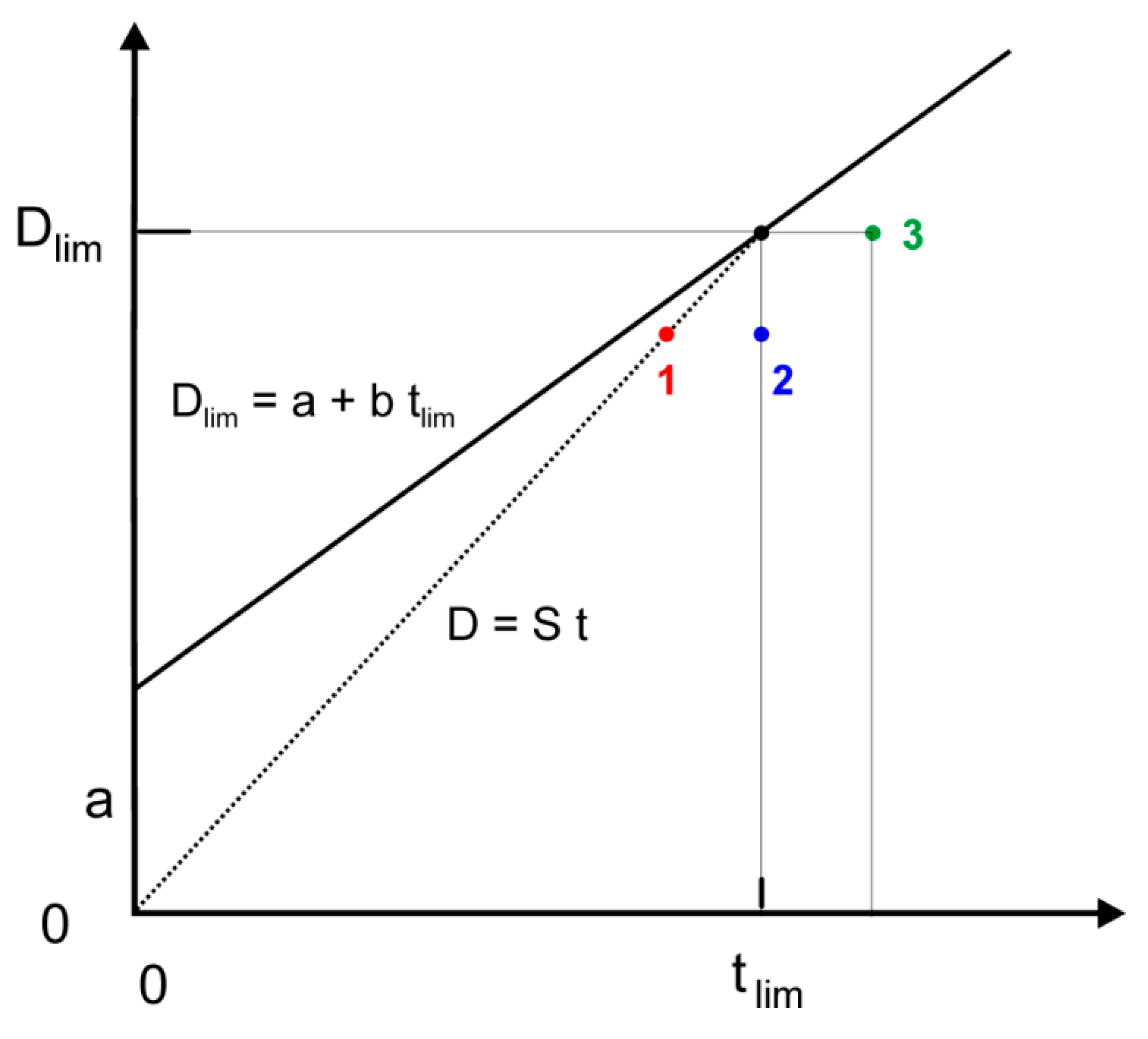
2.1.2. Arbitrary Units in Protocol 3
and tlim3 = Dlim31/g = 5.54711/g
2.2. Coefficients C1 and C2
2.3. Computation of the Effects of Submaximal Performances on SCrit and PCrit
2.3.1. Computation in the Constant-Speed (or Constant Power Output) Protocol (Protocol 1)
2.3.2. Computation in the constant-time protocol (protocol 2)
2.3.3. Computation in the constant-distance protocol
3. Results
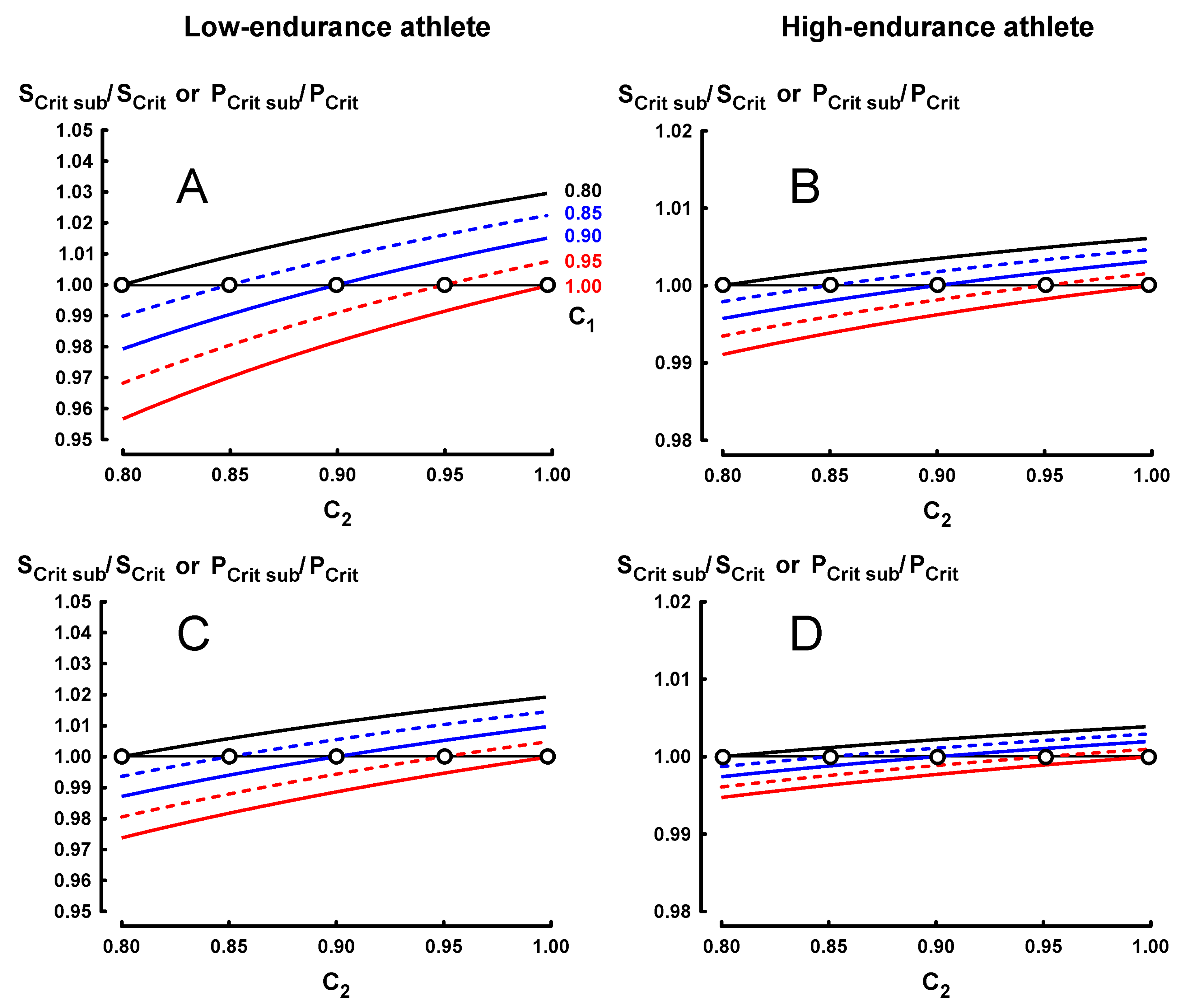
3.1. Results for Protocol 1 (Constant Speed or Power Output Protocol)
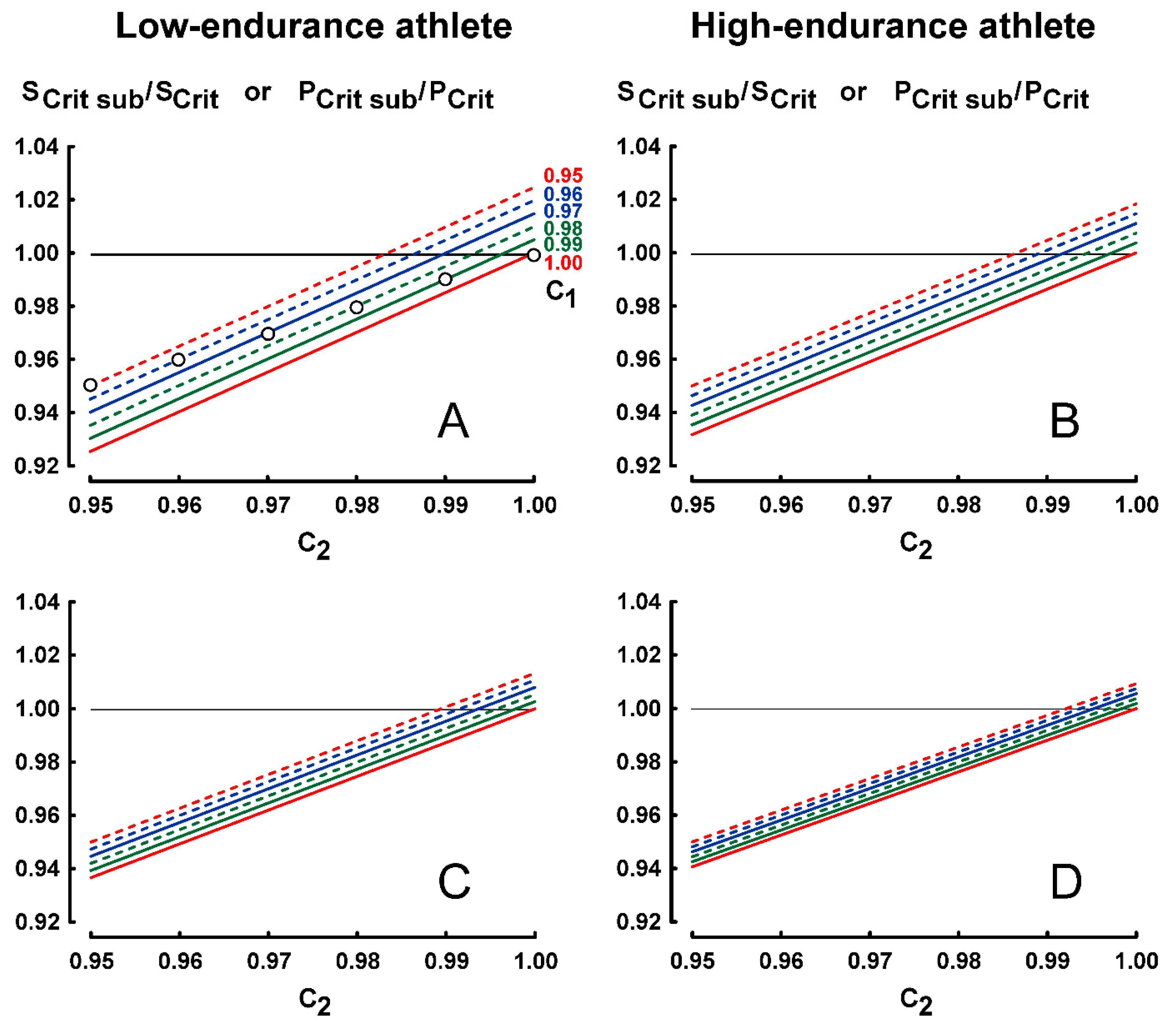
3.2. Results for Protocol 2 (Constant-Time Protocol)
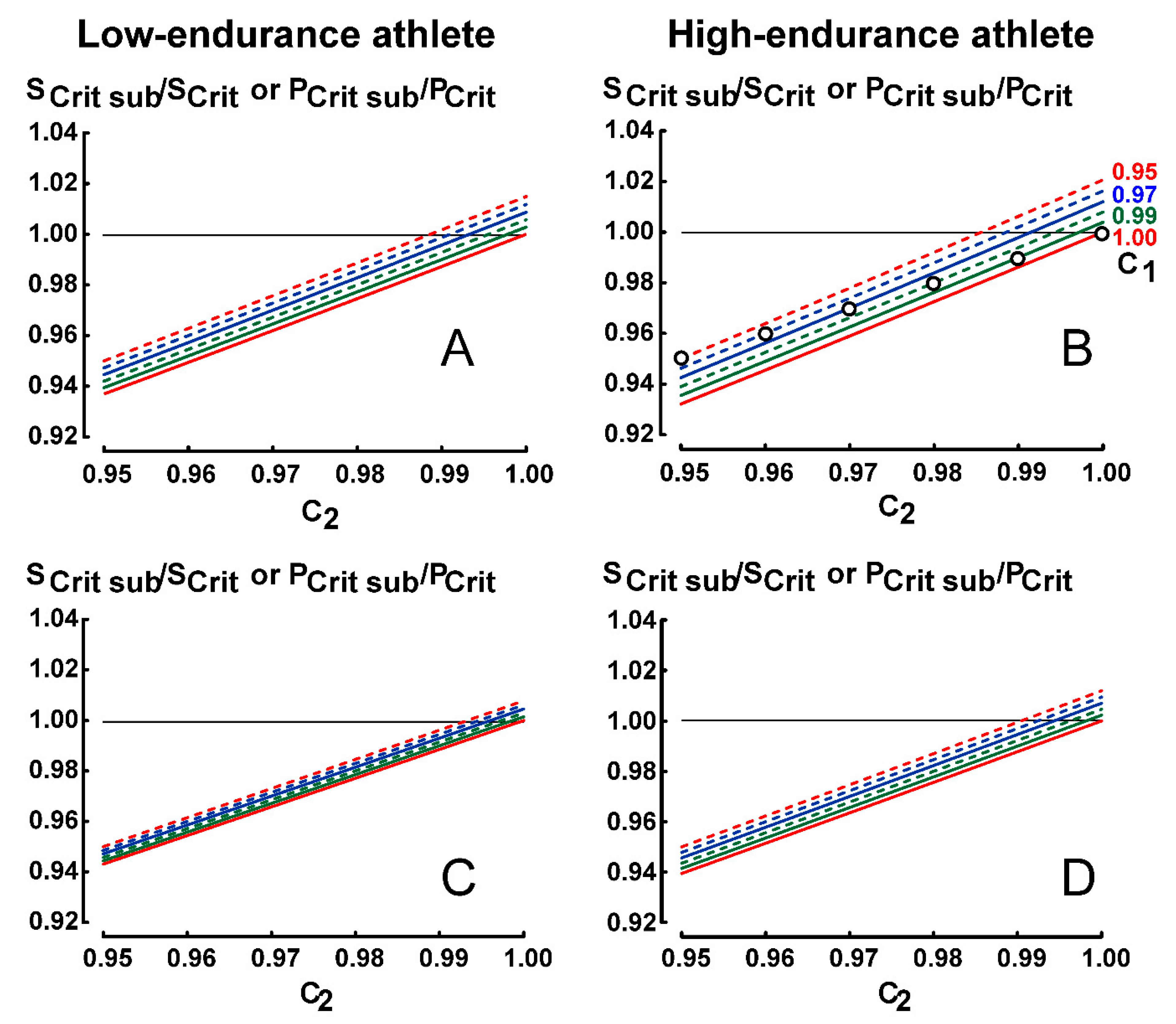
3.3. Results for Protocol 3 (Constant-Distance Protocol)
4. Discussion
- -
- C1 is equal to C2 for protocol 1(empty circles in Figure 1);
- -
- Dlim1 (1 − C1) is equal to Dlim2 (1 − C2) for protocol 2;
- -
- tlim1 (1 − 1/C1) is equal to tlim2 (1 − 1/C2) for protocol 3.
5. Conclusions
Funding
Conflicts of Interest
References
- Kennelly, A.E. An approximate law of fatigue in the speeds of racing animals. Proc. Am. Acad. Arts Sci 1906, 42, 275–331. [Google Scholar] [CrossRef]
- Hill, A.V. The physiological basis of athletic records. Nature 1925, 116, 544–548. [Google Scholar] [CrossRef]
- Scherrer, J.; Samson, M.; Paléologue, A. Etude du travail musculaire et de la fatigue. Données ergométriques obtenues chez l’homme. J. Physiol. 1954, 46, 887–916. [Google Scholar]
- Péronnet, F.; Thibault, G. Mathematical analysis of running performance and world running records. J. Appl. Physiol. 1989, 67, 453–465. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G.; Edmond, I.M.; Hamilton, B.H.; Mac Farlane, D.J.; Ross, B.H. Relation between power and endurance for treadmill running of short duration. Ergonomics 1989, 32, 1565–1571. [Google Scholar] [CrossRef] [PubMed]
- Morton, R.H. A 3-parameter critical power model. Ergonomics 1996, 39, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Ettema, J.H. Limits of human performance and energy-production. Int. J. Angew. Physiol. Einschl. Arb. Physiol. 1966, 22, 45–54. [Google Scholar] [CrossRef]
- Margaria, R.; Cerretelli, P.; Aghemo, P.; Sassi, G. Energy cost of running. J. Appl. Physiol. 1963, 18, 367–370. [Google Scholar] [CrossRef]
- Berthoin, S.; Baquet, G.; Dupont, G.; Blondel, N.; Mucci, P. Critical Velocity and Anaerobic Distance Capacity in Prepubertal Children. Rev. Can. Physiol. Appl. 2003, 28, 561–575. [Google Scholar] [CrossRef]
- Moritani, T.; Ata, A.N.; Devries, H.A.; Muro, M. Critical power as a measure of physical work capacity and anaerobic threshold. Ergonomics 1981, 24, 339–350. [Google Scholar] [CrossRef]
- Whipp, B.J.; Huntsman, D.J.; Storer, T.; Lamarra, N.; Wasserman, K. A constant which determines the duration of tolerance to high-intensity work (Abstract). Fed. Proc. 1982, 41, 1591. [Google Scholar]
- Craig, J.C.; Vanhatalo, A.; Burnley, M.; Jones, A.M.; Poole, D.C. Critical Power: Possibly the Most Important Fatigue Threshold in Exercise Physiology. In Muscle and Exercise Physiology, 1st ed.; Zoladz, J., Ed.; Elsevier Publisher: New York, NY, USA, 2019; Chapter 8; pp. 159–181. [Google Scholar]
- Vandewalle, H.; Kapitaniak, B.; Grun, S.; Raveneau, S.; Monod, H. Comparison between a 30-s all-out test and a time-work test on acycle ergometer. Eur. J. Appl. Physiol. Occup. Physiol. 1989, 58, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Green, S.; Dawson, B.T.; Goodman, C.; Carey, M.F. Y-intercept of the maximal work-duration relationship and anaerobic capacity in cyclists. Eur. J. Appl. Physiol. Occup. Physiol. 1994, 69, 550–556. [Google Scholar] [CrossRef] [PubMed]
- Vandewalle, H. Modelling of Running Performances: Comparisons of Power-Law, Hyperbolic, Logarithmic and Exponential Models in Elite Endurance Runners. Biomed. Res. Int. 2018. [Google Scholar] [CrossRef] [PubMed]
- Gamelin, F.X.; Coquart, J.; Ferrari, N.; Vodougnon, H.; Matran, R.; Léger, L.; Bosquet, L. Prediction of one hour running performance using constant duration tests. J. Strength Cond. Res. 2006, 20, 735–739. [Google Scholar] [PubMed]
- Katz, J.S.; Katz, L. Power laws and athletic performance. J. Sport. Sci. 1999, 17, 467–476. [Google Scholar] [CrossRef]
- Savaglio, S.; Carbone, V. Human performances: Scaling in athletic world records. Nature 2000, 404, 244. [Google Scholar] [CrossRef]
- Carbone, V.; Savaglio, S. Scaling laws and forecasting in athletic world records. J. Sport. Sci. 2001, 19, 477–484. [Google Scholar]
- García-Manso, J.M.; Martín-González, J.M. Laws of potency or scale: Its application to the sportive phenomenon. Fit. Perform. J. 2008, 7, 195–202. [Google Scholar] [CrossRef]
- Dekerle, J.; Nesi, X.; Carter, H. The distance-Time relationship over a century of running Olympic performances: A limit on the critical speed concept. J. Sport. Sci. 2006, 24, 1213–1221. [Google Scholar] [CrossRef]
- Billat, V.; Renoux, J.C.; Pinoteau, J.; Petit, B.; Koralsztein, J.P. Reproducibility of running time to exhaustion at VO2max in subelite runners. Med. Sci. Sport. Exerc. 1994, 26, 254–257. [Google Scholar] [CrossRef]
- Jeukendrup, A.; Saris, W.H.; Brouns, F.; Kester, A.D. A new validated endurance performance test. Med. Sci. Sport. Exerc. 1996, 28, 266–270. [Google Scholar] [CrossRef]
- Hinckson, E.A.; Hopkins, W.G. Reliability of time to exhaustion analysed with critical-power and log-log modeling. Med. Sci. Sport. Exerc. 2005, 37, 696–701. [Google Scholar] [CrossRef]
- Laursen, P.B.; Francis, G.T.; Abbiss, C.R.; Newton, M.J.; Nosaka, K. Reliability of time-to-exhaustion versus time-trial running tests in runners. Med. Sci. Sport. Exerc. 2007, 39, 1374–1379. [Google Scholar] [CrossRef] [PubMed]
- Galbraith, A.; Hopker, J.G.; Jobson, S.A.; Passfield, L. A Novel Field Test to Determine Critical Speed. J. Sport. Med. Doping Stud. 2011, 1, 1–4. [Google Scholar]
- Alberty, M.; Sidney, M.; Huot-Marchand, F.; Dekerle, J.; Bosquet, L.; Gorce, P.; Lensel, G. Reproducibility of performance in three types of training test in swimming. Int. J. Sport. Med. 2006, 27, 623–628. [Google Scholar] [CrossRef][Green Version]
- Galbraith, A.; Hopker, J.; Lelliott, S.; Diddams, L.; Passfield, L. A single-visit field test of critical speed. Int. J. Sport. Physiol. Perform. 2014, 9, 931–935. [Google Scholar] [CrossRef] [PubMed]
- Nimmerichter, A.; Steindl, M.; Williams, C.A. Reliability of the Single-Visit Field Test of Critical Speed in Trained and Untrained Adolescents. Sports 2015, 3, 358–368. [Google Scholar] [CrossRef]
- Vandewalle, H.; Vautier, J.F.; Kachouri, M.; Lechevalier, J.M.; Monod, H. Work-exhaustion time relationships and the critical power concept. A critical review. J. Sport. Med. Phys. Fit. 1997, 37, 89102. [Google Scholar]
- Zinoubi, B.; Vandewalle, H.; Driss, T. Modeling of running performances in humans: Comparison of power laws and critical speed. J. Strength Cond. Res. 2017, 31, 1859–1867. [Google Scholar] [CrossRef]
- Poole, D.C.; Ward, S.A.; Gardner, G.W.; Whipp, B.J. Metabolic and respiratory profile of the upper limit for prolonged exercise in man. Ergonomics 1988, 31, 1265–1279. [Google Scholar] [CrossRef]
- Hill, D.W. The critical power concept. A review. Sport. Med. 1993, 16, 237–254. [Google Scholar] [CrossRef] [PubMed]
- Mattioni Maturana, F.; Fontana, F.Y.; Pogliaghi, S.; Passfield, L.; Muriasa, J.M. Critical power: How different protocols and models affect its determination. J. Sci. Med. Sport. 2018, 21, 742–747. [Google Scholar] [CrossRef]
- Kachouri, M.; Vandewalle, H.; Billat, V.; Huet, M.; Thomaidis, M.; Jousselin, E.; Monod, H. Critical velocity of continuous and intermittent running exercise. An example of the limits of the critical power concept. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 73, 484–487. [Google Scholar] [PubMed]
- Ferguson, C.; Rossiter, H.B.; Whipp, B.J.; Cathcart, A.J.; Murgatroyd, S.R.; Ward, S.A. Effect of recovery duration from prior exhaustive exercise on the parameters of the power-duration relationship. J. Appl. Physiol. 2010, 108, 866–874. [Google Scholar] [CrossRef] [PubMed]
| C1 = 0.9 and C2 = 1 | C1 = 1 and C2 = 0.9 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | tlim 1 | tlim 2 | SCrit | SCritsub | SCritsub/SCrit | SCritsub | SCritsub/SCrit | |
| m.s−1 | m.s−1 | s | S | m.s−1 | m.s−1 | m.s-1 | |||
| A | 4 | 3.0316 | 180 | 720 | 2.709 | 2.750 | 1.015 | 2.659 | 0.982 |
| B | 5 | 3.7895 | 180 | 720 | 3.386 | 3.438 | 1.015 | 3.324 | 0.982 |
| C | 6 | 4.5474 | 180 | 720 | 4.063 | 4.126 | 1.015 | 3.989 | 0.982 |
| D | 4 | 3.0316 | 240 | 960 | 2.709 | 2.750 | 1.015 | 2.659 | 0.982 |
| E | 5 | 3.7895 | 240 | 960 | 3.386 | 3.438 | 1.015 | 3.324 | 0.982 |
| F | 6 | 4.5474 | 240 | 960 | 4.063 | 4.126 | 1.015 | 3.989 | 0.982 |
| C1 = 0.9 and C2 = 1 | C1 = 1 and C2 = 0.9 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | tlim 1 | tlim 2 | PCrit | PCritsub | PCritsub/PCrit | PCritsub | PCritsub/PCrit | |
| W | W | S | S | W | W | W | |||
| A | 240 | 182 | 180 | 720 | 163 | 165 | 1.015 | 160 | 0.982 |
| B | 320 | 243 | 180 | 720 | 217 | 220 | 1.015 | 213 | 0.982 |
| C | 400 | 303 | 180 | 720 | 271 | 275 | 1.015 | 266 | 0.982 |
| D | 240 | 182 | 240 | 960 | 163 | 165 | 1.015 | 160 | 0.982 |
| E | 320 | 243 | 240 | 960 | 217 | 220 | 1.015 | 213 | 0.982 |
| F | 400 | 303 | 240 | 960 | 271 | 275 | 1.015 | 266 | 0.982 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vandewalle, H. Effects of Submaximal Performances on Critical Speed and Power: Uses of an Arbitrary-Unit Method with Different Protocols. Sports 2019, 7, 136. https://doi.org/10.3390/sports7060136
Vandewalle H. Effects of Submaximal Performances on Critical Speed and Power: Uses of an Arbitrary-Unit Method with Different Protocols. Sports. 2019; 7(6):136. https://doi.org/10.3390/sports7060136
Chicago/Turabian StyleVandewalle, Henry. 2019. "Effects of Submaximal Performances on Critical Speed and Power: Uses of an Arbitrary-Unit Method with Different Protocols" Sports 7, no. 6: 136. https://doi.org/10.3390/sports7060136
APA StyleVandewalle, H. (2019). Effects of Submaximal Performances on Critical Speed and Power: Uses of an Arbitrary-Unit Method with Different Protocols. Sports, 7(6), 136. https://doi.org/10.3390/sports7060136





