Changes in Dynamic Strength Index in Response to Strength Training
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Analysis
2.2. Training Intervention
2.3. Statistical Analyses
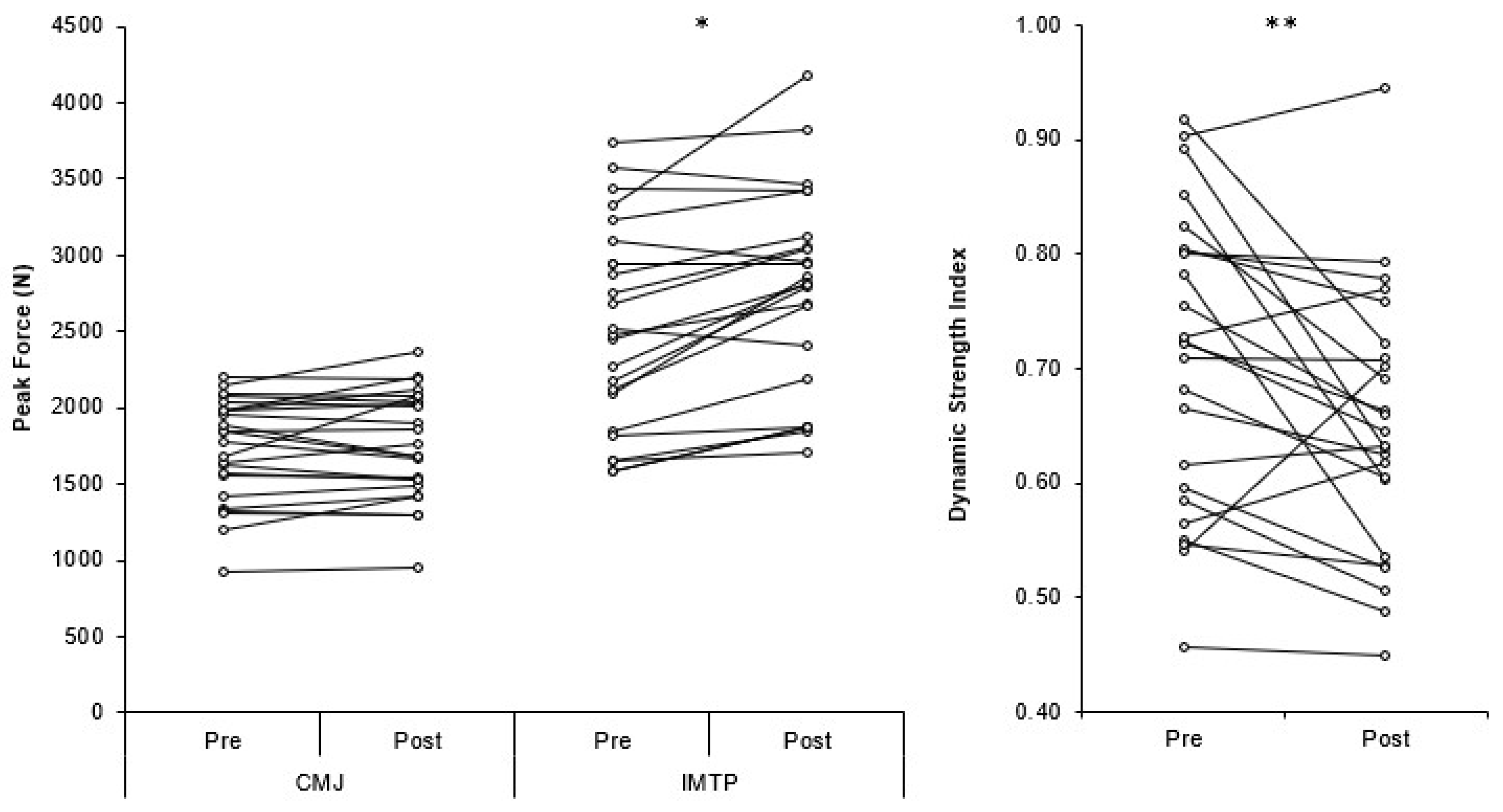
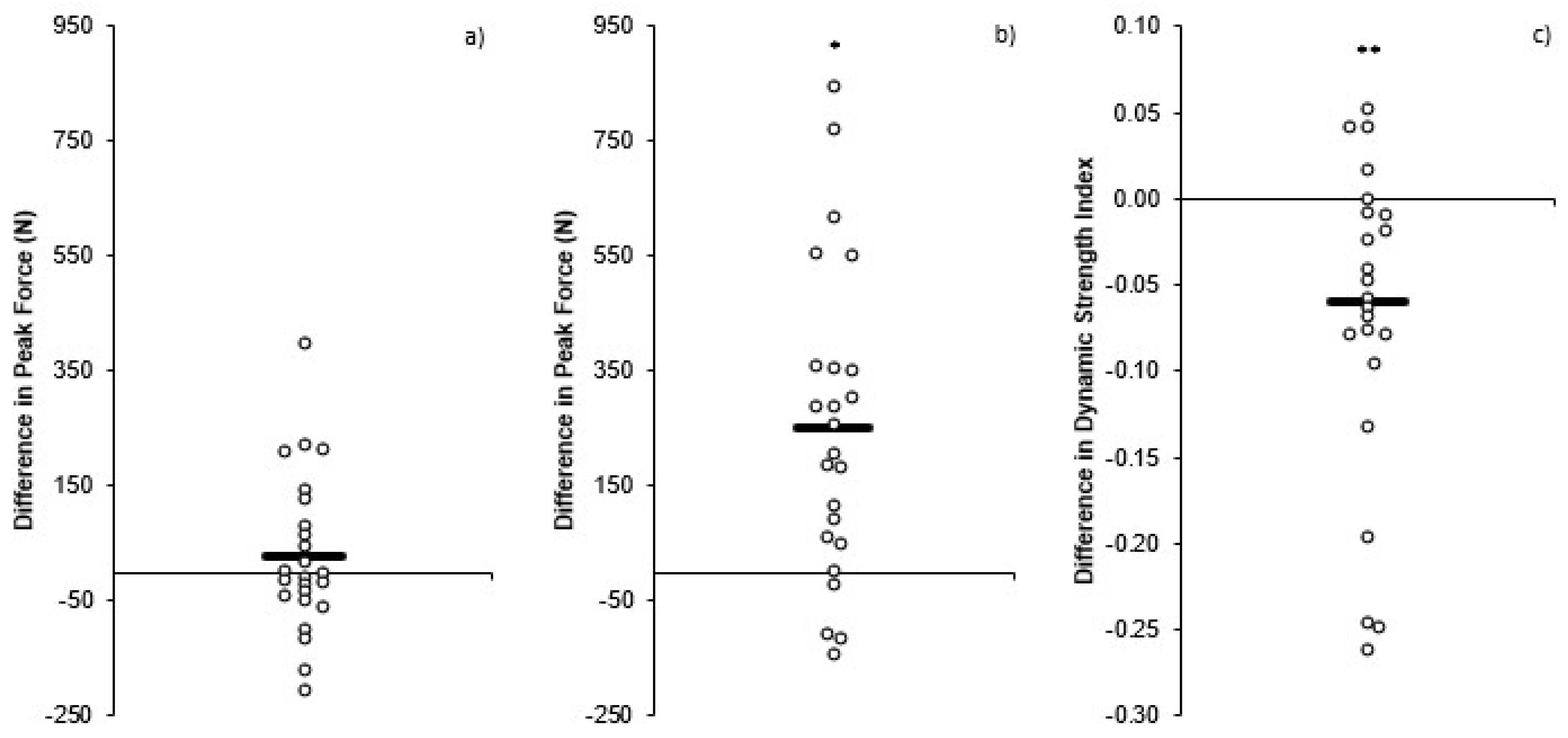
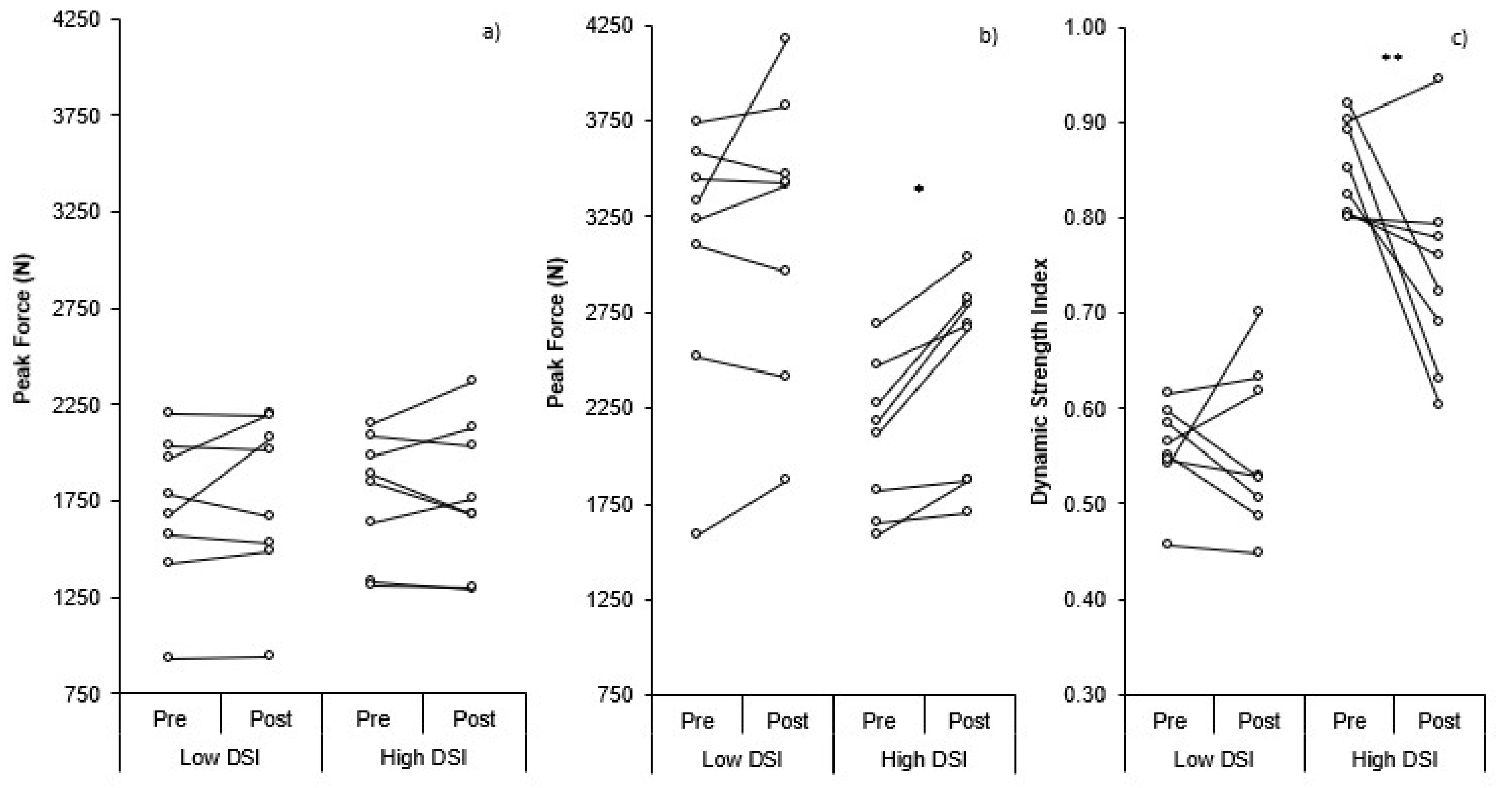
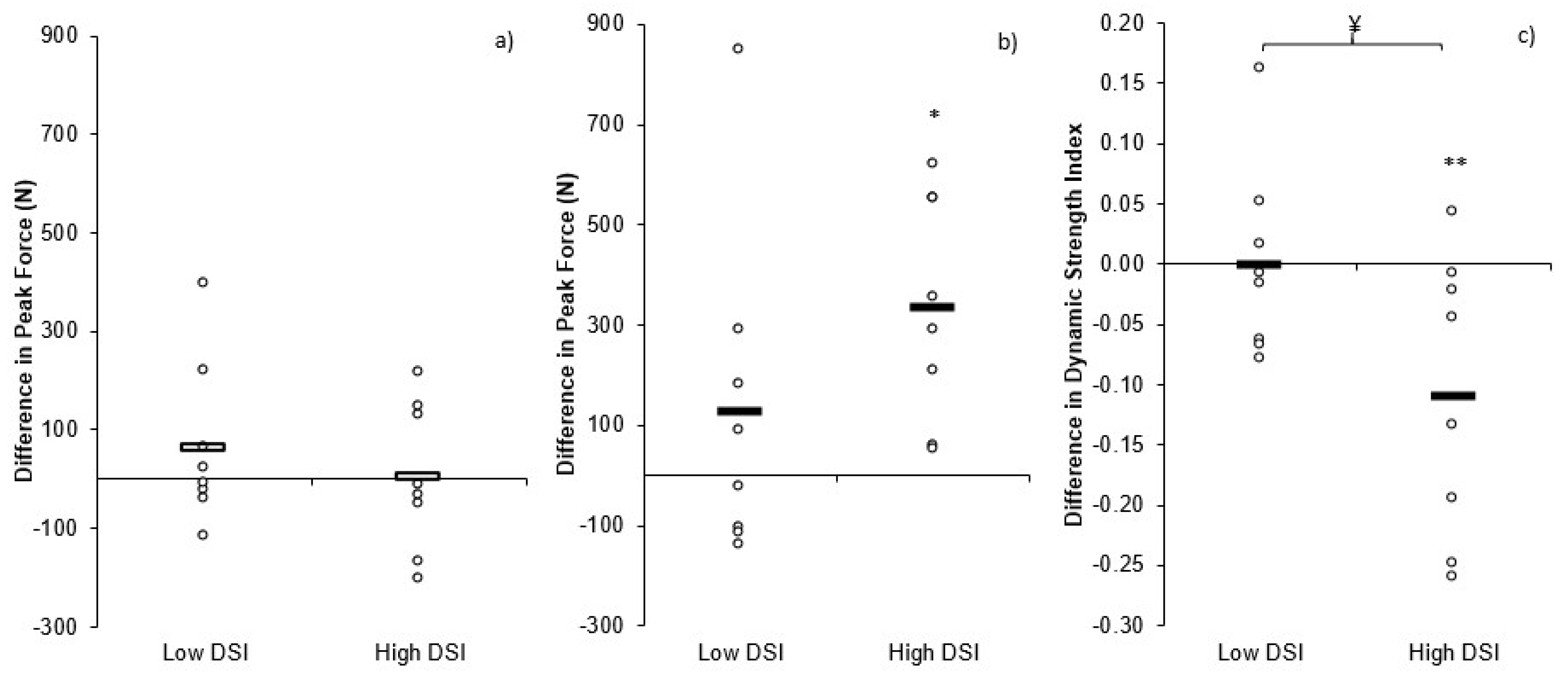
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- DeWeese, B.H.; Hornsby, G.; Stone, M.; Stone, M.H. The training process: Planning for strength–power training in track and field. Part 2: Practical and applied aspects. J. Sport Health Sci. 2015, 4, 318–324. [Google Scholar] [CrossRef]
- McMahon, J.J.; Murphy, S.; Rej, S.J.; Comfort, P. Countermovement-Jump-Phase Characteristics of Senior and Academy Rugby League Players. Int. J. Sports Physiol. Perform. 2017, 12, 803–811. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the Key Phases of the Countermovement Jump Force-Time Curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
- McLellan, C.P.; Lovell, D.I. Neuromuscular Responses to Impact and Collision During Elite Rugby League Match Play. J. Strength Cond. Res. 2012, 26, 1431–1440. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.; Lake, J.; Comfort, P. Reliability of and Relationship between Flight Time to Contraction Time Ratio and Reactive Strength Index Modified. Sports 2018, 6, 81. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.J.; Rej, S.J.; Comfort, P. Sex Differences in Countermovement Jump Phase Characteristics. Sports 2017, 5, 8. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.J.; Jones, P.A.; Suchomel, T.J.; Lake, J.; Comfort, P. Influence of Reactive Strength Index Modified on Force- and Power-Time Curves. Int. J. Sports Physiol. Perform. 2018, 13, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Gathercole, R.; Sporer, B.; Stellingwerff, T.; Sleivert, G. Alternative countermovement-jump analysis to quantify acute neuromuscular fatigue. Int. J. Sports Physiol. Perform. 2015, 10, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Beckham, G.; Mizuguchi, S.; Carter, C.; Sato, K.; Ramsey, M.; Lamont, H.; Hornsby, G.; Haff, G.; Stone, M. Relationships of isometric mid-thigh pull variables to weightlifting performance. J. Sports Med. Phys. Fit. 2013, 53, 573–581. [Google Scholar]
- Thomas, C.; Comfort, P.; Chiang, C.Y.; Jones, P.A. Relationship between isometric mid-thigh pull variables and sprint and change of direction performance in collegiate athletes. J. Trainol. 2015, 4, 6–10. [Google Scholar] [CrossRef]
- McGuigan, M.; Winchester, J.B. The relationship between isometric and dynamic strength in collegiate football players. J. Sports Sci. Med. 2008, 7, 101–105. [Google Scholar] [PubMed]
- Mcguigan, M.R.; Newton, M.J.; Winchester, J.B.; Nelson, A.G. Relationship between isometric and dynamic strength in recreationally trained men. J. Strength Cond. Res. 2010, 24, 2570–2573. [Google Scholar] [CrossRef] [PubMed]
- Secomb, J.L.; Nimphius, S.; Farley, O.R.; Lundgren, L.E.; Tran, T.T.; Sheppard, J.M. Relationships Between Lower-Body Muscle Structure and, Lower-Body Strength, Explosiveness and Eccentric Leg Stiffness in Adolescent Athletes. J. Sports Sci. Med. 2015, 14, 691–697. [Google Scholar] [PubMed]
- Thomas, C.; Jones, P.A.; Comfort, P. Reliability of the Dynamic Strength Index in Collegiate Athletes. Int. J. Sports Physiol. Perform. 2015, 10, 542–545. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, J.M.; Chapman, D.W.; Taylor, K. An evaluation of a strength qualities assessment method for the lower body. J. Aust. Strength Cond. 2011, 19, 4–10. [Google Scholar]
- Comfort, P.; Thomas, C.; Dos’Santos, T.; Jones, P.A.; Suchomel, T.J.; McMahon, J.J. Comparison of Methods of Calculating Dynamic Strength Index. Int. J. Sports Physiol. Perform. 2018, 13, 320–325. [Google Scholar] [CrossRef] [PubMed]
- Thomas, C.; Dos’Santos, T.; Jones, P.A. A Comparison of Dynamic Strength Index between Team-Sport Athletes. Sports 2017, 5, 71. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.J.; Jones, P.A.; Dos’Santos, T.; Comfort, P. Influence of Dynamic Strength Index on Countermovement Jump Force-, Power-, Velocity-, and Displacement-Time Curves. Sports 2017, 5, 72. [Google Scholar] [CrossRef] [PubMed]
- Owen, N.J.; Watkins, J.; Kilduff, L.P.; Bevan, H.R.; Bennett, M.A. Development of a criterion method to determine peak mechanical power output in a countermovement jump. J. Strength Cond. Res. 2014, 28, 1552–1558. [Google Scholar] [CrossRef] [PubMed]
- Moir, G.L. Three Different Methods of Calculating Vertical Jump Height from Force Platform Data in Men and Women. Meas. Phys. Educ. Exerc. Sci. 2014, 12, 207–218. [Google Scholar] [CrossRef]
- Street, G.; McMillan, S.; Board, W.; Rasmussen, M.; Heneghan, J.M. Sources of Error in Determining Countermovement Jump Height with the Impulse Method. J. Appl. Biomech. 2001, 17, 43–54. [Google Scholar] [CrossRef]
- Dos’Santos, T.; Lake, J.; Jones, P.A.; Comfort, P. Effect of low pass filtering on isometric mid-thigh pull kinetics. J. Strength Cond. Res. 2018, 32, 983–989. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Ruben, R.P.; Lider, J.; Twine, C.; Cormie, P. A Comparison of Methods for Determining the Rate of Force Development During Isometric Mid-Thigh Clean Pulls. J. Strength Cond. Res. 2015, 29, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Stone, M.; O’bryant, H.S.; Harman, E.; Dinan, C.; Johnson, R.; Han, K.H. Force-Time Dependent Characteristics of Dynamic and Isometric Muscle Actions. J. Strength Cond. Res. 1997, 11, 269–272. [Google Scholar]
- Halperin, I.; Williams, K.J.; Martin, D.T.; Chapman, D.W. The Effects of Attentional Focusing Instructions on Force Production During the Isometric Midthigh Pull. J. Strength Cond. Res. 2016, 30, 919–923. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Carlock, J.M.; Hartman, M.J.; Kilgore, J.L. Force-time curve characteristics of dynamic and isometric muscle actions of elite women olympic weightlifters. J. Strength Cond. Res. 2005, 19, 741–748. [Google Scholar] [PubMed]
- Dos’Santos, T.; Jones, P.A.; Kelly, J.; McMahon, J.J.; Comfort, P.; Thomas, C. Effect of Sampling Frequency on Isometric Midthigh-Pull Kinetics. Int. J. Sports Physiol. Perform. 2016, 11, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Comfort, P.; Dos’Santos, T.; Thomas, C.; McMahon, J.J.; Suchomel, T.J. An Investigation into the Effects of Excluding the Catch Phase of the Power Clean on Force-Time Characteristics during Isometric and Dynamic Tasks: An Intervention Study. J. Strength Cond. Res. 2018, 32, 2116–2129. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.; Marshall, S.; Batterham, A.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Cormack, S.J.; Newton, R.U.; McGuigan, M.R.; Doyle, T.L. Reliability of measures obtained during single and repeated countermovement jumps. Int. J. Sports Physiol. Perform. 2008, 3, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G. A Scale of Magnitudes of Effect Statistics. Sportsci.org [Website] 2002 7th August. 2006. Available online: http://sportsci.org/resource/stats/index.html (accessed on 18 January 2018).
- Cormie, P.; McGuigan, M.R.; Newton, R.U. Influence of strength on magnitude and mechanisms of adaptation to power training. Med. Sci. Sports Exerc. 2010, 42, 1566–1581. [Google Scholar] [CrossRef] [PubMed]
- Cormie, P.; McGuigan, M.R.; Newton, R.U. Adaptations in athletic performance after ballistic power versus strength training. Med. Sci. Sports Exerc. 2010, 42, 1582–1598. [Google Scholar] [CrossRef] [PubMed]
| Day 1 | ||||
|---|---|---|---|---|
| Exercise | Week 1 | Week 2 | Week 3 | Week 4 |
| Power Clean | 3 × 3 @ 80% | 3 × 3 @ 85% | 3 × 3 @ 90% | 3 × 3 @ 75% |
| Push Press | 3 × 3 @ 80% | 3 × 3 @ 82.5% | 3 × 3 @ 85% | 3 × 3 @ 75% |
| Back Squat | 3 × 3 @ 85% | 3 × 3 @ 87.5% | 3 × 3 @ 90% | 3 × 3 @ 75% |
| Nordic Lowers | 2 × 3 BW | 3 × 3 BW | 3 × 3 BW | 3 × 3 BW |
| Day 2 | ||||
| Mid-thigh Pull | 3 × 3 @ 80% | 3 × 3 @ 82.5% | 3 × 3 @ 85% | 3 × 3 @ 75% |
| RDL | 3 × 3 @ 80% | 3 × 3 @ 82.5% | 3 × 3 @ 85% | 3 × 3 @ 75% |
| Independent Variable | ICC (95% CI) | %CV |
|---|---|---|
| CMJ Height | 0.986 (0.972–0.993) | 3.89 |
| CMJ Peak Force | 0.993 (0.986–0.997) | 3.14 |
| CMJ Time to Take-off | 0.978 (0.943–0.983) | 4.53 |
| IMTP Peak Force | 0.994 (0.989–0.997) | 3.58 |
| Dynamic Strength Index | 0.970 (0.940–0.986) | 4.69 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comfort, P.; Thomas, C.; Dos’Santos, T.; Suchomel, T.J.; Jones, P.A.; McMahon, J.J. Changes in Dynamic Strength Index in Response to Strength Training. Sports 2018, 6, 176. https://doi.org/10.3390/sports6040176
Comfort P, Thomas C, Dos’Santos T, Suchomel TJ, Jones PA, McMahon JJ. Changes in Dynamic Strength Index in Response to Strength Training. Sports. 2018; 6(4):176. https://doi.org/10.3390/sports6040176
Chicago/Turabian StyleComfort, Paul, Christopher Thomas, Thomas Dos’Santos, Timothy J. Suchomel, Paul A. Jones, and John J. McMahon. 2018. "Changes in Dynamic Strength Index in Response to Strength Training" Sports 6, no. 4: 176. https://doi.org/10.3390/sports6040176
APA StyleComfort, P., Thomas, C., Dos’Santos, T., Suchomel, T. J., Jones, P. A., & McMahon, J. J. (2018). Changes in Dynamic Strength Index in Response to Strength Training. Sports, 6(4), 176. https://doi.org/10.3390/sports6040176








