Effects of Different Moments of Inertia on Neuromuscular Performance in Elite Female Soccer Players During Hip Extension Exercise to Prevent Hamstring Asymmetries and Injuries: A Cross-Sectional Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Study Population
2.3. Data Collection
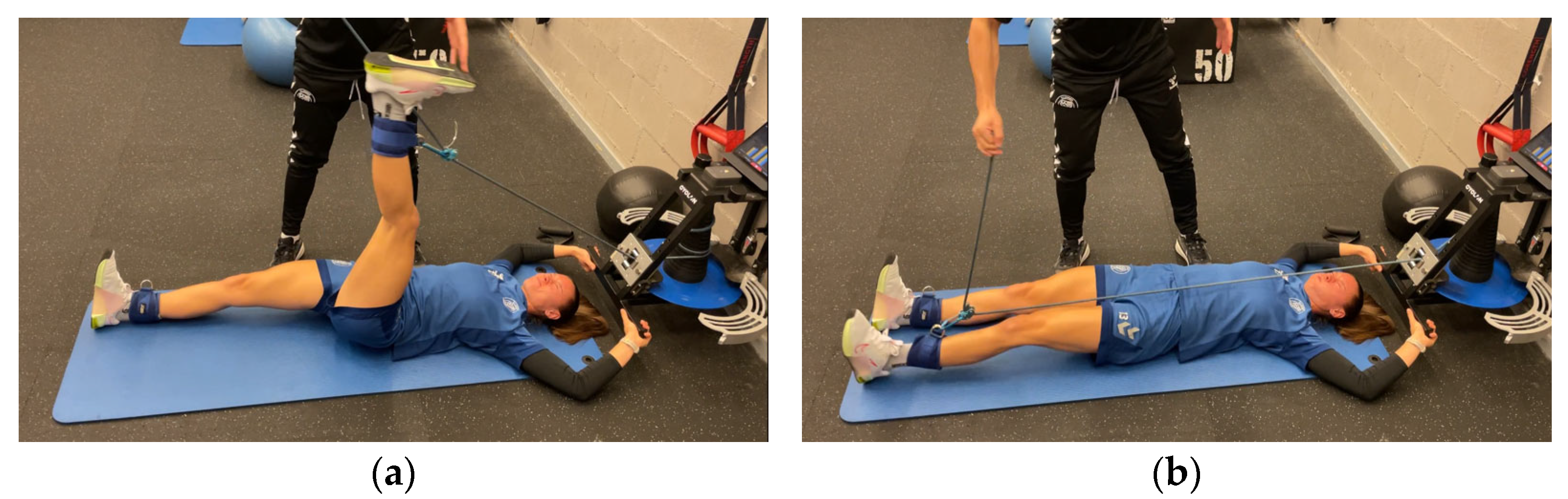
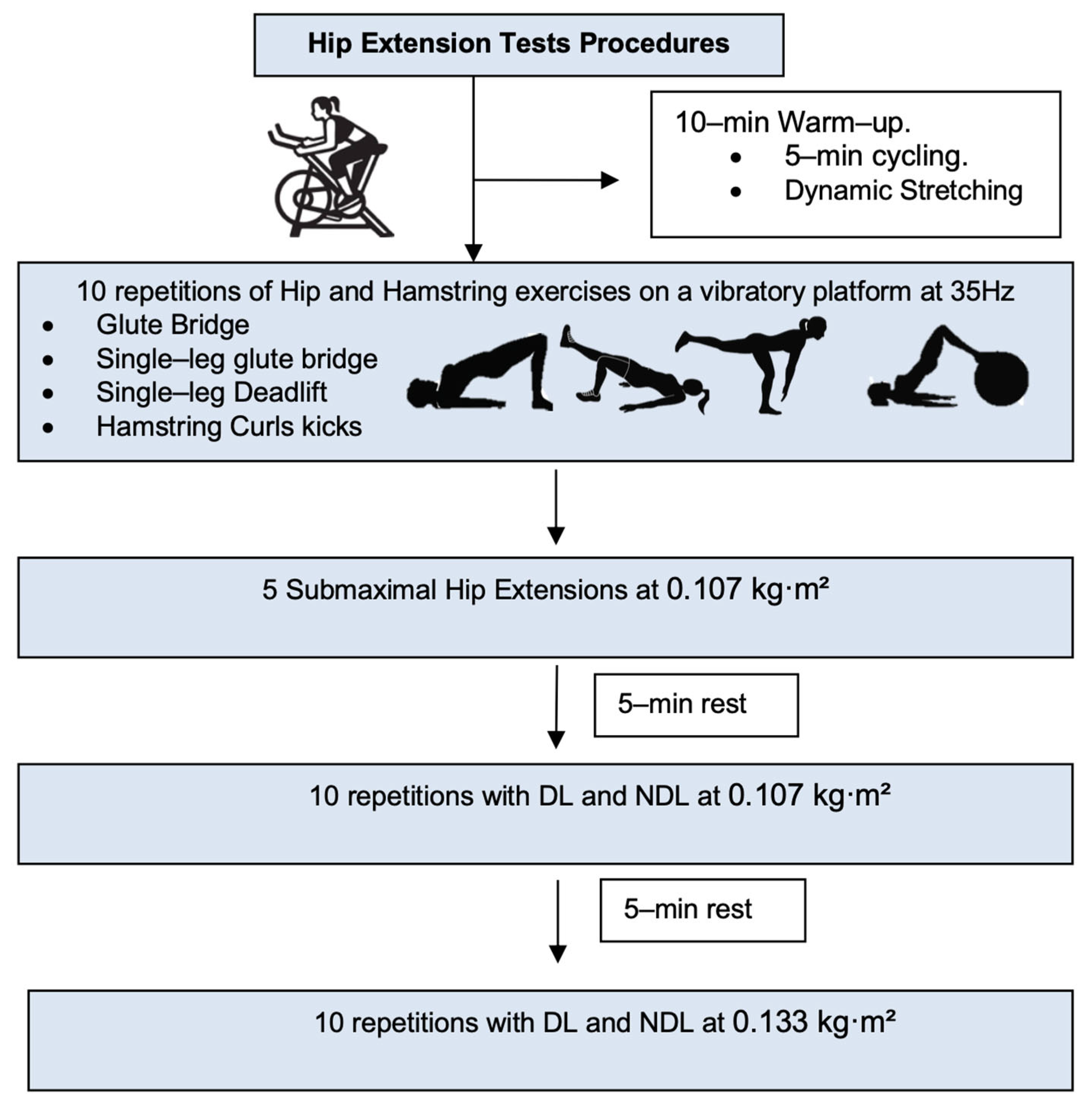
2.4. Testing Procedures
2.5. Statistical Analysis
3. Results
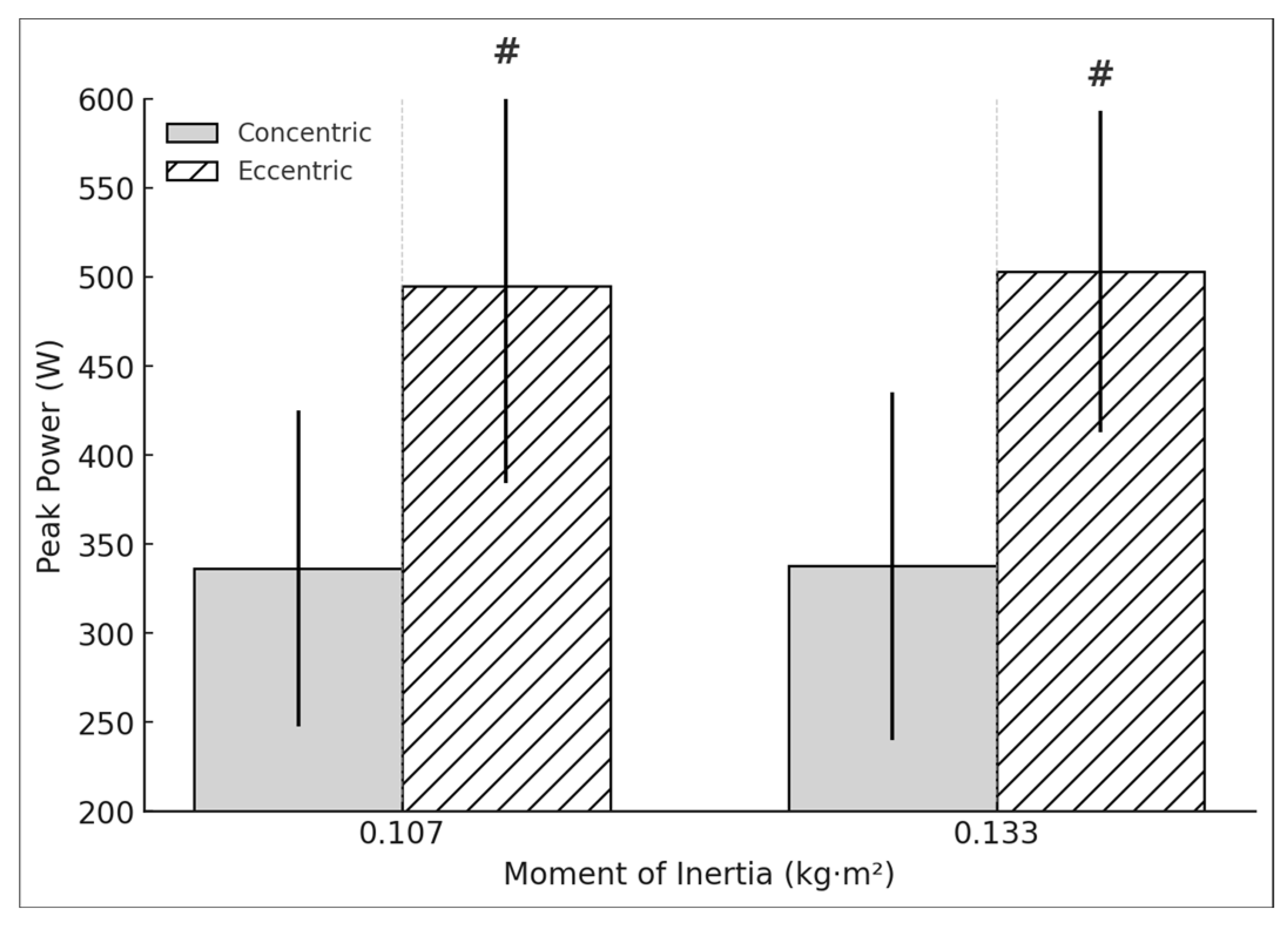
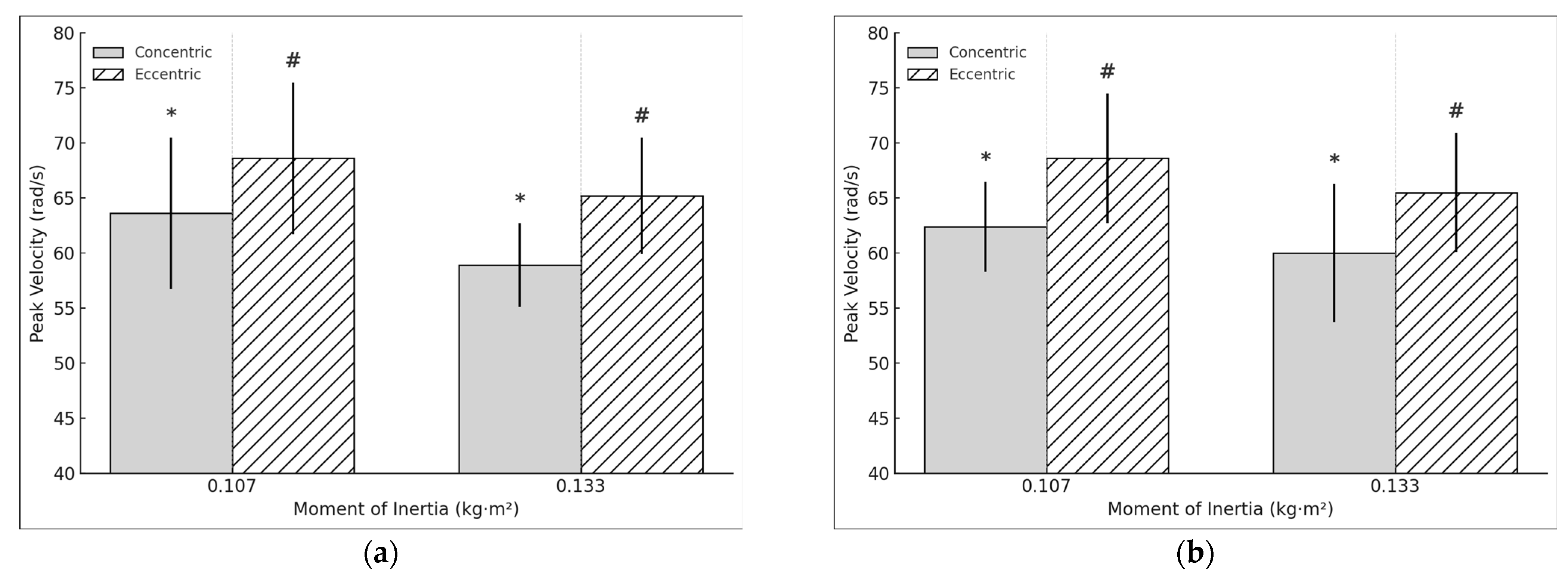
3.1. Peak Mechanical Outputs Dominant and Non-Dominant Limb Comparisons with Different Moments of Inertia (0.107 kg·m2 and 0.133 kg·m2)
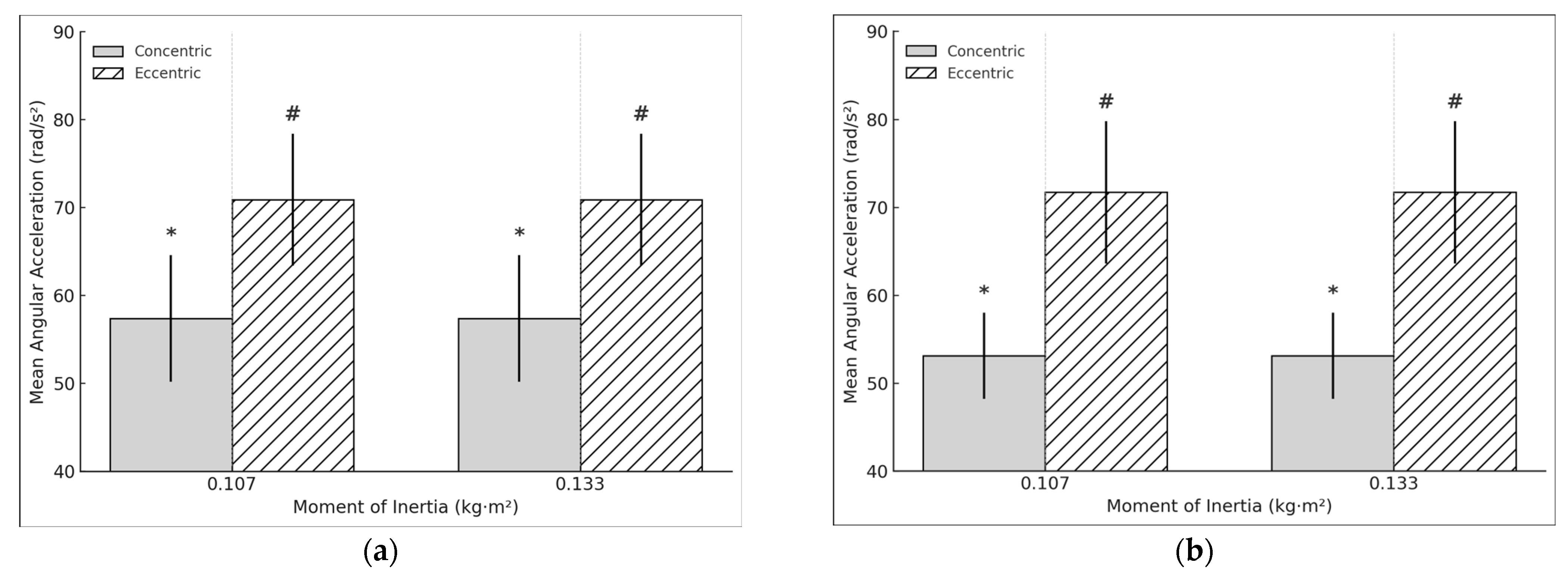
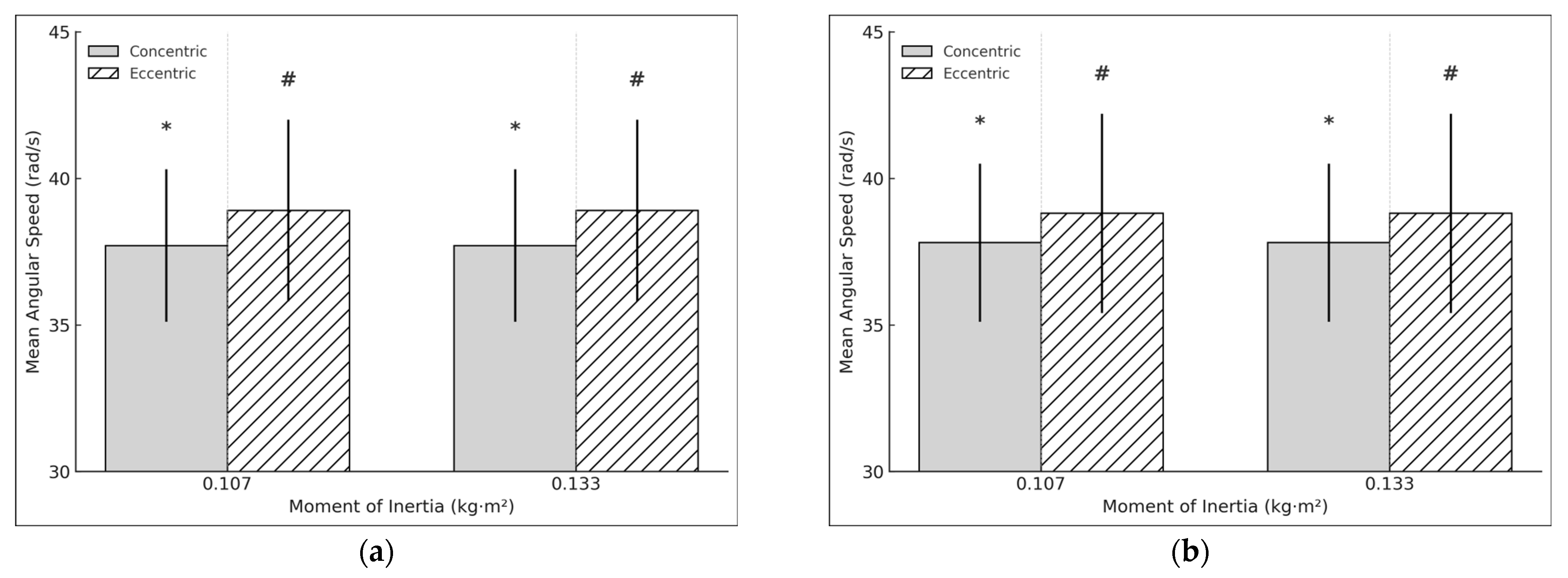
3.2. Mean Mechanical Outputs Dominant and Non-Dominant Limb Comparisons with Different Moments of Inertia (0.107 kg·m2 and 0.133 kg·m2)
4. Discussion
4.1. Practical Implications
4.2. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Griffin, J.; Newans, T.; Horan, S.; Keogh, J.; Andreatta, M.; Minahan, C. Acceleration and High-Speed Running Profiles of Women’s International and Domestic Football Matches. Front. Sport Act. Living 2021, 3, 604605. [Google Scholar] [CrossRef] [PubMed]
- Trewin, J.; Meylan, C.; Varley, M.C.; Cronin, J.; Ling, D. Effect of Match Factors on the Running Performance of Elite Female Soccer Players. J. Strength Cond. Res. 2018, 32, 2002–2009. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Turner, A.; Maloney, S.; Lake, J.; Loturco, I.; Bromley, T.; Read, P. Drop Jump Asymmetry Is Associated with Reduced Sprint and Change-of-Direction Speed Performance in Adult Female Soccer Players. Sports 2019, 7, 29. [Google Scholar] [CrossRef]
- Bishop, C.; Read, P.; McCubbine, J.; Turner, A. Vertical and Horizontal Asymmetries Are Related to Slower Sprinting and Jump Performance in Elite Youth Female Soccer Players. J. Strength Cond. Res. 2018, 1, 56–63. [Google Scholar] [CrossRef]
- Moreno-Azze, A.; Arjol-Serrano, J.L.; Falcón-Miguel, D.; Bishop, C.; Gonzalo-Skok, O. Effects of Three Different Combined Training Interventions on Jump, Change of Direction, Power Performance, and Inter-Limb Asymmetry in Male Youth Soccer Players. Sports 2021, 9, 158. [Google Scholar] [CrossRef]
- Beato, M.; Dello Iacono, A. Implementing Flywheel (Isoinertial) Exercise in Strength Training: Current Evidence, Practical Recommendations, and Future Directions. Front. Physiol. 2020, 11, 569. [Google Scholar] [CrossRef] [PubMed]
- Suchomel, T.J.; Nimphius, S.; Bellon, C.R.; Stone, M.H. The Importance of Muscular Strength: Training Considerations. Sport Med. 2018, 48, 765–785. [Google Scholar] [CrossRef]
- Norrbrand, L.; Pozzo, M.; Tesch, P.A. Flywheel Resistance Training Calls for Greater Eccentric Muscle Activation than Weight Training. Eur. J. Appl. Physiol. 2010, 110, 997–1005. [Google Scholar] [CrossRef]
- Suchomel, T.J.; Wagle, J.P.; Douglas, J.; Taber, C.B.; Harden, M.; Gregory Haff, G.; Stone, M.H. Implementing Eccentric Resistance Training—Part 1: A Brief Review of Existing Methods. J. Funct. Morphol. Kinesiol. 2019, 4, 38. [Google Scholar] [CrossRef]
- Allen, W.J.C.; De Keijzer, K.L.; Raya-González, J.; Castillo, D.; Coratella, G.; Beato, M. Chronic Effects of Flywheel Training on Physical Capacities in Soccer Players: A Systematic Review. Res. Sport. Med. 2021, 31, 228–248. [Google Scholar] [CrossRef]
- Nuñez Sanchez, F.J.; De Villarreal, E.S. Does Flywheel Paradigm Training Improve Muscle Volume and Force? A Meta-Analysis. J. Strength Cond. Res. 2017, 31, 3177–3186. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-López, A.; De Souza Fonseca, F.; Ramírez-Campillo, R.; Gantois, P.; Javier Nuñez, F.; Nakamura, F.Y. The Use of Real-Time Monitoring during Flywheel Resistance Training Programmes: How Can We Measure Eccentric Overload? A Systematic Review and Meta-Analysis. Biol. Sport 2021, 38, 639–652. [Google Scholar] [CrossRef] [PubMed]
- Sabido, R.; Hernández-Davó, J.L.; Pereyra-Gerber, G.T. Influence of Different Inertial Loads on Basic Training Variables during the Flywheel Squat Exercise. Int. J. Sports Physiol. Perform. 2018, 13, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-López, A.; Floría, P.; Sañudo, B.; Pecci, J.; Pérez, J.C.; Pozzo, M. The Maximum Flywheel Load: A Novel Index to Monitor Loading Intensity of Flywheel Devices. Sensors 2021, 21, 8124. [Google Scholar] [CrossRef]
- Brien, J.O.; Browne, D.; Earls, D.; Lodge, C. The Effects of Varying Inertial Loadings on Power Variables in the Flywheel Romanian Deadlift Exercise. Biol. Sport 2021, 39, 499–503. [Google Scholar] [CrossRef]
- Martinez-Aranda, L.M.; Fernandez-Gonzalo, R. Effects of Inertial Setting on Power, Force, Work, and Eccentric Overload during Flywheel Resistance Exercise in Women and Men. J. Strength Cond. Res. 2017, 31, 1653–1661. [Google Scholar] [CrossRef]
- Piqueras-Sanchiz, F.; Sabido, R.; Raya-González, J.; Madruga-Parera, M.; Romero-Rodríguez, D.; Beato, M.; de Hoyo, M.; Nakamura, F.Y.; Hernández-Davó, J.L. Effects of Different Inertial Load Settings on Power Output Using a Flywheel Leg Curl Exercise and Its Inter-Session Reliability. J. Hum. Kinet. 2020, 74, 215–226. [Google Scholar] [CrossRef]
- Ono, T.; Okuwaki, T.; Fukubayashi, T. Differences in Activation Patterns of Knee Flexor Muscles during Concentric and Eccentric Exercises. Res. Sport. Med. 2010, 18, 188–198. [Google Scholar] [CrossRef]
- Presland, J.D.; Opar, D.A.; Williams, M.D.; Hickey, J.T.; Maniar, N.; Lee Dow, C.; Bourne, M.N.; Timmins, R.G. Hamstring Strength and Architectural Adaptations Following Inertial Flywheel Resistance Training. J. Sci. Med. Sport 2020, 23, 1093–1099. [Google Scholar] [CrossRef]
- de Keijzer, K.L.; Gonzalez, J.R.; Beato, M. The Effect of Flywheel Training on Strength and Physical Capacities in Sporting and Healthy Populations: An Umbrella Review. PLoS ONE 2022, 17, e0264375. [Google Scholar] [CrossRef]
- Beato, M.; Maroto-Izquierdo, S.; Turner, A.N.; Bishop, C. Implementing Strength Training Strategies for Injury Prevention in Soccer: Scientific Rationale and Methodological Recommendations. Int. J. Sports Physiol. Perform. 2020, 16, 456–461. [Google Scholar] [CrossRef]
- Nuñez, F.J.; de Hoyo, M.; Muñoz López, A.; Sañudo, B.; Otero-Esquina, C.; Sanchez, H.; Gonzalo-Skok, O. Eccentric-Concentric Ratio: A Key Factor for Defining Strength Training in Soccer. Int. J. Sport Med. 2019, 40, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Cuschieri, S. The STROBE Guidelines. Saudi J. Anaesth. 2019, 13, S31–S34. [Google Scholar] [CrossRef] [PubMed]
- World Medical Association. World Medical Association Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. J. Am. Med. Assoc. 2013, 310, 2191–2194. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef]
- Maroto-Izquierdo, S.; Raya-González, J.; Hernández-Davó, J.L.; Beato, M. Load Quantification and Testing Using Flywheel Devices in Sports. Front. Physiol. 2021, 12, 739399. [Google Scholar] [CrossRef]
- Tous-Fajardo, J.; Maldonado, R.A.; Quintana, J.M.; Pozzo, M.; Tesch, P.A. The Flywheel Leg-Curl Machine: Offering Eccentric Overload for Hamstring Development. Int. J. Sports Physiol. Perform. 2006, 1, 293–298. [Google Scholar] [CrossRef]

| Variables | Mean ± SD |
|---|---|
| Age (years) | 27 ± 4 |
| Weight (kg) | 59.9 ± 6.5 |
| Height (cm) | 168.2 ± 6.3 |
| IMC | 21.2 ± 1.8 |
| Inclusion Criteria |
|---|
|
| Load (kg·m2) | ||||
|---|---|---|---|---|
| Variable | 0.107 | 0.133 | ||
| Concentric | Eccentric | Concentric | Eccentric | |
| Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | |
| DL Power | 316.8 | 503 | 350.7 | 511 |
| (W) | (49.9) | (114.3) | (111.9) | (91.6) |
| NDL Power | 336.2 | 495.1 | 337.7 | 503 |
| (W) | (88.7) | (110.9) | (97.7) | (90.5) |
| DL Angular acceleration | 246.1 | 477.2 | 192.3 | 390.2 |
| (rad/s2) | (53.9) | (82.5) | (20.7) | (42.5) |
| NDL Angular acceleration | 234.3 | 443.1 | 194.9 | 395.8 |
| (rad/s2) | (41.9) | (57.1) | (25.1) | (54.2) |
| DL Angular Speed | 63.6 | 68.6 | 58.9 | 65.2 |
| (rad/s) | (6.9) | (6.9) | (3.8) | (5.3) |
| NDL Angular speed | 62.4 | 68.6 | 60 | 65.5 |
| (rad/s) | (4.1) | (5.9) | (6.3) | (5.4) |
| Load (kg·m2) | ||||
|---|---|---|---|---|
| Variable | 0.107 | 0.133 | ||
| Concentric | Eccentri | Concentric | Eccentric | |
| Mean (SD) | Mean (SD)c | Mean (SD) | Mean (SD) | |
| DL Power | 155.8 | 173.8 | 153.9 | 173.8 |
| (W) | (24.2) | (27.2) | (22.1) | (27.3) |
| NDL Power | 149.7 | 172.1 | 149.7 | 172.1 |
| (W) | (23.9) | (29.7) | (23.9) | (29.7) |
| DL Angular acceleration | 57.4 | 70.9 | 57.4 | 70.9 |
| (rad/s2) | (7.2) | (7.5) | (7.2) | (7.5) |
| NDL Angular acceleration | 53.1 | 71.7 | 53.1 | 71.7 |
| (rad/s2) | (4.9) | (8.1) | (4.9) | (8.1) |
| DL Angular Speed | 37.7 | 38.9 | 37.7 | 38.9 |
| (rad/s) | (2.6) | (3.1) | (2.6) | (3.1) |
| NDL Angular speed | 37.8 | 38.8 | 37.8 | 38.8 |
| (rad/s) | (2.7) | (3.4) | (2.7) | (3.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pumarola, J.; Badiola-Zabala, A.; Solana-Tramunt, M. Effects of Different Moments of Inertia on Neuromuscular Performance in Elite Female Soccer Players During Hip Extension Exercise to Prevent Hamstring Asymmetries and Injuries: A Cross-Sectional Study. Sports 2025, 13, 212. https://doi.org/10.3390/sports13070212
Pumarola J, Badiola-Zabala A, Solana-Tramunt M. Effects of Different Moments of Inertia on Neuromuscular Performance in Elite Female Soccer Players During Hip Extension Exercise to Prevent Hamstring Asymmetries and Injuries: A Cross-Sectional Study. Sports. 2025; 13(7):212. https://doi.org/10.3390/sports13070212
Chicago/Turabian StylePumarola, Jordi, Alesander Badiola-Zabala, and Mònica Solana-Tramunt. 2025. "Effects of Different Moments of Inertia on Neuromuscular Performance in Elite Female Soccer Players During Hip Extension Exercise to Prevent Hamstring Asymmetries and Injuries: A Cross-Sectional Study" Sports 13, no. 7: 212. https://doi.org/10.3390/sports13070212
APA StylePumarola, J., Badiola-Zabala, A., & Solana-Tramunt, M. (2025). Effects of Different Moments of Inertia on Neuromuscular Performance in Elite Female Soccer Players During Hip Extension Exercise to Prevent Hamstring Asymmetries and Injuries: A Cross-Sectional Study. Sports, 13(7), 212. https://doi.org/10.3390/sports13070212







