Comparative Analysis of Speed-Power Performance and Sport-Specific Skills Among Elite Youth Soccer Players with Different Start Procedures
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Approval
2.2. Participants and Allocation
2.3. Inclusion Criteria
- -
- Participation in regular soccer training for at least 12 months;
- -
- Consistent membership of high-level organised soccer teams.
2.4. Exclusion Criteria
- -
- Presence of injury or illness resulting in absence from more than three training sessions within three months prior to the study;
- -
- Withdrawal from the study at any time;
- -
- Persistence of an injury that prevented full participation in the study.
2.5. Testing Conditions
2.6. Anthropometric Measurements
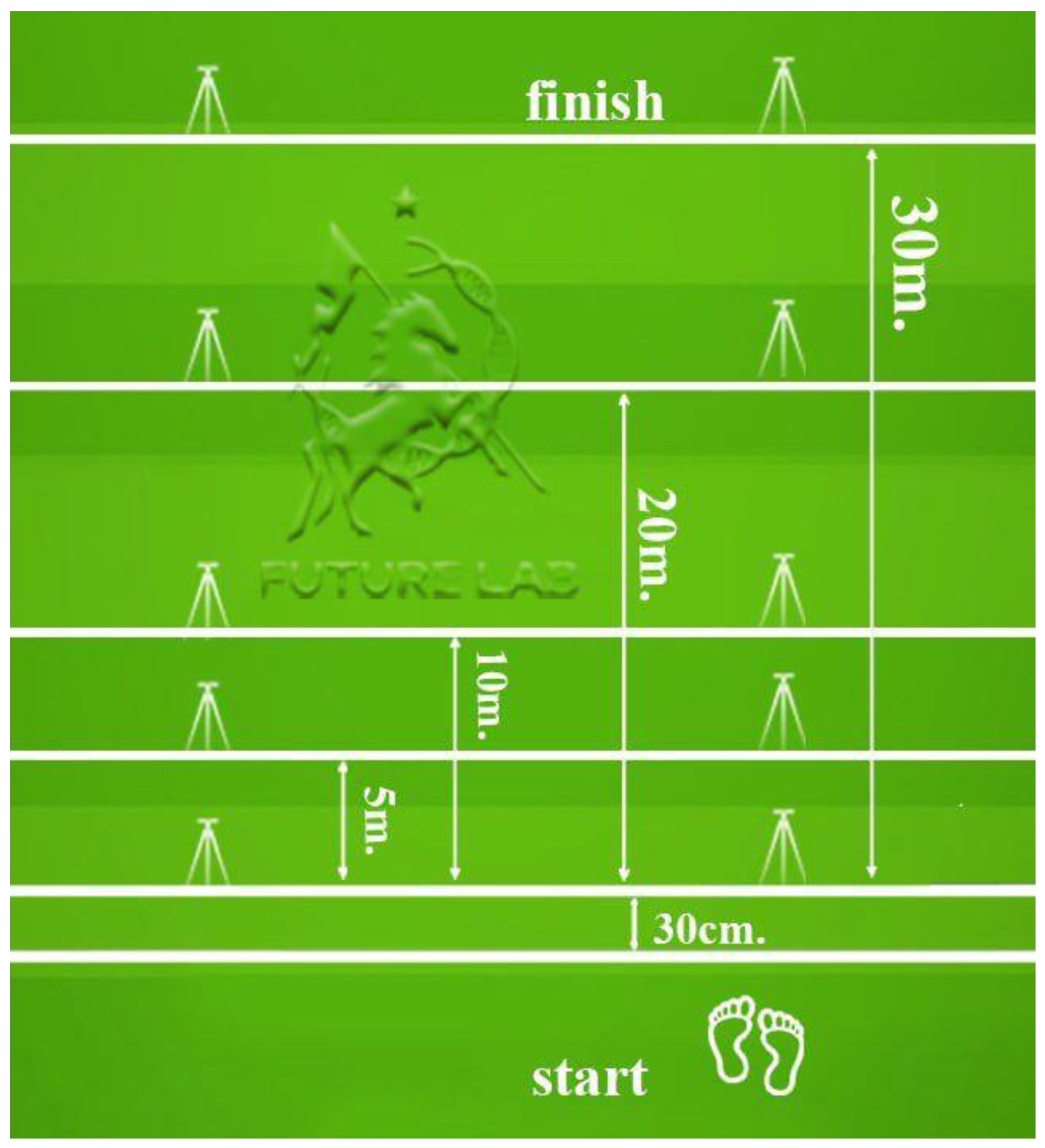
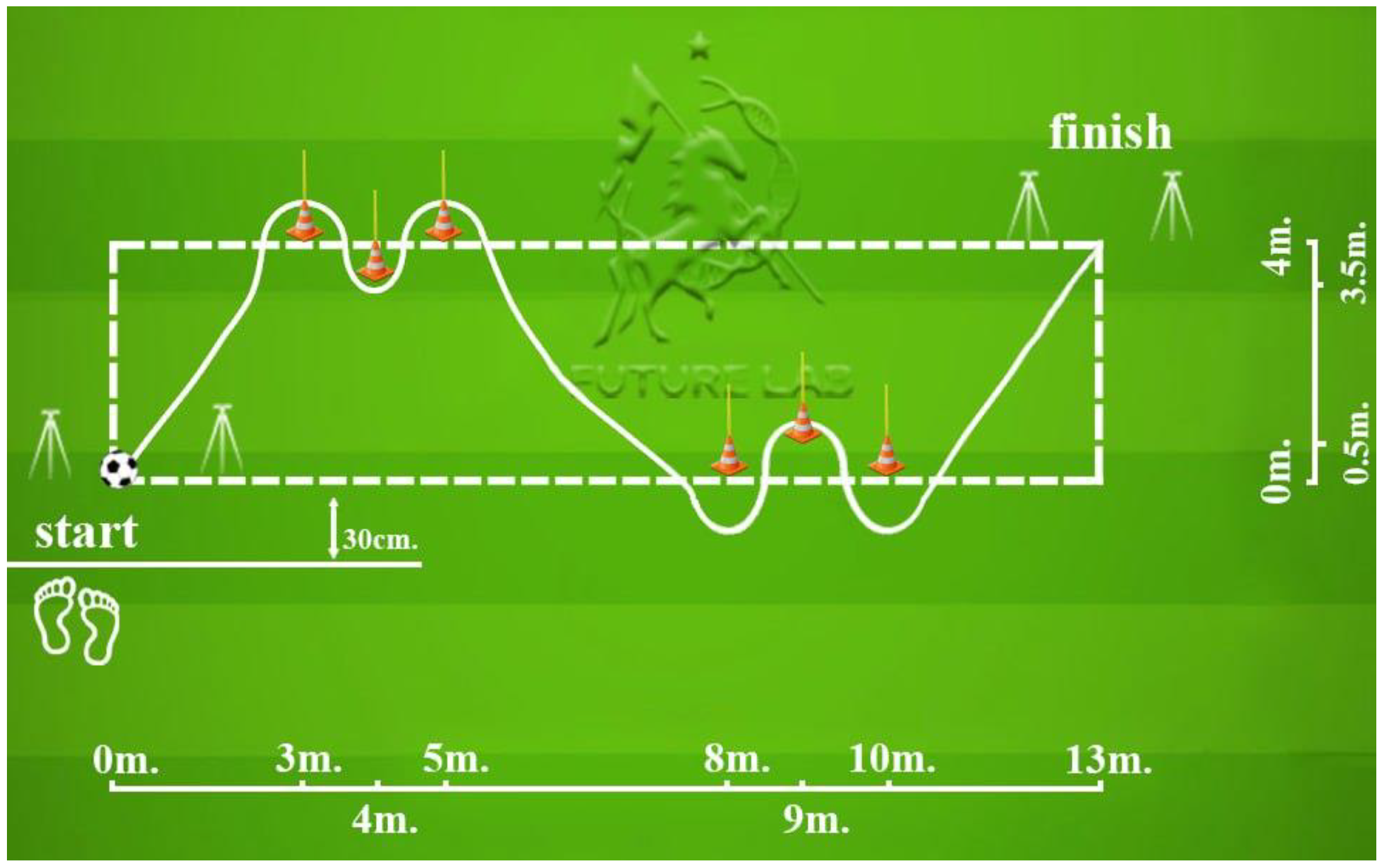
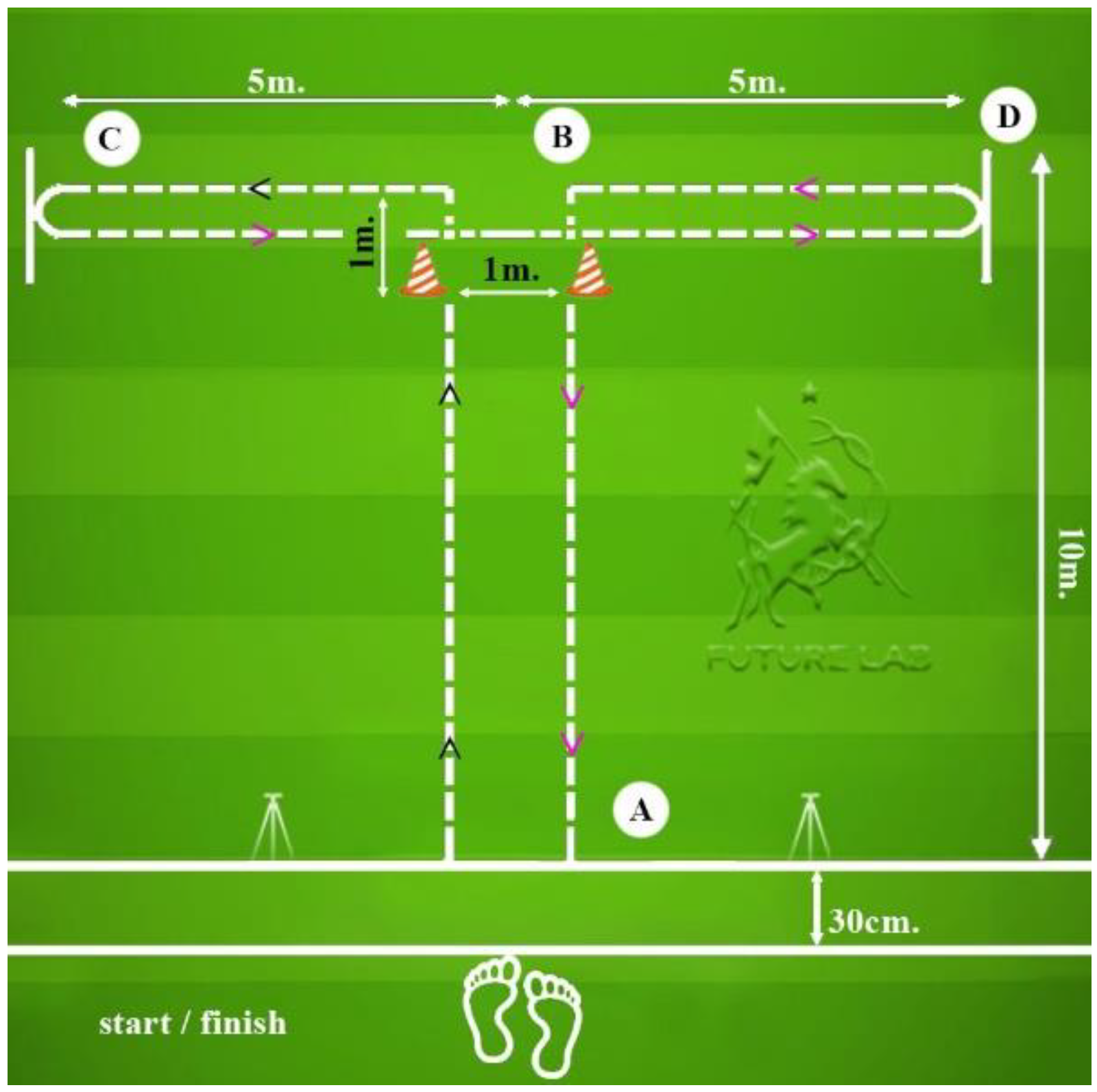
2.7. Testing Battery
2.8. Participant Instructions and Equipment
2.9. Statistical Analysis
- (i)
- Between-group comparisons within each condition (S30 and S100 separately) using Welch’s independent t-test (if both groups were approximately normal) or the Mann–Whitney U test (otherwise), with effect sizes as Cohen’s d (independent) or rank-biserial correlation, respectively;
- (ii)
- Between-group comparisons of the within-subject delta (Δ = S30–S100), which we treat as the primary order-effect test because it directly tests whether the S30→S100 change depends on the order group.
3. Results
3.1. Effect Sizes and Power Analysis
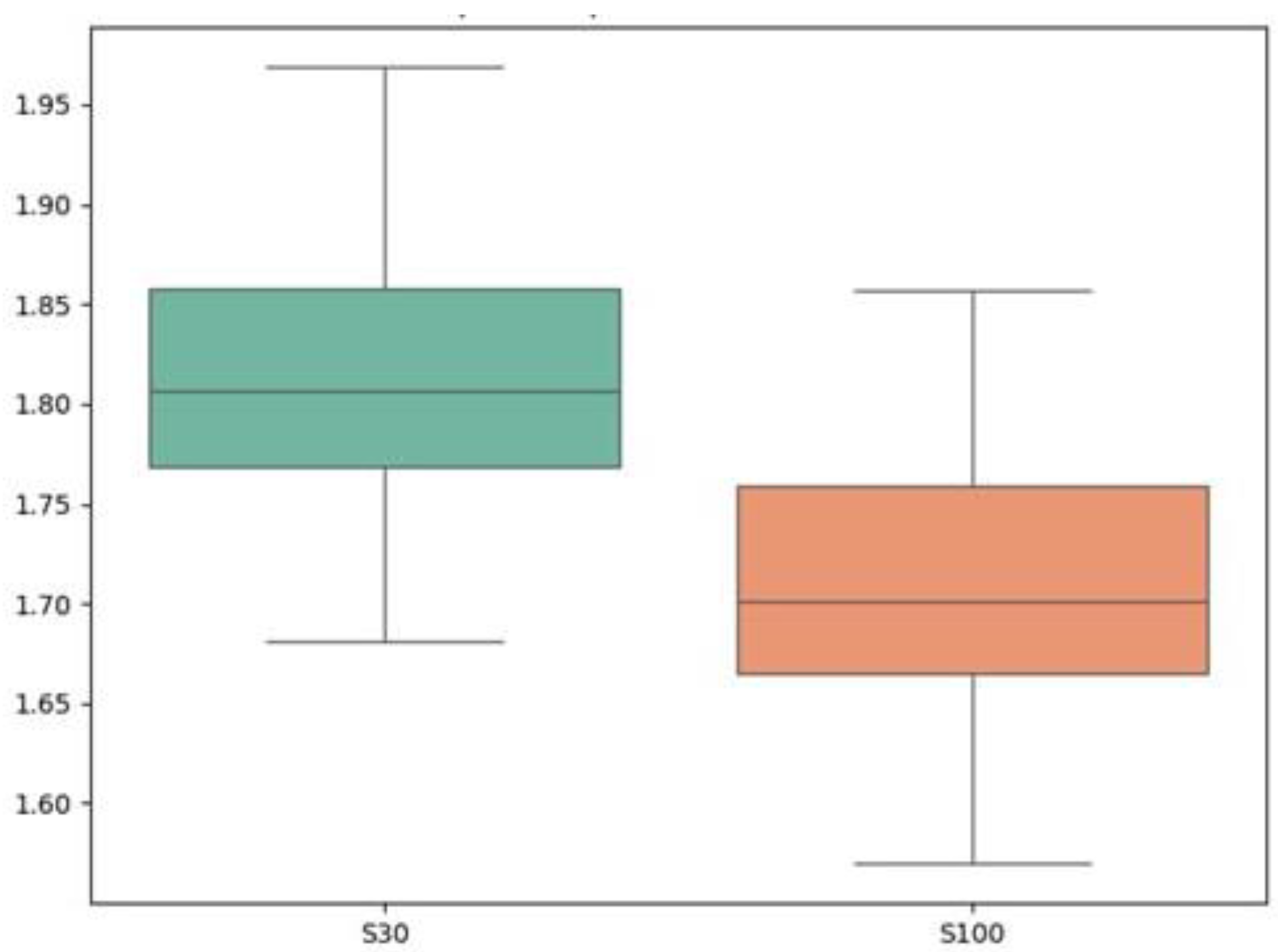
3.2. Magnitude of the S100 Effect on Sprint Performance
3.3. Order Effects Analysis
- (1)
- Condition-wise comparisons (S30 and S100 analysed separately)—summarised in Table 3; and
- (2)
- Within-subject delta comparisons (Δ = S30–S100 between order groups)—our primary order-effect test, detailed in the paragraph below and in Supplementary Table S2.
4. Discussion
4.1. Practical Recommendations
4.2. Limitations and Directions for Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paul, D.J.; Nassis, G.P. Testing Strength and Power in Soccer Players: The Application of Conventional and Traditional Methods of Assessment. J. Strength Cond. Res. 2015, 29, 1748–1758. [Google Scholar] [CrossRef]
- Contreras-Díaz, G.; Chirosa-Ríos, L.J.; Chirosa-Ríos, I.; Intelangelo, L.; Jerez-Mayorga, D.; Martinez-Garcia, D. Reliability of Isokinetic Hip Flexor and Extensor Strength Measurements in Healthy Subjects and Athletes: A Systematic Review and Meta-Analysis. Int. J. Environ. Res. Public Health 2021, 18, 11326. [Google Scholar] [CrossRef]
- Hussain, Z.; Jafar, T.; Zaman, M.U.; Parveen, R.; Saeed, F. Correlations of Skin Fold Thickness and Validation of Prediction Equations Using DEXA as the Gold Standard for Estimation of Body Fat Composition in Pakistani Children. BMJ Open 2014, 4, e004194. [Google Scholar] [CrossRef]
- LourenÇo, T.F.; Martins, L.E.B.; Tessutti, L.S.; Brenzikofer, R.; Macedo, D.V. Reproducibility of an Incremental Treadmill Vo2max Test with Gas Exchange Analysis for Runners. J. Strength Cond. Res. 2011, 25, 1994–1999. [Google Scholar] [CrossRef]
- Oliver, J.M.; Lambert, B.S.; Martin, S.E.; Green, J.S.; Crouse, S.F. Predicting Football Players’ Dual-Energy X-Ray Absorptiometry Body Composition Using Standard Anthropometric Measures. J. Athl. Train. 2012, 47, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Petri, C.; Campa, F.; Holway, F.; Pengue, L.; Arrones, L.S. ISAK-Based Anthropometric Standards for Elite Male and Female Soccer Players. Sports 2024, 12, 69. [Google Scholar] [CrossRef] [PubMed]
- Dugdale, J.H.; Arthur, C.A.; Sanders, D.; Hunter, A.M. Reliability and Validity of Field-based Fitness Tests in Youth Soccer Players. Eur. J. Sport Sci. 2019, 19, 745–756. [Google Scholar] [CrossRef] [PubMed]
- Altmann, S.; Ringhof, S.; Neumann, R.; Woll, A.; Rumpf, M.C. Validity and Reliability of Speed Tests Used in Soccer: A Systematic Review. PLoS ONE 2019, 14, e0220982. [Google Scholar] [CrossRef]
- Book of Rules, WorldAthletics. Available online: https://worldathletics.org/about-iaaf/documents/book-of-rules (accessed on 20 October 2024).
- Sanchez-Sanchez, J.; Martinez-Rodriguez, A.; Felipe, J.L.; Hernandez-Martin, A.; Ubago-Guisado, E.; Bangsbo, J.; Gallardo, L.; Garcia-Unanue, J. Effect of Natural Turf, Artificial Turf, and Sand Surfaces on Sprint Performance. A Systematic Review and Meta-Analysis. Int. J. Environ. Res. Public Health 2020, 17, 9478. [Google Scholar] [CrossRef]
- Cronin, J.B.; Green, J.P.; Levin, G.T.; Brughelli, M.E.; Frost, D.M. Effect of Starting Stance on Initial Sprint Performance. J. Strength. Cond. Res. 2007, 21, 990–992. [Google Scholar] [CrossRef]
- Silva, D.C.F.; Santos, R.; Vilas-Boas, J.P.; Macedo, R.; Montes, A.M.; Sousa, A.S.P. Influence of Cleats-Surface Interaction on the Performance and Risk of Injury in Soccer: A Systematic Review. Appl. Bionics Biomech. 2017, 2017, 1305479. [Google Scholar] [CrossRef]
- Sariati, D.; Hammami, R.; Chtara, M.; Zagatto, A.; Boullosa, D.; Clark, C.C.T.; Hackney, A.C.; Granacher, U.; Souissi, N.; Zouhal, H. Change-of-Direction Performance in Elite Soccer Players: Preliminary Analysis According to Their Playing Positions. Int. J. Environ. Res. Public Health 2020, 17, 8360. [Google Scholar] [CrossRef]
- Loturco, I.; Jeffreys, I.; Abad, C.C.C.; Kobal, R.; Zanetti, V.; Pereira, L.A.; Nimphius, S. Change-of-Direction, Speed and Jump Performance in Soccer Players: A Comparison across Different Age-Categories. J. Sports Sci. 2020, 38, 1279–1285. [Google Scholar] [CrossRef]
- Hasan, S. Effects of Plyometric vs. Strength Training on Strength, Sprint, and Functional Performance in Soccer Players: A Randomized Controlled Trial. Sci. Rep. 2023, 13, 4256. [Google Scholar] [CrossRef]
- Kilit, B.; Chmura, P.; Arslan, E.; Soylu, Y.; Radziminski, Ł. Effects of 2 Combined Training Protocols on the Aerobic and Anaerobic Fitness, Technical Skills, and Psychophysiological Responses in Young Soccer Players. J. Strength. Cond. Res. 2025, 39, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Sal-de-Rellán, A.; Ben Brahim, M.; Hernaiz-Sánchez, A.; Tarwneh, R.; Martín, V. Effects of Resisted Sprint Training with Ball on Speed and Agility Performance in U-19 Elite Soccer Players. PLoS ONE 2024, 19, e0311002. [Google Scholar] [CrossRef] [PubMed]
- Bramah, C.; Tawiah-Dodoo, J.; Rhodes, S.; Elliott, J.D.; Dos’Santos, T. The Sprint Mechanics Assessment Score: A Qualitative Screening Tool for the In-Field Assessment of Sprint Running Mechanics. Am. J. Sports Med. 2024, 52, 1608–1616. [Google Scholar] [CrossRef]
- Meckel, Y.; Machnai, O.; Eliakim, A. Relationship Among Repeated Sprint Tests, Aerobic Fitness, and Anaerobic Fitness in Elite Adolescent Soccer Players. J. Strength Cond. Res. 2009, 23, 163–169. [Google Scholar] [CrossRef]
- Andrašić, S.; Gušić, M.; Stanković, M.; Mačak, D.; Bradić, A.; Sporiš, G.; Trajković, N. Speed, Change of Direction Speed and Reactive Agility in Adolescent Soccer Players: Age Related Differences. Int. J. Environ. Res. Public Health 2021, 18, 5883. [Google Scholar] [CrossRef] [PubMed]
- Fiorilli, G.; Mariano, I.; Iuliano, E.; Giombini, A.; Ciccarelli, A.; Buonsenso, A.; Calcagno, G.; di Cagno, A. Isoinertial Eccentric-Overload Training in Young Soccer Players: Effects on Strength, Sprint, Change of Direction, Agility and Soccer Shooting Precision. J. Sports Sci. Med. 2020, 19, 213–223. [Google Scholar]
- Chaouachi, A.; Manzi, V.; Wong, D.P.; Chaalali, A.; Laurencelle, L.; Chamari, K.; Castagna, C. Intermittent Endurance and Repeated Sprint Ability in Soccer Players. J. Strength Cond. Res. 2010, 24, 2663–2669. [Google Scholar] [CrossRef] [PubMed]
- Fílter, A.; Olivares, J.; Santalla, A.; Nakamura, F.Y.; Loturco, I.; Requena, B. New Curve Sprint Test for Soccer Players: Reliability and Relationship with Linear Sprint. J. Sports Sci. 2020, 38, 1320–1325. [Google Scholar] [CrossRef]
- Krolo, A.; Gilic, B.; Foretic, N.; Pojskic, H.; Hammami, R.; Spasic, M.; Uljevic, O.; Versic, S.; Sekulic, D. Agility Testing in Youth Football (Soccer)Players; Evaluating Reliability, Validity, and Correlates of Newly Developed Testing Protocols. Int. J. Environ. Res. Public Health 2020, 17, 294. [Google Scholar] [CrossRef]
- Altmann, S.; Hoffmann, M.; Kurz, G.; Neumann, R.; Woll, A.; Haertel, S. Different Starting Distances Affect 5-m Sprint Times. J. Strength Cond. Res. 2015, 29, 2361–2366. [Google Scholar] [CrossRef]
- Gioldasis, A.; Theodorou, A.; Bekris, E.; Katis, A.; Smirniotou, A. Sprinting and Dribbling Differences in Young Soccer Players: A Kinematic Approach. Res. Sports Med. 2022, 30, 603–615. [Google Scholar] [CrossRef]
- Asimakidis, N.D.; Bishop, C.J.; Beato, M.; Mukandi, I.N.; Kelly, A.L.; Weldon, A.; Turner, A.N. A Survey into the Current Fitness Testing Practices of Elite Male Soccer Practitioners: From Assessment to Communicating Results. Front. Physiol. 2024, 15, 1376047. [Google Scholar] [CrossRef] [PubMed]
- Gatti, A.; Azzali, G.; Tornaghi, M.; Lovecchio, N.; Giuriato, M. “Who’s Got Talent?” Change of Direction, Anthropometric Characteristics and Maturity Offset Differences Between Elite and Sub-Elite Young Soccer Player. Res. Q. Exerc. Sport 2024, 96, 273–278. [Google Scholar] [CrossRef]
- Ali, A. Measuring Soccer Skill Performance: A Review. Scand. Med. Sci. Sports 2011, 21, 170–183. [Google Scholar] [CrossRef]
- Höner, O.; Murr, D.; Larkin, P.; Schreiner, R.; Leyhr, D. Nationwide Subjective and Objective Assessments of Potential Talent Predictors in Elite Youth Soccer: An Investigation of Prognostic Validity in a Prospective Study. Front. Sports Act. Living 2021, 3, 638227. [Google Scholar] [CrossRef]
- Huijgen, B.C.H.; Elferink-Gemser, M.; Post, W.; Visscher, C. Soccer Skill Development in Professionals. Int. J. Sports Med. 2009, 30, 585–591. [Google Scholar] [CrossRef] [PubMed]
- Buckthorpe, M.; Della Villa, F.; Della Villa, S.; Roi, G.S. On-Field Rehabilitation Part 2: A 5-Stage Program for the Soccer Player Focused on Linear Movements, Multidirectional Movements, Soccer-Specific Skills, Soccer-Specific Movements, and Modified Practice. J. Orthop. Sports Phys. Ther. 2019, 49, 570–575. [Google Scholar] [CrossRef]
- Van Der Horst, N.; Van De Hoef, S.; Reurink, G.; Huisstede, B.; Backx, F. Return to Play After Hamstring Injuries: A Qualitative Systematic Review of Definitions and Criteria. Sports Med. 2016, 46, 899–912. [Google Scholar] [CrossRef]
- Meeusen, R.; Duclos, M.; Foster, C.; Fry, A.; Gleeson, M.; Nieman, D.; Raglin, J.; Rietjens, G.; Steinacker, J.; Urhausen, A. Prevention, Diagnosis, and Treatment of the Overtraining Syndrome: Joint Consensus Statement of the European College of Sport Science and the American College of Sports Medicine. Med. Sci. Sports Exerc. 2013, 45, 186–205. [Google Scholar] [CrossRef]
- Vergani, L.; Cuniberti, M.; Zanovello, M.; Maffei, D.; Farooq, A.; Eirale, C. Return to Play in Long-Standing Adductor-Related Groin Pain: A Delphi Study Among Experts. Sports Med.—Open 2022, 8, 11. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.A.; Tønnessen, E.; Hisdal, J.; Seiler, S. The Role and Development of Sprinting Speed in Soccer. Int. J. Sports Physiol. Perform. 2014, 9, 432–441. [Google Scholar] [CrossRef]
- Sarmento, H.; Anguera, M.T.; Pereira, A.; Araújo, D. Talent Identification and Development in Male Football: A Systematic Review. Sports Med. 2018, 48, 907–931. [Google Scholar] [CrossRef] [PubMed]
- Saward, C.; Hulse, M.; Morris, J.G.; Goto, H.; Sunderland, C.; Nevill, M.E. Longitudinal Physical Development of Future Professional Male Soccer Players: Implications for Talent Identification and Development? Front. Sports Act. Living 2020, 2, 578203. [Google Scholar] [CrossRef]
- Trajković, N.; Sporiš, G.; Krističević, T.; Madić, D.M.; Bogataj, Š. The Importance of Reactive Agility Tests in Differentiating Adolescent Soccer Players. Int. J. Environ. Res. Public Health 2020, 17, 3839. [Google Scholar] [CrossRef] [PubMed]
- Stølen, T.; Chamari, K.; Castagna, C.; Wisløff, U. Physiology of Soccer: An Update. Sports Med. 2005, 35, 501–536. [Google Scholar] [CrossRef]
- Andrzejewski, M.; Chmura, J.; Pluta, B.; Konarski, J.M. Sprinting Activities and Distance Covered by Top Level Europa League Soccer Players. Int. J. Sports Sci. Coach. 2015, 10, 39–50. [Google Scholar] [CrossRef]

| Metric | S30: Mean ± SD | S30: Median [IQR] | S100: Mean ± SD | S100: Median [IQR] |
|---|---|---|---|---|
| Sprint 30 m (s) | 4.21 ± 0.14 | 4.19 [4.16, 4.35] | 4.10 ± 0.14 | 4.07 [4.03, 4.27] |
| Sprint 20 m (s) | 3.05 ± 0.10 | 3.04 [2.96, 3.16] | 2.94 ± 0.10 | 2.92 [2.90, 3.03] |
| Sprint 10 m (s) | 1.81 ± 0.07 | 1.81 [1.73, 1.90] | 1.71 ± 0.07 | 1.70 [1.66, 1.82] |
| Sprint 5 m (s) | 1.09 ± 0.07 | 1.09 [1.02, 1.15] | 1.02 ± 0.06 | 1.02 [0.98, 1.10] |
| COD (s) | 7.49 ± 0.31 | 7.47 [7.32, 7.88] | 7.42 ± 0.35 | 7.38 [7.20, 7.78] |
| T-test (s) | 8.48 ± 0.31 | 8.50 [8.30, 8.74] | 8.38 ± 0.30 | 8.35 [8.20, 8.60] |
| Metric | Test Type | Test Statistic | p-Value | Corrected p-Value (Holm) | Effect Size | Power |
|---|---|---|---|---|---|---|
| Sprint 30 m (s) | Paired t-test | 13.52 | 1.78 × 10−22 | 8.92 × 10−22 | 1.48 | 1.00 |
| Sprint 20 m (s) | Paired t-test | 14.47 | 3.61 × 10−24 | 2.17 × 10−23 | 1.58 | 1.00 |
| Sprint 10 m (s) | Paired t-test | 12.52 | 1.23 × 10−20 | 4.93 × 10−20 | 1.37 | 1.00 |
| Sprint 5 m (s) | Paired t-test | 9.16 | 3.76 × 10−14 | 1.13 × 10−13 | 1.00 | 1.00 |
| COD (s) | Wilcoxon Signed-Rank Test | 824 | 5.03 × 10−5 | 5.03 × 10−5 | 0.52 | N/A |
| T-test (s) | Paired t-test | 5.51 | 4.31 × 10−7 | 8.62 × 10−7 | 0.61 | 1.00 |
| Meric | Test Type | Test Statistic | p-Value | Corrected p-Value (Holm) | Mean (30 cm First) | Mean (100 cm First) | Effect Size (Order Effect) |
|---|---|---|---|---|---|---|---|
| Sprint 30 m (S30) | Mann–Whitney U test | 630 | 0.051 | 0.617 | 4.18 ± 0.13 | 4.24 ± 0.14 | 0.25 |
| Sprint 30 m (S100) | Mann–Whitney U test | 837 | 0.978 | 1 | 4.09 ± 0.15 | 4.10 ± 0.14 | 0.00 |
| Sprint 20 m (S30) | Mann–Whitney U test | 683.5 | 0.147 | 1 | 3.03 ± 0.09 | 3.07 ± 0.10 | 0.19 |
| Sprint 20 m (S100) | Mann–Whitney U test | 834 | 0.956 | 1 | 2.94 ± 0.10 | 2.94 ± 0.10 | 0.01 |
| Split 5 m (S30) | Independent t-test | −0.52 | 0.604 | 1 | 1.09 ± 0.06 | 1.10 ± 0.08 | −0.12 |
| Split 5 m (S100) | Mann–Whitney U test | 894.5 | 0.620 | 1 | 1.02 ± 0.05 | 1.01 ± 0.06 | −0.06 |
| Split 10 m (S30) | Independent t-test | −1.38 | 0.170 | 1 | 1.80 ± 0.06 | 1.83 ± 0.07 | −0.31 |
| Split 10 m (S100) | Independent t-test | −0.25 | 0.799 | 1 | 1.71 ± 0.06 | 1.71 ± 0.07 | −0.06 |
| COD (S30) | Independent t-test | 0.70 | 0.489 | 1 | 7.51 ± 0.28 | 7.47 ± 0.34 | 0.15 |
| COD (S100) | Mann–Whitney U test | 787 | 0.623 | 1 | 7.38 ± 0.28 | 7.45 ± 0.40 | 0.06 |
| T-test (S30) | Independent t-test | −0.35 | 0.727 | 1 | 8.47 ± 0.28 | 8.49 ± 0.36 | −0.08 |
| T-test (S100) | Independent t-test | −0.18 | 0.861 | 1 | 8.37 ± 0.31 | 8.38 ± 0.30 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezuglov, E.; Emanov, A.; Vakhidov, T.; Kapralova, E.; Malyakin, G.; Kolesnichenko, V.; Waśkiewicz, Z.; Smekalkina, L.; Vinogradov, M. Comparative Analysis of Speed-Power Performance and Sport-Specific Skills Among Elite Youth Soccer Players with Different Start Procedures. Sports 2025, 13, 341. https://doi.org/10.3390/sports13100341
Bezuglov E, Emanov A, Vakhidov T, Kapralova E, Malyakin G, Kolesnichenko V, Waśkiewicz Z, Smekalkina L, Vinogradov M. Comparative Analysis of Speed-Power Performance and Sport-Specific Skills Among Elite Youth Soccer Players with Different Start Procedures. Sports. 2025; 13(10):341. https://doi.org/10.3390/sports13100341
Chicago/Turabian StyleBezuglov, Eduard, Anton Emanov, Timur Vakhidov, Elizaveta Kapralova, Georgiy Malyakin, Vyacheslav Kolesnichenko, Zbigniew Waśkiewicz, Larisa Smekalkina, and Mikhail Vinogradov. 2025. "Comparative Analysis of Speed-Power Performance and Sport-Specific Skills Among Elite Youth Soccer Players with Different Start Procedures" Sports 13, no. 10: 341. https://doi.org/10.3390/sports13100341
APA StyleBezuglov, E., Emanov, A., Vakhidov, T., Kapralova, E., Malyakin, G., Kolesnichenko, V., Waśkiewicz, Z., Smekalkina, L., & Vinogradov, M. (2025). Comparative Analysis of Speed-Power Performance and Sport-Specific Skills Among Elite Youth Soccer Players with Different Start Procedures. Sports, 13(10), 341. https://doi.org/10.3390/sports13100341









