Comparing Two Methods of Acute: Chronic Workload Calculations in Girls’ Youth Volleyball
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
2.2.1. HSVB Data
2.2.2. CVB Data
2.3. Measures
2.4. Statistical Analysis
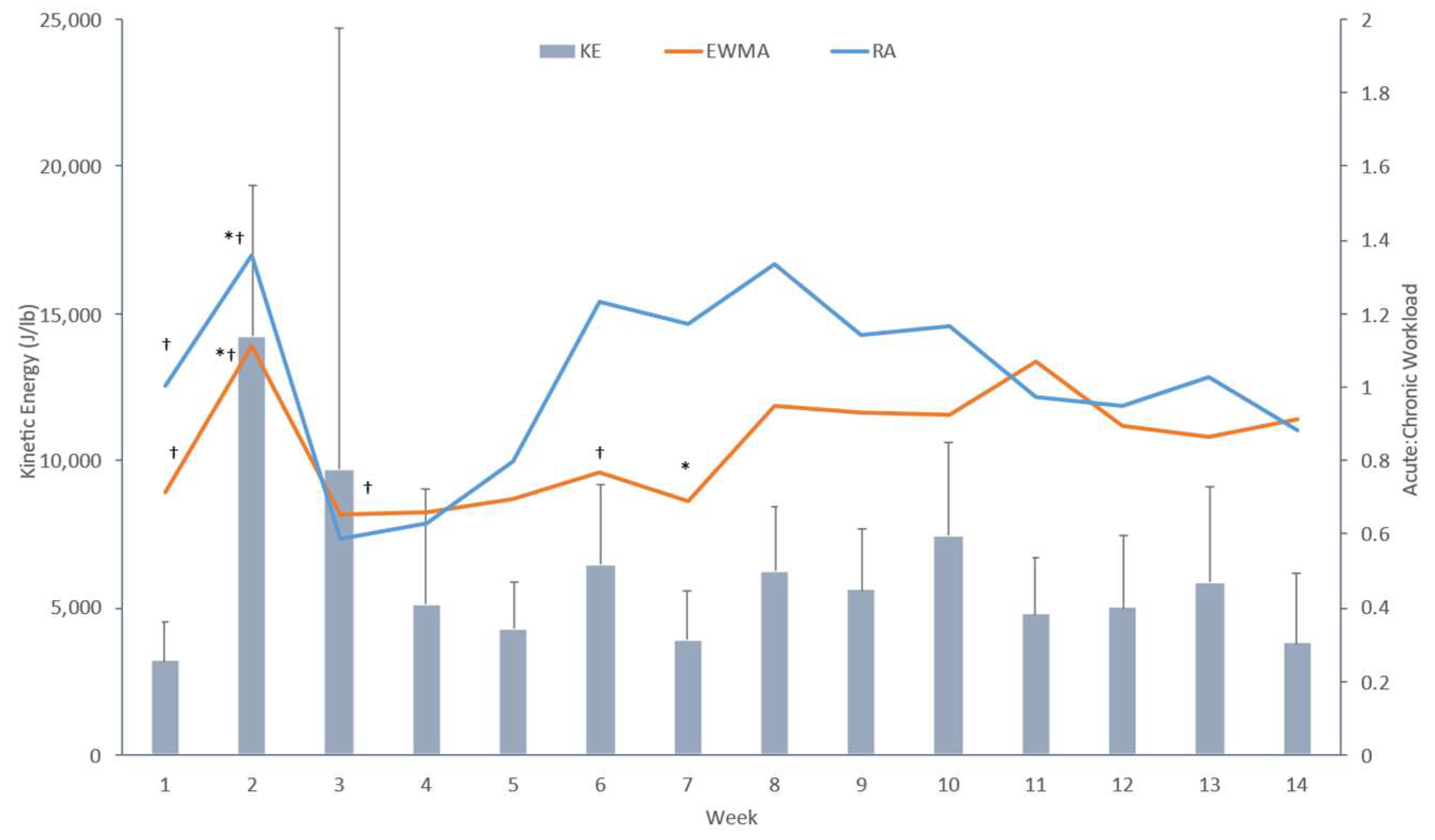
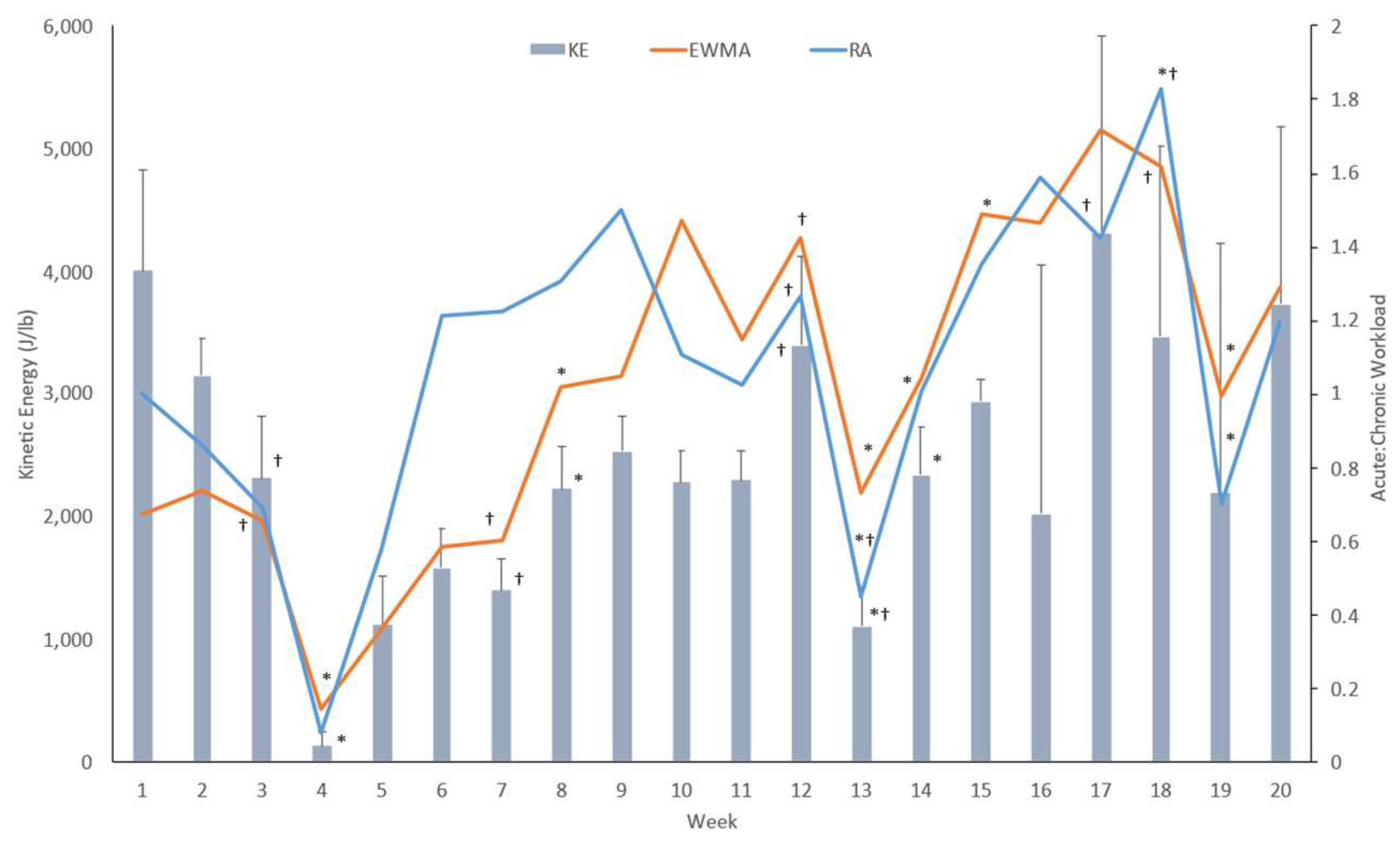
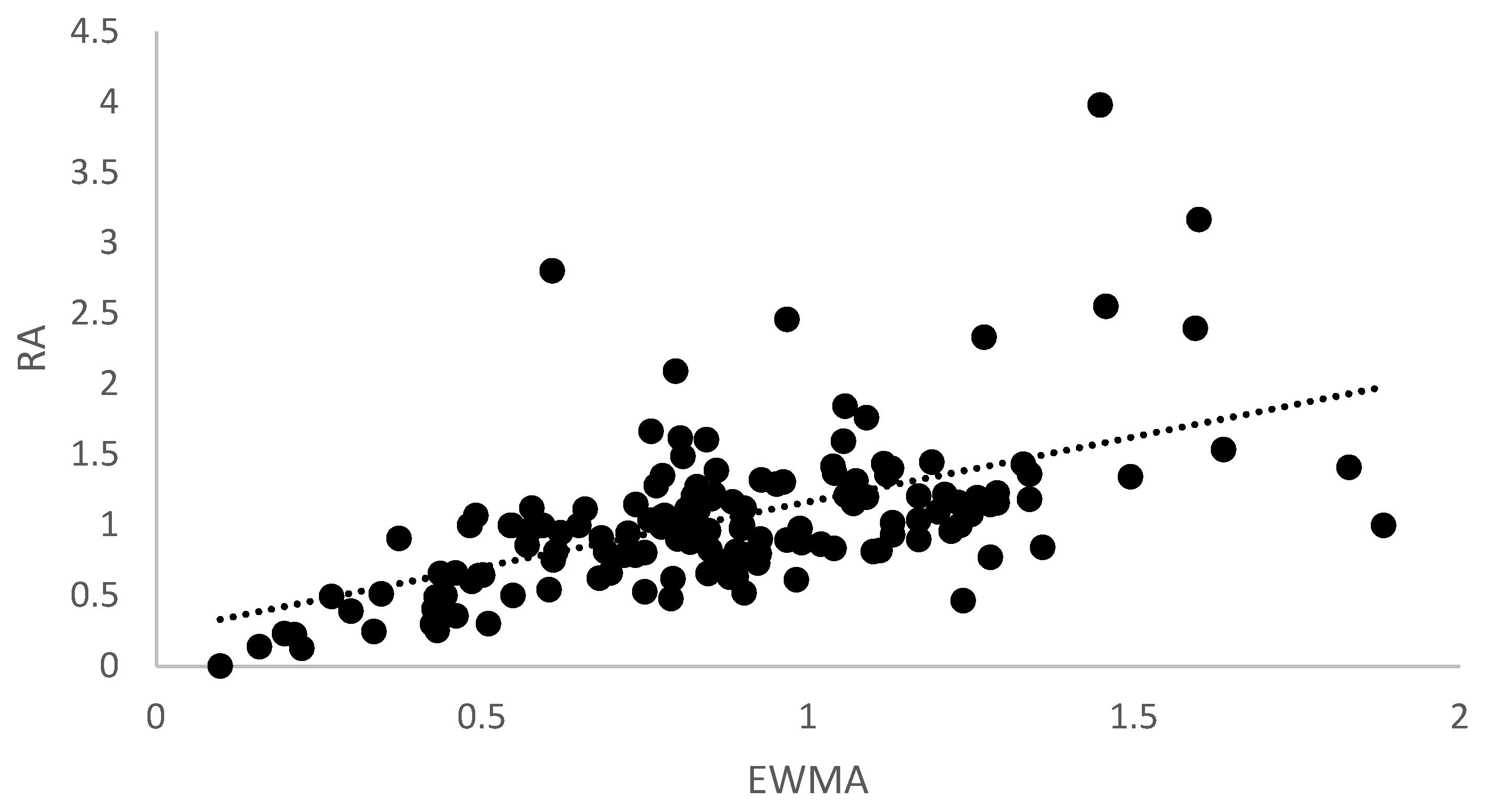
3. Results
3.1. HSVB Data
3.2. CVB Data
4. Discussion
4.1. ACWR in High School Volleyball Season
4.2. ACWR in Club Volleyball Season
4.3. Application of ACWR in Girls’ Volleyball
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gabbett, T.J. The Training-Injury Prevention Paradox: Should Athletes Be Training Smarter and Harder? Br. J. Sports Med. 2016, 50, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Hulin, B.T.; Gabbett, T.J.; Lawson, D.W.; Caputi, P.; Sampson, J.A. The acute: Chronic workload ratio predicts injury: High chronic workload may decrease injury risk in elite rugby league players. Br. J. Sports Med. 2016, 50, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Hawley, J.A. Adaptations of Skeletal Muscle to Prolonged, Intense Endurance Training. Clin. Exp. Pharmacol. Physiol. 2002, 29, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Murray, N.B.; Gabbett, T.J.; Townshend, A.D.; Blanch, P. Calculating acute:chronic workload ratios using exponentially weighted moving averages provides a more sensitive indicator of injury likelihood than rolling averages. Br. J. Sports Med. 2016, 51, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Griffin, A.; Kenny, I.C.; Comyns, T.M.; Lyons, M. The Association Between the Acute:Chronic Workload Ratio and Injury and its Application in Team Sports: A Systematic Review. Sports Med. 2019, 50, 561–580. [Google Scholar] [CrossRef] [PubMed]
- Morton, R.H. Modelling training and overtraining. J. Sports Sci. 1997, 15, 335–340. [Google Scholar] [CrossRef]
- Murray, N.B.; Gabbett, T.J.; Townshend, A.D.; Hulin, B.T.; McLellan, C.P. Individual and combined effects of acute and chronic running loads on injury risk in elite Australian footballers. Scand. J. Med. Sci. Sports 2016, 27, 990–998. [Google Scholar] [CrossRef]
- Foster, C.; Marroyo, J.A.R.; De Koning, J.J. Monitoring Training Loads: The Past, the Present, and the Future. Int. J. Sports Physiol. Perform. 2017, 12, S2-2–S2-8. [Google Scholar] [CrossRef]
- Paulauskas, H.; Kreivyte, R.; Scanlan, A.T.; Moreira, A.; Siupsinskas, L.; Conte, D. Monitoring Workload in Elite Female Basketball Players During the In-Season Phase: Weekly Fluctuations and Effect of Playing Time. Int. J. Sports Physiol. Perform. 2019, 14, 941–948. [Google Scholar] [CrossRef]
- Akyildiz, Z.; Castro, H.D.O.; Çene, E.; Laporta, L.; Parim, C.; Altundag, E.; Akarçeşme, C.; Guidetti, G.; Miale, G.; Silva, A.F.; et al. Within-week differences in external training load demands in elite volleyball players. BMC Sports Sci. Med. Rehabil. 2022, 14, 188. [Google Scholar] [CrossRef]
- Edmonds, R.; Schmidt, B.; Siedlik, J. Eligibility Classification as a Factor in Understanding Student-Athlete Responses to Collegiate Volleyball Competition. Sports 2021, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Pedowitz, D.I.; Reddy, S.; Parekh, S.G.; Huffman, G.R.; Sennett, B.J. Prophylactic Bracing Decreases Ankle Injuries in Collegiate Female Volleyball Players. Am. J. Sports Med. 2007, 36, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Marroyo, J.A.; Medina, J.; García-López, J.; García-Tormo, J.V.; Foster, C. Correspondence Between Training Load Executed by Volleyball Players and the One Observed by Coaches. J. Strength Cond. Res. 2014, 28, 1588–1594. [Google Scholar] [CrossRef] [PubMed]
- Stasinopoulos, D. Comparison of three preventive methods in order to reduce the incidence of ankle inversion sprains among female volleyball players. Br. J. Sports Med. 2004, 38, 182–185. [Google Scholar] [CrossRef]
- High School Volleyball Players in the U.S. 2021/2022|Statista. Available online: https://www.statista.com/statistics/268009/participation-in-us-high-school-volleyball/#:~:text=The%20number%20of%20volleyball%20players,sport%20had%20reached%20520.6%20thousand (accessed on 16 July 2022).
- Munoz, M.A.; Bunn, J.A. Season Phase Comparison of Training and Game Volume in Female High School Volleyball Athletes. J. Athl. Dev. Exp. Under review.
- Verhagen, E.A.L.M.; Van der Beek, A.J.; Bouter, L.M.; Bahr, R.M.; Van Mechelen, W. A one season prospective cohort study of volleyball injuries. Br. J. Sports Med. 2004, 38, 477–481. [Google Scholar] [CrossRef]
- Schafle, M.D.; Requa, R.K.; Patton, W.L.; Garrick, J.G. Injuries in the 1987 National Amateur Volleyball Tournament. Am. J. Sports Med. 1990, 18, 624–631. [Google Scholar] [CrossRef]
- Benson, L.C.; Tait, T.J.; Befus, K.; Choi, J.; Hillson, C.; Stilling, C.; Grewal, S.; Macdonald, K.; Pasanen, K.; Emery, C.A. Validation of a commercially available inertial measurement unit for recording jump load in youth basketball players. J. Sports Sci. 2020, 38, 928–936. [Google Scholar] [CrossRef]
- Charlton, P.C.; Kenneally-Dabrowski, C.; Sheppard, J.; Spratford, W. A simple method for quantifying jump loads in volleyball athletes. J. Sci. Med. Sport 2017, 20, 241–245. [Google Scholar] [CrossRef]
- Brooks, E.R.; Benson, A.C.; Fox, A.S.; Bruce, L.M. Quantifying jumps and external load in netball using VERT inertial measurement units. Sports Biomech. 2021, 6, 1–10. [Google Scholar] [CrossRef]
- Williams, S.; West, S.; Cross, M.J.; Stokes, K.A. Better way to determine the acute:chronic workload ratio? Br. J. Sports Med. 2016, 51, 209–210. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: New York, NY, USA, 1988; ISBN 0805802835. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistics notes: Calculating correlation coefficients with repeated observations: Part 1—correlation within subjects. BMJ 1995, 310, 446. [Google Scholar] [CrossRef] [PubMed]
- Menaspà, P. Are Rolling Averages a Good Way to Assess Training Load for Injury Prevention? Br. J. Sports Med. 2017, 51, 618–619. [Google Scholar] [CrossRef] [PubMed]
- Altundag, E.; Akyildiz, Z.; Lima, R.; Castro, H.D.O.; Çene, E.; Akarçeşme, C.; Miale, G.; Clemente, F.M. Relationships between internal and external training load demands and match load demands in elite women volleyball players. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Foster, C.; Florhaug, J.A.; Franklin, J.; Gottschall, L.; Hrovatin, L.A.; Parker, S.; Doleshal, P.; Dodge, C. A new approach to monitoring exercise training. J. Strength Cond. Res. 2001, 15, 109–115. [Google Scholar] [PubMed]
- Ozkan, A.; Kin-Isler, A. The reliability and validity of regulating exercise intensity by ratings of perceived exertion in step dance sessions. J. Strength Cond. Res. 2007, 21, 296–300. [Google Scholar] [CrossRef] [PubMed]
- Wallace, L.K.; Slattery, K.M.; Impellizzeri, F.M.; Coutts, A.J. Establishing the Criterion Validity and Reliability of Common Methods for Quantifying Training Load. J. Strength Cond. Res. 2014, 28, 2330–2337. [Google Scholar] [CrossRef]
- Esmaeili, A.; Hopkins, W.G.; Stewart, A.M.; Elias, G.P.; Lazarus, B.H.; Aughey, R.J. The Individual and Combined Effects of Multiple Factors on the Risk of Soft Tissue Non-contact Injuries in Elite Team Sport Athletes. Front. Physiol. 2018, 9, 1280. [Google Scholar] [CrossRef]
- Bowen, L.; Gross, A.S.; Gimpel, M.; Li, F.-X. Accumulated workloads and the acute:chronic workload ratio relate to injury risk in elite youth football players. Br. J. Sports Med. 2016, 51, 452–459. [Google Scholar] [CrossRef]
- Myers, N.L.; Aguilar, K.V.; Mexicano, G.; Farnsworth, J.L.; Knudson, D.; BEN Kibler, W. The Acute:Chronic Workload Ratio Is Associated with Injury in Junior Tennis Players. Med. Sci. Sports Exerc. 2019, 52, 1196–1200. [Google Scholar] [CrossRef]
- Raya-González, J.; Nakamura, F.Y.; Castillo, D.; Yanci, J.; Fanchini, M. Determining the Relationship Between Internal Load Markers and Noncontact Injuries in Young Elite Soccer Players. Int. J. Sports Physiol. Perform. 2019, 14, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Mendeley Data, V1. Available online: https://data.mendeley.com/datasets/8hk8k44y7p/1 (accessed on 20 February 2023).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schumann, C.; Wojciechowski, M.; Bunn, J.A. Comparing Two Methods of Acute: Chronic Workload Calculations in Girls’ Youth Volleyball. Sports 2023, 11, 51. https://doi.org/10.3390/sports11030051
Schumann C, Wojciechowski M, Bunn JA. Comparing Two Methods of Acute: Chronic Workload Calculations in Girls’ Youth Volleyball. Sports. 2023; 11(3):51. https://doi.org/10.3390/sports11030051
Chicago/Turabian StyleSchumann, Claire, Monica Wojciechowski, and Jennifer A. Bunn. 2023. "Comparing Two Methods of Acute: Chronic Workload Calculations in Girls’ Youth Volleyball" Sports 11, no. 3: 51. https://doi.org/10.3390/sports11030051
APA StyleSchumann, C., Wojciechowski, M., & Bunn, J. A. (2023). Comparing Two Methods of Acute: Chronic Workload Calculations in Girls’ Youth Volleyball. Sports, 11(3), 51. https://doi.org/10.3390/sports11030051






