Assessing Genetic Diversity and Population Structure of Western Honey Bees in the Czech Republic Using 22 Microsatellite Loci
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
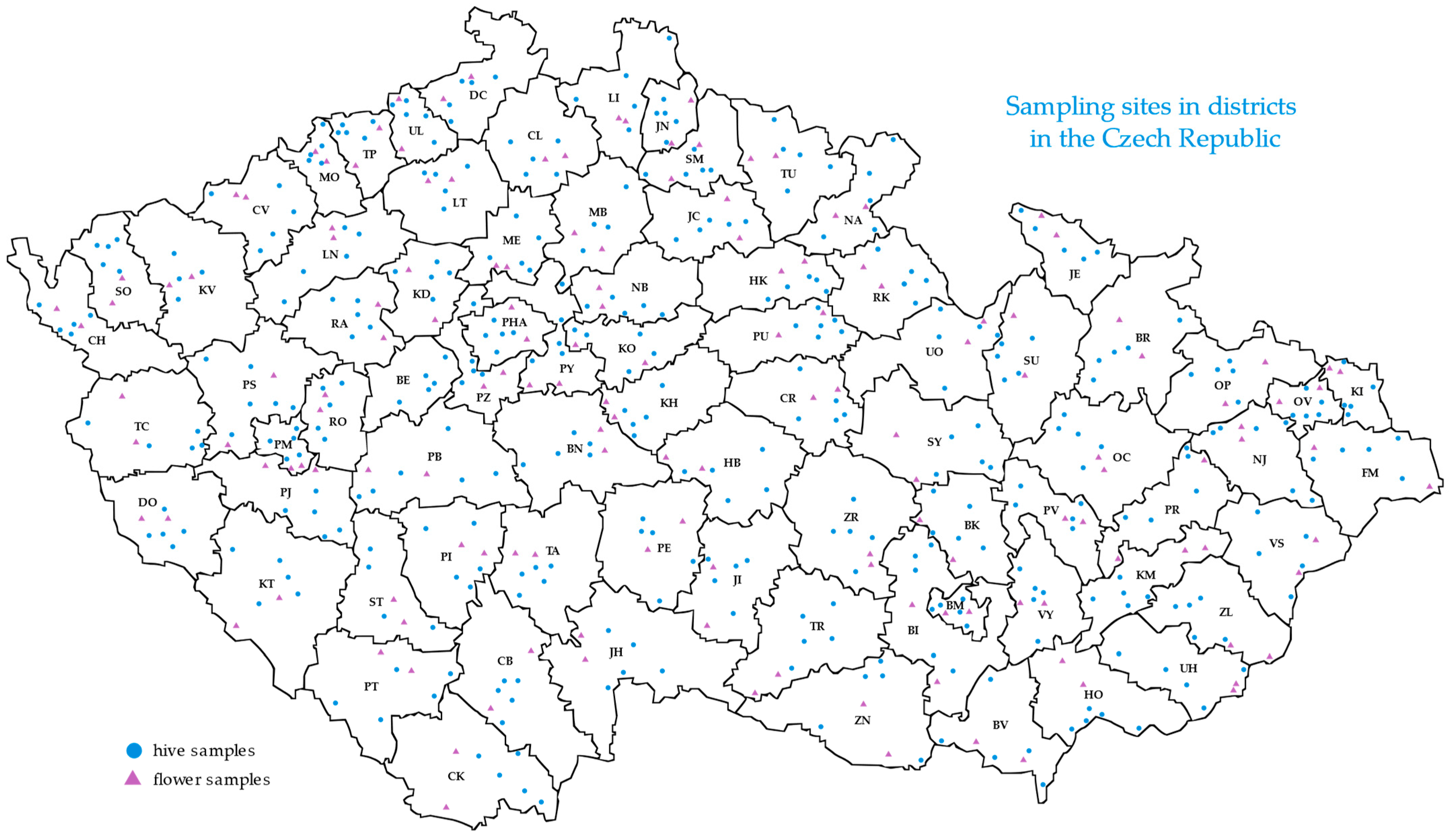
2.1. Sampling of Bees
2.2. DNA Extraction
2.3. PCR Amplification
2.4. Fragment Analysis
2.5. Data Analysis
3. Results
3.1. Genetic Diversity
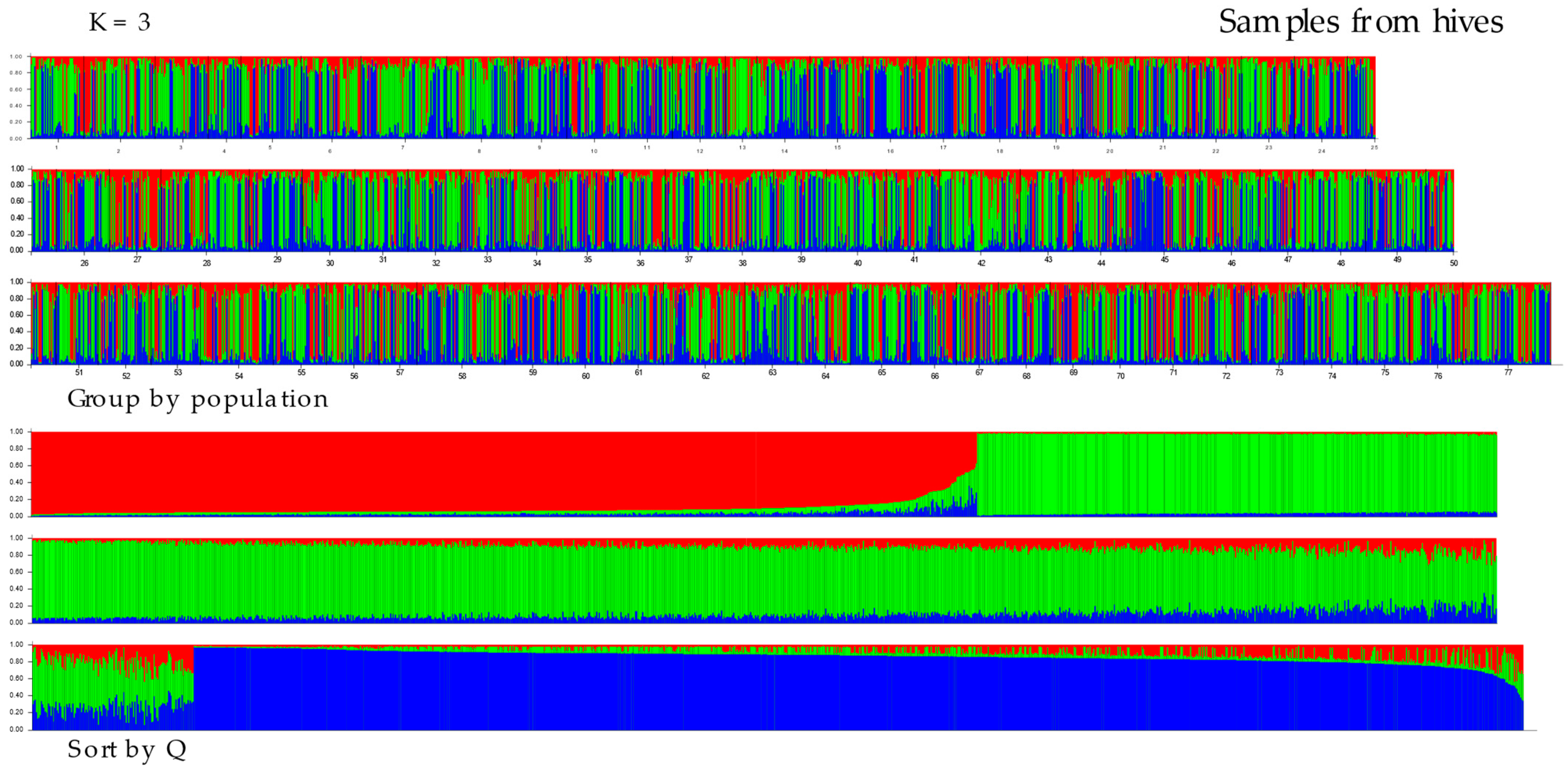
3.2. Population Differentiation and Structure
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krejčík, P.; Scháňková, Š.; Mořický, J.; Chalupa, P. Situační a Výhledová Zpráva—Včely; Ministerstvo Zemědělství: Praha, Czech Republic, 2021; p. 31. ISBN 978-80-7434-656-9. [Google Scholar]
- Engelsdorp, D.; van Meixner, M.D. A historical review of managed honey bee populations in Europe and the United States and the factors that may affect them. J. Inverteb. Pathol. 2010, 103, S80–S95. [Google Scholar] [CrossRef]
- Texl, P.; Vondrák, J. Včely 2011—Co ministerstvo do zprávy nenapsalo. Mod. Včelař 2012, 9, 4–5. [Google Scholar]
- Zahradník, K. České včely a včelaři na mapách. Včelařství 2013, 66, 272–273. [Google Scholar]
- Brus, J.; Biemann, O.; Danihlík, J. Včelaření v Době Klimatické Změny; Univerzita Palackého v Olomouci: Olomouc, Czechia, 2023; ISBN 978-80-244-6321-6. Available online: https://books.google.cz/books?id=qFIrEQAAQBAJ&lpg=PA3&ots=PMHiQSuLx8&dq=V%C4%8Dela%C5%99en%C3%AD%20v%20dob%C4%9B%20klimatick%C3%A9%20zm%C4%9Bny&lr&hl=cs&pg=PA10#v=onepage&q=V%C4%8Dela%C5%99en%C3%AD%20v%20dob%C4%9B%20klimatick%C3%A9%20zm%C4%9Bny&f=true (accessed on 19 October 2024).
- Frey, E.; Rosenkranz, P. Autumn invasion rates of Varroa destructor (Mesostigmata: Varroidae) into honey bee (Hymenoptera: Apidae) colonies and the resulting increase in mite populations. J. Econom. Entomol. 2014, 107, 508–515. [Google Scholar] [CrossRef] [PubMed]
- Von Goetze, G. Die beste Biene: Zuechtungs-und Rassen-kunde der Honigbiene nach dem heutigen Stand von Wissenschaft und Praxis; Liedloff, Loth und Michaelis: Leipzig, Germany, 1940; p. 200. [Google Scholar]
- Ruttner, F. Biogeography and Taxonomy of Honeybees; Springer: Berllin, Germany, 1988; p. xxii+284. [Google Scholar]
- Tomšík, B. Apiar bioclimatical districts of Bohemia and Moravia and appreciation of the bee-family “Iskra II”. Acta Univ. Agricult. Silvicult. Brno 1949, 30, 123. [Google Scholar]
- Tomšík, B. Včela středoevropská žije v Československu. Včelařství 1965, 18, 6–7. [Google Scholar]
- Veselý, V. Bewertung der importierten Rasse der Carnicabiene (Apis mellifera carnica Poll.) und der Hybriden derselben mit der hiesigen Biene in den Bedingungen der ČSR. Sci. Stud. Bee Res. Inst. Dol 1976, 7, 137–157. [Google Scholar]
- Cori, E.O. Včele ušlechtilé a zušlechtění naší obyčejné včely. Český včelař 1875, 9, 49–51, 61–65, 73–75, 85–89, 101–108, 137–139. [Google Scholar]
- Pagač, M.K. Dovozu kraňky do českých zemí. Včelařství 1990, 43, 31. [Google Scholar]
- Živanský, F. Milí ctění členové spolkoví! Včela Brněnská 1872, 6, 1–5. [Google Scholar]
- Büchler, R.; Costa, C.; Hatjina, F.; Andonov, S.; Meixner, M.D.; Conte, Y.L.; Uzunov, A.; Berg, S.; Bienkowska, M.; Bouga, M.; et al. The influence of genetic origin and its interaction with environmental effects on the survival of Apis mellifera L. colonies in Europe. J. Apicult. Res. 2014, 53, 205–214. [Google Scholar] [CrossRef]
- Veselý, V. Strain crossing on mating stations and evaluation of further hybridisation by means of artificial insemination. Sci. Stud. Bee Res. Inst. Dol. 1968, 5, 141–173. [Google Scholar]
- Wragg, D.; Marti-Marimon, M.; Basso, B.; Bidanel, J.P.; Labarthe, E.; Bouchez, O.; Le Conte, Y.; Vignal, A. Whole-genome resequencing of honeybee drones to detect genomic selection in a population managed for royal jelly. Sci. Rep. 2016, 6, 27168. [Google Scholar] [CrossRef] [PubMed]
- De la Rúa, P.; Jaffé, R.; Dall’Olio, R.; Muñoz, I.; Serrano, J. Biodiversity, conservation and current threats to European honeybees. Apidologie 2009, 40, 263–284. [Google Scholar] [CrossRef]
- Bertrand, B.; Alburaki, M.; Legout, H.; Moulin, S.; Mougel, F.; Garnery, L. Mt DNA COI-COII marker and drone congregation area: An efficient method to establish and monitor honeybee (Apis mellifera L.) conservation centers. Mol. Ecol. Resour. 2015, 15, 673–683. [Google Scholar] [CrossRef] [PubMed]
- Parejo, M.; Wragg, D.; Gauthier, L.; Vignal, A.; Neumann, P.; Neuditschko, M. Using whole-genome sequence information to foster conservation efforts for the European dark honey bee, Apis mellifera mellifera. Front. Ecol. Evol. 2016, 4, 140. [Google Scholar] [CrossRef]
- Čermák, K.; Titěra, D.; Janoušek, J.; Sedláček, J.; Cimala, P. Stanovisko chovatelské komise ČSV k článku: “Je to jasná genocida”, autora Bc. Jana Vondráka. Mod. Včelař 2012, 9, 57–58. [Google Scholar]
- Meixner, M.D.; Costa, C.; Kryger, P.; Hatjina, F.; Bouga, M.; Ivanova, E.; Büchler, R. Conserving diversity and vitality for honey bee breeding. J. Apic. Res. 2010, 49, 85–92. [Google Scholar] [CrossRef]
- Pinto, M.A.; Henriques, D.; Chávez-Galarza, J.; Kryger, P.; Garnery, L.; van der Zee, R.; Dahle, B.; Soland-Reckeweg, G.; de la Rúa, P.; Dall’ Olio, R.; et al. Genetic integrity of the Dark European honey bee (Apis mellifera mellifera) from protected populations: A genome-wide assessment using SNPs and mtDNA sequence data. J. Apic. Res. 2014, 53, 269–278. [Google Scholar] [CrossRef]
- Selkoe, K.A.; Toonen, R.J. Microsatellites for ecologists: A practical guide to using and evaluating microsatellite markers. Ecol. Lett. 2006, 9, 615–629. [Google Scholar] [CrossRef] [PubMed]
- Guichoux, E.; Lagache, L.; Wagner, S.; Chaumeil, P.; Léger, P.; Lepais, O.; Lepoittevin, C.; Malausa, T.; Revardel, E.; Salin, F.; et al. Current trends in microsatellite genotyping. Mol. Ecol. Resour. 2011, 11, 591–611. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, I.; Dall’Olio, R.; Lodesani, M.; De la Rúa, P. Population genetic structure of coastal Croatian honeybees (Apis mellifera carnica). Apidologie 2009, 40, 617–626. [Google Scholar] [CrossRef]
- Uzunov, A.; Meixner, M.D.; Kiprijanovska, H.; Andonov, S.; Gregorc, A.; Ivanova, E.; Bouga, M.; Dobi, P.; Büchler, R.; Francis, R. Genetic structure of Apis mellifera macedonica in the Balkan Peninsula based on microsatellite DNA polymorphism. J. Apic. Res. 2014, 53, 288–295. [Google Scholar] [CrossRef]
- Eimanifar, A.; Pieplow, J.T.; Asem, A.; Ellis, J.D. Genetic diversity and population structure of two subspecies of western honey bees (Apis mellifera L.) in the Republic of South Africa as revealed by microsatellite genotyping. PeerJ 2020, 8, e8280. [Google Scholar] [CrossRef]
- Tanasković, M.; Erić, P.; Patenković, A.; Erić, K.; Mihajlović, M.; Tanasić, V.; Kusza, S.; Oleksa, A.; Stanisavljević, L.; Davidović, S. Further Evidence of Population Admixture in the Serbian Honey Bee Population. Insects 2022, 13, 180. [Google Scholar] [CrossRef] [PubMed]
- Bruns, C.E.; Demastes, J.W.; Berendzen, P.B.; Wen, A. The genetic structure of founding bumblebee populations in reconstructed prairie habitat 3 years after planting. Restor. Ecol. 2024, 32, e14176. [Google Scholar] [CrossRef]
- Herrera, C.; Ferragut, J.F.; Leza, M.; Jurado-Rivera, J. Invasion genetics of the yellow-legged hornet Vespa velutina in the Westernmost Mediterranean archipelago. J. Pest. Sci. 2024, 97, 645–656. [Google Scholar] [CrossRef]
- Knoll, A.; Langová, L.; Přidal, A.; Urban, T. Haplotype Diversity in mtDNA of Honeybee in the Czech Republic Confirms Complete Replacement of Autochthonous Population with the C Lineage. Insects 2024, 15, 495. [Google Scholar] [CrossRef] [PubMed]
- Sušnik, S.; Kozmus, P.; Poklukar, J.; Meglic, V. Molecular characterisation of indigenous Apis mellifera carnica in Slovenia. Apidologie 2004, 35, 623–636. [Google Scholar] [CrossRef]
- Nedić, N.; Francis, R.M.; Stanisavljević, L.; Pihler, I.; Kezić, N.; Bendixen, C.; Kryger, P. Detecting population admixture in honey bees of Serbia. J. Apic. Res. 2014, 53, 303–313. [Google Scholar] [CrossRef]
- De La Rúa, P.; Galián, J.; Serrano, J.; Moritz, R.F.A. Genetic structure and distinctness of Apis mellifera L. populations from the Canary Islands. Mol. Ecol. 2001, 10, 1733–1742. [Google Scholar] [CrossRef]
- Coroian, C.O.; Muñoz, I.; Schlüns, E.A.; Paniti-Teleky, O.R.; Erler, S.; Furdui, E.M.; Mărghitaş, L.A.; Dezmirean, D.S.; Schlüns, H.; de la Rúa, P.; et al. Climate rather than geography separates two European honeybee subspecies. Mol. Ecol. 2014, 23, 2353–2361. [Google Scholar] [CrossRef]
- Peakall, R.; Smouse, P.E. GenAlEx 6.5: Genetic analysis in Excel. Population genetic software for teaching and research—An update. Bioinformatics 2012, 28, 2537–2539. [Google Scholar] [CrossRef] [PubMed]
- Weir, B.S.; Cockerham, C.C. Estimating F-statistics for the analysis of population structure. Evolution 1984, 38, 1358–1370. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef]
- Kopelman, N.M.; Mayzel, J.; Jakobsson, M.; Rosenberg, N.A.; Mayrose, I. Clumpak: A program for identifying clustering modes and packaging population structure inferences across K. Mol. Ecol. Resour. 2015, 15, 1179–1191. [Google Scholar] [CrossRef]
- Li, Y.L.; Liu, J.X. StructureSelector: A web based software to select and visualize the optimal number of clusters using multiple methods. Mol. Ecol. Resour. 2021, 18, 176–177. [Google Scholar] [CrossRef] [PubMed]
- Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software structure: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef] [PubMed]
- Puechmaille, S.J. The program structure does not reliably recover the correct population structure when sampling is uneven: Subsampling and new estimators alleviate the problem. Mol. Ecol. Resour. 2016, 16, 608–627. [Google Scholar] [CrossRef] [PubMed]
- Jombart, T.; Devillard, S.; Balloux, F. Discriminant analysis of principal components: A new method for the analysis of genetically structured populations. BMC Genet. 2010, 11, 94. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, I.; De la Rúa, P. Wide genetic diversity in Old World honey bees threaten by introgression. Apidologie 2021, 52, 200–217. [Google Scholar] [CrossRef]
- Péntek-Zakar, E.; Oleksa, A.; Borowik, T.; Kusza, S. Population structure of honey bees in the Carpathian Basin (Hungary) confirms introgression from surrounding subspecies. Ecol. Evol. 2015, 5, 5456–5467. [Google Scholar] [CrossRef] [PubMed]
- Paál, D.; Kopernick, J.; Gasper, J.; Vasícek, D.; Vasícková, K.; Bauerová, M.; Bauer, M. Microsatellite analysis of the Slovak carniolan honey bee (Apis mellifera carnica). J. Microb. Biotech. Food Sci. 2013, 2, 1517–1525. [Google Scholar]
- Gritsenko, D.; Temirbayeva, K.; Taskuzhina, A.; Kostyukova, V.; Pozharskiy, A.; Kolchenko, M.; Khusnitdinova, M.; Krupskiy, O.; Mayer, A.; Nuralieva, U.; et al. First evaluation of genetic diversity among honeybee populations in Kazakhstan. Apidologie 2023, 54, 61. [Google Scholar] [CrossRef]
- Kükrer, M.; Kence, M.; Kence, A. Honey Bee Diversity Is Swayed by Migratory Beekeeping and Trade Despite Conservation Practices: Genetic Evidence for the Impact of Anthropogenic Factors on Population Structure. Front. Ecol. Evol. 2021, 9, 556816. [Google Scholar] [CrossRef]
- Rahimi, A.; Kahrizi, D.; Mirmoayedi, A.; Zarei, L.; Jamali, S. Genetic Characterizations of the Iranian Honey Bee (Apis mellifera meda Skorikov 1929) Populations Using the Microsatellite DNA Markers. Biochem. Genet. 2023, 61, 2293–2317. [Google Scholar] [CrossRef] [PubMed]
- Yıldız, B.İ.; Tüten, E.; Aydın, S.; Karaduman Aslan, Y.; Çetin, R.; Sur, E.; Karabağ, K. A study of whether the genetic variation decreased or not in the protected Caucasian bee, Apis mellifera caucasica Pollmann, 1889 (Hymenoptera: Apidae) population in isolated regions. Turkish J. Ent. 2023, 47, 271–282. [Google Scholar] [CrossRef]




| Locus | N | Na | Ne | I | Ho | He | uHe | F | HWE |
|---|---|---|---|---|---|---|---|---|---|
| A(B)024 | 3626 | 5 | 2.640 | 1.026 | 0.608 | 0.621 | 0.621 | 0.022 | ns |
| A088 | 3637 | 14 | 2.288 | 1.194 | 0.547 | 0.563 | 0.563 | 0.029 | ** |
| Ap043 | 3568 | 14 | 4.072 | 1.634 | 0.718 | 0.754 | 0.755 | 0.049 | *** |
| Ap113 | 3643 | 18 | 1.767 | 0.951 | 0.429 | 0.434 | 0.434 | 0.011 | *** |
| Ap218 | 3412 | 5 | 2.680 | 1.042 | 0.562 | 0.627 | 0.627 | 0.103 | *** |
| Ap249 | 3635 | 12 | 1.868 | 0.865 | 0.451 | 0.465 | 0.465 | 0.030 | *** |
| A007 | 3636 | 25 | 4.511 | 1.838 | 0.762 | 0.778 | 0.778 | 0.022 | *** |
| A014 | 3636 | 26 | 2.030 | 1.290 | 0.502 | 0.508 | 0.508 | 0.011 | *** |
| A079 | 3517 | 17 | 5.986 | 1.968 | 0.819 | 0.833 | 0.833 | 0.017 | *** |
| Ac306 | 3640 | 13 | 2.007 | 1.104 | 0.498 | 0.502 | 0.502 | 0.008 | ns |
| Ap068 | 3632 | 10 | 3.597 | 1.518 | 0.703 | 0.722 | 0.722 | 0.026 | *** |
| Ap223 | 3544 | 7 | 1.722 | 0.796 | 0.413 | 0.419 | 0.419 | 0.016 | *** |
| Ap226 | 3606 | 10 | 2.975 | 1.249 | 0.655 | 0.664 | 0.664 | 0.013 | *** |
| HB-C16-01 | 3292 | 24 | 10.501 | 2.576 | 0.649 | 0.905 | 0.905 | 0.283 | *** |
| A(B)124 | 3553 | 17 | 4.007 | 1.809 | 0.740 | 0.750 | 0.751 | 0.014 | *** |
| AP019 | 3570 | 10 | 2.718 | 1.271 | 0.608 | 0.632 | 0.632 | 0.038 | *** |
| Ap273 | 3643 | 4 | 1.487 | 0.645 | 0.318 | 0.328 | 0.328 | 0.031 | * |
| Ap289 | 3637 | 27 | 1.981 | 1.344 | 0.472 | 0.495 | 0.495 | 0.047 | *** |
| HB-C16-05 | 3615 | 19 | 2.236 | 1.389 | 0.538 | 0.553 | 0.553 | 0.027 | *** |
| A043 | 3513 | 12 | 2.363 | 1.223 | 0.513 | 0.577 | 0.577 | 0.111 | *** |
| Ap049 | 3551 | 8 | 1.728 | 0.905 | 0.370 | 0.421 | 0.421 | 0.121 | *** |
| Ap288 | 3544 | 6 | 1.252 | 0.418 | 0.194 | 0.201 | 0.201 | 0.037 | *** |
| Mean | 3575 | 13.7727 | 3.0189 | 1.2752 | 0.5485 | 0.5796 | 0.5797 | 0.0483 | |
| SE | 18.466 | 1.5146 | 0.4318 | 0.1031 | 0.0329 | 0.0365 | 0.0365 | 0.0131 |
| Locus | N | Na | Ne | I | Ho | He | uHe | F | HWE |
|---|---|---|---|---|---|---|---|---|---|
| A(B)024 | 545 | 4 | 2.605 | 1.018 | 0.591 | 0.616 | 0.617 | 0.041 | ns |
| A088 | 546 | 10 | 2.296 | 1.174 | 0.551 | 0.564 | 0.565 | 0.023 | ns |
| Ap043 | 543 | 10 | 3.984 | 1.593 | 0.729 | 0.749 | 0.750 | 0.026 | ns |
| Ap113 | 550 | 16 | 1.770 | 0.934 | 0.438 | 0.435 | 0.435 | −0.007 | *** |
| Ap218 | 542 | 5 | 2.700 | 1.060 | 0.546 | 0.630 | 0.630 | 0.133 | *** |
| Ap249 | 550 | 8 | 1.847 | 0.832 | 0.467 | 0.459 | 0.459 | −0.019 | ns |
| A007 | 548 | 15 | 4.374 | 1.765 | 0.765 | 0.771 | 0.772 | 0.009 | ns |
| A014 | 548 | 22 | 2.023 | 1.298 | 0.500 | 0.506 | 0.506 | 0.011 | ns |
| A079 | 548 | 13 | 6.169 | 1.992 | 0.816 | 0.838 | 0.839 | 0.026 | ns |
| Ac306 | 548 | 11 | 1.975 | 1.076 | 0.484 | 0.494 | 0.494 | 0.020 | ns |
| Ap068 | 547 | 11 | 3.589 | 1.514 | 0.702 | 0.721 | 0.722 | 0.027 | ns |
| Ap223 | 549 | 5 | 1.744 | 0.796 | 0.439 | 0.427 | 0.427 | −0.029 | ns |
| Ap226 | 549 | 9 | 3.093 | 1.310 | 0.676 | 0.677 | 0.677 | 0.001 | *** |
| HB-C16-01 | 511 | 20 | 10.989 | 2.582 | 0.738 | 0.909 | 0.910 | 0.188 | *** |
| A(B)124 | 532 | 17 | 4.283 | 1.844 | 0.774 | 0.767 | 0.767 | −0.010 | ns |
| AP019 | 541 | 7 | 2.815 | 1.290 | 0.647 | 0.645 | 0.645 | −0.003 | ns |
| Ap273 | 551 | 4 | 1.466 | 0.624 | 0.318 | 0.318 | 0.318 | 0.001 | ns |
| Ap289 | 552 | 24 | 1.942 | 1.317 | 0.476 | 0.485 | 0.485 | 0.018 | ns |
| HB-C16-05 | 546 | 17 | 2.305 | 1.379 | 0.535 | 0.566 | 0.567 | 0.055 | ns |
| A043 | 541 | 8 | 2.250 | 1.162 | 0.505 | 0.556 | 0.556 | 0.092 | *** |
| Ap049 | 541 | 6 | 1.767 | 0.926 | 0.370 | 0.434 | 0.434 | 0.148 | *** |
| Ap288 | 541 | 4 | 1.218 | 0.382 | 0.174 | 0.179 | 0.179 | 0.031 | ns |
| Mean | 544.045 | 11.182 | 3.055 | 1.267 | 0.556 | 0.579 | 0.580 | 0.036 | |
| SE | 1.856 | 1.292 | 0.454 | 0.104 | 0.035 | 0.037 | 0.037 | 0.012 |
| Hive Samples | Flower Samples | |||||
|---|---|---|---|---|---|---|
| Locus | FIS | FIT | FST | FIS | FIT | FST |
| A(B)024 | −0.001 | 0.026 | 0.027 | −0.041 | 0.047 | 0.085 |
| A088 | 0.010 | 0.031 | 0.021 | −0.096 | 0.000 | 0.087 |
| AP043 | 0.022 | 0.046 | 0.025 | −0.067 | 0.021 | 0.083 |
| Ap113 | −0.011 | 0.014 | 0.024 | −0.092 | −0.005 | 0.080 |
| Ap218 | 0.080 | 0.108 | 0.030 | 0.059 | 0.150 | 0.097 |
| Ap249 | 0.005 | 0.031 | 0.026 | −0.100 | −0.011 | 0.081 |
| A007 | −0.001 | 0.023 | 0.023 | −0.067 | 0.017 | 0.079 |
| A014 | −0.013 | 0.010 | 0.023 | −0.085 | 0.004 | 0.082 |
| A079 | −0.007 | 0.017 | 0.024 | −0.061 | 0.030 | 0.086 |
| Ac306 | −0.012 | 0.007 | 0.019 | −0.060 | 0.024 | 0.079 |
| Ap068 | 0.002 | 0.025 | 0.024 | −0.063 | 0.028 | 0.086 |
| Ap223 | −0.006 | 0.015 | 0.021 | −0.124 | −0.031 | 0.082 |
| Ap226 | −0.015 | 0.011 | 0.025 | −0.110 | −0.008 | 0.092 |
| HB-C16-01 | 0.260 | 0.280 | 0.026 | 0.082 | 0.186 | 0.113 |
| A(B)124 | −0.005 | 0.018 | 0.023 | −0.108 | −0.018 | 0.080 |
| AP019 | 0.013 | 0.037 | 0.024 | −0.084 | 0.005 | 0.083 |
| Ap273 | 0.008 | 0.030 | 0.022 | −0.072 | −0.007 | 0.060 |
| Ap289 | 0.031 | 0.049 | 0.019 | −0.064 | 0.019 | 0.078 |
| HB-C16-05 | 0.010 | 0.030 | 0.020 | −0.030 | 0.058 | 0.085 |
| A043 | 0.093 | 0.116 | 0.025 | 0.018 | 0.110 | 0.093 |
| Ap049 | 0.104 | 0.132 | 0.032 | 0.039 | 0.155 | 0.121 |
| Ap288 | 0.009 | 0.036 | 0.026 | −0.066 | 0.015 | 0.076 |
| Mean | 0.026 | 0.050 | 0.024 | −0.054 | 0.036 | 0.086 |
| SE | 0.013 | 0.013 | 0.001 | 0.012 | 0.013 | 0.003 |
| Source | df | Sum of Squares | Mean of Squares | Estimated Variance | Percentage of Variation (%) |
|---|---|---|---|---|---|
| AMOVA (Hive Sample) | |||||
| Between regional populations | 77 | 1251.921 | 16.259 | 0.100 | 2 |
| Among Individuals | 3569 | 24,695.233 | 6.919 | 0.505 | 8 |
| Within Individuals | 3647 | 21,548.000 | 5.908 | 5.908 | 91 |
| Total | 7293 | 47,495.155 | 6.514 | 100 | |
| AMOVA (Flower sample) | |||||
| Between regional populations | 77 | 619.940 | 8.157 | 0.095 | 1 |
| Among Individuals | 476 | 3231.345 | 6.789 | 0.388 | 6 |
| Within Individuals | 553 | 3325.000 | 6.013 | 6.013 | 93 |
| Total | 1105 | 7176.285 | 6.496 | 100 | |
| PCoA via Nei’s Pairwise Distance | PCoA via FST Pairwise Distance | |||||
|---|---|---|---|---|---|---|
| Axis | 1 | 2 | 3 | 1 | 2 | 3 |
| From hives | ||||||
| % | 16.55 | 10.82 | 9.22 | 59.20 | 40.80 | 0.00 |
| Cum. % | 16.55 | 27.37 | 36.59 | 59.20 | 100.00 | 100.00 |
| From flowers | ||||||
| % | 12.59 | 9.15 | 7.49 | 12.44 | 8.61 | 7.94 |
| Cum. % | 12.59 | 21.74 | 29.23 | 12.44 | 21.06 | 29.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knoll, A.; Šotek, M.; Prouza, J.; Langová, L.; Přidal, A.; Urban, T. Assessing Genetic Diversity and Population Structure of Western Honey Bees in the Czech Republic Using 22 Microsatellite Loci. Insects 2025, 16, 55. https://doi.org/10.3390/insects16010055
Knoll A, Šotek M, Prouza J, Langová L, Přidal A, Urban T. Assessing Genetic Diversity and Population Structure of Western Honey Bees in the Czech Republic Using 22 Microsatellite Loci. Insects. 2025; 16(1):55. https://doi.org/10.3390/insects16010055
Chicago/Turabian StyleKnoll, Aleš, Martin Šotek, Jan Prouza, Lucie Langová, Antonín Přidal, and Tomáš Urban. 2025. "Assessing Genetic Diversity and Population Structure of Western Honey Bees in the Czech Republic Using 22 Microsatellite Loci" Insects 16, no. 1: 55. https://doi.org/10.3390/insects16010055
APA StyleKnoll, A., Šotek, M., Prouza, J., Langová, L., Přidal, A., & Urban, T. (2025). Assessing Genetic Diversity and Population Structure of Western Honey Bees in the Czech Republic Using 22 Microsatellite Loci. Insects, 16(1), 55. https://doi.org/10.3390/insects16010055






