Sequential and Binomial Sampling Plans to Estimate Thrips tabaci Population Density on Onion
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
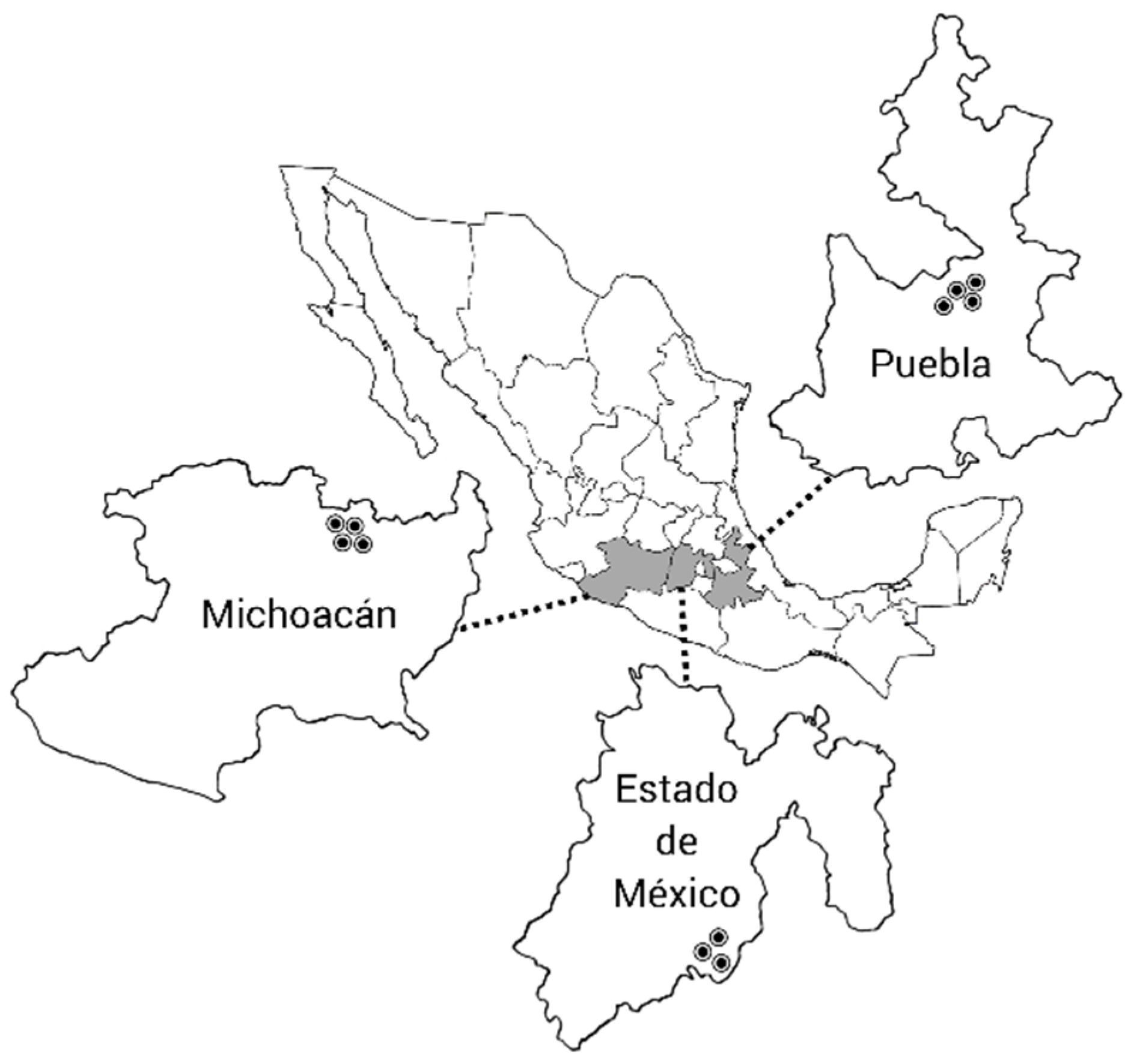
2.1. Sampling of Thrips Populations
2.2. Sequential Enumerative Sampling
2.3. Binomial Sampling
2.4. Validation of Sampling Plans
3. Results
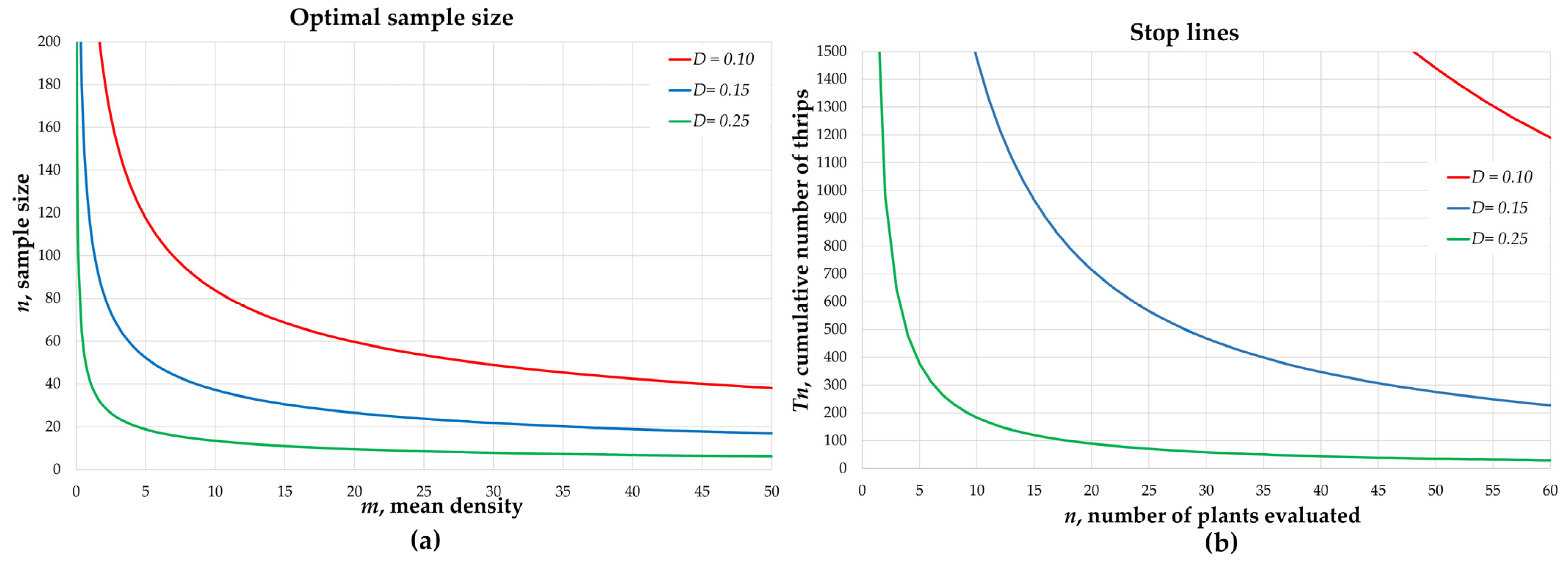
3.1. Sequential Enumerative Sampling
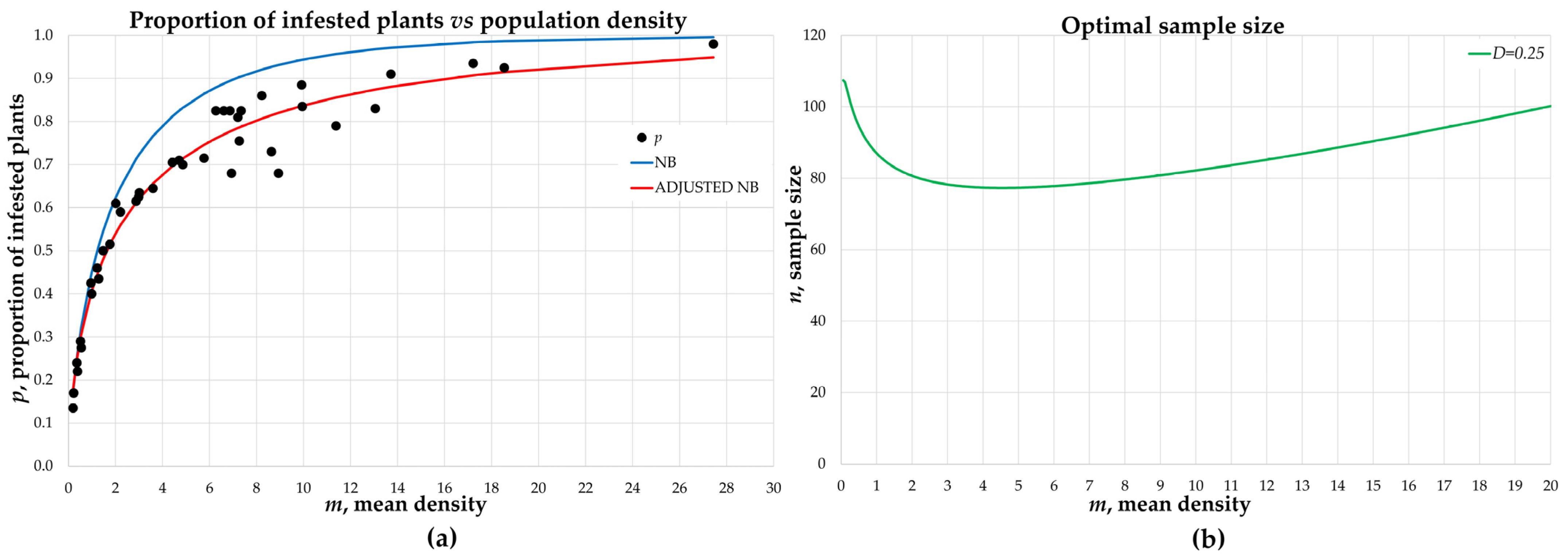
3.2. Binomial Sampling
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gurushidze, M.; Mashayekhi, S.; Blattner, F.R.; Friesen, N.; Fritsch, R.M. Phylogenetic relationships of wild and cultivated species of Allium section cepa inferred by nuclear RDNA ITS sequence analysis. Plant Syst. Evol. 2007, 269, 259–269. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 4 September 2020).
- Diaz-Montano, J.; Fuchs, M.; Nault, B.A.; Fail, J.; Shelton, A.M. Onion thrips (Thysanoptera: Thripidae): A global pest of increasing concern in onion. J. Econ. Entomol. 2011, 104, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Paz, R.; Arrieche, N. Distribución espacial de Thrips tabaci (Lindeman) 1888 (Thysanoptera: Thripidae) en Quíbor, Estado Lara, Venezuela. Bioagro 2017, 29, 123–128. [Google Scholar]
- Kendall, D.M.; Capinera, J.L. Susceptibility of onion growth stages to onion thrips (Thysanoptera: Thripidae) damage and mechanical defoliation. Environ. Entomol. 1987, 16, 859–863. [Google Scholar] [CrossRef]
- Rueda, A.; Badenes-Perez, F.R.; Shelton, A.M. Developing economic thresholds for onion thrips in Honduras. Crop Prot. 2007, 26, 1099–1107. [Google Scholar] [CrossRef]
- Diaz-Montano, J.; Fuchs, M.; Nault, B.A.; Shelton, A.M. Evaluation of onion cultivars for resistance to onion thrips (Thysanoptera: Thripidae) and Iris Yellow Spot Virus. J. Econ. Entomol. 2010, 103, 925–937. [Google Scholar] [CrossRef]
- Sathe, T.V.; Pranoti, M. Occurrence and hosts for a destructive Thrip tabaci Lind. (Thysanoptera: Thripidae). Int. J. Recent Sci. Res. 2015, 6, 2670–2672. [Google Scholar]
- Morse, J.G.; Hoddle, M.S. Invasion biology of thrips. Annu. Rev. Entomol. 2005, 51, 67–89. [Google Scholar] [CrossRef] [PubMed]
- Gill, H.K.; Garg, H.; Gill, A.K.; Gillett-Kaufman, J.L.; Nault, B.A. Onion thrips (Thysanoptera: Thripidae) biology, ecology, and management in onion production systems. J. Integ. Pest Manag. 2015, 6, 6. [Google Scholar] [CrossRef]
- Chatzivassiliou, E.K.; Peters, D.; Katis, N.I. The efficiency by which Thrips tabaci populations transmit Tomato Spotted Wilt Virus depends on their host preference and reproductive strategy. Phytopathology 2002, 92, 603–609. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jacobson, A.L.; Kennedy, G.G. Specific Insect-virus interactions are responsible for variation in competency of different Thrips tabaci Isolines to transmit different Tomato Spotted Wilt Virus isolates. PLoS ONE 2013, 8, e54567. [Google Scholar] [CrossRef]
- Nazemi, A.; Khajehali, J.; Van Leeuwen, T. Incidence and characterization of resistance to pyrethroid and organophosphorus insecticides in Thrips tabaci (Thysanoptera: Thripidae) in onion fields in Isfahan, Iran. Pestic. Biochem. Physiol. 2016, 129, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Castle, S.; Naranjo, S.E. Sampling plans, selective insecticides and sustainability: The case for IPM as ‘Informed Pest Management’. Pest. Manag. Sci. 2009, 65, 1321–1328. [Google Scholar] [CrossRef] [PubMed]
- Romero-Rosales, F. Manejo Ecológico de Patosistemas: Las bases, Los Conceptos y Los Fraudes (o Manejo Integrado de Plagas, MIP); Colección Tlatemoa; Universidad Autónoma Chapingo: Texcoco, México, 2010. [Google Scholar]
- Smith, T.M.; Smith, R.L. Ecología; Addison Wesley: Madrid, Spain, 2007. [Google Scholar]
- Stern, V.M.; van den Bosch, R. The Integration of chemical and biological control of the spotted alfalfa aphid: Field experiments on the effects of insecticides. Hilgardia 1959, 29, 103–130. [Google Scholar] [CrossRef]
- Scheaffer, R.L.; Mendenhall, W.; Ott, L. Elementos de Muestreo; Thomson: Madrid, Spain, 2007. [Google Scholar]
- Southwood, R. Ecological Methods: With Particular Reference to the Study of Insect Populations; Springer: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Taylor, L.R. Assessing and interpreting the spatial distributions of insect populations. Annu. Rev. Entomol. 1984, 29, 321–357. [Google Scholar] [CrossRef]
- Shelton, A.M.; Nyrop, J.P.; North, R.C.; Petzoldt, C.; Foster, R. Development and use of a dynamic sequential sampling program for onion thrips, Thrips tabaci (Thysanoptera: Thripidae), on onions. J. Econ. Entomol. 1987, 80, 1051–1056. [Google Scholar] [CrossRef]
- Fournier, F.; Boivin, G.; Stewart, R.K. Sequential sampling for Thrips tabaci on onions. In Thrips Biology and Management; Parker, B.L., Skinner, M., Lewis, T., Eds.; NATO ASI Series; Springer: Boston, MA, USA, 1995; pp. 557–562. [Google Scholar] [CrossRef]
- Green, R.H. On fixed precision level sequential sampling. Popul. Ecol. 1970, 12, 249–251. [Google Scholar] [CrossRef]
- Kuno, E. Evaluation of statistical precision and design of efficient sampling for the population estimation based on Frequency of occurrence. Popul. Ecol. 1986, 28, 305. [Google Scholar] [CrossRef]
- González, J.E.G.; García, F.; Masiello, L.; Orenga, S.; Ribes, A.; Saques, J. Métodos de muestreo binomial y secuencial para Tetranychus urticae Koch (Acari: Tetranychidae) y Amblyseius californicus (McGregor) (Acari: Phytoseiidae) en fresón. Bol. San. Veg. Plagas 1993, 19, 559–586. [Google Scholar]
- Bechinski, E.J.; Stoltz, R.L. Presence—absence sequential decision plans for Tetranychus urticae (Acari: Tetranychidae) in garden-seed beans, Phaseolus vulgaris. J. Econ. Entomol. 1985, 78, 1475–1480. [Google Scholar] [CrossRef]
- Worner, S.P.; Chapman, R.B. Analysis of binomial sampling data for estimating thrips densities on ornamental plants. N. Z. Plant Prot. 2000, 53, 190–193. [Google Scholar] [CrossRef]
- Carvalho, M.O. Developing and validating sequential sampling plans for integrated pest management on stored products. Adv. Tech. Biol. Med. 2015, 4. [Google Scholar] [CrossRef]
- Namvar, P.; Safaralizadeh, M.H.; Baniameri, V.; Pourmirza, A.A.; Karimzadeh, J. Estimation of larval density of Liriomyza sativae Blanchard (Diptera: Agromyzidae) in cucumber greenhouses using fixed precision sequential sampling plans. Afr. J. Biotechnol. 2012, 11. [Google Scholar] [CrossRef]
- Nakahara, S. The genus Thrips Linnaeus (Thysanoptera: Thripidae) of the New World. In USDA Technical Bulletin No.1822; U.S. Department of Agriculture: Washington, DC, USA, 1994; p. 183. [Google Scholar]
- Mound, L.A.; Masumoto, M. The Genus Thrips (Thysanoptera, Thripidae) in Australia, New Caledonia and New Zealand; Magnolia Press: Auckland, New Zealand, 2005. [Google Scholar]
- Taylor, L.R. Aggregation, variance and the mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Wilson, L.T.; Room, P.M. Clumping patterns of fruit and arthropods in cotton, with implications for binomial sampling. Environ. Entomol. 1983, 12, 50–54. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Grothendieck, G. Nls2: Non-Linear Regression with Brute Force; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Monographs on Statistics and Applied Probability; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Wickham, H. Modelr: Modelling Functions that Work with the Pipe; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Jiménez, S.; Cortiñas, J.; López, D. Temporal and spatial distribution and considerations for the monitoring of Thrips palmi in potato in Cuba. Manejo Integrado Plagas 2000, 57, 54–57. [Google Scholar]
- Quiñones-Valdez, R.; Sánchez-Pale, J.R.; Pedraza-Esquivel, A.K.; Castañeda-Vildozola, A.; Gutierrez-Ibañez, A.T.; Ramírez-Dávila, J.F. Análisis espacial de Thrips Spp. (Thysanoptera) en el cultivo de gladiolo en la región sureste del Estado de México, México. Southwest. Entomol. 2015, 40, 397–408. [Google Scholar] [CrossRef]
- Sardana, H.R.; Bhat, M.; Chaudhary, H.; Sureja, A.K.; Sharma, K.; Ahmad, M. Spatial distribution behaviour of thrips in important cucurbitaceous vegetable crops. Vegetos 2016, 29, 126. [Google Scholar] [CrossRef]
- Sedaratian, A.; Fathipour, Y.; Talebi, A.A.; Farahani, S. Population density and spatial distribution pattern of Thrips tabaci (Thysanoptera: Thripidae) on different soybean varieties. J. Agric. Sci. Tech. 2010, 12, 275–288. [Google Scholar]
- Torres-Vila, L.M.; Lacasa, A.; Meco, R.; Bielza, P. Dinámica Poblacional de Thrips tabaci Lind. (Thysanoptera: Thripidae) sobre liliáceas hortícolas en Castilla-La Mancha. Bol. San. Veg. Plag. 1994, 20, 661–677. [Google Scholar]
- Toledo Arreola, J.; Infante Martínez, F. Manejo Integrado de Plagas; Editorial Trillas: Distrito Federal, México, 2012. [Google Scholar]
- Naranjo, S.E.; Hutchison, W.D. Validation of arthropod sampling plans using a resampling approach: Software and analysis. Am. Entomol. 1997, 43, 48–57. [Google Scholar] [CrossRef]
- Carrizo, P.I.; Klasman, R. Muestreo para el seguimiento poblacional de Frankliniella occidentalis (Pergande, 1895) (Thysanoptera: Thripidae) en cultivo de Dianthus caryophyllus (Cariophyllaceae) en invernadero. Entomotrópica 2002, 17, 7–14. [Google Scholar]
- Cabrera, C.A.; Suris, C.M.; Guerra, B.W.; Nicó, E.D.E. Muestreo secuencial con niveles fijos de precisión para Thrips palmi (Thysanoptera: Thripidae) en papa. Rev. Colomb. Entomol. 2005, 31, 37–42. [Google Scholar]
- Lindenmayer, J.C.; Giles, K.L.; Elliott, N.C.; Knutson, A.E.; Bowling, R.; Brewer, M.J.; Seiter, N.J.; McCornack, B.; Brown, S.A.; Catchot, A.L.; et al. Development of binomial sequential sampling plans for sugarcane aphid (Hemiptera: Aphididae) in commercial grain sorghum. J. Econ. Entomol. 2020, 113, 1990–1998. [Google Scholar] [CrossRef]
- Binns, M.R.; Bostanian, N.J. Robust Binomial decision rules for integrated pest management based on the negative binomial distribution. Am. Entomol. 1990, 36, 50–55. [Google Scholar] [CrossRef]
- Martin, N.A.; Workman, P.J.; Hedderley, D.; Fagan, L.L. Monitoring onion (Allium cepa) crops for onion thrips (Thrips tabaci) (Thysanoptera: Thripidae): Testing a commercial protocol. N. Z. J. Crop. Hort. 2008, 36, 145–152. [Google Scholar] [CrossRef]
- Naranjo, S.E.; Flint, H.M.; Henneberry, T.J. Binomial Sampling plans for estimating and classifying population density of adult Bemisia tabaci in cotton. Entomol. Exp. Appl. 1996, 80, 343–353. [Google Scholar] [CrossRef]
| Fixed Precision | Plot | m ± SE | m′ | Sample Size | D′ ± SE | ||
|---|---|---|---|---|---|---|---|
| Mean | Maximum | Minimum | |||||
| D = 0.10 | 1 | 0.37 ± 0.059 | 0.37 | 440.34 | 797 | 285 | 0.086 ± 0.002 |
| 2 | 0.98 ± 0.112 | 0.97 | 268.88 | 426 | 186 | 0.077 ± 0.001 | |
| 3 | 1.80 ± 0.186 | 1.79 | 197.27 | 300 | 144 | 0.083 ± 0.002 | |
| 4 | 2.97 ± 0.266 | 2.98 | 153.14 | 216 | 109 | 0.077 ± 0.001 | |
| 5 | 5.82 ± 0.416 | 5.81 | 110.67 | 143 | 89 | 0.079 ± 0.002 | |
| 6 | 7.13 ± 0.491 | 7.11 | 99.50 | 124 | 82 | 0.082 ± 0.001 | |
| 7 | 9.82 ± 0.747 | 9.84 | 85.34 | 107 | 68 | 0.093 ± 0.002 | |
| 8 | 13.61 ± 0.907 | 13.62 | 72.42 | 91 | 60 | 0.091 ± 0.002 | |
| 9 | 18.37 ± 1.153 | 18.31 | 62.84 | 76 | 52 | 0.087 ± 0.002 | |
| 10 | 26.97 ± 1.592 | 27.15 | 51.99 | 65 | 44 | 0.097 ± 0.002 | |
| D = 0.15 | 1 | 0.37 ± 0.059 | 0.37 | 196.08 | 395 | 124 | 0.130 ± 0.002 |
| 2 | 0.98 ± 0.112 | 0.98 | 118.19 | 189 | 82 | 0.123 ± 0.002 | |
| 3 | 1.80 ± 0.186 | 1.78 | 88.06 | 143 | 65 | 0.125 ± 0.002 | |
| 4 | 2.97 ± 0.266 | 2.98 | 68.48 | 97 | 52 | 0.118 ± 0.002 | |
| 5 | 5.82 ± 0.416 | 5.82 | 49.07 | 61 | 39 | 0.113 ± 0.002 | |
| 6 | 7.13 ± 0.491 | 7.09 | 44.33 | 59 | 37 | 0.117 ± 0.002 | |
| 7 | 9.82 ± 0.747 | 9.81 | 37.92 | 49 | 31 | 0.137 ± 0.003 | |
| 8 | 13.61 ± 0.907 | 13.65 | 32.29 | 40 | 26 | 0.135 ± 0.003 | |
| 9 | 18.37 ± 1.153 | 18.31 | 27.91 | 34 | 23 | 0.134 ± 0.003 | |
| 10 | 26.97 ± 1.592 | 26.93 | 23.03 | 29 | 20 | 0.137 ± 0.003 | |
| D = 0.25 | 1 | 0.37 ± 0.059 | 0.37 | 69.65 | 164 | 47 | 0.214 ± 0.005 |
| 2 | 0.98 ± 0.112 | 0.98 | 42.56 | 66 | 31 | 0.198 ± 0.004 | |
| 3 | 1.80 ± 0.186 | 1.80 | 31.38 | 51 | 23 | 0.211 ± 0.005 | |
| 4 | 2.97 ± 0.266 | 3.01 | 24.63 | 40 | 20 | 0.206 ± 0.004 | |
| 5 | 5.82 ± 0.416 | 5.80 | 17.62 | 23 | 14 | 0.191 ± 0.004 | |
| 6 | 7.13 ± 0.491 | 7.05 | 15.98 | 21 | 13 | 0.194 ± 0.004 | |
| 7 | 9.82 ± 0.747 | 9.90 | 13.67 | 17 | 11 | 0.226 ± 0.005 | |
| 8 | 13.61 ± 0.907 | 13.52 | 11.64 | 14 | 10 | 0.218 ± 0.005 | |
| 9 | 18.37 ± 1.153 | 18.33 | 10.03 | 12 | 8 | 0.226 ± 0.005 | |
| 10 | 26.97 ± 1.592 | 26.81 | 8.31 | 10 | 7 | 0.224 ± 0.005 | |
| Fixed Precision | Plot | m ± SE | m′ | Sample Size | D′ ± SE | ||
|---|---|---|---|---|---|---|---|
| Mean | Maximum | Minimum | |||||
| D = 0.25 | 1 | 0.37 ± 0.059 | 0.28 | 116.05 | 366 | 90 | 0.31 ± 0.005 |
| 2 | 0.98 ± 0.112 | 1.11 | 121.29 | 193 | 104 | 0.24 ± 0.007 | |
| 3 | 1.80 ± 0.186 | 1.82 | 131.79 | 243 | 110 | 0.17 ± 0.004 | |
| 4 | 2.97 ± 0.266 | 3.03 | 150.14 | 286 | 109 | 0.16 ± 0.004 | |
| 5 | 5.82 ± 0.416 | 5.03 | 165.75 | 419 | 106 | 0.19 ± 0.003 | |
| 6 | 7.13 ± 0.491 | 6.02 | 176.65 | 487 | 108 | 0.20 ± 0.003 | |
| 7 | 9.82 ± 0.747 | 12.31 | 327.87 | 1023 | 118 | 0.26 ± 0.009 | |
| 8 | 13.61 ± 0.907 | 16.23 | 393.46 | 1644 | 113 | 0.21 ± 0.005 | |
| 9 | 18.37 ± 1.153 | 17.99 | 384.77 | 1416 | 124 | 0.13 ± 0.004 | |
| 10 | 26.97 ± 1.592 | 30.25 | 576.04 | 1336 | 154 | 0.16 ± 0.004 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto-Rojas, L.; Rodríguez-Leyva, E.; Bautista-Martínez, N.; Ruíz-Galván, I.; García-Palacios, D. Sequential and Binomial Sampling Plans to Estimate Thrips tabaci Population Density on Onion. Insects 2021, 12, 331. https://doi.org/10.3390/insects12040331
Soto-Rojas L, Rodríguez-Leyva E, Bautista-Martínez N, Ruíz-Galván I, García-Palacios D. Sequential and Binomial Sampling Plans to Estimate Thrips tabaci Population Density on Onion. Insects. 2021; 12(4):331. https://doi.org/10.3390/insects12040331
Chicago/Turabian StyleSoto-Rojas, Lauro, Esteban Rodríguez-Leyva, Néstor Bautista-Martínez, Isabel Ruíz-Galván, and Daniel García-Palacios. 2021. "Sequential and Binomial Sampling Plans to Estimate Thrips tabaci Population Density on Onion" Insects 12, no. 4: 331. https://doi.org/10.3390/insects12040331
APA StyleSoto-Rojas, L., Rodríguez-Leyva, E., Bautista-Martínez, N., Ruíz-Galván, I., & García-Palacios, D. (2021). Sequential and Binomial Sampling Plans to Estimate Thrips tabaci Population Density on Onion. Insects, 12(4), 331. https://doi.org/10.3390/insects12040331








