Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling
Abstract
:1. Introduction
2. Analytical Modelling
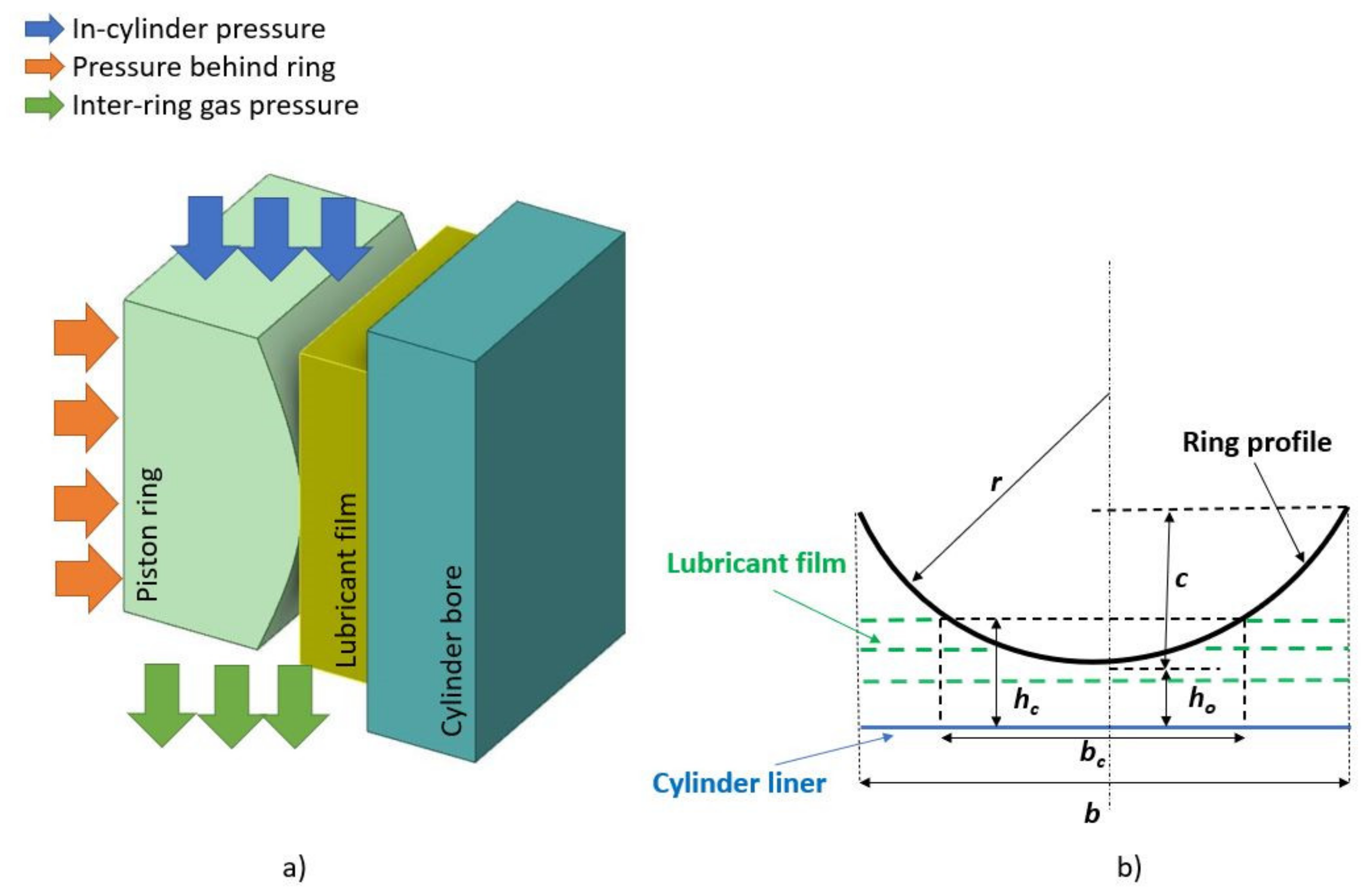
2.1. Description of Piston Ring-Liner Contact
2.2. Determination of Load by Lubricant Film
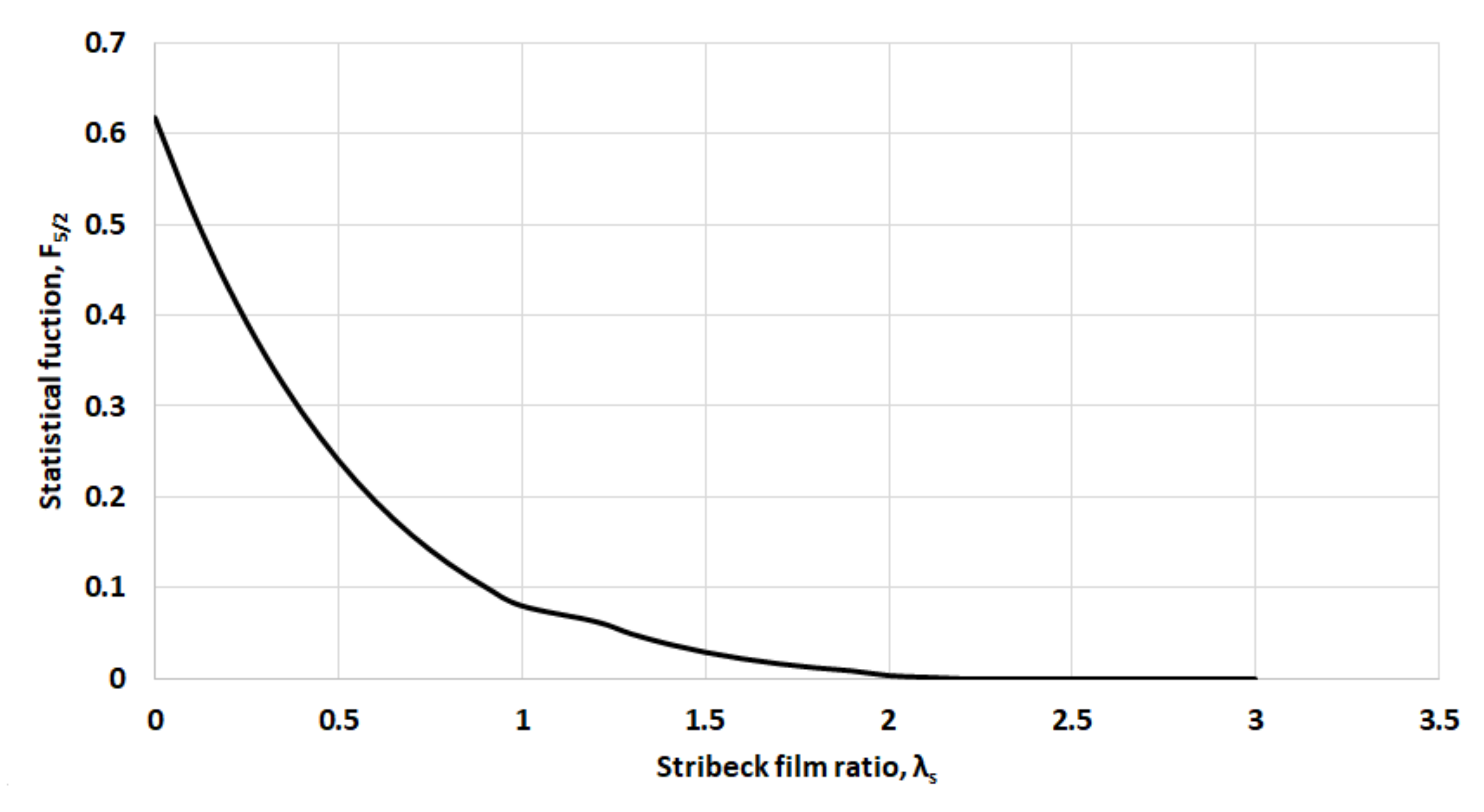
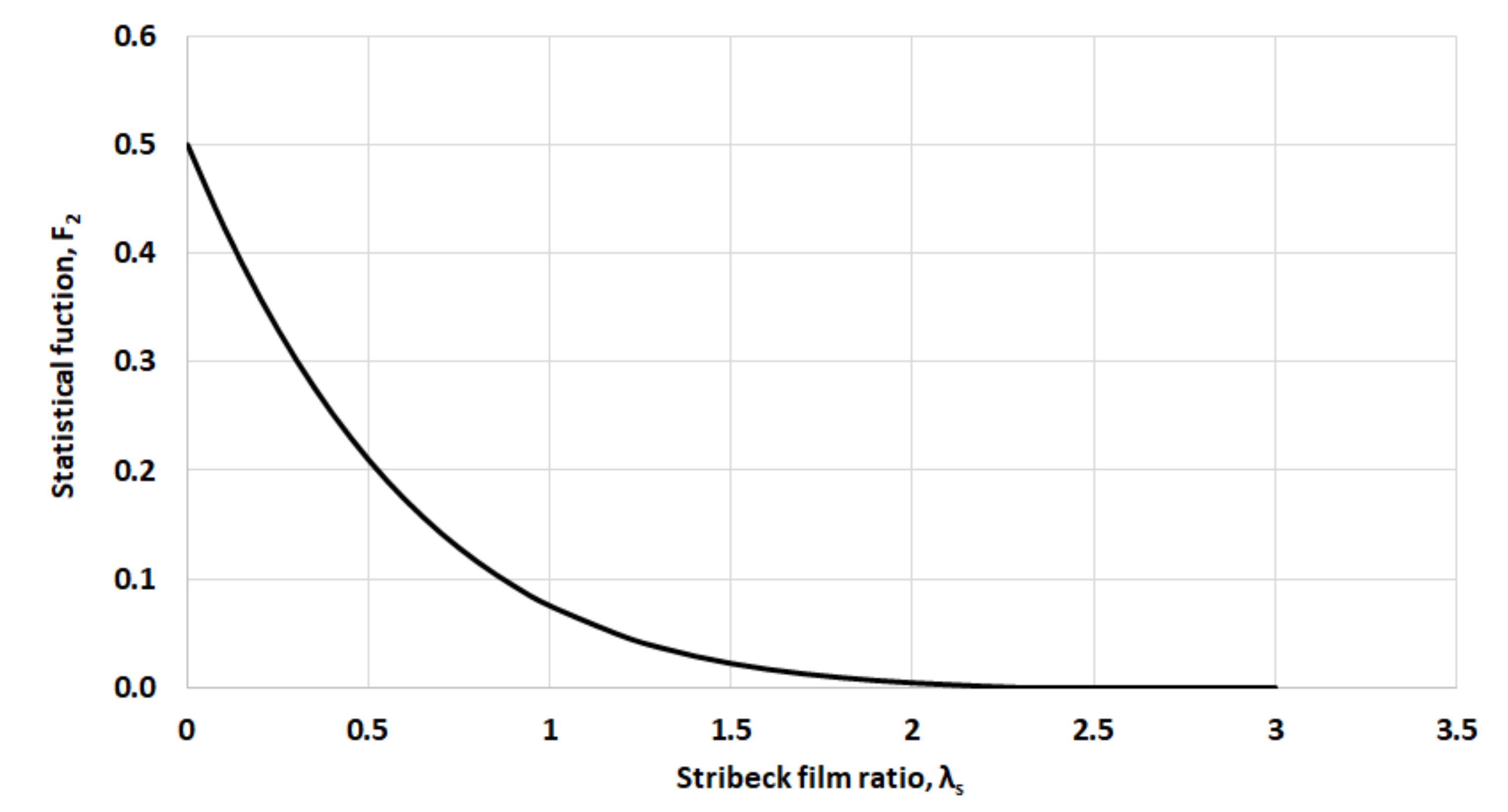
2.3. Determination of Load Carried by the Asperities
2.4. Method of Analytical Solution
2.5. Low Viscosity Oils
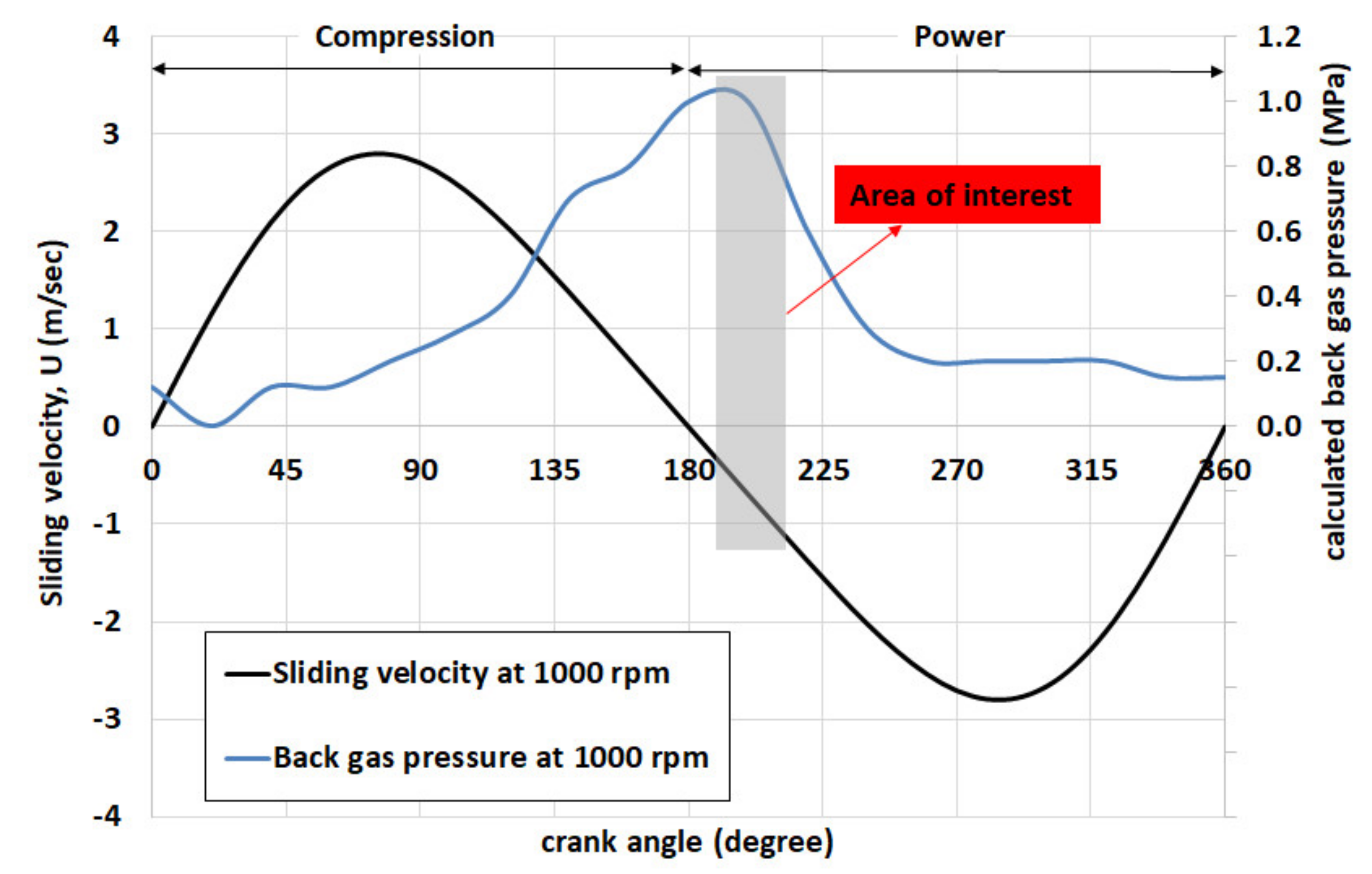
2.6. Ring Friction
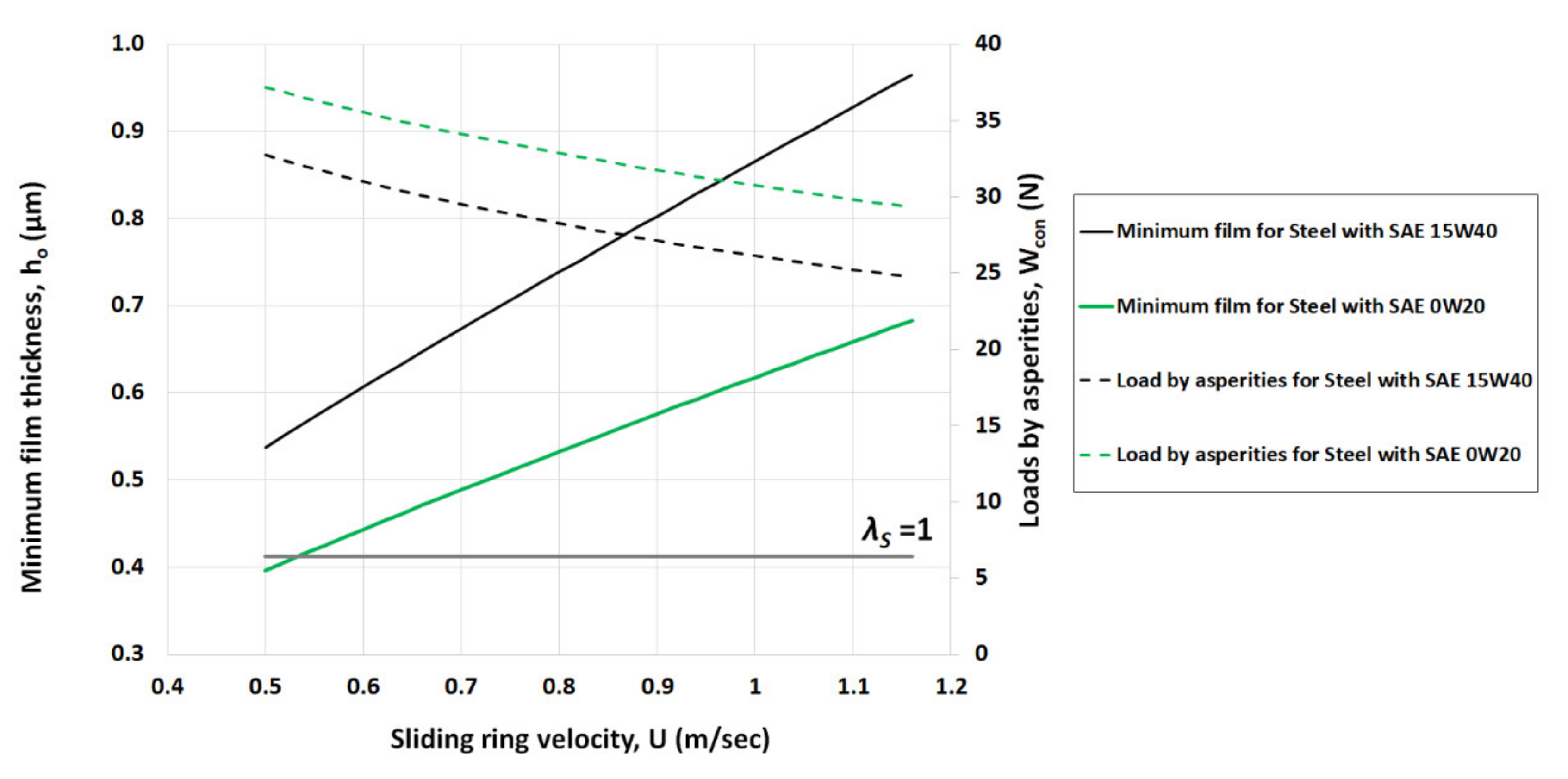
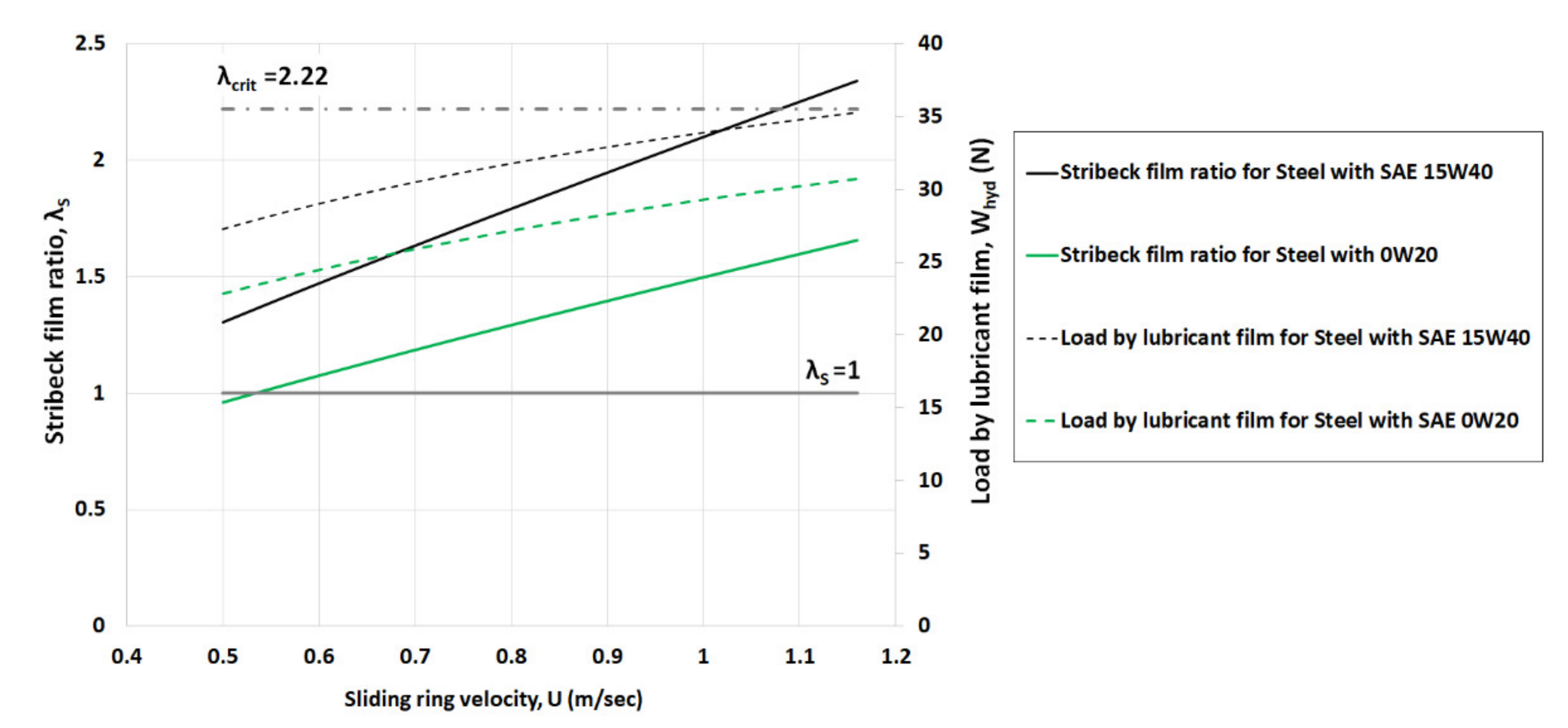
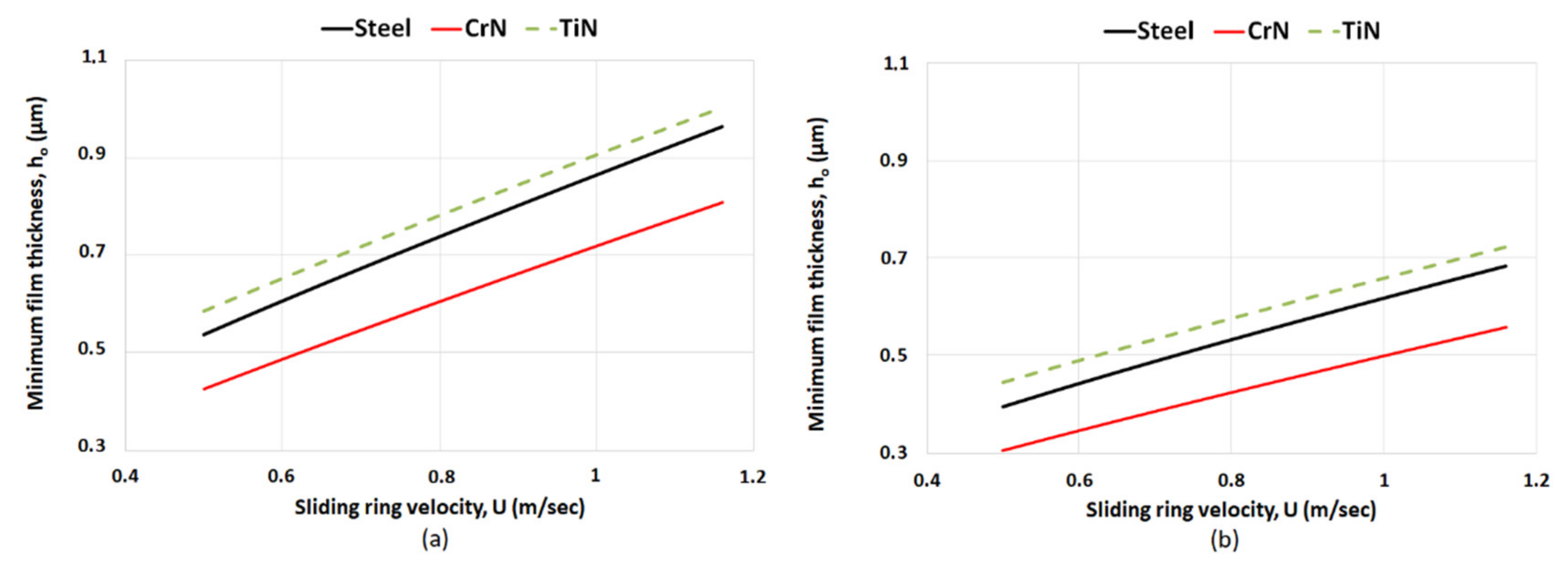
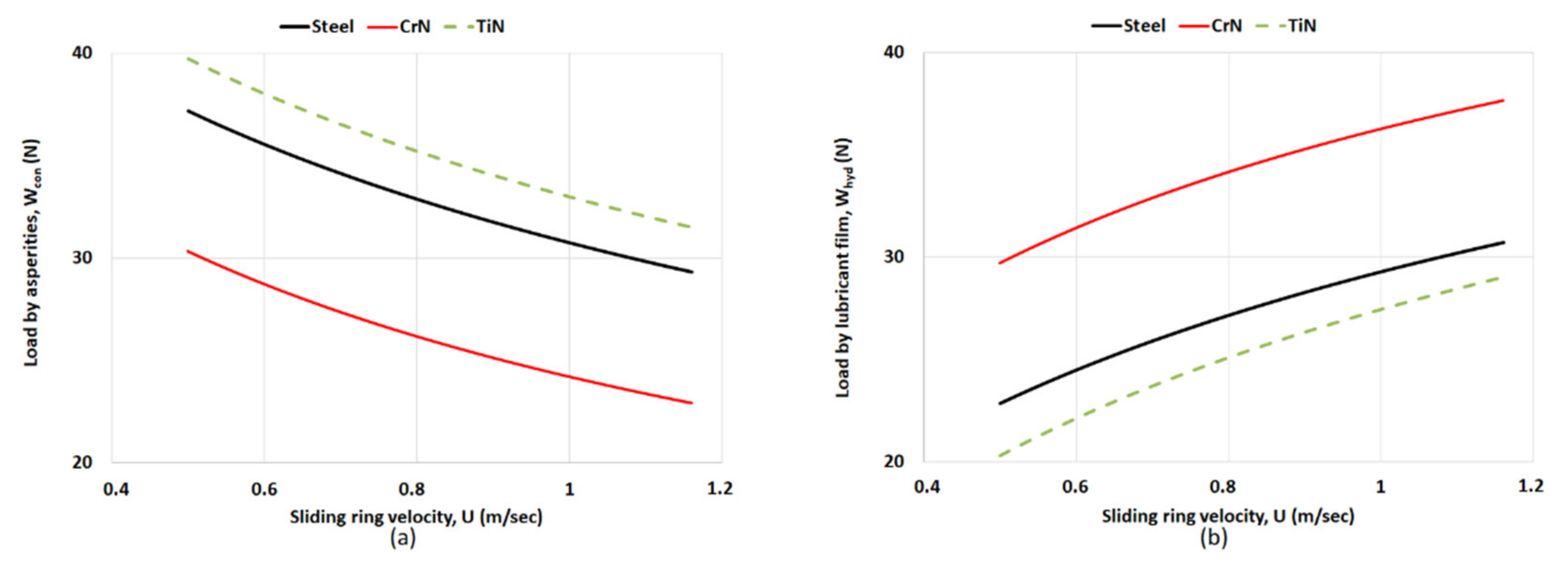
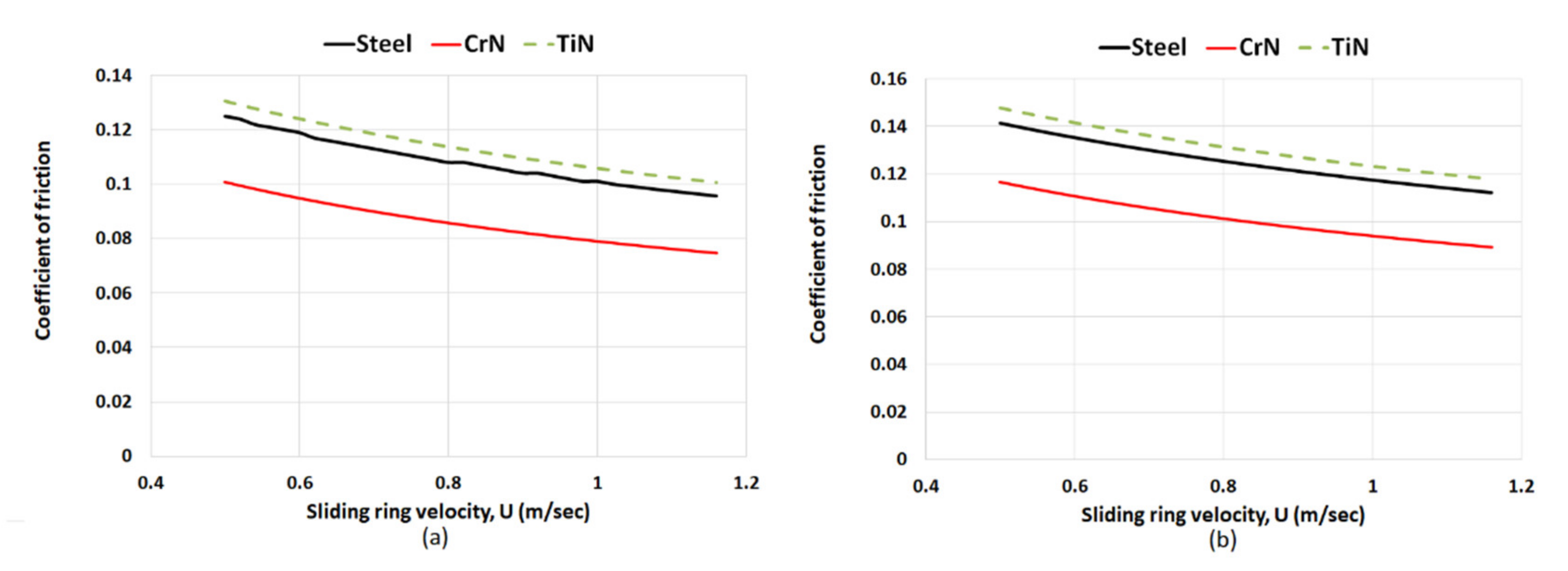
3. Results and Discussion
3.1. Input Coated Piston Rings and Cylinder Liner Data for the Analysis
3.2. Analysis of Minimum Film Thickness and Coefficient of Friction
4. Summary and Conclusions
Funding
Conflicts of Interest
Nomenclature
| A | nominal contact area |
| Acon | asperity contact area |
| b | ring face-width contact |
| bc | critical length along the ring face-width contact |
| c | ring curvature or crown height |
| Ε | Young’s modulus of elasticity |
| Ε* | equivalent Young’s modulus of elasticity |
| F | applied ring load |
| ftot | total friction |
| fv | viscous friction |
| fb | boundary friction |
| F5/2, F2 | statistical functions |
| h | lubricant film thickness |
| hc | critical film thickness |
| ho | minimum film thickness |
| hs | ring face-width profile |
| k | Vogel parameter for describing lubricant viscosity variation with temperature |
| L | ring lateral length |
| phyd | hydrodynamic pressure |
| Pinlet | inlet pressure at the piston ring conjunction |
| Pout | outlet pressure at the piston ring conjunction |
| r | radius of ring curvature |
| M,N | input variables |
| T | lubricant temperature |
| U | sliding velocity |
| Wtot | total load carrying capacity |
| Wcon | load share by the asperities |
| Whyd | load carried by the lubricant film |
| Greek symbols | |
| δ | local contact deformation |
| ε | step for minimum film thickness loop |
| ζ | surface density of asperity peaks |
| θ1,θ2 | Vogel parameters for lubricant viscosity variation with temperature |
| κ | average asperity tip radius |
| λs | Stribeck oil film parameter |
| μ | lubricant dynamic viscosity |
| μasp | coefficient of boundary shear strength |
| ν | Poisson ratio |
| σ | root mean square roughness value of the studied tribo-pair |
| τ | viscous shear stress |
| το | Eyring shear stress of the lubricant film |
| X | parameter for ring balance |
| Superscripts | |
| n | iteration step |
| Subscripts | |
| asp | asperity |
| b | boundary |
| c,crit | critical |
| con | contact |
| hyd | hydrodynamic |
| l | liner |
| r | ring |
| s | shape |
| S | Stribeck |
| tot | total |
| v | viscous |
References
- Tung, S.C.; McMillan, M.L. Automotive tribology overview of current advances and challenges for the future. Tribol. Int. 2004, 37, 517–536. [Google Scholar] [CrossRef]
- Szymanski, P.; Ciuffo, B.; Fontaras, G.; Martini, G.; Pekar, F.; Wozniak, M.; Ozuna, G.; Siczek, K.; Stoeck, T.; Sitnik, L. The future of road transport in Europe. Environmental implications of automated, connected and low-carbon mobility. Combust. Engines 2021, 186, 3–10. [Google Scholar] [CrossRef]
- Golloch, R.; Kessen, U.; Merker, G.P. Tribological investigations on the piston assembly group of a diesel engine. MTZ Worldw. 2002, 63, 21–24. [Google Scholar] [CrossRef]
- Senatore, A.; Aleksendric, D. Advances in piston rings modelling and design. Recent Pat. Eng. 2013, 7, 51–67. [Google Scholar] [CrossRef]
- Livanos, G.A.; Kyrtatos, N.P. Friction model of a marine diesel engine piston assembly. Tribol. Int. 2007, 40, 1441–1453. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A. Piston ring–liner lubrication and tribological performance evaluation: A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 193–209. [Google Scholar] [CrossRef]
- Mishra, P.C. Modeling the root causes of engine friction loss: Transient elastohydrodynamics of a piston subsystem and cylinder liner lubricated contact. Appl. Math. Model. 2015, 39, 2234–2260. [Google Scholar] [CrossRef]
- Marui, E.; Endo, H. Effect of reciprocating and unidirectional sliding motion on the friction and wear of copper on steel. Wear 2001, 249, 582–591. [Google Scholar] [CrossRef]
- Chaudhari, T.; Sutaria, B. Investigation of friction characteristics in segmented piston ring liner assembly of IC engine. Perspect. Sci. 2016, 8, 599–602. [Google Scholar] [CrossRef] [Green Version]
- Furuhama, S. A Dynamic Theory of Piston-Ring Lubrication: 1st Report, Calculation. Bull. JSME 1959, 2, 423–428. [Google Scholar] [CrossRef]
- Furuhama, S. A Dynamic Theory of Piston-Ring Lubrication: 2nd Report, Experiment. Bull. JSME 1960, 3, 291–297. [Google Scholar] [CrossRef] [Green Version]
- Tian, T.; Noordzij, L.; Wong, V.W.; Heywood, J.B. Modeling Piston-Ring Dynamics, Blowby, and Ring-Twist Effects. ASME J. Eng. Gas Turbines Power 1998, 120, 843–854. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. Trans. ASME 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Wolff, A. Influence of piston ring pack configuration on blowby and friction losses in a marine two-stroke engine. Combust. Engines 2017, 170, 164–170. [Google Scholar] [CrossRef]
- Priest, M.; Dowson, D.; Taylor, C.M. Theoretical modelling of cavitation in piston ring lubrication. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2000, 214, 435–447. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Howell-Smith, S.; Teodorescu, M.; Vaughan, N.D. The influence of inter-ring pressures on piston-ring/liner tribological conjunction. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 154–167. [Google Scholar] [CrossRef]
- Nouri, J.M.; Vasilakos, I.; Yan, Y.; Reyes-Aldasoro, C.C. Effect of viscosity and speed on oil cavitation development in a single piston-ring lubricant assembly. Lubricants 2019, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.I.; Morgan, N.; Mainwaring, R.; Davenport, T. How much mixed/boundary friction is there in an engine—And where is it? Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1563–1579. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Fitzsimons, B. The influence of piston ring geometry and topography on friction. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Söderfjäll, M.; Herbst, H.M.; Larsson, R.; Almqvist, A. Influence on friction from piston ring design, cylinder liner roughness and lubricant properties. Tribol. Int. 2017, 116, 272–284. [Google Scholar] [CrossRef]
- Erdemir, A.; Holmberg, K. Energy consumption due to friction in motored vehicles and low-friction coatings to reduce it. In Coating Technology for Vehicle Applications; Springer: Cham, Switzerland, 2015; pp. 1–23. [Google Scholar]
- Ferreira, R.; Martins, J.; Carvalho, Ó.; Sobral, L.; Carvalho, S.; Silva, F. Tribological solutions for engine piston ring surfaces: An overview on the materials and manufacturing. Mater. Manuf. Process. 2020, 35, 498–520. [Google Scholar] [CrossRef]
- Friedrich, C.; Berg, G.; Broszeit, E.; Rick, F.; Holland, J. PVD CrxN coatings for tribological application on piston rings. Surf Coat. Technol. 1997, 97, 661–668. [Google Scholar] [CrossRef]
- Abril, S.O.; García, C.P.; León, J.P. Numerical and Experimental Analysis of the Potential Fuel Savings and Reduction in CO Emissions by Implementing Cylinder Bore Coating Materials Applied to Diesel Engines. Lubricants 2021, 9, 19. [Google Scholar] [CrossRef]
- Barbezat, G. Advanced thermal spray technology and coating for lightweight engine blocks for the automotive industry. Surf. Coat. Technol. 2005, 200, 1990–1993. [Google Scholar] [CrossRef]
- Igartua, A.; Fdez-Pérez, X.; Conte, M.; Illarramendi, I. Tribological tests to simulate wear on piston rings. In Critical Component Wear in Heavy Duty Engines; Lakshminarayanan, P.A., Nayak, N.S., Eds.; John Wiley & Sons Ltd.: Singapore, 2011; pp. 167–195. [Google Scholar]
- Zabala, B.; Igartua, A.; Fernández, X.; Priestner, C.; Ofner, H.; Knaus, O.; Abramczuk, M.; Tribotte, P.; Girot, F.; Roman, E.; et al. Friction and wear of a piston ring/cylinder liner at the top dead centre: Experimental study and modelling. Tribol. Int. 2017, 106, 23–33. [Google Scholar] [CrossRef]
- Gore, M.; Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Howell-Smith, S. A combined analytical-experimental investigation of friction in cylinder liner inserts under mixed and boundary regimes of lubrication. Lubr. Sci. 2017, 29, 293–316. [Google Scholar] [CrossRef] [Green Version]
- Dolatabadi, N.; Forder, M.; Morris, N.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Influence of advanced cylinder coatings on vehicular fuel economy and emissions in piston compression ring conjunction. Appl. Energy 2020, 259, 114129. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P. Thermo-mixed lubrication analysis of coated compression rings with worn cylinder profiles. Ind. Lubr. Tribol. 2017, 69, 15–29. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Grigoriadis, K.; Zavos, A. Contact modeling with a finite element model in piston ring—liner conjunction under dry conditions. Int. J. Struct. Integr. 2019, 10, 393–414. [Google Scholar] [CrossRef]
- Taylor, R.I. Squeeze film lubrication in piston rings and reciprocating contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 977–988. [Google Scholar] [CrossRef]
- Tomanik, E.; Profito, F.; Sheets, B.; Souza, R. Combined lubricant–surface system approach for potential passenger car CO2 reduction on piston-ring-cylinder bore assembly. Tribol. Int. 2018, 149, 105514. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Tribology of new thin compression ring of fired engine under controlled conditions-a combined experimental and numerical study. Tribol. Int. 2018, 128, 214–230. [Google Scholar] [CrossRef]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology; Imperial College Press: London, UK, 2008; ISBN 978-1-84816860-2. [Google Scholar]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Teodorescu, M.; Balakrishnan, S.; Rahnejat, H. Integrated tribological analysis within a multi-physics approach to system dynamics. In Tribology and Interface Engineering Series; Elsevier: Amsterdam, The Netherlands, 2005; Volume 48, pp. 725–737. [Google Scholar]
- Vogel, H. The law of the relation between the viscosity of liquids and the temperature. Phys. Z 1921, 22, 645–646. [Google Scholar]
- Styles, G.; Rahmani, R.; Rahnejat, H.; Fitzsimons, B. In-cycle and life-time friction transience in piston ring–liner conjunction under mixed regime of lubrication. Int. J. Engine Res. 2014, 15, 862–876. [Google Scholar] [CrossRef] [Green Version]
- Arcoumanis, C.; Ostovar, P.; Mortimer, R. Mixed Lubrication Modelling of Newtonian and Shear Thinning Liquids in a Piston-Ring Configuration. SAE Transactions Pap. No. 972924. 1997, 106, 1306–1331. [Google Scholar]
- Rahmani, R.; Rahnejat, H.; Fitzsimons, B.; Dowson, D. The effect of cylinder bore operating temperature on frictional loss and engine emissions in piston ring conjunction. Appl. Energy 2017, 191, 568–581. [Google Scholar] [CrossRef] [Green Version]
- Dowson, D. A central film thickness formula for elasto-hydrodynamic line contacts. In Proceedings of the 5th Leeds-Lyon Symposium, Leeds, UK, 19–22 September 1978. [Google Scholar]
- Tung, S.C.; Gao, H. Tribological Investigation of Piston Ring Coatings Operating in an Alternative Fuel and Engine Oil Blend. Tribol. Trans. 2002, 45, 381–389. [Google Scholar] [CrossRef]
- Howell-Smith, S.; Rahnejat, H.; King, P.D.; Dowson, D. Reducing in-cylinder parasitic losses through surface modification and coating. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 391–402. [Google Scholar] [CrossRef] [Green Version]
- Zavos, A.; Nikolakopoulos, P.G. The effect of square-shaped pockets position in sliding line contacts under mixed regime of lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 490–506. [Google Scholar] [CrossRef]


| Parameter | Cylinder Liner Base Material | Piston Ring Base Material | Ring Coatings | Unit | |
|---|---|---|---|---|---|
| Material | Aluminium | Steel | CrN | TiN | - |
| Young’s modulus of elasticity | 70 | 200 | 400 | 250 | GPa |
| Poisson’s ratio | 0.33 | 0.31 | 0.2 | 0.25 | - |
| Density | 2980 | 7850 | 5900 | 5200 | Kg m−3 |
| SAE 15W40 | SAE 0W20 | |
|---|---|---|
| K (MPA.S) | 0.029 | 0.071 |
| θ1 (°C) | 1424.3 | 983.2 |
| θ2 (°C) | 137.2 | 116.2 |
| M (120 °C) (PA.S) | 0.0073 | 0.0045 |
| Parameter | Piston Ring Uncoated | Piston Ring Coated | Unit | |
|---|---|---|---|---|
| Material | Steel | CrN | TiN | - |
| Ring-face width | 0.5 | 0.5 | 0.5 | mm |
| Ring radius of curvature | 40.5 | 40.5 | 40.5 | mm |
| Ring lateral length | 40 | 40 | 40 | mm |
| Ring surface roughness | 0.40 | 0.25 | 0.31 | μm |
| Liner surface roughness | 0.1 | 0.1 | 0.1 | μm |
| (RMS) surface finish of contact surfaces | 0.412 | 0.269 | 0.325 | μm |
| Equivalent Young’s modulus of elasticity | 115.94 | 132.18 | 121.35 | GPa |
| Roughness parameter | 0.0412 | 0.0486 | 0.0220 | - |
| Asperity slope | 2.51 × 10−5 | 1.16 × 10−5 | 5.50 × 10−4 | - |
| Eyring shear stress | 2 | 2 | 2 | MPa |
| Coefficient of boundary shear strength | 0.22 | 0.22 | 0.22 | - |
| Lubricant temperature | 120 | 120 | 120 | °C |
| Sliding velocity | 0.5–1.16 | 0.5–1.16 | 0.5–1.16 | m/s |
| Applied load | 60 | 60 | 60 | N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavos, A. Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling. Lubricants 2021, 9, 124. https://doi.org/10.3390/lubricants9120124
Zavos A. Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling. Lubricants. 2021; 9(12):124. https://doi.org/10.3390/lubricants9120124
Chicago/Turabian StyleZavos, Anastasios. 2021. "Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling" Lubricants 9, no. 12: 124. https://doi.org/10.3390/lubricants9120124
APA StyleZavos, A. (2021). Effect of Coating and Low Viscosity Oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling. Lubricants, 9(12), 124. https://doi.org/10.3390/lubricants9120124





