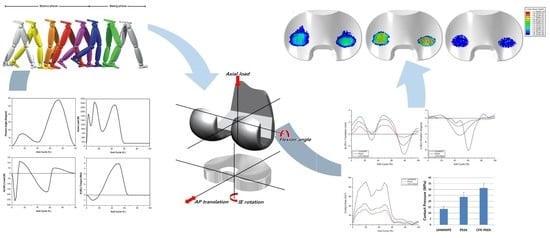
Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Model
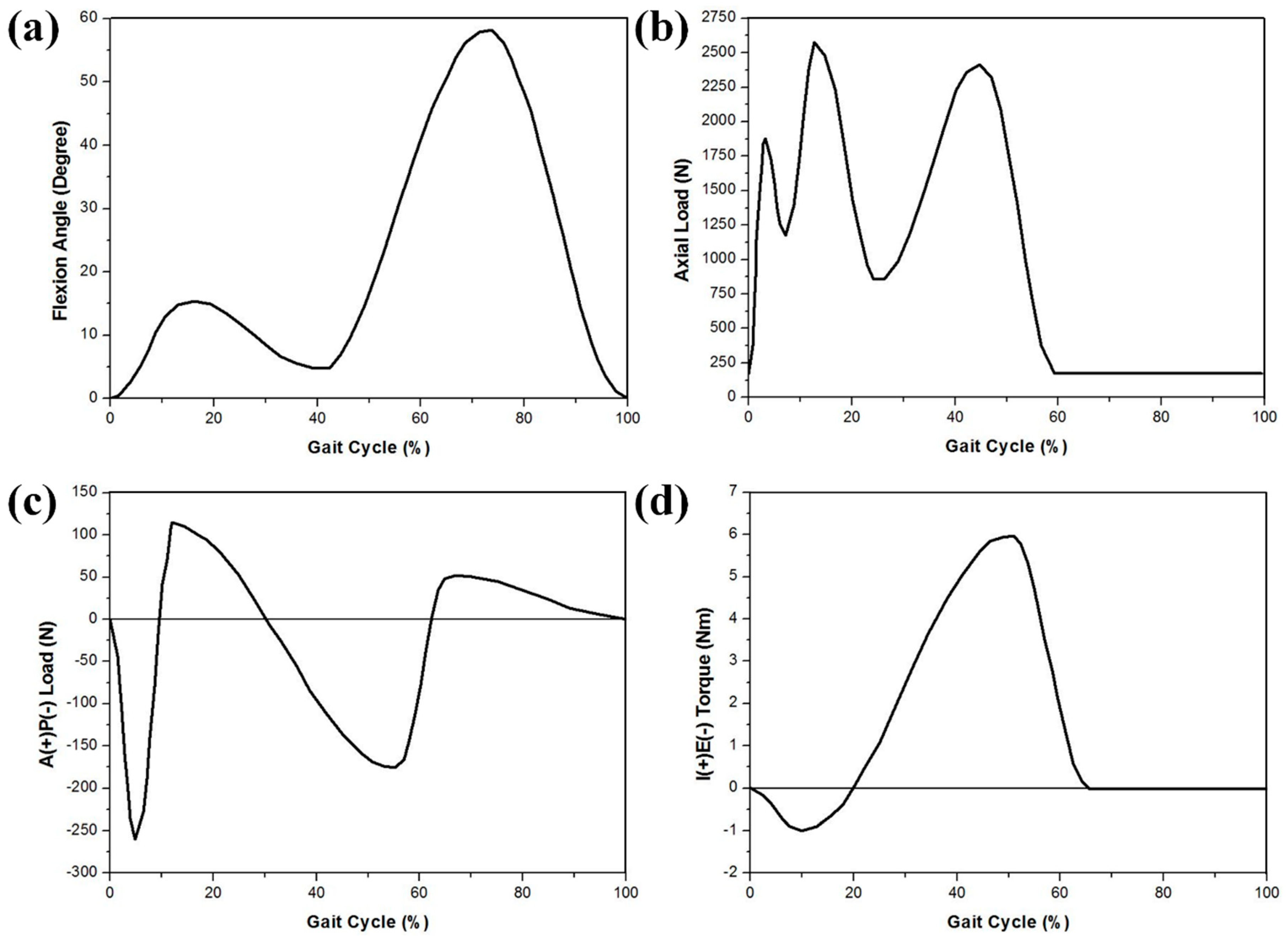
2.2. Boundary and Loading Conditions
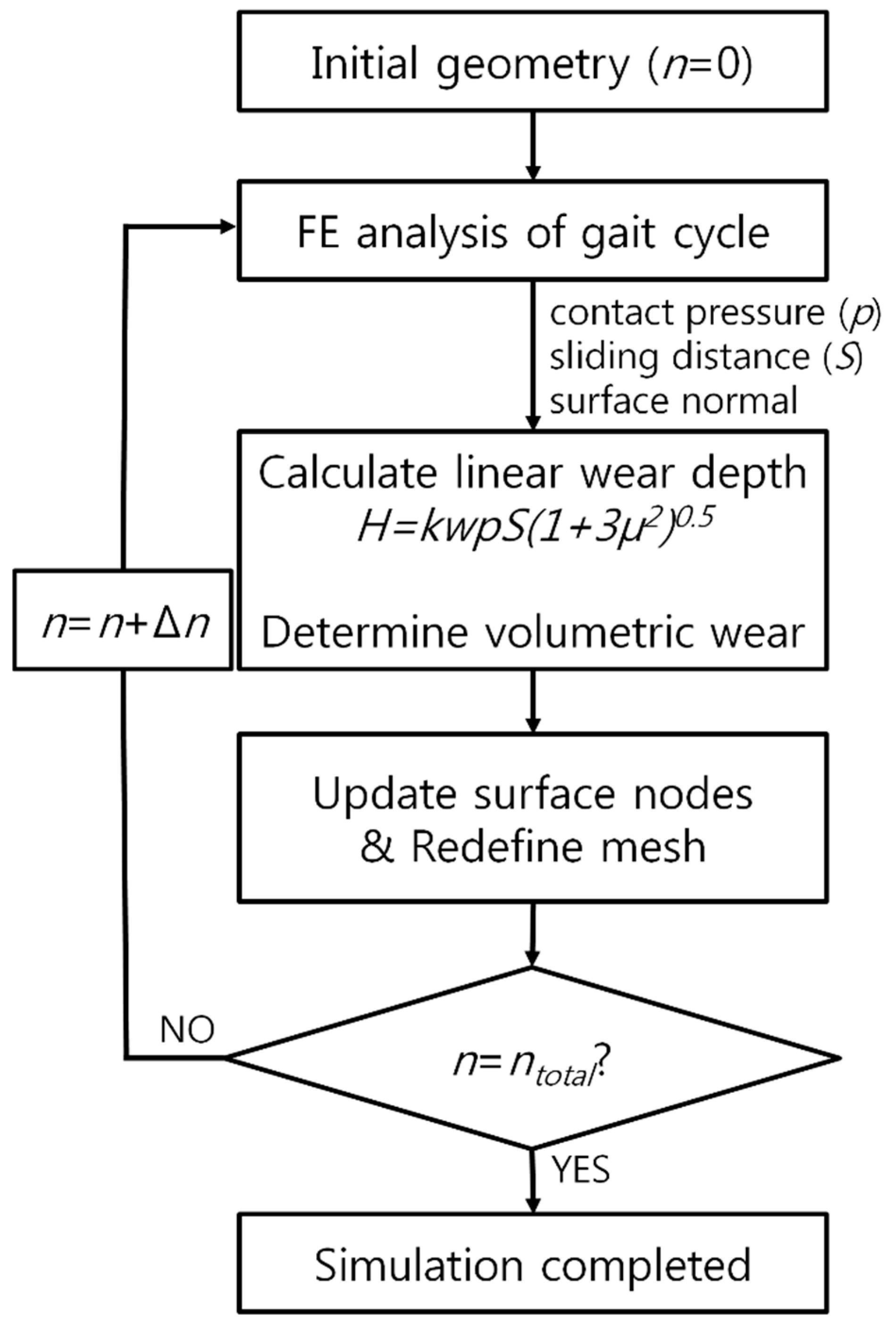
2.3. Computational Wear Simulation
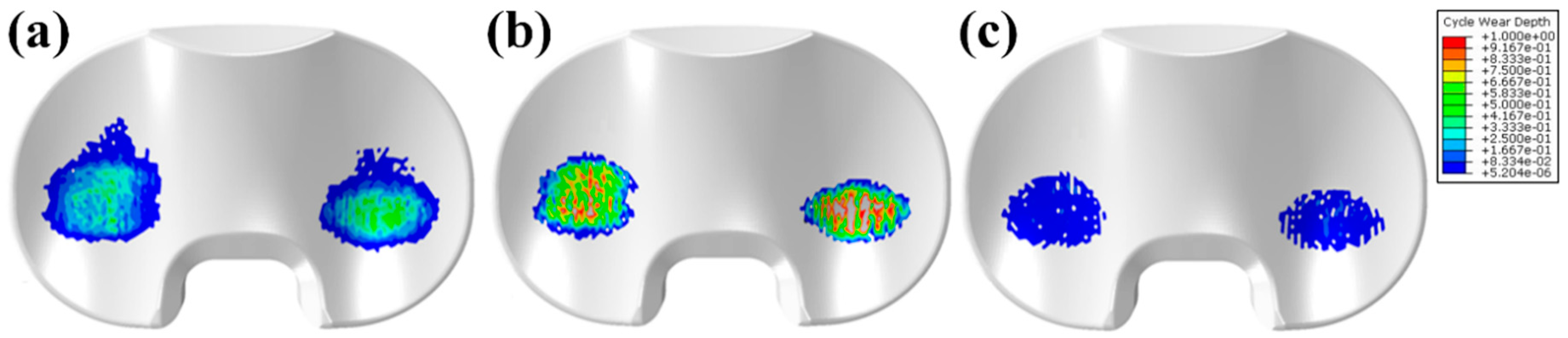
3. Results
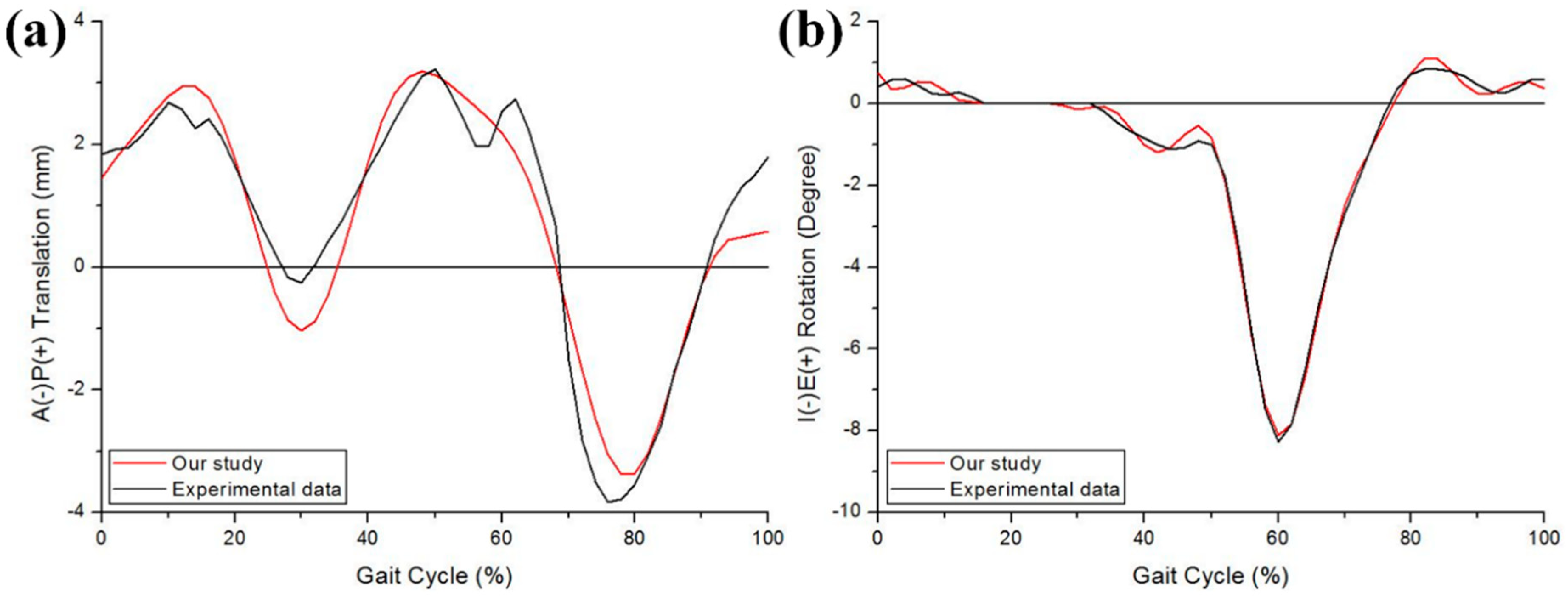
3.1. Validation of UHMWPE Wear Model
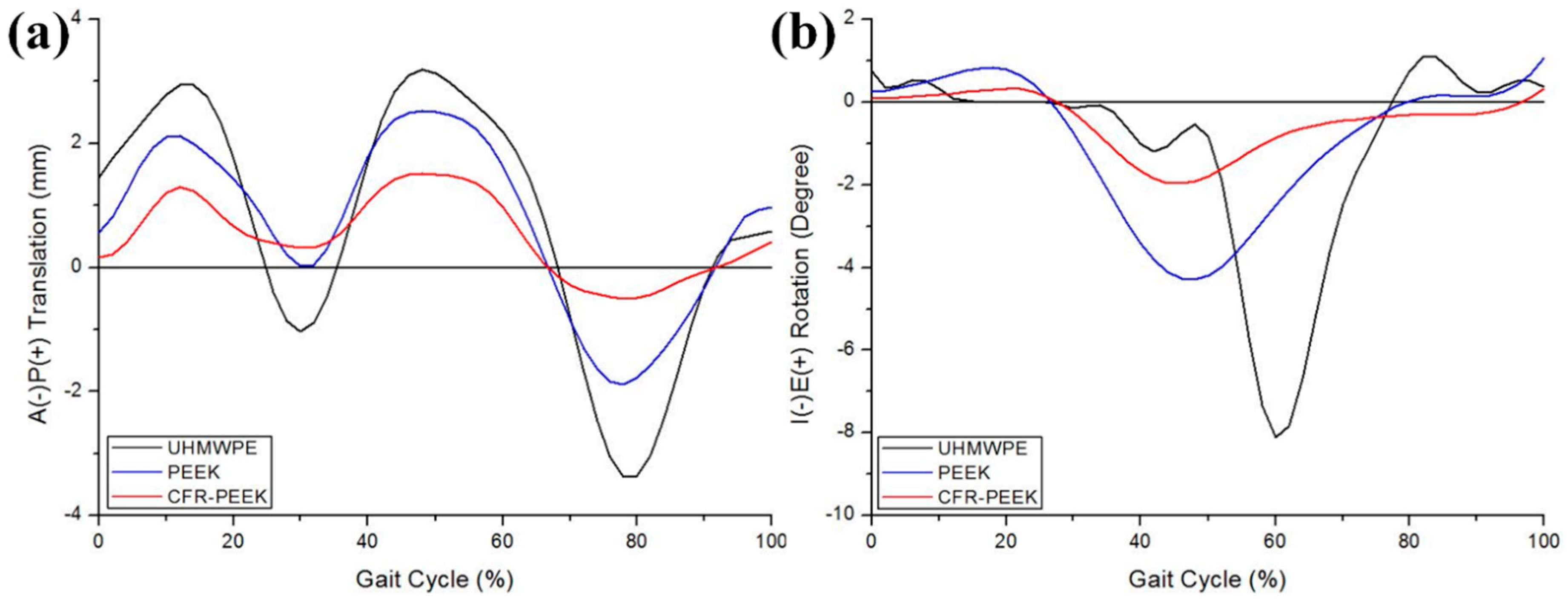
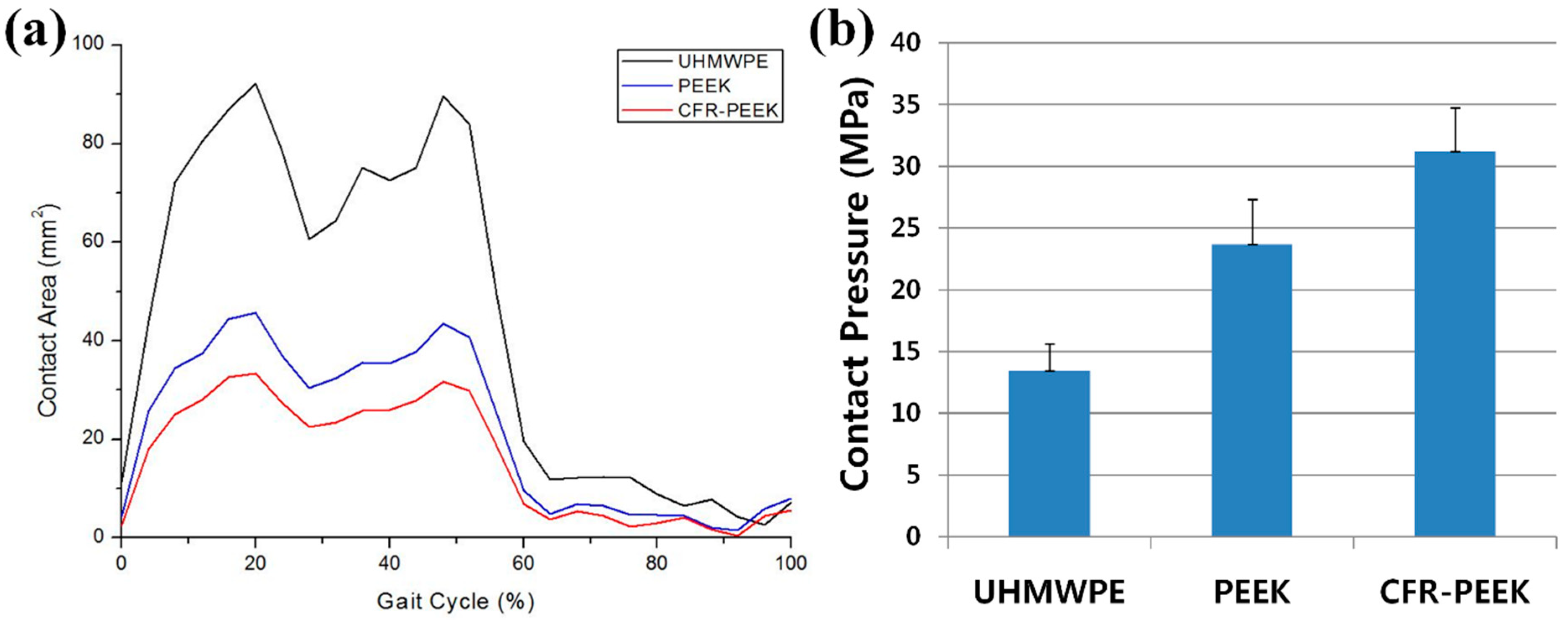
3.2. Comparison of Kinematics, Wear Depth, and Volumetric Wear in UHMWPE, PEEK, and CFR–PEEK Tibial Inserts
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.S.; Vannabouathong, C.; Sprague, S.; Bhandari, M. The use of carbon-fiber-reinforced (cfr) peek material in orthopedic implants: A systematic review. Clin. Med. Insights Arthritis Musculoskelet. Disord. 2015, 8, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Valderrabano, V.; Steiger, C. Treatment and prevention of osteoarthritis through exercise and sports. J. Aging Res. 2010, 2011, 374653. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Smith, B.P.; Plate, J.F.; Casanova, R.; Hsu, F.C.; Li, J.; Xia, L.; Li, K.C.; Poehling, G.G.; Zhou, X. A systematic approach to predicting the risk of unicompartmental knee arthroplasty revision. Osteoarthr. Cartil. 2016, 24, 991–999. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.T.; Son, J.; Kwon, O.R.; Baek, C.; Heo, D.B.; Park, K.M.; Kim, H.J.; Koh, Y.G. Effects of measurement methods for tibial rotation axis on the morphometry in korean populations by gender. Knee 2017, 24, 23–30. [Google Scholar] [CrossRef] [PubMed]
- van der Linden-van der Zwaag, H.M.; Bos, J.; van der Heide, H.J.; Nelissen, R.G. A computed tomography based study on rotational alignment accuracy of the femoral component in total knee arthroplasty using computer-assisted orthopaedic surgery. Int. Orthop. 2011, 35, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Sharkey, P.F.; Hozack, W.J.; Rothman, R.H.; Shastri, S.; Jacoby, S.M. Insall award paper. Why are total knee arthroplasties failing today? Clin. Orthop. Relat. Res. 2002, 404, 7–13. [Google Scholar] [CrossRef]
- Barnett, P.I.; McEwen, H.M.; Auger, D.D.; Stone, M.H.; Ingham, E.; Fisher, J. Investigation of wear of knee prostheses in a new displacement/force-controlled simulator. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2002, 216, 51–61. [Google Scholar] [CrossRef] [PubMed]
- Walker, P.S.; Blunn, G.W.; Broome, D.R.; Perry, J.; Watkins, A.; Sathasivam, S.; Dewar, M.E.; Paul, J.P. A knee simulating machine for performance evaluation of total knee replacements. J. Biomech. 1997, 30, 83–89. [Google Scholar] [CrossRef]
- Fujihara, K.; Teo, K.; Gopal, R.; Loh, P.; Ganesh, V.; Ramakrishna, S.; Foong, K.; Chew, C. Fibrous composite materials in dentistry and orthopaedics: Review and applications. Compos. Sci. Technol. 2004, 64, 775–788. [Google Scholar] [CrossRef]
- Mehboob, H.; Chang, S.-H. Application of composites to orthopedic prostheses for effective bone healing: A review. Compos. Struct. 2014, 118, 328–341. [Google Scholar] [CrossRef]
- Affatato, S.; Ruggiero, A.; Merola, M.; Logozzo, S. Does metal transfer differ on retrieved biolox® delta composites femoral heads? Surface investigation on three biolox® generations from a biotribological point of view. J. Compos. Part B Eng. 2017, 113, 164–173. [Google Scholar] [CrossRef]
- Chohan, J.S.; Singh, R.; Boparai, K.S.; Penna, R.; Fraternali, F. Dimensional accuracy analysis of coupled fused deposition modeling and vapour smoothing operations for biomedical applications. J. Compos. Part B Eng. 2017, 117, 138–149. [Google Scholar] [CrossRef]
- Senatov, F.; Niaza, K.; Stepashkin, A.; Kaloshkin, S. Low-cycle fatigue behavior of 3d-printed pla-based porous scaffolds. J. Compos. Part B Eng. 2016, 97, 193–200. [Google Scholar] [CrossRef]
- Ferreira, O.J.B.; Demétrio, K.B.; dos Santos, L.A.L. Nanostructured hydroxyapatite/polydimethylsiloxane composites obtained by reactive synthesis. J. Compos. Part B Eng. 2017, 121, 152–161. [Google Scholar] [CrossRef]
- Kim, S.H.; Chang, S.H.; Jung, H.J. The finite element analysis of a fractured tibia applied by composite bone plates considering contact conditions and time-varying properties of curing tissues. Compos. Struct. 2010, 92, 2109–2118. [Google Scholar] [CrossRef]
- Jha, D.; Kant, T.; Singh, R. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, S.H.; Chang, S.H. Bio-mechanical analysis of a fractured tibia with composite bone plates according to the diaphyseal oblique fracture angle. Compos. Part B Eng. 2011, 42, 666–674. [Google Scholar] [CrossRef]
- Kang, K.T.; Chun, H.J.; Kim, H.J.; Yeom, J.S.; Park, K.M.; Hwang, I.H.; Lee, K.I. Finite element analysis of instrumented posterior lumbar interbody fusion cages for reducing stress shielding effects: Comparison of the cfrp cage and titanium cage. Compos. Res. 2012, 25, 98–104. [Google Scholar]
- Son, D.S.; Mehboob, H.; Jung, H.J.; Chang, S.H. The finite element analysis for endochondral ossification process of a fractured tibia applied with a composite im-rod based on a mechano-regulation theory using a deviatoric strain. Compos. Part B Eng. 2014, 56, 189–196. [Google Scholar] [CrossRef]
- Son, D.S.; Chang, S.H. The simulation of bone healing process of fractured tibia applied with composite bone plates according to the diaphyseal oblique angle and plate modulus. Compos. Part B Eng. 2013, 45, 1325–1335. [Google Scholar] [CrossRef]
- Kim, S.H.; Chang, S.H.; Son, D.S. Finite element analysis of the effect of bending stiffness and contact condition of composite bone plates with simple rectangular cross-section on the bio-mechanical behaviour of fractured long bones. J. Compos. Part B Eng. 2011, 42, 1731–1738. [Google Scholar] [CrossRef]
- Rankin, K.E.; Dickinson, A.S.; Briscoe, A.; Browne, M. Does a peek femoral tka implant preserve intact femoral surface strains compared with cocr? A preliminary laboratory study. Clin. Orthop. Relat. Res. 2016, 474, 2405–2413. [Google Scholar] [CrossRef] [PubMed]
- Kurtz, S.M. Editorial comment: Advances in peek technology. Clin. Orthop. Relat. Res. 2016, 474, 2362–2363. [Google Scholar] [CrossRef] [PubMed]
- Scholes, S.C.; Unsworth, A. Wear studies on the likely performance of cfr-peek/cocrmo for use as artificial joint bearing materials. J. Mater. Sci. Mater. Med. 2009, 20, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Howling, G.I.; Sakoda, H.; Antonarulrajah, A.; Marrs, H.; Stewart, T.D.; Appleyard, S.; Rand, B.; Fisher, J.; Ingham, E. Biological response to wear debris generated in carbon based composites as potential bearing surfaces for artificial hip joints. J. Biomed. Mater. Res. Part B Appl. Biomater. 2003, 67, 758–764. [Google Scholar] [CrossRef] [PubMed]
- Knight, L.A.; Pal, S.; Coleman, J.C.; Bronson, F.; Haider, H.; Levine, D.L.; Taylor, M.; Rullkoetter, P.J. Comparison of long-term numerical and experimental total knee replacement wear during simulated gait loading. J. Biomech. 2007, 40, 1550–1558. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Sakoda, H.; Sawyer, W.G.; Banks, S.A.; Fregly, B.J. Predicting knee replacement damage in a simulator machine using a computational model with a consistent wear factor. J. Biomech. Eng. 2008, 130, 011004. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J.; Sawyer, W.G.; Harman, M.K.; Banks, S.A. Computational wear prediction of a total knee replacement from in vivo kinematics. J. Biomech. 2005, 38, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.T.; Park, J.H.; Lee, K.I.; Shim, Y.B.; Jang, J.W.; Chun, H.J. Gait cycle comparions of cruciate sacrifice for total knee design-explicit finite element. Int. J. Precis. Eng. Manag. 2012, 13, 2043–2049. [Google Scholar] [CrossRef]
- Kang, K.T.; Son, J.; Kim, H.J.; Baek, C.; Kwon, O.R.; Koh, Y.G. Wear predictions for uhmwpe material with various surface properties used on the femoral component in total knee arthroplasty: A computational simulation study. J. Mater. Sci. Mater. Med. 2017, 28, 105. [Google Scholar] [CrossRef] [PubMed]
- Halloran, J.P.; Easley, S.K.; Petrella, A.J.; Rullkoetter, P.J. Comparison of deformable and elastic foundation finite element simulations for predicting knee replacement mechanics. J. Biomech. Eng. 2005, 127, 813–818. [Google Scholar] [CrossRef] [PubMed]
- Godest, A.C.; Beaugonin, M.; Haug, E.; Taylor, M.; Gregson, P.J. Simulation of a knee joint replacement during a gait cycle using explicit finite element analysis. J. Biomech. 2002, 35, 267–275. [Google Scholar] [CrossRef]
- Sathasivam, S.; Walker, P.S. Computer model to predict subsurface damage in tibial inserts of total knees. J. Orthop. Res. 1998, 16, 564–571. [Google Scholar] [CrossRef] [PubMed]
- Greco, A.; Erck, R.; Ajayi, O.; Fenske, G. Effect of reinforcement morphology on high-speed sliding friction and wear of peek polymers. Wear 2011, 271, 2222–2229. [Google Scholar] [CrossRef]
- Halloran, J.P.; Petrella, A.J.; Rullkoetter, P.J. Explicit finite element modeling of total knee replacement mechanics. J. Biomech. 2005, 38, 323–331. [Google Scholar] [CrossRef]
- Kwon, O.R.; Kang, K.T.; Son, J.; Kwon, S.K.; Jo, S.B.; Suh, D.S.; Choi, Y.J.; Kim, H.J.; Koh, Y.G. Biomechanical comparison of fixed- and mobile-bearing for unicomparmental knee arthroplasty using finite element analysis. J. Orthop. Res. 2014, 32, 338–345. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- McGloughlin, T.M.; Murphy, D.M.; Kavanagh, A.G. A machine for the preliminary investigation of design features influencing the wear behaviour of knee prostheses. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2004, 218, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Grupp, T.M.; Utzschneider, S.; Schroder, C.; Schwiesau, J.; Fritz, B.; Maas, A.; Blomer, W.; Jansson, V. Biotribology of alternative bearing materials for unicompartmental knee arthroplasty. Acta Biomater. 2010, 6, 3601–3610. [Google Scholar] [CrossRef]
- Brockett, C.L.; Carbone, S.; Fisher, J.; Jennings, L.M. Peek and cfr peek as alternative to uhmwpe in total knee replacement. In Proceedings of the ORS 2015 annual meeting, Las Vegas, NV, USA, 24–28 March 2015. [Google Scholar]
- Pal, S.; Haider, H.; Laz, P.J.; Knight, L.A.; Rullkoetter, P.J. Probabilistic computational modeling of total knee replacement wear. Wear 2008, 264, 701–707. [Google Scholar] [CrossRef]
- Netter, J.; Hermida, J.; Flores-Hernandez, C.; Steklov, N.; Kester, M.; D’Lima, D.D. Prediction of wear in crosslinked polyethylene unicompartmental knee arthroplasty. Lubricants 2015, 3, 381–393. [Google Scholar] [CrossRef]
- Sarkar, A.D. Friction and Wear; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Abdelgaied, A.; Liu, F.; Brockett, C.; Jennings, L.; Fisher, J.; Jin, Z. Computational wear prediction of artificial knee joints based on a new wear law and formulation. J. Biomech. 2011, 44, 1108–1116. [Google Scholar] [CrossRef] [PubMed]
- DesJardins, J.D.; Burnikel, B.; LaBerge, M. Uhmwpe wear against roughened oxidized zirconium and cocr femoral knee components during force-controlled simulation. Wear 2008, 264, 245–256. [Google Scholar] [CrossRef]
- Morrison, M.L.; Jani, S.; Parikh, A. Design of an advanced bearing system for total knee arthroplasty. Lubricants 2015, 3, 475–492. [Google Scholar] [CrossRef]
- Papannagari, R.; Hines, G.; Sprague, J.; Morrison, M. Long-term wear performance of an advanced bearing knee technology. Orthop. Proc. 2012, 94, 152. [Google Scholar]
- We Make Taking Decisions Easier. Available online: http://www.Transparencymarketresearch.Com/orthopedic-devices-market.Html (accessed on 1 July 2018).
- Scholes, S.; Unsworth, A. The wear properties of cfr-peek-optima articulating against ceramic assessed on a multidirectional pin-on-plate machine. Proc. Inst. Mech. Eng. Part H 2007, 221, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Scholes, S.; Unsworth, A. Pitch-based carbon-fibre-reinforced poly (ether—ether—ketone) optima® assessed as a bearing material in a mobile bearing unicondylar knee joint. Proc. Inst. Mech. Eng. Part H 2009, 223, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Galvin, A.L.; Kang, L.; Udofia, I.; Jennings, L.M.; McEwen, H.M.; Jin, Z.; Fisher, J. Effect of conformity and contact stress on wear in fixed-bearing total knee prostheses. J. Biomech. 2009, 42, 1898–1902. [Google Scholar] [CrossRef] [PubMed]
- Barbour, P.S.; Barton, D.C.; Fisher, J. The influence of stress conditions on the wear of uhmwpe for total joint replacements. J. Mater. Sci. 1997, 8, 603–611. [Google Scholar]
- Evans, A.; Horton, H.; Unsworth, A.; Briscoe, A. The influence of nominal stress on wear factors of carbon fibre-reinforced polyetheretherketone (peek-optima(r) wear performance) against zirconia toughened alumina (biolox(r) delta ceramic). Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Brockett, C.L.; Carbone, S.; Fisher, J.; Jennings, L.M. Peek and cfr-peek as alternative bearing materials to uhmwpe in a fixed bearing total knee replacement: An experimental wear study. Wear 2017, 374–375, 86–91. [Google Scholar] [CrossRef] [PubMed]
- East, R.H.; Briscoe, A.; Unsworth, A. Wear of peek-optima(r) and peek-optima(r)-wear performance articulating against highly cross-linked polyethylene. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2015, 229, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Scholes, S.; Unsworth, A.J.W. The wear performance of peek-optima based self-mating couples. Wear 2010, 268, 380–387. [Google Scholar] [CrossRef]
- Kang, K.T.; Son, J.; Suh, D.S.; Kwon, S.K.; Kwon, O.R.; Koh, Y.G. Patient-specific medial unicompartmental knee arthroplasty has a greater protective effect on articular cartilage in the lateral compartment: A finite element analysis. Bone Joint Res. 2018, 7, 20–27. [Google Scholar] [CrossRef] [PubMed]

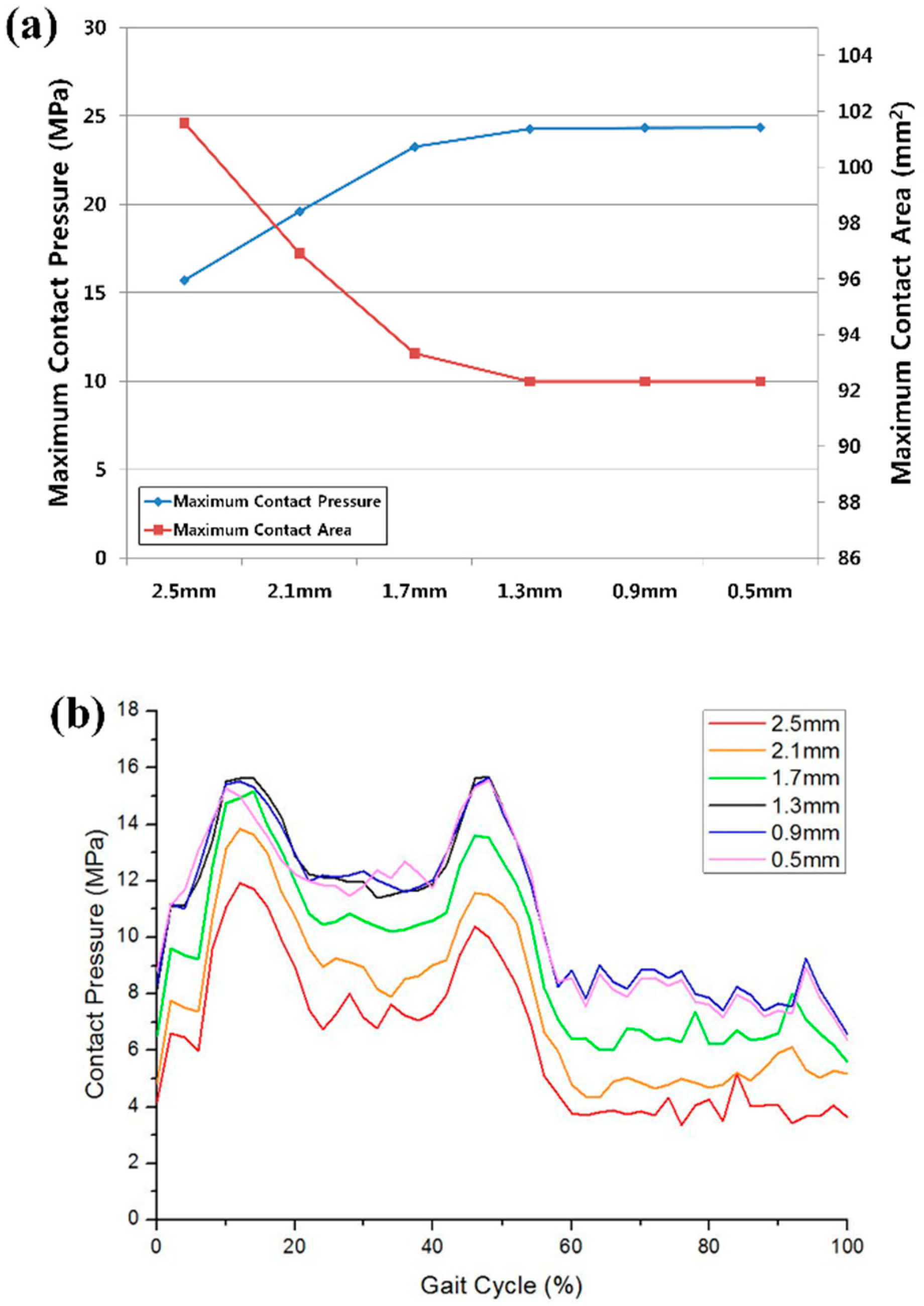
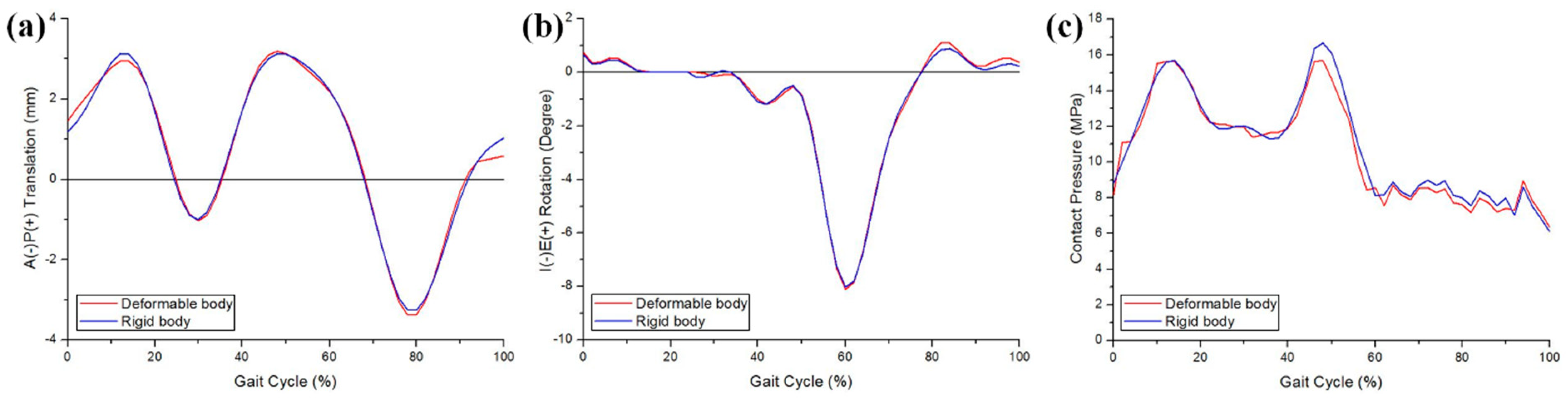
| Term | Our Study | In Vitro Experimental Data |
|---|---|---|
| Wear rate (mm3/million) | 24.90 | 23.4 ± 2.4 |
| Volumetric wear (mm3) | 124.04 | 120.42 ± 12.0 |
| Term | UHMWPE | PEEK | CFR–PEEK |
|---|---|---|---|
| Volumetric wear (mm3) | 124.0 | 300.9 | 15.6 |
| Wear depth (mm) | 0.31 | 0.89 | 0.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koh, Y.-G.; Lee, J.-A.; Kang, K.-T. Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis. Lubricants 2019, 7, 30. https://doi.org/10.3390/lubricants7040030
Koh Y-G, Lee J-A, Kang K-T. Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis. Lubricants. 2019; 7(4):30. https://doi.org/10.3390/lubricants7040030
Chicago/Turabian StyleKoh, Yong-Gon, Jin-Ah Lee, and Kyoung-Tak Kang. 2019. "Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis" Lubricants 7, no. 4: 30. https://doi.org/10.3390/lubricants7040030
APA StyleKoh, Y.-G., Lee, J.-A., & Kang, K.-T. (2019). Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis. Lubricants, 7(4), 30. https://doi.org/10.3390/lubricants7040030