Voltage-Induced Friction with Application to Electrovibration
Abstract
1. Introduction
2. Theory
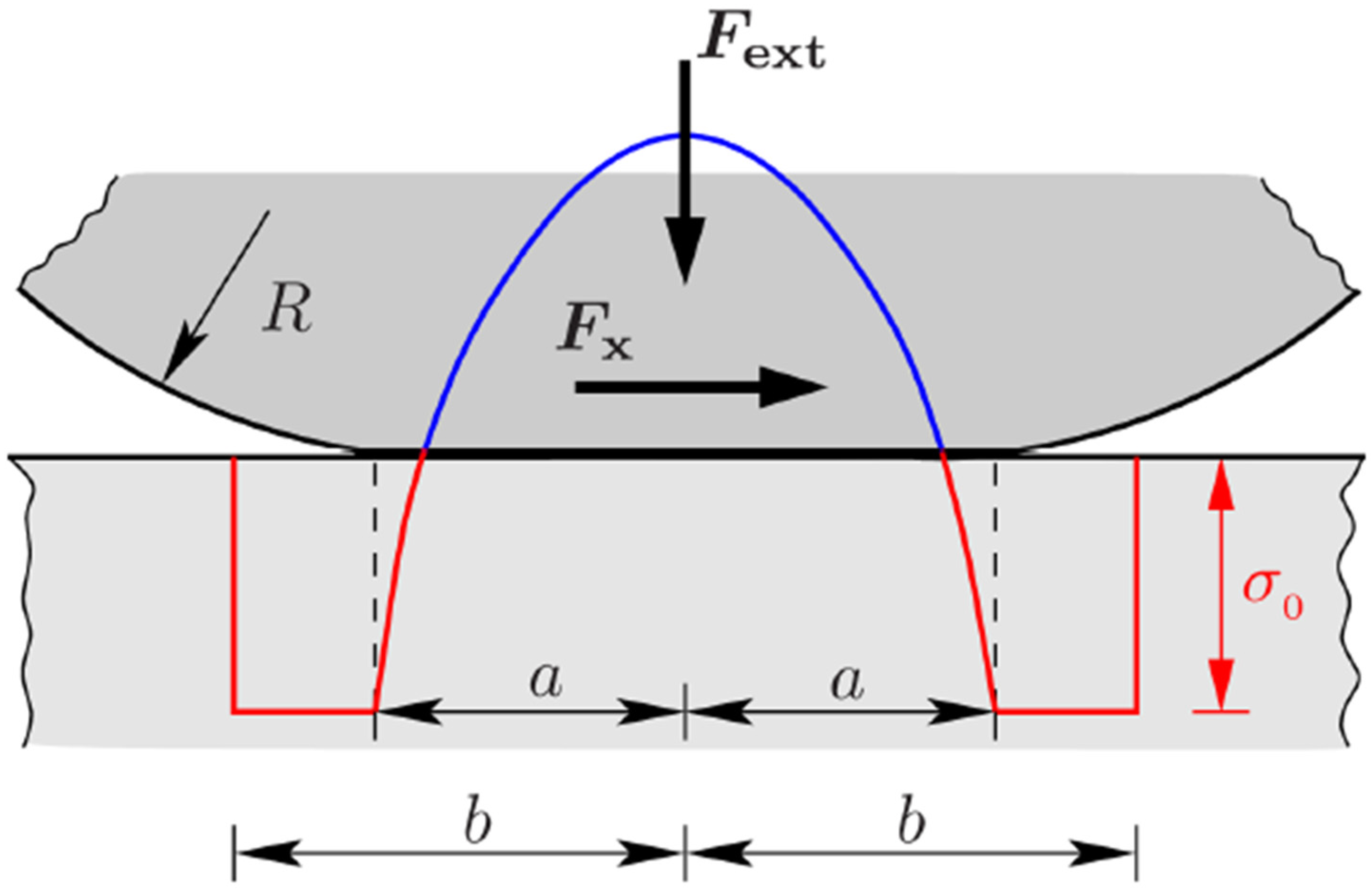
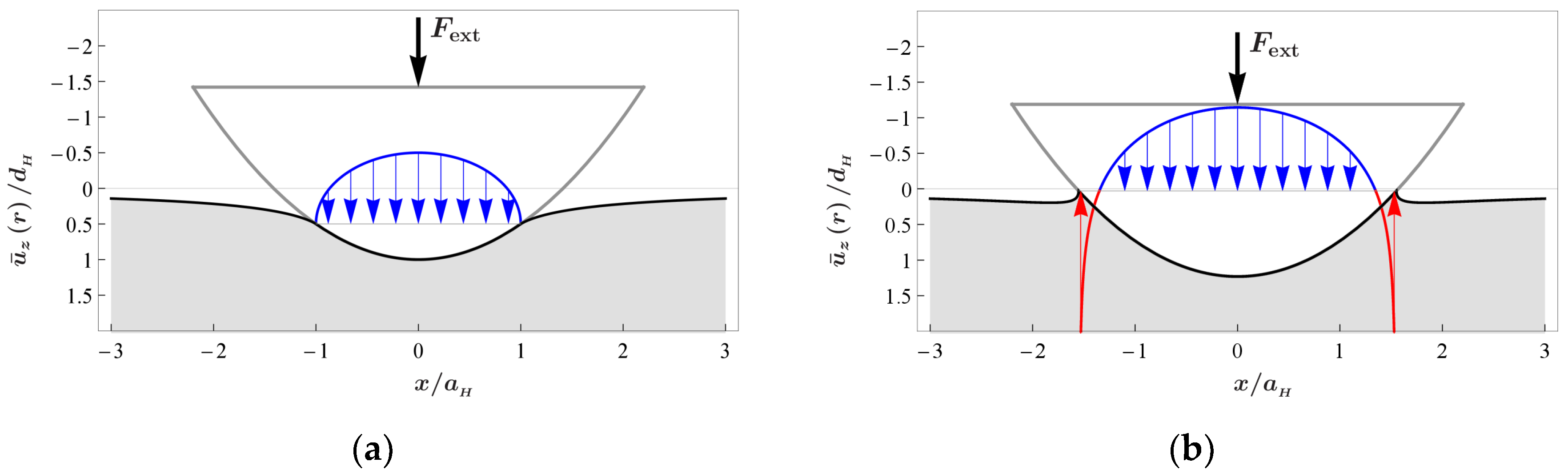
2.1. Contact Mechanics Approach
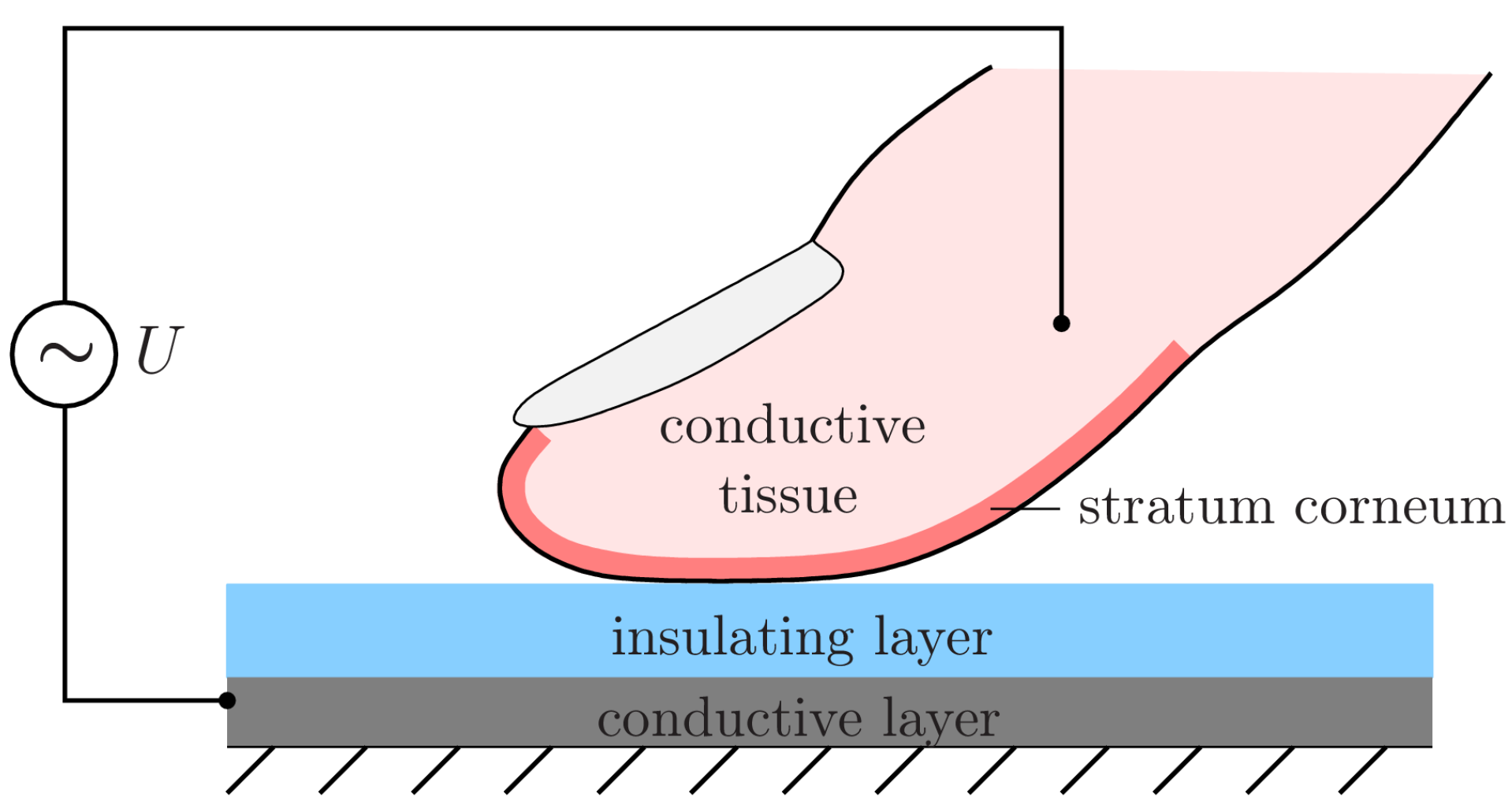
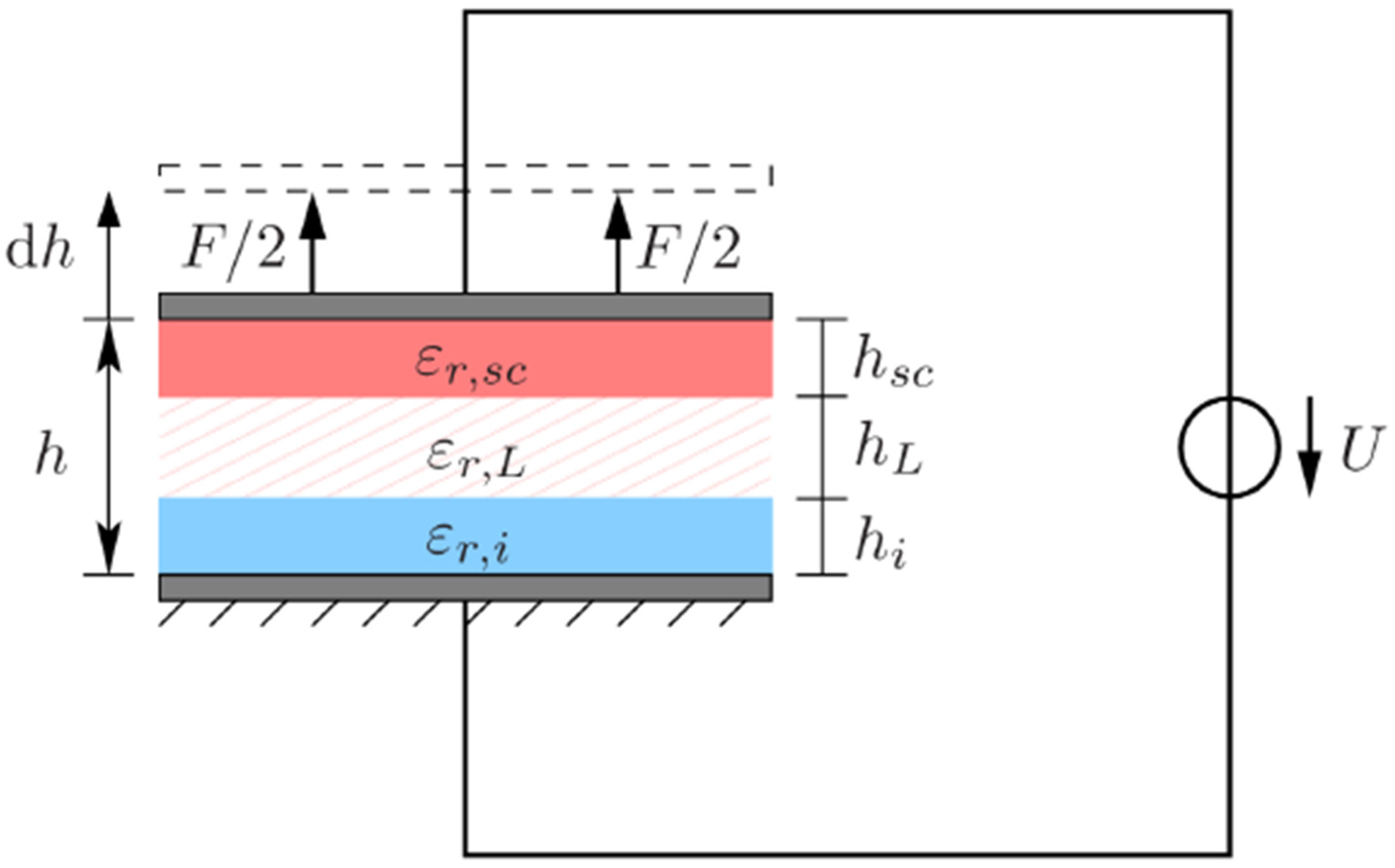
2.2. Electrostatic Approach and Coupling to Contact Mechanics
3. Comparison with Experimental Data
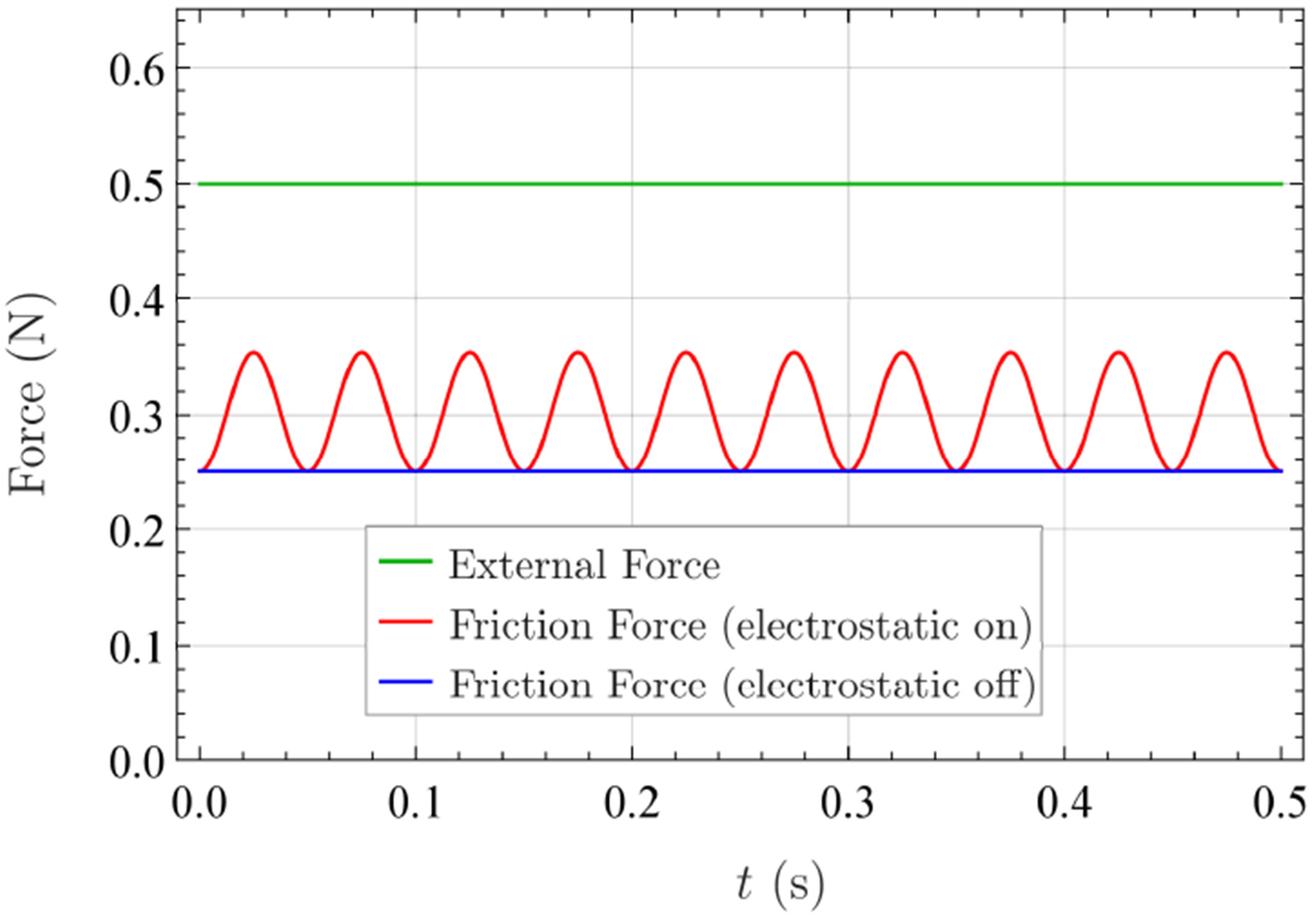
3.1. Friction Force as a Function of Time during Sinusoidal Excitation
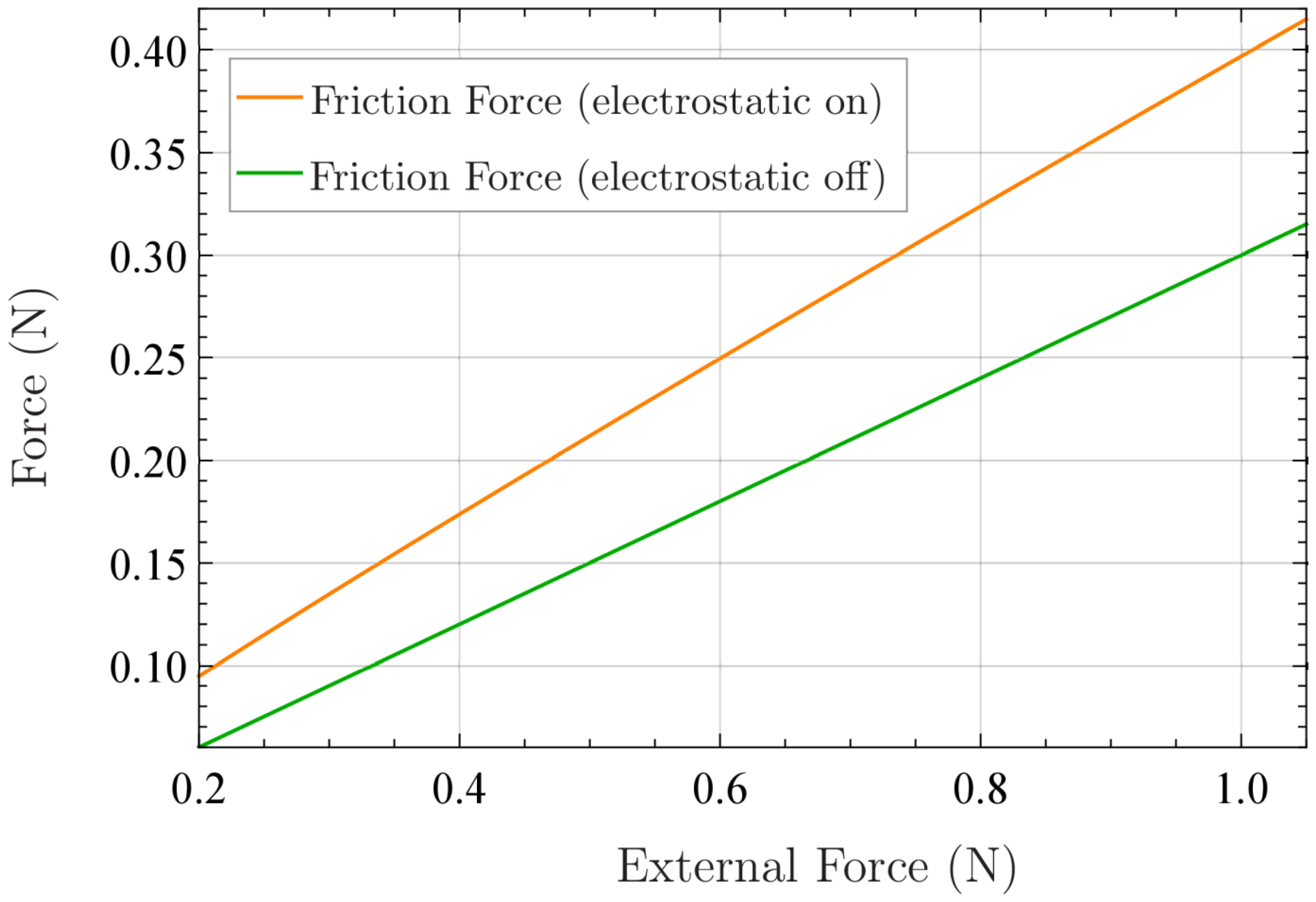
3.2. Friction Force as a Function of Externally Applied Normal Force
3.3. Electrostatic Force as a Function of Applied Voltage Amplitude
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mallinckrodt, E.; Hughes, A.L.; Sleater Jr, W. Perception by skin of electrically induced vibrations. Science 1953, 118, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Bau, O.; Poupyrev, I.; Israr, A.; Harrison, C. TeslaTouch: Electrovibration for touch surfaces. In Proceedings of the 23nd annual ACM symposium on User interface software and technology, New York, NY, USA, 3–6 October 2010; pp. 283–292. [Google Scholar]
- Meyer, D.J.; Peshkin, M.A.; Colgate, J.E. Fingertip friction modulation due to electrostatic attraction. In Proceedings of the IEEE 2013 world haptics conference, Daejeon, Korea, 14–17 April 2013; pp. 43–48. [Google Scholar]
- Shultz, C.D.; Peshkin, M.A.; Colgate, J.E. Surface haptics via electroadhesion: Expanding electrovibration with Johnsen and Rahbek. In Proceedings of the IEEE 2015 world haptics conference, Evanston, IL, USA, 22–26 June 2015; pp. 57–62. [Google Scholar]
- Vardar, Y.; Güçlü, B.; Basdogan, C. Effect of waveform on tactile perception by electrovibration displayed on touch screens. IEEE Trans. Haptics 2017, 10, 488–499. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Yamamoto, A. Modeling and control of electroadhesion force in DC voltage. Robomech J. 2017, 4, 18. [Google Scholar] [CrossRef]
- Kaczmarek, K.A.; Nammi, K.; Agarwal, A.K.; Tyler, M.E.; Haase, S.J.; Beebe, D.J. Polarity effect in electrovibration for tactile display. IEEE Trans. Biomed. Eng. 2006, 53, 2047–2054. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Vezzoli, E.; Amberg, M.; Giraud, F.; Lemaire-Semail, B. Electrovibration modeling analysis. In Proceedings of the International Conference on Human Haptic Sensing and Touch Enabled Computer Applications, Versailles, France, 24–26 June 2014; pp. 369–376. [Google Scholar]
- Vodlak, T.; Vidrih, Z.; Vezzoli, E.; Lemaire-Semail, B.; Peric, D. Multi-physics modelling and experimental validation of electrovibration based haptic devices. Biotribology 2016, 8, 12–25. [Google Scholar] [CrossRef]
- Lyashenko, I.A. Tangential displacement influence on the critical normal force of adhesive contact breakage in biological systems. Facta Univ. Series: Mech. Eng. 2016, 14, 313–320. [Google Scholar] [CrossRef]
- Popov, V.L.; Dimaki, A.V. Friction in an adhesive tangential contact in the Coulomb-Dugdale approximation. J. Adhes. 2017, 93, 1131–1145. [Google Scholar] [CrossRef]
- Popov, V.L.; Hess, M. Voltage induced friction in a contact of a finger and a touchscreen with a thin dielectric coating. arXiv 2018, arXiv:1805.08714, in press. [Google Scholar]
- Maugis, D. Adhesion of spheres: The JKR-DMT transition using a Dugdale model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Popov, V.L.; Heß, M. Method of Dimensionality Reduction in Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Derjaguin, B. Molekulartheorie der äußeren Reibung. Z. Phys. 1934, 88, 661–675. [Google Scholar] [CrossRef]
- Popov, V.L.; Heß, M.; Willert, E. Adhesive Tangential Contact. In Handbook of contact mechanics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Savkoor, A.R.; Briggs, G.A.D. The effect of tangential force on the contact of elastic solids in adhesion. Proc. R. Soc. London A. Math. Phys. Sci. 1977, 356, 103–114. [Google Scholar] [CrossRef]
- Strong, R.M.; Troxel, D.E. An electrotactile display. IEEE Trans. Man-Mach. Syst. 1970, 11, 72–79. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Y.; Wang, D.; Lu, L.; Jiao, J.; Xu, W. The Effect of Applied Normal Force on the Electrovibration. IEEE Trans. Haptics 2019, in press. [Google Scholar] [CrossRef] [PubMed]
- Soneda, T.; Nakano, K. Investigation of vibrotactile sensation of human fingerpads by observation of contact zones. Tribol. Int. 2010, 43, 210–217. [Google Scholar] [CrossRef]
- Van Kuilenburg, J.; Masen, M.A.; van der Heide, E. Contact modelling of human skin: What value to use for the modulus of elasticity? Proc. Inst. Mech. Eng. Part J: J. Eng. Tribol. 2013, 227, 349–361. [Google Scholar] [CrossRef]
- Dzidek, B.M.; Adams, M.J.; Andrews, J.W.; Zhang, Z.; Johnson, S.A. Contact mechanics of the human finger pad under compressive loads. J. R. Soc. Interface 2017, 14, 20160935. [Google Scholar] [CrossRef] [PubMed]

| Symbol | Parameter Name | Value and Unit |
|---|---|---|
| Friction coefficient | 0.5 (0.3) | |
| Radius of fingertip | 1 cm | |
| Equivalent effective elastic modulus | 40 kPa | |
| Relative permittivity of stratum corneum | ||
| Relative permittivity of insulating layer | ||
| Permittivity of free space | ||
| Thickness of stratum corneum | 300 µm | |
| Thickness of insulating layer | 1 µm | |
| Thickness of equivalent air gap | 5 µm | |
| External applied normal force | 0.5 N |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heß, M.; Popov, V.L. Voltage-Induced Friction with Application to Electrovibration. Lubricants 2019, 7, 102. https://doi.org/10.3390/lubricants7120102
Heß M, Popov VL. Voltage-Induced Friction with Application to Electrovibration. Lubricants. 2019; 7(12):102. https://doi.org/10.3390/lubricants7120102
Chicago/Turabian StyleHeß, Markus, and Valentin L. Popov. 2019. "Voltage-Induced Friction with Application to Electrovibration" Lubricants 7, no. 12: 102. https://doi.org/10.3390/lubricants7120102
APA StyleHeß, M., & Popov, V. L. (2019). Voltage-Induced Friction with Application to Electrovibration. Lubricants, 7(12), 102. https://doi.org/10.3390/lubricants7120102






