Abstract
The tribology of lubricated poly(ether ether ketone) (PEEK)—steel tribosystems was investigated in the static and boundary friction regime. Pentaerythrite ester and trimellitic acid ester were used as lubricants. The lubricants differed in their molecular structure but showed only minor differences in their rheological and cohesive energetic properties. In order to investigate the effect of the lubricants on static and dynamic friction, macroscopic oscillatory tribometry experiments and gliding experiments were carried out. The surface and interfacial energies of PEEK, lubricant, and steel, which can be used to determine e.g., the spreading tendency of the lubricant, were employed to explain the tribological characteristics of the system. The gliding experiments exhibited a velocity dependence of the coefficient of friction which indicates a “rate-and-state” type of friction. Trimellitic acid ester resulted in the lowest static and dynamic friction values due to its high tendency to spread. A different static friction behavior was found for pentaerythrite ester, which indicates a possible lubricant-induced mobilization of the polymer surface chains. This finding was supported by an increased interaction energy measured by contact angle measurements. The macroscopic oscillatory tribometry was shown to be a unique and precise method to investigate the transition from static to dynamic friction and to quantify macroscopic adhesive friction. Both types of experiments used a polished steel surface as a frictional partner, which favors the adhesive component of friction. However, the results for the lubricated contacts of polished steel surfaces in the boundary lubrication regime can give some insight into effects of the polymer transfer to rough steel surfaces in the mixed lubrication regime.
1. Introduction
Thermoplastic polymers are increasingly used to replace other materials in tribologically loaded components, e.g., in the automotive industry or in mechanical engineering. This development is largely driven by the need to reduce weight in order to obtain more energy efficient products. A profound understanding of the friction and wear mechanisms is a prerequisite for developing reliable tribological systems. While the interaction between polymer and steel already has been studied in detail for non-lubricated tribological systems, only limited information is available on lubricated tribological systems. Polymer transfer [1] or “temperature hot spots” of the polymer during frictional loading in lubricated systems indicate that the interaction between polymer and its frictional partner for lubricated contacts is complex and includes adhesive interactions. However, in tribological tests in the mixed lubrication regime, the analysis of these effects is often hindered by thermal or mechanical processes (e.g., the “ploughing” of a rough surface through the polymer).
In contrast to the mixed lubrication and the hydrodynamic lubrication regime, the tribology at very low velocities is dominated by the physicochemical interactions [2] between the polymer surface, lubricant, and the surface of the steel counter-body. Measurements of the tribological behavior of lubricated systems in the static and boundary friction regimes might therefore serve as a method by which one can obtain some insight into the interactions between the polymer, lubricant, and steel frictional partner. The chemical characteristics of the lubricant will influence the wetting behavior of the polymer and steel surface and its tendency to migrate into and partially solve the polymer surface. As a result, the interaction between the lubricant and polymer will alter the adhesive and plastic behavior of the polymer, which in turn will ultimately influence the friction and wear characteristics of the entire system over a wide range of sliding velocities.
An understanding of the influence of the lubricant on the tribology near the transition between static friction and the boundary lubrication regime using “rate-and-state” models can furthermore help to explain the performance of the lubricant at local asperity contacts with higher velocities in the mixed lubrication regime. In addition, tribological experiments at very low velocities are not only interesting from a fundamental perspective; they are also relevant for a variety of technical problems, such as the analysis of initial breakaway torques or the emission of noise due to stick-slip phenomena at low gliding speeds.
The current study aims to investigate the relationship between tribological phenomena and the surface and interfacial energies of the tribological partners. The latter can be used to understand adhesion and wetting phenomena observed for the lubricants and frictional partners. The tribology of the lubricated polymer-steel-system was investigated with a tribometer which can be used in an “oscillatory” mode to capture the transition between static friction and dynamic friction, and in a conventional mode to record a Stribeck curve of the lubricated system over a wide range of gliding velocities. The study was carried out with a poly(ether ether ketone) (PEEK)-steel tribosystem which was lubricated with two different ester-based lubricants.
2. Scientific Background
The friction of polymers on smooth surfaces is caused by a continuous forming and breaking of adhesive junctions between the two sliding partners. Schallamach [3] described the adhesive friction as a thermally driven rate process best described by a modified Arrhenius equation. f denotes the rate of bonding and debonding or the “slip-rate”; f0 indicates the reference frequency, E represents the activation energy for rearranging polymer chains to form a bond, W means the work required to break the interfacial contact, and Ω∑ denotes the work done by the applied stress ∑ on the activated volume Ω. Finally, kB is the Boltzmann constant and T is the absolute temperature:
With Schallamach’s approach, the temperature and velocity dependence of the coefficient of friction (COF) µ of a polymer gliding on a smooth surface can be explained. The model predicts a monotonous increasing COF with increasing sliding velocity v until a maximum value is reached. With further increasing v, the COF decreases. Experiments frequently showed that Schallamach’s model and refined versions of the model are able to describe the tribology of polymers.
In the range of static friction and very low sliding speeds v, additional effects can be detected which result in a development of the COF µ(v) differing from the behavior described above. In particular, an initial decrease of the COF leading to a minimum value followed by an increasing COF can be observed. In this velocity range, the tribology cannot solely be described by a thermally driven rate process; the development of the state of the contact area φ (i.e., the “aging” of the contact area) has to be taken into account for describing the tribology of the system. Dieterich [4] and Ruina [5] formulated general “rate-and-state” friction laws in order to describe the COF µ as a function of the slip velocity v and the state φ, where V* denotes a typical sliding velocity which results in the COF µ* and L is a characteristic slip distance. Putelat et al. [6] provided a study on the microphysical foundations of the rate-and-state friction.
Schallamach’s approach is based on an energy-based description of the adhesive processes between the frictional partners. An analysis of the surface and interfacial energies of the frictional partners can give some insight into the influence of the lubricant on the adhesive friction between the polymer and the steel frictional partner. The interactions between the polymer, the lubricant, and the steel counter-body are van-der-Waals interactions which consist of the dispersive London interactions between non-polar molecules and polar interactions arising from dipoles or hydrogen bonds.
The surface and interfacial energies are described in terms of the work of adhesion Wad. The work of adhesion is defined as the amount of free energy required to break the contact interface and separate two surfaces or media to infinity in vacuum. The surface free energy γ corresponds to the free energy change which is associated with increasing the surface area of a medium of a solid by a unit area.
According to Bhushan [7], the free surface energy affects the adhesion between the mating partners: the higher the free surface energy, the stronger are the adhesive forces between the mating surfaces and the higher is the work of adhesion which is required to separate the two surfaces.
In the context of this work, the indexing convention according to Israelachvili [8] will be used. That is, index 1 refers to the polymer, index 2 refers to the steel counter-body, and index 3 refers to the lubricating fluid. The work of cohesion Wii of the frictional partners is related to their surface free energy. For the interfacial energy γ13 between the polymer and lubricant, the Dupré equation holds, where W13 denotes the work of adhesion:
The surface free energies γ and—as a result—the work of adhesion or work of cohesion W can be determined experimentally by contact angle measurements. When a droplet of a lubricant is placed on a solid body, the droplet forms a contact angle with the solid continuum (see Figure 1), unless it spreads and completely wets the surface.
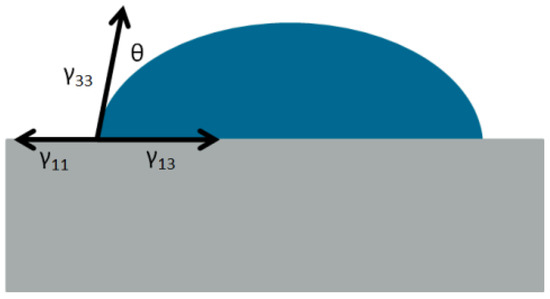
Figure 1.
A droplet rests on a solid surface in atmospheric air.
The surface free energy or the work of adhesion can be calculated using the Young-Dupré equation:
or the Young equation:
The theory of Owens et al. [9] provides an additional approach to calculate the work of adhesion. This theory separates the different interactions between two surfaces into two different groups: the polar component γp and dispersive component γd. The polar component includes the acid-base, London, hydrogen bonding, and induction interactions; the dispersive component corresponds to the dispersion interaction. If it is assumed that only polar-polar and dispersive-dispersive interactions can occur, the work of adhesion between the polymer and the lubricant can be calculated with the geometric means:
The equations above can be used to determine the work of adhesion or one specific surface free energy based on the contact angle and the other surface free energies. Since not all surface free energies which are required are readily available, a range of measurements was carried out which included also fluids and solids with known free surface energies. The required data were obtained by treating the unknown quantities as adjustable parameters and simultaneously varying these parameters to find an optimal solution of a system of equations derived from Equations (5)–(7).
The surface free energy, the work of adhesion, and the work of cohesion of the tribological partners can be used to gain some insight into the energy terms of Equation (1). The work W required breaking the contact between the polymer and steel corresponds to the work-of-spreading Wspreading (mN/m) which defines the natural tendency of the lubricant to wet and spread on the solid surface. A negative value of the work-of-spreading indicates that the lubricating fluid can spontaneously invade and break the interface between the tribological partners. The work-of-spreading can be calculated from the work of adhesion W12 which is required to separate two solid surfaces in contact, the work of cohesion (i.e., the surface free energy) which is required to generate a “free” surface of the lubricating medium W33, and the interfacial energies W13 and W23 which result from the creation of new interfaces between the solid surfaces and the lubricant.
The interfacial energy γ13 of the polymer and the lubricant corresponds to the energy which is required to increase the interfacial area by a unit area. The tendency of the lubricating fluid to “solve” and mobilize the surface chains and thus increase the interfacial area therefore relates to γ13, which can be interpreted in this context as an experimental estimated work-of-solving Wsolving for an intermigrative lubricated surface contact. Its absolute value can be higher than that for the interfacial energy that was obtained by indirect calculation using several nonmigrative lubricated contacts (e.g., of the lubricant with glass, steel, and ceramics). The ratio Wsolving/γ13 is therefore referred to in the literature as an “interaction parameter”.
A lubricant which tends to mobilize surface chains will increase the energy E which is gained after the formation of an increased number of adhesive bonds per real contact area. In addition, the higher mobility of the polymer surface layer will result in a larger effective contact area between the polymer and steel surface.
3. Materials and Methods
3.1. Tribological Experiments
3.1.1. Materials
Tribological experiments were conducted on a lubricated poly(ether ether ketone) (PEEK)-steel tribosystem. Unfilled PEEK450sf (PEEK) was obtained from Ensinger GmbH (Nufringen, Germany). A 100Cr6 steel ball which was integrated in the tribometer was used as tribological partner. Pentaerythrite ester (PEEs, viscosity η = 109 mPas at 25 °C,) and trimellitic acid ester (TAEs, viscosity η = 153 mPas at 25 °C,) were obtained from Klüber Lubrication München SE & Co. KG (Munich, Germany) and used as lubricating media. The PEEK samples were prepared in rectangular plates (6 × 3 × 15 mm3) which were cut from tapered tensile test specimens.
3.1.2. Rheometer
For the characterization of the lubricated polymer-contact, a rotational rheometer developed by Anton Paar GmbH (Ostfildern, Germany) was used (see Figure 2). The instrument includes a tribological measuring unit which can be used to carry out oscillatory tribological experiments or to record a Stribeck curve.

Figure 2.
Rheometer Physika MCR 501 developed by Anton Paar GmbH. A steel ball of 12.7 mm is brought into contact with three poly(ether ether ketone) plates inclined 45° to the rotational axis.
In the oscillatory experiments, a polished steel ball carries out rotational oscillations at very low velocities and deflections. Conducting the oscillatory experiments in this range of sliding speeds enables the acquisition of friction data in the static friction and boundary lubrication regimes. In the Stribeck mode, conventional uni-directional rotational experiments are conducted with gliding speeds ranging from 1 × 10−4 to 1.4 × 103 mm/s. Stribeck experiments collect friction data in the boundary lubrication and mixed lubrication friction regimes.
In the oscillatory experiments, a specimen deflection followed by a gliding motion is induced by the sinusoidal motion of the ball. The storage and loss modulus which describe the viscoelastic deflection properties of the polymer and the viscoelastic gliding properties of the contact surfaces can be calculated from the response of the sample for the deflection and the gliding which is recorded in terms of the phase shift δ and amplitude change. Due to the symmetry of the phase shifting, either the induced torque signal () or the measured deflection signal () can be calculated.
The specimen’s temperature is stabilized at 25 °C during the experiments. The loading situation in the sample holder results in three Hertzian ball contacts on flat surfaces. The normal forces of 3 N and 9 N result in an elastic Hertzian pressure of 33 MPa and 47 MPa. The diameter of the contact area was inspected after the sequence of measurements. The diameter was approximately 20% higher than the estimated diameter of a Hertzian contact area (0.5 mm). An analysis of the specimen’s surface with a profilometer showed that the indentation depth was in the range of the surface roughness.
Based on the orientation of the PEEK plates with respect to the rotational axis, the forces (the normal force Fn and the tangential friction force Ft) which act on the tribological system as well as the sliding distance can be determined.
Prior to the experiments, the specimens were conditioned by carrying out 10 oscillatory experiments and one Stribeck experiment with a normal force of 27 N. The actual measurements were then carried out on the “run-in” specimens, where the same sequence of experiments was carried out, however at reduced normal forces Fn = 9 N and Fn =3 N. A persistent intimate physical contact of the ball to the polymer plates was assured.
3.2. Contact Angle Measurements
Contact angle measurements were conducted with the sessile drop method, using an instrument produced by Data Physics GmbH (Filderstadt, Germany). Three different liquids (water, ethylene glycol, and diiodomethane) with known surface free energies were used to calculate the unknown surface and interfacial energies. A 2-µL droplet (diameter approx. 1–2 mm) of each liquid was dispensed on the surface of the sample, the droplet profile was recognized and recorded by the instrument’s software and the contact angle was calculated automatically. All the calculations and interpolations were carried out according to Equations (5)–(9). PEEs formed an average contact angle of 24° to steel and 6° to PEEK. TAEs formed an average contact angle of 23.5° to steel and 13° to PEEK.
4. Results
4.1. Oscillatory Experiments and Interfacial Energy
Experiments conducted with an oscillatory tribometer make it possible to distinguish between the elastic and viscous response of the system during its transition from sticking to gliding. Two approaches can be taken to differentiate between sample deflection and gliding motion. Deflection and gliding response can be separated by the storage and loss component of their modulus. In addition, viscoelastic deflection and viscoelastic gliding can be distinguished if one assumes that an increase of the tangential friction force Ft with v has to be dominated by a deflection response, and a reduction of Ft with v has to be dominated by a gliding response. In our experiments, both approaches yielded similar results. The oscillation frequency was kept at 1 Hz. The data acquisition rate was chosen to be 10 data points per decade, where the loading torque was increased on a logarithmic scale. When comparing the elastic or storage response of the tribosystem under dry and the two different lubrication conditions (PEEs or TAEs lubrication), a delayed elastic deflection behavior as well as a prolonged and, for Fn = 3 N, an elevated static friction phase before the onset of gliding was observed for the PEEs-lubricated system. Figure 3a shows the velocity dependence of the ratio of tangential force and normal force Ft,storage/Fn which would correspond to the friction coefficient µ in the regime of dynamic friction for dry contact or both lubrication conditions.
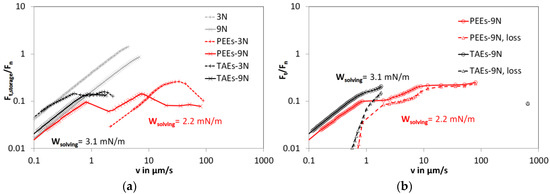
Figure 3.
(a) The storage part of the ratio of tangential and normal loading or coefficient of friction vs. sliding of PEEK against steel 100Cr6 in dry (grey) and a lubricated condition with pentaerythrite ester (PEEs, red symbols) and trimellitic acid ester (TAEs, black symbols). The experiments were conducted at a temperature of 25 °C in the oscillatory mode under a normal force of 3 N or 9 N resulting in an elastic spherical contact with a Hertzian pressure of 33 and 47 MPa. (b) The total and the loss part of the quantity Ft/Fn for PEEK against steel 100Cr6 in lubricated condition with PEEs (red) and TAEs (black). The experimental conditions are the same as in Figure 3a. At the data points with the highest velocities (v ≈ 100 µm/s for PEEs, v ≈ 900 µm/s for TAEs), the ratio Ft/Fn consists essentially of the loss component.
The work-of-spreading Wspreading is negative for both lubricants and therefore a reduced value for the static friction in comparison to the dry contact is found.
The work-of-solving Wsolving for the two lubricated cases is Wsolving(PEEs) = 2.2 mN/m and Wsolving(TAE) = 3.1 mN/m. The estimated interaction parameter Wsolving/γ13 is 0.99 (TAEs) and 1.02 (PEEs). A lower value of Wsolving indicates a stronger tendency of the lubricant to interact with the polymer surface. In case of an interaction parameter larger than unity, a stronger tendency of lubricant and polymer to intermigrate is expected.
Figure 3b shows the velocity dependence of the directly measured quantity Ft/Fn and the viscous component of the response which was identified by its phase shift.
4.2. Stribeck Experiments and Interfacial Energy
In contrast to the oscillatory mode experiments, the Stribeck experiments are true gliding tests. The data acquisition rate was chosen equidistant on a logarithmic scale for increasing velocity. In order to determine the COF, the velocity was kept constant for one second during which the data were acquired. Lower values for the COF were found for lubricated contacts, in particular for the TAEs-lubricated contact. The ranking of the magnitude of the COF qualitatively follows the ranking of the magnitude of Ft/Fn in the oscillatory experiments. Figure 4 shows the Stribeck-curves of PEEK against steel under dry and the two lubrication conditions within the boundary lubrication regime. The beginning of mixed lubrication occurs for the upper limit of the velocities for this experimental setup, at v ~0.1 m/s. The quantity ηv/p for the Fn = 9 N experiments at v = 0.1 m/s is 0.23 µm (PEEs) and 0.32 µm (TAEs). The calculated values of the work of spreading are Wspreading(PEEs) = −1.1 mN/m and Wspreading(TAEs) = −2.5 mN/m and per definition zero for the dry contact.
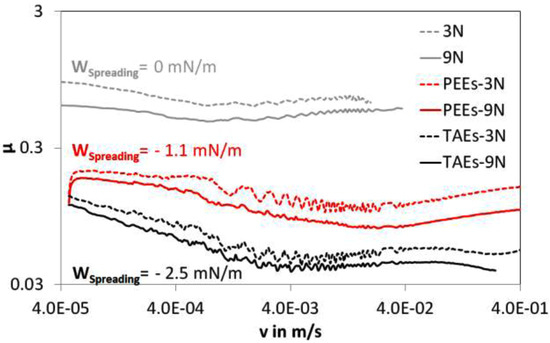
Figure 4.
Friction coefficient vs. sliding speed for PEEK against steel 100Cr6 in dry (grey) and lubricated condition with PEEs (red) and TAEs (black). The experiments were conducted in the Stribeck mode under a normal force of 3 or 9 N resulting in an elastic spherical contact with a Hertzian pressure of 33 and 47 MPa and a temperature of 25 °C.
The overall velocity dependence of the COF confirms a “rate-and-state” friction behavior in the boundary friction regime for all contact conditions. In all cases, the COF decreases with increasing sliding velocity until a minimum value is reached, followed by an increase of the COF with increasing velocity [10,11]. In addition, stick-slip oscillations could be detected predominantly in the velocity weakening regimes followed by a smooth transition to dynamic friction values for increasing velocities. A lower friction coefficient was observed for increased contact pressure, as it is typical for polymers in contact with polished surfaces.
5. Discussion
The negative values for work-of-spreading Wspreading indicate that—from a purely energetic point of view—both lubricants will spontaneously move into the interface between the frictional partners. The wetting of the two frictional partners PEEK and steel does not need to be forced by e.g., applying a suitable sliding speed. Although the energetic point of view neglects the effect of the normal force, we observe for trimellitic acid ester a higher ηv/p factor and an increased film thickness of the lubricant which agrees well with the higher energetic benefit of spreading for TAEs. However, at the applied normal pressures of 33 and 47 MPa, a partial “squeeze out” [12] of the lubricant is likely to occur. The “squeeze out” at higher contact pressure is the origin of an adhesion-driven static friction phenomenon that was observed prior to the breakaway torque in the oscillatory experiments. Since the breakaway torque is substantially higher for the dry contact, only a partial “squeeze out” occurred. After the breakaway point, the adhesion energy which has been stored as elastic energy is dissipated by the sliding processes which can be seen in Ft,loss.
The peak value of the curves measured in the oscillatory mode represents the maximum value of adhesion force which is reached by the tribosystem just prior to the onset of gliding at the end of the static friction regime. At a normal force of Fn = 9 N, both lubricated systems exhibit almost the same maximum value of adhesion force. However, the PEEs-lubricated tribosystem shows a prolonged static friction phase prior to gliding which results in a larger adhesion energy.
The analysis of the surface and interfacial energies supports the results of the tribological findings: a lower positive value of the work-of-solving Wsolving of the PEEs-lubricated system indicates that the PEEK surface chains could possess a higher mobility in a solved-like state. This results in a higher real surface area and thus in a higher total adhesion energy of the PEEK-steel interface, and therefore a higher static and dynamic friction coefficient.
In summary, at velocities beyond the adhesive stiction, both lubricants show a spontaneous wetting and spreading of the frictional partners, where TAEs shows a stronger tendency to invade the interface and thus to reduce the COF. In addition, the higher tendency of PEEs to mobilize the surface polymer chains possibly increases the adhesive interaction between the steel surface and PEEK, thus decreasing the slip-rate υ and by this increasing the COF in the dynamic region.
6. Conclusions
Macroscopic oscillatory tribological experiments and gliding experiments were carried out in order to study the tribological behavior of lubricated PEEK-steel tribosystems. The first results show that the tribological behavior at very low velocities (i.e., at the transition between stiction and gliding) shows the characteristics of adhesive friction. Furthermore, the surface and interfacial energies of the components of the tribosystem can explain the differences which were observed in the tribological behavior. The results suggest that tribological experiments at very low sliding velocities in combination with the analysis of the surface and interfacial energies can give valuable insight into the interaction between lubricants and the tribological partners of PEEK and steel. Future research will focus on applying this approach to a wider range of polymers and lubricants, including systems that do not show spontaneous wetting.
Acknowledgments
Sherif Abdel-Wahed would like to express his deepest gratitude to the German Academic Exchange Service (DAAD) for the GERLS scholarship (programme No. 57147166, ID No. 91567277) which makes it possible to pursue his PhD degree.
Author Contributions
Sherif Abdel-Wahed and Christof Koplin set up the study and designed and performed the experiments; Raimund Jaeger and Matthias Scherge contributed to the analysis and the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Scherge, M.; Kramlich, J.; Böttcher, R.; Hoppe, T. Running-in due to material transfer of lubricated steel/PA46 (aliphatic polyamide) contacts. Wear 2013, 301, 758–762. [Google Scholar] [CrossRef]
- Gellman, A.J.; Spencer, N.D. Surface chemistry in tribology. Proc. Inst. Mech. Eng. J. 2002, 216, 443–461. [Google Scholar] [CrossRef]
- Schallamach, A. A theory of dynamic rubber friction. Wear 1963, 6, 375–382. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction and the mechanics of stick-slip. Pure Appl. Geophys. 1978, 116, 790–806. [Google Scholar] [CrossRef]
- Ruina, A.L. Friction Laws and Instabilities: A Quasistatic Analysis of Some Dry Frictional Behavior; Division of Engineering, Brown University: Providence, RI, USA, 1980. [Google Scholar]
- Putelat, T.; Dawes, J.H.; Willis, J.R. On the microphysical foundations of rate-and-state friction. J. Mech. Phys. Solids 2011, 59, 1062–1075. [Google Scholar] [CrossRef]
- Bhushan, B. Adhesion and stiction: Mechanisms, measurement techniques, and methods for reduction. J. Vac. Sci. Technol. B 2003, 21, 2262–2296. [Google Scholar] [CrossRef]
- Israelachvili, N.J. Intermolecular and Surface Forces, 3rd ed.; Academic Press: San Diego, CA, USA, 2011. [Google Scholar]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Campen, S.; Green, J.; Lamb, G.; Atkinson, D.; Spikes, H. On the Increase in boundary friction with sliding speed. Tribol. Lett. 2012, 48, 237–248. [Google Scholar] [CrossRef]
- Berthoud, P.; Baumberger, T.; G’Sell, C.; Hiver, J.-M. Physical analysis of the state- and rate-dependent friction law: Static friction. Phys. Rev. B 1999, 59, 14313–14327. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Mugele, F. Squeeze-out and wear: Fundamental principles and applications. J. Phys. 2004, 16, R295–R355. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).