Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method
Abstract
:1. Introduction
2. Discrete Wavelet Transform (DWT)
2.1. Multiresolution Analysis
- (i)
- (ii)
- (iii)
- (iv)
- (v)
2.2. Daubechies’s Wavelets
2.3. Discrete Wavelet Transform Matrix
2.4. Discrete Wavelet Transform with Permutation (DWTPer) Matrix
3. Wavelet-Based Decoupled Method for the Numerical Solution of EHL Problem
4. Numerical Experiment
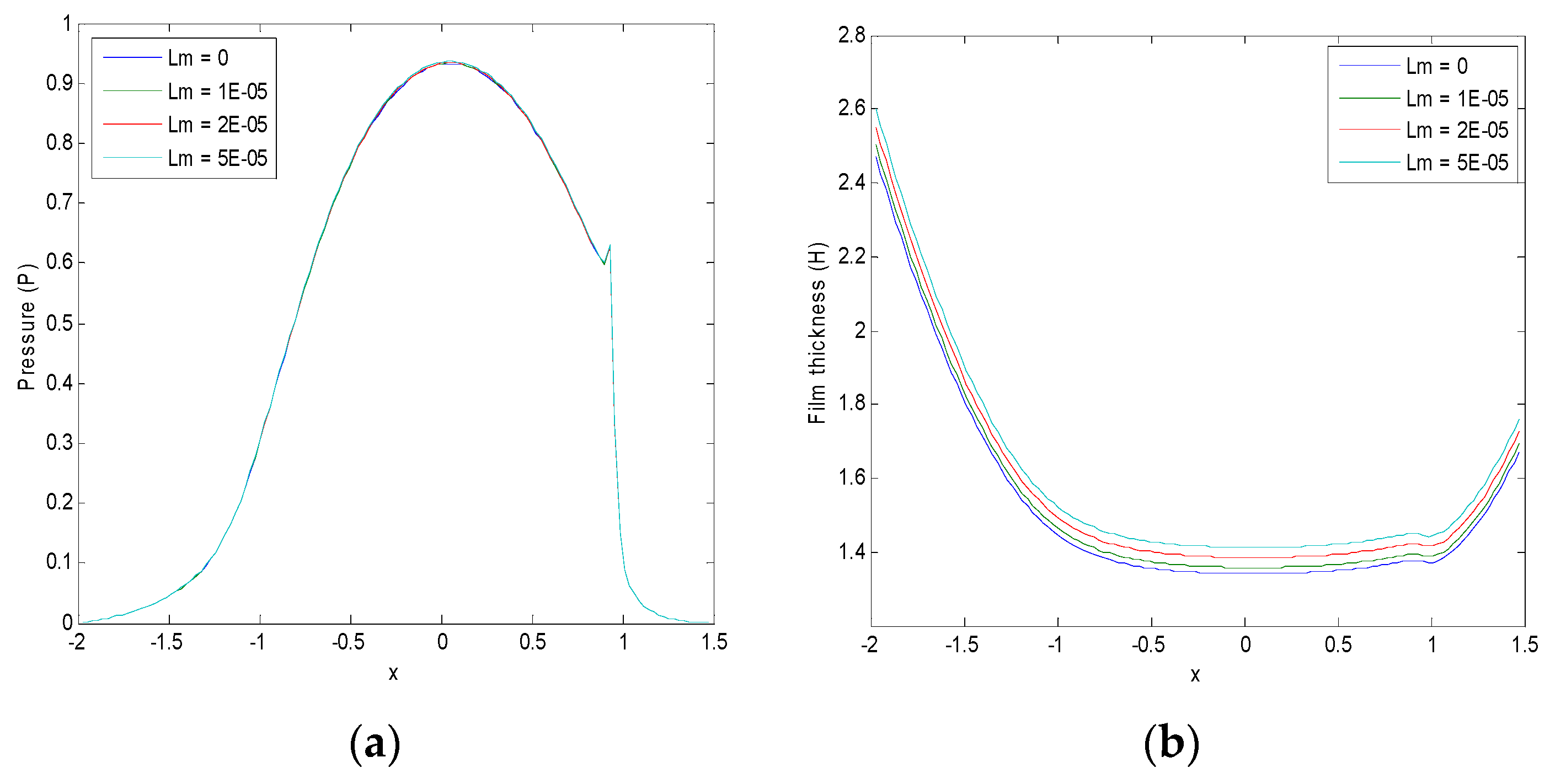
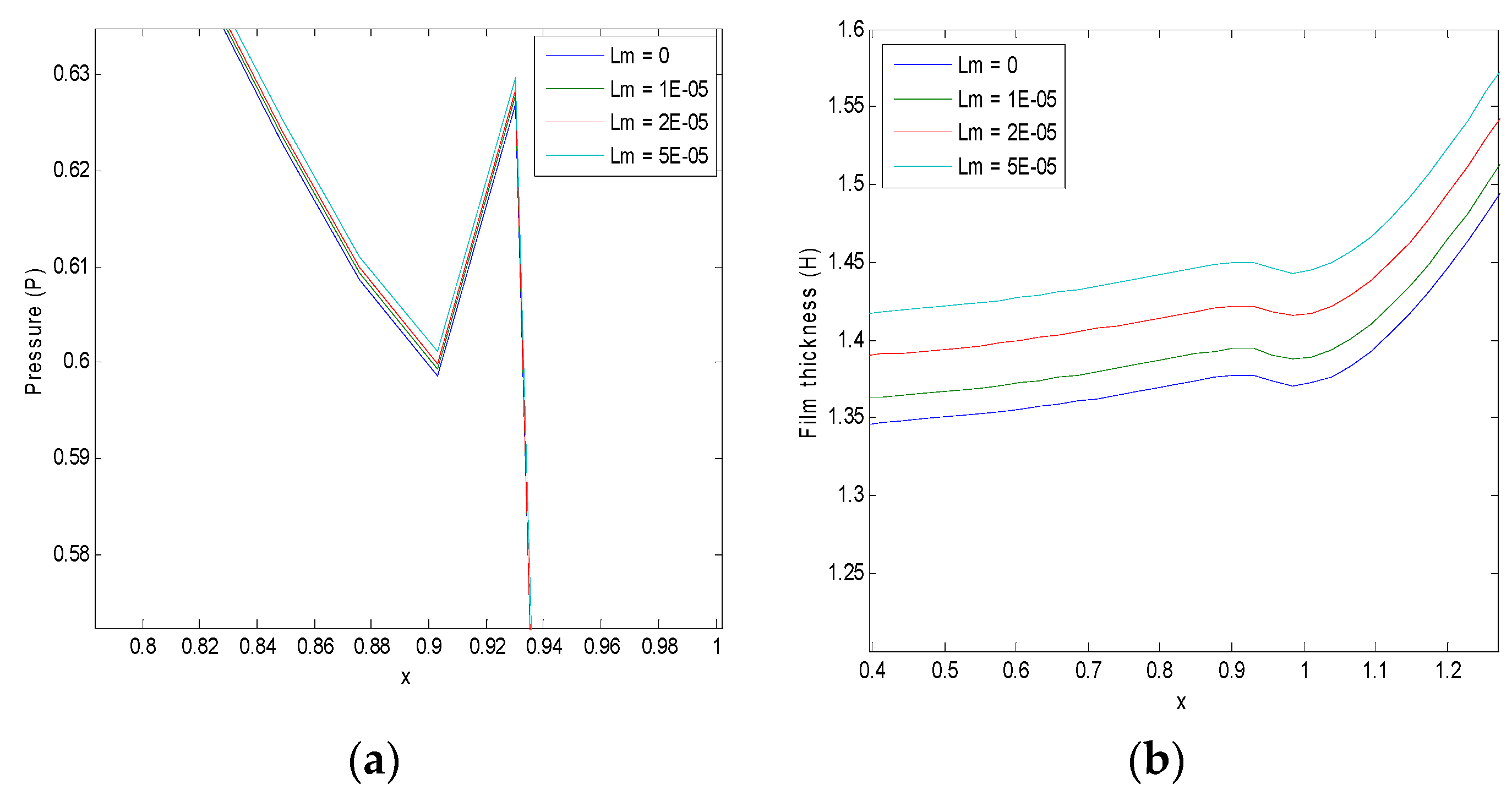
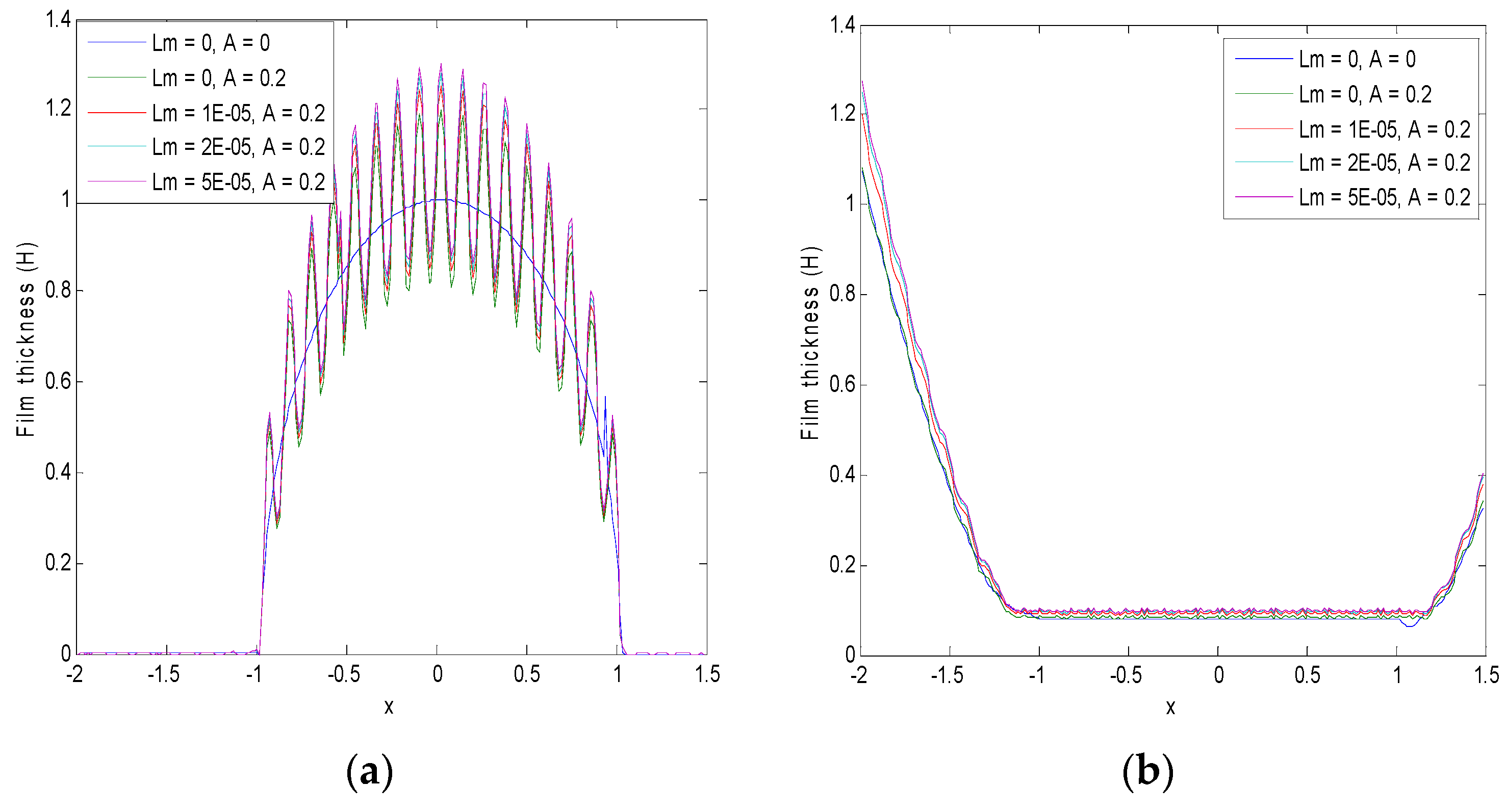
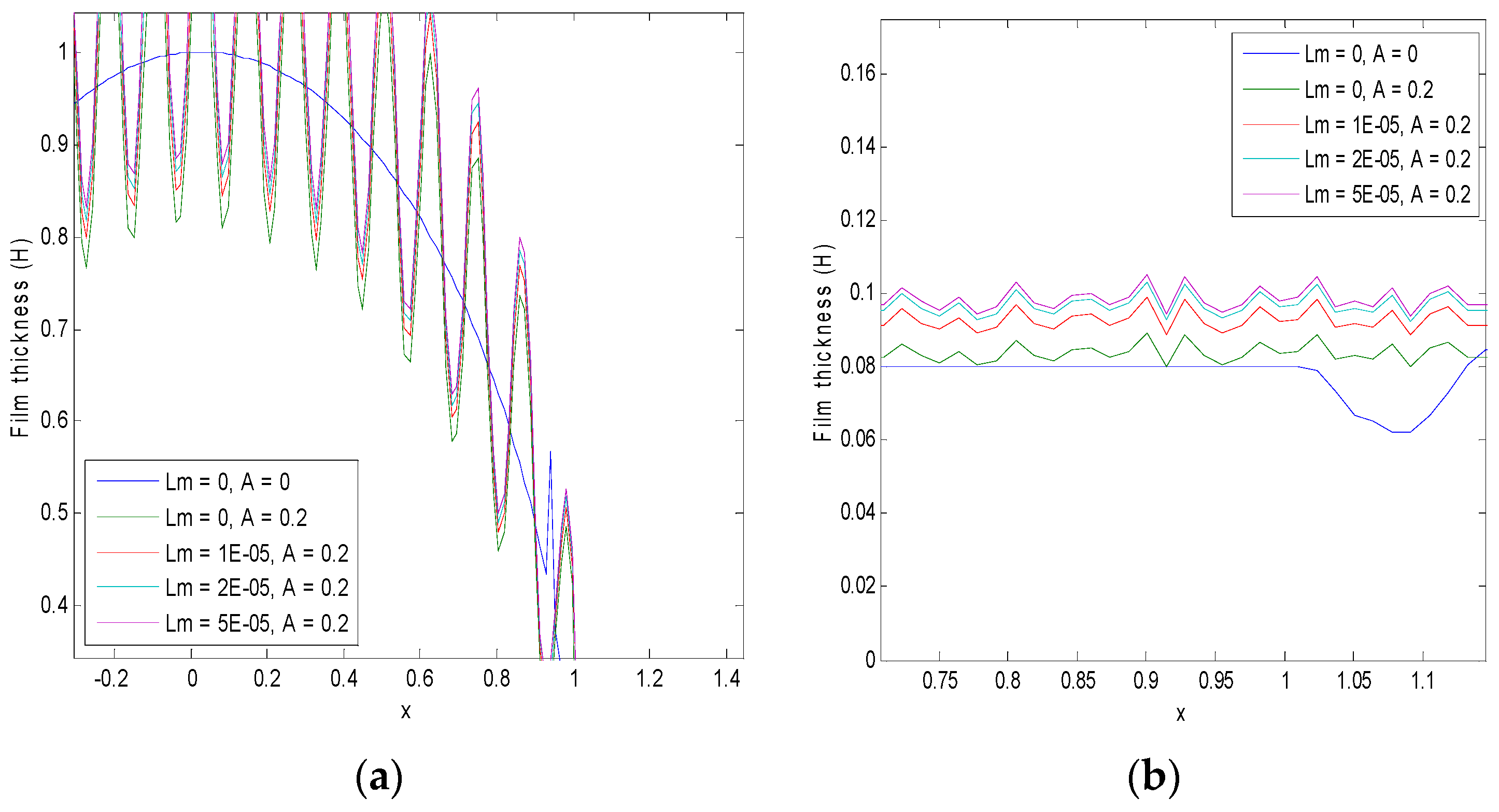
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| half width of the Hertzian contact, | |
| reduced radius of curvature, | |
| reduced modulus of elasticity, | |
| dimensionless speed parameter, | |
| velocity component | |
| sum velocity, | |
| non-dimensional load parameter, | |
| external load per unit width | |
| dimensionless materials parameter, | |
| pressure viscosity parameter | |
| Newtonian viscosity | |
| viscosity at ambient pressure | |
| dimensionless viscosity, | |
| dimensionless location of pressure spike | |
| number of nodes on grid | |
| Couple stress parameter | |
| Density | |
| density at ambient pressure | |
| dimensionless density, | |
| dimensionless film thickness, | |
| film thickness | |
| dimensionless film thickness, | |
| dimensionless constant | |
| discrete approximation of -logarithmic kernel | |
| dimensionless pressure, | |
| Pressure | |
| maximum Hertzian pressure, | |
| mesh size | |
| dimensionless coordinate , coordinate | |
| dimensionless amplitude | |
| dimensionless wavelength |
References
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication; Pergaman Press: Oxford, UK, 1966. [Google Scholar]
- Rao, P.S.; Agarwal, S. Effect of surface roughness on the hydrodynamic lubrication of porous inclined slider bearing considering slip velocity and squeeze velocity with couple stress fluids. Int. J. Eng. Sci. Technol. 2014, 6, 45–64. [Google Scholar] [CrossRef]
- Stokes, V.K. Couple stresses in fluids. Phys. Fluids 1966, 9, 1709–1715. [Google Scholar] [CrossRef]
- Keshavan, S.; Santhana, K.N. Surface roughnss effects on squeeze film behaviour in porous transversely triangular plates with couple stress fluid. Int. J. Mech. Eng. Technol. 2012, 3, 1–12. [Google Scholar]
- Li-Ming, C.; Jaw-Ren, L.; Hsiang-Chen, H.; Yuh-Ping, C. Effects of surface roughness and flow rheology on the EHL of circular contacts with power-law fluid. J. Marine Sci. Technol. 2013, 21, 175–181. [Google Scholar]
- Lin, J.R.; Chu, L.M.; Liang, L.J. Effects of viscosity pressure dependency on the non-Newtonian squeeze film of parallel circular plate. Lubr. Sci. 2013, 25, 1–9. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Apparao, S.; Hiremath, A.G. Effect of Surface Roughness and Viscosity-Pressure Dependency on the Couple Stress Squeeze Film Characteristics of Parallel Circular Plates. Adv. Tribol. 2014. [Google Scholar] [CrossRef] [Green Version]
- Bujurke, N.M.; Salimath, C.S.; Kudenatti, R.B.; Shiralashetti, S.C. A fast wavelet-multigrid method to solve elliptic partial differential equations. Appl. Math. Comp. 2007, 185, 667–680. [Google Scholar] [CrossRef]
- Bujurke, N.M.; Salimath, C.S.; Kudenatti, R.B.; Shiralashetti, S.C. Wavelet-multigrid analysis of squeeze film characteristics of poroelastic bearings. J. Comp. Appl. Math. 2007, 203, 237–248. [Google Scholar] [CrossRef]
- Bujurke, N.M.; Salimath, C.S.; Kudenatti, R.B.; Shiralashetti, S.C. Analysis of modified Reynolds equation using the wavelet-multigrid scheme. Num. Methods Part. Differ. Eqn. 2006, 23, 692–705. [Google Scholar] [CrossRef]
- Zargari, E.A.; Jimack, P.K.; Walkley, M.A. An investigation of the film thickness calculation for elastohydrodynamic lubrication problems. Int. J. Numer. Math. Fluids 2007, 1–6. [Google Scholar]
- Chen, K. Matrix Preconditioning Techniques and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ford, J.M. Wavelet-Based Preconditioning of Dense Linear Systems. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2001. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; PWS Publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving non-symetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Linear and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Lilliam, A.D.; Maria, T.M.; Victoria, V. Daubechies wavelet beam and plate finite elements. Finite Elements Anal. Design 2009, 45, 200–209. [Google Scholar]
- Chen, K. Discrete wavelet transforms accelerated sparse preconditioners for dense boundary element systems. Elec. Trans. Numer. Anal. 1999, 8, 138–153. [Google Scholar]
- Ford, J.M. An improved discrete wavelet transeforms based preconditioner for dense matrix problems. SIAM J. Matrix Anal. Appl. 2003, 25, 642–661. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Multilevel methods in Lubrication; Elsevier: New York, NY, USA, 2000. [Google Scholar]
- Brigges, W.L. A Multigrid Tutorial, 2nd ed.; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Venner, C.H. Multilevel Solution of the EHL Line and Point Contact Problems. Ph.D. Thesis, University of Twente, Byrness Hurd, The Netherlands, 1991. [Google Scholar]
- Dowson, D.; Whitaker, A.V. A numerical procedure for the solution of the elastohydrodynamic lubrication problem of rolling and sliding contacts lubricated by a Newtonian fluid. Proc. Inst. Mech. Eng. 1965, 180, 57–71. [Google Scholar]
- Roelands, C.J.A.; Vluger, J.C.; Waterman, H.I. The viscosity-temperature-pressure relationship for lubricating oils and its correlation with the chemical construction. ASME J. Basic Eng. 1963, 85, 601–610. [Google Scholar] [CrossRef]
- Saini, P.K.; Kumar, P.; Tandon, P. Surface roughness effects in elastohydrodynamic lubrication line contacts using couple stress fluid. Technical Note Proc. IMechE. Part J J. Eng. Trib. 2008, 222, 151–155. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Pressure viscosity coefficient, α | 2.16E−8 |
| Equivalent radius of the disks, R | 0.02 m |
| Equivalent elastic modulus, | 2.2E+11 Pa |
| Inlet viscosity, | 1.98E+8 |
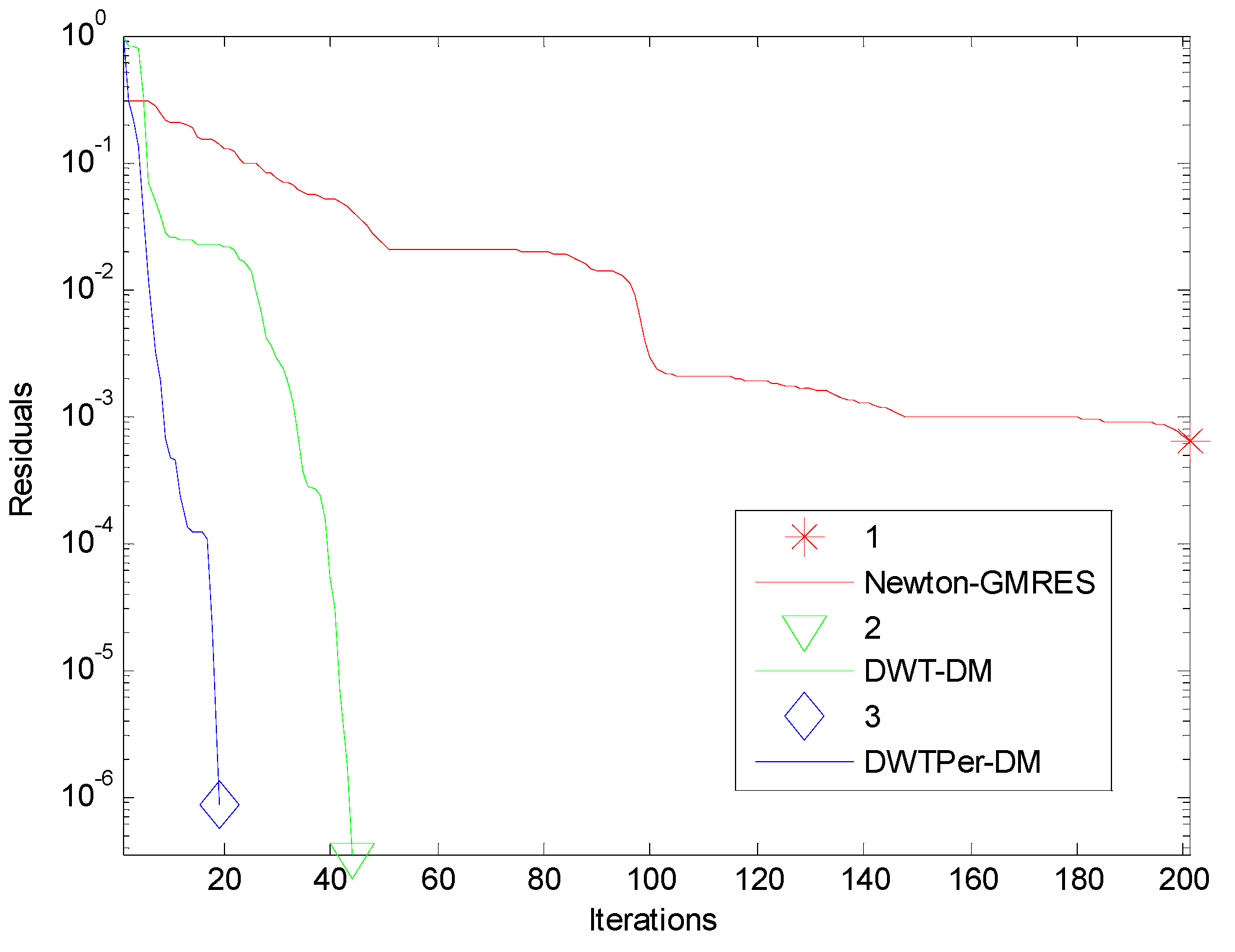
| Converged to the Desired Accuracy (Tol=−1E−6)? (Number of Iterations) | ||||||
|---|---|---|---|---|---|---|
| Newton-GMRES [11] | DWT-DM | DWTPer-DM | ||||
| 2E−11 | 4E−5 | 5E+3 | Yes (201) | Yes (41) | Yes (18) | |
| 64 | 2E−10 | 4E−5 | 5E+3 | No | Yes (43) | Yes (19) |
| 2E−11 | 4E−4 | 5E+3 | Yes (201) | Yes (44) | Yes (19) | |
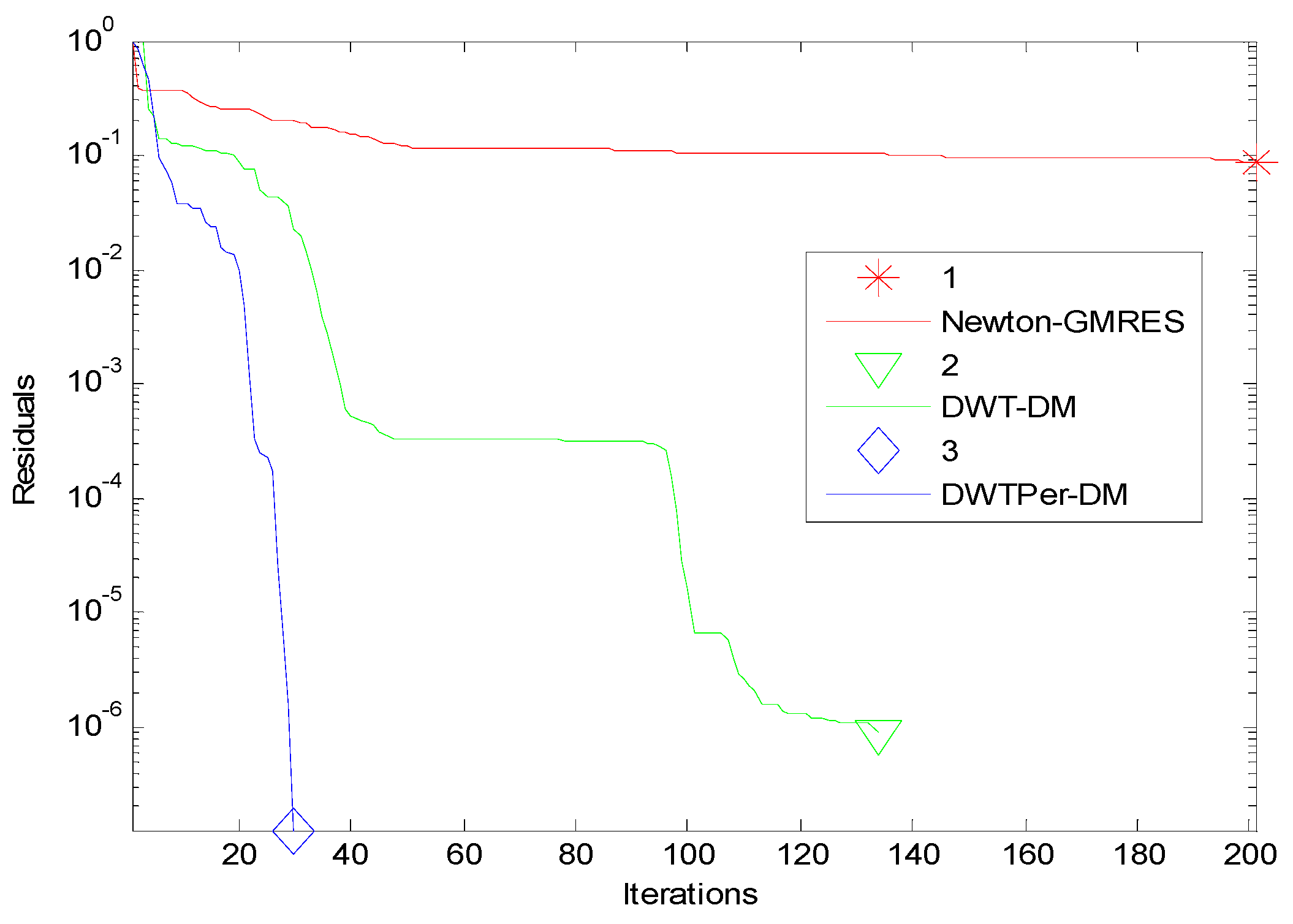
| 2E−11 | 4E−5 | 5E+3 | No | Yes (134) | Yes (30) | |
| 128 | 2E−10 | 4E−5 | 5E+3 | No | Yes (145) | Yes (32) |
| 2E−11 | 4E−4 | 5E+3 | No | Yes (147) | Yes (35) | |
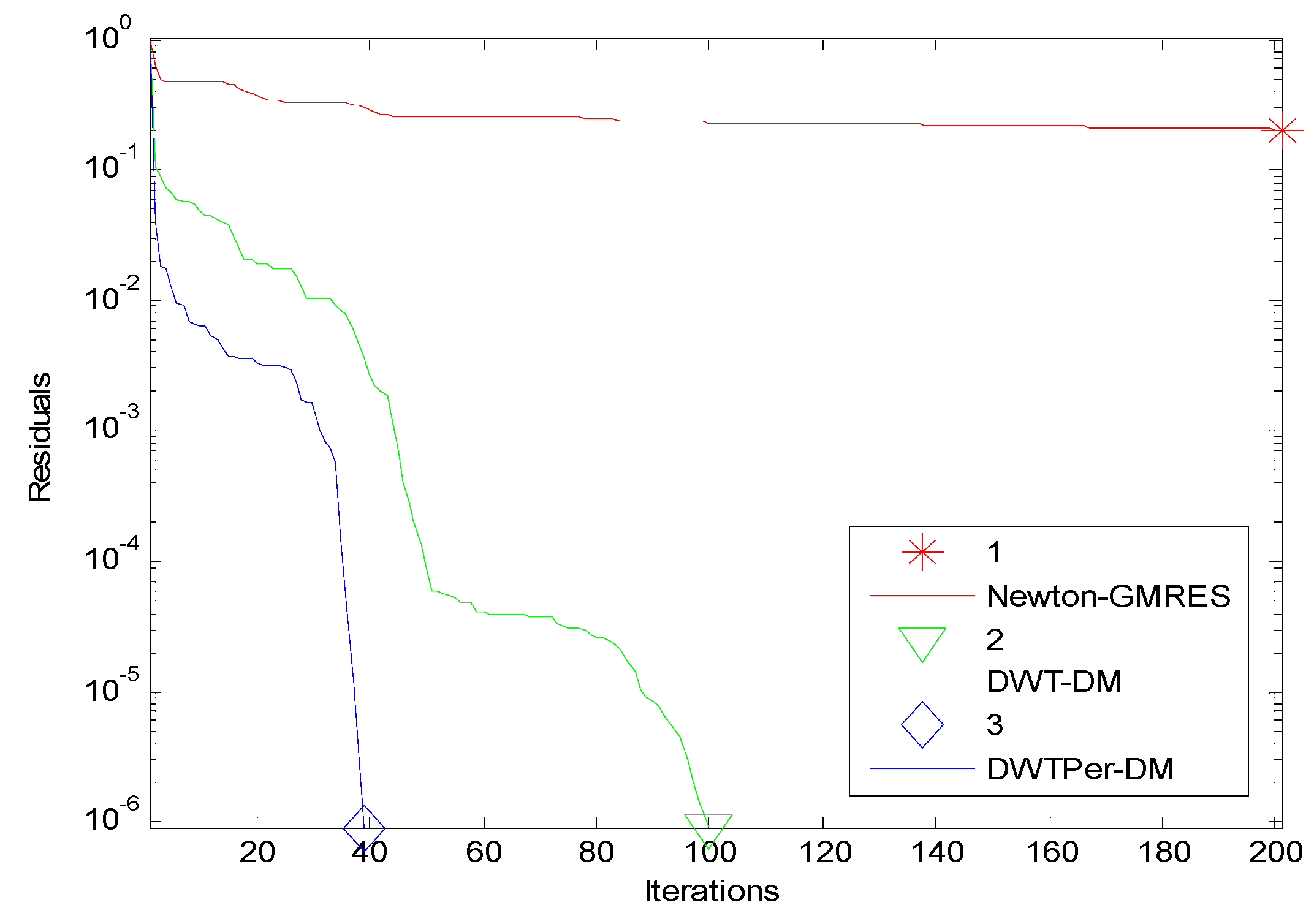
| 2E−11 | 4E−5 | 5E+3 | No | Yes (100) | Yes (39) | |
| 256 | 2E−10 | 4E−5 | 5E+3 | No | Yes (108) | Yes (41) |
| 2E−11 | 4E−4 | 5E+3 | No | Yes (109) | Yes (45) | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiralashetti, S.C.; Kantli, M.H. Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method. Lubricants 2016, 4, 9. https://doi.org/10.3390/lubricants4010009
Shiralashetti SC, Kantli MH. Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method. Lubricants. 2016; 4(1):9. https://doi.org/10.3390/lubricants4010009
Chicago/Turabian StyleShiralashetti, Siddu C., and Mounesha H. Kantli. 2016. "Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method" Lubricants 4, no. 1: 9. https://doi.org/10.3390/lubricants4010009
APA StyleShiralashetti, S. C., & Kantli, M. H. (2016). Investigation of Couple Stress Fluid and Surface Roughness Effects in the Elastohydrodynamic Lubrication Problems using Wavelet-Based Decoupled Method. Lubricants, 4(1), 9. https://doi.org/10.3390/lubricants4010009





